1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 1, 2019

Прикладная математика и механика, 2019, T. 83, № 1, стр. 39-46

ДИНАМИКА УПРУГОГО ЦИЛИНДРА НА УПРУГОМ ОСНОВАНИИ

И. Г. Горячева 1, *, А. А. Зобова 2, **

1 Институт проблем механики им. А.Ю. Ишлинского
Москва, Россия

2 Московский государственный университет им. М.В. Ломоносова
Москва, Россия

* E-mail: goryache@ipmnet.ru
** E-mail: azobova@mech.math.msu.su

Поступила в редакцию 19.04.2018

Полный текст (PDF)

Аннотация

Изучается квазистатическое плоскопараллельное движение бесконечного упругого цилиндра по плоскому горизонтальному основанию из того же материала (ось цилиндра горизонтальна). Распределение нормальных и касательных напряжений в области контактного взаимодействия цилиндра и плоскости берется из решения задачи теории упругости, в которой используется модель сухого трения Амонтона–Кулона на участке относительного проскальзывания и учитывается наличие участка сцепления. Получено аналитическое решение задачи, построен фазовый портрет системы. Проводится сравнение с задачей о движении абсолютно твердого цилиндра по твердой плоскости с сухим трением и без проскальзывания.

Ключевые слова: качение с проскальзыванием, упругий цилиндр, сухое трение

1. Введение. Одна из классических постановок задачи теоретической механики о движении тела по поверхности постулирует контакт твердого тела в единственной точке и отсутствие в этой точке проскальзывания [1]. Это условие приводит к дифференциальной связи, в общем случае неголономной, которая позволяет понизить порядок системы дифференциальных уравнений. Реакция связи вычисляется из динамических уравнений как функция положения и скорости твердого тела. Если реакция не превышает максимальной силы трения Кулона для данных материалов, то говорят, что неголономная связь может быть реализована сухим трения покоя.

Вопрос об обоснованности предположения о том, что контакт реальных выпуклых тел происходит в одной точке, и как следствие, реализуемости неголономных связей сухим трением Кулона был поднят в статье В.Ф. Журавлева [2], что вызвало пристальное внимание специалистов по аналитической механике к контактным задачам и моделированию трения. В частности, были предложены модели контактного взаимодействия, упрощенные по сравнению с решениями контактных задач теории упругости и построенные либо в предположении статического герцевского распределения давлений в пятне контакта, либо из динамических соображений (см. обзор [3]). Отметим, что конечная цель построения этих моделей заключается в изучении динамики абсолютно твердого тела (например, [4–6]). В некоторых случаях исследуется также динамика удара тела о шероховатую поверхность и релаксация колебаний по нормали к опоре [7, 8]. Отметим также экспериментальные работы [9, 10].

Распределение нормальных и касательных напряжений в области контакта взаимодействующих тел является предметом исследования механики контактных взаимодействий [11]. Использование их при анализе задач динамики позволяет выявить новые свойства решений. Простейшей из таких задач является задача о стационарном качении с проскальзыванием упругого цилиндра по упругой плоскости из того же материала [11, 12]. В представленной работе проводится анализ динамики плоскопараллельного движения цилиндра и сопоставление полученных результатов с решениями задач о движении цилиндра по плоскости с сухим трением скольжения Кулона и без проскальзывания.

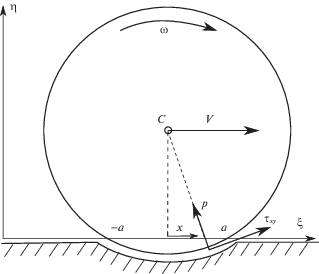
2. Постановка задачи. Рассмотрим плоскопараллельное движение бесконечного упругого цилиндра с удельной (на единицу длины) массой m и радиусом R по плоскому горизонтальному основанию из того же материала с модулем Юнга E и коэффициентом Пуассона ν. Введем инерциальную систему отсчета Oξηζ, ось Oξ которой принадлежит недеформированной опорной плоскости, ось Oη направлена вертикально вверх, ось Oζ перпендикулярна плоскости движения и сонаправлена с осью цилиндра. Распределение масс в цилиндре предполагается осесимметричным, так что центр масс каждого сечения цилиндра C лежит на его оси. Горизонтальную скорость оси цилиндра обозначим V = Veξ, а угловую скорость обозначим ω = –ωeζ. Положительное значение ω соответствует вращению по часовой стрелке, если смотреть с конца оси Oζ (фиг. 1).

Фиг. 1

Распределение нормального давления и касательных напряжений будем брать из решения задачи теории упругости в плоской квазистатической постановке [11, 12]. Предполагается, что скорость движения оси цилиндра мала по сравнению со скоростями распространения возмущений в упругой среде. Введем относительное проскальзывание цилиндра

(2.1)
$\delta = \frac{{\omega R - V}}{V}$

В области контактного взаимодействия введем декартову систему координат C 'xyz с осями, параллельными Oξηζ с началом в точке C ' – проекции центра сечения цилиндра на недеформированную плоскость. Область контактного взаимодействия цилиндра и плоскости – это полоса x ∈ (–a, a), в которой нормальные давления p и касательные напряжения τxy при V > 0 задаются соотношениями

(2.2)
$p(x) = \frac{{E'}}{{4\pi R}}\sqrt {{{a}^{2}} - {{x}^{2}}} ,\quad - a < x < a;\quad E' = \frac{{\pi E}}{{1 - {{\nu }^{2}}}},\quad a = \sqrt {\frac{{8RP}}{{E'}}} $
(2.3)
${{\tau }_{{xy}}}(x) = \left\{ \begin{gathered} \mu p(x),\quad - a < x < c \hfill \\ \mu \left( {p(x) - \frac{{E'}}{{4\pi R}}\sqrt {(a - x)(x - c)} } \right),\quad c < x < a, \hfill \\ \end{gathered} \right.$
где μ – коэффициент сухого трения Амонтона–Кулона, знак которого совпадает со знаком δ (на фиг. 1 изображен случай δ > 0). Полудлина площадки контакта a в контактной задаче вычисляется из статического условия равенства равнодействующей нормального давления внешней прижимающей нагрузке P.

На участке c < x < a области контактного взаимодействия происходит сцепление цилиндра с опорной плоскостью, и касательные напряжения на нем ниже предельного трения (трения покоя). На участке –a < x < c происходит скольжение. Положение границы участка сцепления зависит от величины относительного проскальзывания следующим образом:

(2.4)
$c = a\left( {\frac{{2\delta R}}{{\mu a}} - 1} \right)$

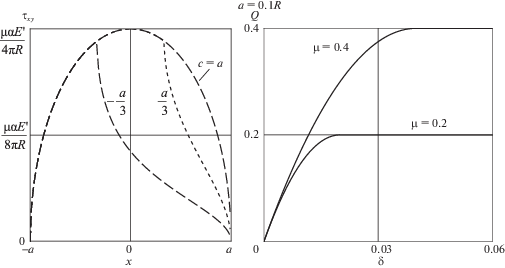
Участок сцепления существует при –a < c < a, т.е. при δ/μ < a/R. Графики распределения касательного напряжения в области контакта изображены в случаях c = a, a/3, –a/3 на фиг. 2 слева при a = 0.1R.

Фиг. 2

Для сведения случая V < 0 к приведенному выше необходимо изменить направление осей C 'x и C 'z и знаки V, ω на противоположные, при этом знак δ не изменится.

Вычислим равнодействующие P и Q нормального давления p(x) (2.2) и касательных напряжений τxy(x) (2.3), а также их моменты ${\mathbf{M}}_{p}^{C}$ и ${\mathbf{M}}_{\tau }^{C}$ относительно оси цилиндра. При V > 0 получим (здесь по-прежнему, signμ = signδ):

${\mathbf{P}} = P{{{\mathbf{e}}}_{\eta }},\quad P = \int\limits_{ - a}^a {p(x)dx} $
(2.5)
${\mathbf{Q}} = Q{{{\mathbf{e}}}_{\xi }},\quad Q = \int\limits_{ - a}^a {{{\tau }_{{xy}}}dx} = \left\{ \begin{gathered} \mu P\frac{{R\delta }}{{a\mu }}\left( {2 - \frac{{R\delta }}{{a\mu }}} \right),\quad \delta {\text{/}}\mu < a{\text{/}}R \hfill \\ \mu P,\quad \delta {\text{/}}\mu > a{\text{/}}R \hfill \\ \end{gathered} \right.$
${\mathbf{M}}_{p}^{C} = 0,\quad {\mathbf{M}}_{\tau }^{C} = RQ{{{\mathbf{e}}}_{\zeta }}$

График зависимости силы трения Q (2.5) от параметра δ представлен на фиг. 2 справа.

Приведем также выражение для силы Q в универсальной форме, которая пригодна как для положительных, так и для отрицательных V при использовании положительного коэффициента трения скольжения |μ|, так что μ = |μ|signδ:

(2.6)
$Q = \left\{ \begin{gathered} \left| \mu \right|P\operatorname{sign} V\frac{{R\delta }}{{a\left| \mu \right|}}\left( {2 - \frac{{R\left| \delta \right|}}{{a\left| \mu \right|}}} \right),\quad \left| \delta \right| < \frac{{a\left| \mu \right|}}{R} \hfill \\ \left| \mu \right|P\operatorname{sign} (\omega R - V),\quad \left| \delta \right| > \frac{{a\left| \mu \right|}}{R} \hfill \\ \end{gathered} \right.$

3. Уравнения движения. Запишем динамические уравнения движения цилиндра

(3.1)
$m{\mathbf{a}} = m{\mathbf{g}} + {\mathbf{P}} + {\mathbf{Q}},\quad \frac{{d{{{\mathbf{K}}}_{C}}}}{{dt}} = {\mathbf{M}}_{p}^{C} + {\mathbf{M}}_{\tau }^{C},$
где a – ускорение центра масс, KC = –Jωeζ – кинетический момент относительно центра масс, J – момент инерции относительно оси цилиндра, g – ускорение свободного падения. В скалярной форме уравнения движения (3.1) имеют вид

(3.2)
$m{{a}_{\eta }} = P - mg,\quad m\dot {V} = Q,\quad J\dot {\omega } = - RQ$

В квазистатической задаче естественно положить aη = 0, поэтому P = mg. Уравнения движения допускают первый интеграл

(3.3)
$mRV + J\omega = mRV(1 + j + j\delta ) = C = \operatorname{const} ,$
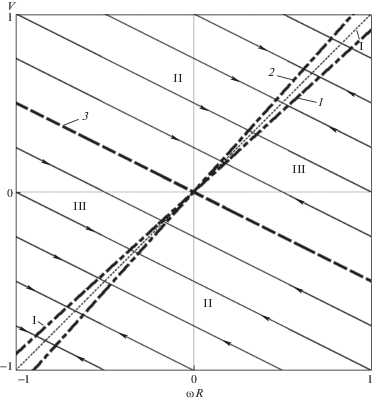
где j = J/(mR2) ≤ 1 – безразмерный момент инерции (в случае однородного цилиндра j = 1/2). Наличие первого интеграла означает, что фазовые траектории на плоскости (ωR, V) лежат на параллельных прямых (фиг. 3). Фазовый портрет системы центрально симметричен: при замене V → –V, ω → –ω в уравнениях (3.2) знак силы трения Q меняется на противоположный, а абсолютная величина не меняется.

Фиг. 3

4. Анализ движения при разных начальных условиях. Найдем решение задачи Коши уравнений (3.2) с начальными условиями V(0) = V0, ω(0) = ω0. При этом δ(0) = (ω0R – – V0)/V0 = δ0 – начальное относительное проскальзывание (напомним, что δ0/μ > 0).

Случай 0 < δ0/μ < a/R. Согласно равенству (2.4), в начальный момент в области контактного взаимодействия существует участок сцепления, т.е. происходит качение цилиндра с проскальзыванием (этот случай был изложен подробно [13]). На фазовой плоскости система находится в области I, ограниченной штрих-пунктирными линиями δ = μa/R при δ > 0 (1) и δ < 0 (2) (фазовый портрет на фиг. 3 построен при μa/R = = ±0.1, j = 1/2). Очевидно, что в этой области на любой фазовой кривой знак скорости V не меняется, поэтому без ограничения общности можно считать V > 0. Константа первого интеграла во всех точках этой области, кроме начала координат, не равна нулю. Используя соотношения (2.1), (3.2) и (3.3), получим дифференциальное уравнение, выражающее изменение переменной δ на фиксированном уровне линейного интеграла:

(4.1)
$\dot {\delta } = - QR\frac{{{{{(1 + j(1 + \delta ))}}^{2}}}}{{Cj}}$

Величина Q определена формулой (2.5), те.

(4.2)
$\dot {\delta } = - P{{R}^{2}}\frac{\delta }{a}\left( {2 - \frac{{R\delta }}{{a\mu }}} \right)\frac{{{{{(1 + j + j\delta )}}^{2}}}}{{Cj}}$

Решение уравнения (4.2) оценивается решениями δmin(t) и δmax(t), имеющими вид [13]:

(4.3)
${{\delta }_{{\min (\max )}}}(t) = \frac{{{{\delta }_{0}}\exp ( - kt)}}{{1 - \frac{{{{\delta }_{0}}R}}{{2\mu a}}(1 - \exp ( - kt))}};\quad k = \frac{{2P{{R}^{2}}}}{a}{{A}_{{\min (\max )}}},$
где

${{A}_{{\min (\max )}}} = \min (\max )\left\{ {\frac{{{{{(1 + j)}}^{2}}}}{{Cj}},\frac{{{{{(1 + j + j{{\delta }_{0}})}}^{2}}}}{{Cj}}} \right\}$

Таким образом, при t → +∞ относительное скольжение δ по модулю экспоненциально убывает и достигает нуля за бесконечное время, причем имеет место асимптотика

$\delta \sim {{\delta }_{0}}\exp \left( { - \frac{{2P{{R}^{2}}{{{(1 + j)}}^{2}}}}{{Caj}}t} \right)\quad {\text{п р и }}\quad t \to \infty $

При этом участок сцепления увеличивается и при t → ∞ занимает всю площадку контакта (см. 2.4), а сила Q монотонно убывает к нулю. Финальное движение цилиндра – чистое качение с постоянной скоростью оси

${{V}^{\infty }} = {{\omega }^{\infty }}R = C{\text{/}}(mR(1 + j))$

Случай δ/μ > a/R. В этом случае величина силы трения не зависит от относительного проскальзывания и равна Q = μP при V > 0 и Q = –μP при V < 0 (напомним, что знак μ совпадает со знаком δ). Участка сцепления нет, то есть происходит полное скольжение цилиндра. Обратимся к уравнениям (3.2), которые имеют следующее решение

$V(t) = {{V}_{0}} \pm \mu gt,\quad \omega (t) = {{\omega }_{0}} \mp \frac{{\mu g}}{{jR}}t$
(Здесь и далее верхний знак берется при V > 0 и нижний – при V < 0.) При этом относительное проскальзывание зависит от времени следующим образом:

$\delta (t) = \frac{{j(R{{\omega }_{0}} - {{V}_{0}}) \mp \mu gt(1 + j)}}{{j({{V}_{0}} \pm \mu gt)}}$

Если начальные условия таковы, что δ0 = –(1 + j)/j и, следовательно, C = 0, получаем δ(t) ≡ δ0. На фазовом портрете этому движению соответствует фазовая кривая 3, проходящая через начало координат. За конечное время

$T = \mp \mu g{\text{/}}{{V}_{0}}$
изображающая точка достигает начала координат, при этом цилиндр останавливается.

В области II

$ - \frac{{1 + j}}{j} < \delta < \mu \frac{a}{R} < 0,$
при V0 > 0 (<0) скорость оси цилиндра линейно убывает (возрастает), а угловая скорость возрастает (убывает). Изображающая точка за конечное время выходит на прямую δ = μa/R, после чего в области контактного взаимодействия возникает сцепление: начинается качение с проскальзыванием. Дальнейшее движение описывается случаем 0 < δ0/μ < a/R.

Осталось рассмотреть область III, в которой

$\left\{ {\delta < - \frac{{1 + j}}{j}} \right\}\bigcup {\left\{ {0 < \delta < \frac{{\mu a}}{R}} \right\}} $
или в координатах (V, ωR)

$\frac{{\omega {{R}^{2}}}}{{\mu a + R}} < V < - j\omega R\quad {\text{п р и }}\quad \omega R < 0$
$ - j\omega R < V < \frac{{\omega {{R}^{2}}}}{{\mu a + R}}\quad {\text{п р и }}\quad \omega R > 0$

В этой области, так же, как и в области II, изображающая точка за конечное время выходит на прямую δ = μa/R, и начинается качение с проскальзыванием: далее динамика описывается случаем 0 < δ0/μ < a/R. Однако при этом направление движения оси цилиндра меняется на противоположное: в некоторый момент времени V(t) обращается в нуль, а угловая скорость ω конечна. Поэтому относительное проскальзывание δ(t) становится бесконечно большим по абсолютной величине. Изображающая точка на фазовом портрете в этот момент пересекает ось абсцисс и переходит из области δ < 0 в область δ > 0. Величина силы трения и ее направление при этом остается постоянным, так как одновременно меняется знак V и δ. Подобное возвратное движение наблюдается при выполнении упражнений с обручем в художественной гимнастике: гимнастка толкает обруч вперед и одновременно подкручивает его “на себя”, и после непродолжительного движения вперед с большим проскальзыванием в контакте обруч меняет направление движения и возвращается в руки спортсменки.

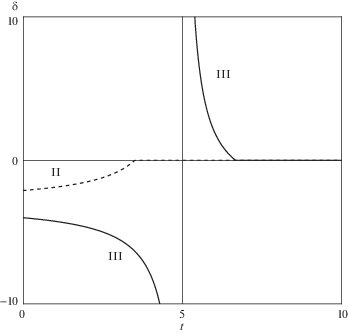
Результаты расчета относительного проскальзывания δ(t) для

$m = 1,\quad g = 1,\quad R = 1,\quad j = 1{\text{/}}2,\quad \mu = 0.2,\quad a{\text{/}}R = 0.1$
и начальных условий из областей II и III показаны на фиг. 4. Начальные условия:

$V(0) = 1,\quad \omega (0) = - 1.1\quad ({\text{п р и }}\;{\text{э т о м }}\;\delta (0) = - 2.1 < 0,\;C > 0)\quad {\text{д л я }}\;{\text{к р и в о й }}\;{\text{II}}$
$V(0) = 1,\quad \omega (0) = - 3\quad (\delta (0) = - 4.1 < 0,\;C < 0)\quad {\text{д л я }}\;{\text{к р и в о й }}\;{\text{III}}$
Фиг. 4

На кривой III функция δ(t) стремится к –∞ при t → 5, что соответствует смене направления движения центра масс. При t > 5 кривая III монотонно убывает от +∞ до 0.

5. Обсуждение результатов. Для почти всех начальных условий финальное движение – это чистое качение с постоянными скоростью оси цилиндра и угловой скоростью. Исключения составляют лишь движения с нулевой константой линейного интеграла C = 0: происходит полное скольжение цилиндра, который за конечное время останавливается. Во всех остальных случаях (C ≠ 0) полной диссипации кинетической энергии не происходит, поскольку сила трения при нулевом относительном проскальзывании равна нулю. В натурном эксперименте, конечно, чистое качение не будет наблюдаться бесконечно долго из-за потерь энергии, не учитываемых в рассмотренной модели (неидеальная упругость, сопротивление воздушной среды, тепловые потери и т.п.).

В отличие от классической постановки задачи с сухим трением скольжения Кулона, где время прекращения относительного проскальзывания конечно, в рассмотренной модели учет сцепления и, следовательно, уменьшения величины трения при качении с проскальзыванием приводит к экспоненциальному стремлению относительного проскальзывания к нулю.

Заметим также, что при стремлении модуля упругости Юнга E к бесконечности область контакта уменьшается (a → 0), и в пределе получим точечный контакт цилиндра и плоскости. При этом, если δ = 0, то Q = 0. Эта предельная задача полностью соответствует классической задаче теоретической механики о качении диска по горизонтальной прямой с наложенной идеальной дифференциальной связью V = ωR, выражающей отсутствие проскальзывания; касательная реакция указанной связи равна нулю.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А17-117021310379-5) и частично – в рамках проектов Российского фонда фундаментальных исследований (17-20-01147-офи_м_РЖД, 16-01-00338-а).

Список литературы

  1. Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. М.: Наука. Гл. ред. физ-мат. лит., 1967. 520 с.

  2. Журавлев В.Ф. О модели сухого трения в задаче качения твердых тел // ПММ. 1998. Т. 62. Вып. 5. С. 762–767.

  3. Зобова А.А. Обзор моделей распределенного сухого трения // ПММ. 2016. Т. 80. № 2. С. 194–206.

  4. Журавлев В.Ф., Климов Д.М. Глобальное движение кельтского камня // Изв. РАН. МТТ. 2008. № 3. С. 8–16.

  5. Ишханян М.В., Карапетян А.В. Динамика однородного шара на горизонтальной плоскости с учетом трения скольжения, верчения и качения // Изв. РАН. МТТ. 2010. № 2. С. 3–14.

  6. Сальникова Т.В., Трещев Д.В., Галлямов С.Р. Движение свободной шайбы по шероховатой горизонтальной плсокости // Нелин. дин. 2012. Т. 8. № 1. С. 83–101.

  7. Кулешов А.С., Трещев Д.В., Иванова Т.Б., Наймушина О.С. Твердый цилиндр на вязкоупругой плоскости // Нелин. дин. 2011. Т. 7. № 3. С. 601–625.

  8. Зобова А.А., Трещев Д.В. Шар на вязкоупругой плоскости // Труды МИАН. 2013. Т. 281. С. 98–126.

  9. Киреенков А.А., Семендяев С.В, Филатов В.Ф. Экспериментальное исследование связанных двумерных моделей трения скольжения и верчения // Изв. РАН. МТТ. 2010. № 6. С. 192–202.

  10. Borisov A.V., Erdakova N.N., Ivanova T.B., Mamaev I.S. The dynamics of a body with an axisymmetric base sliding on a rough plane // Regular Chaotic Dyn. 2014. V. 19. № 6. P. 607–634.

  11. Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.

  12. Carter F.W. On the action of a locomotive driving wheel // Proc. Roy. Soc. London A. V. 112. P. 151–157.

  13. Горячева И.Г., Зобова А.А. Динамическая задача о качении с проскальзыванием упругого цилиндра по упругому основанию // Докл. РАН. 2018. Т. 481. № 1. Принята в печать.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал