Прикладная математика и механика, 2019, T. 83, № 2, стр. 175-201
О ПЕРИОДИЧЕСКИХ ДВИЖЕНИЯХ БЛИЗКОЙ К АВТОНОМНОЙ СИСТЕМЫ В СЛУЧАЯХ ДВОЙНОГО ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА
О. В. Холостова *
Московский авиационный институт (НИУ)
Москва, Россия
* E-mail: kholostova_o@mail.ru
Поступила в редакцию 12.03.2018
После доработки 10.02.2019
Принята к публикации 19.03.2019
Аннотация
Рассматриваются движения близкой к автономной, $2\pi $-периодической по времени гамильтоновой системы с двумя степенями свободы в окрестности положения равновесия. Предполагается, что гамильтониан системы зависит от трех параметров $\varepsilon $, $\alpha $ и $\beta $, и при $\varepsilon = 0$ система автономна. Пусть для некоторых значений $\alpha $ и $\beta $ в невозмущенной ($\varepsilon = 0$) системе реализуется двойной параметрический резонанс, когда одна из частот малых линейных колебаний системы в окрестности положения равновесия является целым, а другая полуцелым числом. Для достаточно малых, но отличных от нуля значений $\varepsilon $ в малой окрестности резонасной точки, рассматриваемой при фиксированном резонансном значении одного из параметров ($\beta $), решен вопрос о существовании, бифуркациях и устойчивости в линейном приближении периодических движений системы. В случаях кратных резонансов исследуемого типа построены периодические движения динамически симметричного спутника в окрестности его стационарного вращения (цилиндрической прецессии) на слабоэллиптической орбите и проведен линейный и нелинейный анализ их устойчивости.
Была иссследована устойчивость положений равновесия гамильтоновых систем при наличии однократного параметрического резонанса [1]. Изучены периодические и условно-периодические движения близкой к автономной гамильтоновой системы с одной степенью свободы в случае параметрического резонанса [2–4]. Рассмотрены резонансные периодические движения в системе с двумя степеням свободы при однократном параметрическом резонансе основного типа [5]. Изучались случаи кратных параметрических резонансов в близких к автономным линейных гамильтоновых системах [6–8] (см. также монографию [9]), установлено существование нескольких областей параметрического резонанса, выходящих из порождающей точки. Эти области были построены при исследовании ряда задач динамики спутника (моделируемого твердым телом) относительно центра масс в центральном ньютоновском гравитационном поле. Были рассмотрены периодические движения близкой к автономной, периодической по времени гамильтоновой системы с двумя степенями свободы, их бифуркации и устойчивость в случаях, когда одна из частот малых колебаний невозмущенной системы равна целому или полуцелому числу, а другая равна нулю [10].
В работе для аналогичных систем исследуется другой случай кратного параметрического резонанса, когда одна из частот малых линейных колебаний невозмущенной системы целое, а другая полуцелое число. Описаны периодичские движения системы, исследована их бифуркация и устойчивость в линейном приближении. Исследованы резонансные периодические движения динамически симметричного спутника в окрестности стационарного вращения на слабоэллиптической орбите.
1. Постановка задачи. Рассмотрим движения близкой к автономной, $2\pi $-периодической по времени гамильтоновой системы с двумя степенями свободы. Пусть гамильтониан системы зависит от малого параметра $\varepsilon $ ($0 < \varepsilon \ll 1$) и параметров $\alpha $ и $\beta $, меняющихся в некотором диапазоне, и аналитичен по ним. При достаточно малых значениях $\varepsilon $ представим гамильтониан в виде ряда
(1.1)
$\begin{gathered} H = {{H}^{{(0)}}}({{q}_{j}},{{p}_{j}},\alpha ,\beta ) + \varepsilon {{H}^{{(1)}}}({{q}_{j}},{{p}_{j}},t,\alpha ,\beta ) + {{\varepsilon }^{2}}{{H}^{{(2)}}}({{q}_{j}},{{p}_{j}},t,\alpha ,\beta ) + O({{\varepsilon }^{3}}) \hfill \\ \end{gathered} ,$Будем считать, что начало координат ${{q}_{j}} = {{p}_{j}} = 0$ ($j = 1,2$) фазового пространства – положение равновесия системы, в его окрестности гамильтониан (1.1) аналитичен по ${{q}_{j}}$, ${{p}_{j}}$, а функции ${{H}^{{(k)}}}$ записываются в виде рядов, содержащих слагаемые четных степеней по координатам и импульсам:
(1.2)
$\begin{gathered} {{H}^{{(k)}}} = {{H}_{{2k}}} + {{H}_{{4k}}} + \ldots \hfill \\ \end{gathered} $Здесь ${{H}_{{lk}}}$ ($l = 2,4,\; \ldots $; $k = 0,1,2,\; \ldots $) – совокупности слагаемых степени $l$ по ${{q}_{j}}$ и ${{p}_{j}}$ с постоянными (при $k = 0$) или $2\pi $-периодическими по времени (при $k = 1,2,\; \ldots $) коэффициентами, а многоточие означает совокупность слагаемых не менее шестой степени по ${{q}_{j}}$ и ${{p}_{j}}$.
Пусть при $\varepsilon = 0$ имеется область изменения параметров $\alpha $ и $\beta $, в которой рассматриваемое положение равновесия устойчиво в линейном приближении, корни $ \pm i{{\omega }_{j}}(\alpha ,\beta )$ ($j = 1,2$) характеристического многочлена линеаризованных уравнений возмущенного движения чисто мнимые. Пусть, кроме того, для некоторых значений – $\alpha = {{\alpha }_{{\text{*}}}}$ и $\beta = {{\beta }_{{\text{*}}}}$ из этой области одна из частот ${{\omega }_{j}}$ – целое (отличное от нуля), а другая – полуцелое число и, таким образом, в системе реализуется двойной параметрический резонанс. При достаточно малых, но отличных от нуля значениях $\varepsilon $ в окрестности резонансной точки (0, ${{\alpha }_{{\text{*}}}}$, ${{\beta }_{{\text{*}}}}$) трехмерного пространства параметров появляются области неустойчивости (области параметрического резонанса).
Цель данной работы – решение задачи о существовании, бифуркациях и устойчивости (в линейном приближении) периодических движений системы с гамильтонианом (1.1), (1.2) в малой окрестности точки (0, ${{\alpha }_{{\text{*}}}}$, ${{\beta }_{{\text{*}}}}$) кратного параметрического резонанса рассматриваемого типа. Исследование будет проводиться в сечениях $\beta = {{\beta }_{{\text{*}}}}$ трехмерного пространства параметров при достаточно малых, но отличных от нуля значениях $\varepsilon $ и близких к резонансным значениям $\alpha $.
В качестве приложения будут построены (в соответствующих сечениях трехмерного пространства параметров) резонансные периодические движения динамически симметричного спутника в окрестности его цилиндрической прецессии на слабоэллиптической орбите. Для одной из резонансных точек предложенный в теории алгоритм будет обобщен и применен при рассмотреннии трехмерной окрестности этой точки. Будет проведен полный, линейный и нелинейный, анализ устойчивости найденных периодических движений спутника.
2. Преобразование гамильтониана. Модельные гамильтонианы. Пусть при $\varepsilon = 0$, α = = ${{\alpha }_{{\text{*}}}}$ и $\beta = {{\beta }_{{\text{*}}}}$ в системе с гамильтонианом (1.1), (1.2) выполнены соотношения ${{\omega }_{1}} = n$, $2{{\omega }_{2}} = m$, где $n$ – целое число и $m$ – целое нечетное число.
Будем рассматривать движения системы в малой окрестности резонансной точки (0, ${{\alpha }_{{\text{*}}}}$, ${{\beta }_{{\text{*}}}}$) при $\beta = {{\beta }_{{\text{*}}}}$, полагая
Тогда гамильтониан (1.1), (1.2) может быть переписан в виде
(2.1)
$H = {{H}_{2}} + {{H}_{4}} + \ldots ,\quad {{H}_{4}} = {{H}_{{40}}}({{q}_{j}},{{p}_{j}},{{\alpha }_{{\text{*}}}},{{\beta }_{{\text{*}}}}) + O(\varepsilon )$(2.2)
${{H}_{2}} = {{H}_{{20}}} + \varepsilon [{{\mu }_{1}}H_{{20}}^{'} + {{H}_{{21}}}] + {{\varepsilon }^{2}}[{{\mu }_{2}}H_{{20}}^{{''}}{\text{/}}2 + {{\mu }_{1}}H_{{21}}^{'} + {{H}_{{22}}}] + O({{\varepsilon }^{3}}),$2.1. Преобразование гамильтониана. Осуществим ряд канонических преобразований, упрощающих структуру гамильтониана (2.1), (2.2) в слагаемых до четвертого порядка включительно по ${{q}_{j}}$, ${{p}_{j}}$ ($j = 1,2$) с учетом имеющихся резонансов.
Сначала нормализуем автономную (при $\varepsilon = 0$) часть гамильтониана (2.1), (2.2). Оставляя за переменными прежние обозначения, запишем результат в виде (${{c}_{{ij}}}$ = const)
(2.3)
${{H}^{{(0)}}} = {{H}_{{20}}} + {{H}_{{40}}} + \ldots ,\quad {{H}_{{20}}} = \frac{n}{2}(q_{1}^{2} + p_{1}^{2}) + \frac{m}{4}(q_{2}^{2} + p_{2}^{2})$(2.4)
${{H}_{{40}}} = \frac{{{{c}_{{20}}}}}{4}{{(q_{1}^{2} + p_{1}^{2})}^{2}} + \frac{{{{c}_{{11}}}}}{4}(q_{1}^{2} + p_{1}^{2})(q_{2}^{2} + p_{2}^{2}) + \frac{{{{c}_{{02}}}}}{4}{{(q_{2}^{2} + p_{2}^{2})}^{2}}$Далее упростим структуру квадратичной части гамильтониана при $\varepsilon \ne 0$. Результат будем представлять в виде
Рассмотрим слагаемые порядка $\varepsilon $. Пусть после нормализации автономной части гамильтониана функции $H_{{20}}^{'}$ и ${{H}_{{21}}}$ из (2.2) преобразуются к виду
Осуществим унивалентное, $4\pi $-периодическое по времени преобразование поворота по обеим парам переменных, определяемое формулами
При этом в гамильтониане (2.3) исчезнет квадратичная часть ${{H}_{{20}}}$, а форма ${{H}_{{40}}}$ (2.4) с точностью до обозначений переменных не изменится.
Сделаем затем линейное, близкое к тождественному (и отличающееся от него слагаемыми порядка $\varepsilon $), $4\pi $-периодическое по времени каноническое преобразование ${{x}_{j}}$, ${{X}_{j}} \to {{\tilde {x}}_{j}}$, ${{\tilde {X}}_{j}}$, уничтожающее время $t$ в слагаемых порядка $\varepsilon $ в квадратичной части гамильтониана. В результате в квадратичной части, вместо исходных десяти, останется шесть слагаемых, разбитых на две группы, зависящие от своей пары сопряженных переменных:
(2.5)
$\begin{gathered} {{{K}_{{21}}} = ({{\mu }_{1}}{{\gamma }_{1}} - {{\beta }_{1}})\tilde {x}_{1}^{2} + ({{\mu }_{1}}{{\gamma }_{1}} + {{\beta }_{1}})\tilde {X}_{1}^{2} + {{\beta }_{2}}{{{\tilde {x}}}_{1}}{{{\tilde {X}}}_{1}} + } \\ + \;({{\mu }_{1}}{{\gamma }_{2}} - {{\beta }_{3}})\tilde {x}_{2}^{2} + ({{\mu }_{1}}{{\gamma }_{2}} + {{\beta }_{3}})\tilde {X}_{2}^{2} + {{\beta }_{4}}{{{\tilde {x}}}_{2}}{{{\tilde {X}}}_{2}}, \\ \end{gathered} $(2.6)
$\begin{gathered} {{\gamma }_{1}} = \frac{1}{2}({{a}_{1}} + {{a}_{3}}),\quad {{\gamma }_{2}} = \frac{1}{2}({{a}_{2}} + {{a}_{4}}) \\ {{\beta }_{1}} = - \frac{1}{2}\overline {[{{b}_{1}}(t) - {{b}_{3}}(t)]cos2nt} + \frac{1}{2}\overline {{{b}_{6}}(t)sin2nt} ,\quad {{\beta }_{2}} = \overline {[{{b}_{1}}(t) - {{b}_{3}}(t)]sin2nt} + \overline {{{b}_{6}}(t)cos2nt} \\ {{\beta }_{3}} = - \frac{1}{2}\overline {[{{b}_{2}}(t) - {{b}_{4}}(t)]cosmt} + \frac{1}{2}\overline {{{b}_{5}}(t)sinmt} ,{\quad {{\beta }_{4}} = \overline {[{{b}_{2}}(t) - {{b}_{4}}(t)]sinmt} + \overline {{{b}_{5}}(t)cosmt} } \\ \end{gathered} $Проведем дальнейшее упрощение квадратичной формы (2.5), осуществив еще одно преобразоование поворота по каждой паре переменных, описываемое соотношениями
Углы ${{\varphi }_{{0j}}}$ задаются равенствами
Предполагается, что $\beta {\text{'}} \ne 0$ и $\beta {\text{''}} \ne 0$.
В результате получаем
(2.7)
${{K}_{{21}}} = ({{\mu }_{1}}{{\gamma }_{1}} - \beta {\text{'}})y_{1}^{2} + ({{\mu }_{1}}{{\gamma }_{1}} + \beta {\text{'}})Y_{1}^{2} + ({{\mu }_{1}}{{\gamma }_{2}} - \beta {\text{''}})y_{2}^{2} + ({{\mu }_{1}}{{\gamma }_{2}} + \beta {\text{''}})Y_{2}^{2}$Тривиальное положение равновесия линейной системы с гамильтонианом (2.7) устойчиво при выполнении условий
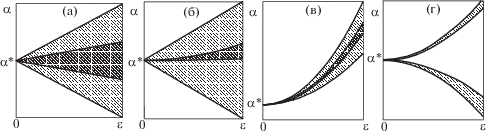
Области устойчивости и неустойчивости в плоскости параметров $\varepsilon $, $\alpha $ показаны в этом случае на фиг. 1а. Здесь и далее области неустойчивости тривиального равновесия закрашены серым или, при наложении двух областей неустойчивости, темно-серым цветом, области устойчивости (в линейном приближении) не закрашены. Границы внешней и внутренней областей неустойчивости на фиг. 1а задаются соответственно уравнениями
Если обе величины $\mu _{1}^{'}$ и $\mu _{1}^{{''}}$ отличны от нуля, то процесс нормализации квадратичной части гамильтониана заканчивается.
В случаях, когда квадратичная форма ${{H}_{{21}}}$ имеет специальную структуру, величины $\beta {\text{'}}$ и $\beta {\text{''}}$ могут обратиться в нуль. Пусть, например, в разложениях функций ${{b}_{k}}(t)$ в ряды Фурье содержатся только гармоники $sin(2k + 1)t$ и $cos(2k + 1)t$, где $k$ – целые числа. Тогда, как следует из формул (2.6), ${{\beta }_{1}} = {{\beta }_{2}} = 0$, и значит, $\beta {\text{'}} = 0$. В этом случае нормализованная квадратичная часть ${{K}_{{21}}}$ имееет вид
(2.8)
$\begin{gathered} {{K}_{{21}}} = {{\mu }_{1}}{{\gamma }_{1}}(y_{1}^{2} + Y_{1}^{2}) + ({{\mu }_{1}}{{\gamma }_{2}} - \beta {\text{''}})y_{2}^{2} + ({{\mu }_{1}}{{\gamma }_{2}} + \beta {\text{''}})Y_{2}^{2} \hfill \\ \end{gathered} $Если, кроме того, в разложении функций ${{b}_{2}}(t)$, ${{b}_{4}}(t)$ и ${{b}_{5}}(t)$ не содержатся гармоники $cosmt$ и $sinmt$, то $\beta {\text{''}} = 0$, и исчезает (в данном приближении) также и вторая область неустойчивости, а функция ${{K}_{{21}}}$ принимает вид
(2.9)
$\begin{gathered} {{K}_{{21}}} = {{\mu }_{1}}{{\gamma }_{1}}(y_{1}^{2} + Y_{1}^{2}) + {{\mu }_{1}}{{\gamma }_{2}}(y_{2}^{2} + Y_{2}^{2}) \hfill \\ \end{gathered} $В этих случаях полагаем ${{\mu }_{1}} = 0$; для того чтобы выявить расщепление в уравнениях границ областей неустойчивости, рассматриваем следующие приближения по $\varepsilon $.
На этапе второго приближения сначала, как и ранее, уничтожаем время в слагаемых $O({{\varepsilon }^{2}})$ квадратичной части гамильтониана, а затем, при необходимости, делаем преобразования поворота. В случае, отвечающем соотношению (2.8), получаем в итоге (${{\eta }_{j}}$ – постоянные, а за переменными оставляем прежние обозначения)
(2.10)
$\begin{gathered} {{K}_{{21}}} = \beta {\text{''}}(Y_{2}^{2} - y_{2}^{2}) \hfill \\ \end{gathered} $(2.11)
${{K}_{{22}}} = ({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{1}})y_{1}^{2} + ({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{2}})Y_{1}^{2} + ({{\mu }_{2}}{{\gamma }_{2}} - {{\eta }_{3}})y_{2}^{2} + ({{\mu }_{2}}{{\gamma }_{2}} - {{\eta }_{4}})Y_{2}^{2}$Этому случаю соответствует фиг. 1б, уравнения границ областей параметрического резонанса имеют вид ($\mu _{2}^{'} = {{\eta }_{1}}{\text{/}}{{\gamma }_{1}}$, $\mu _{2}^{{{\text{''}}}} = {{\eta }_{2}}{\text{/}}{{\gamma }_{1}}$)
(2.12)
$\alpha = {{\alpha }_{*}} \pm \varepsilon \mu _{1}^{{''}} + O({{\varepsilon }^{2}}),\quad \alpha = {{\alpha }_{*}} + {{\varepsilon }^{2}}\mu _{2}^{'} + O({{\varepsilon }^{3}}),\quad \alpha = {{\alpha }_{*}} + {{\varepsilon }^{2}}\mu _{2}^{{''}} + O({{\varepsilon }^{3}})$Если в соотношении (2.11) ${{\eta }_{1}} = {{\eta }_{2}}$, то $\mu _{2}^{'} = \mu _{2}^{{''}}$, и вторая область неустойчивости на этом этапе еще не определяется. Полагая ${{\mu }_{2}} = \mu _{2}^{'}$, проводим нормализацию квадратичной части в слагаемых порядка ${{\varepsilon }^{3}}$. Получаем в этом случае (${{\xi }_{j}}$ – постоянные, за переменными оставлены прежние обозначения)
(2.13)
${{K}_{{21}}} = \beta {\text{''(}}Y_{2}^{2} - y_{2}^{2}{\text{)}},\quad {{K}_{{22}}} = (\mu _{2}^{'}{{\gamma }_{2}} - {{\eta }_{3}})y_{2}^{2} + (\mu _{2}^{'}{{\gamma }_{2}} - {{\eta }_{4}})Y_{2}^{2}$(2.14)
${{K}_{{23}}} = ({{\mu }_{3}}{{\gamma }_{1}} - {{\xi }_{1}})y_{1}^{2} + ({{\mu }_{3}}{{\gamma }_{1}} - {{\xi }_{2}})Y_{1}^{2} + ({{\mu }_{3}}{{\gamma }_{2}} - {{\xi }_{3}})y_{2}^{2} + ({{\mu }_{3}}{{\gamma }_{2}} - {{\xi }_{4}})Y_{2}^{2}$Границы второй области неустойчивости задаются соотношениями
Рассмотрим теперь случай $\mu _{1}^{'} = \mu _{1}^{{''}} = 0$, отвечающий квадратичной форме (2.9). При ${{\mu }_{1}} = 0$ имеем ${{K}_{{21}}} = 0$, а нормализованная квадратичная часть ${{K}_{{22}}}$ определяется выражением (2.11). При ${{\eta }_{1}} \ne {{\eta }_{2}}$ и ${{\eta }_{3}} \ne {{\eta }_{4}}$ в этом приближении получаем две области неустойчивости, которые могут располагаться одна внутри другой (аналогично фиг. 1а), либо частично пересекаться, либо не иметь общих точек.
В случае выполнения одного из равенств ${{\eta }_{1}} = {{\eta }_{2}}$ или ${{\eta }_{3}} = {{\eta }_{4}}$ в данном приближении определяется только одна область параметричекого резонанса. При ${{\eta }_{3}} = {{\eta }_{4}}$ ее границы задаются вторым и третьим соотношениями в (2.12). В этом случае для ${{\mu }_{2}} = {{\hat {\mu }}_{2}}$ = ${{{{\eta }_{3}}} \mathord{\left/ {\vphantom {{{{\eta }_{3}}} {{{\gamma }_{2}}}}} \right. \kern-0em} {{{\gamma }_{2}}}}$ проводится нормализация квадратичной части в слагаемых третьей степени по $\varepsilon $. Получаем
(2.15)
$\begin{gathered} {{K}_{{21}}} = 0,\quad {{K}_{{22}}} = ({{{\hat {\mu }}}_{2}}{{\gamma }_{1}} - {{\eta }_{1}})y_{1}^{2} + ({{{\hat {\mu }}}_{2}}{{\gamma }_{1}} - {{\eta }_{2}})Y_{1}^{2} \hfill \\ \end{gathered} ,$(2.16)
$\alpha = {{\alpha }_{*}} + {{\varepsilon }^{2}}{{\hat {\mu }}_{2}} + {{\varepsilon }^{3}}\hat {\mu }{{_{3}^{'}}_{3}},\quad \alpha = {{\alpha }_{*}} + {{\varepsilon }^{2}}{{\hat {\mu }}_{2}} + \varepsilon {\text{'}}{{{\kern 1pt} }^{3}}\hat {\mu }_{3}^{{''}},\quad \hat {\mu }_{3}^{'} = {{{{\xi }_{3}}} \mathord{\left/ {\vphantom {{{{\xi }_{3}}} {{{\gamma }_{3}}}}} \right. \kern-0em} {{{\gamma }_{3}}}},\;{\text{ }}\hat {\mu }_{3}^{{''}} = {{{{\xi }_{4}}} \mathord{\left/ {\vphantom {{{{\xi }_{4}}} {{{\gamma }_{3}}}}} \right. \kern-0em} {{{\gamma }_{3}}}}$Если величина ${{\hat {\mu }}_{2}}$ находится в интервале между $\mu _{2}^{'}$ и $\mu _{2}^{{''}}$, то вторая область лежит внутри первой (фиг. 1в), а если вне этого интервала, то две области параметрического резонанса не пересекаются (фиг. 1а).
В случае, когда в соотношении (2.11) выполнены оба равенства ${{\eta }_{1}} = {{\eta }_{2}}$ и ${{\eta }_{3}} = {{\eta }_{4}}$, области параметрического резонанса могут проявиться в слагаемых не менее третьего порядка по $\varepsilon $. Границы одной из них (при ${{\mu }_{2}} = {{\hat {\mu }}_{2}}$) определяются соотноошениями (2.16), а границы другой (при ${{\mu }_{2}} = {{\tilde {\mu }}_{2}}$ = ${{{{\eta }_{1}}} \mathord{\left/ {\vphantom {{{{\eta }_{1}}} {{{\gamma }_{1}}}}} \right. \kern-0em} {{{\gamma }_{1}}}}$) – аналогичными соотношениями ($\tilde {\mu }_{3}^{'}$, $\tilde {\mu }_{3}^{{''}}$ – постоянные)
Если ${{\hat {\mu }}_{2}} = {{\tilde {\mu }}_{2}}$, то для этого общего значения параметра μ2 имеем ${{K}_{{22}}} = 0$, а нормализованная форма ${{K}_{{23}}}$ определена равенством (2.14). Процесс нормализации заканчивается, если в этом случае выделяются обе области неустойчивости; если это не так, то рассматриваются следующие приближения по $\varepsilon $.
Замечание. Для всех рассмотренных случаев предполагалось, что величины $\beta {\text{'}}$ и $\beta {\text{''}}$ имеют порядок единицы (по сравнению с ε). Случаи, когда величины $\beta {\text{'}}$ и/или $\beta {\text{''}}$ малы (вместе с ε), требуют дополнительного исследования; в данной работе такое исследование не проводится.
2.2. Модельные гамильтонианы. Нормализованный гамильтониан возмущенного движения, полученный в результате преобразований, описанных в разд. 2.1, представляется в виде
(2.17)
$\begin{gathered} K = {{K}_{2}} + {{K}_{4}} + \ldots ,\quad {{K}_{2}} = K_{2}^{'} + O({{\varepsilon }^{{k + 1}}}),\quad K_{2}^{'} = \sum\limits_{l = 1}^k \,{{\varepsilon }^{l}}{{K}_{{2l}}} \\ {{K}_{4}} = {{K}_{{40}}} + O(\varepsilon ),\quad {{K}_{{40}}} = \frac{{{{c}_{{20}}}}}{4}{{(y_{1}^{2} + Y_{1}^{2})}^{2}} + \frac{{{{c}_{{11}}}}}{4}(y_{1}^{2} + Y_{1}^{2})(y_{2}^{2} + Y_{2}^{2}) + \frac{{{{c}_{{02}}}}}{4}{{(y_{2}^{2} + Y_{2}^{2})}^{2}} \\ \end{gathered} $Квадратичные формы ${{K}_{{2l}}}$ вычисляются по формулам из разд. 2.1, а многоточие означает совокупность слагаемых не менее шестой степени по ${{y}_{j}}$, ${{Y}_{j}}$ с $4\pi $-периодическими по времени коэффициентами.
Наименьший порядок $k$ нормализованных слагаемых квадратичной части (для которого в окрестности резонансной точки обнаруживаются обе области неустойчивости тривиального равновесия системы) определяется структурой периодических слагаемых исходного гамильтониана возмущенного движения и рассматриваемым резонансным соотношением. Далее считаем, что $k \leqslant 3$. Сценарием $k + l$ будем называть случай, когда области неустойчивости проявляются в слагаемых порядков ${{\varepsilon }^{k}}$ и ${{\varepsilon }^{l}}$ ($l \leqslant k$).
Случай $k = 1$. При $k = 1$ (сценарий 1 + 1) перейдем в малую, порядка ${{\varepsilon }^{{1/2}}}$, окрестность начала координат фазового пространства, полагая
(2.18)
$\begin{gathered} {{{\tilde {\Gamma }}}^{{(1)}}} = {{\Gamma }^{{(1)}}} + O(\varepsilon ),\quad {{\Gamma }^{{(1)}}} = {{\Gamma }_{{21}}} + {{\Gamma }_{{40}}} \hfill \\ \end{gathered} $Здесь и далее ${{\Gamma }_{{2l}}}$ и ${{\Gamma }_{{40}}}$ – это формы ${{K}_{{2l}}}$ и ${{K}_{{40}}}$ из соотношений (2.17), в которых сделана замена ${{y}_{j}} = {{z}_{j}}$, ${{Y}_{j}} = {{Z}_{j}}$ ($j = 1,2$). В равенствах (2.18) выражение для ${{\Gamma }_{{21}}}$ определяется из соотношения (2.7). Приближенный гамильтониан ${{\Gamma }^{{(1)}}}$ будем называть модельным для отвечающего ему резонансного случая. Слагаемое $O(\varepsilon )$ в равенствах (2.18) периодично по ${{\tau }_{1}}$ (с периодом ${{T}_{1}} = 4\pi \varepsilon $) и в достаточно малой окрестности начала координат фазового пространства аналитично по переменным ${{z}_{j}}$, ${{Z}_{j}}$ ($j = 1,2$).
Случай $k = 2$. Если $k = 2$, то при ${{\mu }_{1}} \ne 0$ исследование также проводится ${{\varepsilon }^{{1/2}}}$-окрестности начала координат и гамильтониан приводится к виду (2.18), в котором ${{\Gamma }_{{21}}}$ вычисляется при помощи формул (2.8) для сценария 2 + 1 или (2.9) для сценария 2 + 2.
При ${{\mu }_{1}} = 0$ нормализованная квадратичная часть в слагаемых первого и второго порядков по $\varepsilon $ определяется формулами (2.10) и (2.11). Перейдем в $\varepsilon $-окрестность начала координат, полагая
Если в равенстве (2.10) ${{K}_{{21}}} \ne 0$ (сценарий 2 + 1), то, вводя новую независимую переменную ${{\tau }_{1}}$, получим гамильтониан вида
(2.19)
$\begin{gathered} {{{\tilde {\Gamma }}}^{{(2)}}} = {{\Gamma }^{{(21)}}} + O({{\varepsilon }^{2}}),\quad {{\Gamma }^{{(21)}}} = {{\Gamma }_{{21}}} + \varepsilon ({{\Gamma }_{{22}}} + {{\Gamma }_{{40}}}) \hfill \\ \end{gathered} $Если же ${{K}_{{21}}} = 0$ (сценарий 2 + 2), то вводим ${{\tau }_{2}} = {{\varepsilon }^{2}}t$. Тогда имеем
(2.20)
$\begin{gathered} {{{\tilde {\Gamma }}}^{{(2)}}} = {{\Gamma }^{{(22)}}} + O(\varepsilon ),\quad {{\Gamma }^{{(22)}}} = {{\Gamma }_{{22}}} + {{\Gamma }_{{40}}} \hfill \\ \end{gathered} $Модельными для данного случая будут гамильтонианы ${{\Gamma }^{{(1)}}}$ (при ${{\mu }_{1}} \ne 0$) и ${{\Gamma }^{{(21)}}}$ или ${{\Gamma }^{{(22)}}}$ (при ${{\mu }_{1}} = 0$). Слагаемые $O({{\varepsilon }^{2}})$ и $O(\varepsilon )$ в равенствах (2.19) и (2.20) аналитичны по ${{z}_{j}}$, ${{Z}_{j}}$ и периодичны по ${{\tau }_{1}}$ и ${{\tau }_{2}}$ с периодами ${{T}_{1}}$ и ${{T}_{2}} = 4\pi {{\varepsilon }^{2}}$ соответственно.
Случай $k = 3$. При ${{\mu }_{1}} \ne 0$ исследуется ${{\varepsilon }^{{1/2}}}$-окрестность начала координат и модельный гамильтониан ${{\Gamma }^{{(1)}}}$, в котором функция ${{\Gamma }_{{21}}}$ вычисляется с учетом формулы (2.8) для сценария 3 + 1 и формулы (2.9) для сценариев 3 + 2 и 3 + 3.
Если ${{\mu }_{1}} = 0$, то переходим в $\varepsilon $-окрестность начала координат. Для сценария 3 + 1 модельным на этом этапе будет гамильтониан ${{\Gamma }^{{(21)}}}$, в котором функции ${{\Gamma }_{{21}}}$ и ${{\Gamma }_{{22}}}$ вычисляются с учетом формул (2.10) и (2.11) (при ${{\eta }_{1}} = {{\eta }_{2}}$). Для сценариев 3 + 2 и 3 + 3 имеем ${{K}_{{21}}} = 0$, модельным будет гамильтониан ${{\Gamma }^{{(22)}}}$, в котором функция ${{\Gamma }_{{22}}}$ вычисляется с учетом формулы (2.11) при ${{\eta }_{3}} = {{\eta }_{4}}$ и ${{\eta }_{1}} = {{\eta }_{2}}$, ${{\eta }_{3}} = {{\eta }_{4}}$ соответственно.
На этапе третьего приближения по $\varepsilon $ следует перейти в ${{\varepsilon }^{{3/2}}}$-окрестность начала координат по формулам
Проводя нормализацию для сценария 3 + 1 и вводя независимую переменную ${{\tau }_{1}}$, получим
(2.21)
$\begin{gathered} {{{\tilde {\Gamma }}}^{{(3)}}} = {{\Gamma }^{{(31)}}} + O({{\varepsilon }^{3}}),\quad {{\Gamma }^{{(31)}}} = {{\Gamma }_{{21}}} + \varepsilon {{\Gamma }_{{22}}} + {{\varepsilon }^{2}}({{\Gamma }_{{23}}} + {{\Gamma }_{{40}}}) \hfill \\ \end{gathered} $Формы ${{\Gamma }_{{21}}}$, ${{\Gamma }_{{22}}}$, ${{\Gamma }_{{23}}}$ вычисляются с учетом соотношений (2.13) и (2.14).
При выполнении сценария 3 + 2 после нормализации и введения в качестве независимой переменной ${{\tau }_{2}}$ имеем
(2.22)
$\begin{gathered} {{{\tilde {\Gamma }}}^{{(3)}}} = {{\Gamma }^{{(32)}}} + O({{\varepsilon }^{2}}),\quad {{\Gamma }^{{(32)}}} = {{\Gamma }_{{22}}} + \varepsilon ({{\Gamma }_{{23}}} + {{\Gamma }_{{40}}}) \hfill \\ \end{gathered} $Учтено, что ${{K}_{{21}}} = 0$, а формы ${{\Gamma }_{{22}}}$ и ${{\Gamma }_{{23}}}$ определяются из соотношений (2.15) и (2.14).
Наконец, при условии ${{\eta }_{1}} = {{\eta }_{2}}$, ${{\eta }_{3}} = {{\eta }_{4}}$ (сценарий 3 + 3) и ${{\hat {\mu }}_{2}} \ne {{\tilde {\mu }}_{2}}$ получаем тот же гамильтониан (2.22), в котором следует принять
(2.23)
${{\Gamma }_{{22}}} = ({{\hat {\mu }}_{2}}{{\gamma }_{1}} - {{\eta }_{1}})(z_{1}^{2} + Z_{1}^{2})\quad {\text{и л и }}\quad \begin{gathered} {{\Gamma }_{{22}}} = ({{{\tilde {\mu }}}_{2}}{{\gamma }_{2}} - {{\eta }_{3}})(z_{2}^{2} + Z_{2}^{2}) \hfill \\ \end{gathered} ,$Если же ${{\hat {\mu }}_{2}} = {{\tilde {\mu }}_{2}}$, то имеем ${{\Gamma }_{{22}}} = 0$, и тогда
(2.24)
$\begin{gathered} {{{\tilde {\Gamma }}}^{{(3)}}} = {{\Gamma }^{{(33)}}} + O(\varepsilon ),\quad {{\Gamma }^{{(33)}}} = {{\Gamma }_{{23}}} + {{\Gamma }_{{40}}} \hfill \\ \end{gathered} $Независимой для этого гамильтониана является переменная ${{\tau }_{3}} = {{\varepsilon }^{3}}t$
Слагаемые $O({{\varepsilon }^{3}})$, $O({{\varepsilon }^{2}})$ и $O(\varepsilon )$ в соотношениях (2.21), (2.22) и (2.24) аналитичны по ${{z}_{j}}$, ${{Z}_{j}}$ и периодичны по $\tau $ с периодами ${{T}_{1}}$ , ${{T}_{2}}$ и ${{T}_{3}} = 4\pi {{\varepsilon }^{3}}$ соответственно.
При рассмотрении соответствующей окрестности резонансной точки модельными для случаев $k = 3$ будут гамильтонианы ${{\Gamma }^{{(1)}}}$, ${{\Gamma }^{{(2i)}}}$ ($i = 1$ или 2) и ${{\Gamma }^{{(3j)}}}$ ($j = 1$, 2 или 3).
3. Резонансные периодические движения системы. Решим вопрос о существовании, числе и устойчивости (в линейном приближении) периодических движений систем с гамильтонианами ${{\tilde {\Gamma }}^{{(k)}}}$ ($k = 1,2,3$), определяемыми формулами (2.18)–(2.22), (2.24). На первом этапе найдем отличные от тривиального положения равновесия соответствующих им модельных систем.
3.1. Случай $k = 1.$ Рассмотрим сначала модельную систему с гамильтонианом ${{\Gamma }^{{(1)}}}$ (2.18), в котором квадратичная часть вычисляется с помощью формулы (2.7) при $\beta {\text{'}} \ne 0$, $\beta {\text{''}} \ne 0$ (сценарий 1 + 1). Приравнивая нулю частные производные ${{\Gamma }^{{(1)}}}$ по ${{z}_{j}}$ и ${{Z}_{j}}$ ($j = 1,2$), получим систему уравнений для определения положений равновесия этой модельной системы
(3.1)
$\begin{gathered} [2({{\mu }_{1}}{{\gamma }_{1}} - \beta {\text{'}}) + {{c}_{{20}}}(z_{1}^{2} + Z_{1}^{2}) + ({{c}_{{11}}}{\text{/}}2)(z_{2}^{2} + Z_{2}^{2})]{{z}_{1}} = 0 \\ [2({{\mu }_{1}}{{\gamma }_{1}} + \beta {\text{'}}) + {{c}_{{20}}}(z_{1}^{2} + Z_{1}^{2}) + ({{c}_{{11}}}{\text{/}}2)(z_{2}^{2} + Z_{2}^{2})]{{Z}_{1}} = 0 \\ [2({{\mu }_{1}}{{\gamma }_{2}} - \beta {\text{''}}) + ({{c}_{{11}}}{\text{/}}2)(z_{1}^{2} + Z_{1}^{2}) + {{c}_{{02}}}(z_{2}^{2} + Z_{2}^{2})]{{z}_{2}} = 0 \\ [2({{\mu }_{1}}{{\gamma }_{2}} + \beta {\text{''}}) + ({{c}_{{11}}}{\text{/}}2)(z_{1}^{2} + Z_{1}^{2}) + {{c}_{{02}}}(z_{2}^{2} + Z_{2}^{2})]{{{Z}_{2}} = 0} \\ \end{gathered} $Исключим комбинации $z_{2}^{2} + Z_{2}^{2}$ и $z_{1}^{2} + Z_{1}^{2}$ соответственно из первых двух и последних двух уравнений (3.1), в результате получим два уравнения-следствия вида ${{z}_{1}}{{Z}_{1}} = 0$, ${{z}_{2}}{{Z}_{2}} = 0$. Рассматривая их совместно с системой (3.1), определим две группы положений равновесия.
К первой группе относятся четыре пары равновесий, задаваемые сооотношениями
(3.2)
$\begin{gathered} {{z}_{2}} = {{Z}_{1}} = {{Z}_{2}} = 0,\quad z_{1}^{2} = - 2({{\gamma }_{1}}{{\mu }_{1}} - \beta {\text{'}})c_{{20}}^{{ - 1}}\quad ({{c}_{{20}}}({{\gamma }_{1}}{{\mu }_{1}} - \beta {\text{'}}) < 0) \\ \begin{gathered} {{z}_{1}} = {{z}_{2}} = {{Z}_{2}} = 0,\quad Z_{1}^{2} = - 2({{\gamma }_{1}}{{\mu }_{1}} + \beta {\text{'}})c_{{20}}^{{ - 1}}\quad \hfill \\ \end{gathered} ({{c}_{{20}}}({{\gamma }_{1}}{{\mu }_{1}} + \beta {\text{'}}) < 0) \\ {{z}_{1}} = {{Z}_{1}} = {{Z}_{2}} = 0,\quad z_{2}^{2} = - 2({{\gamma }_{2}}{{\mu }_{1}} - \beta {\text{''}})c_{{02}}^{{ - 1}}\quad ({{c}_{{02}}}({{\gamma }_{2}}{{\mu }_{1}} - \beta {\text{''}}) < 0) \\ {{z}_{1}} = {{z}_{2}} = {{Z}_{1}} = 0,\quad Z_{2}^{2} = - 2({{\gamma }_{2}}{{\mu }_{1}} + \beta {\text{''}})c_{{02}}^{{ - 1}}\quad ({{c}_{{02}}}({{\gamma }_{2}}{{\mu }_{1}} + \beta {\text{''}}) < 0) \\ \end{gathered} $В скобках здесь и далее в аналогичных соотношениях указаны условия существования решений. Из этих условий следует, что данные положения равновесия появляются (или исчезают), в зависимости от знаков коэффициентов ${{c}_{{20}}}$ и ${{c}_{{02}}}$, при переходе через бифуркационные точки ${{\mu }_{1}} = \pm \mu _{1}^{'}$ и ${{\mu }_{1}} = \pm \mu _{1}^{{''}}$.
Вторую группу положений равновесия составляют четверки решений, описываемые соотношениями
(3.3)
$\begin{gathered} {{z}_{1}} = {{z}_{2}} = 0,\quad Z_{1}^{2} = 4({{\kappa }_{1}}{{\mu }_{1}} + 2\beta {\text{'}}{{c}_{{02}}} - {{c}_{{11}}}\beta {\text{''}}){{\Delta }^{{ - 1}}},\quad Z_{2}^{2} = - 4({{\kappa }_{2}}{{\mu }_{1}} + {{c}_{{11}}}\beta {\text{'}} - 2{{c}_{{20}}}\beta {\text{''}}){{\Delta }^{{ - 1}}} \\ {{z}_{1}} = {{Z}_{2}} = 0,\quad Z_{1}^{2} = 4({{\kappa }_{1}}{{\mu }_{1}} + 2{{c}_{{02}}}\beta {\text{'}} + {{c}_{{11}}}\beta {\text{''}}){{\Delta }^{{ - 1}}},\quad z_{2}^{2} = - 4({{\kappa }_{2}}{{\mu }_{1}} + {{c}_{{11}}}\beta {\text{'}} + 2{{c}_{{20}}}\beta {\text{''}}){{\Delta }^{{ - 1}}} \\ {{Z}_{1}} = {{z}_{2}} = 0,\quad z_{1}^{2} = 4({{\kappa }_{1}}{{\mu }_{1}} - 2{{c}_{{02}}}\beta {\text{'}} - {{c}_{{11}}}\beta {\text{''}}){{\Delta }^{{ - 1}}},\quad Z_{2}^{2} = - 4({{\kappa }_{2}}{{\mu }_{1}} - {{c}_{{11}}}\beta {\text{'}} - 2{{c}_{{20}}}\beta {\text{''}}){{\Delta }^{{ - 1}}} \\ {{Z}_{1}} = {{Z}_{2}} = 0,\quad z_{1}^{2} = 4({{\kappa }_{1}}{{\mu }_{1}} - 2{{c}_{{02}}}\beta {\text{'}} + {{c}_{{11}}}\beta {\text{''}}){{\Delta }^{{ - 1}}},\quad z_{2}^{2} = - 4({{\kappa }_{2}}{{\mu }_{1}} - {{c}_{{11}}}\beta {\text{'}} + 2{{c}_{{20}}}\beta {\text{''}}){{\Delta }^{{ - 1}}} \\ \end{gathered} $Здесь введены обозначения
Решения (3.3) существуют, если правые части в выражениях с квадратами неотрицательны. Бифуркационными являются восемь точек
(3.4)
$\begin{gathered} {{\mu }_{1}} = ( \pm 2{{c}_{{02}}}\beta {\text{'}} \pm {{c}_{{11}}}\beta {\text{''}})\kappa _{1}^{{ - 1}},\quad {{\mu }_{1}} = ( \pm {{c}_{{11}}}\beta {\text{'}} \pm 2{{c}_{{20}}}\beta {\text{''}})\kappa _{2}^{{ - 1}} \hfill \\ \end{gathered} $Здесь верхние и нижние знаки берутся в любом сочетании.
Рассмотрим вопрос об устойчивости в линейном приближениии найденных решений. Зададим возмущения ${{\tilde {z}}_{j}}$, ${{\tilde {Z}}_{j}}$ ($j = 1,2$) переменных ${{z}_{j}}$, ${{Z}_{j}}$ системы относительно их равновесных значений. Для обоих решений из первой пары в равенствах (3.2) квадратичная часть гамильтониана возмущенного движения имеет вид
Отсюда следует, что в области существования данного решения условия устойчивости сводятся к неравенствам
Для решений из второй, третьей и четвертой пар аналогичные условия имеют соответственно вид ${{c}_{{20}}} < 0$, ${{({{\kappa }_{2}}{{\mu }_{1}} + {{c}_{{11}}}\beta {\text{'}})}^{2}}$ > $4({{c}_{{20}}}\beta {\text{''}}{{)}^{2}}$; ${{c}_{{02}}} > 0$, ${{({{\kappa }_{1}}{{\mu }_{1}} + {{c}_{{11}}}\beta {\text{''}})}^{2}}$ > $4({{c}_{{02}}}\beta {\text{'}}{{)}^{2}}$ и ${{c}_{{02}}} < 0$, ${{({{\kappa }_{1}}{{\mu }_{1}} - {{c}_{{11}}}\beta {\text{''}})}^{2}}$ > $4({{c}_{{02}}}\beta {\text{'}}{{)}^{2}}$. Таким образом, характер устойчивости исследуемых равновесных точек определяется расположением величины ${{\mu }_{1}}$ относительно бифуркационных значений (3.4).
Для решений (3.3) составляем характеристические уравнения соответствующих линеаризованных уравнений возмущенного движения
Если выполнены соотношения
то корни уравнения (3.5) чисто мнимые, и исследуемое решение устойчиво в линейном приближении. При изменении знака хотя бы одного неравенства на противоположный уравнение (3.5) имеет корни с положительными вещественными частями, и имеет место неустойчивость.Рассмотрим первую четверку решений (3.3), существующих при выполнении неравенств
(3.7)
$\begin{gathered} {{{\kappa }_{1}}\Delta ({{\mu }_{1}} - {{\mu }_{{11}}}) > 0,\quad {{\kappa }_{2}}\Delta ({{\mu }_{1}} - {{\mu }_{{12}}}) < 0} \\ {{\mu }_{{11}}} = \kappa _{1}^{{ - 1}}({{c}_{{11}}}\beta {\text{''}} - 2{{c}_{{02}}}\beta {\text{'}}),\quad {{\mu }_{{12}}} = \kappa _{2}^{{ - 1}}(2{{c}_{{20}}}\beta {\text{''}} - {{c}_{{11}}}\beta {\text{'}}) \\ \end{gathered} $Коэффициенты уравнения (3.5) для каждого из этих решений таковы:
Отсюда находим, что в области существования первые два неравенства (3.6) сводятся к системе
(3.8)
$\begin{gathered} \delta ({{\mu }_{1}} - {{\mu }_{{10}}}) > 0,\quad \Delta < 0 \hfill \\ \end{gathered} $Таким образом, при $\Delta > 0$ данные равновесия всегда неустойчивы.
Пусть $\Delta < 0$. Величина $d$ из третьего условия (3.6) представляет собой квадратный относительно ${{\mu }_{1}}$ трехчлен с положительным старшим коэффициентом
(3.9)
${{d}_{2}} = 1024{{\Delta }^{{ - 2}}}[c_{{20}}^{2}{{\beta }^{{'2}}}\kappa _{1}^{2} + (2{{c}_{{20}}}{{c}_{{02}}} - c_{{11}}^{2})\beta {\text{'}}\beta {\text{''}}{{\kappa }_{1}}{{\kappa }_{2}} + c_{{02}}^{2}\beta {\text{'}}{{{\text{'}}}^{2}}\kappa _{2}^{2}]$Рассматривая систему неравенств (3.7), (3.8), находим, что если ${{\kappa }_{1}}{{\kappa }_{2}} > 0$ и ${{c}_{{20}}}f < 0$, то ее решение задается интервалом $min({{\mu }_{{11}}},{{\mu }_{{12}}})$ < ${{\mu }_{1}}$ < $max({{\mu }_{{11}}},{{\mu }_{{12}}})$. Если ${{\kappa }_{1}}{{\kappa }_{2}} < 0$ и ${{c}_{{20}}} < 0$, то при $\delta < 0$ имеем ${{\mu }_{1}} < min({{\mu }_{{11}}},{{\mu }_{{12}}})$, а при $\delta > 0$ получаем ${{\mu }_{1}} > max({{\mu }_{{11}}},{{\mu }_{{12}}})$. Для невыписанных значений параметров из области существования имеем неустойчивость.
Вторая четверка равновесий (3.3) существует при выполнении условий (3.7), в которых величину $\beta {\text{''}}$ следует взять с противоположным знаком. Аналогично предыдущему заключаем, что в области существования неравенство $b > 0$ удовлетворяется при условии $\Delta > 0$; при $\Delta < 0$ имеем неустойчивость.
В случае $\Delta > 0$ дискриминант квадратного относительно ${{\mu }_{1}}$ трехчлена $d$ из третьего условия (3.6), равный $s{{\Delta }^{{ - 1}}}{{\beta }^{{'2}}}{{\beta }^{{''2}}}c_{{11}}^{2}f_{1}^{2}$ (${{f}_{1}} = {{\gamma }_{1}}\beta {\text{''}} + {{\gamma }_{2}}\beta {\text{'}}$), положителен, и $d$ имеет два вещественных корня, обозначим их через ${{\mu }_{1}}_{*}$ и ${{\mu }_{1}}{{{\kern 1pt} }_{{{\text{**}}}}}$ (${{\mu }_{1}}_{*}$ < ${{\mu }_{1}}{{{\kern 1pt} }_{{{\text{**}}}}}$). При этом старший коэффициент трехчлена $d$, вычисляемый по формуле (3.9) при замене $\beta {\text{''}}$ на $ - \beta {\text{''}}$, может быть как положительным, так и отрицательным.
Если ${{\kappa }_{1}}{{\kappa }_{2}} > 0$, то всегда ${{d}_{2}} > 0$, и в случае ${{c}_{{20}}}{{c}_{{02}}} < 0$ условия устойчивости удовлетворяются для значений ${{\mu }_{1}}$ из двух интервалов
(3.10)
$\begin{gathered} min({{\mu }_{{11}}},{{\mu }_{{12}}}) < {{\mu }_{1}} < {{\mu }_{1}}_{*},\quad {{\mu }_{{\text{1}}}}{{{\kern 1pt} }_{{{\text{**}}}}} < {{\mu }_{1}} < max({{\mu }_{{11}}},{{\mu }_{{12}}}) \hfill \\ \end{gathered} $В случае же ${{c}_{{20}}}{{c}_{{02}}} > 0$ условия устойчивости при ${{\delta }_{1}} > 0$ и ${{\delta }_{1}} < 0$ задаются первым и вторым неравенством (3.10) соответственно.
Исследование устойчивости при ${{\kappa }_{1}}{{\kappa }_{2}} < 0$ несколько сложнее. Приведем его результаты для случая ${{\kappa }_{1}} > 0$, ${{\kappa }_{2}} < 0$ (случай ${{\kappa }_{1}} < 0$, ${{\kappa }_{2}} > 0$ рассматривается аналогично). Выражение в квадратных скобках в равенстве (3.9) при замене $\beta {\text{''}}$ на $ - \beta {\text{''}}$ можно переписать, выделив в нем квадратный трехчлен относительно величины $x = \beta {\text{'}}{{\kappa }_{1}}{\text{/}}(\beta {\text{''}}{{\kappa }_{2}})$, где $x < 0$. Его дискриминант, равный $c_{{11}}^{2}\Delta $, положителен, поэтому квадратный трехчлен имеет два вещественных (отрицательных) корня, обозначим из через ${{x}_{1}}$ и ${{x}_{2}}$ (${{x}_{1}} < {{x}_{2}}$). При $x < {{x}_{1}}$ и $x > {{x}_{2}}$ справедливо неравенство ${{d}_{2}} > 0$, а при ${{x}_{1}} < x < {{x}_{2}}$ имеем ${{d}_{2}} < 0$.
Пусть сначала ${{d}_{2}} > 0$. Если ${{c}_{{20}}} > 0$, ${{c}_{{02}}} > 0$, то в случаях ${{\delta }_{1}} > 0$ и ${{\delta }_{1}} < 0$ условия устойчивости приводятся к неравенствам
(3.11)
$\begin{gathered} max({{\mu }_{{11}}},{{\mu }_{{12}}}) < {{\mu }_{1}} < {{\mu }_{1}}_{*}\quad {\text{и }}\quad {{\mu }_{1}} > max({{\mu }_{{11}}},{{\mu }_{{12}}}) \hfill \\ \end{gathered} $(3.12)
$\begin{gathered} {{\mu }_{1}} > {{\mu }_{1}}{{{\kern 1pt} }_{{{\text{**}}}}} \hfill \\ \end{gathered} $Если же ${{c}_{{20}}} < 0$, ${{c}_{{02}}} > 0$, то в случае ${{f}_{1}} > 0$ на левой ($x < {{x}_{1}}$) ветви положительных значений ${{d}_{2}}$ условие устойчивости определяется объединением первого неравенства из (3.11) и неравенства (3.12), а на правой ($x > {{x}_{2}}$) ветви – вторым неравенством (3.11). При ${{f}_{1}} < 0$ условия устойчивости на левой и правой ветвях меняются местами.
В случае ${{d}_{2}} < 0$ исследуемые решения устойчивы, если ${{c}_{{02}}} > 0$ и выполнено неравенство
Для третьей четверки решений (3.3) из условия $b > 0$ имеем в области существования $\Delta > 0$, а для четвертой $\Delta < 0$; проверка других условий устойчивости проводится так же, как для второй и первой четверок решений соответственно.
3.2. Случай $k = 2$. Рассмотрим два сценария, возможных в случае $k = 2.$
3.2.1. Сценарий 2 + 1. В случае $\beta {\text{'}} = 0$, $\beta {\text{''}} \ne 0$ реализуется сценарий 2 + 1; картина устойчивости имеет вид, представленный на фиг. 1б.
Первое приближение. В модельной системе с гамильтонианом ${{\Gamma }^{{(1)}}}$, в котором квадратичная часть определяется формулой (2.8) при ${{\mu }_{1}} \ne 0$, в ${{\varepsilon }^{{1/2}}}$-окрестности резонансной точки происходит перестройка фазового пространства (по сравнению со случаем, рассмотренным в разд. 3.1). В системе появляется первый интеграл $z_{1}^{2} + Z_{1}^{2} = 2c$ = = const. Приведенной системе с одной степенью свободы отвечает гамильтониан вида
(3.13)
$h = \left( {{{\mu }_{1}}{{\gamma }_{2}} - \beta {\text{''}} + \frac{1}{2}{{c}_{{11}}}c} \right)z_{2}^{2} + \left( {{{\mu }_{1}}{{\gamma }_{2}} + \beta {\text{''}} + \frac{1}{2}{{c}_{{11}}}c} \right)Z_{2}^{2} + \frac{1}{4}{{c}_{{02}}}{{(z_{2}^{2} + Z_{2}^{2})}^{2}}$Тривиальное положение равновесия этой системы устойчиво при выполнении условия
и неустойчиво в противном случае. Точки бифуркации задаются соотношениямиДругие положения равновесия системы с гамильтонианом (3.13) определяются формулами
(3.14)
${{{z}_{2}} = 0,\quad Z_{2}^{2} = - 2{{\gamma }_{2}}({{\mu }_{1}} - \mu _{1}^{ - })c_{{02}}^{{ - 1}}\quad ({{c}_{{02}}}{{\gamma }_{2}}({{\mu }_{1}} - \mu _{1}^{ - }) < 0)}{\text{ }}$(3.15)
${{Z}_{2}} = 0,\quad z_{2}^{2} = - 2{{\gamma }_{2}}({{\mu }_{1}} - \mu _{1}^{ + })c_{{02}}^{{ - 1}}\quad ({{c}_{{02}}}{{\gamma }_{2}}({{\mu }_{1}} - \mu _{1}^{ + }) < 0)$В области существования равновесия (3.14) устойчивы в линейном приближении, если $\beta {\text{''}}{{c}_{{02}}} < 0$, и неустойчивы, если $\beta {\text{''}}{{c}_{{02}}} > 0$. Для равновесий (3.15) эти условия устойчивости и неустойчивости меняются местами.
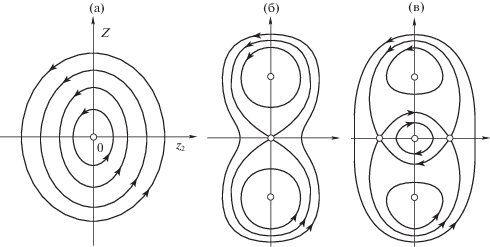
Фазовые портреты системы с гамильтонианом (3.13) показаны на фиг. 2а–2в для случаев
Вернемся к модельной системе с двумя степенямии свободы с гамильтонианом ${{\Gamma }^{{(1)}}}$. Ее положениями равновесия будут точки
(3.16)
${{z}_{1}} = {{z}_{2}} = {{Z}_{1}} = 0,\quad Z_{2}^{2} = - 2({{\mu }_{1}}{{\gamma }_{2}} + \beta {\text{''}})c_{{02}}^{{ - 1}}\quad ({{c}_{{02}}}({{\mu }_{1}}{{\gamma }_{2}} + \beta {\text{''}}) < 0)$(3.17)
${{z}_{1}} = {{Z}_{1}} = {{Z}_{2}} = 0,\quad z_{2}^{2} = - 2({{\mu }_{1}}{{\gamma }_{2}} - \beta {\text{''}})c_{{02}}^{{ - 1}}\quad ({{c}_{{02}}}({{\mu }_{1}}{{\gamma }_{2}} - \beta {\text{''}}) < 0),$Квадратичная часть гамильтониана возмущенного движения для решений (3.16) имеет вид
Для значений ${{\mu }_{1}} = {{c}_{{11}}}\beta {\text{''}}\kappa _{1}^{{ - 1}}$ и ${{\mu }_{1}} = - {{c}_{{11}}}\beta {\text{''}}\kappa _{1}^{{ - 1}}$ (если они находятся в области существования) равновесия (3.16) и (3.17) соответственно являются сложными особыми точками.
Кроме изолированных положений равновесия, в модельной системе с гамильтонианом ${{\Gamma }^{{(1)}}}$ могут существовать семейства положений равновесия. Так, при выполнении условия ${{\mu }_{1}}{{\gamma }_{1}}{{c}_{{20}}} < 0$ в системе имеется семейство неустойчивых положений равновесия (сложных особых точек), образующих в плоскости переменных ${{z}_{1}}$, ${{Z}_{1}}$ окружность вида
Еще две пары симметричных семейств (окружностей) из неустойчивых сложных особых точек, задаваемых соотношениями
Второе приближение. При ${{\mu }_{1}} = 0$ переходим в $\varepsilon $-окрестность тривиального равновесия и рассматриваем модельную систему с гамильтонианом ${{\Gamma }^{{(21)}}}$, квадратичная часть которой вычисляется при помощи выражений (2.10) и (2.11). Положения равновесия модельной системы таковы:
(3.18)
$\begin{gathered} {{z}_{1}} = {{z}_{2}} = {{Z}_{2}} = 0,\quad Z_{1}^{2} = - 2({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{2}})c_{{20}}^{{ - 1}} \\ ({{c}_{{20}}}({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{2}}) < 0)\quad ({{z}_{1}} \leftrightarrow {{Z}_{1}},\;{{\eta }_{1}} \leftrightarrow {{\eta }_{2}}) \\ \end{gathered} $Квадратичная часть гамильтониана возмущенного движения имеет вид
(3.19)
$\begin{gathered} - \varepsilon ({{\eta }_{1}} - {{\eta }_{2}})\tilde {z}_{1}^{2} - 2\varepsilon ({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{2}})\tilde {Z}_{1}^{2} - (\beta {\text{''}} + O(\varepsilon ))\tilde {z}_{2}^{2} + (\beta {\text{''}} + O(\varepsilon ))\tilde {Z}_{2}^{2} \\ {\text{(}}{{{\tilde {z}}}_{1}} \leftrightarrow {{{\tilde {Z}}}_{1}},\;{{\eta }_{1}} \leftrightarrow {{\eta }_{2}}) \\ \end{gathered} $Таким образом, при достаточно малых значениях $\varepsilon $ данные равновесия неустойчивы в области существования.
Объединяя результаты исследования модельных систем первого и второго приближений и исключая отмеченные случаи сложных особых точек, приходим к следующему выводу. Внутри большей области неустойчивости (см. фиг. 1б) существует, в зависимости от знаков величин ${{\gamma }_{2}}$ и ${{c}_{{02}}}$, одна из пар устойчивых в линейном приближении положений равновесия (3.16) или (3.17). Вне этой зоны неустойчивости по одну сторону существует та же пара равновесий, оставаясь устойчивой, и другая, неустойчивая, пара равновесий; по другую сторону в модельной системе отсутствуют положения равновесия, отличные от тривиального. Исключение составляет внутренняя зона неустойчивости и ее малая, ширины $O({{\varepsilon }^{2}})$, окрестность. В этой окрестности, аналогично, существуют, по одну сторону от зоны неустойчивости, две пары равновесий (3.18), по другую сторону – ни одной, а внутри самой зоны – одна из этих пар, и все эти равновесия неустойчивы.
3.2.2. Сценарий 2+2. В этом случае $\beta {\text{'}} = \beta {\text{''}} = 0$. При ${{\mu }_{1}} \ne 0$ модельная система с гамильтонианом ${{\Gamma }^{{(1)}}}$, вычисляемым с учетом выражения (2.9) для квадратичной части, не имеет положений равновесия, отличных от тривиального. Переходя при ${{\mu }_{1}} = 0$ в $\varepsilon $-окрестность тривиального равновесия, получим систему с модельным гамильтонианом ${{\Gamma }^{{(22)}}}$ (второе равенство (2.20)), квадратичная часть которого определена равенством (2.11). По своей структуре гамильтониан ${{\Gamma }^{{(22)}}}$ аналогичен модельному гамильтониану ${{\Gamma }^{{(1)}}}$ (с квадратичной частью (2.7)), исследование которого проведено в разд. 3.1.
3.3. Случай $k = 3$. 3.3.1. Сценарий 3+1. При реализации сценария 3 + 1 взаимное расположение областей неустойчивости аналогично показанному на фиг. 1б, только внутренняя область неустойчивости имеет ширину $O({{\varepsilon }^{3}})$.
При ${{\mu }_{1}} \ne 0$ для квадратичной части модельного гамильтониана ${{\Gamma }^{{(1)}}}$ первого приближения используется выражение (2.8), и имеем случай, рассмотренный в разд. 3.2.1.
На этапе второго приближения (случай ${{\mu }_{1}} = 0$) исследуется модельный гамильтониан ${{\Gamma }^{{(21)}}}$ из (2.19), в котором формы ${{\Gamma }_{{21}}}$ и ${{\Gamma }_{{22}}}$ вычисляются с помощью соотношений (2.10) и (2.11) при ${{\eta }_{1}} = {{\eta }_{2}}$. В модельной системе имеется первый интеграл $z_{1}^{2} + Z_{1}^{2} = 2c$ = = const. Кроме тривиального равновесия, в области ${{c}_{{20}}}({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{1}}) < 0$ существуют два семейства неустойчивых сложных особых точек, для которых
Других положений равновесия нет.
Модельный гамильтониан ${{\Gamma }^{{(31)}}}$ третьего приближения определен вторым равенством (2.21), а положения равновесия отвечающей ему модельной системы таковы:
Как и в описанных выше аналогичных случаях, во внутренней зоне неустойчивости тривиального равновесия существует одна пара положений равновесия, вне ее по одну сторону имеются две пары равновесий, а по другую сторону ни одной. Найденные положения равновесия, находясь в зоне неустойчивости тривиального равновесия системы, неустойчивы в области своего существования. Квадратичная часть гамильтониана возмущенного движения имеет вид
3.3.2. Сценарий 3 + 2. При ${{\mu }_{1}} \ne 0$ квадратичная часть первого приближения имеет вид (2.9); в модельной системе с гамильтонаном ${{\Gamma }^{{(1)}}}$ нет положений равновесия, отличных от тривиального.
В модельном гамильтониане второго приближения (случай ${{\mu }_{1}} = 0$) имеем ${{\Gamma }_{{21}}} = 0$. Форма ${{\Gamma }_{{22}}}$ определяется соотношением (2.11), в котором ${{\eta }_{1}} = {{\eta }_{2}}$ или ${{\eta }_{3}} = {{\eta }_{4}}$, и с точностью до обозначений совпадает с формой (2.8); соответствующее ей исследование проведено в разд. 3.2.1. Изолированными положениями равновесия в случае, например, ${{\eta }_{3}} = {{\eta }_{4}}$ будут точки
(3.20)
${{z}_{1}} = 0,\quad Z_{1}^{2} = - (2{{\mu }_{2}}{{\gamma }_{1}} - 2{{\eta }_{2}})c_{{20}}^{{ - 1}}\quad ({{c}_{{20}}}({{\mu }_{2}}{{\gamma }_{1}} - {{\eta }_{2}}) < 0),$Кроме того, существуют еще два положения равновесия, соответствующие точкам (3.20) при замене ${{\tilde {z}}_{1}} \leftrightarrow {{Z}_{1}}$, ${{\eta }_{1}} \leftrightarrow {{\eta }_{2}}$, устойчивые в линейном приближении в области существования, если ${{c}_{{20}}}({{\eta }_{2}} - {{\eta }_{1}}) < 0$ (кроме, может быть, точки ${{\mu }_{2}} = ({{\eta }_{1}}{{c}_{{11}}}$ – $2{{\eta }_{4}}{{c}_{{20}}})\kappa _{2}^{{ - 1}}$), и неустойчивые, при ${{c}_{{20}}}({{\eta }_{2}} - {{\eta }_{1}}) > 0$.
При ${{\mu }_{2}} = {{\hat {\mu }}_{2}}$ рассматриваем модельный гамильтониан ${{\Gamma }^{{(32)}}}$ третьего приближения (второе равенство (2.22)) с квадратичными формами согласно равенствам (2.15) и (2.14). В модельной системе имеются положения равновесия вида
Квадратичная часть гамильтонианов возмущенного движения задается выражением
Отсюда следует, что если значение ${{\mu }_{2}} = {{\hat {\mu }}_{2}}$ находится в зоне неустойчивости тривиального равновесия (см. фиг. 1в), то в области существования эти положения равновесия неустойчивы. В случае двух непересекающихся областей параметрического резонанса (как на фиг. 1г) первая пара равновесных точек устойчива в области существования при ${{c}_{{02}}}({{\xi }_{3}} - {{\xi }_{4}}) > 0$, а вторая – при ${{c}_{{02}}}({{\xi }_{3}} - {{\xi }_{4}}) < 0$.
Таким образом, в рассматриваемом случае отличные от тривиального равновесия системы могут существовать в ${{\varepsilon }^{2}}$-окрестности резонансной точки при ${{\mu }_{1}} = 0$. В случае, относящемся к фиг. 1в, описание положений равновесия и характера их устойчивостии аналогично сделанному в разд. 3.2.1 описанию, относящемуся к фиг. 1б. Для случая (фиг. 1г) двух непересекающихся областей параметрического резонанса (ширины порядка $O({{\varepsilon }^{2}})$ и $O({{\varepsilon }^{3}})$) вблизи каждой из них существуют либо две пары равновесных точек (одна устойчивая в линейном приближении и одна неустойчивая), либо ни одной, а в самой области – одна (устойчивая) пара.
3.3.3. Сценарий 3 + 3. На этапах первого и второго приближений в соответствующих модельных системах нет положений равновесия, отличных от тривиального. При рассмотрении третьего приближения в случае ${{\hat {\mu }}_{2}} \ne {{\tilde {\mu }}_{2}}$ имеем модельный гамильтониан ${{\Gamma }^{{(32)}}}$ (второе равенство (2.22)), вычисляемый с учетом соотношений (2.23) и (2.14), и два значения ${{\mu }_{2}} = {{\hat {\mu }}_{2}}$ и ${{\mu }_{2}} = {{\tilde {\mu }}_{2}}$, для которых в третьем приближении строятся две непересекающиеся области параметрического резонанса. Описание результатов аналогично предыдущему описанию, относящемуся к фиг. 1г.
Если ${{\hat {\mu }}_{2}} = {{\tilde {\mu }}_{2}}$, то для обеих областей параметрического резонанса имеем ${{\mu }_{1}} = {{\mu }_{2}}$ = 0, значения ${{\mu }_{3}}$ на граничных кривых определяются при помощи соотношения (2.14) для формы ${{K}_{{23}}}$. Модельным будет гамильтониан ${{\Gamma }^{{(33)}}}$ (второе равенство (2.24)), аналогичный по структуре гамильтониану ${{\Gamma }^{{(1)}}}$, равновесные точки которого описаны в разд. 3.1.
В таблице 1 представлена сводка результатов исследования отличных от тривиального изолированных положений равновесия рассмотренных модельных систем. Указано максимальное число равновесных точек для каждого сценария и соответствующих ему приближений.
Таблица 1
| $k$ | Сценарий | Приближения | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| 1 | 1 + 1 | 24 | – | – |
| 2 | 2 + 1 | 4 | 4 | – |
| 2 + 2 | 0 | 24 | – | |
| 3 | 3 + 1 | 4 | 0 | 4 |
| 3 + 2 | 0 | 4 | 4 | |
| 3 + 3 | 0 | 0 | 4 + 4 | |
| 0 | 0 | 24 | ||
Для сценариев $k + k$ в случаях, когда различия в уравнениях всех четырех границ областей неустойчивости выявляются в слагаемых порядка $k$, в модельной системе имеется до 24 положений равновесия, при этом существует большое число вариантов их взаимного расположения и характера их устойчивости (см. разд. 3.1). Для сценариев $k + l$ ($l < k$), а также первого варианта сценария 3 + 3 внутри каждой области неустойчивости и вблизи нее существуют от нуля до двух пар положений равновесия. Если при этом одна из областей лежит внутри другой, то все положения равновесия, относящиеся к внутренней области, неустойчивы. Для внешней области имеем внутри одну устойчивую равновесную пару, а вне ее по одну из сторон от нее устойчивую и неустойчивую пары; этот же вывод относится к каждой из двух непересекающихся областей для первого варианта сценария 3 + 3.
3.4. Периодические движения системы и их устойчивость. Вернемся к исследованию полных систем с гамильтонианами (2.18)–(2.22). В окрестности каждого положения равновесия ${{z}_{j}} = {{z}_{{j*}}}$, ${{Z}_{j}} = {{Z}_{{j*}}}$ ($j = 1,2$) (исключим из рассмотрения равновесия, являющиеся сложными особыми точками) соответствующих модельных систем полные системы являются квазилинейными с возмущениями $O(\varepsilon )$ (для случаев (2.18), (2.20) и (2.24)), $O({{\varepsilon }^{2}})$ (для случаев (2.19) и (2.22)) или $O({{\varepsilon }^{2}})$ (для случая (2.21)). Корни характеристических уравнений линеаризованных, в окрестности рассматриваемых положений равновесия, уравнений возмущенного движения либо $O(1)$ (для ${{\Gamma }^{{(1)}}}$, ${{\Gamma }^{{(22)}}}$ и ${{\Gamma }^{{(33)}}}$), либо $O(1)$ и $O(\varepsilon )$ (для ${{\Gamma }^{{(21)}}}$ и ${{\Gamma }^{{(32)}}}$), либо $O(1)$ и $O({{\varepsilon }^{2}})$ (для ${{\Gamma }^{{(31)}}}$). Возмущения же имеют по соответствующим независимым переменным периоды ${{T}_{1}}$ (для случаев (2.18), (2.19) и (2.21)), ${{T}_{2}}$ (для случаев (2.20) и (2.22)) или ${{T}_{3}}$ (для случая (2.24)), где ${{T}_{k}} = 4\pi {{\varepsilon }^{k}}$, $k = 1,2,3$.
Во всех случаях имеет место нерезонансный случай теории периодических движений Пуанкаре [13], и из каждого положения равновесия модельной системы рождается единственное, ${{T}_{k}}$-периодическое по ${{\tau }_{k}}$, периодическое решение полной системы, представляемое сходящимся рядом по целым степеням $\varepsilon $ и имеющее вид
Производя в обратной последовательности замены переменных, описанные в разд. 2, получим единственное резонансное периодическое (с периодом $4\pi $) движение исходной системы. При этом, если порождающими для данного движения являются положения равновесия системы с гамильтонианом ${{\Gamma }^{{(1)}}}$ или с гамильтонианами ${{\Gamma }^{{(21)}}}$, ${{\Gamma }^{{(22)}}}$ , то получаемое движение аналитично по ${{\varepsilon }^{{1/2}}}$ или $\varepsilon $ соответственно. Если порождающим является положение равновесия системы, определяемой одним из гамильтонианов ${{\Gamma }^{{(31)}}}$, ${{\Gamma }^{{(32)}}}$, ${{\Gamma }^{{(33)}}}$, то в исходных переменных резонансное периодическое движение представляется в виде
Периодические движения, рождающиеся из устойчивых в линейном приближении или неустойчивых положений равновесия модельных систем, также устойчивы в линейном приближении или неустойчивы. Это следует из непрерывности по малому параметру соответствующих характеристических показателей линеаризованных уравнений возмущенного движения.
4. Резонансные периодические движения спутника на слабоэллиптической орбите в окрестности цилиндрической прецессии. Рассмотрим движение динамически симметричного спутника (твердого тела) относительно центра масс в центральном ньютоновском гравитационном поле. Орбиту центра масс спутника предполагаем слабоэллиптической с эксцентриситетом $e$ ($0 < e \ll 1$). Пусть ${{\omega }_{0}}$ – среднее движение центра масс спутника по орбите, $r$ – проекция вектора угловой скорости тела в орбитальной системе координат на ось динамической симметрии ($r = {{r}_{0}} = {\text{const}}$), $A$ и $C$– его экваториальный и осевой моменты инерции. Ориентацию системы главных центральных осей инерции спутника в орбитальной системе координат определим при помощи углов Эйлера $\psi $, $\theta $, $\phi $.
Движение динамически симметричного спутника относительно центра масс на эллиптической орбите произвольного эксцентриситета описывается каноническими дифференциальными уравнениями с функцией Гамильтона [11]
(4.1)
$\begin{gathered} H = \frac{{p_{\psi }^{2}}}{{2(1 + ecos\nu {{)}^{2}}{{{\sin }}^{2}}\theta }} + \frac{{p_{\theta }^{2}}}{{2(1 + ecos\nu {{)}^{2}}}} - \frac{{cos\psi \cos \theta }}{{sin\theta }}{{p}_{\psi }} - \\ - \;\frac{{\alpha \beta {{{(1 - {{e}^{2}})}}^{{3/2}}}{{p}_{\psi }}cos\theta }}{{{{{(1 + ecos\nu )}}^{2}}{{{\sin }}^{2}}\theta }} - {{p}_{\theta }}sin\psi + \frac{{\alpha \beta {{{(1 - {{e}^{2}})}}^{{3/2}}}cos\psi }}{{sin\theta }} + \\ { + \;\frac{{{{\alpha }^{2}}{{\beta }^{2}}{{{(1 - {{e}^{2}})}}^{3}}{{{\cos }}^{2}}\theta }}{{2(1 + ecos\nu {{)}^{2}}{{{\sin }}^{2}}\theta }} + \frac{3}{2}(\alpha - 1)(1 + ecos\nu ){{{\cos }}^{2}}\theta } \\ \end{gathered} $Здесь $\nu $ – истинная аномалия, принимаемая за независимую переменную, а безразмерные параметры $\alpha $ и $\beta $ вычисляются по формулам $\alpha = C{\text{/}}A$ ($0 \leqslant \alpha \leqslant 2$) и $\beta = {{r}_{0}}{\text{/}}{{\omega }_{0}}$.
Система уравнений движения спутника допускает частное решение
соответствующее стационарному вращению – цилиндрической прецессии, для которой спутник равномерно вращается вокруг оси динамической симметрии, расположенной перпендикулярно плоскости орбиты. Вводя в функцию (4.1) возмущения по формуламВ невозмущенной ($e = 0$) задаче, отвечающей круговой орбите центра масс спутника, в плоскости параметров $\alpha $, $\beta $ имеются три точки
(4.2)
${\text{т о ч к а }}\;{{P}_{2}}{\text{:}}\quad \alpha = \frac{{17}}{{12}},\quad \beta = \frac{{24}}{{17}}\quad \left( {{{\omega }_{1}} = \frac{3}{2},\;{{\omega }_{2}} = 1} \right)$Ранее [8] в окрестности этих точек при малых значениях $e$ построены области параметрического резонанса. Опираясь на теоретические результаты, полученные в предыдущих разделах данной работы, опишем резонансные периодические движения оси симметрии спутника для значений параметров, лежащих в малых окрестностях точек (4.2).
4.1. Точка ${{P}_{1}}.$ Рассмотрим окрестность точки ${{P}_{1}}$, полагая
Первое приближение. Проведем нормализацию гамильтониана возмущенного движения в слагаемых второй и четвертой степеней относительно возмущений. Нормализованные при $e = 0$ слагаемые четвертой степени представляются в виде
(4.3)
$\begin{gathered} {{H}_{{40}}} = \frac{1}{{32}}{{(y_{1}^{2} + Y_{1}^{2})}^{2}} + \frac{1}{4}(y_{1}^{2} + Y_{1}^{2})(y_{2}^{2} + Y_{2}^{2}) + \frac{5}{{16}}{{(y_{2}^{2} + Y_{2}^{2})}^{2}} \hfill \\ \end{gathered} ,$(4.4)
$\begin{gathered} {{K}_{{21}}} = \frac{3}{{16}}{{\mu }_{1}}(y_{1}^{2} + Y_{1}^{2}) + \left( {\frac{3}{8}{{\mu }_{1}} - \frac{9}{{16}}} \right)y_{2}^{2} + \left( {\frac{3}{8}{{\mu }_{1}} + \frac{9}{{16}}} \right)Y_{2}^{2} \hfill \\ \end{gathered} $Отсюда находим точки бифуркации ${{\mu }_{1}} = \pm 3{\text{/}}2$, задающие границы внешней области параметрического резонанса, и точку ${{\mu }_{1}} = 0$, вблизи которой далее определится внутренняя область неустойчивости (фиг. 1б).
При помощи формул (4.3) и (4.4) приведем гамильтониан к виду (2.18). В соответствующей модельной системе с гамильтонианом ${{\Gamma }^{{(1)}}}$ (см. разд. 3.2.1) при ${{\mu }_{1}} < 0$ имеется семейство неустойчивых сложных особых точек вида ${{z}_{2}} = {{Z}_{2}} = 0$, $z_{1}^{2} + Z_{1}^{2} = - 3{{\mu }_{1}}$, а на интервале $ - 6 < {{\mu }_{1}} < - 3{\text{/}}2$ еще два семейства вида
Изолированными положениями равновесия системы являются точки
(4.5)
$\begin{gathered} {{Z}_{1}} = {{Z}_{2}} = {{z}_{1}} = 0,\quad z_{2}^{2} = - \frac{3}{5}{{\mu }_{1}} + \frac{9}{{10}}\quad \left( {{{\mu }_{1}} < \frac{3}{2}} \right) \hfill \\ \end{gathered} ,$(4.6)
$\begin{gathered} {{Z}_{1}} = {{z}_{1}} = {{z}_{2}} = 0,\quad Z_{2}^{2} = - \frac{3}{5}{{\mu }_{1}} - \frac{9}{{10}}\quad \left( {{{\mu }_{1}} < - \frac{3}{2}} \right) \hfill \\ \end{gathered} $Исключим из дальнейшего рассмотрения значения ${{\mu }_{1}} = 0$, ${{\mu }_{1}} = - 6$, относящиеся к решению (4.5). Используя результаты разд. 3.4 заключаем, что из каждого положения равновесия (4.5) и (4.6) модельной системы в ${{e}^{{1/2}}}$-окрестности начала координат фазового пространства рождается единственное $4\pi $-периодическое решение исходной полной системы, отвечающее периодическому движению оси симметрии спутника. В переменных ${{q}_{1}}$, ${{q}_{2}}$ эти движения определяются соотношениями
(4.7)
$\begin{gathered} {{q}_{1}} = \sqrt {2e} {{z}_{{20}}}cos\frac{\nu }{2} + O({{e}^{{3/2}}}) \\ {{q}_{2}} = - \frac{{\sqrt 2 }}{{50}}{{e}^{{3/2}}}\left[ {15({{\mu }_{1}} + 1)sin\frac{\nu }{2} + (71 + 6{{\mu }_{1}})sin\frac{3}{2}\nu } \right]{{z}_{{20}}} + O({{e}^{{5/2}}}) \\ \end{gathered} $(4.8)
$\begin{gathered} {{q}_{1}} = \sqrt {2e} {{Z}_{{20}}}sin\frac{\nu }{2} + O({{e}^{{3/2}}}) \\ {{q}_{2}} = \frac{{\sqrt 2 }}{{50}}{{e}^{{3/2}}}\left[ {15({{\mu }_{1}} - 1)cos\frac{\nu }{2} + (71 - 6{{\mu }_{1}})cos\frac{3}{2}\nu } \right]{{Z}_{{20}}} + O({{e}^{{5/2}}}) \\ \end{gathered} $Равновесные значения ${{z}_{{20}}}$ и ${{Z}_{{20}}}$ заданы последними равенствами (4.5) и (4.6) соответственно.
Замена $\nu $ на $\nu + 2\pi $ меняет знаки решений (4.7) и (4.8) на противоположные. Поэтому каждой паре положений равновесия (4.5) и (4.6) отвечает одно и то же периодическое движение спутника.
Если в соотношениях (4.7) и (4.8) отбросить слагаемые $O({{e}^{{3/2}}})$ и выше, то получаем гармонические колебания вдоль оси $O{{q}_{1}}$ с амплитудами $O({{e}^{{1/2}}})$. В случае существования обоих движений (${{\mu }_{1}} < - 3{\text{/}}2$) они имеют друг относительно друга сдвиг по фазе, равный $\pi $; при этом движение с меньшей ($\sim {\kern 1pt} {{Z}_{{20}}}$) и большей ($\sim {\kern 1pt} {{z}_{{20}}}$) по модулю амплитуде соответственно неустойчиво и устойчиво в линейном приближении.
Для строгого решения вопроса об устойчивости периодического движения (4.7) следует провести нормализацию гамильтониана в окрестности этого движения в слагаемых до четвертой степени включительно относительно возмущений. Частоты малых колебаний линеаризованных уравнений возмущенного движения вычисляются по формулам
Если величины ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ не связаны резонансным соотношением четвертого порядка, то в симплектических полярных координатах ${{\varphi }_{j}}$, ${{r}_{j}}$ ($j = 1,2$), задаваемых формулами ${{z}_{j}} = \sqrt {2{{r}_{j}}} sin{{\varphi }_{j}}$, ${{Z}_{j}} = \sqrt {2{{r}_{j}}} cos{{\varphi }_{j}}$, нормализованный гамильтониан имеет вид
(4.9)
$\begin{gathered} \begin{gathered} H = {{\Omega }_{1}}{{r}_{1}} + {{\Omega }_{2}}{{r}_{2}} + {{C}_{{20}}}r_{1}^{2} + {{C}_{{11}}}{{r}_{1}}{{r}_{2}} + {{C}_{{02}}}r_{2}^{2} + O(e) \hfill \\ \end{gathered} \\ {{C}_{{20}}} = - \frac{3}{{40}} + O(e),\quad {{C}_{{11}}} = - \frac{3}{{\sqrt {9 - 6{{\mu }_{1}}} }} + O(e),\quad {{C}_{{02}}} = - \frac{{5({{\mu }_{1}} - 6)}}{{4(2{{\mu }_{1}} - 3)}} + O(e) \\ \end{gathered} $“Поправки” $O(e)$ в выражениях для ${{C}_{{ij}}}$ постоянны, а слагаемое $O(e)$ в гамильтониане (4.9) имеет по ${{r}_{j}}$ порядок, не меньший трех, и периодично по независимой переменной ${{\tau }_{1}} = e\nu $ с периодом ${{T}_{1}} = 4\pi e$.
Для выписанных значений коэффициентов ${{C}_{{ij}}}$ имеем
В области существования данных движений для значений
Расчеты показывают, что соответствующие им резонансные слагаемые имеют порядок не меньший, чем $e$. В этих резонансных случаях можно продолжить нормализацию в членах шестой, восьмой и т.д. степеней относительно возмущений, учитывая наличие резонансов восьмого, двенадцатого и т.д. порядков при $3{{\Omega }_{1}} = {{\Omega }_{2}}$ и ${{\Omega }_{1}} = 3{{\Omega }_{2}}$, или резонансов четных порядков, начиная с шестого, при ${{\Omega }_{1}} = {{\Omega }_{2}}$.
Так как частоты ${{\Omega }_{j}}$ несоизмеримы с частотой внешнего возмущения ($\sim {\kern 1pt} {{e}^{{ - 1}}}$), то независимая переменная ${{\tau }_{1}}$ на каждом этапе будет уничтожаться. В результате получаем автономный гамильтониан, являющийся формальным первым интегралом, главная (линейная по ${{r}_{j}}$) часть которого положительно определена. В достаточно малой окрестности начала координат этот формальный интеграл также положительно определен, поэтому для рассматриваемых резонансных случаев периодическое движение (4.7) формально устойчиво.
Второе приближение. При ${{\mu }_{1}} = 0$ имеем
(4.10)
$\begin{gathered} {{K}_{{21}}} = \frac{9}{{16}} \hfill \\ \end{gathered} (Y_{2}^{2} - y_{2}^{2}),$(4.11)
$\begin{gathered} {{K}_{{22}}} = \left( {\frac{3}{{16}}{{\mu }_{2}} - \frac{{33}}{{20}}} \right)y_{1}^{2} + \left( {\frac{3}{{16}}{{\mu }_{2}} - \frac{3}{{20}}} \right)Y_{1}^{2} + \left( {\frac{3}{8}{{\mu }_{2}} - \frac{{357}}{{1280}}} \right) \hfill \\ \end{gathered} (y_{2}^{2} + Y_{2}^{2})$Точками бифуркации, задающими внутреннюю область неустойчивости (фиг. 1б), будут ${{\mu }_{2}} = 4{\text{/}}5$, ${{\mu }_{2}} = 44{\text{/}}5$.
Используя соотношения (4.10) и (4.11), составим гамильтониан (2.19) с модельной частью ${{\Gamma }^{{(21)}}}$. В соответствующей модельной системе имеются положения равновесия
В исходной полной системе этим решениям отвечают два неустойчивых, аналитических по $e$ периодических движения оси симметрии спутника, определяемые формулами
Если пренебречь слагаемыми $O({{e}^{2}})$ и выше, то эти соотношения описывают гармонические колебания вдоль оси $O{{q}_{2}}$, происходящие с амплитудами порядка $e$ и имеющие друг относительно друга (в случае существования обоих движений) сдвиг по фазе, равный $\pi $.
4.2. Точка ${{P}_{2}}$. Рассмотрим теперь окрестность точки ${{P}_{2}}$, полагая
Нормализованная форма четвертой степени ${{H}_{{40}}}$ имеет вид
(4.12)
$\begin{gathered} {{H}_{{40}}} = - \frac{1}{{48}}{{(y_{1}^{2} + Y_{1}^{2})}^{2}} + \frac{1}{{12}}(y_{2}^{2} + Y_{2}^{2})(y_{1}^{2} + Y_{1}^{2}) + \frac{1}{{32}}{{(y_{2}^{2} + Y_{2}^{2})}^{2}} \hfill \\ \end{gathered} ,$При ${{\mu }_{1}} \ne 0$ тривиальное положение равновесия устойчиво в линейном приближении. Других положений равновесия модельная система первого приближения не имеет (см. разд. 3.3.2).
Второе приближение. При ${{\mu }_{1}} = 0$ имеем ${{K}_{{21}}} = 0$, а
(4.13)
${{K}_{{22}}} = \left( {\frac{{17}}{{72}}{{\mu }_{2}} - \frac{{1965}}{{3584}}} \right)(y_{1}^{2} + Y_{1}^{2}) + \left( {\frac{{17}}{{48}}{{\mu }_{2}} + \frac{{15}}{{28}}} \right)Y_{2}^{2} + \left( {\frac{{17}}{{48}}{{\mu }_{2}} + \frac{{205}}{{252}}} \right)y_{2}^{2}$Точки бифуркации ${{\mu }_{2}}$ = –820/357 и ${{\mu }_{2}}$ = –180/119 задают границы первой области неустойчивости, а для значения ${{\mu }_{2}}$ = 17685/7616 на этапе следующего приближения будет определена вторая область неустойчивости. Две области неустойчивости не имеют общих точек, их взаимное расположение соответствует фиг. 1г.
При помощи соотношений (4.12) и (4.13) получаем гамильтониан (2.20) с модельной частью ${{\Gamma }^{{(22)}}}$. Положениями равновесия соответствующей модельной системы являются семейства неустойчивых сложных особых точек
(4.14)
$\begin{gathered} {{Z}_{1}} = {{Z}_{2}} = {{z}_{1}} = 0,\quad z_{2}^{2} = - \frac{{17}}{3}{{\mu }_{2}} - \frac{{820}}{{63}}\quad \left( {{{\mu }_{2}} < - \frac{{820}}{{357}}} \right) \hfill \\ \end{gathered} $(4.15)
$\begin{gathered} {{Z}_{1}} = {{z}_{1}} = {{z}_{2}} = 0,\quad Z_{2}^{2} = - \frac{{17}}{3}{{\mu }_{2}} - \frac{{60}}{7}\quad \left( {{{\mu }_{2}} < - \frac{{180}}{{119}}} \right) \hfill \\ \end{gathered} $Для каждого из случаев (4.14) и (4.15), исключив сложные особые точки, найдем аналитические по $e$ резонансные периодические движения исходной полной системы. Получаем неустойчивое движение вида
(4.16)
$\begin{gathered} {{q}_{1}} = {{z}_{{20}}}{{e}^{2}}\left( {\frac{4}{9} - \frac{{12}}{7}cos2\nu } \right) + O({{e}^{3}}),\quad {{q}_{2}} = e{{z}_{{20}}}sin\nu + O({{e}^{2}}) \hfill \\ \end{gathered} $(4.17)
$\begin{gathered} {{q}_{1}} = - \frac{{12}}{7}{{e}^{2}}{{Z}_{{20}}}sin2\nu + O({{e}^{3}}),\quad {{q}_{2}} = - e{{Z}_{{20}}}cos\nu + O({{e}^{2}}) \hfill \\ \end{gathered} $При учете в этих выражениях слагаемых не выше первого порядка по $e$, имеем гармонические колебания вдоль оси $O{{q}_{2}}$ с амплитудой порядка $O(e)$.
Проведем нелинейный анализ устойчивости движения (4.17). Частоты малых линейных колебаний линеаризованных уравнений возмущенного движения определяются выражениями
Нормализованный гамильтониан возмущенного движения при отсутствии резонансов четвертого порядка приводится к виду (4.9), причем
Точка ${{\mu }_{2}}$ = –3560/3927, для которой главная часть величины $\tilde {\Delta }$ обращается в нуль, не входит в область существования движения (4.17). Кроме того, в области существования коэффициенты ${{C}_{{ij}}}$ отрицательны при достаточно малых значениях $e$. Поэтому в нерезонансном случае рассматриваемое движение устойчиво для большинства начальных условий и формально устойчиво (кроме исключенной точки ${{\mu }_{2}}$ = –40725/7616).
Резонанс $2{{\Omega }_{1}} = 2{{\Omega }_{2}}$ четвертого порядка реализуется для ${{\mu }_{2}}$ ≈ –11.1922, причем резонансные слагаемые в членах четвертой степени нормализованного гамильтониана имеют порядок не меньший, чем $e$. Повторяя рассуждения, проведенные для резонансных случаев решения (4.7), заключаем, что в данном резонансном случае движение (4.17) формально устойчиво.
Третье приближение. Для значений ${{\mu }_{1}} = 0$, ${{\mu }_{2}}$ = 17685/7616 проводим нормализацию в слагаемых $O({{e}^{3}})$ в квадратичной части гамильтониана. Имеем в результате
(4.18)
$\begin{gathered} {{K}_{{22}}} + e{{K}_{{23}}} = \left( {\frac{{17}}{{48}}e{{\mu }_{3}} + \frac{{105\,535}}{{64\,512}}} \right)y_{2}^{2} + \left( {\frac{{17}}{{48}}e{{\mu }_{3}} + \frac{{9735}}{{7168}}} \right)Y_{2}^{2} + \\ + \;\frac{{17}}{{72}}e[({{\mu }_{3}} + \mu _{3}^{ + })y_{1}^{2} + ({{\mu }_{3}} + \mu _{3}^{ - })Y_{1}^{2}] \\ \mu _{3}^{ \pm } = \pm \frac{{40\,285}}{{8704}} \\ \end{gathered} $Отсюда находим, что точками бифуркации, определяющими границы второй области неустойчивости, будут ${{\mu }_{3}} = \mu _{3}^{ \pm }$.
При помощи соотношений (4.12) и (4.18) получим гамильтониан (2.22). Положения равновесия модельной системы с гамильтонианом ${{\Gamma }^{{(32)}}}$ описываются соотношениями
В области существования равновесия из первой пары устойчивы в линейном приближении, а из второй неустойчивы.
В исходных переменных первой паре соответствует устойчивое (в линейном приближении) $4\pi $-периодическое движение оси спутника вида
(4.19)
$\begin{gathered} {{q}_{1}} = - \frac{{\sqrt 6 }}{3}{{e}^{{3/2}}}{{z}_{{10}}}cos\frac{3}{2}\nu + \frac{{\sqrt 6 }}{{32}}{{e}^{{5/2}}}{{z}_{{10}}}\left( { - 6cos\frac{\nu }{2} + 11cos\frac{5}{2}\nu } \right) + O({{e}^{{7/2}}}) \\ {{q}_{2}} = \frac{{8\sqrt 6 }}{{63}}{{e}^{{5/2}}}{{z}_{{10}}}\left( { - 7sin\frac{\nu }{2} + 2sin\frac{5}{2}\nu } \right) + O({{e}^{{7/2}}}), \\ \end{gathered} $Если пренебречь слагаемыми $O({{e}^{{5/2}}})$ и выше, то данные движения – гармонические колебания вдоль оси $O{{q}_{1}}$ с амплитудой $O({{e}^{{3/2}}})$.
Продолжая нормализацию, приведем гамильтониан возмущенного движения для решения (4.19) к виду (4.9), где с точностью до слагаемых O(e) включительно
Отсюда находим
При достаточно малых значениях $e$ частоты ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ несоизмеримы и, кроме того, в области существования рассматриваемого решения справедливы соотношения ${{C}_{{20}}} > 0$ и $\tilde {\Delta } < 0$. Таким образом, для всех значений ${{\mu }_{3}}$ из области существования периодическое движение (4.19) устойчиво для большинства начальных условий и формально устойчиво.
Замечание. Исследование резонансных точек P1 и P2 и их окрестностей, проведенное при фиксированном значении одного из параметров (α), опирается на теоретические результаты, полученные в разд. 1–3. Разработанные подходы могут быть применены и при рассмотрении полной (трехмерной) окрестности резонансной точки. При этом общая теория была бы слишком громоздкой из-за большого числа вариантов взаимного расположения областей параметрического резонанса и бифуркационных поверхностей в пространстве параметров. Поэтому такие рассмотрения лучше проводить для конкретной задачи, что в качестве примера будет выполнено для третьей резонансной точки P3.
4.3. Точка ${{P}_{3}}$. Рассмотрим окрестность точки ${{P}_{3}}$, полагая
(4.20)
$\begin{gathered} \alpha = 1 + e{{\nu }_{1}},\quad \beta = \frac{3}{2} + e{{\mu }_{1}} + {{e}^{2}}{{\mu }_{2}}\quad ({{\nu }_{1}} \ne 0) \hfill \\ \end{gathered} $Нормализация гамильтониана возмущенного движения в слагаемых четвертой степени при $e = 0$ и квадратичной части в слагаемых порядка $O(e)$ дает
(4.21)
${{K}_{{40}}} = \frac{1}{8}{{(y_{2}^{2} + Y_{2}^{2})}^{2}},\quad {{K}_{{21}}} = \frac{{{{\nu }_{1}}}}{2}(y_{1}^{2} + Y_{1}^{2}) + \frac{1}{4}(2{{\mu }_{1}} + 5{{\nu }_{1}})(y_{2}^{2} + Y_{2}^{2})$При ${{\nu }_{1}} \ne - (2{\text{/}}5){{\mu }_{1}}$ тривиальное положение равновесия системы устойчиво в линейном приближении. В модельной системе первого приближения других положений равновесия нет.
В случае ${{\nu }_{1}} = - (2{\text{/}}5){{\mu }_{1}}$ проведем нормализацию квадратичной части гамильтониана в слагаемых порядка до $O({{e}^{2}})$ включительно, получая в итоге
(4.22)
$\begin{gathered} {{{K}_{{21}}} + e{{K}_{{22}}} = \left( { - \frac{{{{\mu }_{1}}}}{5} + e\frac{{3\mu _{1}^{2}}}{{25}}} \right)(y_{1}^{2} + Y_{1}^{2}) + e\frac{{{{\mu }_{2}} - \mu _{2}^{ + }}}{2}y_{2}^{2} + e\frac{{{{\mu }_{2}} - \mu _{2}^{ - }}}{2}Y_{2}^{2}} \\ \mu _{2}^{ \pm } = \pm \frac{7}{5}{{\mu }_{1}} + \frac{{22}}{{25}}\mu _{1}^{2} \\ \end{gathered} $Отсюда следует, что на границах области параметрического резонанса
При помощи соотношений (4.21) и (4.22) составим гамильтониан (2.19) с модельной частью ${{\Gamma }^{{(21)}}}$. При выполнении условий ${{\mu }_{2}} < \mu _{2}^{ + }$ и ${{\mu }_{2}} < \mu _{2}^{ - }$ в отвечающей ему модельной системе имеются положения равновесия, для которых ${{z}_{1}} = {{Z}_{1}} = 0$, а
(4.24)
${{Z}_{2}} = 0,\quad z_{2}^{2} = 2(\mu _{2}^{ + } - {{\mu }_{2}})\quad {\text{и }}\quad {{z}_{2}} = 0,{\text{ }}Z_{2}^{2} = 2(\mu _{2}^{ - } - {{\mu }_{2}})$В исходных переменных каждой паре точек (4.24) отвечает аналитическое по $e$, $4\pi $-периодическое по $\nu $ движение, описываемое с точностью до слагаемых $O({{e}^{2}})$ включительно соотношениями
(4.25)
$\begin{gathered} {{q}_{1}} = - \frac{{\sqrt 6 e{{z}_{{20}}}}}{3}cos\frac{\nu }{2} - \frac{{\sqrt 6 {{e}^{2}}{{z}_{{20}}}}}{{18}}\left[ {(8{{\mu }_{1}} + 9)cos\frac{\nu }{2} - 9cos\frac{3}{2}\nu } \right] \\ {{q}_{2}} = - \frac{{\sqrt 6 e{{z}_{{20}}}}}{3}sin\frac{\nu }{2} + \frac{{\sqrt 6 {{e}^{2}}{{z}_{{20}}}}}{{90}}\left[ {(32{{\mu }_{1}} + 45)sin\frac{\nu }{2} + 45sin\frac{3}{2}\nu } \right] \\ \end{gathered} $(4.26)
$\begin{gathered} {{q}_{1}} = - \frac{{\sqrt 6 e{{Z}_{{20}}}}}{3}sin\frac{\nu }{2} - \frac{{\sqrt 6 {{e}^{2}}{{Z}_{{20}}}}}{{18}}\left[ {(8{{\mu }_{1}} - 9)sin\frac{\nu }{2} - 9sin\frac{3}{2}\nu } \right] \\ {{q}_{2}} = \frac{{\sqrt 6 e{{Z}_{{20}}}}}{3}cos\frac{\nu }{2} - \frac{{\sqrt 6 {{e}^{2}}{{Z}_{{20}}}}}{{90}}\left[ {(32{{\mu }_{1}} - 45)cos\frac{\nu }{2} + 45cos\frac{3}{2}\nu } \right] \\ \end{gathered} $Если в этих соотношениях пренебречь слагаемыми $O({{e}^{2}})$ и выше, то в плоскости величин ${{q}_{1}}$, ${{q}_{2}}$ имеем движения по окружностям с радиусами $O(e)$, происходящие в направлении против часовой стрелки. В областях существования обоих движений их фазы различаются на $\pi $.
Выводы об устойчивости (в линейном приближении) и неустойчивости найденных периодических движений совпадают, в соответствующих областях, с аналогичными выводами для порождающих их положений равновесия модельной системы.
Для геометрической интерпретации полученных результатов перепишем уравнения границ области параметрического резонанса (в данном приближении) в эквивалентном виде, с учетом соотношений (4.20) и (4.23):
Верхний и нижний знаки отвечают аналогичным знакам в условии (4.23).
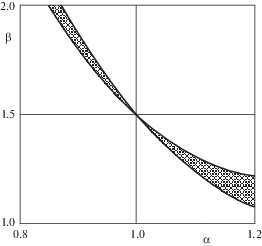
На фиг. 3 область параметрического резонанса в окрестности точки ${{P}_{3}}$ построена в плоскости параметров $\alpha $, $\beta $ для значения $e = 0.15$. В части плоскости, расположенной выше и правее этой области, в окрестности невозмущенного движения (цилиндрической прецессии) нет периодических движений спутника. Внутри части области параметрического резонанса, задаваемой условием $\alpha < 1$, существует и устойчиво в линейном приближении периодическое движение (4.25). В малой ($O({{e}^{2}})$) окрестности, расположенной ниже и левее этой части области неустойчивости, существуют оба периодических движения (4.25) и (4.26), первое из которых остается устойчивым в линейном приближении, а второе неустойчиво. В случае $\alpha > 1$ при описании области существования и результатов устойчивости движения (4.25) и (4.26) следует поменять местами.
Работа выполнена в рамках государственного задания (3.3858.2017/4.6).
Список литературы
Якубович В.А., Старжинский В.М. Параметрический резонанс в линейных системах. М.: Наука, 1987. 328 с.
Маркеев А.П. О поведении нелинейной гамильтоновой системы с одной степенью свободы на границе области параметрического резонанса // ПММ. 1995. Т. 59. Вып. 4. С. 569–580.
Маркеев А.П. Параметрический резонанс и нелинейные колебания тяжелого твердого тела в окрестности его плоских вращений // Изв. РАН. МТТ. 1995. № 5. С. 34–44.
Холостова О.В. Параметрический резонанс в задаче о нелинейных колебаниях спутника на эллиптической орбите // Космич. исслед. 1996. Т. 3. Вып. 3. С. 312–316.
Холостова О.В. О периодических движениях неавтономной гамильтоновой системы с двумя степенями свободы при параметрическом резонансе основного типа // ПММ. 2002. Т. 66. Вып. 4. С. 540–551.
Маркеев А.П. О кратном резонансе в линейных системах Гамильтона // ДАН. 2005. Т. 402. № 3. С. 539–343.
Маркеев А.П. Об одном особом случае параметрического резонанса в задачах небесной механики // Письма в Астрон. ж. 2005. Т. 31. Вып. 5. С. 388–394.
Маркеев А.П. О кратном параметрическом резонансе в системах Гамильтона // ПММ. 2006. Т. 70. Вып. 2. С. 200–220.
Маркеев А.П. Линейные гамильтоновы системы и некоторые задачи об устойчивости движения спутника относительно центра масс. М.; Ижевск: НИЦ “Регул. и хаотич. динамика”, Ин-т компьют. исследований, 2009. 396 с.
Холостова О.В. О периодических движениях неавтономной гамильтоновой системы в одном случае кратного параметрического резонанса // Нелин. дин. 2017. Т. 13. № 4. С. 477–504.
Маркеев А.П. О вращательном движении динамически симметричного спутника на эллиптической орбите // Космич. исслед. 1967. Т. 5. Вып. 4. С. 530–539.
Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука, 1978. 312 с.
Малкин И.Г. Некоторые задачи теории нелинейных колебаний. М.: Гостехиздат, 1956. 492 с.
Glimm J. Formal stability of Hamiltonian systems // Comm. Pure Appl. Math. 1964. № 4. P. 509–526.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика