1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 3, 2019

Прикладная математика и механика, 2019, T. 83, № 3, стр. 354-369

НЕУСТОЙЧИВОСТЬ СТАЦИОНАРНЫХ ТЕЧЕНИЙ В КАНАЛАХ ПЕРЕМЕННОЙ ПЛОЩАДИ ПОПЕРЕЧНОГО СЕЧЕНИЯ С ДЕТОНАЦИОННОЙ ВОЛНОЙ ЧЕПМЕНА–ЖУГЕ

А. Н. Крайко 1, 2, *

1 Центральный институт авиационного моторостроения им. П.И. Баранова
Москва, Россия

2 Московский физико-технический институт
Долгопрудный, Россия

* E-mail: akraiko@ciam.ru

Поступила в редакцию 11.03.2019
После доработки 10.04.2019
Принята к публикации 24.04.2019

Полный текст (PDF)

Аннотация

Исследована устойчивость стационарных течений идеального (невязкого и нетеплопроводного) газа в каналах переменной площади поперечного сечения, в расширяющейся части которых располагается (“стоит”) детонационная волна Чепмена–Жуге (ДВCJ). Стационарные и нестационарные течения описываются уравнениями одномерного приближения с детонационной волной – плоской, нормальной оси канала поверхностью разрыва. Горючая смесь до детонационной волны и продукты сгорания за ней – совершенные газы с постоянными теплоемкостями, которые, как и аддитивные постоянные в выражениях для внутренней энергии и энтальпии, разные до и после волны. Так как число Маха за ДВCJ равно единице, то в стационарном потоке она может стоять только в расширяющейся части канала. При этом в зависимости от условий на выходе из канала поток за ней может быть и сверх-, и дозвуковым. В первом случае начальное возмущение может прийти на ДВCJ только слева (газ течет слева направо), во втором – с обеих сторон. При исследовании устойчивости сначала предполагается, что и после начального возмущения детонационная волна, слегка сместившись, продолжает оставаться ДВCJ. При этом анализ устойчивости сводится к вычислению производной числа Маха ДВCJ по числу Маха стационарного потока перед волной. В принятой постановке величина этой производной всегда такая, что рассматриваемое течение неустойчиво. На самом деле, малые возмущения ДВCJ делают ее слегка пересжатой. Однако и с учетом этого стационарное течение с ДВCJ в расширяющемся канале всегда неустойчиво.

Ключевые слова: устойчивость течения в канале переменной площади, детонационная волна Чепмена–Жуге, слегка пересжатая детонационная волна, инварианты линеаризованных уравнений, особенности линеаризованных соотношений для детонационной волны Чепмена–Жуге

Введение. Согласно модели Зельдовича–Неймана–Дёринга (ЗНД-модели) [1–3] структура детонационной волны включает интенсивную ударную волну (поверхность разрыва) и примыкающую к ней “зону реакций” конечной ширины. Действительная толщина ударной волны – несколько длин свободного пробега при на порядки более протяженной зоне реакций. Химические реакции, скорость которых сильно зависит от температуры, начинаются благодаря нагреву горючей смеси ударной волной и заканчиваются достижением продуктами сгорания термодинамического равновесия. Получающиеся в рамках ЗНД-модели детонационные адиабаты полностью определяются термодинамикой смеси в исходном (холодном, метастабильном) и в конечных равновесных состояниях, не завися от кинетики процесса горения. На детонационных адиабатах особый интерес представляют точки, которые отвечают детонационным волнам, названным по именам их открывателей [4, 5] детонационными волнами Чепмена–Жуге (ДВCJ). Важная особенность ДВCJ – равная звуковой нормальная к волне скорость газа за ней [6–8]. Благодаря этому ДВCJ оказывается самоподдерживающейся, ибо волны разрежения, идущие от “инициатора детонации”, не могут ее догнать и ослабить.

Экспериментально обнаруженные в середине ХХ века случаи развала ожидаемых в рамках ЗНД-модели стационарных структур детонационных волн вызвали поток исследований их “структурной” устойчивости. В соответствующих, как правило, одномерных моделях [9–20] реальная кинетика заменяется одной реакцией с некоторой “энергией активации” и последующим мгновенным или протяженным по времени тепловыделением. В таком приближении условие структурной устойчивости приводит к ограничениям на энергию активации. В настоящее время выяснение одномерной структурной устойчивости ДВCJ в любой смеси при известной кинетике ее горения (реакциях, их энергиях и константах скоростей) возможно в процессе численного решения сравнительно простой нестационарной задачи о неравновесном одномерном течении невязкого и нетеплопроводного газа. Если такое решение выходит на стационарную структуру, то ДВCJ в рассматриваемой горючей смеси структурно устойчива. Если же выхода на стационарную структуру не происходит, то в такой смеси ДВCJ структурно неустойчива.

Наряду со структурной устойчивостью ДВCJ представляет интерес устойчивость стационарных течений в каналах переменной площади со структурно устойчивой и поэтому рассматриваемой как поверхность разрыва ДВCJ. Интерес к таким течениям – следствие их привлечения (см., например, [21–25]) в качестве элемента прямоточных двигателей с горением в стационарной ДВCJ. Стационарная ДВCJ располагается на входе двигателя летательного аппарата, летящего со скоростью ДВCJ [21, 22]; она стоит в камере сгорания двигателя аппарата, летящего со скоростью, превышающей скорость ДВCJ [23, 24]; рассмотрены оба варианта [25]. При этом отмечено [23]: “Устойчивость таких режимов требует самостоятельного исследования. Вероятно, она может быть обеспечена лишь при специальном регулировании”. При допущении, что сдвинутая по потоку волна остается самоподдерживающейся, расчеты, показали [24], что в рассматриваемых там примерах течения с ДВCJ в расширяющихся каналах неустойчивы. Ниже анализ устойчивости стационарных течений с ДВCJ в расширяющемся канале выполнен сначала с таким же допущением, а затем в более полной нестационарной постановке.

1. Формулы и уравнения одномерного приближения для течения с детонационной волной в канале переменной площади. Пусть невязкий и нетеплопроводный газ течет слева направо по каналу переменной площади поперечного сечения F = F(x), где х – расстояние, отсчитываемое далее от стационарного положения ДВCJ. Если t – время, u, ρ, p, e и h = e + p/ρ – скорость, плотность, давление, удельные внутренняя энергия и энтальпия газа, то в одномерном приближении нестационарное течение в канале удовлетворяет дифференциальным уравнениям

(1.1)
$\begin{gathered} \frac{{\partial (\rho F)}}{{\partial t}} + \frac{{\partial (\rho uF)}}{{\partial x}} = 0,\quad \frac{{\partial (\rho uF)}}{{\partial t}} + \frac{{\partial [(p + \rho {{u}^{2}})F]}}{{\partial x}} = pF{\kern 1pt} {\text{'}} \\ \frac{{\partial [\rho F(e + {{u}^{2}}{\text{/}}2)]}}{{\partial t}} + \frac{{\partial [\rho uF(h + {{u}^{2}}{\text{/}}2)]}}{{\partial x}} = 0 \\ \end{gathered} $
и соотношениям на детонационной волне

(1.2)
$\begin{gathered} {{\rho }_{1}}({{u}_{1}} - D) = {{\rho }_{2}}({{u}_{2}} - D),\quad {{p}_{1}} + {{\rho }_{1}}({{u}_{1}} - D)({{u}_{1}} - {{u}_{2}}) = {{p}_{2}} \\ 2{{h}_{1}} + {{({{u}_{1}} - D)}^{2}} = 2{{h}_{2}} + {{({{u}_{2}} - D)}^{2}} \\ \end{gathered} $

Здесь F ' = dF(x)/dx, детонационная волна – плоская поверхность разрыва, нормальная оси х, D – ее скорость, а индекс 1 (2) метит параметры слева (справа) от разрыва.

В стационарном течении детонационная волна покоится (D = 0), а обыкновенные дифференциальные уравнения, получающиеся из системы (1.1), интегрируются и дают три конечных соотношения [6–8]

(1.3)
$\rho uF = G = const,\quad 2h + {{u}^{2}} = 2H = const,\quad s = {{s}_{{1,2}}} = const,\quad {{s}_{2}} \ne {{s}_{1}}$

Постоянные G (расход) и H (полная энтальпия) в них на детонационной волне не изменяются в отличие от растущей удельной энтропии s и изменяющейся любой ее функции (“энтропийной функции”). Независимо от этого в силу интегралов (1.3) произведение ρu (“плотность тока”) – функция числа Маха М = u/a, где a – скорость звука, с максимумом при М = 1. Поэтому согласно первому равенству (1.3) стационарная ДВCJ, за которой М2 = 1, не может располагаться в сужающемся канале. Второе равенство (1.3) – условие сохранения полной энтальпии выполняется и на стационарных ударных волнах, в том числе, на косых скачках.

При стационарной ДВCJ в некотором сечении расширяющегося участка канала для реализации сверхзвукового течения за ней давление в среде, в которую происходит истечение (“внешнее давление” ре), должно быть ниже некоторого. Напротив, при ре, большем давления р2 за ДВCJ, к ней может примыкать дозвуковой поток. Разумеется, для реализации любой из перечисленных возможностей каждое стационарное течение должно быть устойчивым.

Для дальнейшего уравнения (1.1) запишем в характеристической форме

(1.4)
$\begin{gathered} \rho a\left[ {\frac{{\partial u}}{{\partial t}} + (u + a)\frac{{\partial u}}{{\partial x}}} \right] + \frac{{\partial p}}{{\partial t}} + (u + a)\frac{{\partial p}}{{\partial x}} + \rho u{{a}^{2}}f = 0,\quad f = \frac{{F{\kern 1pt} {\text{'}}}}{F} \\ \rho a\left[ {\frac{{\partial u}}{{\partial t}} + (u - a)\frac{{\partial u}}{{\partial x}}} \right] - \frac{{\partial p}}{{\partial t}} - (u - a)\frac{{\partial p}}{{\partial x}} - \rho u{{a}^{2}}f = 0 \\ \frac{{\partial p}}{{\partial t}} + u\frac{{\partial p}}{{\partial x}} - {{a}^{2}}\left( {\frac{{\partial \rho }}{{\partial t}} + u\frac{{\partial \rho }}{{\partial x}}} \right) = 0 \\ \end{gathered} $

Первое и второе из этих уравнений определяют изменение инвариантов Римана (для изэнтропических течений), из-за переменности площади поперечного сечения канала, вдоль С+- и С–-характеристик, а третье – следствие сохранения энтропии на траекториях частиц (С0-характеристиках).

Для замыкания уравнений и условий (1.1)–(1.4) примем далее, что горючая смесь до детонационной волны (k = 1) и продукты сгорания за ней (k = 2) – совершенные газы с постоянными, но разными теплоемкостями и иными константами, т.е.

(1.5)
$\begin{gathered} p\omega = {{R}_{k}}T,\quad {{R}_{k}} = {{c}_{{pk}}} - {{c}_{{vk}}} = \frac{{{{\gamma }_{k}} - 1}}{{{{\gamma }_{k}}}}{{c}_{{pk}}},\quad {{\gamma }_{k}} = \frac{{{{c}_{{pk}}}}}{{{{c}_{{vk}}}}},\quad {{a}^{2}} = {{\gamma }_{k}}p\omega \\ h = \frac{{{{a}^{2}}}}{{{{\gamma }_{k}} - 1}} + {{q}_{k}},\quad {{q}_{1}} = q,\quad {{q}_{2}} = 0,\quad s(p,\rho ) = \frac{p}{{{{\rho }^{{{{\gamma }_{k}}}}}}} \\ \end{gathered} $

Здесь ω = 1/ρ – удельный объем, Т – температура, R – газовая постоянная, cp и ${{c}_{{v}}}$ – удельные теплоемкости, γ – показатель адиабаты и q – удельная теплота сгорания горючей смеси. Для таких газов получающееся из условий (1.2) уравнение детонационной адиабаты принимает вид

(1.6)
$\frac{{{{\gamma }_{2}} + 1}}{{{{\gamma }_{2}} - 1}}\frac{{{{p}_{2}}{{\omega }_{2}}}}{{{{p}_{1}}{{\omega }_{1}}}} - \frac{{{{\gamma }_{1}} + 1}}{{{{\gamma }_{1}} - 1}} - \frac{{{{p}_{2}}}}{{{{p}_{1}}}} + \frac{{{{\omega }_{2}}}}{{{{\omega }_{1}}}} = \frac{{2q}}{{{{p}_{1}}{{\omega }_{1}}}}$

Если для уравнений состояния (1.5) к соотношениям (1.2), записанным для неподвижной детонационной волны (D = 0), добавить равенство

$u_{2}^{2} = a_{2}^{2} = {{\gamma }_{2}}{{p}_{2}}{{\omega }_{2}},$
то оно из всех точек адиабаты (1.6) определит две “точки Жуге”. Верхняя (в плоскости ωp) из них с p2 > p1 отвечает ДВCJ, а нижняя с p2 < p1 – фронту дефлаграции. Проделав необходимые выкладки, для ДВCJ, следуя известному подходу [6], найдем

$M_{J}^{2} \equiv \frac{{u_{1}^{2}}}{{a_{1}^{2}}} = \frac{{\chi + \sqrt {{{\chi }^{2}} - {{{({{\gamma }_{1}} - 1)}}^{2}}\gamma _{2}^{2}} }}{{{{\gamma }_{1}}({{\gamma }_{1}} - 1)}} = 1 + \frac{{\gamma + 1}}{\psi }{{q}^{o}} + \sqrt {{{{\left( {1 + \frac{{\gamma + 1}}{\psi }{{q}^{o}}} \right)}}^{2}} - 1} $
(1.7)
$\begin{gathered} \chi = {{\gamma }_{1}}\frac{{\gamma _{2}^{2} - 1}}{\psi }{{q}^{o}} - {{\gamma }_{1}} + \gamma _{2}^{2},\quad \psi = \frac{{{{T}_{1}}}}{{{{T}_{0}}}},\quad {{q}^{o}} = \frac{q}{{{{c}_{{p1}}}{{T}_{0}}}} \\ \frac{{{{p}_{2}}}}{{{{p}_{1}}}} = \frac{{1 + {{\gamma }_{1}}M_{J}^{2}}}{{{{\gamma }_{2}} + 1}} = \frac{{1 + \gamma M_{J}^{2}}}{{\gamma + 1}} \\ \end{gathered} $
$\frac{1}{{{{{\text{M}}}_{{\text{J}}}}}}\frac{{{{a}_{2}}}}{{{{a}_{1}}}} = \frac{{{{\omega }_{2}}}}{{{{\omega }_{1}}}} = \frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = \frac{{{{\gamma }_{2}}(1 + {{\gamma }_{1}}M_{J}^{2})}}{{{{\gamma }_{1}}({{\gamma }_{2}} + 1)M_{J}^{2}}} = \frac{{1 + \gamma M_{J}^{2}}}{{(\gamma + 1)M_{J}^{2}}}$

Здесь и далее Т0 – температура, фиксированная в данной задаче, а вторые выражения (последние звенья в цепочках равенств) справедливы для неизменных показателей адиабаты: γ2 = γ1 = γ.

Согласно формулам (1.7), при qo → ∞ число Маха МJ, а вместе с ним отношения давлений p2/p1, скоростей звука а2/a1 и температур T2/T1 также растут неограниченно. В то же время, как и для ударных волн, отношения плотностей, удельных объемов и скоростей стремятся к конечным пределам

(1.8)
$\frac{{{{u}_{2}}}}{{{{u}_{1}}}} = \frac{{{{\omega }_{2}}}}{{{{\omega }_{1}}}} = \frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}} = \frac{{{{\gamma }_{2}}}}{{{{\gamma }_{2}} + 1}} > \frac{{{{\gamma }_{2}} - 1}}{{{{\gamma }_{2}} + 1}}$

Хотя реальные значения qo не очень велики, эти формулы полезны для оценок входящих в них параметров. Так, согласно соотношению (1.8), удельный объем и скорость могут уменьшиться при переходе через ДВCJ чуть меньше чем вдвое. С другой стороны, так как подкоренное выражение в формуле для $M_{J}^{2}$ не может быть отрицательным, то при γ2 < γ1 возникает ограничение

${{q}^{o}} \geqslant \frac{{{{\gamma }_{1}} - {{\gamma }_{2}}}}{{{{\gamma }_{1}}({{\gamma }_{2}} - 1)}}$

В действительности, однако, различие показателей адиабаты связано с изменением химического состава при сгорании горючей смеси. Поэтому с уменьшением qo уменьшается разность γ1 – γ2 и происходит естественный переход в отношениях (1.7) к последнему равенству в цепочке равенств для $M_{J}^{2}$ без такого ограничения.

2. Неустойчивость стационарного течения с детонационной волной Чепмена–Жуге в расширяющемся канале. Сжигание горючей смеси в стационарной ДВCJ, стоящей в некотором сечении расширяющегося участка канала, интересно для ряда приложений. Построение таких течений реализуется в рамках конечных уравнений (1.3), описывающих стационарные течения в каналах переменной площади, уравнений состояния (1.5) и соотношений (1.6) и (1.7), выполняющихся на ДВCJ.

При числе Маха полета летательного апарата М0 > MJ поток в канале воздухозаборника, оставаясь сверхзвуковым, сначала тормозится до Mm < МJ в минимальном сечении канала, а затем разгоняется в его расширяющейся части. При разгоне число Маха потока М1 растет, его температура Т1 в силу условия сохранения полной энтальпии уменьшается, а обратная ей величина

(2.1)
$\frac{1}{\psi } \equiv \frac{{{{T}_{0}}}}{{{{T}_{1}}}} = \frac{{2 + ({{\gamma }_{1}} - 1)M_{1}^{2}}}{{2 + ({{\gamma }_{1}} - 1)M_{0}^{2}}}$
увеличивается. Поэтому согласно соотношениям (1.7), МJ также растет, но, как показано ниже, медленнее, чем М1 и в некотором сечении расширяющегося канала выполнится равенство МJ = М1. В такое сечение можно поставить ДВCJ.

Правда, уже в воздухозаборнике к воздуху добавляется топливо, неучтенное в равенстве (2.1). До начала горения учет такой добавки сводится к некоторой коррекции входящих в это равенство величин. Обычно расход топлива много меньше расхода воздуха, и это может лишь слегка сказаться на результатах расчетов.

Сказанное выше поясняет рис. 1 со схемами двух прямоточных двигателей с горением в ДВCJ и с примыкающими к ней соответственно сверхзвуковым и дозвуковым потоками. На рис. 1а цифры 1 и 2 метят потоки до и после детонационной волны, контур расширяющегося сопла первого двигателя – сплошная кривая cf, а пунктирная ломанная cf ° – контур дозвуковой части и сопла Лаваля (со скругляющей вблизи минимального сечения окружностью) второго двигателя. Горизонтальный отрезок сg показывает, что в рассматриваемом приближении минимальная площадь сопла Лаваля равна площади канала в сечении стационарного положения ДВCJ.

Рис. 1. Схемы двух прямоточных двигателей с горением в стационарной детонационной волне Чепмена–Жуге (а) и распределения чисел Маха в их воздухозаборнике, детонационных камерах и соплах (б).

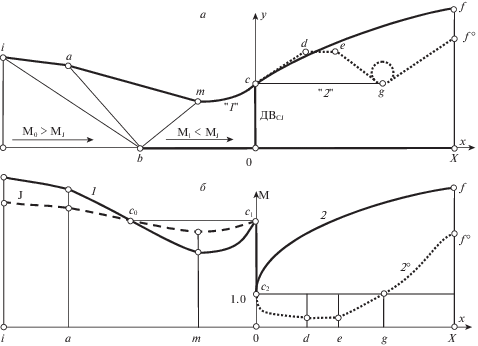
На рис. 1б сплошная кривая 1 и штриховая J дают M1 = M1(x) и MJ = MJ(x) до детонационной волны, сплошная кривая 2 и пунктирная 2° дают распределения чисел Маха для двух двигателей за ДВCJ, а вертикальный отрезок с1с2 – детонационную волну. Так как за ДВCJ число Маха М2 = 1 при производной F ' > 0, то при х = +0 касательные к кривым 2 и 2° вертикальны. Горизонтальный отрезок c0c1 определяет точку с0, в которой, как и в точке с1, MJ = M1 и скорость ДВCJ равна скорости потока перед ней, однако такое положение волны невозможно из-за сужения канала. Везде, включая трехскачковый воздухозаборник, перечисленные кривые отвечают решениям уравнений одномерного приближения с единственным разрывом – ДВCJ.

Анализ устойчивости стационарного течения с ДВCJ начнем, допустив, следуя указанному ранее подходу [24], что при смещении х1 = х1(t) ДВCJ от стационарного положения х1 = 0 она остается самоподдерживающейся. При сделанном допущении справедливы формулы (1.7) и (2.1) и их следствие $M_{J}^{2}$ = $M_{J}^{2}(M_{1}^{2})$. Учтя, что $M_{J}^{2}$ = $M_{1}^{2}$ при х1 = 0, найдем

${{M}^{2}} \approx M_{1}^{2} + \frac{{dM_{1}^{2}}}{{dx}}{{x}_{1}},\quad M_{J}^{2} \approx M_{1}^{2} + \frac{{dM_{J}^{2}}}{{dM_{1}^{2}}}\frac{{dM_{1}^{2}}}{{dx}}{{x}_{1}}$
$\frac{{d{{x}_{1}}}}{{dt}} = a(M - {{M}_{J}}) = a\frac{{{{M}^{2}} - M_{J}^{2}}}{{M + {{M}_{J}}}} \approx \lambda {{x}_{1}},\quad \lambda = \frac{{{{a}_{1}}}}{{2{{M}_{1}}}}{{\left( {1 - \frac{{dM_{J}^{2}}}{{dM_{1}^{2}}}} \right)}_{1}}\frac{{dM_{1}^{2}}}{{dx}}$

При сверхзвуковом течении в расширяющемся канале число Маха – растущая функция х и знак λ определяется знаком разности в скобке, т.е. величиной стоящей в ней производной. Проделав необходимые выкладки, получим

(2.2)
$\begin{gathered} \frac{{dM_{J}^{2}}}{{dM_{1}^{2}}} = \frac{{({{\gamma }_{1}} - 1)M_{J}^{2}}}{{2 + ({{\gamma }_{1}} - 1)M_{J}^{2}}}{{\left[ {1 + 2\frac{{\gamma _{2}^{2} - {{\gamma }_{1}}}}{{\gamma _{2}^{2} - 1}}\left( {\frac{\psi }{{{{\gamma }_{1}}{{q}^{o}}}}} \right) + \frac{{\gamma _{2}^{2} - \gamma _{1}^{2}}}{{\gamma _{2}^{2} - 1}}{{{\left( {\frac{\psi }{{{{\gamma }_{1}}{{q}^{o}}}}} \right)}}^{2}}} \right]}^{{ - 1/2}}} = \\ = \frac{{(\gamma - 1)M_{J}^{2}}}{{[2 + (\gamma - 1)M_{J}^{2}]\sqrt {1 + 2\psi {\text{/}}[(\gamma + 1){{q}^{o}}]} }} < 1, \\ \end{gathered} $
где, как и ранее, второе выражение отвечает γ2 = γ1 = γ.

Согласно равенствам (2.2), при одинаковых показателях адиабаты указанная производная меньше единицы, λ > 0 и стационарное течение с ДВCJ неустойчиво. При разных показателях адиабаты исследование усложняется, однако и в этом случае анализ выражения в квадратной скобке в формуле (2.2) показывает, что при реальных значениях входящих в нее параметров ситуация не изменяется, т.е. положительная производная $dM_{J}^{2}{\text{/}}dM_{1}^{2}$ < 1. Кстати, именно это неравенство учтено при построении рис. 1б. На нем и при разгоне, и при торможении сверхзвукового потока MJ изменяется медленнее, чем М1.

Допущение возмущенной ДВCJ оставаться самоподдерживающейся предполагает бесконечно медленное изменение исследуемого течения, включая нулевую скорость сместившейся от своего стационарного положения детонационной волны. Однако при найденных положительных λ ее скорость λх1 равна нулю только при х1 = 0. Если же х1 ≠ 0, то скорость волны конечна, вопреки допущению о бесконечно медленной эволюции течения. С другой стороны, возмущенная ДВCJ, став пересжатой, будет при тех же параметрах набегающего потока иметь большую скорость, чем ДВCJ. При смещении ДВCJ вправо это может изменить вывод о неустойчивости исследуемого течения. Напротив, при смещении ДВCJ влево большая скорость пересжатой волны подтвердит правильность такого вывода, а этого более чем достаточно. Правда, тут же возникает вопрос о возмущениях, приходящих на пересжатую волну справа и весьма важных в похожих задачах с ударной волной [26–32]. В связи этим ниже анализ устойчивости стационарных течений с ДВCJ в расширяющемся канале проведен в более полной нестационарной постановке.

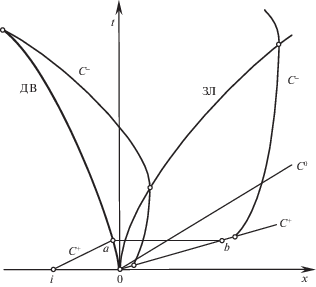
При произвольном малом возмущении ДВCJ становится пересжатой с числом Маха за ней М2 чуть меньше единицы. Для варианта со сверхзвуковым потоком за стационарной ДВCJ возможный сценарий эволюции течения поясняет xt-диаграмма рис. 2. Начальные возмущения на ней приходят на детонационную волну (ДВ) только слева. В силу этого, пусть при t = 0 поток возмущен лишь на малом отрезке i0 оси х, причем так, что ДВ, став слегка пересжатой, начала двигаться влево. При t = ta отрезок ia С+-характеристики пересечется с ДВ, а течение станет возмущенным на отрезке ab, ограниченном справа С+-характеристикой, пришедшей из начала координат x = t = 0. Эта же характеристика ограничивает возмущенное течение справа, по крайней мере, до ее прихода к выходу из канала x = X. Слева возмущенное течение ограничивает движущаяся ДВ.

Рис. 2. xt-диаграмма течения за возмущенной (слегка пересжатой) детонационной волной Чепмена–Жуге.

При t > 0 к слегка пересжатой ДВ станет примыкать вначале небольшая дозвуковая область, ограниченная снизу по потоку траекторией “звуковой линии” (ЗЛ), на которой u = a. Справа от ЗЛ течение сверхзвуковое и идущие против потока С–-характеристики сносятся им вправо. На ЗЛ их скорость равна нулю (С–-характеристики “останавливаются” с вертикальной касательной на xt-диаграмме), а после пересечения со ЗЛ С–-характеристики начинают движение влево вдогонку ДВ. Из сказанного и из рис. 2 видно, что С–-характеристики возмущенного течения – сильно искривленные кривые. Хотя все характеристики невозмущенных стационарных потоков до и за ДВCJ также сильно искривлены (правда, без изменения направления движения), их форма определяется стационарным решением, т.е. известна заранее. При анализе устойчивости в задачах, рассмотренных ранее [26–34], все характеристики возмущенных и невозмущенных течений совпадают и потому также известны заранее.

В задаче с xt-диаграммой рис. 2 ситуация намного сложнее, чем в [26–34], не только из-за отличия возмущенных и невозмущенных характеристик, но и потому, что теперь возмущенное течение в целом не близко ни к какому известному. Исключение – значения параметров в той части примыкающей к ДВ дозвуковой области, где они близки к величинам за ДВCJ. Приписав последним величинам звездочку и взяв за масштабы скорости, плотности и давления ${{a}_{*}}$, ${{\rho }_{*}}$ и ${{\rho }_{{\text{*}}}}a_{{\text{*}}}^{{\text{2}}}$, будем иметь

(2.3)
$u = 1 + \delta u,\quad a = 1 + \delta a,\quad \rho = 1 + \delta \rho ,\quad p = \frac{1}{{{{\gamma }_{2}}}} + \delta p,\quad h = \frac{{{{{(1 + \delta a)}}^{2}}}}{{{{\gamma }_{2}} - 1}}$
с (|δu|, |δa|, |δρ|, |δp|) $ \ll $ 1. В дополнение за масштабы площади, длины и времени возьмем F(0), l = 1/f(0) и l/${{a}_{*}}$ с функцией f = f(х), введенной в уравнениях (1.4).

При выбранных масштабах после подстановки представлений (2.3) в уравнения (1.4) и их линеаризации характеристические уравнения в таком (“околозвуковом”) приближении примут вид

$\begin{gathered} {{C}^{ + }}{\text{:}}\quad \frac{{dx}}{{dt}} = 2,\quad \frac{{d\delta u}}{{dt}} + \frac{{d\delta p}}{{dt}} + \frac{{1 + \delta u + {{\gamma }_{2}}\delta p}}{2}f = 0,\quad f = f(x),\quad f(0) = 1 \\ {{C}^{ - }}{\text{:}}\quad \frac{{dx}}{{dt}} = \delta u - \delta a,\quad \frac{{d\delta u}}{{dt}} - \frac{{d\delta p}}{{dt}} - (1 + \delta u + {{\gamma }_{2}}\delta p)f = 0 \\ {{C}^{0}}{\text{:}}\quad \frac{{dx}}{{dt}} = 1,\quad \frac{{d\delta p}}{{dt}} - \frac{{d\delta \rho }}{{dt}} = 0 \\ \end{gathered} $

После введения инвариантов Римана (“правого” δR и “левого” δL) и “энтропийного” δS

$2\delta R = \delta u + \delta p,\quad 2\delta L = \delta u - \delta p,\quad \delta S = \delta p - \delta \rho $
характеристические уравнения перепишутся в форме

(2.4)
$\begin{gathered} {{C}^{ + }}{\text{:}}\quad \frac{{dx}}{{dt}} = 2,\quad \frac{{d\delta R}}{{dt}} + \frac{{1 + ({{\gamma }_{2}} + 1)\delta R - ({{\gamma }_{2}} - 1)\delta L}}{4}f = 0 \\ {{C}^{ - }}{\text{:}}\quad \frac{{dx}}{{dt}} = \frac{{(3 - {{\gamma }_{2}})\delta R + ({{\gamma }_{2}} + 1)\delta L - \delta S}}{2},\quad \frac{{d\delta L}}{{dt}} = \frac{{1 + ({{\gamma }_{2}} + 1)\delta R - ({{\gamma }_{2}} - 1)\delta L}}{2}f \\ {{C}^{0}}{\text{:}}\quad \frac{{dx}}{{dt}} = 1,\quad \frac{{d\delta S}}{{dt}} = 0 \\ \end{gathered} $

В околозвуковом приближении нестационарные возмущения параметров потока выражаются через введенные инварианты равенствами

(2.5)
$\begin{gathered} \delta u = \delta R + \delta L,\quad \delta p = \delta R - \delta L, \\ \delta \rho = \delta R - \delta L - \delta S,\quad \delta a = \frac{{({{\gamma }_{2}} - 1)(\delta R - \delta L) + \delta S}}{2} \\ \end{gathered} $

Для параметров за ДВ, пока ее отход от стационарного положения, т.е. ее координата еще мала: |x2(t)| = |x1(t)| $ \ll $ 1, справедливы представления (2.3) и равенства (2.5). При этом для t > ta сверхзвуковой стационарный поток перед ДВ невозмущен. Поэтому отличие δφ1 любого параметра φ от его стационарного значения дается формулой: $\delta {{\varphi }_{1}}(t)$ = = $\varphi _{1}^{'}(0){{x}_{1}}(t)$, в которой, как и ранее, штрих означает дифференцирование по х соответствующего стационарного параметра. Если, учтя сказанное и то, что на стационарной ДВCJ (при ее нулевой скорости D = 0) условия (1.2) выполняются, провести их линеаризацию, то это приведет к равенствам (δD = dx1/dt – скорость ДВ)

$\begin{gathered} (1 - {{\rho }_{1}})\delta D - {{x}_{1}} = 2\delta {{R}_{2}} - \delta {{S}_{2}} \\ {{\rho }_{1}}(1 - {{u}_{1}})\delta D - ({{u}_{1}} - 1){{x}_{1}} = 2\delta {{R}_{2}} \\ ({{\gamma }_{2}} - 1)(1 - {{u}_{1}})\delta D = 2({{\gamma }_{2}} - 1)\delta {{R}_{2}} + \delta {{S}_{2}}, \\ \end{gathered} $
в которых нет левого инварианта δL2.

Отсутствие δL2 в линеаризованных законах сохранения на ДВ означает, что в каждом из них коэффициенты при δL2, вычисленные при отбрасывании вторых слагаемых в соотношениях (2.3), равны нулю. Обнаруженная особенность ДВ, получающихся при возмущении стационарных течений с неподвижной ДВCJ, указывает на то, что для таких течений при “линеаризации” уравнений

$\begin{gathered} (1 - {{\rho }_{1}})\delta D - {{x}_{1}} = \delta {{u}_{2}} + \delta {{\rho }_{2}} + \delta {{u}_{2}}\delta {{\rho }_{2}} \\ ({{\rho }_{1}} - 1)\delta D - ({{u}_{1}} - 1){{x}_{1}} = \delta {{u}_{2}} + \delta {{p}_{2}} \\ 2({{\gamma }_{2}} - 1)(1 - {{u}_{1}})\delta D = 4\delta {{a}_{2}} + 2{{(\delta {{a}_{2}})}^{2}} + 2({{\gamma }_{2}} - 1)\delta {{u}_{2}} + ({{\gamma }_{2}} - 1){{(\delta {{u}_{2}})}^{2}}, \\ \end{gathered} $
полученных из условий (1.2), нужно сохранять (δL2)2. Проделав необходимые выкладки, придем к разрешенным относительно δD, δR2 и δS2 равенствам

(2.6)
$\begin{gathered} \delta D = \frac{{4({{\gamma }_{2}} + 1 - {{\gamma }_{2}}{{u}_{1}}){{x}_{1}} - (5 - \gamma _{2}^{2}){{{(\delta {{L}_{2}})}}^{2}}}}{{4(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]}} < 0 \\ \delta {{R}_{2}} = \frac{{4[({{\gamma }_{2}} - 1){{u}_{1}} - {{\gamma }_{2}}]{{u}_{1}}{{x}_{1}} + (5 - \gamma _{2}^{2}){{{(\delta {{L}_{2}})}}^{2}}}}{{8[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]}} > 0 \\ \delta {{S}_{2}} = \frac{{({{\gamma }_{2}} - 1)({{u}_{1}} - 1){{u}_{1}}{{x}_{1}}}}{{{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}}} - {{(\delta {{L}_{2}})}^{2}} < 0 \\ \end{gathered} $

При t = ta неравенства в формулах (2.6) – следствие того, что, во-первых, в этот момент x1 отрицательно в силу выбора начальных возмущений (см. ниже), во-вторых, всегда ρ1 < ρ2 = 1 и u1 > u2 = 1, и в-третьих, максимально возможная величина u1 определяется формулой (1.8) с u2 = 1, как и ρ2 = 1, в силу выбранных масштабов скорости и плотности. Итак, при t = ta

(2.7)
$\frac{{d{{x}_{1}}}}{{dt}} = \delta D = \frac{{4({{\gamma }_{2}} + 1 - {{\gamma }_{2}}{{u}_{1}}){{x}_{1}} - (5 - \gamma _{2}^{2}){{{(\delta {{L}_{2}})}}^{2}}}}{{4(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]}} < 0$

Следовательно, отрицательная координата x1(t) движущейся влево детонационной волны будет продолжать уменьшаться, увеличивая модуль ее также отрицательной скорости δD. Через (δL2)2 независимо от знака δL2(t) разгону детонационной волны и ее удалению от стационарного положения х = 0 в большей или в меньшей степени будут способствовать и приходящие на нее справа отраженные акустические волны. Сказанное – доказательство неустойчивости стационарного течения с ДВCJ, к которой в стационарном решении справа примыкал бы разгоняющийся сверхзвуковой поток.

Уравнения (2.6) и (2.7) и неравенства в них в согласии со способом их получения справедливы и для дозвукового варианта, изображенного на рис. 1. Его xt-диаграмма проще представленной на рис. 2. Действительно, теперь вновь возникшая дозвуковая область, примыкающая к возмущенной слегка пересжатой детонационной волне всего лишь расширяет существовавшую до этого большую дозвуковую область. В плоскости xt правая граница дозвуковой области в отличие от заранее неизвестной звуковой линии (ЗЛ) рис. 2 – вертикаль x = xm с постоянной координатой xm минимального сечения сопла Лаваля. Наконец, теперь возмущенное течение почти везде при малых t близко к стационарному потоку. Существенно, однако, то, что и здесь для сместившейся влево детонационной волны (при х2(t) = х1(t) < 0) такой близости по-прежнему нет справа от нее. Поэтому, поступая так же, как в предыдущем варианте, придем к равенствам (2.6) и (2.7) и к выводу о неустойчивости течения с дозвуковым потоком за стационарной ДВCJ.

3. О смещении детонационной волны возмущениями, пришедшими по потоку. Рассмотрим ключевой для выполненного выше анализа вопрос о смещении детонационной волны начальными возмущениями (рис. 2), принесенными характеристиками набегающего на волну сверхзвукового потока с отрезка i0 оси х. В противоположность потоку за ДВCJ течение перед ней независимо от направления смещения волны при малых нестационарных возмущениях близко к стационарному сверхзвуковому потоку. Поэтому для него при прежнем выборе масштабов вместо представлений (2.3) имеем

(3.1)
$\begin{gathered} u = {{u}_{1}}(x) + \delta u,\quad a = {{a}_{1}}(x) + \delta a,\quad \rho = {{\rho }_{1}}(x) + \delta \rho ,\quad p = {{p}_{1}}(x) + \delta p \\ h = {{h}_{1}}(x) + \frac{{2{{a}_{1}}(x)}}{{{{\gamma }_{1}} - 1}}\delta a,\quad {{p}_{1}}(x) = \frac{1}{{{{\gamma }_{1}}}}{{\rho }_{1}}(x)a_{1}^{2}(x),\quad {{h}_{1}}(x) = \frac{{a_{1}^{2}(x)}}{{{{\gamma }_{1}} - 1}}, \\ \end{gathered} $
где переменные с индексом 1 удовлетворяют конечным равенствам (1.3), описывающим стационарное течение, или обыкновенным дифференциальным уравнениям (как и выше, штрих означает дифференцирование по х)

$({{\rho }_{1}}{{u}_{1}}){\text{'}} + {{\rho }_{1}}{{u}_{1}}f = 0,\quad p_{1}^{'} + {{\rho }_{1}}{{u}_{1}}u_{1}^{'} = 0,\quad h_{1}^{'} + {{u}_{1}}u_{1}^{'} = 0,\quad f = F{\kern 1pt} {\text{'/}}F$

Подстановка представлений (3.1) в уравнения (1.4) приводит к характеристической системе для нестационарных добавок

$\begin{gathered} {{\rho }_{1}}{{a}_{1}}\left[ {\frac{{\partial \delta u}}{{\partial t}} + ({{u}_{1}} \pm {{a}_{1}})\frac{{\partial \delta u}}{{\partial x}}} \right] \pm \frac{{\partial \delta p}}{{\partial t}} \pm ({{u}_{1}} \pm {{a}_{1}})\frac{{\partial \delta p}}{{\partial x}} + \\ + \;{{\rho }_{1}}{{a}_{1}}({{u}_{1}} \pm {{a}_{1}})\left[ {\left( {\frac{{\delta \rho }}{{{{\rho }_{1}}}} + \frac{{\delta a}}{{{{a}_{1}}}}} \right)u_{1}^{'} \pm \left( {\frac{{\delta \rho }}{{{{\rho }_{1}}}} + \frac{{{{a}_{1}}}}{{{{u}_{1}} \pm {{a}_{1}}}}\frac{{\delta u}}{{{{u}_{1}}}} + \frac{{2{{u}_{1}} \pm {{a}_{1}}}}{{{{u}_{1}} \pm {{a}_{1}}}}\frac{{\delta a}}{{{{a}_{1}}}}} \right)\frac{{{{u}_{1}}{{a}_{1}}f}}{{{{u}_{1}} \pm {{a}_{1}}}}} \right] = 0 \\ \frac{{\partial \delta p}}{{\partial t}} + {{u}_{1}}\frac{{\partial \delta p}}{{\partial x}} - a_{1}^{2}\left( {\frac{{\partial \delta \rho }}{{\partial t}} + {{u}_{1}}\frac{{\partial \delta \rho }}{{\partial x}}} \right) - 2{{u}_{1}}{{a}_{1}}\rho _{1}^{'}\delta a = 0, \\ \end{gathered} $
где верхние (нижние) знаки отвечают С+(С–)-характеристикам. При использовании этих уравнений вблизи волны (при |x| $ \ll $ 1) все величины с индексом 1 можно заменить их значениями при х = 0.

Введя с учетом последнего замечания инварианты δR, δL и δS

$2\delta R = {{\rho }_{1}}{{a}_{1}}\delta u + \delta p,\quad 2\delta L = {{\rho }_{1}}{{a}_{1}}\delta u - \delta p,\quad \delta S = \delta p - a_{1}^{2}\delta \rho $
запишем уравнения, определяющие их при |x| $ \ll $ 1, в виде

(3.2)
$\begin{gathered} {{C}^{ \pm }}{\text{:}}\quad \frac{{dx}}{{dt}} = {{u}_{1}} \pm {{a}_{1}} \\ \frac{{d\delta R}}{{dt}} = - {{\rho }_{1}}{{a}_{1}}({{u}_{1}} \pm {{a}_{1}})\left[ {\left( {\frac{{\delta \rho }}{{{{\rho }_{1}}}} + \frac{{\delta a}}{{{{a}_{1}}}}} \right)u_{1}^{'} \pm \left( {\frac{{\delta \rho }}{{{{\rho }_{1}}}} + \frac{{{{a}_{1}}}}{{{{u}_{1}} \pm {{a}_{1}}}}\frac{{\delta u}}{{{{u}_{1}}}} + \frac{{2{{u}_{1}} \pm {{a}_{1}}}}{{{{u}_{1}} \pm {{a}_{1}}}}\frac{{\delta a}}{{{{a}_{1}}}}} \right)\frac{{{{u}_{1}}{{a}_{1}}f}}{{{{u}_{1}} \pm {{a}_{1}}}}} \right] \\ {{C}^{0}}{\text{:}}\quad \frac{{dx}}{{dt}} = {{u}_{1}},\quad \frac{{d\delta S}}{{dt}} = 2{{u}_{1}}{{a}_{1}}\rho _{1}^{'}\delta a \\ \end{gathered} $

Правые части каждого второго из этих уравнений – линейные комбинации δR, δL и δS, ибо согласно определениям инвариантов

$\begin{gathered} \delta u = \frac{{\delta R + \delta L}}{{{{\rho }_{1}}{{a}_{1}}}},\quad \delta p = \delta R - \delta L,\quad \delta \rho = \frac{{\delta R - \delta L - \delta S}}{{a_{1}^{2}}} \\ \delta a = \frac{{({{\gamma }_{1}} - 1)(\delta R - \delta L) + \delta S}}{{2{{\rho }_{1}}{{a}_{1}}}} \\ \end{gathered} $

Поэтому заданные на отрезке i0 малые ненулевые значения инвариантов приносятся на малый начальный отрезок 0а возмущенной детонационной волны, практически не изменяясь вдоль своих характеристик.

Построим пример начальных возмущений на отрезке i0 оси х, которые к моменту t = ta сместят детонационную волну влево. Для этого, допустив отличные от нуля нестационарные возмущения параметров набегающего сверхзвукового потока и выразив их вблизи волны (в треугольнике i0a) через инварианты с индексом 1, подставим их в дополнение к δD, х1, δR2, δS2 и δL2 в выполняющиеся на волне законы сохранения (1.2). Проделав необходимые выкладки, придем к выражению для скорости детонационной волны

(3.3)
$\begin{gathered} \delta D = \frac{{4({{\gamma }_{2}} + 1 - {{\gamma }_{2}}{{u}_{1}}){{x}_{1}} - (5 - \gamma _{2}^{2}){{{(\delta {{L}_{2}})}}^{2}}}}{{4(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]}} + \frac{{[1 - ({{\gamma }_{2}} - 1)a_{1}^{2}{\text{/}}({{\gamma }_{1}} - 1)]{{u}_{1}}\delta {{S}_{1}}}}{{(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]a_{1}^{2}}} + \\ + \;\frac{{[1 - ({{\gamma }_{2}} - 1){{u}_{1}}{{a}_{1}}]({{u}_{1}} - {{a}_{1}})\delta {{L}_{1}} - [1 + ({{\gamma }_{2}} - 1){{u}_{1}}{{a}_{1}}]({{u}_{1}} + {{a}_{1}})\delta {{R}_{1}}}}{{(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]a_{1}^{2}}} \\ \end{gathered} $
из-за возмущений, приходящих на волну слева (с индексом “1”) и справа (δL2), и ее смещения (х1). Коэффициенты перед всеми возмущениями – константы.

Пусть i0a и i–a – отрезки С0- и С–-характеристик, которые (см. рис. 2), как и отрезок С+-характеристики ia, приходят с оси х в точку а. Тогда начальные возмущения, т.е. величины δR1, δS1 и δL1 отличны от нуля только на отрезках i0, i00 и i–0, а согласно уравнениям для dx/dt из (3.2) ${{x}_{i}} < {{x}_{{{{i}^{0}}}}} < {{x}_{{{{i}^{ - }}}}}$. Воспользовавшись произволом в выборе δR1, δS1 и δL1, зададим их постоянными одного порядка ε2$ \ll $ 1 с отрицательным суммарным вкладом (–ε2) в правую часть равенства (3.3). Для таких возмущений, учтя сказанное выше, придем к справедливому на отрезке 0а возмущенной детонационной волны уравнению

(3.4)
$\begin{gathered} \frac{{d{{x}_{1}}}}{{dt}} = k{{x}_{1}} - {{\varepsilon }^{2}} - K{{(\delta {{L}_{2}})}^{2}} \\ k = \frac{{{{\gamma }_{2}} + 1 - {{\gamma }_{2}}{{u}_{1}}}}{{(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]}} > 0,\quad K = \frac{{5 - \gamma _{2}^{2}}}{{4(1 - {{\rho }_{1}})[{{\gamma }_{2}} + 1 - ({{\gamma }_{2}} - 1){{u}_{1}}]}} > 0 \\ \end{gathered} $

Последнее слагаемое в полученном уравнении неизвестно. Однако оно, как и в уравнении (2.7), при любых отличных от нуля отраженных возмущениях уменьшает координату волны х1. Проинтегрировав уравнение (3.4) без этого слагаемого при начальном условии х1(0) = 0, убедимся в отрицательном знаке требуемого смещения возмущенной детонационной волны

${{x}_{{1a}}} \equiv {{x}_{1}}({{t}_{a}}) = \frac{{{{\varepsilon }^{2}}}}{k}(1 - {{e}^{{k{{t}_{a}}}}}) < 0$

Заключение. Отметим несколько моментов, проявившихся при выполнении данного исследования. Начиная с заведомо неверного допущения о том, что малые возмущения ДВCJ оставляют ее самоподдерживающейся. По этой причине приведший к выражениям (2.2) почти элементарный подход может также показаться неверным. Строго говоря, это так, но сделанный в результате вывод о неустойчивости стационарного течения с ДВCJ в расширяющемся канале оказывается верным благодаря двум дополнительным соображениям. Очевидно, что при одинаковых параметрах перед ДВ скорость ставшей слегка пересжатой ДВ больше скорости ДВCJ. Далее нужно ограничиться смещениями ДВ против потока. Для них важен лишь сам факт большей скорости пересжатой ДВ без знания ее величины. Для смещений ДВ по потоку нужна дополнительная информация, которую элементарный подход дать не может. Поскольку, однако, смещения ДВ против потока ведут к неустойчивости, то знать, что будет при смещениях ДВ по потоку и не требуется.

Казалось бы, все ясно, но тут возникает вопрос об “игре возмущений” в дозвуковых областях, примыкающих к пересжатой ДВ. В похожих задачах с ударными волнами без выяснения особенностей таких игр обойтись невозможно. Здесь же уже первое знакомство с проблемой (см. рис. 2) пугает казалось бы неразрешимыми трудностями. Все, однако, получается и проще, и интереснее. Главная особенность возникшей проблемы – отсутствие в линеаризованных законах сохранения на возмущенной ДВCJ первой степени инварианта, приносимого С–-характеристиками на слегка пересжатую ДВ справа. В результате влияние отраженных акустических волн проявляется через квадрат этого инварианта, не завися от его знака. При этом, как и в элементарном подходе, ограничение возмущениями, смещающими ДВCJ против потока, приводит к выводу о неустойчивости исследуемого течения.

Автор признателен Н.И. Тилляевой за обсуждения, А.Г. Куликовскому за полезный совет, П.С. Уткину за библиографию и Х.Ф. Валиеву за расчеты, предварившие данное исследование.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (№ 17-01-00126).

Список литературы

  1. Зельдович Я.Б. К теории распространения детонационных волн в газообразных системах // ЖЭТФ. 1940. Т. 10. Вып. 5. С. 542–569.

  2. von Neumann J. Progress report on theory of detonation waves // OSRD Rep., 1942. № 549.

  3. Döring W. Über den Detonationsvorgang in Gasen // Ann. Physic. 1943. Bd. 43. S. 421–436.

  4. Chapman D.L. On the rate of explosions in gases // Phil. Mag. 1899. V. 47. 5th Ser. № 284. P. 90–104.

  5. Jouguet E. Sur la propagation des reactions chimiques dans les gaz // J. Maths. Pures Appl. 6e ser. 1905. T. 1. V. 60. Fasc. 4. P. 347–425; 1906. T. 2. V. 61. Fasc. 1. P. 5–86.

  6. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. Москва: Наука, 1986. 733 с.

  7. Черный Г.Г. Газовая динамика. Москва: Наука, 1988. 424 с.

  8. Крайко А.Н. Теоретическая газовая динамика: классика и современность. Москва: Торус пресс, 2010. 440 с.

  9. Зайдель Р.М. Об устойчивости детонационных волн в газовых смесях // Докл. АН СССР. 1961. Т. 136. № 5. С. 1142–1145.

  10. Erpenbeck J.J. Stability of steady-state equilibrium detonations // Phys. Fluids. 1962. V. 5. № 5. P. 604–614.

  11. Пухначев В.В. Об устойчивости детонации Чепмена–Жуге // Докл. AH CCCP. 1963. Т. 149. № 4. С. 798–801.

  12. Зайдель Р.М., Зельдович Я.Б. Одномерная неустойчивость и затухание детонации // ПМТФ. 1964. № 6. С. 59–65.

  13. Щелкин К.И. Об одномерной неустойчивости детонации // Докл. AH CCCP. 1965. Т. 160. № 5. С. 1144–1146.

  14. Щёлкин К.И. Избранные труды. Снежинск: Изд-во РФЯЦ–ВНИИТФ, 2011. 268 с.

  15. Fickett W., Wood W.W. Flow calculations for pulsating one-dimensional detonations // Phys. Fluids. 1966. V. 9. № 5. P. 903–916.

  16. Lee H.I., Stewart D.S. Calculation of linear detonation instability: one-dimensional instability of plane detonation // J. Fluid Mech. 1990. V. 216. P. 103–132.

  17. Bourlioux A., Majda A.J., Roytburd V. Theoretical and numerical structure for unstable one-dimensional detonations // SIAM J. Appl. Math. 1991. V. 51. № 2. P. 303–343.

  18. Sharpe G.J., Falle S.A.E.G. One-dimensional numerical simulations of idealized detonations // Proc. R. Soc. A. 1999. V. 455. P. 1203–1214.

  19. Daimon Yu., Matsuo A. Detailed features of one-dimensional detonations // Phys. Fluids. 2003. V. 15. № 1. P. 112–122.

  20. Kasimov A.R., Stewart D.S. On the dynamics of self-sustained one-dimensional detonations: a numerical study in the shock-attached frame // Phys. Fluids. 2004. V. 16. № 10. P. 3566–3578.

  21. Зельдович Я.Б. К вопросу об энергетическом использовании детонационного горения // ЖТФ. 1940. Т. 10. Вып. 17. С. 1453–1461.

  22. Zeldovich Ya.B. To the question of energy use of detonation combustion // J. Propuls. Power. 2006. V. 22. № 3. P. 588–592.

  23. Александров В.Г., Крайко А.Н., Реент К.С. Определение характеристик сверхзвукового пульсирующего детонационного прямоточного двигателя (СПДПД) // Аэромеханика и газовая динамика. 2001. № 2. С. 3–15.

  24. Крайко А.Н. Теоретическое и экспериментальное обоснование концепции пульсирующего двигателя с детонационной волной, движущейся против сверхзвукового потока. Импульсные детонационные двигатели / Под ред. С.М. Фролова. Москва: Торус пресс, 2006. С. 569–590.

  25. Kraiko A.N., Egoryan A.D. Comparison of thermodynamic efficiency and thrust characteristics of air-breathing jet engines with subsonic combustion and burning in stationary and nonstationary detonation waves, AIP Conf. Proc. V. 2027: Proc. of the 19th Intern. Conf. on the Methods of Aerophysical Research (ICMAR 2018) / Ed. by V. Fomin, AIP, 2018. P. 020006-1–020006-5.

  26. Черный Г.Г. Неустановившиеся движения газа в каналах с проницаемыми стенками. Об устойчивости скачка уплотнения в каналах // Тр. ЦИАМ. 1953. № 244. 12 с. = Черный Г.Г. Неустановившиеся движения газа в каналах. Устойчивость замыкающего скачка // Газовая динамика. Избранное. Издание второе исправленное. В 2-х т. Т. 1. Ред.-сост.: А.Н. Крайко. Москва: Физматлит, 2005. С. 590–609.

  27. Бабицкий А.Б. Отражение малых возмущений от поверхности скачка и устойчивость скачка в канале переменного сечения при Т01 ≠ Т02. Королев: ЦНИИМаш, 1963. 19 с.

  28. Гринь В.Т., Крайко А.Н., Тилляева Н.И. Исследование устойчивости течения идеального газа в квазицилиндрическом канале // ПММ. 1975. Т. 39. Вып. 3. С. 473–484.

  29. Гринь В.Т., Крайко А.Н., Тилляева Н.И. Об устойчивости течения идеального газа в канале с замыкающим скачком уплотнения при одновременном отражении от сечения выхода акустических и энтропийных волн // ПММ. 1976. Т. 40. Вып. 3. С. 469–478.

  30. Крайко А.Н., Широносов В.А. Исследование устойчивости течения идеального газа в канале с замыкающим скачком уплотнения при околозвуковой скорости потока // ПММ. 1976. Т. 40. Вып. 4. С. 579–586.

  31. Гринь В.Т., Крайко А.Н., Тилляева Н.И., Широносов В.А. Анализ устойчивости одномерного течения в канале при произвольном изменении параметров стационарного потока между сечением замыкающего скачка и выходом из канала // ПММ. 1977. Т. 41. Вып. 4. С. 637–645.

  32. Гринь В.Т., Крайко А.Н., Тилляева Н.И., Широносов В.А. Исследование устойчивости течения идеального газа в каналах с замыкающим скачком уплотнения // Тр. ЦИАМ. 1982. № 1020. С. 6–21.

  33. Галин Г.Я., Куликовский А.Г. Об устойчивости течений, возникающих при распадении произвольного разрыва // ПММ. 1975. Т. 39. Вып. 1. С. 95–102.

  34. Галин Г.Я., Куликовский А.Г. Об устойчивости одномерных течений газа в расширяющихся областях // Изв. АН СССР МЖГ. 1981. № 2. С. 112–119.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал