Прикладная математика и механика, 2019, T. 83, № 3, стр. 377-383

В сборнике статей [1], посвященном гиперзвуковым течениям газа, помещено сообщение, в котором академик А.А. Дородницын пишет: “При нулевом угле атаки на поверхности тела вращения энтропия принимает максимальное значение. Многие расчеты и эксперименты показывают, что и при углах атаки, отличных от нуля, с точностью, которая получена в этих расчетах или эксперименте, энтропия сохраняет свое максимальное значение. Однако никакого строгого доказательства этого факта нет”. Затем А.А. Дородницын приводит одно доказательство, которое в разговоре ему сообщил М.Д. Ладыженский. Это доказательство основано на предположении, что завихренность на поверхности тела непрерывно зависит от угла атаки. С использованием этого предположения выкладки М.Д. Ладыженского приводят к выводу о существовании некоторого ненулевого диапазона углов атаки, при которых энтропия на поверхности тела вращения будет оставаться максимальной. Предположение о непрерывной зависимости завихренности на поверхности тела вращения от угла атаки и отсутствие не только точного значения, но и каких-либо приближенных оценок упомянутого диапазона углов атаки, – все это означало, что вопрос решен лишь частично и только для тел вращения.

В.В. Сычев в предисловии к [1] замечает, что “проблема величины энтропии на поверхности тела вращения под углом атаки … вызывала в последние годы оживленные дискуссии”. Несмотря на это, в известной автору данной статьи отечественной и зарубежной литературе, кроме упомянутого доказательства М.Д. Ладыженского, удалось найти только еще одну статью [2]. В ней приведено доказательство важного для рассматриваемого вопроса промежуточного результата, состоящего в том, что градиент энтропии на критической линии равен нулю. Как будет показано ниже, это утверждение верно для течений с постоянной полной энтальпией. Однако предложенное в [2] доказательство не опирается на факт постоянства полной энтальпии во всем потоке. Согласно [2] градиент энтропии на критической линии должен быть равен нулю даже в течениях с переменной полной энтальпией. Но это неверно (соответствующий пример приведен в четвертом разделе данной работы). Поэтому в доказательстве [2] содержится ошибка, и проблема величины энтропии на поверхности тела в общем 3D- случае до сих пор оставалась открытой.

При сверхзвуковом (число Маха $\operatorname{M} > 1$) обтекании тел с гладкой выпуклой носовой частью возникает отошедший головной скачок. Если осесимметричное тело расположено так, что ось симметрии параллельна скорости набегающего потока (нулевой угол атаки), то критическая линия тока AB, лежащая на этой оси (рис. 1 (a)), заканчивается на теле в критической точке $B$. При этом точка $A{\kern 1pt} $ расположена на скачке там, где касательная к скачку плоскость перпендикулярна скорости набегающего потока. Поэтому параметры течения в критической точке $B$ можно рассчитывать по параметрам набегающего потока. Для этого достаточно использовать условия Ренкина–Гюгонио на прямом скачке в точке A и условие сохранения энтропии на критической линии тока. Очевидно, что в этом случае энтропия принимает максимальное значение на критической линии тока и на поверхности тела.

Рис. 1.

Гладкая выпуклая носовая часть в сверхзвуковом потоке: (а) – осесимметричное обтекание; (б) – не осесимметричное обтекание.

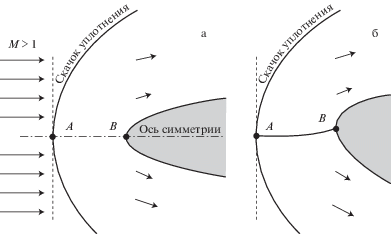
В данной статье рассмотрен общий 3D-случай; в частности, если есть угол атаки или тело не осесимметрично. Доказано, что, как и в симметричном случае, точка $A$ расположена на скачке там, где касательная к скачку плоскость перпендикулярна направлению набегающего потока (рис. 1 (б)). Как следствие энтропия принимает максимальное значение на критической линии тока и на поверхности тела.

1. Обозначения и уравнения движения. Рассмотрим стационарное обтекание тела с гладкой выпуклой носовой частью однородным сверхзвуковым потоком идеального совершенного газа без предположения о какой-либо симметрии. Поскольку носовая часть гладкая и выпуклая, отошедший головной скачок уплотнения также будет иметь гладкую выпуклую форму. При этом ниже по течению могут находиться другие скачки уплотнения и тангенциальные разрывы. Будем считать, что в течении существует замкнутая область $\bar {G}$, расположенная между головным скачком и носовой частью и обладающая следующими свойствами. Критическая линия $AB$, за исключением точки A начала критической линии на скачке и критической точки $B$ на теле, лежит внутри замкнутой области $\bar {G}$. При этом часть границы $\bar {G}$, лежащая на (гладкой) поверхности тела, представляет собой замыкание двухмерной окрестности точки $B$, а часть границы, лежащая на скачке, представляет собой замыкание двухмерной окрестности точки A. Оставшаяся же часть границы вместе с внутренними точками $\bar {G}$ находится внутри зоны течения, в которой отсутствуют скачки и разрывы.

Критическая точка $B$ является точкой растекания, и в ней начинаются линии тока, растекающиеся во всех направлениях по поверхности тела. При этом по крайней мере в некоторой окрестности точки $B$ только критическая линия имеет точки внутри течения и одну точку на поверхности тела (точку $B$). Остальные линии тока в этой окрестности либо не контактируют с поверхностью тела (линии тока, проходящие над поверхностью), либо целиком лежат на поверхности тела (линии тока, начинающиеся в точке $B$).

Дальнейшее исследование будет существенным образом опираться на сформулированное выше предположение о единственности критической линии тока (которая имеет точки внутри течения и одну точку на поверхности тела). Однако это предположение исключает из рассмотрения плоские течения, поскольку в таких течениях критическая поверхность тока состоит из бесконечного числа критических линий тока. Автору данной статьи не удалось найти подход к решению вопроса о начале критической линии в плоском случае, и вопрос о начале критической линии в плоских течениях в данной статье оставлен без ответа.

Обозначим: ${\mathbf{u}}$ – вектор скорости, $\rho $ – плотность, $p$ – давление, ${\mathbf{w}} = \operatorname{rot} {\mathbf{u}}$ – вектор завихренности. Давление $p$ и плотность $\rho $ в области $\bar {G}$ связаны соотношением $p{{\rho }^{{ - \gamma }}} = \sigma $, где $\gamma $ – показатель адиабаты, $\sigma $ – энтропийная функция, которая может быть различной на различных линиях тока.

Поскольку точки области $\bar {G}$, за исключением граничных точек на скачке и на теле, являются внутренними точками зоны течения, в которой отсутствуют скачки и разрывы, то будем считать, что в этих точках параметры течения (компоненты скорости, $\rho $ и $p$) являются дважды непрерывно дифференцируемыми функциями пространственных координат. Кроме того, поскольку поверхности скачка и тела являются гладкими, будем считать, что параметры течения и их первые и вторые производные допускают непрерывное продолжение из внутренних точек области $\bar {G}$ как на поверхность скачка, так и на поверхность тела. Под значениями производных на упомянутых поверхностях будем понимать их непрерывные продолжения из внутренних точек $\bar {G}$. (Таким образом, предполагается непрерывность первых и вторых производных во всех точках замкнутой области $\bar {G}$)

Замечание. Предположение о непрерывности первых и вторых производных во всех точках $\bar {G}$ не противоречит тому, что кривизна линий тока не ограничена в окрестности критической точки. Подобная картина имеет место, например, в точном решении уравнений для несжимаемой жидкости в окрестности критической точки, приведенном Бэтчелором в [3, параграф 2.7]. В точном решении Бетчелора компоненты скорости и их первые и вторые производные допускают непрерывное продолжение на поверхность тела. При этом максимальная кривизна линий тока неограниченно возрастает по мере их приближения к критической точке.

Течение газа в области $\bar {G}$ подчиняется уравнению неразрывности $\operatorname{div} {\kern 1pt} (\rho \operatorname{u} ) = 0$. Набегающий поток однороден. Поэтому полная энтальпия ${{i}_{0}}$ = $(\gamma {\text{/(}}\gamma - 1{\text{)}})(p{\text{/}}\rho )$ + ${{{\mathbf{u}}}^{2}}{\text{/}}2$ одинакова во всех точках течения $(\nabla {{i}_{0}} = 0)$. В этом случае уравнения Эйлера в форме Крокко [3, 4] записываются следующим образом:

2. Завихренность в критической точке. Первая теорема Гельмгольца о вихрях может быть сформулирована следующим образом. Частицы жидкости, составляющие вихревую линию (векторную линию завихренности) в некоторый момент времени, составляют одну из вихревых линий в каждый последующий момент времени. Критерий Зоравского [5], который также называется теоремой Фридмана [6], обобщает теоремы Гельмгольца о вихрях и в некоторых случаях позволяет исследовать векторные линии других векторов (а не только вектора завихренности). В этом случае частицы, составляющие векторные линии, движутся со скоростью, вообще говоря, не совпадающей со скоростью жидкости. Поэтому обычно [7–9] при использовании критерия Зоравского вводится понятие воображаемой жидкости, состоящей из таких частиц.

Используем критерий Зоравского и понятие воображаемой жидкости для исследования векторных линий вектора $\rho {\mathbf{u}}$, совпадающих с линиями тока газа. Для этого в области $\bar {G}$ наряду с течением (реального) газа рассмотрим течение воображаемой жидкости, частицы которой, в дальнейшем называемые q-частицами, движутся со скоростью ${\mathbf{q}} = \alpha {\mathbf{w}}{\text{/}}p$, где коэффициент $\alpha = 1$ кг/с² обеспечивает для ${\mathbf{q}}$ размерность скорости ([q] = м/с). Эти q-частицы не взаимодействуют с газом и не влияют на течение газа.

Уравнение (1.1) может быть записано в виде: $(\rho {\mathbf{u}}) \times {\mathbf{q}}$ = $ - \alpha {{(\gamma - 1)}^{{ - 1}}}\nabla \ln \sigma $. Поэтому $\operatorname{rot} ((\rho {\mathbf{u}}) \times {\mathbf{q}})$ = 0. Вместе с уравнением неразрывности это означает, что в области $\bar {G}$ выполняется равенство $({\mathbf{q}} \cdot \nabla )(\rho {\mathbf{u}})$ – $(\rho {\mathbf{u}} \cdot \nabla ){\mathbf{q}}$ + $\rho {\mathbf{u}}\operatorname{div} {\mathbf{q}}$ = 0. Согласно критерию Зоравского, из последнего равенства следует, что q-частицы, составляющие сегмент линии тока газа (то есть сегмент векторной линии $\rho {\mathbf{u}}$), лежащий в области $\bar {G}$ в некоторый момент времени, двигаясь со скоростью ${\mathbf{q}}$, будут составлять сегмент одной из линий тока газа в каждый последующий момент времени (до тех пор, пока эти q-частицы находятся в области $\bar {G}$).

Докажем, что ${\mathbf{w}}(B) = 0$. Допустим, что завихренность в критической точке $B$ не равна нулю. Тогда ${\mathbf{q}}(B) \ne 0$. Точка $B$ есть точка растекания газа. Поэтому энтропийная функция на поверхности тела равна своему значению в точке $B$, и вектор $\nabla \ln \sigma $ ортогонален поверхности тела. Вместе с уравнением (1.1) это означает, что в точках поверхности тела, где ${\mathbf{u}} \ne 0$ (то есть всюду, кроме точки $B$), вектор ${\mathbf{q}}$ лежит в касательной к поверхности тела плоскости. Из непрерывности ${\mathbf{q}}$ следует, что в точке $B$ вектор ${\mathbf{q}}$ также лежит в касательной к поверхности тела плоскости.

Проекция скорости ${\mathbf{q}}$ в произвольной точке области $\bar {G}$ на вектор ${\mathbf{q}}(B) \ne 0$ равна $({\mathbf{q}} \cdot {\mathbf{q}}(B)){\text{/|}}{\mathbf{q}}(B){\text{|}}$, где $({\mathbf{q}} \cdot {\mathbf{q}}(B))$ – скалярное произведение векторов ${\mathbf{q}}$ и ${\mathbf{q}}(B)$. В точке $B$ эта проекция равна ${\text{|}}{\mathbf{q}}(B){\text{|}}$. В силу непрерывности ${\mathbf{q}}$, существует такая (достаточно малая) шаровая окрестность ${{G}_{B}}$ точки $B$, что часть этой окрестности, занятая течением газа, лежит в $\bar {G}$, и в этой части $({{G}_{B}} \cap \bar {G})$ проекция скорости ${\mathbf{q}}$ на вектор ${\mathbf{q}}(B) \ne 0$ не меньше $0.5{\text{|}}{\mathbf{q}}(B){\text{|}}$. Все q-частицы, находящиеся в этой окрестности, движутся с ненулевой скоростью, и их координата в направлении ${\mathbf{q}}(B)$ меняется со скоростью не менее $0.5{\text{|}}{\mathbf{q}}(B){\text{|}}$. Согласно теории автономных систем обыкновенных дифференциальных уравнений [10], поскольку скорость ${\mathbf{q}}$ не равна нулю, траектории q-частиц, лежащие внутри окрестности ${{G}_{B}}$, не пересекаются (не имеют общих точек). Кроме того, поскольку на поверхности тела вектор ${\mathbf{q}} \ne 0$ лежит в касательной к поверхности тела плоскости, траектории, имеющие хотя бы одну точку на поверхности тела, целиком лежат на этой поверхности (в окрестности ${{G}_{B}}$).

Пусть C – точка на критической линии $A{\kern 1pt} B$; Обозначим: CB – сегмент критической линии между точками C и $B$. Выберем точку $C{\kern 1pt} $ так, чтобы сегмент CB целиком лежал внутри окрестности ${{G}_{B}}$. Обозначим: $Q(C{\kern 1pt} B)$ – совокупность q-частиц, которые составляют сегмент CB в момент времени ${{t}_{0}}$; $Q(B)$ ⊂ $Q(C{\kern 1pt} B)$ – q-частица, которая находится в точке $B$ в момент времени ${{t}_{0}}$. Частицы $Q(C{\kern 1pt} B)$ движутся со скоростью ${\mathbf{q}}$. При этом, как следует из перечисленных выше свойств траекторий q-частиц в окрестности ${{G}_{B}}$, в течение некоторого промежутка времени $[{{t}_{0}},{\kern 1pt} \,{{t}_{1}}]$ частица $Q(B)$ будет двигаться по поверхности тела, а остальные частицы $Q(C{\kern 1pt} B)$ будут при движении оставаться во внутренних точках течения. Кроме того, поскольку проекция скорости ${\mathbf{q}}$ на вектор ${\mathbf{q}}(B) \ne 0$ не меньше $0.5{\text{|}}{\mathbf{q}}(B){\text{|}} > 0$, для любого момента времени $t \subset \;]{{t}_{0}},{{t}_{1}}]$ частица $Q(B)$ будет находиться на поверхности тела в точке $D = D(t) \ne B$. Но, согласно критерию Зоравского, частицы $Q(C{\kern 1pt} B)$ в момент времени $t \subset \;]{{t}_{0}},{{t}_{1}}]$ должны составлять сегмент одной из линий тока газа. Поэтому в сколь угодно малой окрестности точки $B$ должна существовать линия тока газа, имеющая как точку $D \ne B$ на поверхности тела, так и точки, лежащие внутри течения. Но это невозможно (см. второй абзац раздела 1). Поэтому предположение, о том, что ${\mathbf{w}}(B) \ne 0$, неверно, то есть ${\mathbf{w}}(B) = 0$.

3. Точка начала критической линии на скачке. Выше рассматривался сегмент CB критической линии, лежащий в окрестности ${{G}_{B}}$. Из-за ограниченности ${{G}_{B}}$ возможна ситуация, при которой начало этого сегмента (точка $C$) не может быть выбрано как угодно близко к точке $A$ на скачке. Теперь рассмотрим сегмент, начало которого может быть как угодно близко к точке $A$. Пусть E – произвольная точка на критической линии AB, лежащая внутри области $\bar {G}$, то есть $E \subset A{\kern 1pt} B{\kern 1pt} $, $E \ne A$, $E \ne B$. Обозначим: $EB$ – сегмент критической линии между точками $E{\kern 1pt} $ и $B$. Согласно критерию Зоравского, q-частицы, составляющие сегмент $EB$ в момент времени ${{t}_{0}}$, двигаясь со скоростью ${\mathbf{q}}$, в каждый последующий момент составляют сегмент одной из линий тока газа. При этом, как показано выше, q-частица $Q(B)$ покоится в точке $B$. Это означает, что остальные q-частицы, составляющие сегмент $EB$ в момент времени ${{t}_{0}}$, в каждый последующий момент времени продолжают лежать на критической линии. Поэтому они или покоятся, или движутся вдоль этой линии. В обоих случаях на сегменте $EB$ выполнено равенство ${\mathbf{q}} \times {\mathbf{u}} = 0$. Вместе с уравнением (1.1) это означает, что во всех точках сегмента $EB$ градиент энтропийной функции равен нулю $(\nabla \sigma = 0)$. Поскольку точка E была выбрана произвольно, то, в силу непрерывности $\nabla \sigma $, имеем: $\nabla \sigma (A) = 0$ (речь идет о непрерывном продолжении $\nabla \sigma $ из внутренних точек области $\bar {G}$ на поверхность скачка).

Обозначим: $A'$ – точка на скачке, в которой касательная к скачку плоскость перпендикулярна направлению набегающего потока. Параметры течения на разных сторонах скачка связаны условиями на косом скачке уплотнения [4, 11]. Из этих условий и из того, что скачок имеет искривленную выпуклую форму, следует, что проекция $\nabla \sigma $ на поверхность скачка равна нулю только в точке $A'$. В точке $A'$ скачок перпендикулярен скорости ${\mathbf{u}}(A')$. Поэтому, используя уравнение (1.1), получаем, что проекция $\nabla \sigma (A')$ на нормаль к скачку также равна нулю.

Итак, $A'$ – единственная точка на скачке, где $\nabla \sigma = 0$, а энтропия максимальна на линии тока, начинающейся в этой точке. Выше было показано, что $\nabla \sigma (A) = 0$. Поэтому точка $A$ совпадает с точкой $A'$. Таким образом, приходим к основному результату. В течениях с отошедшим головным скачком при обтекании тел с гладкой выпуклой носовой частью критическая линия начинается там, где касательная к скачку плоскость перпендикулярна скорости набегающего потока (рис. 1 (а,б)), а энтропия принимает максимальное значение на критической линии тока и на поверхности тела.

4. О постоянстве полной энтальпии. Рассмотрим стационарное обтекание тела с гладкой выпуклой носовой частью однородным сверхзвуковым потоком идеального совершенного газа. В таком течении всюду $\nabla {{i}_{0}} = 0$ и, как показано в данной работе, градиент энтропии на критической линии равен нулю, а сама энтропия принимает максимальное значение на поверхности тела. Выберем произвольную точку $E$ на критической линии AB, не совпадающую с точками $A$ и $B$ (рис. 1 (б)). Существует бесконечное число функций $m$, постоянных на линиях тока и таких, что в точке $E$ функция $m$ имеет ненулевой градиент $(\nabla m(E) \ne 0)$. Выберем одну из таких функций $m$. Применим к параметрам течения преобразование Мунка–Прима [12]. Согласно [12], новое стационарное течение с параметрами ${{{\mathbf{u}}}_{1}} = m{\mathbf{u}}$, ${{\rho }_{1}} = {{m}^{{ - 2}}}\rho $ и ${{p}_{1}} = p$ удовлетворяет всем уравнениям движения идеального газа и имеет те же самые линии тока, что и старое $({\mathbf{u}},\rho ,p)$ течение. В частности, новая и старая критические линии совпадают. Поэтому новая энтропийная функция ${{\sigma }_{1}} = \sigma {{m}^{{2\gamma }}}$ на поверхности тела равна своему значению в точке $E$, которое, в силу неравенства $\nabla m(E) \ne 0$, является промежуточным (не максимальным). Это не противоречит результату предыдущих разделов о максимальности энтропии на поверхности тела, поскольку в новом течении полная энтальпия ${{i}_{{01}}} = {{i}_{0}}{{m}^{2}}$ уже не будет постоянной во всем потоке.

Приведенный пример показывает, что постоянство полной энтальпии во всем потоке существенно для вывода о максимальности энтропии на поверхности тела.

Заключение. С использованием уравнений Эйлера исследованы стационарные 3D- течения (исключая плоские течения) за отошедшим головным скачком, возникающим при сверхзвуковом обтекании тела с гладкой выпуклой носовой частью. Набегающий сверхзвуковой поток считался однородным. Доказано, что критическая линия начинается на скачке в точке, в которой касательная к скачку плоскость перпендикулярна направлению набегающего потока.

В частности, это означает, что давление и плотность в передней критической точке можно вычислять по параметрам набегающего потока с использованием условий Ренкина–Гюгонио на прямом скачке в точке начала критической линии. Следовательно, при заданных параметрах набегающего потока, давление и плотность в критической точке и энтропийная функция на поверхности тела будут одинаковыми для различных тел, распложенных под различными углами атаки.