Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 817-822

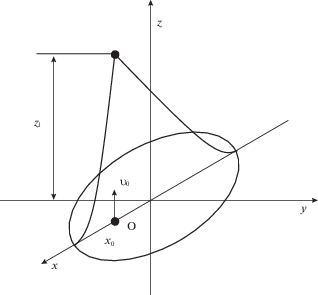
Рассмотрим движение частицы единичной массы после столкновения ее с упругой, невесомой пленкой, натянутой на каркас в виде жесткого неподвижного кольца единичного радиуса. В начальный момент частица со скоростью ${{{\mathbf{v}}}_{0}}$ пересекает плоскость кольца (рис. 1).

Выберем неподвижную декартову систему координат $x$, $y$, $z$ так, чтобы ее начало совпало с центром кольца, ось $z$ направлена по нормали к плоскости кольца в сторону начальной скорости частицы, а ось $x$ – через точку столкновения $\left( {{{x}_{0}},0,0} \right)$ ($0 < x \ll 1$).

Если точка падения совпадает с центром кольца ${{x}_{0}} = 0$, то ось $x$ направлена в ту же сторону, что и проекция скорости частицы на плоскость кольца.

Предположим, что сила трения частицы на пленке, как и другие внешние силы, кроме силы упругой деформации пленки отсутствуют.

Приняв за единицу времени отношение радиуса кольца к скорости частицы в момент столкновения, уравнение ее движения будем считать безразмерным.

Ранее показано [1], что при центральном столкновении тела в форме диска с упругой пленкой, натянутой на кольцо, она принимает одну из двух возможных экстремальных форм в виде катеноида. Площадь его поверхности, в частности, меньше площади соответствующего описанного усеченного конуса и близка к площади последнего. Можно предположить, что при переходе от тела в форме диска к телу в форме шара весьма малого радиуса при малом отклонении точки падения (${{x}_{0}}$) от центра пленки площадь боковой поверхности соответствующего описанного косого конуса будет близка к площади поверхности деформированной пленки (оставаясь бόльшей последней).

1. Площадь косого конуса с круглым опорным контуром. Для удобства временно введем еще систему координат $OXYZ$, которая получается из системы $oxyz$ сдвигом вдоль оси $x$ на величину $\Delta \geqslant 0$, соответствующую проекции вершины косого конуса на ось $x$. Пусть ${{Z}_{1}}$ обозначает аппликату вершины конуса (в момент столкновения $\Delta = {{x}_{0}}$).

Точку $O$ примем за начало полярной системы координат $\rho $, $\beta $, в которой угол $\beta $ отсчитывается от оси $X$ (или $x$), а $\rho $ – расстояние от точки $O$ до окружности радиуса единица с центром в точке $o$. В этих координатах уравнение окружности имеет вид

Элемент площади сектора $d{{S}_{c}} = \frac{1}{2}{{\rho }^{2}}d\beta $ и элемент площади конуса, проектирующегося в этот сектор, связаны соотношением $d{{S}_{0}} = d{{S}_{c}}{\text{/}}\cos \varphi $, где $\varphi $ – угол между нормалью ${\mathbf{N}}$ к элементу $d{{S}_{0}}$ и осью $Z$.

Вектор ${\mathbf{N}}$ определяется векторным произведением ${\mathbf{N}} = \left[ {{\mathbf{m\dot {m}}}} \right]$ [3], где вектор ${\mathbf{m}}$ лежит на образующей конуса: ${\mathbf{m}} = \left( { - \rho \cos \beta , - \rho \sin \beta ,{{Z}_{1}}} \right)$, $\left( {0,0,{{Z}_{1}}} \right)$ – координаты вершины конуса,

Таким образом, площадь поверхности косого конуса определяется формулой

Для случая, когда смещение $\Delta \ll 1$ приведем асимптотическое представление формулы (1.5). Учитывая, что ${{\rho }^{2}} = 1 - 2\Delta \cos \beta + {{\Delta }^{2}}\cos 2\beta + {{\Delta }^{3}}\cos \beta + o\left( {{{\Delta }^{3}}} \right)$, с точностью до $o\left( {{{\Delta }^{2}}} \right)$ получаем

Следовательно

или

2. Косое столкновение частицы с пленкой, натянутой на круглое кольцо. Вернемся к исходной системе координат $oxyz$. Заменяя $\Delta $ на ${{x}_{0}}$, $Z$ на $z$ запишем приближенное выражение приращения площади пленки по сравнению с исходным значением $\pi $

Энергия $U$ упругой пленки, имеющей некоторое предварительное натяжение на каркасе пропорциональна приращению ее площади после столкновения с частицей, т.е. $U = \mu S$ ($\mu = \operatorname{const} $ – коэффициент пропорциональности. В случае мыльной пленки $\mu $ – коэффициент поверхностного натяжения).

Для описания траектории частицы воспользуемся уравнением (2.2) [2], в котором координаты $\beta $, $q$, заменим на координаты плоскости $x$, $z$, соответственно. При этом коэффициенты первой квадратичной формы $E = G = 1$ и V = –U = $ - \frac{{\pi \mu }}{8}(4{{z}^{2}}$ – z⁴ + + $2{{x}^{2}}{{z}^{2}}) + o({{x}^{4}},{{z}^{4}})$.

Это уравнение здесь имеет вид

где $h$ – полная энергия системы частица-пленка $h = \frac{1}{2}\left( {{{{\dot {x}}}^{2}} + {{{\dot {z}}}^{2}}} \right) + U$, $z{\text{'}} = dz{\text{/}}dx$, $\dot {z} = dz{\text{/}}dt$. $V_{x}^{'} = - \frac{1}{2}\pi \mu x{{z}^{2}}$, $V_{z}^{'} = - \frac{1}{2}\pi \mu \left( {2z - {{z}^{3}} + {{x}^{2}}z} \right)$.

Таким образом, уравнение траектории принимает вид:

Если в числителе оставить слагаемые не выше первого порядка малости относительно координат и их производных, а в знаменателе – не выше второго порядка, и, если частица падает на пленку не по нормали к последней, то приближенно

После интегрирования (2.4) получим

где ${{c}_{0}} = z{\text{'}}$ при $x = {{x}_{0}}$.

При этом скорость частицы в каждой точке траектории определяется из интеграла энергии $h$.

Если горизонтальная составляющая скорости падения частицы направлена к центру ($x < {{x}_{0}}$), то в (2.5) выбираем знак минус и максимальное значение прогиба пленки $\sqrt {2h{{c}_{1}}{\text{/}}\pi \mu } $ достигаются при $\sqrt {\pi \mu {\text{/}}2h} \left( {x - {{x}_{0}}} \right)$ = $ - \frac{\pi }{2}$, а точка отделения частицы от пленки ${{x}_{0}}$ определяется из соотношения $\sqrt {\pi \mu {\text{/}}2h} \left( {{{x}_{\rho }} - {{x}_{0}}} \right) = - \pi $ и наоборот.

Заметим, что траектория частицы, определенная уравнением (2.3) лежит несколько ниже реальной траектории, так как площадь конуса всегда больше площади деформации пленки.

3. Скольжение частицы с учетом трения. Влияние сухого трения (как наиболее важного здесь фактора диссипации энергии) на скольжение частицы в плоскости $x$, $z$ выясним исходя из модели кулоновского трения $\left| {\mathbf{F}} \right| = \nu \left| {\mathbf{Q}} \right|$, где ${\mathbf{F}}$ – сила трения, направленная по касательной к траектории частицы, ${\mathbf{Q}}$ – сила давления частицы на пленку $\left| {\mathbf{Q}} \right|$ = $\mu \sqrt {{{{\left( {\partial S{\text{/}}\partial x} \right)}}^{2}} + {{{\left( {\partial S{\text{/}}\partial z} \right)}}^{2}}} $, $\nu $ – коэффициент трения

Пусть $\gamma $ обозначает острый угол между касательной к траектории и осью х. Тогда ${{F}_{x}} = - \nu \left| {\mathbf{Q}} \right|\cos \gamma $, ${{F}_{z}} = - \nu \left| {\mathbf{Q}} \right|\sin \gamma $, $\gamma = \operatorname{arctg} \left( {z{\text{/}}\left| x \right|} \right)$.

В процессе скольжения частицы знак $x$, (а значит и знак ${{F}_{x}}$) может меняться. Однако, в рассматриваемом (типичном) случае будем считать, что от начала движения и до размыкания контакта частицы и пленки знак $\dot {x}$ совпадает со знаком $\dot {x}\left( o \right) > 0$. Тогда ${{F}_{x}} \leqslant 0$ и ${{F}_{z}} \leqslant 0$. (В противном случае надо следить за сменой знака $\dot {x}$ и менять знак ${{F}_{x}}$.)

Присутствие в уравнениях движения угла $\gamma $ как функции $x$ существенно усложняет эти уравнения. Для упрощения задачи воспользуемся ее решением без учета трения в разд. 2 с прежними начальными условиями. Таким образом, приближенное решение будет определяться из лагранжевой системы уравнений

4. Площадь конуса с произвольным опорным контуром. Пусть вершина конуса лежит на оси $z$, а опорный контур $L$ описывается уравнением в полярных координатах $\rho = \rho \left( \beta \right)$. Тогда, как следует из предыдущего, площадь конуса определяется интегралом

где ${\mathbf{N}} = \left[ {{\mathbf{m\dot {m}}}} \right] = \left( {{{z}_{1}}\left( {\rho \cos \beta - \dot {\rho }\sin \beta } \right),{{z}_{1}}\left( {\rho \sin \beta - \dot {\rho }\cos \beta } \right),{{\rho }^{2}}} \right)$, $\cos \varphi = {\mathbf{kN}}{\text{/}}\left| {\mathbf{N}} \right|$, ${\mathbf{k}} = (0,0$, 1), ${{z}_{1}}$ – аппликата вершины конуса.

Таким образом, в случае произвольного гладкого контура $L$ площадь конуса определяется интегралом

5. О движении частицы в более общих случаях. Если опорный контур имеет центр симметрии, то при падении частицы на пленку по нормали в этот центр, частица будет продолжать двигаться по этой нормали (по оси $z$).

Перемещению частицы $z$ можно дать оценку снизу, если контур $L$ заменим некоторым выпуклым симметричным контуром ${{L}_{0}}$, вписанным в контур $L$. В качестве контура ${{L}_{0}}$ можно взять, например, окружность или замкнутую линию, состоящую из двух полуокружностей, раздвинутых по направлению нормали к разрезу окружности. (В последнем случае площадь конической поверхности будет состоять из площадей пары треугольников с основаниями равными величине раздвижения полуокружностей с общей вершиной на оси $z$ и – пары кусков площадей косых конусов, опирающихся на дуги полуокружностей.)

В более общих случаях параметр $\rho \left( \beta \right)$ можно представить в виде конечной суммы ряда Фурье по косинусам $\beta \in \left[ {0,\pi } \right]$. Тогда подкоренное выражение в интеграле (4.1) с известной точностью можно представить так же в виде конечной суммы ряда Фурье

(${{m}_{1}}$, ${{m}_{2}}$ – определяются заданной точностью вычислений).

Для краткости последнее выражение обозначим как ${{f}_{1}}\left( \beta \right) + {{f}_{2}}\left( \beta \right)z_{1}^{2}$.

Для приближенного вычисления интеграла (4.1) или интеграла

Воспользуемся неравенством Коши–Буняковского

Это неравенство усиливает оценку деформации снизу, то есть со стороны перехода к более жесткой упругой системе.

В случае малых деформаций (${{z}_{1}} \ll 1$) получим

где $A = {{\left[ {\int_0^\pi {\left[ {{{f}_{1}}\left( \beta \right)d\beta } \right]} } \right]}^{{1/2}}} > 0$,

Следовательно, движение частицы после столкновения с пленкой будет приближенно описываться одним дифференциальным уравнением второго порядка относительно ${{z}_{1}}$ с постоянными коэффициентами.

Замечание 1. В случае зеркальной симметрии опорного контура с учетом формулы (4.1) решается задача о плоском движении частицы при косом столкновении как в разд. 2.

Замечание 2. Наличие иных потенциальных сил, кроме сил упругости, например, силы тяжести частицы, не исключает применение формулы траектории [1]. При этом формулы разд. 2 и 5 несколько усложнятся.

Рассмотренная задача может быть полезной при разработке аварийных гасителей скорости.