Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 808-816

При решении задачи о действии на балку простейших подвижных нагрузок – сосредоточенной силы или груза с переменными скоростями движения – применяются методы, связанные c интегральными преобразованиями Фурье и Лапласа, использованием метода Бубнова–Галеркина [1, 2], интеграла Френеля, функций Уиттекера и метода малого параметра для решения обыкновенного дифференциального уравнения с переменными коэффициентами [1–5]. Кроме того, используются методы, связанные с численным решением интегральных уравнений относительно динамической реакции путем построения рекуррентных зависимостей с помощью формулы Гаусса [6, 7] и решением системы интегральных уравнений посредством замены ее системой алгебраических уравнений [8]. Предлагаемый в данной работе метод решения указанных задач учитывает любое необходимое число форм колебаний в разложении функции прогиба и приводит к разрешающей системе уравнений, для решения которой применяется безусловно-устойчивая схема интегрирования [9, 10] с минимальным числом неизвестных, как и в методе интегральных уравнений при решении задач с постоянной скоростью движения. В качестве нагрузки на стержни рассматриваются движущиеся с переменной скоростью сосредоточенные силы, грузы и экипажи.

1. Постановка задачи, общие формулы и тестовые примеры. Обратимся сначала к решению классической задачи о движении груза по балке с переменной скоростью, а затем перейдем к случаю более сложной нагрузки. Используются безусловно-устойчивая шаговая процедура по времени и метод учета действия безмассовой подвижной нагрузки на стержневые системы, предложенные ранее [9]. Рассматриваются случаи равнопеременного движения подвижной нагрузки по конструкциям.

Дифференциальное уравнение колебаний балки при движении по ней груза весом $P$ и массой $M$ имеет вид

Здесь $EJ$ – жесткость балки на изгиб, ${{\mu }_{1}}$ – коэффициент, учитывающий диссипацию энергии, $q{\text{*}}\left( {y,t} \right)$ – прогиб балки, y – координата по длине, $\delta \left( {y - s(t)} \right)$ – дельта-функция, $s(t) = {{v}_{0}}t + w{{t}^{2}}{\text{/}}2$ – закон движения груза по балке, t – время, ${{v}_{0}}$ – скорость груза при въезде на балку, $v = {{v}_{0}} + wt$ и $w$ – скорость и ускорение движения груза, $m$ – масса балки.

Прогиб шарнирно опертой балки в момент ${{t}_{{j + 1}}}$ при движении по ней сосредоточенной силы

можно записать в виде [9] где использованы обозначения

Здесь $q_{{ij}}^{{}}$ – обобщенные координаты балки, ${{W}_{i}}\left( {{{\eta }_{1}}} \right)$ – фундаментальные функции, ${{\tilde {\omega }}_{i}}$ – круговая частота изгибных колебаний, $n$ – число удерживаемых форм колебаний, $\ell $ – длина балки, $\ddot {q}_{1}^{{}}$ – вертикальное ускорение груза.

Полагая ${{\ddot {q}}_{{1j + 1/2}}} = {{d}^{2}}q{\text{*}}\left( {s(t),t} \right){\text{/}}d{{t}^{2}}$, при $t = {{t}_{{j + 1/2}}}$, запишем полное вертикальное ускорение груза в виде

Используя (1.2) и (1.3), имеем на шаге [t_j, t_j + 1]

где введены следующие обозначения

Из условий динамического равновесия груза следует

После подстановки (1.5) в (1.4), имеем на шаге [t_j, t_j + 1] уравнение относительно ${{\ddot {q}}_{{1j + {\text{1/2}}}}}$. Выражение (1.2) с учетом (1.5) позволяет вычислить начальные условия задачи для следующего шага интегрирования.

Шаговая процедура (1.2)–(1.5) реализована для расчета равнопеременного движения груза по балке со следующими параметрами [1, 6, 7].

где ${{v}_{0}}$ и ${{v}_{1}}$ – скорости, соответственно, въезда и схода груза с балки.

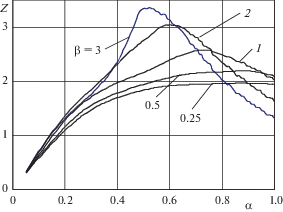
На рис. 1 показан характер возрастания и убывания динамического коэффициента $Z = {{Z}_{D}}{\text{/}}{{Z}_{0}}$, где ${{Z}_{D}}$– смещение груза и ${{Z}_{0}} = 2P{{l}^{3}}{\text{/}}\left( {{{\pi }^{4}}EJ} \right)$ – статический прогиб под силой в центре балки, в зависимости от скорости движения, определяемой коэффициентом $\alpha $. Результаты получены при ${{v}_{1}}{\text{/}}{{v}_{0}} = 2{\text{/}}3$ и различных значениях параметра $\beta $, определяющего соотношение масс груза и балки 3, 2, 1, 0.5 и 0.25. Результаты, полученные по разным методикам и представленные на рис. 1 и в работе [7] (стр. 210), практически совпадают. Заметим, что предложенная методика (1.2)–(1.5) при $M$ = 0 может быть использована для решения классической задачи о движении с переменной скоростью вдоль стержня сосредоточенной силы. В зависимости от перемещения груза по балке, определяемого, при $\alpha $ = 0.5 и $\beta $ = 0.25, отрезком $\xi = \pi tv{\text{/}}\ell $ [1], на рис. 2 показаны изменения следующих величин: динамических коэффициентов для перемещений в центре балки при равнопеременном движении сосредоточенной силы ${{\left. Z \right|}_{{y = \ell /2}}} = {{Z}_{D}}{\text{/}}{{Z}_{0}}$ (рис. 2, a) и груза $\tilde {Z}$ (рис. 2, б); динамического коэффициента для изгибающего момента $\tilde {\mu } = {{M}_{D}}{\text{/}}{{M}_{0}}$, где ${{M}_{D}}$ – момент в середине балки, при ${{M}_{0}} = P\ell {\text{/}}4$ (рис. 2, в); динамического коэффициента $R = {{P}_{D}}{\text{/}}P$ для динамического давления под грузом ${{P}_{D}}$ (рис. 2, г).

Во всех рассмотренных случаях на рис. 2 пунктирные линии соответствуют равнозамедленному движению при $w = - v_{0}^{2}{\text{/}}2\ell $, ${{v}_{1}} = 0$, ${{t}_{1}} = 2\ell {\text{/}}v{}_{0}$, $B = - 0.5$, $v = {{v}_{0}}$, а линии сплошные – равноускоренному движению при $w = v_{1}^{2}{\text{/}}2\ell $, ${{v}_{0}} = 0$, ${{t}_{2}} = 2\ell {\text{/}}v{}_{1}$, $B = 0.5$, $v = {{v}_{1}}$, где ${{t}_{{1,2}}}$ – время движения груза, $\Delta {{t}_{j}}$ = 0.0005 с, $n$ = 45, $B = w\ell {\text{/}}{{v}^{2}}$ [1]. Результаты, полученные по разным методикам для случая движения силы и представленные на рис. 2, a и в работе [1] (стр. 313), практически совпадают.

2. Метод решения уравнений для системы “состав–мост”. Алгоритм (1.2)–(1.4) легко реализуется в случае движения системы грузов по балке (системе балок). Выражения вида (1.4) при движении N грузов формируют систему N линейных, алгебраических уравнений

Здесь $А,\;B$ – блочно-диагональная матрица и вектор (число блоков равно числу балок), $E$ – единичная матрица, $R{}_{{ko}}$ – вектор динамических добавок к статическим давлениям грузов на балку, ${{\ddot {q}}_{K}}$ – вектор вертикальных ускорений движущихся грузов.

Рассмотрим модель для изучения вертикальной динамики системы “состав-мост”. Будем далее ее обозначать через $\{ {{e}_{h}},e_{{h^\circ }}^{^\circ }\} $, при $h = 1,2,...,{{m}_{*}}$, $h^\circ = 1,2,..,m^\circ $, где ${{m}_{*}}$, $m^\circ $ – число последовательно расположенных шарнирно опертых балок и, соответственно, число экипажей в составе. На рис. 3 представлена модель вагона из скоростного состава, на рис. 4 изображен скоростной состав при движении по многопролетному балочному мосту в момент торможения.

Построим систему уравнений, описывающих вертикальную динамику состава $\{ e_{{h^\circ }}^{^\circ }\} $, состоящего из несвязанных между собой вагонов (рис. 3, 4). Будем считать при этом, что начальные условия задачи нулевые, а параметры, определяющие положение $\{ e_{{h^\circ }}^{^\circ }\} $ в системе ${{O}_{*}}{{X}_{*}}{{Y}_{*}}{{Z}_{*}}$, движущейся со скоростью состава $v$ поступательно, отсчитываются от их значений в статическом равновесии. При этом в момент изменения скорости к кузову каждого вагона прикладываются горизонтальные силы инерции, влияющие на вертикальную динамику вагонов (продольная динамика состава не рассматривается). Обозначим через элементы $\{ e_{{h^\circ }}^{^\circ }\} $, вовлеченные к моменту времени t в совместные колебания с $\left\{ {{{e}_{h}}} \right\}$. Тогда для системы имеем

Здесь ${{\bar {q}}_{c}}$ – вектор независимых обобщенных координат, определяющих в системе ${{O}_{*}}{{X}_{*}}{{Y}_{*}}{{Z}_{*}}$, ${{M}_{*}} = [M_{*}^{r}]$, ${{C}_{*}} = [C_{*}^{r}]$, ${{K}_{*}} = [K_{*}^{r}]$ – блочно-диагональные матрицы масс, демпфирования и жесткости для , $M_{*}^{r}$, $C_{*}^{r}$, $K_{*}^{r}$ – блоки матриц ${{M}_{*}}$, ${{C}_{*}}$, ${{K}_{*}}$, соответствующие экипажу с номером $r$ [10], ${{\Pi }_{*}}$ – матрица соединения векторов ${{\bar {R}}_{*}}$ и ${{R}_{*}}$, ${{R}_{*}}$ – вектор динамических добавок к статическим реакциям в точках контакта $\{ e_{{h^\circ }}^{^\circ }\} $ с проезжей частью (системой $\left\{ {{{e}_{h}}} \right\}$ и жестким внемостовым полотном).

Будем считать, что торможение состава происходит в момент $t{\text{*}}$, когда первая колесная пара состава достигает середины второго пролета, при этом в момент $t{\text{*}}$ к кузовам состава прикладываются инерционные пары сил ${{M}^{{(ин)}}} = {{M}^{{(куз)}}}w \times L$ (см. рис. 4), где ${{M}^{{(куз)}}}$– масса кузова вагона, $L$ – расстояние по вертикали от центра масс кузова до оси колесной пары. Введем в рассмотрение следующие величины: ${{P}_{*}}$ и ${{R}_{{ko}}}$ – векторы статических давлений колесных пар системы на проезжую часть и соответствующие динамические добавки к ним; ${{q}_{{ck}}}$ – вектор смещений колес вагона (подвектор ${{\bar {q}}_{c}}$); ${{q}_{{ko}}}$ – вектор смещений проезжей части в точках контакта с ним колесных пар состава. Выделим из ${{R}_{{ko}}}$, ${{R}_{*}}$, ${{q}_{{ko}}}$, ${{q}_{{ck}}}$ подвекторы, соответственно, $R_{{ko}}^{^\circ }$, $R_{*}^{{^{^\circ }}}$, $q_{{ko}}^{^\circ }$, $q_{{ck}}^{^\circ }$, отвечающие только взаимодействию с $\left\{ {{{e}_{h}}} \right\}$, где $R_{{ko}}^{^\circ }$, $R_{*}^{^\circ }$ – динамические добавки к статическим давлениям колес и добавки к реакциям колес, $q_{{ko}}^{^\circ }$, $q_{{ck}}^{^\circ }$ – смещения балки и смещения колес на мосту. В любой момент времени элементы вектора ${{q}_{{ko}}}$, относящиеся к проезжей части вне моста, остаются нулевыми, а при движении состава по мосту выполняются условия неразрывности перемещений и скоростей $q_{{ko}}^{^\circ } = q_{{ck}}^{^\circ }$, $\dot {q}_{{ko}}^{^\circ } = \dot {q}_{{ck}}^{^\circ }$ и условия равновесия в движущихся узлах (в точках контакта колес с проезжей частью моста):

Для системы $\left\{ {{{e}_{h}}} \right\}$, по которой происходит движение состава, на шаге [t_j, t_j + 1] можно записать

Здесь А – блочно-диагональная матрица, характеризующая жесткостные, диссипативные и инерционные характеристики системы {е_h}, Е – единичная матрица, В – вектор, учитывающий начальные условия для {е_h} в момент t_j и действие на проезжую часть моста системы движущихся сил ${{P}_{*}}$.

Проведем дискретизацию (2.2) по времени ( j = 0, 1, 2…), используя шаговую процедуру из [9], в итоге имеем

Выделим из (2.5) подсистему уравнений, отвечающих в левой части подвектору $\ddot {q}_{{ckj + 1/2}}^{^\circ }$, далее выразим эту подсистему относительно вектора динамических добавок к статическим реакциям колес, представив ее в виде

Подставим в (2.3) векторы $R_{{k0}}^{^\circ }$, $R_{*}^{^\circ }$ из (2.4) и (2.7), в итоге имеем разрешающую систему уравнений на шаге [t_j, t_j + 1]

где $D,D^\circ $ – блочно-диагональная матрица и вектор, характеризующие на шаге [t_j, t_j + 1] движение системы “состав – мост”.

Проследим ход решения всей задачи при j = 0, 1, 2, … На шаге [t_j, t_j + 1] при начальных условиях задачи в момент t_j определяется, применяя (2.8), вектор $\ddot {q}_{{koj + 1/2}}^{^\circ }$, далее, используя (2.7), (2.6) и (1.2), вычисляются поля смещений, скоростей и ускорений для системы в момент t_j + 1. Далее процесс повторяется.

3. Результаты численного моделирования. Шаговая процедура (2.8) реализована для высокоскоростного состава из [12] при движении по многопролетному мосту. Система $\{ {{e}_{h}},e_{h}^{^\circ }\} $ состоит из четырех типовых железобетонных балочных пролетных строений одинаковой длины при ЕJ = 2.15 × 10⁷ кНм², т = 8.2 т/м, µ₁ = 0.00202 с, $\ell $ = 18 м и шести вагонов. Положение состава на мосту определяется отрезком $s(t)$ (рис. 4), т.е. положением первого колеса первого вагона на мосту.

Система уравнений (2.8) меняла свой порядок с 1 до 12 в процессе численной реализации, при движении состава со скоростью ${{v}_{0}}$ = 250 км/ч и торможении состава в момент, когда s = 1.5$\ell $ и $w = - 2$ м/c² [13]. На рис. 5, а показаны зависимости вертикальных смещений первого колеса первого вагона $\mathop q\nolimits_1 $ [м] (пунктирная линия) и середины второго пролетного строения ${{q}_{{1b}}}$ (сплошная линия) от положения состава, определяемого отрезком $s(t)$, на проезжей части моста (рис. 4). На рис. 5, б показана зависимость от $s(t)$ динамической добавки R(кН) первой колесной пары первого вагона. Шаг интегрирования $\Delta {{t}_{j}}$ при п = 45 в (2.8) выбирался равным $\Delta {{t}_{j}}$ = 0.0036 с, при числе шагов по времени равном 300 и статической нагрузке от каждой колесной пары 170 кН. Отметим ожидаемое совпадение ординат графика на рис. 5, а, соответствующее моменту, когда колесо первого вагона достигает середины второго пролета при s = 27 м.

4. Заключение. Предложенный метод позволяет исследовать, используя шаговую процедуру, предложенную в [9], действие подвижной инерционной нагрузки с переменной скоростью, на стержни при различных граничных условиях, применяя соответствующие фундаментальные функции [10, 11, 14]. В задачах железнодорожного транспорта метод позволяет исследовать поведение системы “состав–мост” при различных скоростях движения состава в режимах начала торможения или разгона состава при любом его положении по длине пролетного строения моста. В задачах, связанных с подвижной нагрузкой, метод позволяет оценивать поведение конструкции и поведение объекта (системы с конечным числом степеней свободы) при резком торможении.