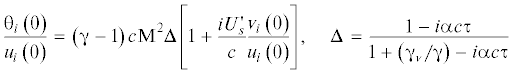Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 749-769
АСИМПТОТИЧЕСКАЯ ОЦЕНКА УСТОЙЧИВОСТИ СВЕРХЗВУКОВОГО ПОГРАНИЧНОГО СЛОЯ В КОЛЕБАТЕЛЬНО ВОЗБУЖДЕННОМ ГАЗЕ НА ПЛАСТИНЕ
Ю. Н. Григорьев 1, *, И. В. Ершов 2, **
1 Институт вычислительных технологий СО РАН
Новосибирск, Россия
2 Новосибирский государственный аграрный университет
Новосибирск, Россия
* E-mail: grigor@ict.nsc.ru
** E-mail: ivershov1969@gmail.com
Поступила в редакцию 17.03.2019
После доработки 18.06.2019
Принята к публикации 21.06.2019
Аннотация
Построена асимптотическая теория кривой нейтральной устойчивости сверхзвукового пограничного слоя колебательно возбужденного молекулярного газа на плоской пластине. В качестве исходной математической модели течения рассматривались уравнения двухтемпературной вязкой теплопроводной газовой динамики. На основе их линеаризации на автомодельном погранслойном решении для совершенного газа получена спектральная задача для системы линейных обыкновенных дифференциальных уравнений восьмого порядка. Из линейной комбинации граничных значений ее решений, убывающих вне пограничного слоя, выведено алгебраическое “вековое” уравнение с характерным разделением на “невязкую” и “вязкую” части, которое решалось численно. Показано, что рассчитанные таким образом кривые нейтральной устойчивости подтверждают эффект повышения устойчивости течения на фоне релаксационного процесса и в пределах 12–15% согласуются с полученными ранее результатами прямого численного решения полной спектральной задачи. Решение упрощенной системы уравнений для расчета критического числа Рейнольдса дает аналогичный результат.
Введение. В современной аэродинамике большое место занимают проблемы, в которых необходим учет реальных свойств газов. В частности, возник интерес к задачам гидродинамической устойчивости течений химически реагирующих, оптически активных и термически неравновесных молекулярных газов (см., например, библиографию в монографиях [1, 2]).
Влияние сильной термической неравновесности колебательных степеней свободы молекул и диссоциации молекул на ламинарно-турбулентный переход при гиперзвуковом обтекании тонких конусов систематически изучалось в серии экспериментальных и численных исследований [3–5].
Первые численные расчеты устойчивости пограничного слоя термически неравновесного газа на пластине в полной постановке были выполнены Bertolotti [6]. Неравновесность соответствовала стационарным условиям полета в атмосфере на высоте $H$ = 12 км при числе Маха M = 4.5, когда происходит возбуждение колебательных мод, и условиям эксперимента в аэродинамической трубе, где, наоборот, энергия колебательных мод, “замороженных” при температуре торможения в расширяющемся потоке, в процессе релаксации повышает статическую температуру газа.
Устойчивость сверхзвукового пограничного слоя на пластине рассчитывалась [7] в более широком диапазоне чисел Маха M = 1.6–4.8 и для предельного уровня колебательного возбуждения при отсутствии диссоциации.
При этом использовалась наиболее полная постановка данной задачи, опирающаяся на аналогию с известными расчетами для совершенного газа [8]. Релаксационный процесс соответствовал мгновенному отклонению колебательной энергии (температуры) от нулевого значения, что в реальности может быть вызвано импульсной лазерной накачкой колебательной моды.
В обеих работах для специально рассчитанных профилей стационарного течения были получены графики инкрементов нарастания наиболее неустойчивых первой и второй невязких и вязких мод, а также кривые нейтральной устойчивости последних.
Асимптотические оценки влияния колебательного возбуждения в условиях доступности численных расчетов устойчивости в достаточно полной постановке, полезны для относительно простого получения приближенных значений минимального критического числа Рейнольдса в зависимости от способа и уровня возбуждения, рода газа и т.п. Кроме того, они могут дать независимое подтверждение численных результатов, в частности, для плоской пластины, где в хорошо изученном случае совершенного газа результаты обоих подходов находятся в удовлетворительном соответствии.
Асимптотические оценки критического числа Рейнольдса в пограничном слое колебательно возбужденного газа на пластине для случая двумерных дозвуковых возмущений впервые были получены в работе [9]. В близкой постановке [10] рассматривался случай трехмерных возмущений. Неравновесность создавалась введением в уравнение Ландау–Теллера для колебательной энергии (температуры) стационарного источника накачки, что представляет интерес в свете возможных приложений. Однако из-за несовершенства и противоречивости использованной в этих работах модели полученные результаты вызывают серьезную критику.
В первую очередь надо сказать, что влияние возбуждения описывается на основе нефизического понятия знакопеременной второй вязкости, которое только по названию совпадает с введенным еще Стоксом [11] коэффициентом при дивергентной части тензора напряжений.
Не углубляясь в анализ адекватности такого подхода, можно ограничиться указанием на очевидные недостатки данной модели. Так, несмотря на используемую терминологию, в исходных уравнениях импульсов и полной энергии опущены дивергентные слагаемые с коэффициентом второй (объемной) вязкости (ср. [12]).
В отличие от более полной постановки [6, 7], в [9] рассматривается пространственно однородное уравнение Ландау–Теллера, не включающее конвективный перенос возбуждения стационарным течением. При этом процесс диффузии колебательного возбуждения, существенный из-за градиента колебательной энергии поперек пограничного слоя не учитывается [6, 7, 9]. Введенный в это уравнение источник никак не компенсируется отводом энергии из поступательных степеней свободы, что можно было бы сделать либо теплоотводом с поверхности пластины, либо включением в уравнение энергии однородной по пространству эндотермической реакции [13]. Очевидно, что это противоречит стационарности невозмущенного течения. Можно привести и ряд других более мелких, но неочевидных недостатков.
Собственно задача линейной устойчивости исследовалась в рамках упрощенной асимптотической теории [9, 10], аналогичной первым работам по устойчивости пограничного слоя совершенного газа на пластине [14, 15]. При этом основной результат состоял в модификации асимптотической оценки критического числа Рейнольдса, показывающей возможность его понижения, начиная с определенного уровня накачки колебательной моды. В свете отмеченных выше недостатков в постановке задачи этот вывод представляется дискуссионным, хотя факт понижения устойчивости дозвукового пограничного слоя, рассматривавшегося ранее [9, 10], при подводе энергии, например, при нагревании поверхности, хорошо известен.
В настоящей работе строится асимптотическая теория кривой нейтральной устойчивости сверхзвукового пограничного слоя колебательно возбужденного газа на плоской пластине. В качестве исходной математической модели течения использовались уравнения двухтемпературной вязкой теплопроводной газовой динамики. В рамках классической линейной теории устойчивости получена спектральная задача для системы линейных обыкновенных дифференциальных уравнений восьмого порядка. Основные этапы вывода секулярного (“векового”) уравнения, единые для всех сдвиговых течений, совпадают с предложенными в работах [14, 15]. Показано, что рассчитанные на основе полученного уравнения кривые нейтральной устойчивости хорошо согласуются с результатами прямого численного решения исходной спектральной задачи [7]. Близкие результаты дает решение упрощенного уравнения для критического числа Рейнольдса.
1. Исходные уравнения спектральной задачи. На основе линейной теории гидродинамической устойчивости рассматривается развитие двумерных дозвуковых возмущений при сверхзвуковом обтекании колебательно возбужденным газом плоской полубесконечной пластины. Начало декартовой системы координат $\left( {x,~y} \right)$ совпадает с носиком пластины, координата $x$ ориентирована по направлению невозмущенного потока, координата $y$ направлена в поток по нормали к пластине. Течение описывается системой уравнений двухтемпературной газовой динамики [5, 12].
В качестве характерных величин для обезразмеривания выбраны текущее расстояние $x = L$ вдоль пластины, параметры невозмущенного потока вне пограничного слоя, отмеченные индексом “∞”: скорость ${{U}_{\infty }}$, плотность ${{{\rho }}_{\infty }}$ и температура ${{T}_{\infty }}$, коэффициенты сдвиговой ${{{\eta }}_{\infty }}$ и объемной ${{{\eta }}_{{{\text{b}}\infty }}}$ вязкостей, коэффициент теплопроводности, обусловленный переносом энергии в поступательных и вращательных степенях свободы, ${{k}_{\infty }} = {{k}_{{t\infty }}} + {{k}_{{r\infty }}}$, коэффициент теплопроводности, описывающий диффузионный перенос энергии колебательных квантов, ${{k}_{{{v}\infty }}}$. Для обезразмеривания давления и времени используются комбинированные величины ${{{\rho }}_{\infty }}U_{\infty }^{2}$ и $L{\text{/}}{{U}_{\infty }}$, соответственно.
Исходная двухтемпературная система уравнений в отсутствие внешних источников не имеет стационарных решений, в частности, в приближении пограничного слоя. Поэтому она приближенно линеаризуется на стационарном автомодельном решении уравнений пограничного слоя в отсутствии колебательного возбуждения [11]. На основе полученной таким образом системы уравнений для возмущений рассматривалась устойчивость периодических по продольной координате $x$ решений в форме бегущих плоских волн
Подстановка ${\mathbf{q}}{\text{'}}$ в систему уравнений для возмущений приводит к уравнениям для их амплитуд, которые имеют вид [7]
(1.2)
$\begin{gathered} \frac{{{{{\eta }}_{s}}}}{{{\text{Re}}}}{\Delta }u - {{{\rho }}_{s}}Du - {\alpha }{{{\rho }}_{s}}v\frac{{d{{U}_{s}}}}{{dy}} - i{\alpha \varepsilon } + \frac{{{{{\eta }}_{{Ts}}}}}{{{\text{Re}}}}~\frac{{d{{T}_{s}}}}{{dy}}~\left( {\frac{{du}}{{dy}} + i{{{\alpha }}^{2}}v} \right) + \\ \, + \frac{{\theta }}{{{\text{Re}}}}{\text{\;}}\frac{d}{{dy}}{\text{\;}}\left( {{{{\eta }}_{{Ts}}}\frac{{d{{U}_{s}}}}{{dy}}} \right) + \frac{{{{{\eta }}_{{Ts}}}}}{{{\text{Re}}}}{\text{\;}}\frac{{d{{U}_{s}}}}{{dy}}{\text{\;}}\frac{{d{\theta }}}{{dy}} = 0 \\ \end{gathered} $(1.3)
$\frac{{\alpha {{\eta }_{s}}}}{{{\text{Re}}}}{\Delta }v - {\alpha }{{{\rho }}_{s}}Dv - \frac{{d{\varepsilon }}}{{dy}} + \frac{{{\alpha }{{{\eta }}_{{Ts}}}}}{{{\text{Re}}}}~\frac{{d{{T}_{s}}}}{{dy}}~\left( {\frac{{dv}}{{dy}} - iu} \right) + \frac{{i{\alpha }{{{\eta }}_{{Ts}}}}}{{{\text{Re}}}}{\text{\;}}\frac{{d{{U}_{s}}}}{{dy}}~{\theta } = 0$(1.4)
$\begin{gathered} \frac{{\gamma {{k}_{s}}}}{{{\text{RePr}}}}\Delta \theta - {{\rho }_{s}}D\theta - \alpha {{\rho }_{s}}~\frac{{d{{T}_{s}}}}{{dy}}~v - \alpha \left( {\gamma - 1} \right)\sigma - \frac{{{{{\gamma }}_{v}}{{{\rho }}_{s}}}}{{\tau }}~\left( {{\theta } - {{{\theta }}_{v}}} \right) + \\ \, + \frac{{2{\gamma }\left( {{\gamma } - 1} \right){{{\eta }}_{s}}{{{\text{M}}}^{2}}}}{{{\text{Re}}}}{\text{\;}}\frac{{d{{U}_{s}}}}{{dy}}~\left( {\frac{{du}}{{dy}} + i{{\alpha }^{2}}v} \right) + \frac{{2{\gamma }{{k}_{{Ts}}}}}{{{\text{RePr}}}}{\text{\;}}\frac{{d{{T}_{s}}}}{{dy}}{\text{\;}}\frac{{d{\theta }}}{{dy}} + \\ \, + \left[ {\frac{{\gamma }}{{{\text{RePr}}}}{\text{\;}}\frac{d}{{dy}}{\text{\;}}\left( {{{k}_{{Ts}}}\frac{{d{{T}_{s}}}}{{dy}}} \right) + \frac{{{\gamma }\left( {{\gamma } - 1} \right){{{\eta }}_{{Ts}}}{{{\text{M}}}^{2}}}}{{{\text{Re}}}}{\text{\;}}{{{\left( {\frac{{d{{U}_{s}}}}{{dy}}} \right)}}^{2}}} \right]{\theta } = 0 \\ \end{gathered} $(1.5)
$\begin{gathered} \frac{{{\gamma }{{{\mu }}_{2}}{{k}_{{vs}}}}}{{{\text{RePr}}}}{\Delta }{{{\theta }}_{v}} - {{{\gamma }}_{v}}{{{\rho }}_{s}}D{{{\theta }}_{v}} - {\alpha }{{{\gamma }}_{v}}{{{\rho }}_{s}}~\frac{{d{{T}_{s}}}}{{dy}}~v + \frac{{{{{\gamma }}_{v}}{{{\rho }}_{s}}}}{{\tau }}~\left( {{\theta } - {{{\theta }}_{v}}} \right) + \\ + \;\frac{{{\gamma }{{{\mu }}_{2}}}}{{{\text{RePr}}}}\frac{d}{{dy}}{\text{\;}}\left( {{{k}_{{vTs}}}\frac{{d{{T}_{s}}}}{{dy}}} \right){\theta } + \frac{{{\gamma }{{{\mu }}_{2}}{{k}_{{vTs}}}}}{{{\text{RePr}}}}{\text{\;}}\frac{{d{{T}_{s}}}}{{dy}}\left( {\frac{{d{\theta }}}{{dy}} + \frac{{d{{{\theta }}_{v}}}}{{dy}}} \right) = 0 \\ \end{gathered} $Индексом “s” здесь и далее обозначены значения соответствующих величин в стационарном невозмущенном течении. В качестве граничных условий принималось, что при $y = 0$ и на условной верхней границе пограничного слоя $y = {\delta }$ все возмущения обращаются в нуль.
В монографиях [2, 12] показано, что для двухатомных газов при умеренном уровне термической неравновесности
поведение температурных зависимостей коэффициентов сдвиговой ${\eta }$ и объемной ${{{\eta }}_{b}}$ вязкостей практически совпадает, при этом их отношение 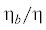 меняется в диапазоне:
меняется в диапазоне:  = 0–2. Ввиду этого, а также для последующего сопоставления полученных результатов
расчетов с данными [7], в уравнениях (1.1)–(1.6) в качестве температурной зависимости для коэффициента объемной вязкости аналогично
[7] используется формула ${{{\eta }}_{b}}\left( T \right) = {{{\mu }}_{1}}{\eta }\left( T \right)$, где ${{{\mu }}_{1}} = {{{\eta }}_{{b\infty }}}{\text{/}}{{{\eta }}_{\infty }}$ = 0–2, а температурная зависимость коэффициента сдвиговой вязкости ${\eta }\left( T \right)$ описывается законом Сазерленда [17].
= 0–2. Ввиду этого, а также для последующего сопоставления полученных результатов
расчетов с данными [7], в уравнениях (1.1)–(1.6) в качестве температурной зависимости для коэффициента объемной вязкости аналогично
[7] используется формула ${{{\eta }}_{b}}\left( T \right) = {{{\mu }}_{1}}{\eta }\left( T \right)$, где ${{{\mu }}_{1}} = {{{\eta }}_{{b\infty }}}{\text{/}}{{{\eta }}_{\infty }}$ = 0–2, а температурная зависимость коэффициента сдвиговой вязкости ${\eta }\left( T \right)$ описывается законом Сазерленда [17].
Коэффициенты теплопроводности $k = {{k}_{t}} + {{k}_{r}}$ и ${{k}_{v}}$, обусловленные поступательно-вращательным и колебательным движением молекул, выражены через коэффициент сдвиговой вязкости с помощью полуэмпирических соотношений Эйкена [7, 16]:
В уравнениях системы (1.1)–(1.6) коэффициент ${\gamma } = {{c}_{{p\infty }}}{\text{/}}{{c}_{{V\infty }}}$ – показатель адиабаты, ${{c}_{{V\infty }}} = {{c}_{{Vt\infty }}} + {{c}_{{Vr\infty }}}~$ и ${{c}_{{p\infty }}} = {{c}_{{Vt\infty }}} + {{c}_{{Vr\infty }}} + R~$ – соответственно удельные теплоемкости при постоянных объеме и давлении при температуре ${{T}_{\infty }}$. Параметр ${{{\gamma }}_{v}}$ = ${{c}_{{V{v}\infty }}}{\text{/}}\left( {{{c}_{{Vt\infty }}} + {{c}_{{Vr\infty }}}} \right)$ = = ${{c}_{{V{v}\infty }}}{\text{/}}{{c}_{{V\infty }}}$ характеризует степень неравновесности колебательной моды молекул, ${\tau }$ – характерное время релаксации колебательной степени свободы молекул. Критерии подобия ${\text{Re}} = {{{\rho }}_{\infty }}L{{U}_{\infty }}{\text{/}}{{{\eta }}_{\infty }}$, ${\text{M}} = {{U}_{\infty }}{\text{/}}\sqrt {{\gamma }R{{T}_{\infty }}} $ и ${\text{Pr}} = {{c}_{{p\infty }}}{{{\eta }}_{\infty }}{\text{/}}\left( {{{k}_{{t\infty }}} + {{k}_{{r\infty }}}} \right)$ = ${{c}_{{p\infty }}}{{{\eta }}_{\infty }}{\text{/}}{{k}_{\infty }}$ – соответственно числа Рейнольдса, Маха и Прандтля невозмущенного потока. С использованием формул Эйкена параметр ${{{\mu }}_{2}}$ для двухатомных газов выражается как μ2 = = ${{k}_{{v\infty }}}{\text{/}}\left( {{{k}_{{t\infty }}} + {{k}_{{r\infty }}}} \right)$ = $20{{{\gamma }}_{v}}{\text{/}}33$.
Система линейных уравнений (1.1)–(1.6) имеет восьмой порядок и вместе с однородными граничными условиями определяет несамосопряженную спектральную задачу для развивающихся во времени возмущений, где собственными значениями являются комплексные фазовые скорости возмущений $c = {{c}_{r}} + i{{c}_{i}}$. Необходимо отметить, что соотношение ε, содержащее параметр (объемную вязкость), исключается из системы. Для этого достаточно продифференцировать уравнение (1.2) по y, уравнение (1.3) умножить на $i\alpha $ и вычесть одно из другого полученные уравнения. Уравнения пограничного слоя в приближении Прандтля, которые используются для расчета невозмущенного стационарного течения, также не зависят от объемной вязкости. Это позволяет констатировать, что объемная вязкость, как и прямо связанная с ней вторая вязкость в понимании Стокса [11], не влияют на линейную устойчивость течения в пограничном слое.
2. Параметры стационарного течения. Автомодельные профили скорости и температуры рассчитывались численным интегрированием системы уравнений в автомодельных переменных
(2.1)
$\frac{d}{{d{\xi }}}\left( {C\frac{{{{d}^{2}}f}}{{d{{{\xi }}^{2}}}}} \right) + f\frac{{{{d}^{2}}f}}{{d{{{\xi }}^{2}}}} = 0~$(2.2)
$\frac{d}{{d{\xi }}}\left( {{{k}_{s}}\frac{{d{{T}_{s}}}}{{d{\xi }}}} \right) + \frac{{\left( {{\gamma } - 1} \right)}}{4}{\text{Pr}}{{{\text{M}}}^{2}}C{{\left( {\frac{{{{d}^{2}}f}}{{d{{{\xi }}^{2}}}}} \right)}^{2}} + {\text{Pr}}f\frac{{d{{T}_{s}}}}{{d{\xi }}} = 0~$Здесь ${\xi }$ – автомодельная переменная Дородницына–Хоуарта [11]
(2.3)
$\begin{gathered} {\xi } = \frac{{\zeta }}{{\sqrt x }},\quad {\zeta } = \frac{1}{2}~\,\mathop \smallint \limits_0^y \,{{{\rho }}_{s}}~dy~ \\ \frac{{df}}{{d{\xi }}} = 2u\left( {\xi } \right),\quad C = {\rho }\left( {{{T}_{s}}} \right){\eta }\left( {{{T}_{s}}} \right) = {{{\rho }}_{s}}{{{\eta }}_{s}} = \frac{{{{{\eta }}_{s}}}}{{{{T}_{s}}}}, \\ \end{gathered} $Для расчета гидродинамических параметров невозмущенного течения система (2.1), (2.2) приводилась к системе в нормальной форме, которая интегрировалась численно методом “стрельбы” с помощью процедуры Рунге–Кутты четвертого порядка на интервале [0, δc]. Точкой “прицеливания” служила середина интервала, где требовалось совпадение значений вычисляемых величин с точностью до 10–8.
В расчетах здесь и далее использовалось число Прандтля ${\text{Pr}}$ = 0.75, за условную верхнюю границу пограничного слоя принималось значение ${{{\delta }}_{c}}$ = 8, зависимость сдвиговой вязкости от температуры описывалась формулой Сазерленда в виде [17]
Как известно, константа Сазерленда слабо зависит от температуры и в основном определяется родом газа. При этом относительная константа $\bar {C} = C{\text{/}}{{T}_{\infty }}$ меняется в пределах $\bar {C}$ = 0.3–1.0 [17]. В данном случае выбор $\bar {C}$ = 0.5 связан с необходимостью сравнения результатов с данными работ [7, 8].
Расчеты были выполнены для чисел Маха ${\text{M}}$ = 2.2, 4.5, 4.8. Примеры рассчитанных профилей скорости ${{U}_{s}}$, плотности ${{{\rho }}_{s}}$ и температуры ${{T}_{s}}$ приведены на рис. 1.
Рис. 1.
Автомодельные профили скорости ${{U}_{s}}$, плотности ${{\rho }_{s}}$ и температуры ${{T}_{s}}$.

3. Асимптотика “невязких” решений. Асимптотические решения системы (1.1)–(1.6) для больших значений чисел Рейнольдса ищутся в виде ряда теории возмущений
В нулевом приближении, эквивалентном предельному переходу ${\text{Re}} \to \infty $ в уравнениях (1.1)–(1.6), приходим к системе уравнений для невязких возмущений, которая рассматривалась ранее в [15]. Было показано, что она может быть сведена к линейному уравнению второго порядка для возмущения давления. Таким образом, в этом приближении могут быть построены только два линейно независимых решения. Остальные шесть решений должны быть получены с учетом вязких слагаемых. При этом для вывода секулярного уравнения здесь надо использовать только затухающие при $y \to \infty $ решения [19].
Так как в коэффициентах уравнения для возмущения давления используются автомодельные профили скорости ${{U}_{s}}$ и температуры ${{T}_{s}}$, удобно перейти в нем к дифференцированию по автомодельной переменной (2.3) в соответствии с соотношением
Преобразованное таким образом уравнение в несамосопряженной форме записывается в виде
(3.1)
$p{\text{''}} - a\left( {\psi } \right)p{\text{'}} - b\left( {\psi } \right)p = 0,\quad a\left( {\psi } \right) = \frac{{2W{\text{'}}}}{W},\quad b\left( {\psi } \right) = 4{{\alpha }^{2}}\chi {{T}_{s}}~$Для дальнейших вычислений в уравнении (3.1) проводится линейная замена независимой переменной ${\psi } = {\xi } - {{{\xi }}_{c}}$, которая, не меняя форму уравнения, переносит начало отсчета поперечной координаты в критический слой, где реальная фазовая скорость возмущения равна местной скорости невозмущенного потока ${{c}_{r}} = {{U}_{{sc}}}$. Для рассматриваемых ниже нейтральных возмущений примем ${{c}_{r}} \equiv c$. Индексом “c” будут обозначаться величины, вычисляемые в критическом слое при ${\psi } = 0$.
В уравнении (3.1) введены обозначения
Для нейтральных возмущений, как и для растущих, необходимо выполнение первого условия (теоремы) Рэлея [18]
Поэтому ${\psi } = 0$ представляет собой регулярную особую точку уравнения (3.1). Так как коэффициент $a\left( {\psi } \right)$ имеет в этой точке полюс первого порядка, а $b\left( {\psi } \right)$ является гладкой функцией, решение в окрестности особой точки строится методом Фробениуса [20] в виде обобщенного степенного ряда
(3.2)
$p\left( {\psi } \right) = {{{\psi }}^{r}}\,\sum\limits_{k = 0}^\infty {{{c}_{k}}{{{\psi }}^{k}}} $Предварительно разложим коэффициенты уравнения (3.1) в степенные ряды по переменной ${\psi }$ в окрестности особой точки ${\psi } = 0$. Очевидно, что разложение функции $W$ имеет вид
При этом разложение коэффициента $a\left( {\psi } \right)$ строится исходя из соотношения
Получаем
(3.3)
$a\left( {\psi } \right) = \frac{2}{{\psi }} + A + B{\psi } + ~ \cdots ,\quad A = \frac{{U_{{sc}}^{{''}}}}{{U_{{sc}}^{'}}},\quad B = \frac{{4U_{{sc}}^{{'''}}}}{{3U_{{sc}}^{'}}} - {{A}^{2}}$Первые члены разложения коэффициента $b\left( {\psi } \right)$ записываются как
(3.4)
$b\left( {\psi } \right) = 4{{\alpha }^{2}}[(T_{{sc}}^{2} + 2{{T}_{{sc}}}T_{{sc}}^{'}{\psi } + \ldots ) - {{m}^{2}}{{{\text{M}}}^{2}}({{T}_{{sc}}}U_{{sc}}^{'}{{{\psi }}^{2}} + T_{{sc}}^{'}U_{{sc}}^{{'2}}{{{\psi }}^{3}} + \ldots )]~$Подставляя представление (3.2) в уравнение (3.1) с учетом разложений (3.3), (3.4) и приравнивая нулю выражение при низшей степени ${{{\psi }}^{{r - 2}}}$, получаем следующее определяющее уравнение для показателя r [20]
Так как ${{c}_{0}} \ne 0$, то отсюда следует, что (3.5) имеет два корня ${{r}_{1}} = 3$ и ${{r}_{2}} = 0$. Поскольку ${{r}_{1}} \ne {{r}_{2}}$ и ${{r}_{1}} - {{r}_{2}} = 3$ – целому числу, то в соответствии с общей теорией [20] два линейно независимых решения уравнения (3.1) строятся в виде
В силу однородности уравнения (3.1) без ограничения общности можно положить $c_{0}^{{\left( 1 \right)}} = c_{0}^{{\left( 2 \right)}} = 1$. Подстановка разложения ${{p}_{1}}\left( {\psi } \right)$ в (3.1) позволяет получить рекуррентные выражения для коэффициентов $\{ c_{k}^{{\left( 1 \right)}}\} $. В результате имеем
(3.6)
${{p}_{1}}\left( {\psi } \right) = {{{\psi }}^{3}} + \frac{4}{3}A{{{\psi }}^{4}} + c_{2}^{{\left( 1 \right)}}{{{\psi }}^{5}} + \ldots ,\quad c_{2}^{{\left( 1 \right)}} = \frac{{3{{A}^{2}} + 3B + 4{{\alpha }^{2}}T_{{sc}}^{2}}}{{10}}$При подстановке ${{p}_{2}}\left( {\psi } \right)$ в (3.1) сингулярная часть отделяется, а неизвестные коэффициенты $\{ c_{k}^{{\left( 2 \right)}}\} $ также определяются по рекуррентным соотношениям, что позволяет записать второе решение в виде
(3.7)
${{p}_{2}}\left( {\psi } \right) = 1 - 2{{\alpha }^{2}}T_{{sc}}^{2}{{{\psi }}^{2}} - \frac{4}{3}{{\alpha }^{2}}T_{{sc}}^{2}A{{p}_{1}}\left( {\psi } \right){\text{Ln}}\left( {\psi } \right),$Фундаментальное решение строится численно в виде
(3.8)
$p\left( {\psi } \right) = {{p}_{2}}\left( {\psi } \right) + C{{p}_{1}}\left( {\psi } \right)~$Интегрирование ведется в двух интервалах – $\left[ {{{{\psi }}_{{\varepsilon }}},{\delta } - {{{\xi }}_{c}}} \right]$ для ${\psi } > 0$ и $\left[ {{{{\psi }}_{{ - {\varepsilon }}}}, - {{{\xi }}_{c}}} \right]$ для ${\psi } < 0$. В первом из интервалов краевая задача решается методом стрельбы. На верхней границе ${\psi } = - {{{\xi }}_{с}}$ ставится условие $p = 0$. В окрестности критического слоя в обоих случаях в качестве условий берутся асимптотические разложения фундаментального решения (3.8) при малых значениях $~{{{\psi }}_{{ \pm {\varepsilon }}}}$. Константа $C$ заранее неизвестна и определяется итеративно. Задается ее некоторое значение при фиксированных значениях $c$ и $\alpha $. Уравнение интегрируется к внешней границе $~{{{\psi }}_{{\delta }}} = {\delta } - {{{\xi }}_{c}}~$, и константа меняется до тех пор, пока не будет удовлетворено граничное условие $p = 0$. С найденной константой уравнение (3.1) интегрируется с асимптотическим условием при ${\psi } < 0$ до нижней границы ${\psi } = ~ - {{{\xi }}_{c}}~$.
Расчеты выполнялись для чисел Маха ${\text{M}}$ = 2.2, 4.5 и 4.8. Для каждого числа Маха ${\text{M}}$ находилась координата обобщенной точки перегиба ${{{\xi }}_{s}}$ из уравнения
и соответствующее значение фазовой скорости ${{c}_{s}} = {{U}_{s}}\left( {{{{\xi }}_{s}}} \right)$. Диапазон изменения фазовой скорости для первой моды выбирался аналогично [8] в соответствии с неравенством а для остальных мод из интервалаШаг по $c$ был выбран $\Delta c = {{10}^{{ - 4}}}$. Волновые числа изменялись в диапазоне $\alpha \in \left[ {0,0.3} \right]$ с шагом $\Delta \alpha = {{10}^{{ - 4}}}$.
При интегрировании в интервале ${\psi } > 0$ в выражении ${{m}^{2}}$ пренебрегалось мнимой частью $m_{i}^{2}$ в силу ее малости, как это было сделано в асимптотике. При этом отпадает необходимость расщеплять решение уравнения (3.1) на реальную и мнимую части. При интегрировании в интервале ${\psi } < 0$ решение расщеплялось на реальную и мнимую части.
После расчета массива значений $p~\left( { - {{{\xi }}_{c}}} \right) = P~\left( {c,{\alpha }} \right)$ граничные значения “невязкой” части фундаментального решения, входящие в секулярное уравнение, рассчитывались по формулам для возмущений скоростей и температур, следующих из системы (1.1)–(1.6) при ${\text{Re}} \to \infty $:
(3.10)
${{\theta }_{i}}\left( y \right) = {{T}_{s}}\left[ {\frac{{\left( {\gamma - 1} \right)\left( {1 + i\alpha \tau W} \right)p{{{\text{M}}}^{2}}}}{{1 + \frac{{{{\gamma }_{v}}}}{\gamma } + i\alpha \tau W}} - \frac{{p{\text{'}}T_{s}^{'}}}{{{{\alpha }^{2}}{{W}^{2}}}}} \right]~$4. Асимптотика “вязких” решений. Построение асимптотики “вязких” решений осуществляется на основе упрощения полной линеаризованной системы (1.1)–(1.6), как это было сделано в [15, 19]. Упрощенная система имеет вид
(4.2)
$u{\text{'''}} - i\alpha \left( {{{U}_{s}} - c} \right)\frac{{\operatorname{Re} u{\text{'}}}}{{{{{\eta }}_{s}}{{T}_{s}}}} = 0$(4.3)
${\theta ''} - i\alpha \left( {{{U}_{s}} - c} \right)\frac{{\Pr \operatorname{Re} ~\theta }}{{{{{\eta }}_{s}}{{T}_{s}}}} + \frac{{{{{\gamma }}_{v}}\Pr \operatorname{Re} }}{{{\gamma }{{{\eta }}_{s}}{{T}_{s}}}}\frac{{\left( {{{{\theta }}_{v}} - {\theta }} \right)}}{{\tau }} = 0$(4.4)
${\theta }_{v}^{{''}} - i\alpha \left( {{{U}_{s}} - c} \right)\frac{{33\Pr \operatorname{Re} ~{{{\theta }}_{v}}}}{{20\gamma {{\eta }_{s}}{{T}_{s}}}} - \frac{{33\Pr \operatorname{Re} }}{{20{\gamma }{{{\eta }}_{s}}{{T}_{s}}}}\frac{{\left( {{{{\theta }}_{v}} - {\theta }} \right)}}{{\tau }} = 0$Следует отметить, что упрощенная система, как и исходная, имеет восьмой порядок. Если перейти здесь к совершенному газу: ${{{\gamma }}_{v}} = {{{\theta }}_{v}} = 0$, то система трансформируется в “вязкую” систему Дана–Линя шестого порядка [21].
Надо отметить, что у системы (4.1)–(4.4) есть два тривиальных решения u = = $v = {\theta } = {{{\theta }}_{v}} = 0$ и $u = 1$, $v = - iy$, ${\theta } = {{{\theta }}_{v}} = 0$. Поскольку здесь необходимы только убывающие (ограниченные) при $y \to \infty $ решения, то единственное удовлетворяющее этому условию нулевое тривиальное решение будет заменяться “невязким” решением (3.10):
Процесс построения “вязких” решений покажем на примере уравнения импульсов (4.2), которое преобразуем следующим образом. Введем замены независимой [22] и зависимой [21] переменных по формулам
(4.5)
$Y\left( y \right) = {{\left[ {\frac{3}{2}~\mathop \smallint \limits_{{{y}_{c}}}^y \sqrt {\frac{{{{U}_{s}} - c}}{{{{{\eta }}_{s}}{{T}_{s}}}}} ~dt} \right]}^{{2/3}}},\quad U\left( Y \right) = u{\text{'}}~\sqrt {\frac{{dY}}{{dy}}} $В новых переменных входящие в (4.2) производные выражаются как
Подстановка этих выражений в (4.2) дает
Поскольку строится асимптотическая теория для ${\text{Re}} \gg 1$, можно пренебречь, как это было сделано в [21], слагаемым $P\left( Y \right)$. Заметив еще, что
приходим к уравнению Эйри [22]
(4.6)
$\frac{{{{d}^{2}}U}}{{d{{\zeta }^{2}}}} - \zeta U = 0,\;\;\;\;\zeta = {{\left( {i\alpha \operatorname{Re} } \right)}^{{1/3}}}Y$Линейно независимые решения (4.6) могут быть представлены в нескольких эквивалентных формах, например, функциями Эйри первого и второго рода ${\text{A}}{{{\text{i}}}_{{1,2}}}\left( z \right)$. В нашем случае удобно воспользоваться аппаратом обобщенных функций Эйри ${{A}_{k}}\left( {z,p} \right)$ [23], для которых имеется ряд необходимых в дальнейшем анализе соотношений. В частности,
(4.7)
${{A}_{k}}\left( {z,0} \right) = {{A}_{k}}\left( z \right) \equiv {\text{A}}{{{\text{i}}}_{k}}\left( z \right),\quad {{A}_{k}}\left( {z, - 1} \right) = ~{\text{Ai}}_{k}^{'}\left( z \right)$(4.8)
${\text{\;}}{{A}_{k}}\left( {z,1~} \right) = \mathop \smallint \limits_\infty ^z \,{{A}_{k}}\left( t \right)~dt,\quad {{A}_{k}}\left( {z,2~} \right) = \mathop \smallint \limits_\infty ^z \,{{A}_{k}}\left( {t,1} \right)~dt$(4.9)
${{A}_{k}}\left( {z,~j - 3~} \right) - z{{A}_{k}}\left( {z,j - 1~} \right) + \left( {j - 1} \right){{A}_{k}}\left( {z,j~} \right) = 0,$Асимптотическое представление для обобщенных функций Эйри имеет вид [23]
(4.10)
${{A}_{ \pm }}\left( {z,j} \right) = \frac{{{{{\left( { \pm 1} \right)}}^{j}}}}{{2\sqrt \pi }}~{{z}^{{ - \left( {2j + 1} \right)}}}~\exp \left( { \pm \frac{{2\sqrt {{{z}^{3}}} }}{3}~} \right)$При этом ${{A}_{1}}\left( {z,j~} \right)\sim {{A}_{ - }}\left( {z,j~} \right)$, ${{A}_{2}}\left( {z,j~} \right)\sim {{A}_{ + }}\left( {z,j~} \right)$.
Первое из соотношений (4.7) позволяет записать два линейно независимых решения (4.6) как
Из выражений (4.5), (4.11) для производной возмущения продольной скорости следует
Чтобы найти решение для возмущения продольной скорости, необходимо проинтегрировать последнее. Из перехода к независимой переменной ${\zeta }$ имеем для дифференциалов
Интегрируя $u_{{1,2}}^{{\text{'}}}$, получаем два “вязких” решения
(4.12)
${{u}_{{v1,2}}} = \mathop \smallint \limits_\infty ^\zeta \frac{{dY}}{{d{\zeta }}}~{{\left( {\frac{{dy}}{{dY}}} \right)}^{{3/2}}}{{A}_{{1,2}}}\left( t \right)~dt = \frac{{dY}}{{d{\zeta }}}~{{\left( {\frac{{dy}}{{dY}}} \right)}^{{3/2}}}{{A}_{{1,2}}}\left( {{\zeta },1} \right)$Здесь при интегрировании из-под знака интеграла были вынесены медленно меняющиеся функции, как это сделано в [21].
Только одно из полученных решений удовлетворяет необходимому асимптотическому условию убывания при $y \to \infty $. Как следует из выражений (4.10), (4.12), оно выражается через обобщенную функцию Эйри первого рода первого порядка. Таким образом, используемое в дальнейшем анализе решение записывается в виде
(4.13)
${{u}_{v}}\left( y \right) = \frac{{dY}}{{d{\zeta }}}~{{\left( {\frac{{dy}}{{dY}}} \right)}^{{3/2}}}{{A}_{1}}\left( {\zeta ,1} \right)$Чтобы построить решения уравнений (4.3) и (4.4) для возмущений температур, выполним в них следующие преобразования. Приближенно примем, что ${\text{33/}}\left( {20\gamma } \right) \approx 1$. Введем вспомогательные функции
Переход обратно к температурам, получаем
(4.14)
${\theta } = \frac{{{\gamma }{{{\theta }}_{ + }} - {{{\gamma }}_{v}}{{{\theta }}_{ - }}}}{{{\gamma } + {{{\gamma }}_{v}}}},\quad {{{\theta }}_{v}} = \frac{{{\gamma }\left( {{{{\theta }}_{ + }} + {{{\theta }}_{ - }}} \right)}}{{{\gamma } + {{{\gamma }}_{v}}}}$Складывая и вычитая уравнения (4.3) и (4.4), получаем уравнения для введенных функций, которые записываются в универсальном виде
(4.15)
${\theta }_{ \pm }^{{''}} - {{p}_{ \pm }}\left( y \right){\text{Re}}{{{\theta }}_{ \pm }} = 0,$Как и выше, делаем в уравнении (4.15) замену зависимых и независимых переменных
В результате приходим к уравнениям
Отсюда в соответствии с соотношениями (4.14) получаем решение уравнения (4.3) для возмущения статической температуры
(4.16)
${{{\theta }}_{v}}\left( y \right) = \frac{1}{{\left( {{\gamma } + {{{\gamma }}_{v}}} \right)}}~\left[ {{\gamma }{{A}_{1}}\left( {{{{\zeta }}_{ + }}} \right)\sqrt {\frac{{dy}}{{d{{Y}_{ + }}}}} - {{{\gamma }}_{v}}{{A}_{1}}\left( {{{{\zeta }}_{ - }}} \right)\sqrt {\frac{{dy}}{{d{{Y}_{ - }}}}} } \right]~$Поскольку в связанные уравнения (4.1), (4.2) входит только ${\theta }\left( y \right)$, то найденное решение позволяет отщепить уравнение (4.4), понизив таким образом порядок определителя в секулярном уравнении.
Два линейно независимых решения для возмущения поперечной скорости строятся следующим образом. Полагая в (4.1) ${\theta } = 0$, $u \ne 0$ и интегрируя с учетом (4.13), получаем
(4.17)
${{v}_{{v1}}}\left( y \right) = - i\,\mathop \smallint \limits_\infty ^{\zeta } \,\frac{{dY}}{{d{\zeta }}}\frac{{dy}}{{dY}}~{{u}_{{vis}}}~dt = - i{{\left( {\frac{{dy}}{{dY}}} \right)}^{{5/2}}}{{\left( {\frac{{dY}}{{d{\zeta }}}} \right)}^{2}}{{A}_{1}}\left( {\zeta ,2} \right),$Аналогично, при ${\theta } \ne 0$, $u = 0$ выполняя интегрирование в (4.1) с подстановкой (4.16), находим
(4.18)
${{v}_{{v2}}}\left( y \right) = \frac{{i\left( {{{U}_{s}} - c} \right)}}{{\left( {1 + \frac{{{{{\gamma }}_{v}}}}{{\gamma }}} \right){{T}_{s}}}}~\left[ {\left( {\frac{{d{{Y}_{ + }}}}{{d{{{\zeta }}_{ + }}}}} \right){{{\left( {\frac{{dy}}{{d{{Y}_{ + }}}}} \right)}}^{{3/2}}}{{A}_{1}}\left( {{{{\zeta }}_{ + }},1} \right) - } \right.\left. {\frac{{{{{\gamma }}_{v}}}}{{\gamma }}\left( {\frac{{d{{Y}_{ - }}}}{{d{{{\zeta }}_{ - }}}}} \right){{{\left( {\frac{{dy}}{{d{{Y}_{ - }}}}} \right)}}^{{3/2}}}{{A}_{1}}\left( {{{{\zeta }}_{ - }},1} \right)} \right]~$В результате два линейно независимых решения усеченной “вязкой” системы (4.1)–(4.3) записываются в виде
(4.19)
${{{\mathbf{V}}}_{2}}\left( y \right) = {{\left[ {{{u}_{v}}\left( y \right),~{{v}_{{v1}}}\left( y \right),0~} \right]}^{T}},\quad {{{\mathbf{V}}}_{3}}\left( y \right) = {{\left[ {0,~{{v}_{{v2}}}\left( y \right),{{{\theta }}_{v}}\left( y \right)~} \right]}^{T}}$5. Секулярное уравнение. Для перехода к спектральной задаче необходимо потребовать, чтобы линейная комбинация независимых решений (3.10) и (4.19) удовлетворяла однородным граничным условиям системы (1.1)–(1.6), тогда
(5.1)
${{c}_{1}}{{{\mathbf{V}}}_{1}}\left( 0 \right) + {{c}_{2}}{{{\mathbf{V}}}_{2}}\left( 0 \right) + {{c}_{3}}{{{\mathbf{V}}}_{3}}\left( 0 \right) = 0$Чтобы однородная система (5.1) имела нетривиальное решение $\left( {{{c}_{1}},~{{c}_{2}},{{c}_{3}}} \right)$, ее определитель должен быть равен нулю
(5.2)
$\left| {\begin{array}{*{20}{c}} {{{u}_{i}}\left( 0 \right)}&{{{u}_{v}}\left( 0 \right)}&0 \\ {{{v}_{i}}\left( 0 \right)}&{{{v}_{{v1}}}\left( 0 \right)}&{{{{v}}_{{v2}}}\left( 0 \right)} \\ {{{{\theta }}_{i}}\left( 0 \right)}&0&{{{{\theta }}_{v}}\left( 0 \right)} \end{array}} \right| = 0$Равенство (5.2) представляет исходную форму секулярного уравнения, структурно совпадающего с аналогичным уравнением Дана–Линя для совершенного газа. Для дальнейших преобразований удобно раскрыть определитель через отношения элементов в каждом из столбцов. Имеем
(5.3)
$\frac{{{{v}_{i}}\left( 0 \right)}}{{{{u}_{i}}\left( 0 \right)}} = \frac{{{{{\theta }}_{i}}\left( 0 \right)}}{{{{u}_{i}}\left( 0 \right)}}\frac{{{{v}_{{v2}}}\left( 0 \right)}}{{{{{\theta }}_{v}}\left( 0 \right)}} + \frac{{{{v}_{{v1}}}\left( 0 \right)}}{{{{u}_{v}}\left( 0 \right)}}~$Используя систему уравнений для невязких возмущений и формулы (3.9), получим выражение
Соотношение (5.4) позволяет разделить в уравнении (5.3) “невязкую” и “вязкую” части. В результате имеем
(5.5)
$\frac{{{{v}_{i}}\left( 0 \right)}}{{{{u}_{i}}\left( 0 \right)}} = \frac{{\frac{{{{v}_{{v1}}}\left( 0 \right)}}{{{{u}_{v}}\left( 0 \right)}} + \left( {{\gamma } - 1} \right)c{{{\text{M}}}^{2}}{\Delta }\frac{{{{v}_{{v2}}}\left( 0 \right)}}{{{{{\theta }}_{v}}\left( 0 \right)}}}}{{1 - i\left( {{\gamma } - 1} \right){{{\text{M}}}^{2}}U_{s}^{'}{\Delta }\frac{{{{v}_{{v2}}}\left( 0 \right)}}{{{{{\theta }}_{v}}\left( 0 \right)}}}}~$Для преобразования “вязкой” правой части уравнения (5.5) введем функцию Титьенса
Функция Эйри первого рода связана с функцией Ханкеля первого рода порядка 1/3 соотношением [23]
(5.6)
$F\left( z \right) = - \frac{{{{A}_{1}}\left( { - z,2} \right)}}{{z{{A}_{1}}\left( { - z,1} \right)}}~,\quad G\left( z \right) = - \frac{{{{A}_{1}}\left( { - z,1} \right)}}{{z{{A}_{1}}\left( { - z} \right)}}$Выполнив в решениях (4.13) и (4.17) замену ${\zeta } = - z$, с учетом соотношений (5.6) получаем
(5.7)
$\frac{{{{v}_{{v1}}}\left( 0 \right)}}{{{{u}_{v}}\left( 0 \right)}} = iz\frac{{dY}}{{d{\zeta }}}\frac{{dy}}{{dY}}\left( { - \frac{{{{A}_{1}}\left( { - z,2} \right)}}{{z{{A}_{1}}\left( { - z,1} \right)}}} \right) = iz\frac{{dY}}{{d{\zeta }}}\frac{{dy}}{{dY}}F\left( z \right) = KF\left( z \right)$Другое отношение “вязких” решений, входящее в уравнения (5.5), преобразуем следующим образом:
На основе численных расчетов кривых нейтральной устойчивости [7] имеет место оценка
В результате получаем
(5.8)
$\frac{{{{v}_{{v2}}}\left( 0 \right)}}{{{{{\theta }}_{v}}\left( 0 \right)}} = \frac{{ic}}{{{{T}_{s}}\left( 0 \right)}}\frac{{dy}}{{d{{Y}_{ + }}}}\frac{{dY}}{{d{{{\zeta }}_{ + }}}}G\left( {{{z}_{ + }}} \right) = {{K}_{{\theta }}}G\left( {{{z}_{ + }}} \right)$Вычислив производные при $y = 0$, множители перед функциями в (5.7) и (5.8) можно записать в виде
(5.9)
$\begin{gathered} K = \frac{3}{2}\sqrt {\frac{{{{{\eta }}_{s}}{{T}_{s}}\left( 0 \right)}}{c}} \,\mathop \smallint \limits_0^{{{y}_{c}}} \,\sqrt {\frac{{{{U}_{s}} - c}}{{{{{\eta }}_{s}}{{T}_{s}}}}} ~dt,\quad {{K}_{{\theta }}} = \frac{3}{2}\frac{{\sqrt c }}{{{{T}_{s}}\left( 0 \right)}}\sqrt {{{{\eta }}_{s}}{{T}_{s}}\left( 0 \right)} \,\mathop \smallint \limits_0^{{{y}_{c}}} \,\sqrt {\frac{{{{U}_{s}} - c}}{{{{{\eta }}_{s}}{{T}_{s}}}}} ~dt \\ K = \frac{{{{T}_{s}}\left( 0 \right)}}{c}{{K}_{{\theta }}} \\ \end{gathered} $Используя соотношения (5.7)–(5.9), преобразуем уравнение (5.5), разрешив полученное выражение относительно ${\Pi }\left( 0 \right)$. В результате получаем секулярное уравнение в виде
(5.10)
${\Pi }\left( 0 \right) = \frac{{p{\text{'}}\left( 0 \right)}}{{{{\alpha }^{2}}p\left( 0 \right)}} = \frac{{c\left( {1 + {\lambda }} \right)\left[ {F\left( z \right) + N{\Delta }G\left( {{{z}_{ + }}} \right)} \right]}}{{\left( {1 + {\lambda }} \right)U_{s}^{'}\left( 0 \right)F\left( z \right) - i}},$6. Асимптотики секулярного уравнения. Функции $F\left( z \right)$ и $G\left( z \right)$ табулированы [24, 25] до значений $z \leqslant 10$. В проводимых расчетах требуется знать решение секулярного уравнения для больших значений $z$. Для расчета функций $F\left( z \right)$ и $G\left( z \right)$ для больших значений аргумента использовались асимптотические представления [19, 21]:
Представляет интерес приближенная оценка минимального критического числа Рейнольдса ${\text{R}}{{{\text{e}}}_{{{\text{cr}}}}}$, подобная полученной ранее [15, 25] для совершенного газа. Необходимо отметить, что для оценки отдельных членов секулярного уравнения (5.10) при асимптотиках $\alpha \operatorname{Re} \gg 1$, $\alpha \ll 1$ в [15, 25] использовались профили параметров несущего потока, близкие к автомодельным профилям, получаемым из системы (2.1), (2.2). В частности, профиль скорости аппроксимировался сочленением прямой и дуги параболы, а температура получалась из интеграла Крокко аналогичной системы. Это позволяет воспользоваться с минимальными изменениями ранее полученными результатами [26], детально изложенными в [15, 25]: $1 + {\lambda } \cong 1$ и $N\Delta G \ll 1$. При этом уравнение (5.10) преобразуется к виду
(6.1)
${\Pi }\left( 0 \right) = \frac{{F\left( z \right)}}{{1 - F\left( z \right)}} = \tilde {F}\left( z \right) - 1 = {{\tilde {F}}_{r}}\left( z \right) + i{{\tilde {F}}_{i}}\left( z \right) - 1,$(6.2)
$\begin{gathered} c{\Pi }\left( 0 \right) = c{{{\Pi }}_{r}}\left( 0 \right) + ic{{{\Pi }}_{i}}\left( 0 \right) \equiv u + iv = \\ = \frac{{cU_{s}^{'}\left( 0 \right)}}{{{{T}_{s}}\left( 0 \right)}}~\left[ {{{K}_{1}}\left( c \right) + \frac{{{{T}_{s}}\left( 0 \right)}}{{cU_{s}^{'}\left( 0 \right)}} + \frac{{\sqrt {1 - m_{r}^{2}{{M}^{2}}{{{\left( {1 - c} \right)}}^{2}}} }}{{\alpha {{{\left( {1 - c} \right)}}^{2}}}}} \right]~ \\ \end{gathered} $При выводе соотношения (6.2) использовано представление “невязких” решений системы (1.1)–(1.6) рядами по степеням ${{\alpha }^{2}}$, в котором удержаны только первые члены разложения [15, 25], а функция ${{K}_{1}}\left( c \right)$ здесь имеет вид
При малых волновых числах ${\alpha }$
Вершине кривой нейтральной устойчивости, дающей значение ${\text{R}}{{{\text{e}}}_{{{\text{cr}}}}}$, соответствует максимум ${{\tilde {F}}_{i}}\left( z \right)$ = 0.58, при значении аргумента $z$ = 3.24. При этом ${{\tilde {F}}_{r}}\left( z \right)$ = 1.46. Из соотношений (6.1) и (6.2) следует система для определения критических значений ${{c}_{{{\text{cr}}}}}$ и ${{{\alpha }}_{{{\text{сr}}}}}$:
(6.3)
$\frac{{{{c}_{{{\text{cr}}}}}U_{s}^{'}\left( 0 \right)}}{{{{T}_{s}}\left( 0 \right)}}{{K}_{{{\text{1}}i}}}\left( {{{c}_{{{\text{cr}}}}}} \right) = 0.58,\quad \frac{{{{c}_{{{\text{cr}}}}}U_{s}^{'}\left( 0 \right)}}{{{{T}_{s}}\left( 0 \right)}}~\frac{{\sqrt {1 - m_{r}^{2}{{{\text{M}}}^{2}}{{{\left( {1 - {{c}_{{{\text{cr}}}}}} \right)}}^{2}}} }}{{\alpha {{{\left( {1 - {{c}_{{{\text{cr}}}}}} \right)}}^{2}}}} = 0.46$Здесь
После нахождения значений ${{c}_{{{\text{cr}}}}}$ и ${{\alpha }_{{{\text{сr}}}}}$ критическое число Рейнольдса, определенное по текущей длине $L$ пластины, вычисляется как
(6.4)
${\text{R}}{{{\text{e}}}_{{{\text{cr}}}}} = {{\left[ {\frac{{{{\alpha }_{{{\text{cr}}}}}}}{{{{{3.24}}^{3}}}}{{{\left( {\frac{3}{2}\,~\mathop \smallint \limits_{{{y}_{c}}}^y \,\sqrt {\frac{{{{U}_{s}} - c}}{{{{{\eta }}_{s}}{{T}_{s}}}}} } \right)}}^{2}}} \right]}^{{ - 1}}},$(6.5)
${\text{R}}{{{\text{e}}}_{{{\delta },{\text{cr}}}}} = \sqrt {{\text{R}}{{{\text{e}}}_{{{\text{cr}}}}}} $В табл. 1 представлены полученные из решения уравнений (6.3)–(6.5) числовые оценки критических чисел Рейнольдса ${\text{R}}{{{\text{e}}}_{{{\delta },{\text{cr}}}}}$, волновых чисел ${{{\alpha }}_{{{\text{cr}}}}}$ и фазовых скоростей ${{c}_{{{\text{cr}}}}}$ для совершенного (${{{\gamma }}_{v}} = 0$) и колебательно возбужденного (${{{\gamma }}_{v}} = 0.667$) газов. Видно, что при максимальном уровне колебательного возбуждения оценки значений критических чисел Рейнольдса ${\text{R}}{{{\text{e}}}_{{{\delta },{\text{cr}}}}}$ примерно на 7% выше, чем их значения в совершенном газе.
Таблица 1.
Оценки критических чисел Рейнольдса ${{\operatorname{Re} }_{{\delta ,\operatorname{cr} }}}$ и волновых чисел ${{\alpha }_{{\operatorname{cr} }}}$
| M | ${{\operatorname{Re} }_{{\delta ,\operatorname{cr} }}}$ | ${{\alpha }_{{\operatorname{cr} }}}$ | ${{c}_{{\operatorname{cr} }}}$ | |||
|---|---|---|---|---|---|---|
| ${{\gamma }_{{v}}} = 0$ | 0.667 | 0 | 0.667 | 0 | 0.667 | |
| 2.2 | 230 | 245 | 0.0637 | 0.0697 | 0.6161 | 0.5988 |
| 4.5 | 183 | 194 | 0.2051 | 0.2109 | 0.9083 | 0.8830 |
| 4.8 | 138 | 147 | 0.1754 | 0.1812 | 0.9164 | 0.8907 |
7. Численные расчеты нейтральных кривых. В расчетах спектров вязких возмущений число Рейнольдса ${\text{Re}}$, определенное по текущей длине $L$, было заменено на число ${\text{R}}{{{\text{e}}}_{{\delta }}} = \sqrt {{\text{Re}}} $, определенное по местной толщине пограничного слоя. Секулярное уравнение (5.10) имеет структуру, аналогичную структуре уравнений, рассматривавшихся ранее [15, 19]. Левая “невязкая” часть этого уравнения зависит от фазовой скорости $c$ и волнового числа ${\alpha }$, а правая “вязкая” часть выражается через табулированные функции переменной $z$ и также зависит от $c$. Поэтому координаты точки на кривых нейтральной устойчивости ${\text{R}}{{{\text{e}}}_{{\delta }}}\left( {{\alpha },~{{{\gamma }}_{{v}}},{\text{M}}} \right)$ на плоскости $\left( {{{{\operatorname{Re} }}_{\delta }},~\alpha } \right)$ рассчитывались в той же последовательности, что и в [15, 19]. Все вычисления проводились для времени колебательной релаксации $\tau $ = 1.
Для фиксированных значений числа Маха M и степени колебательной неравновесности ${{{\gamma }}_{v}}$ задавалось очередное значение фазовой скорости $c$ в интервале $c$ = [0, 1] с шагом ${\Delta }c = {{10}^{{ - 4}}}$. Интеграл в правой части секулярного уравнения (5.10) рассчитывался по формуле Симпсона [27]. Действительные и мнимые значения правой части уравнения (5.10) вычислялись для интервала $z$ = [0, 10] с помощью таблиц [24, 25], а для интервала $z$ = [10, 50] – с помощью асимптотической формулы [19, 21]. В расчетах принимался в обоих случаях табличный шаг ${\Delta }z$ = 0.04.
После расчета массивов правой части секулярного уравнения (5.10) вычислялись массивы его левой части для заданного значения $c$ в зависимости от волнового числа $c$ = [0, 0.5] с шагом $\Delta \alpha = {{10}^{{ - 4}}}$. Рассчитанные массивы правой и левой частей (5.10) сравнивались между собой до получения равенства с точностью до ${{10}^{{ - 8}}}$, если оно достигалось при фиксированном значении $c$. Далее расчет повторялся для очередного значения фазовой скорости. В результате были сформированы массивы значений волновых чисел ${{\alpha }_{k}}$, фазовых скоростей ${{c}_{k}}$ и переменной ${{z}_{k}}$, соответствующие точкам на нейтральной кривой. С использованием формулы
Нейтральные кривые для различных мод возмущений при фиксированном значении числа Маха M определялись по интервалам значений фазовой скорости ${{c}_{k}}$ на них. При этом в случае ${{c}_{k}} = \left( {1 - {{{\text{M}}}^{{ - 1}}},~{{c}_{{s1}}}} \right]~$ точки принадлежат кривой нейтральной устойчивости моды I, а в случае ${{c}_{k}} = \left( {{{c}_{{s1}}},{{c}_{{s2}}}} \right]~$ кривым нейтральной устойчивости моды II. Для моды $n$ (где $n$ = 1, 2, …) значения фазовых скоростей ${{c}_{{sn}}}$ при заданном числе Маха определялись из равенства ${{c}_{{sn}}} = {{U}_{s}}\left( {{{{\xi }}_{{sn}}}} \right)$, а координаты точек перегиба ${{{\xi }}_{{sn}}}$ – из уравнения (3.9).
На рис. 2 приведены результаты расчетов кривых нейтральной устойчивости ${\text{R}}{{{\text{e}}}_{{\delta }}}\left( {\alpha } \right)$ для совершенного (${{{\gamma }}_{{v}}} = 0$) и колебательно возбужденного (${{{\gamma }}_{{v}}}$ = 0.667) газов при числах Маха ${\text{M}}$ = 2.2 и 4.5. Сплошные кривые соответствуют решению исходной спектральной задачи (1.1)–(1.6), а штриховые – асимптотическому решению (5.10). Точки ${{K}_{1}}$, $K_{1}^{'}$ и ${{K}_{2}}$, $K_{2}^{'}$ на нейтральных кривых представляют собой критические точки для мод I и II, а прямые ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ – асимптоты при ${\text{R}}{{{\text{e}}}_{{\delta }}} \to \infty $ для первой и второй мод, полученные ранее Мэком в работе [8]. Области неустойчивости мод I и II на фигуре обозначены, соответственно, римскими цифрами I и II.
Рис. 2.
Кривые нейтральной устойчивости ${{\operatorname{Re} }_{\delta }}\left( \alpha \right)$ для мод I и II.

Расчеты показали, что при ${\text{M}}$ = 2.2 существует только первая неустойчивая мода, представляющая собой обобщение волны Толлмина–Шлихтинга на сжимаемый пограничный слой [8]. Из графиков видно, что асимптотические кривые удовлетворительно согласуются с результатами, полученными для исходной спектральной задачи (1.1)–(1.6). При этом переход к асимптотической теории приводит к расширению областей неустойчивости обеих мод и уменьшению критических значений их чисел Рейнольдса.
Из поведения кривых нейтральной устойчивости следует, что учет колебательной релаксации в уравнениях исходной спектральной задачи (1.1)–(1.6) и секулярном уравнении (5.10) (асимптотической теории) приводит к уменьшению размеров областей неустойчивости обеих мод и росту критических значений их чисел Рейнольдса.
В табл. 2 сравниваются значения критических чисел Рейнольдса ${\text{R}}{{{\text{e}}}_{{{\delta },{\text{cr}}}}}$ и волновые числа ${{\alpha }_{{{\text{cr}}}}}$, полученные из численного решения исходной спектральной задачи и даваемые асимптотической теорией. Видно, что для обеих мод критические значения чисел Рейнольдса, вычисленные по асимптотической теории, приблизительно на 14–15% меньше соответствующих значений, полученных при численном решении полной спектральной задачи. При этом учет колебательной релаксации приводит к возрастанию значений критических чисел Рейнольдса ${\text{R}}{{{\text{e}}}_{{{\delta },{\text{cr}}}}}$ обеих мод примерно на 12–13% относительно их значений в совершенном газе.
Таблица 2.
Критические числа Рейнольдса ${\text{R}}{{{\text{e}}}_{{{\delta },{\text{cr}}}}}$ и волновые числа ${{\alpha }_{{\operatorname{cr} }}}$ для мод I и II
| M | ${{\operatorname{Re} }_{{\delta ,\operatorname{cr} }}}$ | ${{\alpha }_{{\operatorname{cr} }}}$ | ||||||
|---|---|---|---|---|---|---|---|---|
| Решение уравнений (1.1)–(1.6) | Решение уравнения (5.10) | Решение уравнений (1.1)–(1.6) | Решение уравнения (5.10) | |||||
| ${{\gamma }_{v}} = 0$ | 0.667 | 0 | 0.667 | 0 | 0.667 | 0 | 0.667 | |
| Мода I | ||||||||
| 2.2 | 281 | 317 | 240 | 271 | 0.0580 | 0.0635 | 0.0626 | 0.0685 |
| 4.5 | 462 | 521 | 396 | 446 | 0.0650 | 0.0708 | 0.0653 | 0.0712 |
| 4.8 | 440 | 496 | 377 | 425 | 0.0701 | 0.0763 | 0.0705 | 0.0767 |
| Мода II | ||||||||
| 4.5 | 221 | 250 | 191 | 214 | 0.2001 | 0.2060 | 0.2015 | 0.2072 |
| 4.8 | 168 | 191 | 144 | 163 | 0.1710 | 0.1772 | 0.1722 | 0.1783 |
Заключение. Для сверхзвукового пограничного слоя колебательно возбужденного газа на плоской пластине в рамках линейной теории устойчивости выведено секулярное уравнение и построены асимптотические решения спектральной задачи в случае двумерных дозвуковых возмущений.
Рассчитаны кривые нейтральной устойчивости рассматриваемого течения, удовлетворительно согласующиеся с результатами прямого численного решения исходной спектральной задачи.
Получена система для упрощенного расчета критических чисел Рейнольдса, решения которой также удовлетворительно согласуются как с численными расчетами в полной постановке, так и с решениями асимптотического секулярного уравнения.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 17-01-00209а).
Список литературы
Гапонов С.А., Петров Г.В. Устойчивость пограничного слоя неравновесного диссоциирующего газа. Новосибирск: Наука, 2013
Grigoryev Yu.N., Ershov I.V. Stability and Suppression of Turbulence in Relaxing Molecular Gas Flows. Cham: Springer, 2017. 233 p.
Johnson H.B., Seipp T., Candler G.V. Numerical study of hypersonic reacting boundary layer transition on cones // Phys. Fluids. 1998. V. 10. P. 2676–2685.
Fujii K., Hornung H.G. Experimental investigation of high-enthalpy effects on attachment-line boundary layer // AIAA J. 2003. V. 41. № 7. P. 1282–1291.
Wagnild R.M., Candler G.V., Leyva I.A., Jewell J.S., Hornung H.G. Carbon dioxide injection for hypervelocity boundary layer stability // AIAA Paper 2010–1244. 2010. P. 1–16.
Bertolotti F.B. The influence of rotational and vibrational energy relaxation on boundary layer stability // J. Fluid Mech. 1998. V. 372. P. 93–118.
Григорьев Ю.Н., Ершов И.В. Линейная устойчивость сверхзвукового пограничного слоя релаксирующего газа на пластине // Изв. РАН. МЖГ. 2019. № 3. С. 3–15.
Mack L.M. Boundary Layer Stability Theory. JPL Technical Rep., Document 900–277. Pasadena: California Instit. Technology, 1969. 272 p.
Молевич Н.Е. Асимптотический анализ устойчивости плоскопараллельного пограничного слоя сжимаемого релаксирующего газа // Изв. РАН. МЖГ. 1999. № 5. С. 82–88.
Завершинский И.П., Кнестяпин В.Н. Устойчивость трехмерных возмущений малой амплитуды в неравновесном сжимаемом пограничном слое // Теплофиз. высоких температур. 2007. Т. 45. № 2. С. 235–242.
Лойцянский Л.Г. Механика жидкости и газа. М.; Л.: ГИТТЛ, 1950. 676 с.
Нагнибеда Е.А., Кустова Е.В. Кинетическая теория процессов переноса и релаксации в потоках неравновесных реагирующих газов. С.-Петербург: Изд-во СПбГУ, 2003. 272 с.
Осипов А.И., Уваров А.В. Кинетические и газодинамические процессы в неравновесной молекулярной физике // УФН. 1992. Т. 162. № 11. С. 1–42.
Dunn D.W., Lin C.C. On the stability of the laminar boundary layer in a compressible fluid // J. Aeron. Sci. 1955. V. 22. № 7. P. 455–477.
Линь Цзя-цзяо Теория гидродинамической устойчивости. М.: Изд-во иностр. лит., 1958. 194 с.
Ферцигер Дж., Капер Г.К. Математическая теория процессов переноса в газах. М.: Мир, 1976. 555 с.
Кэй Дж., Лэби Т. Таблицы физических и химических постоянных. М.: Физматгиз, 1962. 248 с.
Григорьев Ю.Н., Ершов И.В. Линейная устойчивость невязкого сдвигового течения колебательно возбужденного двухатомного газа // ПММ. 2011. Т. 75. Вып. 4. С. 581–593.
Григорьев Ю.Н., Ершов И.В. Асимптотическая теория кривой нейтральной устойчивости течения Куэтта сжимаемого и колебательно-возбужденного газа // ПМТФ. 2017. Т. 58. № 1. С. 3–21.
Трикоми Ф. Дифференциальные уравнения. М.: Изд-во иностр. лит., 1962. 351 с.
Reshotko E. Stability of the Compressible Laminar Boundary Layer. GALCIT Hypersonic Res. Proj. Memorandum № 52. Pasadena: California Inst. Technol., 1960. 168 p.
Фок В.А. Проблемы дифракции и распространения радиоволн. М.: Советское радио, 1970. 520 с.
Drazin P.G., Reid W.H. Hydrodynamic Stability. Cambridge: Univ. Press, 2004. 605 p.
Miles J.W. The hydrodynamic stability of a thin film of liquid in uniform shearing motion // J. Fluid Mech. 1960. V. 8. P. 593–610.
Гапонов С.А., Маслов А.А. Развитие возмущений в сжимаемых потоках, Новосибирск: Наука, 1980. 144 с.
Lees L. The Stability of the Laminar Boundary Layer in a Compressible Fluid. NACA Technical note, No.1360. Washington: NACA, 1947. 169 p.
Корн Г., Корн Т. Справочник по математике. М.: Наука, 1973. 720 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика