Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 734-748

Введение. В середине ХХ века стали актуальны задачи построения оптимальных головных частей, которые, примыкая к заданному телу вращения, обладали бы минимальным сопротивлением при полете со сверх- и гиперзвуковыми скоростями. Взяв для определения давления на искомых головных частях весьма простую локальную формулу, предложенную еще Ньютоном, аэродинамики США и СССР попытались решить возникшие задачи при разных дополнительных ограничениях. Решение одной из таких задач (“задачи Ньютона”), отвечающей заданному удлинению головной части, в форме краткого “Поучения” из 30 строк и двух рисунков дано Ньютоном в его “Математических началах натуральной философии”. В России “Начала” в переводе с латыни А.Н. Крылова были изданы сначала в 1916 г., затем в 1936 г. в собрании сочинений А.Н. Крылова и только в 1989 г. в том же переводе – отдельным изданием. Несомненное достоинство крыловского перевода – подробные примечания и разъяснения, в том числе, упомянутого “Поучения”, многократно превышающие по объему оригинальный текст Ньютона. Ничего подобного нет в зарубежных переводах “Начал”: у нас британского гения переводил русский гений.

Несмотря на наличие, казалось бы, готового решения (правда, без объяснений, зато с бесценными разъяснениями А.Н. Крылова), и задача Ньютона, и ее обобщения (например, с заменой заданного удлинения фиксированным объемом головной части) оказались не по зубам аэродинамикам середины ХХ века. Причина – их математическая подготовка, в которой место только входившей в жизнь “Математической теории оптимального управления” занимало “Вариационное исчисление” в основном с двусторонними экстремалями, определяемыми уравнением (или уравнениями) Эйлера. В обсуждаемых задачах для решения также нужны односторонние экстремали, место которых в “Началах” и в комментариях А.Н. Крылова заняли геометрические построения, эквивалентные, но непривычные и поэтому трудные для понимания читателям ХХ века.

Более полное описание сказанного выше, а также захватывающего (почти детективного) продолжения с середины ХХ до начала XXI века истории решения задачи построения оптимальных головных частей, в которой автору и его учителям Горимиру Горимировичу Черному и Юрию Дмитриевичу Шмыглевскому посчастливилось участвовать, – основной предмет данной статьи.

1. Задача Ньютона и проблемы с ее решением. В середине ХХ века выяснилось, что предложенная Ньютоном формула для давления р на поверхности тела с внутренней нормалью n к его контуру:

неплохо работает при гиперзвуковых скоростях полета. Здесь ρ – плотность газа, V – вектор его скорости, θ – угол касательной к контуру тела с осью х, а индексом 0 отмечены параметры набегающего потока. Формула (1.1) получается, если принять, что частицы газа движутся до поверхности тела, не изменяя своей начальной скорости V₀, а при соударении с телом, потеряв ее нормальную к поверхности составляющую, продолжают движение вдоль его поверхности. Тогда же аэродинамики, используя формулу (1.1), обратились к решению задачи Ньютона о построении контура if плоской симметричной или осесимметричной головной части минимального сопротивления при заданных длине L и полувысоте или радиусе основания Y для плоских и осесимметричных тел (рис. 1, декартовы или цилиндрические координаты х и у отнесены к Y, l = = L/Y – удлинение головной части) и ее обобщений и сразу столкнулись с неожиданными, на первый взгляд, трудностями. Поясним их суть.

При выборе полувысоты или радиуса основания в качестве линейного масштаба 0 ≤ х ≤ l, 0 ≤ у ≤ 1, и для головной части с образующей х = х(у) в согласии с формулой (1.1) коэффициент волнового сопротивления имеет вид (ν = 0 для плоских тел и ν = 1 для осесимметричных)

Отсюда при малых варьированиях контура, т.е. при замене х и x' на x + δx и x' + δx' с точностью до квадратов вариаций для приращения с_х получим

Поэтому, если контур if реализует минимум с_х, то при малых δх и δx' в силу выражения (1.2) условия оптимальности сведутся к равенству (необходимому условию экстремума с_х – уравнению Эйлера) и неравенству (необходимому условию минимума с_х – условию Лежандра)

Уравнение Эйлера интегрируется и дает интеграл

В плоском случае отсюда следует, что

т.е. оптимальный контур – прямая: х = lу при 0 ≤ y ≤ 1. Правда, возникает вопрос: при любых ли x' = l будет выполняться условие Лежандра: φ_х'х' ≥ 0 и что делать, если оно нарушится? Согласно формуле для φ(х') имеем и это условие в осесимметричном и в плоском случаях выполняется при

Для плоской головной части x' = l, и при l < 1/3^1/2 условие Лежандра нарушается, т.е. найденное решение непригодно.

Еще хуже ситуация с осесимметричными головными частями, для которых в силу интеграла (1.4): yφ_x' = const = (yφ_x')_i = 0⋅(φ_x')_i. = 0. Отсюда в общем случае φ_x' = 0, а в силу формулы (1.5) φ_x' = 0 при x' = 0 и x' = ∞. Значению x' = 0 отвечают торцы: х ≡ const, а x' = ∞ – цилиндрические участки: у ≡ const. При 0 < l < ∞ любая соединяющая точки i и f их ступеньчатая комбинация дает не минимум, а максимум c_x = 1.

С такими же проблемами столкнулись Г.Г. Черный и его аспирант А.Л. Гонор [1], которые попытались решить ту же задачу в рамках формулы (1.1), подправленной А. Буземаном (“закона сопротивления Ньютона–Буземана”). В результате они ограничились контурами тел вращения с протоком.

2. К решению задачи Ньютона в Советском Союзе. Немного предыстории. С осени 1956 г. автор – студент МФТИ (Московского физико-технического института) с базовой кафедрой в ЦИАМ (Центральном институте авиационного моторостроения им. П.И. Баранова) проходил практику в лаборатории “Газовой динамики” (лаб. № 4) этого института. Начальником лаб. № 4 был тогда 33-х летний Горимир Горимирович Черный, а руководителем автора – экспериментатор Владимир Васильевич Поляков.

По окончании в начале 1959 г. МФТИ автор стал постоянным сотрудником лаб. № 4, а с осени того же года по инициативе В.В. Полякова был командирован в Вычислительный центр (ВЦ) АН СССР для овладения численными методами газовой динамики и опытом работы на лучшей отечественной вычислительной технике. Там ему посчастливилось сблизиться с Юрием Дмитриевичем Шмыглевским – признанным специалистом по вариационным задачам газовой динамики, заведующим лаборатории “Механики сплошной среды” ВЦ. Общение с ним оказалось весьма плодотворным, и вскоре после докладов на руководимом Г.Г. Черным семинаре в лаб. № 4 ЦИАМ автора также признали специалистом в указанной области.

Обсуждая с Ю.Д. Шмыглевским разные проблемы, автор, как и его новый коллега и учитель, всерьез интересовался оптимальным профилированием “в точной постановке” – в рамках полных уравнений газовой динамики идеального (невязкого и нетеплопроводного) газа. Приближенные постановки с привлечением локальных формул для давления типа формулы Ньютона или Ньютона–Буземана интересовали его слегка (“для общего развития”). Так было и со статьей [1], прочитанной “по диагонали” без попыток разобраться, в чем дело.

Ситуация резко изменилась в конце осени – начале зимы 1962 г. В декабре того года фирма “Боинг” проводила в своей штаб-квартире в Сиэтле конференцию по оптимальным аэродинамическим формам. Из советских аэродинамиков на нее был приглашен Г.Г. Черный. Один из его докладов касался работы [1] и, естественно, описанной выше проблемы с осью симметрии, которую они с Александром Львовичем (тогда “Сашей”) Гонором не могли решить. Поэтому А.Л. Гонор, повстречав в ЦИАМ своего тезку и, вроде бы, специалиста, сказал: “Саша, подумай, вдруг, чего-нибудь сообразишь”.

Приехав в ВЦ, автор этой статьи взял в библиотеке “Основы вариационного исчисления” М.А. Лаврентьева и Л.А. Люстерника, вспомнил то, чему его учили в МФТИ, проделал необходимые выкладки, пришел к результатам, описанным в разд. 1, и, ничего не сообразив, пошел домой, чтобы утром проснуться с готовым решением.

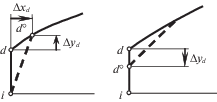
На следующее утро автор проделал такой мысленный эксперимент [2]. Ранее, как само собой разумеющееся, полагалось, что из точки i образующая if идет сразу вправо. А если не так? Составим ее из двух участков (рис. 2): идущего влево отрезка ii° оси х и наклонного участка i°f. Для такой образующей в рамках формулы Ньютона (1.1) и без вариационного исчисления с_х → 0 при х_i° → –∞. Но – тут же спохватился экспериментатор – мы ведь задавали длину головной части, и потому нельзя вылезать за ось у! Значит, оптимальный контур может содержать передний торец id (рис. 3), появляющийся из-за ограничения длины головной части как участок краевого экстремума (КЭ). На нем допустимые вариации δх ≥ 0, и потому в отличие от участков двустороннего экстремума (ДЭ) с допустимыми δх любого знака на нем уравнение Эйлера выполняться не обязано.

Правда, как установлено выше, на торце id – вертикальном участке КЭ уравнение Эйлера, тем не менее, выполняется, зато нарушается условие Лежандра. Однако это несущественно. Важно другое: по формуле Ньютона величину с_х уменьшают выемки на любом участке образующей (рис. 3), и чем их больше, тем меньше с_х. Для контура в виде “ежа” с бесконечным числом таких выемок и выступов с_х = 0. Однако, несмотря на это, решение с передним торцом верно, поскольку торец – участок КЭ не только из-за ограничения по длине головной части, но и как граница применимости формулы Ньютона. Для головной части она справедлива, если 0 ≤ θ ≤ π/2, и передний торец – участок КЭ одновременно и по х, и по θ.

Итак, при решении задачи Ньютона и ее обобщений в рамках формулы (1.1) на искомом оптимальном контуре х, у и θ удовлетворяют ограничениям

Любое равенство в них может приводить к появлению участка КЭ.

Решение любой задачи современной теории оптимального управления начинается с записи всех ограничений типа неравенств (2.1), и участки КЭ в ней столь же обычны, как и участки ДЭ. В классическом вариационном исчислении об участках КЭ вспоминали лишь в исключительных случаях. Современная теория оптимального управления в середине ХХ века только начинала свое развитие и обязательная запись ограничений типа (2.1) и появление вместе с ними участков КЭ были незнакомы аэродинамикам того времени. Притом, что участки КЭ столь же естественны, как значения функции на границах области изменения независимых переменных при поиске ее максимальной или минимальной величины.

Вооруженный знанием структуры искомого контура автор в то далекое время вернулся к решению заинтриговавшей его задачи. Если оптимальный контур содержит передний торец id_– и пологий участок d₊ f, то при варьировании наряду с допустимыми в силу условий (2.1) вариациями δх' и δх на id_– и d₊ f появятся (рис. 4) приращения координат точки их стыковки Δу_d и Δx_d. Индексы – и + метят параметры до и после точки стыковки при движении по if от точки i. На рис. 4 штрихами даны измененные участки контура и учтено, что в силу условий (2.1) на торце допустимые δх' ≥ 0.

Из-за варьирования координат точки d в выражении (1.2) для приращения с_х добавится слагаемое

Здесь многоточием обозначен интеграл из правой части равенства (1.2) от y_d до 1. Учтено, что на торце х' = 0, φ_х'(0) ≡ 0, а в силу формулы для Δx_d интегральное слагаемое от 0 до y_d с (δх')² много меньше, чем Δx_d.

Как видно из рис. 4, в точке d допустимы приращения Δу_d любого знака при допустимых Δх_d ≥ 0. Поэтому для оптимального контура

Положительность при $x_{{d + }}^{'} = 1$ коэффициента при Δх_d в первом равенстве (2.2) показывает, что с_х при допустимых Δх_d ≥ 0 растет, и передний торец – участок КЭ.

В силу сказанного выше, оптимальные контуры плоских головных частей при l ≥ 1 – наклонные прямые, а при l < 1 – комбинация торца и отрезка прямой х' = 1 (рис. 5). Как показало прямое сравнение значений с_х, при 1/3^1/2 ≤ l < 1 удовлетворяющие условию Лежандра наклонные прямые дают большее сопротивление, чем контуры с торцом.

Следствия утреннего “эксперимента” были получены в тот же день. Рассказ же о них Ю.Д. Шмыглевскому вызвал бурю восторга: “Александр Николаевич, немедленно пишите статью” – его совет. У Александра Николаевича, однако, были естественные сомнения: “Неужели этого никто не знал?” – спрашивал он себя и с этим вопросом отправился в библиотеку соседнего с ВЦ Математического института им. В.А. Стеклова АН СССР.

Начав искать в картотеке Ньютона, был удивлен отсутствием его сочинений на русском языке. Стал искать на английском и нашел издание [3] с картинкой в примечаниях, эквивалентной рис. 3 (в “Началах” поток течет справа налево, иные обозначения точек и нет остроконечных “выемок”). С Ньютоном все стало ясно (“Наверняка, он знал изложенное выше”). А как с другими? Авторы отчета NACA [4], столкнувшись в задаче Ньютона с “проблемой оси симметрии” для ее разрешения, “следуя Ньютону”, ввели передний торец без объяснения причин его появления. Почему появился торец у Ньютона, автора тогда не интересовало, ибо ничего отличного от его “эксперимента” он себе просто не представлял.

Через пару дней уже в ЦИАМ произошла встреча с А. Гонором. “Все это – чушь” сказал тот. “Но ведь то же самое – у Ньютона и американцев”. “И Ньютон, и американцы ничего не понимали” – окончательное резюме А. Гонора. “Ну что ж, пусть нас рассудит Учитель” – сказал автор и подал заявку на семинар Г.Г. Черного. Доклад на ближайшем семинаре вызвал уже описанную реакцию А. Гонора. Автор произносит “заключительное слово” и еще стоит у доски, когда руководитель семинара, ничего не объяснив (вопреки традиции, но ведь А. Гонор – его первый аспирант), объявляет: “Семинар окончен. Александр Николаевич и Александр Львович, останьтесь”.

Остаются трое, и сразу вопрос Г.Г. Черного: “Александр Николаевич, где Вы это у Ньютона нашли?” То, что его искренний ответ: “В американском издании [3]” не соответствовал действительности, автор ничего не подозревая, узнал только через 40 лет, но об этом позже. Пока же заметим, что на самом деле, объяснения причин появления в решении торца не было ни в одном издании “Начал”, включая [3]. Несмотря на это, после вопроса Г.Г. Черного стало ясно, что Учитель признал правоту автора. С тех пор передний торец фигурирует как участок КЭ не только в рамках формулы Ньютона [5, 6], но и в приближении полных уравнений течения идеального газа [7–10].

Казалось бы, с оптимальными в рамках формулы Ньютона головными частями все стало ясно. Однако через 25 лет эта увлекательная история получила неожиданное развитие. В конце лета 1988 г. во время конференции, проходившей на озере Байкал, к автору обратилась аспирантка из Иркутска Ольга Гильман: “Александр Николаевич, я решила задачу, которую не смог решить Эггерс [11]. Об оптимальной головной части заданного объема Ω или ω = Ω/(πY³) вместо заданной длины L или удлинения l. Вы же должны знать об этой проблеме как один из переводчиков сборника докладов конференции в Сиэтле в 1962 году. Эггерс, а еще раньше он с коллегами [4], не сумели построить решение для всех возможных значений ω от 0 до ∞. Я же, введя внутренний торец, его построила”.

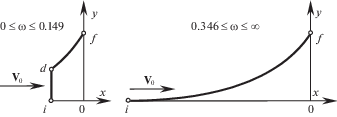
Вернувшись в Москву, автор выяснил, что Эггерс с коллегами [4, 11] при малых ω, “следуя Ньютону”, искали решение с передним торцом (рис. 6, слева). Однако в задаче с заданным объемом и свободной длиной головной части тела он мог быть участком КЭ только по θ (в задаче Ньютона передний торец – участок КЭ и по θ, и по х), но, как сразу было установлено, он таковым не является (впрочем, как и внутренние торцы, введенные аспиранткой из Иркутска). Согласившись поэтому с оценкой А. Гонором работ американцев, напомним их “решение”.

Начнем с того, что тут, в отличие от задачи Ньютона, образующая df не выпуклая, а вогнутая, и при движении от точки d к точке f угол θ растет. В точке d по-прежнему θ_d+ = 45°. Поэтому величина θ_f > 45°, причем она тем больше, чем больше ω, достигая 60° при ω = 0.149. При еще больших ω из-за нарушения условия Лежандра (1.6) решения [4, 11] с передним торцом непригодны. Похожая ситуация с большими ω. Для них оптимальны остроконечные головные части (рис. 6, справа), а θ_f растет с уменьшением ω, достигая 60° при ω = 0.346. В результате был сделан [4, 11] ошибочный вывод: при 0.149 < ω < 0.346 “решение, если и существует, то не может быть получено в данной постановке”.

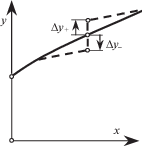
Случилось так, что построение правильного решения [12] совпало с выводом необходимого условия минимума с_х, более сильного, чем условие Лежандра. Для этого наряду с малыми (слабыми) вариациями δх' в окрестности произвольной внутренней точки участка ДЭ вводится малая вертикальная ступенька (рис. 7) с х' = 0 и высотами Δу_– ≤ 0 и Δу₊ ≥ 0. В рассматриваемой задаче величины разнознаковых приращений Δу_– и Δу₊ близки по модулю (для сохранения объема), а в задаче Ньютона произвольны. Из-за такого (сильного) варьирования х' в выражении для приращения с_х добавится слагаемое

где многоточием обозначены вклады отличных от Δу_– и Δу₊ вариаций и приращений.

Согласно принятому способу сильного варьирования (рис. 7) во внутренних точках участка ДЭ допустимые Δу_– ≤ 0, а Δу₊ ≥ 0. Значит, в согласии с условием (2.4) на участке ДЭ должно выполняться необходимое условие минимума с_х

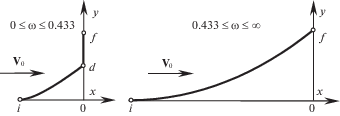
более сильное, чем условие Лежандра (1.6). Все контуры с торцом и часть остроконечных рис. 6 (с θ_f > 45°) этому условию не удовлетворяют. При l < 1 нарушается оно и на прямолинейных образующих рис. 5. Как стало известно автору в начале XXI века (см. ниже), на 75 лет раньше его это условие в задаче Ньютона установил А.Н. Крылов. Поэтому, как и ранее [2], будем называть его “условием Крылова”.

Найденное автором тогда же, хотя и опубликованное с задержкой [12] решение обсуждаемой задачи поясняет рис. 8. Согласно ему и вопреки рис. 6 заостренная головная часть оптимальна при 0.433 ≤ ω ≤ ∞. При 0 < ω < 0.433 в рамках формулы Ньютона (1.1) оптимальны головные части принципиально нового типа: острие, выступающее из заднего торца – участка КЭ, также появляющегося в силу ограничений (2.1) с тем отличием, что теперь начало координат лежит в основании головной части, и первое условие (2.1) заменяется на х ≤ 0. В точке стыковки d острия и заднего торца аналогично задаче Ньютона $x_{{d - }}^{'} = 1$, однако образующая острия id_– вогнутая, что при 0 ≤ у < у_d и обеспечивает выполнение условия Крылова.

В приближении формулы Ньютона в развитие ранее опубликованных результатов [6, 12] построены [13] головные части, оптимальные при заданных L, Y и Ω, точнее, l = = L/Y и с_Ω = Ω/(πLY ²). При этом под заданием Y и l понималось задание габаритов. Так, при больших l и малых с_Ω отнесенная к Y длина головной части может быть меньше l. С другой стороны, при больших с_Ω понимаемое в этом смысле ограничение (2.1) величины у приводит к участку КЭ нового типа – цилиндрическому отрезку: у = 1. Результаты [13] суммирует рис. 9, сплошные кривые которого дают с_х = с_х(с_Ω, l) оптимальных головных частей тел вращения, построенных по формуле Ньютона (1.1). Крайние точки этих кривых отвечают минимально и максимально возможным объемам (с_Ω = 0 и с_Ω = 1). Для них по формуле (1.1) с_x = 1. Для каждого удлинения l кружок дает величину с_x головной части задачи Ньютона, которая для этого значения l минимальна. Между кружками и треугольниками оптимальные контуры состоят из переднего торца и выпуклого участка ДЭ. Треугольники отвечают предельно толстым головным частям такого типа с горизонтальной касательной в точке f. Справа от них оптимальны контуры, состоящие из переднего торца, выпуклого участка ДЭ и концевого участка КЭ: у = 1. Между кружками и квадратиками оптимальные контуры состоят из переднего торца и сначала выпуклых участков ДЭ. С уменьшением с_Ω на участках ДЭ появляются вогнутые участки, а начиная с квадратиков – задний торец. Штрихами даны рассчитанные по формуле Ньютона значения с_х = с_х(с_Ω, l) затупленных или острых конусов, удовлетворяющих тем же, что и оптимальные тела габаритным ограничениям.

Определенные интегрированием уравнений течения идеального газа значения с_х головных частей [14], оптимальных в приближении формулы Ньютона, подтвердили преимущества выпуклых оптимальных контуров. В противоположность этому значения с_х головных частей с вогнутыми участками, а тем более с задним торцом, как правило, получались больше значений с_х эквивалентных конусов. В тех же примерах, где преимущество сохранялось, оно было заметно меньше, найденного по формуле Ньютона. Следствие этих результатов – изменение постановки задачи. На практике задание объема головной части обусловлено размещением в ней полезного груза заданного объема Ω^m. Объем же головной части должен удовлетворять неравенству Ω ≥ Ω^m. Если Ω_PN отвечает решению задачи Ньютона с тем же значением l и со свободным объемом, и Ω_PN ≥ Ω^m, то именно оно со значением с_х = с_хPN, минимальным для заданного l, дает решение задачи. Согласно рис. 9 при этом возможно значительное (при l ≥ ≥ 1 – в разы) уменьшение с_х. С математической точки зрения, такая головная часть – пустотелый обтекатель с располагающимся внутри него (если Ω_PN = Ω^m, то толщина его стенок нулевая) полезным объемом Ω^m. Итак, оптимальные в рамках формулы Ньютона головные части, отвечающие на рис. 9 участкам кривых слева от кружков (с с_Ω < с_ΩPN), не представляют интереса.

3. Возвращение к Ньютону в переводе А.Н. Крылова. История с задачей Ньютона получила неожиданное продолжение в 2002 г. В январе 2003 г. предстоял 80-летний юбилей Г.Г. Черного, который решили отметить выпуском сборника ранее опубликованных работ Учителя, его учеников и ближайших коллег “Механика жидкости и газа. Избранное”. Ответственным редактором этого ретроспективного юбилейного сборника [15] стал автор.

Мировую славу Г.Г Черному принес его метод аналитического расчета обтекания тел при больших сверхзвуковых скоростях. С учетом этого редакторы-составители сборника решили включить в него первый отчет ЦИАМ [16] с описанием метода Черного. Работая с указанным отчетом, ответственный редактор обнаружил заключительный § 4. “О теле с наименьшим сопротивлением и о теореме Ньютона, относящейся к нахождению тела с наименьшим сопротивлением” и ссылку на “Начала” Ньютона в VII томе вышедшего в 1936 г. собрания сочинений переводившего “Начала” с латыни на русский язык академика Алексея Николаевича Крылова. К стыду автора это было его первое знакомство с трудами ученого, гениальность которого еще предстояло оценить, но “лучше поздно, чем никогда”.

Стало ясно, что § 4 отчета [16] – предшественник статьи [1] и знакомство с А.Н. Крыловым могло состояться на 40 лет раньше. Однако тогда (в 1962 г.) после ознакомления с американским изданием “Начал” Ньютона [3] “с Ньютоном все было понятно”, и он ни на каком языке не интересовал автора. Теперь же причина появления торца в решении Ньютона стала интересна, но том VII собрания сочинений А.Н. Крылова в библиотеке ЦИАМ оказался утерян. Зато нашлось издание “Начал” Ньютона [17] в том же переводе А.Н. Крылова, вышедшее в СССР в 1989 г. Остается позавидовать автору – так много нового и интересного он узнал.

Итак, вместе с ним вернемся к труду Ньютона в переводе А.Н. Крылова. Замечательная особенность перевода А.Н. Крылова – разъяснение всех, как правило, постулируемых без доказательств и объяснений утверждений Ньютона, что видно и по обсуждаемой задаче. Как уже отмечалось, у Ньютона к ней имеют отношение лишь несколько кратких (в американском издании “Начал” [3] – чуть больше страницы с 2-мя рисунками), приведенных без доказательств утверждений, составивших одно “Поучение”. Последнее включает три темы.

1. О построении при заданных длине L и радиусе основания Y усеченного конуса, реализующего в рамках формулы (1.1) минимум сопротивления;

2. Об уменьшении сопротивления тела вращения при замене прилегающего к носику овального участка пересекающимися отрезками прямых с углами наклона к оси вращения 90° и 45°;

3. О примыкающем к переднему торцу выпуклом участке оптимального контура, определяемого словесным равенством, в которое входят длины четырех связанных с этим участком отрезков прямых.

По первой теме Ньютон дает такой способ построения. На составленном из отрезков прямых рис. 10: x_c = x_i/2 = – L/2, y_f = Y, и длины отрезков bc и cf равны. Тогда прямой отрезок bf определяет контур оптимального усеченного конуса – ломаную iaf.

Вторую тему “Поучения” Ньютона поясняет рис. 11. Речь идет о замене начального участка ic контура осесимметричного тела (у Ньютона “образованного вращением эллипса или овала”) двумя отрезками прямых – вертикальным id и наклонным dc. Наклонный отрезок касается исходного контура в точке с, в которой касательная образует с осью х угол θ_с = 45°. Согласно “Поучению” при большем объеме новое тело имеет меньшее сопротивление. Заканчивает Ньютон вторую тему словами: “Я считаю, что это предложение может быть небесполезно при построении судов”.

По объему разъяснения А.Н. Крылова к двум первым темам “Поучения” более чем вдвое превышают текст Ньютона, но не это главное. Главное в том, что именно здесь А.Н. Крыловым выведено необходимое условие минимума сопротивления (2.5), названное ранее [2] его именем. Приведем рассуждения А.Н. Крылова со ссылками на рис. 10 и на рис. 12, эквивалентный добавленному им в переводе, и с непринципиальной коррекцией.

Далее почти цитата: “Прежде всего заметим (рис. 10), что, когда длина усеченного конуса L приближается к нулю, то угол наклона отрезка af приближается к 45°. Таким образом, если (см. рис. 12) вблизи точки контура с θ > 45° взять бесконечно тонкий оптимальный усеченный конус adce, то при большем объеме тело с контуром adc будет испытывать меньшее сопротивление, нежели тело с контуром abc также усеченного, но неоптимального конуса. Отсюда следует также, что сопротивление конической поверхности bc больше суммы сопротивлений конической поверхности dc и кольцевой поверхности bd. Следовательно, если имеется какая-либо поверхность вращения, касательная к контуру которой в какой-либо точке составляет с осью угол, больший 45°, то, взяв поверхность, образованную вращением ломаной cdbi, элемент cd которой составляет 45° с осью, получим тело, объем которого больше объема первоначального тела, сопротивление же меньше. Значит, наименьшим сопротивлением будет обладать в этом случае такое тело, для которого ни в одной точке вышеуказанной замены сделать нельзя … ”.

Очевидно, что в приведенном абзаце А.Н. Крылов, опираясь на две первые темы “Поучения” Ньютона, доказал необходимое условие минимума сопротивления (2.5), более сильное, чем условие Лежандра. Выделенные в приведенной цитате курсивом слова “в этом случае” и опущенная заключительная часть цитаты (многоточие) не умаляют заслуг гениального переводчика. Ведь кроме него никто, включая Лежандра, специально изучавшего то же “Поучение” и получившего для задачи Ньютона свое, более слабое условие, не сделал этого.

Заключительная третья тема “Поучения” (из восьми строк) – инструкция по построению осесимметричной головной части минимального сопротивления. В XVII веке решения записывались в геометрической форме – в виде равенств из комбинаций длин разных отрезков. Чтобы сформулировать завершающее инструкцию словесное равенство, Ньютон вводит в рисунок второй темы дополнительные отрезки прямых, изображенные на рис. 11 штрихами. Точка n – произвольная точка выпуклого участка, а наклон отрезка rd равен наклону касательной в точке n. Наряду с длинами штриховых отрезков в приведенное равенство входит радиус торца y_d. Сформулированное Ньютоном равенство определяет форму выпуклого участка контура оптимальной головной части и условие его стыковки (θ_d+ = 45°) с торцом. Согласно примечанию А.Н. Крылова (на трех страницах!), “геометрическое” решение Ньютона эквивалентно интегралу (1.4) уравнения Эйлера (1.3) и условию (2.3) стыковки участка ДЭ с участком КЭ.

И Ньютон, и А.Н. Крылов нигде не пишут о торце как об участке КЭ. Однако в свете двух первых тем обсуждаемого “Поучения” и их следствия для усеченного конуса малой длины в этом и не было особой необходимости. Нужно было лишь помнить об ограничениях на допустимые х и θ, а о них оба гения забыть не могли.

Заключение. История решения задачи об оптимальной головной части тела вращения при больших скоростях полета, ставшей актуальной в середине ХХ века, может заинтересовать не только аэродинамиков. Не аэродинамик и не специалист в вариационном исчислении А.Н. Крылов перевел “Начала” Ньютона с решением этой задачи еще в 1914 г. Тем поразительней уровень проявленного им понимания отнюдь не близких ему проблем.

Автор признателен А.Г. Терентьеву, только благодаря настойчивости которого появилась эта статья, опубликованная первоначально [18] в трудах конференции “Гидродинамика больших скоростей и кораблестроение” (Чебоксары, 24–29 июня 2018 г.), посвященной 155-летию со дня рождения академика А.Н. Крылова.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (17-01-00126).