Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 779-789

1. Введение. Исследуется обобщение структурно-феноменологической модели Покровского–Виноградова (МПВ), описывающей течения растворов и расплавов несжимаемых вязкоупругих полимерных сред, на неизотермический случай, причем дополнительно предполагается, что среда испытывает воздействие магнитного поля. В МПВ полимерная система рассматривается как суспензия макромолекул полимера, движущихся в анизотропной жидкости, образованной, например, растворителем и другими макромолекулами. Воздействие окружающей среды на макромолекулу аппроксимируется воздействием на линейную цепочку из броуновских частиц, каждая из которых представляет собой достаточно большую часть макромолекулы. Броуновские частицы (“бусинки”) связаны между собой последовательно упругими силами (“пружинками”). В случае медленно меняющихся движений макромолекулу моделируют цепочкой из двух частиц (“гантелью”).

Описанное физическое представление о процессе течения линейных полимеров приводит к формулировке МПВ [1–3]

где $\rho $ – плотность полимера, ${{v}_{i}}$ – $i$-я компонента скорости, ${{\sigma }_{{ik}}}$ – тензор напряжений, $p$ – гидростатическое давление, ${{\eta }_{0}}$, ${{\tau }_{0}}$ – начальные значения сдвиговой вязкости и времени релаксации для вязкоупругой составляющей, ${{a}_{{ik}}}$ – симметрический тензор дополнительных напряжений второго ранга, ${{v}_{{ij}}}$ – тензор градиентов скорости, $I$ – первый инвариант тензора дополнительных напряжений, ${{\gamma }_{{ik}}}$ – симметризованный тензор градиентов скорости, $k$ и $\beta $ – феноменологические параметры, учитывающие в уравнениях динамики макромолекулы полимера размеры и форму молекулярного клубка. Здесь (1.1) – уравнение движения и условие несжимаемости, а (1.2) и (1.3) – реологические соотношения, устанавливающие связь между кинематическими характеристиками потока и его термодинамическими параметрами.

Некоторые обобщения модели (1.1)–(1.3), например, когда в уравнение (1.2) добавляется слагаемое, учитывающее сдвиговую вязкость, а параметр $\beta $ дополнительно зависит от первого инварианта тензора анизотропии, дают хорошие результаты в вычислительных экспериментах для вискозиметрических течений [4]. Поэтому можно предположить, что модификации МПВ окажутся полезными при моделировании движения полимеров в сложных условиях деформирования, например, для стационарных и нестационарных течений в каналах кругового сечения, в каналах с резко изменяющейся площадью сечения и течениях со свободной поверхностью. Важная особенность таких течений – их двумерный и трехмерный характер.

Здесь рассматривается одно из таких обобщений: учитываются влияние тепла и магнитного поля на процесс движения полимерной жидкости. Основной интерес будет связан с аналогом известного сдвигового течения в бесконечном плоском канале – течения Пуазейля, имеющего ряд особенностей. Так, например, как показывают расчеты, при определенных значениях параметров профиль скорости движения вытянут в сторону, противоположную направлению сил давления (разд. 3).

Основные результаты сформулированы в разделе 4: во-первых получено асимптотическое представление спектра линеаризованной проблемы относительно течения типа Пуазейля, а во-вторых, как следствие, выписано условие, при выполнении которого основное решение асимптотически устойчиво в выбранном классе возмущений, периодических по переменной, меняющейся вдоль границы бесконечного плоского канала.

Для случая вязкой жидкости известен результат А.Н. Крылова о линейной неустойчивости течения Пуазейля при достаточно больших числах Рейнольдса [5], подтверждающий гипотезу Хайзенберга [6] (было получено уточнение результата А.Н. Крылова [7]).

2. Нелинейная модель течения полимерной жидкости в плоском канале в присутствии внешнего магнитного поля. Используя известные результаты [3, 8–12], сформулируем математическую модель магнитогидродинамических течений несжимаемой полимерной жидкости; рассмотрим вариант, когда в уравнение, характеризующее изменение внутренней энергии (уравнение притока тепла) жидкости, по аналогии с работой Шибаты [13] введены диссипативные слагаемые. В безразмерном виде получим (далее мы будем придерживаться ранее принятых обозначений [12])

Здесь ${\mathbf{u}} = (u,v)$, ${\mathbf{H}} = (L,1 + M)$ – вектор скорости и вектор напряженности магнитного поля в декартовой системе координат $(x,\;y)$, $t$ – время, $Z = \frac{T}{{{{T}_{0}}}}$, $T$ – температура, ${{T}_{0}}$ – некоторое среднее значение температуры (комнатная температура, далее будем полагать ${{T}_{0}} = 300$ К), $\Pi = \frac{1}{{\operatorname{Re} }}({{a}_{{ij}}})$ $i,j$ = $1,2$, $\operatorname{Re} = \frac{{{{u}_{H}}l}}{{\eta _{0}^{*}}}$ – число Рейнольдса, $\rho = 1$ – плотность среды, ${{u}_{H}}$ – характерная скорость, $l$ – характерная длина, $\eta _{0}^{*}$ – начальное значение сдвиговой вязкости при комнатной температуре ${{T}_{0}}$, ${{a}_{{11}}}$, ${{a}_{{22}}}$, ${{a}_{{12}}}$ – компоненты симметрического тензора анизотропии второго ранга, $\operatorname{Gr} = \frac{{{\text{Ra}}}}{{{\text{Pr}}}}$ – число Грасгофа, $\operatorname{Ra} = \frac{{lbg{{T}_{0}}{\text{Pr}}}}{{u_{H}^{2}}}$ – число Релея, $b$ – коэффициент теплового расширения полимерной жидкости, $g$ – величина ускорения свободного падения, $\Pr = \frac{{l{{u}_{H}}{{c}_{v}}}}{\varepsilon }$ = $\frac{{{{c}_{v}}\eta _{0}^{*}\operatorname{Re} }}{\varepsilon }$ – число Прандтля, ${{c}_{v}}$ – теплоемкость, $\varepsilon $ – коэффициент теплопроводности полимерной жидкости, $p$ – давление, ${{\sigma }_{m}} = \frac{{\mu {{\mu }_{0}}H_{0}^{2}}}{{\rho u_{H}^{2}}}$ – коэффициент магнитного давления, $\mu $ – магнитная проницаемость полимерной жидкости, ${{\mu }_{0}}$ – магнитная проницаемость в вакууме, ${{H}_{0}}$ – характерная величина напряженности магнитного поля, ${{A}_{i}} = {{\operatorname{We} }^{{ - 1}}} + {{a}_{{ii}}}$, $i = 1,2$, $\operatorname{We} = \frac{{\tau _{0}^{*}{{u}_{H}}}}{l}$ – число Вайсенберга, $\tau _{0}^{*}$ – начальное значение временной релаксации при комнатной температуре ${{T}_{0}}$ [3, 12], ${{L}_{{ii}}} = \frac{{{{K}_{I}}{{a}_{{ii}}} + (a_{{ii}}^{2} + a_{{12}}^{2})}}{{_{0}(Z)}}$, $i = 1,2$, ${{K}_{I}} = {{\operatorname{We} }^{{ - 1}}} + \frac{{\bar {k}}}{3}I$, $\bar {k}$ = = k–, $I = {{a}_{{11}}} + {{a}_{{22}}}$ – первый инвариант тензора анизотропии; $k$, ($0 < \beta < 1$) – феноменологические параметры реологической модели [3], ${{\tilde {K}}_{I}} = {{K}_{I}} + I$, $I = {{a}_{{11}}} + {{a}_{{22}}}$ – первый инвариант тензора анизотропии, ${{\tau }_{0}}(Z) = \frac{1}{{ZJ(Z)}}$, $J(Z) = exp\left\{ {{{{\bar {E}}}_{A}}\frac{{Z - 1}}{Z}} \right\}$, ${{\bar {E}}_{A}} = \frac{{{{E}_{A}}}}{{{{T}_{0}}}}$, ${{E}_{A}}$ – энергия активации, ${{A}_{r}} = \frac{{\alpha u_{H}^{2}\Pr }}{{\operatorname{Re} {{T}_{0}}{{c}_{v}}}}$ = $\frac{{\alpha u_{H}^{2}\eta _{0}^{*}}}{{{{T}_{0}}\varepsilon }}$, ${{D}_{\Gamma }} = {{a}_{{11}}}{{u}_{x}}$ + $({{v}_{x}} + {{u}_{y}}){{a}_{{12}}}$ + ${{a}_{{22}}}{{v}_{y}}$, ${{A}_{m}} = \frac{{{{\alpha }_{m}}u_{H}^{2}\Pr }}{{{{T}_{0}}{{c}_{v}}}}$, $\alpha $ – термический эквивалент работы [14], ${{\alpha }_{m}}$ – магнитотермический эквивалент работы, ${{D}_{m}} = {{L}^{2}}{{u}_{x}}$ + $L(1 + M)({{v}_{x}} + {{u}_{y}})$ + ${{(1 + M)}^{2}}{{v}_{y}}$, ${{b}_{m}} = \frac{1}{{{{{\operatorname{Re} }}_{m}}}}$, Re_m = = ${{\sigma }_{m}}\mu {{\mu }_{0}}{{u}_{H}}l$ – магнитное число Рейнольдса, $\sigma $ – электропроводность среды, $\frac{d}{{dt}} = \frac{\partial }{{\partial t}} + u\frac{\partial }{{\partial x}} + v\frac{\partial }{{\partial y}}$, ${{\Delta }_{{x,y}}} = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}$.

В системе (2.1)–(2.4) переменные и совокупности переменных $t$, $(x,y)$, $(u,v)$, $p$, $({{a}_{{11}}},{{a}_{{22}}},{{a}_{{12}}})$, $L$ и $M$ – результат отнесения соответствующих размерных переменных к следующим характерным величинам: $l{\text{/}}{{u}_{H}}$, $l$, ${{u}_{H}}$, $\rho u_{H}^{2}$, ${\text{We/3}}$, ${{H}_{0}}$ (рис. 1).

Замечание 1. Магнитогидродинамические уравнения (2.1)–(2.4) выведены с привлечением уравнений Максвелла [9, 10], причем вектор магнитной индукции берется в виде

где $\chi $ – магнитная восприимчивость, при этом [15, 16]: ${{\chi }_{0}}$ – магнитная восприимчивость при комнатной температуре ${{T}_{0}}$ (=300 K). Далее будем полагать, что для полимерной жидкости $\mu = 1$ (${{\chi }_{0}} = 0$).

В качестве главной будем рассматривать задачу о решении системы (2.1)–(2.4), описывающей магнитогидродинамическое течение несжимаемой полимерной жидкости в плоском канале толщиной 1, ограниченном горизонтальными стенками – электродами ${{C}^{ + }}$ и ${{C}^{ - }}$, вдоль которых пропущены электрические токи проводимости с силой тока ${{J}^{ + }}$ и ${{J}^{ - }}$. Канал помещен в однородное внешнее магнитное поле с компонентами $L = 0$, $M = 0$ (рис. 1).

Внешние по отношению к каналу области $S_{1}^{ + }$ и $S_{1}^{ - }$ – магнетики с магнитными восприимчивостями $\chi _{1}^{ + }$ и $\chi _{1}^{ - }$, на них также воздействует описанное внешнее магнитное поле; на рисунке его компоненты снабжены соответствующими индексами. На стенках канала выполнены граничные условия прилипания

условие $T = {{T}_{0}}$ в области $S_{1}^{ + }$ и на электроде ${{C}^{ + }}$и условие $T$ – температура в области $S_{1}^{ - }$ и на электроде ${{C}^{ - }}$, т.е. при $\bar {\theta } > 0$ нагрев происходит снизу, при $\bar {\theta } < 0$ – сверху.

В силу соотношения (2.5) и условий (2.6)–(2.8) получаем

Замечание 2. Далее будем полагать либо $k = \beta $, либо $k = 1.2\beta $. Заметим, что, как было показано [3], при $k = 1.2\beta $ для расплавов полимеров получаются результаты, наилучшим образом соответствующие экспериментальным данным.

Замечание 3. Границы ${{C}^{ + }}$ и ${{C}^{ - }}$ – границы раздела двух однородных изотропных магнетиков. Следовательно, на них выполняются следующие краевые условия [15, 17]:

В качестве основного режима течения несжимаемой полимерной жидкости будет рассмотрен аналог течения Пуазейля.

Замечание 4. Еще раз отметим, что в отличие, например, от работ [12, 18–20] первое из уравнений (2.4), описывающее изменение внутренней энергии (уравнение притока тепла), содержит диссипативные слагаемые, характеризующие поток тепла, возникающий при ненулевых градиентах скорости. Наличие диссипативных членов приводит, в частности, к тому, что неизотермичность имеет место и $\bar {\theta } = 0$ (и это правильно, поскольку приток тепла будет происходить за счет влияния компонент тензора анизотропии ${{\hat {a}}_{{11}}}$, ${{\hat {a}}_{{12}}}$, ${{\hat {a}}_{{22}}}$).

Напротив, в ранее принятой модели [12] при $\bar {\theta } = 0$ имеем $\hat {Z} = 1$, ${{\bar {\tau }}_{0}}(\hat {Z}) = 1$, т.е. возникает изотермический процесс (крышкой обозначено основное решение и величины, которые вычисляются на основном решении).

3. Магнитогидродинамическое течение типа Пуазейля. Обозначим ${\mathbf{U}}(t,x,y) = (u,v,{{a}_{{11}}},{{a}_{{12}}},{{a}_{{22}}},Z,L,M{{)}^{T}}$. Будем искать у системы (2.1)–(2.4) частное решение специального вида

соответствующее стационарному течению несжимаемой полимерной жидкости в плоском бесконечном канале (рис. 1) под действием постоянного перепада давления вдоль оси канала $y = 0$. Здесь а $\hat {P}(y)$ ($\hat {P}(0) = 0$) – некоторая функция, подлежащая определению, ${{\hat {p}}_{0}}$ – значение давления на оси канала $y = 0$ при $x = 0$, $\hat {A}$ – взятый с обратным знаком безразмерный перепад давления на отрезке $h$, причем $\widehat {\Delta p} > 0$ (рис. 1).

Для определения величин как функций от $y$ из равенств (2.1)–(2.4), (2.6)–(2.8), (2.19) получаем соотношения, позволяющие сформулировать итерационный алгоритм для нахождения $\hat {Z}(y,\bar {C})$ (точнее $\hat {Q}(y,\bar {C})$: $\hat {Z}(y,\bar {C})$ = $\hat {Q}(y,\bar {C})$ + 1 + $\bar {\theta }\left( {\frac{1}{2} - y} \right)$), $\hat {L}(y,\bar {C})$, ${{\hat {a}}_{{22}}}(y,\bar {C})$ и постоянной $\bar {C}$, результаты проведенных расчетов подробно описаны ранее [21].

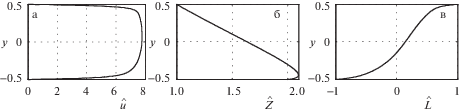
Некоторые решения, точнее, компоненты решения $\hat {u}$, $\hat {Z}$, $\hat {L}$, представлены на рис. 2–5. В первом (основном) случае $\hat {A} = 1$, = 1, $m = 1$, ${\text{Re}} = 1$, ${\text{We}} = 1$, = 0.5, ${{A}_{r}} = 1$, ${{A}_{m}} = 1$, = 1, ${{b}_{m}} = 1$, ${{\bar {E}}_{A}} = 1$, ${{J}^{ + }} = 2$, ${{J}^{ - }} = 1$, а во втором, третьем и четвертом случаях меняется один из параметров $A$, ${{J}^{ + }}$ и $\theta $, соответственно, а остальные параметры остаются неизменными.

Отметим важные качественные моменты в поведении стационарных режимов течения полимерной жидкости: в отличие от работы [12], в которой было обнаружено влияние параметра ${{\bar {E}}_{A}}$, связанного с энергией активации ${{E}_{A}}$, ${{\bar {E}}_{A}} = {{E}_{A}}{\text{/}}{{T}_{0}}$, на форму профиля скорости – он теряет симметричность, характерную для параболического профиля скорости течения Пуазейля для вязкой жидкости [11], решения модели (2.1)–(2.10) обладают более широким спектром интересных свойств.

Так, в основном случае (рис. 2) профиль скорости вытянут против направления сил давления (что обусловлено влиянием магнитного поля!), на рис. 3 перепад давления (по абсолютной величине) увеличен – в результате профиль скорости развернулся вправо, на рис. 4 абсолютная величина давления снова невелика, но за счет того, что на верхнем электроде направление тока изменено на противоположное, профиль скорости развернут вновь вправо. Наконец, сильное охлаждение нижней границы канала приводит к тому, что скорость жидкости в нижней части канала стала практически нулевой (рис. 5).

Важнейший вопрос, который возникает в связи со стационарным решением проблемы (2.1)–(2.10), течением типа Пуазейля – физическая реализуемость полученного решения, которая, в частности, предполагает, что исследуемое решение устойчиво по Ляпунову.

4. Линеаризованная модель течения полимерной жидкости в плоском канале. Формулировка основных результатов. Проведя линеаризацию модели (2.1)–(2.10) относительно описанного в предыдущем параграфе аналога течения Пуазейля с учетом дополнительных условий (2.1), получаем громоздкую систему, которую в структурном виде можно записать так

где ${{B}_{0}} = (b_{{ij}}^{0})_{{i,j = 1}}^{5}$, $C = ({{c}_{{ij}}})_{{i,j = 1}}^{5}$ – достаточно разреженные матрицы с элементами, зависящими от $\hat {Z}$ и ${{\hat {a}}_{{ij}}}$, $\Omega = P - {{\hat {Z}}_{{22}}} - {{Z}_{{22}}}$, ${{\alpha }_{{ij}}} = \frac{{{{a}_{{ij}}}}}{{{\text{Re}}}}$, компоненты вектора ${\mathbf{\Gamma }}$, функции $F$ и $G$ – линейные функции от неизвестных и их производных по переменным $x,\;y$, коэффициенты системы определяются основным решением и параметрами исходной системы (2.1)–(2.4).

К системе (4.1)–(4.5) добавляем граничные условия:

и начальные данные. При этом начальные данные должны удовлетворять уравнению (4.2) и дополнительным условиям (2.1).

Далее мы будем искать у сформулированной выше задачи частные решения специального вида

Сформулируем основные результаты работы.

Теорема 1. Если задача (4.1)–(4.7) имеет решение вида (4.8) (параметр $\omega $ фиксирован), то для $\lambda $ справедливо следующее асимптотическое представление

где ${{\hat {\alpha }}_{2}} = {{\hat {\alpha }}_{{22}}} + \frac{1}{{\operatorname{Re} \operatorname{We} }}$, ${{R}_{{34}}} = - 2\hat {u}{\kern 1pt} '\; + 2\beta {{\hat {a}}_{{12}}}\hat {\chi }_{0}^{*}$, $\hat {\chi }_{0}^{*} = \frac{1}{{{{{\bar {\tau }}}_{0}}(\hat {Z})}}$, ${{R}_{{44}}} = \hat {\chi }_{0}^{*}{{\hat {\tilde {K}}}_{{\hat {I}}}}$ (${{R}_{{34}}}$, ${{R}_{{44}}}$ – компоненты матрицы $R$ в системе (4.1)).

Из представления (4.9) вытекает необходимое условие асимптотической устойчивости найденного в разд. 3 течения типа Пуазейля.

Теорема 2. Для асимптотической устойчивости течения типа Пуазейля необходимо выполнение неравенства

Доказательства теорем вследствие громоздкости не приводятся. Заметим только, что при доказательстве используются идеи работ [22–24], связанные с асимптотическим представлением фундаментальных решений систем обыкновенных дифференциальных уравнений в случае роста модуля параметра.

Утверждения теорем обобщают результаты [18–20, 25–28] на случай неизотермических течений полимеров под воздействием магнитного поля.

Заключение. Найдена формула, описывающая распределение точек спектра (при возрастании их модуля) для линейной смешанной задачи, полученной после линеаризации МГД модели несжимаемой полимерной жидкости относительно аналога течения Пуазейля в бесконечном плоском канале в классе периодических возмущений. Сформулировано необходимое условие его асимптотической устойчивости, определяющее область допустимых значений модели, для которых это свойство справедливо.

Авторы благодарят А.В. Егитова за помощь в оформлении работы.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (17-01-00791а, 19-01-00261а).