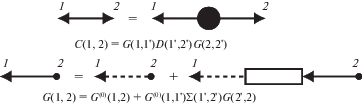Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 790-807

1. Введение. При описании поля скоростей рассматриваются пространственно-временные распределения скоростей ${\mathbf{u}}({\mathbf{r}},t)$, которые будем называть реализациями поля скоростей, а статистическое описание турбулентного поля скоростей подразумевает задание распределения плотности вероятности различных реализаций поля $P[{\mathbf{u}}({\mathbf{r}},t)]$. Знание этой функции позволяет вычислить всевозможные средние, описывающие усредненное поведение турбулизованной жидкости и ее характеристики, такие как распределение энергии по спектру волновых чисел, усредненные коэффициенты переноса типа турбулентной вязкости, диффузии, теплопроводности и проч.

Возникновение стохастичности обычно связывают с развитием неустойчивости крупномасштабных течений жидкости. В теории случайных процессов стохастичность моделируется введением внешних случайных сил (сил Ланжевена) путем задания функции распределения внешних случайных сил (аддитивный шум). В ряде случаев стохастичность моделируется случайными коэффициентами в описывающих процессы уравнениях (мультипликативный шум), например, перенос пассивной примеси в случайном поле скоростей. Каждой реализации поля скоростей соответствует заданная величина внешней случайной силы, а усреднение по реализациям поля скоростей соответствует усреднению по реализациям внешней случайной силы при заданной функции распределения реализаций случайных сил.

Функциональная формулировка статистической теории турбулентности означает, что вместо статистического описания в терминах функции распределения плотности вероятности реализаций поля $P[{\mathbf{u}}({\mathbf{r}},t)]$ и вычисления различных средних согласно формуле

где $d[{\mathbf{u}}]$ – элементарный объем в пространстве реализаций поля скоростей, используется более удобный метод характеристического функционала (ХФ) ([1], п. (3.4)).

Метод ХФ представляет собой обобщение метода характеристических функций, используемого при статистическом описании случайных величин, на случай описания случайных полей. В теории случайных величин характеристическая функция определяется как среднее от Фурье-образа плотности вероятности распределения случайных величин. Соответственно, в теории случайных полей ХФ определяется как функциональный аналог Фурье-образа распределения плотности вероятности реализаций случайных полей

При этом средние величины вычисляются путем выполнения операции функционального (вариационного) дифференцирования согласно формуле

Понятие ХФ применяется не только в статистической гидродинамике, оно широко используется также в математике и разных областях физики [2]. Хотя возможность описания случайных полей на языке ХФ была сформулирована еще в 1935 г. А.Н. Колмогоровым [3], в физике это понятие стало использоваться несколько позднее. В статистической механике соответствующий ХФ так называемый производящий функционал был введен в 1946 г. Н.Н. Боголюбовым [4], а в квантовой теории поля – в 1949 г. Ю. Швингером с целью формулировки теории вне рамок теории возмущений [5]. Несколько позднее им же были выписаны уравнения в функциональных (вариационных) производных для производящего функционала (уравнения Швингера) [6]. В 1954 г. И.М. Гельфандом и Р.А. Минлосом [7], а также независимо Эдвардсом и Пайерлсом [8] было получено представление решения уравнений в функциональных производных теории поля в виде функциональных интегралов (континуальных интегралов, интегралов по путям).

В статистической теории турбулентности метод ХФ был впервые предложен Хопфом [9] для описания корреляционных функций поля скоростей в различных точках в заданный момент времени (пространственный ХФ)

Хопф получил уравнение в функциональных производных, описывающее временную эволюцию ХФ при заданном начальном значении ХФ.

Обобщением этого метода, позволяющего описывать корреляции полей скорости в различных точках и при различных временах был предложен Льюисом и Крейчнаном (метод пространственно-временного ХФ) [10] (см. также [11]). Пространственно-временной ХФ Льюиса–Крейчнана определяется формулой (1.1). Для пространственно-временного ХФ было получено уравнение в функциональных производных [10], которое, по мнению авторов, позволяет найти ХФ. Однако вопрос о том, как происходит усреднение и какова статистика ансамбля, по которому производится усреднение, остался открытым, вследствие чего уравнение Льюиса–Крейчнана содержит произвол и правила избавления от этого произвола не формулируются. Отметим, что для пространственного ХФ Хопфа этого произвола нет, так как статистические свойства ансамбля учтены в задаваемом начальном значении ХФ.

В теории турбулентности использование ланжевеновского подхода для моделирования возникновения стохастичности за счет развития неустойчивости крупномасштабных течений было впервые предложено Уайлдом [12] (см. также [13]). В противоположность традиционному способу статистического описания турбулентности в терминах статистических моментов, Уайлд при построении решения уравнения Навье–Стокса (УНС) для поля скоростей применил метод возмущений. В его теории в качестве возмущения рассматривался нелинейный член в УНС и решение для скорости представлялось в виде ряда по степеням внешней случайной силы. При вычислении статистических моментов поля скоростей ряды перемножались и затем проводилось почленное усреднение получившегося ряда с использованием правил вычисления статистических моментов в случае центрированного нормального распределения внешних случайных сил. Подобная процедура связана с выполнением громоздких вычислений, требующих аккуратности и внимания. Для упрощения вычислений было предложено при анализе получающихся рядов использовать технику фейнмановских диаграмм – графическое представление математических выражений (см. также [14, 15]).

Основными элементами диаграммной техники Уайлда являются функция Грина линейной задачи ${{G}^{{(0)}}}(1,2)$, которую будем изображать на рисунках отрезком из штриховых линий между точками 1 и 2 с входящей в точку 1 стрелкой (прямая линия в диаграммной технике Уайлда), так называемая вершина $V({\text{1|2}},3)$, изображаемая светлым кружком с двумя входящими стрелками 2 и 3 и одной выходящей 1 (точка в обозначениях Уайлда), и парная корреляционная функция внешних случайных сил ${{D}^{{(0)}}}(1,2)$, изображаемая светлым кружком с двумя выходящими стрелками (волнистая линия у Уайлда). Правила соответствия фейнмановских диаграмм теории возмущений аналитическим выражениям представлены на рис. 1.

Использование теории возмущений и соответствующей ей скелетной диаграммной техники (СДТ) Фейнмана предполагает малость возмущения и возможность судить о поведении рассматриваемой системы на основе знания нескольких первых членов полного ряда. Однако в случае развитой турбулентности фактический параметр разложения (эффективное число Рейнольдса) не является малым и встает вопрос о поведении полного ряда, т.е. суммирования диаграмм теории возмущений. Это достигается с помощью перехода к скелетным диаграммам Фейнмана, соответствующим сумме некоторой бесконечной подпоследовательности диаграмм теории возмущений, и описанию системы в терминах скелетных диаграмм.

Аналогичная проблема возникла в теории квантованных полей при формулировке способа описания сильных взаимодействий. В 1973 г. в работе П. Мартина, Е. Сиджиа и Х. Роуза [16] была сформулирована теорема об эквивалентности статистической задачи для произвольной классической системы и некоторой квантовой теории поля (так называемый “формализм удвоения полей”). В монографии [17] приводится формулировка утверждения, что в квантовой теории поля представление для производящего функционала для всевозможных функций Грина может быть получено путем усреднения экспоненты от действия для классической частицы во внешнем поле по квантовым флуктуациям внешнего поля, что согласуется с теоремой эквивалентности [16]. Теорема эквивалентности позволяет при построении статистической теории турбулентности применять развитый в квантовой теории поля мощный математический аппарат, использующий улучшенную теорию возмущений, идею перенормировок, представление решения уравнения в функциональных производных для производящего функционала (уравнения Швингера) в форме функционального интеграла. В статистической теории турбулентности переход к СДТ осуществляется естественным образом при функциональной формулировке теории в терминах ХФ, а не на основе кропотливого анализа диаграмм теории возмущений, к тому же чреватого ошибками [12–16].

В данной работе описывается формулировка статистической теории турбулентности в терминах ХФ, приводится способ получения представления для пространственно-временного ХФ, вытекающий непосредственно из УНС при наличии внешней случайной и регулярной силы. Из этого представления можно получить уравнение в функциональных производных для ХФ и использовать его для нахождения различных соотношений между статистическими моментами поля скоростей, функциями Грина и другими величинами, описывающими поле турбулентных пульсаций скорости. Полученные уравнения представлены графически с помощью СДТ. Также показано как функциональная формулировка статистического описания турбулентности позволяет прийти к СДТ вне рамок теории возмущений.

2. Математическая постановка задачи. С целью упрощения записи для совокупности координат пространственно-временной точки и номеров компонент вектора будем в дальнейшем использовать цифровые обозначения $\{ {{{\mathbf{r}}}_{1}},{{t}_{1}},{{\alpha }_{1}}\} \equiv 1$, согласно которым ${{u}_{{{{\alpha }_{1}}}}}({{{\mathbf{r}}}_{1}},{{t}_{1}}) \equiv u(1)$. Также будет подразумеваться интегрирование по пространственно-временным переменным и суммирование по повторяющимся индексам (правило Эйнштейна), т.е.

Когда векторные или тензорные индексы выписываются явно, цифровые обозначения будут относиться только к пространственно-временным переменным.

В основе рассмотрения лежит УНС для несжимаемой жидкости при наличии задаваемой статистически внешней случайной силы $X(1)$ и регулярной силы $f(1)$. В используемых обозначениях УНС имеет вид (более подробно см. [18])

Внешнюю случайную силы $X(1)$ без потери общности можно полагать соленоидальной (бездивергентной) и подчиняющейся центрированному нормальному распределению с парной корреляционной функцией вида

где ${{P}_{{\alpha \beta }}}(1,2)$ – оператор поперечного проектирования, Фурье-образ которого имеет вид ${{P}_{{\alpha \beta }}}(k) = {{\delta }_{{\alpha \beta }}} - {{k}_{\alpha }}{{k}_{\beta }}{\text{/}}{{k}^{2}}$, при этом ${{k}_{\alpha }}{{P}_{{\alpha \beta }}}(k) = 0$.

Согласно определению (1.1) для получения представления ХФ необходимо знать плотность вероятности распределения различных реализаций поля скоростей $P[u(1)]$, которая может быть представлена в виде среднего от $\delta $-функционала

где $\tilde {u}(1,X)$ – решение УНС (2.1) при фиксированных $f(1)$ и $X(1)$, угловые скобки означают усреднение по $\tilde {u}(1)$, что соответствует усреднению по реализациям поля внешних случайных сил $X$.

Воспользовавшись функциональным аналогом известной в теории обобщенных функций формулы $\delta [\varphi (x)] = \delta (x - {{x}_{0}}{\text{)|}}\varphi {\kern 1pt} '{\kern 1pt} (x{\text{)}}{{{\text{|}}}^{{ - 1}}}$, ${\kern 1pt} \varphi ({{x}_{0}}) = 0$, записанном в виде

и функциональным аналогом разложения Фурье для $\delta $-функции получим представление для ХФ в форме двукратного функционального интеграла по полям $u$ и $\hat {u}$

Обычно принимается, что вклад якобиана функционального преобразования $L[u] \to u$ (березиниана) $\left| {\delta L[u]{\text{/}}\delta u} \right|$ может быть сведен к переопределению интегральной меры путем включения его в $d[u]$, что позволяет в равенстве (2.3) принять ${\text{|}}\delta L[u]{\text{/}}\delta u{\text{|}} = 1$. Однако, поскольку представляет интерес не сам интеграл (2.3), а только вытекающее из него уравнение для ХФ, явная форма этой величины оказывается несущественной.

В случае гауссовой статистики поля $X(1)$ усреднение по реализациям внешней случайной силы дает

где

В результате приходим к представлению ХФ вида

Задаваемое формулой (2.4) представление ХФ совпадает с представлением производящего функционалом некоторой квантовой теории поля. В 1962 г. В.И. Татарский [19] впервые обратил внимание на тесную аналогию между уравнением Хопфа для ХФ и уравнением Швингера для производящего функционала, что позднее было сформулировано в форме теоремы эквивалентности Мартина–Сиджиа–Роуза [16]. В частности, В.И. Татарский показал, что решение уравнения в функциональных производных Хопфа может быть записано в виде континуального интеграла. (Отметим различие в терминологиях: характеристическому функционалу, функциональному интегралу и функциональной производной в используемой в данной работе терминологии соответствуют производящий функционал, континуальный интеграл и вариационная производная в квантовой теории поля.) Представление для ХФ (2.3) в виде функционального интеграла по двум полям является иллюстрацией упомянутого выше формализма. Отметим, что второе поле $\hat {u}$ возникает при использовании представления для $\delta $-функционала в форме функционального разложения Фурье.

Используя свойство инвариантности функционально интеграла относительно операции сдвига функциональной переменной $\hat {u} \to \hat {u} + \delta \hat {u}$, приходим к уравнению в функциональных производных для пространственно-временного ХФ

Оно отличается от уравнения для пространственно-временного ХФ [10] учетом внешней регулярной силы $f$ и наличием слагаемого, содержащего дисперсию внешних случайных сил ${{D}^{{(0)}}}$, определяющих статистику ансамбля реализаций поля скоростей.

Выпишем еще уравнение для логарифма ХФ, функциональные производные которого дают представление для различных неприводимых статистических моментов (кумулятивных средних) поля скоростей и на языке фейнмановских диаграмм теории возмущений функциональные производные этого функционала соответствуют учету только одночастично неприводимых (one-particle irreducible) диаграмм, т.е. диаграмм, которые нельзя разбить на две независимые части разрывом одной линии

Следуя предложенному ранее подходу [18, 20], перейдем далее к новым функциональным переменным $\hat {\eta }$ и $\hat {f}$:

При $\eta \to 0$ получим $\hat {\eta }(1) \to \left\langle {u(1)} \right\rangle $, т.е. эта величина стремится к среднему значению компоненты скорости ${{\alpha }_{1}}$ в пространственно-временной точке $\{ {{{\mathbf{r}}}_{1}},{{t}_{1}}\} $ в поле внешней регулярной силы ${{f}_{{\alpha 2}}}({{{\mathbf{r}}}_{2}},{{t}_{2}})$.

Переход к новым функциональным переменным осуществляется с помощью функционального преобразования Лежандра путем ведения нового функционала

В этом случае

В пределе $\eta \to 0$ функциональные производные $\ln \Phi $ в уравнениях (2.9) допускают простую интерпретацию: $C(1,2)$ – парная корреляционная функция (дисперсия) поля скоростей, функция $G(1,2)$ описывает отклик среднего поля скорости в пространственно-временной точке 1 на действие силового источника, локализованного в точке 1, иными словами, является функцией (тензором) Грина. В СДТ функцию $C(1,2)$ (называемую также коррелятором) будем изображать сплошной линией, соединяющей точки 1 и 2 с входящими в эти точки стрелками, а функцию $G(1,2)$ (называемую пропагатором) изобразим сплошной линией с входящей в точку 1 стрелкой (рис. 2).

Для функционала $\Psi [\hat {\eta },\hat {f}]$ уравнение в функциональных производных будет иметь вид

В диаграммной технике теории возмущений функциональным производным функционала $\Psi [\hat {\eta },\hat {f}]$ соответствует совокупность (бесконечная) одночастично-неприводимых диаграмм с “ампутированными” внешними линиями. В СДТ (берется сумма некоторой бесконечной подпоследовтельности диаграмм теории возмущений) функционал $\Psi [\hat {\eta },\hat {f}]$ будем изображать темным кружком, а действию на него операторами функционального дифференцирования $\delta {\text{/}}i{\kern 1pt} \delta \hat {\eta }(1)$ и $\delta {\text{/}}{\kern 1pt} \delta \hat {f}(1)$ изображать соответственно вставкой входящей в него или выходящей из него стрелками (см. рис. 2). Из анализа диаграммных рядов теории возмущений следует, что выражения, содержащие производные функционала $\Psi $ только по полям $\hat {\eta }$ (что соответствует только входящим в темный кружок стрелкам), равны нулю, также как производные $ln\Phi $ только по полям $f$:

Для дальнейшего анализа рассмотрим смешанные функциональные производные функционала $\Psi $

3. Уравнения для парной корреляционной функции и функции Грина. Из формулы (2.11) и определения функции Грина (2.9) следует

${{G}^{{ - 1}}}$ – обратная функция Грина, определенная соотношением

При учете равенства (3.1) формула (2.12) запишется в виде

или

В статистической теории турбулентности уравнение (3.3) впервые было получено Уайлдом [12] путем анализа рядов теории возмущений с использованием СДТ. Функцию $D(1,2) = {{D}^{{(0)}}}(1,2) + {{D}^{{(1)}}}(1,2)$ в уравнении Уайлда (3.3) следует интерпретировать как парную корреляционную функцию эффективных случайных сил, ${{D}^{{(1)}}}$ – поправка с исходной (затравочной) корреляционной функции случайных сил ${{D}^{{(0)}}}$, обусловленная межмодовыми взаимодействиями. Отметим, что при выводе уравнения Уайлда УНС и вытекающее из него уравнение для характеристического функционала не использовалось, и можно интерпретировать это уравнение как введение новой статистической характеристики турбулентного поля скоростей $D(1,2)$, определенной формулой (3.3).

Для нахождения уравнений для функций ${{G}^{{ - 1}}}$ и $D$ подействуем на уравнение (2.10) для функционала $\Psi $ оператором $\delta {\text{/}}\delta \hat {\eta }(2)$. Используя соотношения (2.9) и (3.1), получим

где а при действии на уравнение (2.10) оператором $\delta {\text{/}}i\delta \hat {f}(2)$ и учете равенства (3.2) найдем

Из уравнений (3.4) и (3.6) следует, что определяемые формулами (3.5) и (3.7) величины $\Sigma (1,2)$ и ${{D}^{{(1)}}}(1,2)$ следует интерпретировать соответственно как обусловленные влиянием турбулентного перемешивания поправки к вязкости жидкости и корреляционной функции внешних случайных сил.

Уравнение (3.4) можно переписать в виде

${{G}^{{(0)}}}$ – функция Грина линейного уравнения

Уравнение (3.8) – аналог уравнения Дайсона в квантовой теории поля, а величина $\Sigma $ – аналог “оператора собственной энергии”. Парной корреляционной функции (ПКФ) эффективных случайных сил $D(1,2)$ поставим в соответствие темный кружок с двумя выходящими стрелками, поправке к корреляционной функции внешних случайных сил ${{D}^{{(1)}}}(1,2)$ – прямоугольник с двумя выходящими стрелками, а величине $\Sigma (1,2)$, описывающей поправку к вязкому слагаемому в УНС, вызванную переносом импульса турбулентными пульсациями скорости, поставим в соответствие прямоугольник с входящей в точку 2 и выходящей из точки 1 стрелками. В СДТ уравнения Дайсона (3.8) и Уайлда (3.3) изображаются диаграммами, представленными на рис. 3.

При действии на уравнение (2.6) для $\ln \Phi $ оператором $\delta {\text{/}}i\delta \eta (4)$ может быть получено уравнение для ПКФ

где $C(2,3,4)$ – трехточечный статистический момент третьего порядка;

С целью получения замкнутого уравнения для представляющей непосредственный интерес ПКФ традиционно используются различные феноменологические гипотезы замыкания типа турбулентной вязкости, согласно которой вклад нелинейного члена в уравнении (3.8) принимается пропорциональным парной корреляционной функции и записывается в виде ${{\nabla }^{{(1)}}}[{{\nu }_{T}}(1,4){{\nabla }^{{(2)}}}C(2,4)]$, где интегральное ядро ${{\nu }_{T}}(1,2)$ интерпретируется как коэффициент турбулентной вязкости. Следует однако отметить, что третий статистический момент входит в уравнение (3.6) в виде комбинации $T(1,4)$ = = $\frac{1}{2}V({\text{1|2}},3)C(2,3,4)$, представляющей собой тензор второго ранга, именуемый также инерционным тензором. Именно эта величина нужна для получения замкнутого уравнения для ПКФ. Оказывается, что указанная величина может быть выражена через величины, связанные с ПКФ и функцией Грина.

Момент третьего порядка с учетом формул (2.9) может быть записан в виде

Использование формул (3.5) и (3.7) для тензора второго ранга $T(1,4)$, приводит к представлению

и задача сводится к нахождению величин ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ определенных формулами (3.5) и (3.7).

Для нахождения явного вида величин ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ согласно (3.5) и (3.7) следует предварительно найти функциональные производные $C$ по полям $\hat {\eta }$ и $\hat {f}$.

Дифференцируя тождество $G(1,1{\kern 1pt} '){{G}^{{ - 1}}}(1{\kern 1pt} ',2) = \delta (1 - 2)$ по функциональной переменной $\hat {\eta }(3)$ и используя определение обратной функции Грина (3.1), найдем

и аналогично

Дифференцирование уравнения Уайлда (3.3) по $\hat {\eta }(3)$ и $\hat {f}(3)$ с использованием равенств (3.12) и (3.13) дает

где были введены три новые функции называемые в диаграммной технике вершинами и интерпретируемые в квантовой теории поля как величины, описывающие соответственно процессы слияния двух квантов в один (вершина первого типа), распад одного кванта на два (вершина второго типа) и порождение трех квантов внешним полем (вершина третьего типа). На необходимость учета вершин всех трех типов впервые было указано в работе [16] (см. также [18, 19]).

В СДТ вершинам $\Gamma (1{\kern 1pt} {\text{|}}{\kern 1pt} 2,3)$, $\Gamma (1,2{\kern 1pt} {\text{|}}{\kern 1pt} 3)$ и $\Gamma (1,2,3)$ будем ставить в соответствие темный кружок с двумя входящими и одной выходящей стрелками, одной входящей и двумя выходящими стрелками и с тремя выходящими стрелками (рис. 2). Согласно определениям (3.16) в рамках СДТ вершины изображаются стрелками, входящими и выходящими в соответствующие ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ прямоугольники (рис. 4). Используя соотношения (3.14) и (3.15), для величин ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}(1,2)$ получим

В рамках СДТ операции функционального дифференцирования будут графически отображаться вставкой входящих и выходящих стрелок в линии пропагаторов, корреляторов и вершин. Вытекающие из формул (3.12)–(3.15) правила действия операторов $\delta {\text{/}}\delta \hat {\eta }$ и $\delta {\text{/}}i\delta \hat {f}$ на функции пропагатора $G$ и коррелятора $C$ приведены на рис. 4, также приведены диаграммы для изображаемых прямоугольниками величин ${{\Sigma }^{{(1)}}}(1,2)$ и ${{D}^{{(1)}}}(1,2)$, которые согласно формулам (3.5) и (3.7) выражаются через функциональные производные коррелятора $C(3,4)$ по полям $\hat {\eta }(2)$ и $\hat {f}(2)$, изображаемые вставкой входящих и выходящих стрелок в линию коррелятора, что приводит к диаграммным представлениям для ${{\Sigma }^{{(1)}}}(1,2)$ и ${{D}^{{(1)}}}(1,2)$, приведенным на рис. 4 и соответствующим формулам (3.17) и (3.18).

Система уравнений (3.3), (3.8), (3.17), (3.18) – точное следствие уравнения для ХФ (2.6) и вытекающего из него уравнения (2.10).

При выводе этих уравнений никакие приближения или дополнительные предположения феноменологического характера не были использованы. Однако эта система не является замкнутой, т.к. содержит три неизвестные функции $\Gamma $, для которых в свою очередь можно получить уравнения, содержащие моменты более высокого порядка, т.е. возникает цепочка уравнений, в чем-то аналогичная цепочке уравнений Фридмана–Келлера при традиционной формулировке статистической теории турбулентности в терминах статистических моментов. Следует отметить, что неизвестные функции $\Gamma $ входят только в выражения для $\Sigma $ и ${{D}^{{(1)}}}$, определяемых формулами (3.17), (3.18) и следующих из УНС при наличии внешней случайной силы.

Была предложена схема [21] приближенного замыкания цепочки путем использования на некотором этапе теории возмущений, что позволяет найти, по крайней мере, некоторую бесконечную подпоследовательность полного ряда теории возмущений. В частности, при вычислении величин ${{\Sigma }^{{(1)}}}(1,2)$ и ${{D}^{{(1)}}}(1,2)$ предлагалось использовать низшее приближение теории возмущений для вершин, положив

что с точки зрения цепочки Фридмана–Келлера в какой-то мере соответствует схеме замыкания уравнений для статистических моментов. Однако в рассматриваемом случае замыкание осуществляется без привлечения основанных на феноменологических соображениях гипотез типа приближения квазинормальности Миллионщикова [22] о связи высших статистических моментов с низшими или приближения прямых взаимодействий Крейчнана [23]. Приближению (3.19) соответствует известное в квантовой теории поля и успешно применяемое в ряде других областей “однопетлевое приближение”, в котором учитывается вклад всех диаграмм теории возмущений, не содержащих пересекающихся петель.

Решение полученной системы уравнений может строиться методом итераций, при котором в качестве нулевого приближения используются выражения для $\Sigma $ и ${{D}^{{(1)}}}$, вычисленные в низшем приближении теории возмущений, подстановка которых в уравнения Уайлда (3.3) и Дайсона (3.8) с последующим их решением соответствует суммированию некоторой бесконечной подпоследовательности ряда теории возмущений для функции Грина и ПКФ.

Улучшение однопетлевого приближения (3.19) может быть осуществлено при вычислении вершин с помощью операции функционального дифференцирования выражений для ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ по полям $\hat {\eta }$ и $\hat {f}$ согласно формулам (3.16). В рамках СДТ операции функционального дифференцирования будут отображаться вставкой входящих и выходящих стрелок в линии пропагаторов, корреляторов и вершин.

На рис. 4 приведены графические представления результатов действия операторов функционального дифференцирования на линии пропагаторов и корреляторов, соответствующие формулам (3.12)–(3.15). Согласно формулам (3.5) и (3.7) диаграммы для ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ содержат вставку в линию коррелятора входящей и выходящей стрелок, а использование формул (3.16) позволяет графически представить вершины в виде прямоугольников со вставками входящих и выходящих стрелок (рис. 4).

Для получения представлений для вершин с применением операции функционального дифференцирования выражений для ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ согласно формулам (3.16) требуется проведение длительных вычислений с использованием громоздких формул. Эта процедура может быть существенно упрощена в рамках СДТ при использовании сформулированных выше правил графического выполнения операций функционального дифференцирования.

На рис. 5 приведен результат применения СДТ при вычислении вершины $\Gamma (1{\kern 1pt} {\text{|}}{\kern 1pt} 2,3)$. Графическое представление вершин двух других типов может быть получено при замене одной или двух входящих стрелок на выходящие. Отметим, что полученные графические представления для вершин $\Gamma $ содержат еще вершины с четырьмя входящими и выходящими стрелками (четыреххвостые вершины); для них с помощью графического выполнения операций функционального дифференцирования можно получить представление, которое будет содержать пятихвостые вершины. Так возникает цепочка уравнений, в некотором смысле аналогичная цепочке уравнения Фридмана–Келлера при статистическом описании турбулентности в терминах статистических моментов. Отметим, что при графическом представлении уравнений левая вершина всегда оказывается затравочной (bare).

Однако в рассматриваемом случае приближение строится не в виде разложения по некоторому параметру, как в теории возмущений, а по другой схеме. Как уже говорилось, приближение (3.19) соответствует учету всех диаграмм теории возмущений, не содержащих пересекающихся петель. Если в диаграммном представлении для вершин отбросить четыреххвостые вершины, то полученная система диаграммных уравнений будет соответствовать учету всех диаграмм теории возмущений, не содержащих дважды пересекающихся петель.

Из однопетлевого приближения (3.19) следует, что поправки к корреляционной функции внешних случайных сил ${{D}^{{(1)}}}$, которые согласно формуле (3.18) выражаются через вершины $\Gamma (1,{\text{2|3}})$ и $\Gamma (1,2,3)$, содержащие две и три выходящие стрелки, равны нулю. Однако оказывается, что существует возможность выразить вершины с двумя и тремя выходящими стрелками через вершину с одной выходящей стрелкой $\Gamma (1{\kern 1pt} {\text{|}}{\kern 1pt} 2,3)$.

Для нахождения дополнительных соотношений, связывающих вершины разных типов, подействуем на уравнение (2.11) оператором функционального дифференцирования $\delta {\text{/}}\delta \hat {f}(4)$ и получим

И аналогично, при действии на уравнение (2.12) этим оператором, найдем

Используя уравнение Уайлда (3.3), приходим к представлению вершин с двумя и тремя выходящими стрелками через вершину с двумя входящими и одной выходящей стрелками

Графические представления соотношений (3.20) и (3.21) приведены на рис. 6, также изображены диаграммные представления для величин ${{\Sigma }^{{(1)}}}$ и ${{D}^{{(1)}}}$ и вершин $\Gamma $, полученные после исключения вершин второго и третьего типов.

4. Обсуждение. Поскольку функциональная формулировка статистической теории турбулентности и вытекающей из нее СДТ является некоторой альтернативой теории возмущений и соответствующей диаграммной техники, представляется целесообразным сравнение этих двух подходов. В теории возмущений решение для скорости в виде степенного ряда строится с помощью итерационной процедуры, при которой в качестве нулевого приближения используется решение линеаризованного УНС в поле внешней случайной силы ${{u}^{{(0)}}}(1)$ = ${{G}^{{(0)}}}(1,2)X(2)$, которое подставляется в нелинейный член УНС и для нахождения следующего приближения для скорости получившееся уравнение решается с учетом поправки к внешней случайной силе. Итерационная процедура приводит к представлению решения для скорости в виде ряда по степеням внешней случайной силы. Уже выполнение первой итерации оказывается очень громоздкой процедурой и для упрощения записи и анализа последующих приближений используется техника фейнмановских диаграмм. Учет высших приближений осуществляется путем процедуры перенормировок, сводящейся к замене базовых элементов теории возмущений ${{G}^{{(0))}}}$, $V({\text{1|2}},3)$ и ${{D}^{{(0)}}}$ на перенормированные значения $G$, $\Gamma ({\text{1|2}},3)$ и $D$, что на языке диаграмм соответствует переходу от диаграммной техники теории возмущений к СДТ. Подобная процедура неоднозначна и это проявляется, например, при подсчете числа топологически эквивалентных диаграмм или в том, что в СДТ имеются вершины трех типов (см. формулы (3.16), тогда как в диаграммной технике теории возмущений имеется единственная вершина.

При функциональной формулировке теории на основе метода ХФ и связанного с ним метода скелетных диаграмм Фейнмана следует, что ошибки при переходе от диаграмм теории возмущений к скелетным диаграммам, исключаются автоматически [20], а уравнения Уайльда и Дайсона следуют напрямую из формализма ХФ вне рамок теории возмущений. Полученное в рамках функциональной формулировки соотношение между вершинами различных типов позволяет выразить вершины второго и третьего типов (с двумя и тремя выходящими стрелками) через вершину первого типа (две входящие стрелки и одна выходящая). Кроме того становится ясным, какие диаграммы не учитываются при использовании однопетлевого и двухпетлевого приближений. Можно надеяться, что с ростом “запутанности” скелетных диаграмм вклад соответствующих диаграмм будет уменьшаться.

Работа выполнена в рамках государственного задания № АААА-А17-117021310375-7.