Прикладная математика и механика, 2020, T. 84, № 1, стр. 64-76
СТРУКТУРА ТЕМПЕРАТУРНОГО ФРОНТА ПРИ ФИЛЬТРАЦИИ В ТРЕЩИНОВАТО-ПОРИСТОЙ СРЕДЕ
А. А. Афанасьев *
Научно-исследовательский институт механики МГУ им. М.В. Ломоносова
Москва, Россия
* E-mail: afanasyev@imec.msu.ru
Поступила в редакцию 30.01.2019
После доработки 03.10.2019
Принята к публикации 05.10.2019
Аннотация
Исследована структура фронта температуры при неизотермической однофазной фильтрации в трещиновато-пористой среде с учетом неравновесных эффектов, обусловленных различными значениями температуры в трещинах и вмещающей их низкопроницаемой среде. В рамках модели двойной пористости даны оценки для толщины фронта и ограничены области значений параметров подобия, при которых она определяется процессами теплопроводности или неравновесным теплообменом в среде. Для различных пространственных масштабов неизотермического течения выделено три асимптотических случая распределения температуры в структуре фронта, описывающихся конечными соотношениями.
1. Постановка задачи. При закачке нагретой жидкости в однородную холодную пористую среду, насыщенную той же самой жидкостью, образуется фронт температуры $S$. Предположим, что в одномерном течении он распространяется от границы $x = 0$ в область $x > 0$ (рис. 1). Перед фронтом сохраняется начальная температура ${{T}_{ - }}$, а за ним пористая среда нагревается до температуры закачиваемой жидкости ${{T}_{ + }}$. Предполагая локальное тепловое равновесие и малость кондуктивного переноса тепла по сравнению с конвективным, фронт можно рассматривать как сильный разрыв, на котором температура скачком возрастает от ${{T}_{ - }}$ до ${{T}_{ + }}$ (рис. 1, линия 1). Решения с такими разрывами, скорость которых выражается из конечного соотношения, рассматривались ранее (напр. [1, 2]). Если кондуктивный перенос тепла сопоставим с конвективным, то теплопроводность сглаживает разрывное распределение температуры. В результате фронт $S$ представляет собой протяженную область, в которой температура непрерывно возрастает от ${{T}_{ - }}$ до ${{T}_{ + }}$ (рис. 1, кривая 2). Фильтрация с подобными температурными слоями, протяженность которых растет со временем, $t$, как $\sqrt t $, рассматривалась в [3–5].
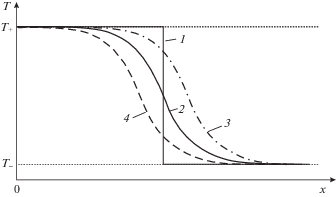
Рис. 1.
Схема распределения температуры $T$ в фронте $S$ при локальном равновесии (кривые 1, 2), в случаях если конвективный поток тепла существенно больше кондуктивного потока (кривая 1) и если эти потоки сопоставимы (кривые 2–4). Разрывные линии 3 и 4 показывают распределения $T$ в средах ${{\Phi }_{f}}$ и ${{\Phi }_{m}}$ при отсутствии локального теплового равновесия.
При высоких скоростях фильтрации течение осложняется отсутствием локального теплового равновесия между жидкостью и скелетом пористой среды. В этом случае время, за которое фронт проходит некоторое характерное расстояние, имеет тот же или больший порядок величины, что и время, за которое в элементарном объеме выравниваются температуры жидкости и скелета пористой среды. Подобные неравновесные эффекты, также как и теплопроводность, могут привести к образованию переходного слоя $S$ конечной толщины, в котором температура непрерывна. Структура таких фронтов рассматривалась в работах [6, 7], в которых показано, что при характерных размерах зерен геологических пористых сред (100–104 мкм) подобные неравновесные эффекты несущественны для геофизических приложений теории фильтрации.
В настоящей работе рассмотрена структура температурного фронта при фильтрации в трещиновато-пористых средах, когда течение осложняется наличием двух различных масштабов пористости и проницаемости. Существуют высокопроницаемые трещины или каналы, между которыми располагаются низкопроницаемые пористые блоки. Для прогнозирования фильтрации в таких средах часто используют модель двойной пористости [8, 9]. В этой модели трещиновато-пористая среда рассматривается в виде двух взаимопроникающих континуумов (пористых сред) – трещин, ${{\Phi }_{f}}$, и блоков, ${{\Phi }_{m}}$, между которыми происходит тепломассообмен [8, 10]. В практических приложениях часто рассматривается предельный случай, когда ${{\Phi }_{f}}$ имеет малую пористость и высокую проницаемость, а ${{\Phi }_{m}}$, наоборот, – высокую пористость и малую проницаемость [11–13]. В этом случае течение жидкости в основном происходит по трещинам, тогда как больший ее объем находится в блоках. В настоящей работе для общности исследования данных предположений о ${{\Phi }_{f}}$ и ${{\Phi }_{m}}$ не делается, а существенным для дальнейшего изложения является только наличие двух различных масштабов пористости проницаемости.
При фильтрации в трещиновато-пористой среде нагретая жидкость может переносить высокие значения температуры ${{T}_{ + }}$ существенно быстрее по трещинам ${{\Phi }_{f}}$, чем по блокам ${{\Phi }_{m}}$ (рис. 1, кривые 3 и 4). В результате локальное тепловое равновесие между ${{\Phi }_{f}}$ и ${{\Phi }_{m}}$ нарушается, а фронт $S$ имеет конечную толщину. При этом в обоих взаимопроникающих континуумах возможен конвективный перенос тепла жидкостью, который в отличие от [6, 7, 14, 15] учитывается в настоящей работе. Так как характерный размер низкопроницаемых блоков в среде ${{\Phi }_{m}}$ (>1 м) существенно больше характерного размера зерен (100–104 мкм), то неравновесное распределение температуры в трещиновато-пористых средах может развиваться в существенно большем диапазоне параметров течения, чем в случаях, рассмотренных ранее [6, 7]. Подобную неравновесность необходимо учитывать в геофизических приложениях, связанных с получением геотермальной энергии и природными процессами [11, 13].
2. Основные уравнения. Поровое пространство трещиновато-пористой среды охарактеризуем параметром $\gamma = {{{{V}_{f}}} \mathord{\left/ {\vphantom {{{{V}_{f}}} V}} \right. \kern-0em} V}$ – относительным объемом среды ${{\Phi }_{f}}$, где $V = {{V}_{f}} + {{V}_{m}}$ – полный элементарный объем среды, а ${{V}_{i}}$, $i = f,m$ – объем, относящийся к континууму ${{\Phi }_{i}}$. Тогда относительный объем среды ${{\Phi }_{m}}$ равен $1 - \gamma = {{{{V}_{m}}} \mathord{\left/ {\vphantom {{{{V}_{m}}} V}} \right. \kern-0em} V}$. Для каждого континуума зададим пористость ${{\phi }_{i}} = {{{{V}_{{\operatorname{por} ,i}}}} \mathord{\left/ {\vphantom {{{{V}_{{\operatorname{por} ,i}}}} {{{V}_{i}}}}} \right. \kern-0em} {{{V}_{i}}}}$, абсолютную проницаемость ${{K}_{i}}$, и коэффициент теплопроводности насыщенной пористой среды ${{\lambda }_{i}}$, где ${{V}_{{\operatorname{por} ,i}}}$ – объем пустот, заполненных жидкостью в соответствующем континууме. Тогда поровые пространства в средах ${{\Phi }_{f}}$ и ${{\Phi }_{m}}$ занимают, соответственно, доли $\gamma {{\phi }_{f}}$ и $(1 - \gamma ){{\phi }_{m}}$ элементарного объема $V$.
Неизотермическая фильтрация несжимаемой жидкости в тонком горизонтальном слое трещиновато-пористой среды описывается системой уравнений [8, 11, 13, 16, 17]
(2.3)
${{\partial }_{t}}{{(\rho e)}_{i}} + \nabla \left( {\rho {{e}_{i}}{{{\mathbf{u}}}_{i}}} \right) = - \nabla ({{P}_{i}}{{{\mathbf{u}}}_{i}}) + {{n}_{i}}{{{v}}_{{mf}}}{{P}_{i}} + {{\lambda }_{i}}\Delta {{T}_{i}} + {{n}_{i}}{{{v}}_{{mf}}}\rho C{{T}_{{mf}}} + {{n}_{i}}{{q}_{{mf}}}$(2.4)
${{{v}}_{{mf}}} = \sigma \frac{{{{K}_{m}}}}{\mu }({{P}_{m}} - {{P}_{f}}),\quad {{q}_{{mf}}} = \sigma {{\lambda }_{m}}({{T}_{m}} - {{T}_{f}})$Здесь ${{{{\partial }_{t}} = \partial } \mathord{\left/ {\vphantom {{{{\partial }_{t}} = \partial } {\partial t}}} \right. \kern-0em} {\partial t}}$, ${\mathbf{u}}$ – скорость фильтрации, $\mu = {\text{const}}$ – динамическая вязкость жидкости, $P$ – давление, $\sigma = 12{\text{/}}(L_{0}^{2})$ – параметр формы блоков в изотропной среде ${{\Phi }_{m}}$, характеризующий форму и размер блоков и, следовательно, интенсивность тепломассообмена между трещинами и блоками [12], ${{L}_{0}}$ – характерный размер блоков, $\rho = {\text{const}}$ – плотность жидкости, а $e$ – ее удельная внутренняя энергия, ${{(\rho e)}_{i}}$ – эффективная внутренняя энергия насыщенной пористой среды ${{\Phi }_{i}}$, $T$ – температура, ${{{v}}_{{mf}}}$ и ${{q}_{{mf}}}$ – потоки жидкости и энергии, передающейся посредством теплопроводности, из среды ${{\Phi }_{m}}$ в ${{\Phi }_{f}}$, введены константы ${{n}_{f}} = 1$, ${{n}_{m}} = - 1$, а индекс $i = m,f$ обозначает параметры, относящиеся к среде ${{\Phi }_{i}}$.
Соотношение (2.1) – закон фильтрации Дарси, а (2.2) – уравнения неразрывности для каждого ${{\Phi }_{i}}$. Закон сохранения энергии (2.3) основывается на предположении о малой скорости фильтрации ${\mathbf{u}}$, которое заведомо выполняется для широкого класса течений в пористых средах [16]. Тогда, считая ${\mathbf{u}}$ малым, при записи баланса энергии можно пренебречь изменением кинетической энергии $E\sim {{{\mathbf{u}}}^{2}}$ и притоком тепла вследствие диссипации кинетической энергии $dQ{\text{**}}\sim {{{\mathbf{u}}}^{2}}$. В результате закон сохранение энергии для каждого континуума ${{\Phi }_{i}}$ постулируем в виде
где $dU$ – изменение внутренней энергии, $d{{A}^{{(e)}}}$ – элементарная работа внешних сил, $d{{Q}^{{(e)}}}$ – элементарный приток тепла [18]. В сформулированной задаче массовые силы отсутствуют, поэтому член $d{{A}^{{(e)}}}$ содержит работу только поверхностных сил. Левые части уравнений (2.3) соответствуют приращению $d{{U}_{i}}$ в законе (2.5). Члены $ - \nabla \left( {{{P}_{i}}{{{\mathbf{u}}}_{i}}} \right)$ и ${{n}_{i}}{{P}_{i}}{{{v}}_{{mf}}}$ соответствуют работе внешних сил давления $dA_{i}^{{(e)}}$, приводящих к течению по средам ${{\Phi }_{i}}$ и между ${{\Phi }_{m}}$ и ${{\Phi }_{f}}$, соответственно. Последние три члена в правой части (2.3), равны кондуктивному (т.е. из-за теплопроводности) притоку тепла $dQ_{i}^{{(e)}}$ по среде ${{\Phi }_{i}}$, а также конвективному и кондуктивному перетоку тепла между ${{\Phi }_{m}}$ и ${{\Phi }_{f}}$, соответственно.Соотношения (2.4) задают переток жидкости и кондуктивный поток тепла между взаимопроникающими средами, согласно которым ${{{v}}_{{mf}}}$ прямо пропорционально разности давлений ${{P}_{m}} - {{P}_{f}}$, а ${{q}_{{mf}}}$ – температур ${{T}_{m}} - {{T}_{f}}$.
Температура ${{T}_{{mf}}}$ жидкости во втором слагаемом в правой части уравнения (2.3), ответственном за конвективный перенос тепла между ${{\Phi }_{i}}$, сносится против направления потока. Если течение происходит из ${{\Phi }_{m}}$ в ${{\Phi }_{f}}$, т.е. при ${{P}_{m}} \geqslant {{P}_{f}}$, ${{{v}}_{{mf}}} \geqslant 0$, то ${{T}_{{mf}}} = {{T}_{m}}$, а если, наоборот, – из ${{\Phi }_{f}}$ в ${{\Phi }_{m}}$, т.е. при ${{P}_{m}} < {{P}_{f}}$, ${{{v}}_{{mf}}} < 0$, то ${{T}_{{mf}}} = {{T}_{f}}$.
Эффективная плотность внутренней энергии ${{(\rho e)}_{i}}$ (и теплоемкость ${{(\rho С)}_{i}}$) бесконечно малого объема среды ${{\Phi }_{i}}$ записывается в виде суммы объемных энергий (и теплоемкостей) жидкости и скелета пористой среды:
(2.6)
$\begin{gathered} {{\left( {\rho y} \right)}_{f}} = \gamma ({{\phi }_{f}}\rho {{y}_{f}} + (1 - {{\phi }_{f}}){{\rho }_{r}}y_{{r,f}}^{{}}),\quad y = e,C \\ {{\left( {\rho y} \right)}_{m}} = (1 - \gamma )\left( {{{\phi }_{m}}\rho {{y}_{m}} + (1 - {{\phi }_{m}}){{\rho }_{r}}{{y}_{{r,m}}}} \right), \\ \end{gathered} $3. Уравнения в безразмерной форме и предложения. Учитывая сформулированную задачу (рис. 1), определим безразмерные параметры в виде
(3.1)
$x = {{x}_{ * }}L,\quad t = {{t}_{ * }}{{t}_{s}},\quad u = {{u}_{ * }}\Omega ,\quad P = {{P}_{ * }}{{P}_{s}},\quad T = {{T}_{ * }}{{T}_{s}},$(3.2)
$\begin{gathered} L = \frac{{\Omega {{t}_{s}}}}{{\bar {\phi }}},\quad \Omega = \frac{{\bar {K}{{P}_{s}}}}{{\mu L}},\quad {{T}_{s}} = {{T}_{ + }} - {{T}_{ - }} \\ \bar {\phi } = \gamma {{\phi }_{f}} + (1 - \gamma ){{\phi }_{m}},\quad \bar {K} = {{K}_{f}} + {{K}_{m}},\quad \bar {\lambda } = {{\lambda }_{f}} + {{\lambda }_{m}}, \\ \end{gathered} $Подставляя соотношения (2.4)–(3.2) в уравнения (2.1)–(2.3) и всюду далее опуская символ звездочки у безразмерных величин, систему уравнений фильтрации в трещиновато-пористой среде представим в виде
(3.5)
$\begin{gathered} {\text{S}}{{{\text{h}}}_{i}}{{\partial }_{t}}{{T}_{i}} + {{{\mathbf{u}}}_{i}}\nabla {{T}_{i}} + \Upsilon {{{\mathbf{u}}}_{i}}\nabla {{P}_{i}} = \\ = \frac{{{{\Lambda }_{i}}}}{{{\text{Pe}}}}\Delta {{T}_{i}} + {{n}_{i}}\frac{{{{\kappa }_{m}}}}{B}({{P}_{m}} - {{P}_{f}})({{T}_{{mf}}} - {{T}_{i}}) + \frac{{{{n}_{i}}{{\Lambda }_{m}}}}{{B{\text{Pe}}}}({{T}_{m}} - {{T}_{f}}), \\ \end{gathered} $(3.6)
$\begin{gathered} {{\kappa }_{i}} = \frac{{{{K}_{i}}}}{{\bar {K}}},\quad {{\Lambda }_{i}} = \frac{{{{\lambda }_{i}}}}{{\bar {\lambda }}},\quad {\text{S}}{{{\text{h}}}_{i}} = \frac{{{{{(\rho C)}}_{i}}}}{{\bar {\phi }\rho С}} \\ \Upsilon = \frac{{{{P}_{s}}}}{{\rho C{{T}_{s}}}},\quad B = \frac{1}{{\sigma {{L}^{2}}}},\quad {\text{Pe}} = \frac{{\rho C\Omega L}}{{\bar {\lambda }}} \\ \end{gathered} $Так как ${{\kappa }_{f}} + {{\kappa }_{m}} = 1$ и ${{\Lambda }_{f}} + {{\Lambda }_{m}} = 1$, то из параметров ${{\kappa }_{i}}$ и ${{\Lambda }_{i}}$ только ${{\kappa }_{m}}$ и ${{\Lambda }_{m}}$ независимые, а ${{\kappa }_{f}} = 1 - {{\kappa }_{m}}$, ${{\Lambda }_{f}} = 1 - {{\Lambda }_{m}}$.
Параметр подобия $\Upsilon $ характеризует влияние работы внешних поверхностных сил (давления) на распределение температуры. Для типичных параметров течения воды, рассматривающихся в данной работе ($\rho = 1000$ кг/м3, $С = 4200$ Дж/(кг K), ${{P}_{s}} = {{10}^{5}}$ Па, ${{T}_{s}} \geqslant 1$°C), выполняется условие $\Upsilon \ll 1$, поэтому всюду далее полагаем $\Upsilon \equiv 0$.
Параметр подобия $B$ характеризует интенсивность тепломассообмена между ${{\Phi }_{i}}$. Если $B \to 0$, то множители перед разностями давлений ${{P}_{m}} - {{P}_{f}}$ и температур ${{T}_{m}} - {{T}_{f}}$ в правых частях уравнений (3.4) и (3.5) стремятся к бесконечности, а, следовательно, эти разности стремятся к нулю. Это означает, что при $B \to 0$ $P$ и $T$ в средах ${{\Phi }_{i}}$ быстро выравниваются. Чем больше $B$, тем больше могут различаться давления ${{P}_{i}}$ и температуры ${{T}_{i}}$, а локальное равновесие между средами нарушается. Таким образом, $B$ есть мера неравновесности течения из-за различной динамики процессов в средах ${{\Phi }_{i}}$.
В условиях локального теплового равновесия ($B = 0$) фильтрация описывается уравнениями, полученными попарным суммированием уравнений (3.3)–(3.5) при $i = f$ с $i = m$:
(3.7)
$\begin{gathered} {\mathbf{\bar {u}}} = - \nabla P,\quad \nabla {\mathbf{\bar {u}}} = 0,\quad {\kern 1pt} \overline {{\text{Sh}}} {{\partial }_{t}}T + {\mathbf{\bar {u}}}\nabla T = \frac{{\Delta T}}{{{\text{Pe}}}} \\ P = {{P}_{f}} = {{P}_{m}},\quad T = {{T}_{f}} = {{T}_{m}},\quad {\mathbf{\bar {u}}} = {{{\mathbf{u}}}_{f}} + {{{\mathbf{u}}}_{m}},\quad \overline {{\text{Sh}}} = {\text{S}}{{{\text{h}}}_{f}} + {\text{S}}{{{\text{h}}}_{m}} \\ \end{gathered} $Заметим, что система уравнений (3.3)–(3.5) расщепляется на две подсистемы, которые можно решить последовательно одну за другой. Сначала достаточно решить уравнения (3.3), (3.4) относительно ${{P}_{i}}$ и ${{{\mathbf{u}}}_{i}}$, а затем, используя полученные распределения давления и скорости, решить два уравнения на температуру (3.5).
Далее ограничимся случаем, когда на границе $x = 0$ давления в средах равны, а объемы жидкости, закачиваемой в среды ${{\Phi }_{i}}$, пропорциональны соответствующей проницаемости ${{K}_{i}}$, т.е. в безразмерных переменных заданы граничные условия
(3.8)
$x = {\text{0:}}\quad {{P}_{i}} = {{P}_{ + }},\quad {{T}_{i}} = 1,\quad {{{{u}_{m}}} \mathord{\left/ {\vphantom {{{{u}_{m}}} {{{u}_{f}}}}} \right. \kern-0em} {{{u}_{f}}}} = {{{{\kappa }_{m}}} \mathord{\left/ {\vphantom {{{{\kappa }_{m}}} {{{\kappa }_{f}}}}} \right. \kern-0em} {{{\kappa }_{f}}}},$Таким образом, давления в средах ${{\Phi }_{i}}$ равны друг другу во всей области $x > 0$ и, согласно соотношениям (2.4), переток жидкости между ${{\Phi }_{i}}$ равен нулю: ${{{v}}_{{mf}}} = 0$. Тогда второй член в правой части уравнения (3.5) тождественно равен нулю, а уравнения на температуру упрощаются:
(3.10)
$\begin{gathered} {\text{S}}{{{\text{h}}}_{i}}{{\partial }_{t}}{{T}_{i}} + {{\kappa }_{i}}\nabla {{T}_{i}} = {{\Lambda }_{i}}\alpha \Delta {{T}_{i}} + {{n}_{i}}{{\Lambda }_{m}}\beta ({{T}_{m}} - {{T}_{f}}) \\ \alpha = \frac{1}{{{\text{Pe}}}},\quad \beta = \frac{1}{{B{\text{Pe}}}} \\ \end{gathered} $Учитывая уравнения (3.7) и соотношения (2.5), получим, что температура в равновесном течении ($B = 0$) удовлетворяет уравнению
4. Малые возмущения и сильные разрывы. При ${\text{Pe}} \to \infty $ система двух уравнений (1.16) на распределение температуры в неравновесном течении имеет две характеристические скорости [1]
С характеристикой ${{c}_{m}}$ (или ${{c}_{f}}$) в среде ${{\Phi }_{m}}$ (или ${{\Phi }_{f}}$) переносятся малые возмущения температуры ${{T}_{m}}$ (или ${{T}_{f}}$), а параметры в смежной среде ${{\Phi }_{f}}$ (или ${{\Phi }_{m}}$) не изменяются. Таким образом, малые возмущения (4.1) описывают перенос возмущений ${{T}_{i}}$ жидкостью в условиях пренебрежимо малой теплопроводности и отсутствия теплообмена между средами ${{\Phi }_{i}}$.
Из интегральной формы записи законов сохранения (3.10) [18, 19] следует, что при ${\text{Pe}} \to \infty $ и любом $B$ возможны разрывы двух типов, ${{S}_{f}}$ и ${{S}_{m}}$, распространяющихся со скоростями ${{c}_{f}}$ и ${{c}_{m}}$. Разрывы ${{S}_{f}}$ (и ${{S}_{m}}$) переносят возмущения ${{T}_{f}}$ (и ${{T}_{m}}$), а температура ${{T}_{m}}$ (и ${{T}_{f}}$) в них непрерывна. На каждом разрыве ${{S}_{i}}$ выполняется два условия, соответствующие законам сохранения (3.10), поэтому для эволюционности разрыва ${{S}_{i}}$ необходимо потребовать, чтобы от него уходила ровно одна характеристика [19]. Так как в среде ${{\Phi }_{i}}$ скорость разрыва равна ${{c}_{i}}$, то, в случае общего положения ${{c}_{f}} \ne {{c}_{m}}$, и от разрыва ${{S}_{i}}$ уходит только одна характеристика другого типа ${{c}_{j}}$, $j \ne i$. Это означает, что любой разрыв ${{S}_{i}}$ эволюционен.
При ${\text{Pe}} \to \infty $ уравнение (3.11) на распределение температуры в равновесном течении имеет одну характеристическую скорость
Заметим, что из выражения (4.2) ясен физический смысл параметра $\overline {{\text{Sh}}} $. Температурное число Струхаля $\overline {{\text{Sh}}} > 1$ показывает во сколько раз в равновесном течении частица жидкости движется быстрее, чем распространяются возмущения температуры $T$, вызванные конвективным переносом тепла. Действительно, если частица нагретой жидкости догоняет $S$, то далее она в переходном слое отдает тепло скелету пористой среды, охлаждается и движется дальше, обгоняя $S$. Числа ${\text{S}}{{{\text{h}}}_{i}}$ характеризуют те же самые процессы в средах ${{\Phi }_{i}}$ при $B \to \infty $.
Из интегральной формы записи уравнения (3.11) следует, что в равновесном течении возможны разрывы только одного типа $S$, распространяющегося с характеристической скоростью $c$. При $B = 0$ на разрыве $S$ выполняется одно условие, соответствующее закону сохранения (3.11), поэтому для эволюционности разрыва $S$ необходимо потребовать, чтобы характеристики (4.2) от него не уходили. Так как разрыв распространяется со скоростью $c$, то в равновесной модели разрыв $S$ всегда эволюционен.
Рассмотрим разрыв $S$ в рамках более общей неравновесной модели (3.10), из которой в пределе $B = 0$ получено уравнение (3.11). В случае общего положения $c \ne {{c}_{i}}$, поэтому при $B \ne 0$ разрыв $S$ неэволюционен, так как от него обязательно уходит одна характеристика ${{c}_{m}}$ и одна ${{c}_{f}}$. Таким образом, имеется кажущееся противоречие, связанное с тем, что разрыв $S$ эволюционен только в предельном случае $B = 0$ и неэволюционен при любом $B > 0$, несмотря на то, что уравнение (3.11) есть частный случай системы (3.10). Для разрешения противоречия рассмотрим структуру фронта разрыва $S$ в неравновесном течении.
5. Характерные масштабы в температурном фронте. Введем переменную
равную числу вовлеченных в неизотермическое течение блоков в среде ${{\Phi }_{m}}$, умноженному на коэффициент ${1 \mathord{\left/ {\vphantom {1 {\sqrt {12} }}} \right. \kern-0em} {\sqrt {12} }}$. Таким образом, $X$ характеризует пространственный масштаб течения, если за единицу длины взят размер одного блока. Тогда, согласно (3.2), возрастание $X$ соответствует пропорциональному росту времени закачки нагретой жидкости ${{t}_{s}}$.Используя переменную $X$, параметры $\alpha $ и $\beta $ в уравнениях (3.10) представим в виде
(5.1)
$\alpha = \frac{1}{{{\text{P}}{{{\text{e}}}_{0}}X}},\quad \beta = \frac{X}{{{\text{P}}{{{\text{e}}}_{0}}}},\quad {\text{P}}{{{\text{e}}}_{0}} = \frac{{\rho C\Omega }}{{\bar {\lambda }\sqrt \sigma }}$Здесь ${\text{P}}{{{\text{e}}}_{0}}$ – число Пекле, если масштаб длины равен ${1 \mathord{\left/ {\vphantom {1 {\sqrt \sigma }}} \right. \kern-0em} {\sqrt \sigma }}\sim {{L}_{0}}$. Таким образом, параметр $\alpha $, пропорциональный кондуктивному переносу тепла внутри каждой среды ${{\Phi }_{i}}$, убывает с $X$ как ${{X}^{{ - 1}}}$, а параметр $\beta $, пропорциональный интенсивности теплообмена между средами, возрастает прямопропорционально $X$. Согласно (5.1), кривые $\alpha (X)$ и $\beta (X)$ на рис. 2 пересекаются в точке $O$ с координатами $X = 1$, $\alpha = \beta = {1 \mathord{\left/ {\vphantom {1 {{\text{P}}{{{\text{e}}}_{0}}}}} \right. \kern-0em} {{\text{P}}{{{\text{e}}}_{0}}}}$.
Рис. 2.
Зависимость $\alpha $ и $\beta $ от $X$ в логарифмических осях – прямые 1 и 2 соответственно.
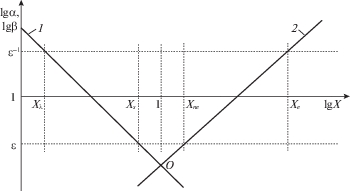
Введем малую величину $\varepsilon \ll 1$, такую что при $\alpha < \varepsilon $ и $\beta < \varepsilon $ можно пренебречь правой частью уравнения (3.10) по сравнению с конвективным членом ${{\kappa }_{i}}\nabla {{T}_{i}}$, имеющим порядок единицы в силу выбранных единиц измерения (3.1), (3.2). Определим значения ${{X}_{\lambda }}$, ${{X}_{s}}$, ${{X}_{{ne}}}$ и ${{X}_{e}}$ так, чтобы выполнялись равенства (рис. 2)
Тогда, согласно (5.1), получим
(5.2)
${{X}_{\lambda }} = \frac{\varepsilon }{{{\text{P}}{{{\text{e}}}_{0}}}},\quad {{X}_{s}} = \frac{1}{{\varepsilon {\text{P}}{{{\text{e}}}_{0}}}},\quad {{X}_{{ne}}} = {\text{P}}{{{\text{e}}}_{0}}\varepsilon ,\quad {{X}_{e}} = \frac{{{\text{P}}{{{\text{e}}}_{0}}}}{\varepsilon }$В силу введенных определений, при $t\sim 1$ и $X \geqslant {{X}_{s}}$ (${\text{Pe}} \gg 1$) влиянием теплопроводности на распределение параметров в пространстве можно пренебречь, а при $X < {{X}_{\lambda }}$ (${\text{Pe}} \ll 1$) кондуктивный перенос тепла преобладает над конвективным. При ${{X}_{\lambda }} \leqslant X < {{X}_{s}}$ необходимо учитывать оба механизма переноса тепла внутри каждого континуума ${{\Phi }_{i}}$. При $X \geqslant {{X}_{e}}$ ($B{\text{Pe}} \ll 1$) происходит течение близкое к локальному тепловому равновесию, т.е. ${{T}_{f}} \approx {{T}_{m}}$, а при $X < {{X}_{{ne}}}$ ($B{\text{Pe}} \gg 1$) теплообмен между средами пренебрежимо мал и, следовательно, распределения температур ${{T}_{m}}$ и ${{T}_{f}}$ не зависят друг от друга. При ${{X}_{{ne}}} \leqslant X < {{X}_{e}}$ существенны неравновесные эффекты из-за теплообмена между средами ${{\Phi }_{i}}$.
Предположим, что ${{X}_{s}} < {{X}_{{ne}}}$, т.е., согласно обозначениям (5.2), ${\text{P}}{{{\text{e}}}_{0}} \gg 1$, а точка $O$ на рис. 2 лежит ниже горизонтальной прямой с ординатой $\varepsilon $. Тогда выполняется следующая цепочка неравенств
Введем переменные
(5.4)
$\begin{gathered} {{\xi }_{0}} = \sqrt {\frac{{\overline {{\text{Sh}}} {\kern 1pt} {\text{Pe}}x}}{t}} ,\quad \xi = (\overline {{\text{Sh}}} x - t)\sqrt {\frac{{{\text{Pe}}}}{{\overline {{\text{Sh}}} {\kern 1pt} t}}} ,\quad \eta = \frac{{\overline {{\text{Sh}}} {\kern 1pt} x - t}}{{\overline {{\text{Sh}}} {\kern 1pt} t}} \\ \xi = {{\xi }_{0}} - \sqrt {\frac{{{\text{P}}{{{\text{e}}}_{0}}Xt}}{{\overline {{\text{Sh}}} }}} ,\quad \xi = \eta \sqrt {\overline {{\text{Sh}}} {\kern 1pt} {\text{P}}{{{\text{e}}}_{0}}Xt} \\ \end{gathered} $На масштабах $X < {{X}_{\lambda }}$, $t\sim 1$ уравнения (3.10) сводятся к системе двух уравнений теплопроводности, решение которых зависит только от переменной ${{\xi }_{0}}$:
(5.5)
${\text{S}}{{{\text{h}}}_{i}}{{\partial }_{t}}{{T}_{i}} = \frac{{{{\Lambda }_{i}}}}{{{\text{Pe}}}}\Delta {{T}_{i}},\quad {{T}_{i}} = 1 - {\text{erf}}\left( {\frac{{{{\xi }_{0}}}}{2}\sqrt {\frac{{{\text{S}}{{{\text{h}}}_{i}}}}{{\overline {{\text{Sh}}} {{\Lambda }_{i}}}}} } \right),$(5.6)
$\Delta {{x}_{i}}\sim \sqrt {\frac{{t{{\Lambda }_{i}}}}{{{\text{S}}{{{\text{h}}}_{i}}{\text{Pe}}}}} = \sqrt {\frac{{{{\Lambda }_{i}}}}{{{\text{S}}{{{\text{h}}}_{i}}{\text{P}}{{{\text{e}}}_{0}}}}} {{\left( {\frac{t}{X}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$Рис. 3.
Асимптотические случаи распределения ${{T}_{i}}$ при ${\text{S}}{{{\text{h}}}_{m}} = 1.86$, ${\text{S}}{{{\text{h}}}_{f}} = 0.53$, ${{\kappa }_{m}} = {{\Lambda }_{m}} = 0.3$, ${\text{P}}{{{\text{e}}}_{0}} = 18.3$. Кривые 1, 2 и 3, 4 – распределения ${{T}_{f}}$, ${{T}_{m}}$ при $X < {{X}_{\lambda }}$, $t \ll 1$ и ${{X}_{s}} \leqslant X < {{X}_{{ne}}}$, соответственно. Кривая 5 – равновесное распределение $T = {{T}_{f}} = {{T}_{m}}$ при $X \geqslant {{X}_{e}}$. Стрелки показывают направление смещения кривых при возрастании $Xt$.
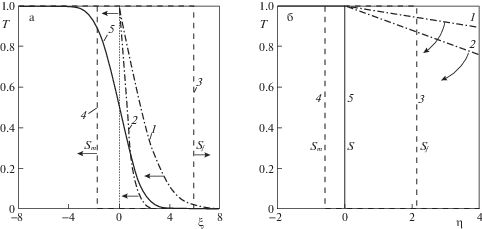
При $X < {{X}_{\lambda }}$ и возрастании $Xt$ кривые 1 и 2 на плоскости $\left\{ {\xi ,T} \right\}$ смещаются влево, так как переменная $\xi $ убывает при ${{\xi }_{0}} = {\text{const}}$ (рис. 3а). Решение (5.5) на плоскости $\left\{ {\eta ,T} \right\}$, $\eta \sim 1$ дает прямые линии (рис. 3б). В пределе $Xt \to 0$ они совпадают с горизонтальной прямой $T = 1$, а при возрастании $Xt$ их наклон к оси $\eta $ увеличивается.
На масштабах ${{X}_{\lambda }} < X < {{X}_{s}}$, $t\sim 1$, когда члены ${{\kappa }_{i}}\nabla {{T}_{i}}$ и ${{{{\Lambda }_{i}}\Delta {{T}_{i}}} \mathord{\left/ {\vphantom {{{{\Lambda }_{i}}\Delta {{T}_{i}}} {{\text{Pe}}}}} \right. \kern-0em} {{\text{Pe}}}}$ в уравнениях (3.10) сравнимы, а теплообмен между средами ${{\Phi }_{i}}$ еще пренебрежимо мал ($X < {{X}_{e}}$), распределение температуры описывается уравнениями
(5.7)
${\text{S}}{{{\text{h}}}_{i}}{{\partial }_{t}}{{T}_{i}} + {{\kappa }_{i}}\nabla {{T}_{i}} = \frac{{{{\Lambda }_{i}}}}{{{\text{Pe}}}}\Delta {{T}_{i}}$Решение системы (5.7) имеет вид
(5.8)
${{T}_{i}} = 1 - {\text{erf}}\left( {\frac{{{{\xi }_{i}}}}{2}} \right),\quad {{\xi }_{i}} = \left( {{\text{S}}{{{\text{h}}}_{i}}x - {{\kappa }_{i}}t} \right)\sqrt {\frac{{{\text{Pe}}}}{{{{\Lambda }_{i}}{\text{S}}{{{\text{h}}}_{i}}t}}} $Следовательно, температуры ${{T}_{i}}$ имеют автомодельные распределения от различных переменных ${{\xi }_{i}}$. Решения (5.8) описывают постепенное формирование двух различных фронтов температуры ${{S}_{i}}$ в средах ${{\Phi }_{i}}$, для толщины которых $\Delta {{x}_{i}}$ остается справедливой оценка (5.6). C возрастанием $Xt$ толщины фронтов на плоскости $\left\{ {\xi ,T} \right\}$ уменьшаются и в результате переходных процессов при ${{X}_{\lambda }} \leqslant X < {{X}_{s}}$ распределения температуры непрерывным образом эволюционируют к следующему асимптотическому распределению при ${{X}_{s}} \leqslant X < {{X}_{{ne}}}$.
На масштабах ${{X}_{s}} \leqslant X < {{X}_{{ne}}}$, $t\sim 1$ можно пренебречь как теплопроводностью (${{X}_{s}} \leqslant X$), так и теплообменом между средами ($X < {{X}_{{ne}}}$), а (3.10) сводится к двум уравнениям переноса
Система (5.9) описывает разрывные распределения температуры в среде ${{\Phi }_{i}}$, связанные с распространением со скоростями ${{c}_{i}}$ (4.1) двух сильных разрывов ${{S}_{i}}$ (рис. 3, кривые 3, 4). В результате ${{T}_{i}}$ в структуре фронта $S$ имеют автомодельные распределения от переменной $\eta $
где $\theta (x)$ – функция Хевисайда. Если эти решения построить на плоскости $\left\{ {\xi ,T} \right\}$, то график ${{T}_{i}}$ имеет форму “ступеньки”, смещающейся в случае разрыва ${{S}_{f}}$ (или ${{S}_{m}}$) в положительном (или отрицательном) направлении оси $\xi $ (предполагается, что ${{c}_{m}} < {{c}_{f}}$). На плоскости $\left\{ {\eta ,T} \right\}$ распределения (5.10) при возрастании $X$ не изменяются, т.е. при ${{X}_{s}} \leqslant X < {{X}_{{ne}}}$ реализуется автомодельное распределение температуры ${{T}_{i}}$ от переменной $\eta $. Для толщины $\Delta x$ фронта $S$, определяемой как расстояние от разрыва ${{S}_{m}}$ до ${{S}_{f}}$, справедлива оценка(5.11)
$\Delta x\sim \left( {{{c}_{f}} - {{c}_{m}}} \right)t = \left( {\frac{{{{\kappa }_{f}}}}{{{\text{S}}{{{\text{h}}}_{f}}}} - \frac{{{{\kappa }_{m}}}}{{{\text{S}}{{{\text{h}}}_{m}}}}} \right)t\sim 1$При этом разрывы ${{S}_{i}}$ нужно понимать как узкие температурные подслои, имеющие толщины (5.6).
На промежуточных масштабах ${{X}_{{ne}}} \leqslant X < {{X}_{e}}$ температуры ${{T}_{i}}$ непрерывным образом эволюционируют к следующему асимптотическому распределению при $X \geqslant {{X}_{e}}$. Здесь при возрастании $Xt$ температуры ${{T}_{i}}$ между разрывами ${{S}_{m}}$ и ${{S}_{f}}$ начинают выравниваться из-за теплообмена между средами ${{\Phi }_{i}}$, сближаясь при $X\sim {{X}_{e}}$.
При $X > {{X}_{e}}$, $t\sim 1$ можно пренебречь как теплопроводностью (${{X}_{s}} \leqslant X$), так и считать течение равновесным ($X > {{X}_{e}}$), происходящим при локально однородной температуре $T = {{T}_{i}}$. В этом случае уравнение на температуру (3.11) сводится к уравнению переноса (${\text{Pe}} \gg 1$)
которое описывает разрывное распределение $T$, связанное с распространением со скоростью $c$ (4.2) сильного разрыва $S$ (рис. 3б, линия 5):Для оценки толщины температурного слоя при $X \geqslant {{X}_{e}}$ заметим, что, в соответствии с (3.10), время установления локального теплового равновесия ${{t}_{e}}$ пропорционально константе $B{\text{Pe}}$, т.е. ${{t}_{e}}\sim B{\text{Pe}}$. Следовательно, так как скорость разрыва $S$ постоянна и равна $c$ (4.2), то для протяженности переходного слоя $\Delta {{x}_{e}}$, определяющегося только теплообменом между средами ${{\Phi }_{i}}$ ($B{\text{Pe}}\sim 1$, ${\text{Pe}} \to \infty $), получим оценку
(5.14)
$\Delta {{x}_{{ne}}}\sim cB\operatorname{Pe} = \frac{{B{\text{Pe}}}}{{\overline {{\text{Sh}}} }} = \frac{{{\text{P}}{{{\text{e}}}_{0}}}}{{\sigma L_{0}^{2}\overline {{\text{Sh}}} }}\frac{1}{X}$Если же пренебречь неравновесными эффектами, рассмотрев фронт, определяющийся только теплопроводностью ($B = 0$, ${\text{Pe}}{\kern 1pt} {\kern 1pt} {\sim 1}$), то, согласно (3.11), для его протяженности $\Delta {{x}_{\lambda }}$ получим
(5.15)
$\Delta {{x}_{\lambda }}\sim \sqrt {\frac{t}{{\overline {{\text{Sh}}} {\text{Pe}}}}} = \sqrt {\frac{1}{{\overline {{\text{Sh}}} {\text{P}}{{{\text{e}}}_{0}}}}} {{\left( {\frac{t}{X}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$Таким образом, согласно выражениям (3.6), (3.10) и (5.1), при $X > {{X}_{e}}$, $t\sim 1$ имеем $\Delta {{x}_{{ne}}}\sim {{X}^{{ - 1}}}$, $\Delta {{x}_{\lambda }}\sim {{X}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$. Следовательно, при $X \gg 1$ выполняется неравенство $\Delta {{x}_{\lambda }} > \Delta {{x}_{e}}$, а толщина фронта $S$ определяется теплопроводностью. В этом случае $T$ есть решение уравнения (3.11)
Соотношение (5.16) определяет кривую 5 на рис. 3а, которая с возрастанием $Xt$ не перемещается на плоскости $\left\{ {\xi ,T} \right\}$. Заметим, что устремив в выражении для температуры (5.16) $t$ к бесконечности и перейдя к переменной $\eta $, получим решение (5.13).
Таким образом, при $X < {{X}_{{ne}}}$ толщина $\Delta x$ фронта $S$, в соответствии с соотношением (5.11), растет прямо пропорционально времени $t$. При этом фронт содержит два температурных подслоя, соответствующих разрывам ${{S}_{i}}$, толщины которых $\Delta {{x}_{i}}$ растут как $\sqrt t $ (см. (5.6)). При ${{X}_{{ne}}} \leqslant X < {{X}_{e}}$ $\Delta x$ достигает значения $\Delta x\sim {{B{\text{Pe}}} \mathord{\left/ {\vphantom {{B{\text{Pe}}} {\overline {{\text{Sh}}} }}} \right. \kern-0em} {\overline {{\text{Sh}}} }}$ (см. (5.14)) и при $X > {{X}_{e}}$ растет как $\sqrt t $ (см. (5.15)), а внутренние температурные подслои исчезают из-за теплообмена между средами ${{\Phi }_{i}}$. Следовательно, неэволюционный в рамках неравновесной модели разрыв $S$ всегда имеет структуру конечной протяженности. В рамках неравновесной модели на таких масштабах, что $B \ll 1$, фронт $S$ нужно понимать не как сильный разрыв, а бесконечно узкий переходный слой.
В заключение отметим, что если не выполняется условие ${\text{P}}{{{\text{e}}}_{0}} \gg 1$, то ${{X}_{s}} > {{X}_{{ne}}}$, а цепочка неравенств (5.3) нарушается. При ${\text{P}}{{{\text{e}}}_{0}}\sim 1$ сразу после образования температурных слоев в средах ${{\Phi }_{i}}$ при $X < {{X}_{\lambda }}$ может становиться существенным теплообмен между средами ${{\Phi }_{i}}$, а промежуточный асимптотический этап ${{X}_{s}} \leqslant X < {{X}_{{ne}}}$, на котором фронт ограничен сильными разрывами ${{S}_{i}}$, не реализуется.
Работа выполнена при финансовой поддержке Совета по грантам Президента РФ (МД-3567.2018.1)
Список литературы
Афанасьев А.А. Исследование эволюционности разрывов при фильтрации бинарной смеси // Изв. РАН. МЖГ. 2014. № 1. С. 90–102.
Афанасьев А.А., Султанова Т.В. Исследование гидродинамической неустойчивости фронта вытеснения при закачке углекислого газа в водонасыщенный пласт // Изв. РАН МЖГ. 2016. № 4. С. 85–96.
Бармин А.А., Цыпкин Г.Г. Математическая модель инжекции воды в геотермальный пласт, насыщенный паром // Изв. РАН. МЖГ. 1996. № 6. С. 92–98.
Шагапов В.Ш., Ильясов У.Р., Насырова Л.А. Об инжекции воды в геотермальный пласт // ПМТФ. 2002. Т. 43. № 4. С. 127–138.
Афанасьев А.А., Бармин А.А. Нестационарные одномерные фильтрационные течения воды и пара с учетом фазовых переходов // Изв. РАН. МЖГ. 2007. № 4. С. 134–143.
Gandomkar A., Gray K.E. Local thermal non-equilibrium in porous media with heat conduction // Int. J. Heat Mass Trans. 2018. V. 124. P. 1212–1216.
Gelet R., Loret B., Khalili N. The significance of local thermal non-equilibrium in simulations of enhanced geothermal recovery // 14th IACMAG, Kyoto, Japan. 2014. P. 1713–1718.
Баренблатт Г.И., Желтов Ю.П., Кочина И.Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах // ПММ. 1960. Т. 24. Вып. 5. С. 852–864.
Warren J.E., Root P.J. The behavior of naturally fractured reservoirs // SPE J. 1963. V. 3. № 3. P. 245–255.
Нигматуллин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987. 464 с.
Pruess K., Narasimhan T.N. A practical method for modelling fluid and heat flow in fractured porous media // SPE. J. 1985 V. 25. № 1. P. 14–26.
Kazemi H., Merill L.S., Porterfield K.L., Zeman P.R. Numerical simulation of water-oil flow in naturally fractured reservoirs // SPE J. 1976. V. 16. № 6. P. 317–326.
Afanasyev A. Reservoir simulation with MUFITS code: Extension for double porosity reservoirs and flows in horizontal wells // Energy Proc. 2017. V. 125. P. 596–603.
Lu W., Xiang Y. Analysis of the instantaneous local thermal equilibrium assumption for heat exchange between rock matrix and fracture water // Adv. Mater. Res. 2012. V. 594–597. P. 2430–2437.
Nield D.A. A note on local thermal non-equilibrium in porous media near boundaries and interfaces // Transp. Porous Media. 2012. V. 95. P. 581–584.
Баренблат Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. М.: Недра, 1984. 208 с.
Афанасьев А.А. Об одном представлении уравнений многокомпонентной многофазной фильтрации // ПММ. 2012. Т. 76. Вып. 2. С. 265–274.
Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1970. 492 с.
Куликовский А.Г., Свешникова Е.И. Нелинейные волны в упругих средах. М.: Моск. лицей, 1998. 412 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


