Прикладная математика и механика, 2020, T. 84, № 5, стр. 570-589

1. Введение. Решения уравнений движения вязкого газа, описывающие достаточно простые течения, помогают нам понять физические особенности сложных течений. Исследование задачи о диффузии точечного вихря в вязкой несжимаемой жидкости можно найти практически во всех учебниках по гидродинамике. Вместе с тем известно, что поле окружных скоростей точечного вихря

где $2\pi {{\Gamma }_{0}}$ – циркуляция вихря, $r$ – расстояние от вихря, является и точным решением уравнений Эйлера, и точным решением уравнений Навье–Стокса. Во втором случае для поддержания поля скоростей (1.1) необходим постоянный подвод энергии [1]. Кроме того, жидкость, движущаяся со скоростью (1.1), обладает бесконечной кинетической энергией. Поле скоростей (1.1) в трехмерном течении индуцирует бесконечная прямолинейная вихревая нить интенсивности $2\pi {{\Gamma }_{0}}$. Выделим в направлении оси вихревой нити слой жидкости единичной протяженности и вычислим кинетическую энергию этого слоя

Здесь $m$ – масса жидкости, $\rho $ – плотность.

Интеграл (1.2) имеет логарифмическую особенность и в нуле и на бесконечности. Следовательно, встает вопрос о том, как в принципе такое поле скоростей могло быть создано. Создать поле (1.1) во всем пространстве невозможно. Обычно в физически реализуемых течениях образуется не один, а, например, два вихря с противоположной интенсивностью. Тогда поле скоростей имеет более быстро затухающее асимптотическое представление на больших удалениях. Таким образом, устраняется особенность при $r \to \infty $. Особенность при $r \to 0$ устраняется за счет того, что образующийся вихрь не является бесконечно тонким, а имеет структуру.

Можно предложить один из способов создания поля (1.1) в ограниченной области пространства. Это можно сделать в несжимаемой вязкой жидкости с помощью вращающегося вокруг своей оси бесконечного по протяженности цилиндра [2, 3].

Ранее [3, 4] исследовались нестационарное и предельное стационарное течение, порождаемые вращающимся цилиндром с заданным расходом жидкости через его поверхность. Задачи, связанные с взаимодействием набегающего потока с вращающимся цилиндром, рассмотрены во многих публикациях, например, [4–6]. Изучалась устойчивость подвижного цилиндра в циркуляционном потоке [7].

В данной статье рассматривается задача о вращении бесконечного цилиндра, но уже в сжимаемом газе с вязкостью, зависящей от температуры. Показано, что решение задачи во всем пространстве можно получить только в рамках нестационарной постановки. Нигде, кроме ограниченной области у поверхности цилиндра, течение не выходит на стационарный режим, что не было учтено ранее [8], где была предпринята попытка получить стационарное решение во всем пространстве.

2. Постановка задачи. Пусть бесконечный по протяженности круговой цилиндр радиуса ${{r}_{*}}$ помещен в покоящийся вязкий совершенный газ с температурой $T = {{T}_{0}}$, плотностью $\rho = {{\rho }_{0}}$ и коэффициентами динамической вязкости $\mu = {{\mu }_{0}}$ и теплопроводности $\lambda = {{\lambda }_{0}}$. В момент времени $t = 0$ цилиндр начинает вращаться вокруг своей оси с угловой скоростью ${{{{w}_{*}}} \mathord{\left/ {\vphantom {{{{w}_{*}}} {{{r}_{*}}}}} \right. \kern-0em} {{{r}_{*}}}}$, которая поддерживается постоянной. Исследуется возмущенное состояние газа при $t > 0$ при условии, что температура газа на поверхности цилиндра также сохраняется постоянной $T = {{T}_{*}}$.

Предполагается, что в цилиндрической системе координат $\left( {x,r,\theta } \right)$ нестационарное течение зависит только от координаты $r$ и имеет ламинарный характер. Таким образом, пренебрегается возможной неустойчивостью течения. Уравнения и краевые условия, определяющие состояние газа, имеют вид [9]

где $2\pi \Gamma $ – циркуляция азимутальной составляющей скорости $w$, $v$ – радиальная составляющая скорости, $p$ – давление газа, $\Pr = {{\mu {{c}_{p}}} \mathord{\left/ {\vphantom {{\mu {{c}_{p}}} \lambda }} \right. \kern-0em} \lambda }$ ~ $O\left( 1 \right)$ – число Прандтля, ${{c}_{p}}$ – удельная теплоемкость при постоянном давлении, $R$ – универсальная газовая постоянная, $(\,){\kern 1pt} ' \equiv {\partial \mathord{\left/ {\vphantom {\partial {\partial r}}} \right. \kern-0em} {\partial r}}$. Число Прандтля Pr и ${{c}_{p}}$ полагаются постоянными.

Согласно уравнениям (2.1) радиальный масштаб области, в которой возникают вязкие возмущения, является величиной пропорциональной $\sqrt {{{\nu }_{0}}t} $, где ${{\nu }_{0}} = {{{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{\mu }_{0}}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}$. Безразмерный параметр ${{\sqrt {{{\nu }_{0}}t} } \mathord{\left/ {\vphantom {{\sqrt {{{\nu }_{0}}t} } {{{r}_{*}}}}} \right. \kern-0em} {{{r}_{*}}}}$ – отношение характерных независимых линейных размеров рассматриваемой задачи – может меняться при $t > 0$ в широких пределах. В настоящей работе ставится задача о построении асимптотического решения уравнений (2.1), (2.2) при относительно больших временах, когда ${{\sqrt {{{\nu }_{0}}t} } \mathord{\left/ {\vphantom {{\sqrt {{{\nu }_{0}}t} } {{{r}_{*}}}}} \right. \kern-0em} {{{r}_{*}}}} = {{\varepsilon }^{{ - 1}}} \gg 1$. Для определенности рассматривается случай линейной зависимости коэффициента вязкости от температуры газа ${{{{\mu \left( T \right)} \mathord{\left/ {\vphantom {{\mu \left( T \right)} \mu }} \right. \kern-0em} \mu }}_{0}} = {T \mathord{\left/ {\vphantom {T {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$.

Для решения задачи всю область течения можно разбить на три асимптотические подобласти. Линейные размеры ${{r}_{*}}$ и $\sqrt {{{\nu }_{0}}t} $ соответствуют внутренней и внешней областям вязких возмущений (соответственно области ${{G}_{1}}$ и ${{G}_{2}}$). Как будет показано ниже, внешнему пределу решения в области ${{G}_{2}}$ соответствуют нулевая азимутальная скорость и конечный (но малый при больших числах Рейнольдса) расход, вызванный переменной по времени радиальной скоростью. Поскольку при ограниченной скорости распространения возмущений в газе расход должен обращаться в нуль на больших расстояниях от цилиндра, возникает третья асимптотическая область ${{G}_{3}}$, за размер которой отвечают акустические возмущения. Линейный размер области ${{G}_{3}}$ равен ${{a}_{0}}t$, где ${{a}_{0}}$ – скорость звука в невозмущенном газе, и является наибольшим из трех масштабов: его отношение к размеру области ${{G}_{2}}$ составляет ${{{{a}_{0}}t} \mathord{\left/ {\vphantom {{{{a}_{0}}t} {\sqrt {{{\nu }_{0}}t} }}} \right. \kern-0em} {\sqrt {{{\nu }_{0}}t} }}$ = ${{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } {\left( {{{M}_{1}}\varepsilon } \right)}}} \right. \kern-0em} {\left( {{{M}_{1}}\varepsilon } \right)}} \gg 1$, где Re = = ${{{{w}_{*}}{{r}_{*}}} \mathord{\left/ {\vphantom {{{{w}_{*}}{{r}_{*}}} {{{\nu }_{0}}}}} \right. \kern-0em} {{{\nu }_{0}}}} \gg 1$, ${{\operatorname{M} }_{1}} = {{{{w}_{*}}} \mathord{\left/ {\vphantom {{{{w}_{*}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$, ${{a}_{0}} = \sqrt {\left( {\unicode{230} - 1} \right){{c}_{p}}{{T}_{0}}} $, $\unicode{230} $ – показатель адиабаты.

Цель данной статьи – определить характеристики течения в областях ${{G}_{1}}$ и ${{G}_{2}}$. В каждой из этих областей вместо независимых переменных $r$, $t$ введем новые независимые переменные: $\eta = {r \mathord{\left/ {\vphantom {r {{{r}_{*}}}}} \right. \kern-0em} {{{r}_{*}}}}$, $\varepsilon $ в области ${{G}_{1}}$ и $\tau = {r \mathord{\left/ {\vphantom {r {\sqrt {{{\nu }_{0}}t} }}} \right. \kern-0em} {\sqrt {{{\nu }_{0}}t} }}$, $\varepsilon $ в области ${{G}_{2}}$.

Зависимые переменные в уравнениях (2.1), (2.2) представим в безразмерном виде

Далее черточки над безразмерными переменными будут опущены. Уравнения (2.1), (2.2) можно переписать в безразмерном виде. В области ${{G}_{1}}$ $\left( {1 \leqslant \eta < \infty } \right)$

В области ${{G}_{2}}$ $\left( {0 < \tau < \infty } \right)$

Здесь

Из уравнений (2.3)–(2.6) следует, что при $\varepsilon \to 0$ и ${{\operatorname{M} }_{1}}\sim {{F}_{*}}\sim O(1)$ искомые функции в областях ${{G}_{1}}$ и ${{G}_{2}}$ являются величинами порядка $O(1)$ или меньше. Очевидно, что граничных условий (2.4), (2.6) недостаточно для однозначного определения этих функций в каждой из областей ${{G}_{1}}$, ${{G}_{2}}$. Необходимо потребовать, чтобы выполнялось сращивание асимптотического решения в области ${{G}_{1}}$ при $\eta \to \infty $ с асимптотическим решением в области ${{G}_{2}}$ при $\tau \to 0$.

3. Асимптотическое решение уравнений в области G₂. Из третьего уравнения (2.5) следует, что с точностью до членов порядка $O({{\varepsilon }^{2}})$ статическое давление в области ${{G}_{2}}$ является при $\tau \sim O\left( 1 \right)$ постоянной величиной $p = 1$ и имеет координатную особенность $p\sim {{{{\varepsilon }^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }^{2}}} {{{\tau }^{2}}}}} \right. \kern-0em} {{{\tau }^{2}}}}$ при $\tau \to 0$. Из уравнений (2.5) можно получить, что с точностью до членов порядка $O({{\varepsilon }^{2}})$ плотность газа и радиальная составляющая скорости выражаются через функцию $F$:

Зависимость $c\left( \varepsilon \right)$ пока оставим неизвестной. Эта величина должна определяться из условия $v(\tau ,\varepsilon ) \leqslant O\left( 1 \right)$ при $\tau \leqslant O\left( 1 \right)$, вытекающего из условий сращивания с решением в области ${{G}_{1}}$.

В главном приближении функция $F\left( {\tau ,\varepsilon } \right)$ удовлетворяет уравнению

Асимптотическое поведение решения уравнения (3.2) при $\tau \to 0$ имеет вид

Из условия, что при $\tau \to 0$ функция $F\left( {\tau ,\varepsilon } \right)$ должна сращиваться с решением в области ${{G}_{1}}$, а ее величина сохранять порядок $O\left( 1 \right)$ при $\tau \sim O\left( \varepsilon \right)$, следует

С учетом соотношений (3.3), (3.4) функции $F\left( {\tau ,\varepsilon } \right)$, $\gamma \left( {\tau ,\varepsilon } \right)$ представим в виде степенного ряда по малому параметру ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }}$:

Таким образом, в главном приближении решение для температуры и циркуляции зависит только от автомодельной переменной $\tau $. Функция ${{F}_{0}}$ удовлетворяет нелинейному уравнению

и краевым условиям

Единственным решением для ${{F}_{0}}\left( \tau \right)$, удовлетворяющим (3.6), (3.7), является

Согласно выражениям (3.1),

Функции ${{F}_{1}}$, ${{\gamma }_{0}}$ удовлетворяют линейным дифференциальным уравнениям

и граничным условиям

Решение уравнений (3.9), удовлетворяющих условиям (3.3)–(3.5) и (3.10):

где $x = \tau \sqrt {\Pr } $. В главном приближении распределение циркуляции отличается от случая несжимаемой жидкости на постоянный множитель $A\left( {{{\operatorname{M} }_{1}},{{F}_{*}},\Pr } \right)$ – неизвестную константу, которая определяется из условия асимптотического сращивания решения (3.11) с решением в области ${{G}_{1}}$.

Из представлений (3.1) и (3.5), решения (3.11) и условия ${v} \leqslant O\left( 1 \right)$ при $\tau \sim O\left( \varepsilon \right)$ (область перекрытия с решением в ${{G}_{1}}$)

Для следующего приближения функций, определяющих температуру и циркуляцию, имеем

Граничные условия для уравнений (3.12)

В решение уравнений (3.12) с граничными условиями (3.13) войдут еще две пока неизвестные константы ${{c}_{1}}$ и ${{c}_{2}}$.

В двух первых приближениях при $\tau \to \infty $ функции $F,\,\,\gamma ,\,\,\rho $ отличаются от своих предельных значений (2.6) на экспоненциально малые величины. Безразмерная радиальная составляющая скорости ${v} \to 0$ затухает по степенному закону ${v}\sim {{{{\alpha }_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}} {\left( {{{\tau }^{2}}\ln \varepsilon } \right)}}} \right. \kern-0em} {\left( {{{\tau }^{2}}\ln \varepsilon } \right)}}$. Такое поведение ${v}\left( \tau \right)$ соответствует тому, что расширение области ${{G}_{2}}$ с течением времени индуцирует при $\tau \to \infty $ поле радиальных скоростей, эквивалентных источнику (или стоку) с отношением интенсивности источника к циркуляции вихря, неограниченно убывающему при возрастании числа Рейнольдса, малому по сравнению с характерной циркуляцией вихря ${{\Gamma }_{*}}$ и зависящему от времени

В области ${{G}_{3}}$ возникает задача о распространении возмущений от источника, который “включается” в момент времени $t = 0$ и на больших временах имеет вид (3.15). Так как со временем $\varepsilon \left( t \right)$ уменьшается, то интенсивность источника убывает. Из асимптотики (3.15) и уравнений (2.1) следует, что радиальная скорость $v$ и возмущения температуры $\tilde {T} = T - 1$, плотности $\tilde {\rho } = \rho - 1$ и давления $\tilde {p} = p - 1$ имеют порядок $O\left( {{{\operatorname{M} _{1}^{2}{{\varepsilon }^{2}}} \mathord{\left/ {\vphantom {{\operatorname{M} _{1}^{2}{{\varepsilon }^{2}}} {{{{\operatorname{Re} }}^{2}}\ln \varepsilon }}} \right. \kern-0em} {{{{\operatorname{Re} }}^{2}}\ln \varepsilon }}} \right)$ и удовлетворяют линейным уравнениям Эйлера, которые преобразуются к виду

При $r \geqslant {{a}_{0}}t$ характеристики течения соответствуют невозмущенному состоянию газа. В отличие от главного приближения уравнений в областях ${{G}_{1}}$ (4.12) и ${{G}_{2}}$ (3.5), уравнения в области ${{G}_{3}}$ не сводятся к обыкновенным дифференциальным уравнениям и решение не является автомодельным.

Из представлений (3.5), решений (3.8) и (3.11) следует, что на масштабе $\tau \sim O\left( \varepsilon \right)$, т.е. в области ${{G}_{1}}$, первые два приближения становятся членами одного порядка малости. Для проведения процедуры сращивания решения в области ${{G}_{2}}$ с решением в области ${{G}_{1}}$ выпишем поведение функций $F,\,\,\gamma $ при $\tau \to 0$ (внутренний предел внешнего разложения):

где ${{c}_{F}} = - \ln 2 + {c \mathord{\left/ {\vphantom {c 2}} \right. \kern-0em} 2}$, $c = 0.5772$ – постоянная Эйлера.

Первое из соотношений (3.16), переписанное в переменных $\eta $ ($\tau = \varepsilon \eta $), определяет граничные условия для функции $F$ в области ${{G}_{1}}$ при $\eta \to \infty $ (внешний предел внутреннего разложения). С точностью до членов порядка $O(1{\text{/}}\ln \varepsilon )$

Из-за логарифмического характера особенности в решении задачи при $\tau \to 0$ (3.16) возникает ситуация, когда для сращивания решений в переменных области ${{G}_{1}}$ (3.17) с точностью до членов $O\left( {{{{\ln }}^{{ - n}}}\varepsilon } \right)$ необходимо в области ${{G}_{2}}$ построить решение (3.5), (3.8), (3.11), (3.14) с точностью до $O\left( {{{{\ln }}^{{ - (n + 1)}}}\varepsilon } \right)$.

4. Асимптотическое решение уравнений в области ${{G}_{1}}$. Решение уравнений (2.3) будем искать, пренебрегая в них членами порядка $O\left( {{{\varepsilon }^{2}}} \right)$. Тогда для функций $F$ и $\gamma $ имеем

Легко проверить, что циркуляция $\gamma \left( \eta \right)$, не имеющая особенность при $\eta \to \infty $ и удовлетворяющая условию $\gamma \left( 1 \right) = 1$, выражается через функцию $F\left( \eta \right)$:

Подстановка представления (4.2) во второе уравнение (4.1) приводит к тождеству. С учетом уравнений (4.1) из уравнений (2.3) следует, что $p\left( \eta \right)$ и $\rho \left( \eta \right)$ также выражаются через интегралы функции $F\left( \eta \right)$. Сосредоточимся на решении первого уравнения (4.1), т.к. остальные гидродинамические функции могут быть найдены по виду функции $F$. Подставляя представления (4.2) в первое уравнение (4.1) и учитывая граничное условие и условие сращивания решений, имеем

Введем новую зависимую переменную $y\left( \eta \right)$

Выпишем уравнения и краевые условия, которым с точностью до $O\left( {{1 \mathord{\left/ {\vphantom {1 {{{{\ln }}^{2}}\varepsilon }}} \right. \kern-0em} {{{{\ln }}^{2}}\varepsilon }}} \right)$ удовлетворяет функция $y\left( \eta \right)$. Из задачи (4.3) с учетом замены (4.5) приходим к уравнению

Используя определение величины $b$ и замену (4.5), получаем

где $\lambda = {{{{{{F}_{*}}} \mathord{\left/ {\vphantom {{{{F}_{*}}} {[2\left( {\unicode{230} - 1} \right)\Pr \operatorname{M} _{1}^{2}]}}} \right. \kern-0em} {[2\left( {\unicode{230} - 1} \right)\Pr \operatorname{M} _{1}^{2}]}}}^{2}} = {{{1 \mathord{\left/ {\vphantom {1 {[2\left( {\unicode{230} - 1} \right)\Pr \operatorname{M} _{*}^{2}]}}} \right. \kern-0em} {[2\left( {\unicode{230} - 1} \right)\Pr \operatorname{M} _{*}^{2}]}}}^{2}}$, ${{\operatorname{M} }_{*}} = {{{{w}_{*}}} \mathord{\left/ {\vphantom {{{{w}_{*}}} {{{a}_{*}}}}} \right. \kern-0em} {{{a}_{*}}}}$, ${{a}_{*}}$ – скорость звука в газе у поверхности цилиндра. Из асимптотики (4.4) получаем

Уравнение (4.6) можно переписать в виде

Откуда

Следовательно, для задачи (4.6)–(4.8) вместо соотношения (4.7) можно использовать граничное условие

Асимптотическое поведение решения уравнения (4.6) при $\eta \to \infty $ имеет вид

Решение уравнений (4.6), (4.8), (4.10) будем искать в виде асимптотического ряда

Из решений (4.8), (4.11), (4.12) следует, что ${{y}_{0}}\left( \eta \right)$ не содержит логарифмического члена при $\eta \to \infty $. Уравнение и граничные условия для функции ${{y}_{0}}\left( \eta \right)$ имеют вид

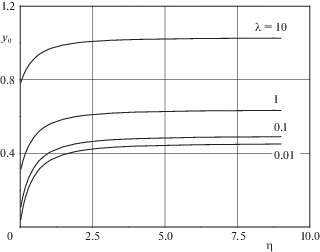
При заданных параметрах течения около цилиндра параметр $\lambda $ фиксирован. Тогда если в дополнение к граничным условиям (4.14), (4.15) задавать произвольное значение $y_{0}^{'}\left( 1 \right)$, то система (4.13)–(4.15) будет переопределенной. Варьируя $y_{0}^{'}\left( 1 \right)$ и решая задачу Коши, можно найти такое его значение, при котором система (4.13)–(4.15) разрешима. В качестве примеров на рис. 1 приведены решения (снизу вверх) при $\lambda = 0.01$ и $y_{0}^{'}\left( 1 \right) = 1.1731$, $\lambda = 0.1$ и $y_{0}^{'}\left( 1 \right) = 0.9754$, $\lambda = 1$ и $y_{0}^{'}\left( 1 \right) = 0.7396$, $\lambda = 10$ и $y_{0}^{'}\left( 1 \right) = 0.5275$.

Из (4.4), (4.5) следует, что параметр ${{\alpha }_{1}}$ определяется главным приближением решения в области ${{G}_{1}}$

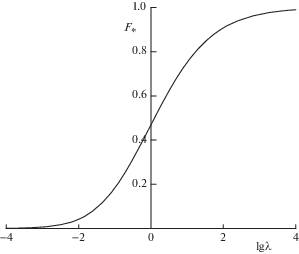
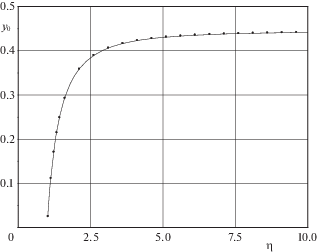
При ${{F}_{*}}\sim O(1)$ и $\lambda \sim O(1)$ параметр ${{\alpha }_{1}}$ есть также величина порядка $O(1)$, которая может принимать как положительные, так и отрицательные значения. Взаимодействие температурного и вихревого полей в области ${{G}_{1}}$ приводит к переходу энергии вращательного движения газа в энергию тепловую. Относительная температура газа ${{T\left( \eta \right)} \mathord{\left/ {\vphantom {{T\left( \eta \right)} {{{T}_{*}}}}} \right. \kern-0em} {{{T}_{*}}}}$ вблизи поверхности цилиндра возрастает. Зависимость ${{F}_{*}} = {{\tilde {F}}_{*}}\left( \lambda \right)$, представленная на рис. 2, соответствует ${{\alpha }_{1}}\left( {{{F}_{*}},\lambda } \right) = 0$. Если ${{F}_{*}} > {{\tilde {F}}_{*}}\left( \lambda \right)$, то поток тепла поступает из области ${{G}_{1}}$ в область ${{G}_{2}}$; в противном случае поток тепла меняет свое направление.

Согласно граничному условию (4.8) функция ${{y}_{1}}\left( \eta \right)$ должна иметь логарифмическую особенность при $\eta \to \infty $. Из-за этой особенности оба слагаемых в асимптотике (4.12) становятся одного порядка при переходе из области ${{G}_{1}}$ в область ${{G}_{2}}$. Сращивание решений становится возможным, если в представлении (4.12) учитываются оба члена асимптотического разложения.

Уравнения и краевые условия для функции ${{y}_{1}}\left( \eta \right)$:

При произвольном значении $y_{1}^{'}\left( 1 \right)$ система (4.17)–(4.19) также является переопределенной. Варьируя $y_{1}^{'}\left( 1 \right)$, можно найти его значение, при котором выполняется условие (4.19).

С точностью до членов порядка $O\left( {{{{\ln }}^{{ - 2}}}\varepsilon } \right)$ решение для $F\left( {\eta ,\lambda } \right)$ в области ${{G}_{1}}$ можно считать известным. При $\eta \to \infty $ это решение имеет вид

где

Используя решения (4.4), (4.20), (4.21) можно найти неизвестный коэффициент ${{c}_{2}}$ в асимптотическом представлении для функции $F$ в области ${{G}_{2}}$.

Через известные функции ${{y}_{0}}\left( \eta \right)$ и ${{y}_{1}}\left( \eta \right)$ можно из представлений (4.2) и уравнения (4.9) выразить с точностью до членов $O\left( {{{{\ln }}^{{ - 2}}}\varepsilon } \right)$ решение для циркуляции

Интегрируя два раза выражение (4.2) по частям, с учетом (4.20) получаем при $\eta \to \infty $

Откуда внешний предел внутреннего разложения представляется формулой

где ${{k}_{\eta }} = 1 + {{\alpha }_{1}} + \left( {{{\alpha }_{1}}\ln \eta + h} \right){\text{/}}\ln \varepsilon $.

Соотношение (4.24), переписанное в переменных $\tau $, определяет вид внутреннего предела внешнего разложения для функции $\gamma $ в области ${{G}_{2}}$

где ${{k}_{\tau }} = 1 + \left( {{{\alpha }_{1}}\ln \tau + h} \right){\text{/}}\ln \varepsilon $.

Раскладывая (4.25) в ряд по степеням ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }}$, получим

Сравнение асимптотику (4.26) с (3.16) позволяет определить неизвестные константы $A$ и ${{c}_{1}}$, входящие в представление величин в области ${{G}_{2}}$. Для константы $A$ получаем соотношение

Выражение (4.27) можно переписать в виде

Из уравнений и граничных условий (4.13)–(4.15) следует, что $y_{0}^{'}(\eta ) > 0$. Заменяя в подынтегральном выражении (4.28) ${{y}_{0}}(\eta )$ на меньшую величину ${{y}_{0}}(1)$, приходим к неравенству

В случае ${{F}_{*}} \geqslant 1$ температура газа во всем пространстве будет превосходить температуру невозмущенного газа ($F \geqslant 1$), поскольку нет причин, противодействующих нагреву газа вследствие перехода энергии вращательного движения в тепло. В этом случае из (4.29) следует, что $A > 1$. Можно показать, что тот же результат будет иметь место при произвольной монотонно возрастающей зависимости $\mu \left( T \right)$. Это позволяет сформулировать теорему о скачке циркуляции: если ${{F}_{*}} \geqslant 1$ и ${{d\mu } \mathord{\left/ {\vphantom {{d\mu } {dT > 0}}} \right. \kern-0em} {dT > 0}}$, то циркуляция в сжимаемом газе в области $r\sim \sqrt {{{\nu }_{0}}t} $ будет превышать циркуляцию в несжимаемой жидкости при тех же $r$ и $t$ (сравнение приведено на рис. 5, см. ниже). Название теоремы связано с тем, что внутренний предел внешнего решения ($\tau \to 0$) для циркуляции ${{\gamma }_{0}}\left( \tau \right)$ не совпадает со значением циркуляции на поверхности цилиндра.

Пользуясь промежуточными асимптотиками температуры (3.17) и циркуляции (4.23), можно в главном приближении вычислить кинетическую энергию течения

где ${{E}_{0}} = \pi {{\rho }_{0}}\Gamma _{*}^{2}\left| {\ln \varepsilon } \right|$ – кинетическая энергия для случая несжимаемой жидкости в тот же момент времени. Почти вся энергия приходится на течение в промежуточной области ${{r}_{*}} \ll r \ll \sqrt {{{\nu }_{0}}t} $ и со временем неограниченно растет вместе с размером этой области. В случае ${{M}_{1}} = {{F}_{*}} = \Pr = 1$, численное решение дает значения констант $A \approx 1.19$, ${{\alpha }_{1}} = 0.88$. Кинетическая энергия течения сжимаемого газа оказывается меньше, чем у несжимаемой жидкости: в пределе $\varepsilon \to 0$ из (4.30) получается ${E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}} \approx 0.87$.

5. Составное решение. С точностью до членов $O\left( {{{{\ln }}^{{ - 2}}}\varepsilon } \right)$ равномерно пригодное решение для функций $F$ и $\gamma $ в области ${{G}_{1}} \cap {{G}_{2}}$ представляется в виде [10]

где ${{F}^{{\left( 1 \right)}}}\left( \tau \right)$ и ${{\gamma }^{{\left( 1 \right)}}}\left( \tau \right)$ – решения (4.5), (4.12), (4.22) в области ${{G}_{1}}$, переписанные в переменных $\tau $, ${{F}^{{\left( 2 \right)}}}\left( \tau \right)$ и ${{\gamma }^{{\left( 2 \right)}}}\left( \tau \right)$ – решения (3.5) в области ${{G}_{2}}$, $F_{{пред}}^{{\left( 2 \right)}}\left( \tau \right)$ и $\gamma _{{пред}}^{{\left( 2 \right)}}\left( \tau \right)$ – внутренний предел внешнего разложения (3.16).

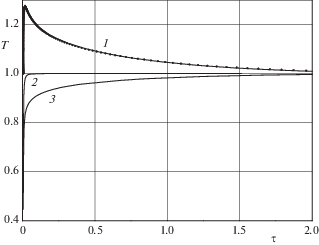
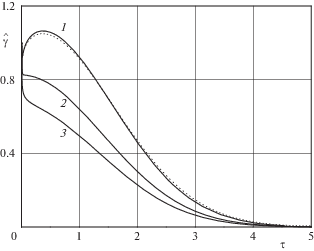
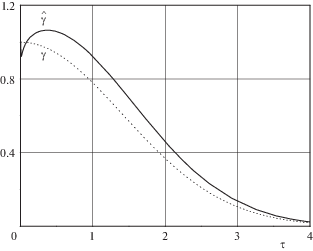
На рис. 3–4 представлено поведение зависимостей $\hat {T}\left( \tau \right) = \sqrt {\hat {F}\left( \tau \right)} $ и $\hat {\gamma }\left( \tau \right)$, соответствующих случаю ${{M}_{1}} = \Pr = 1$, ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} = - 0.189$ и трем разным значениям ${{F}_{*}}$: кривые 1 соответствуют значениям параметров ${{F}_{*}} = 1$, ${{\alpha }_{1}} > 0$; 2 – ${{F}_{*}} = 0.407$, ${{\alpha }_{1}} = 0$; 3 – ${{F}_{*}} = 0.2$, ${{\alpha }_{1}} < 0$; пунктирами изображено численное решение уравнений Навье–Стокса при ${{F}_{*}} = 1$ (см. разд. 8). В случае ${{\alpha }_{1}} > 0$ температура имеет максимум в области ${{G}_{1}}$; при ${{\alpha }_{1}} \leqslant 0$ – монотонно возрастает при удалении от поверхности цилиндра. Переход энергии вращательного движения в тепловую вызывает рост температуры газа в области ${{G}_{1}}$, в области ${{G}_{2}}$ – влияние на изменение температуры газа в основном оказывает диффузия тепла. Рост температуры газа вызывает увеличение коэффициента динамической вязкости $\left( {\mu \sim T} \right)$ и появление градиента вязкости $\left( {{{\partial \mu } \mathord{\left/ {\vphantom {{\partial \mu } {\partial r}}} \right. \kern-0em} {\partial r}}\sim {{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial r}}} \right. \kern-0em} {\partial r}}} \right)$, что в случае ${{\alpha }_{1}} > 0$ приводит к немонотонному изменению циркуляции вращательного движения вдоль координаты $r$. По мере удаления от поверхности цилиндра завихренность

дважды меняет свой знак. Имеется участок, на котором генерируется положительная завихренность. В случае, соответствующем рис. 3 при ${{F}_{*}} = 1$, он включает $2.3\varepsilon < \tau < 0.36$. Из второго уравнения системы (4.1) можно получить соотношение из которого следует, что экстремум завихренности в области ${{G}_{1}}$ достигается в той же точке ($\tau \approx 3.4\varepsilon $, рис. 3), что экстремум температуры. Циркуляция окружной скорости на участке $0.084{\kern 1pt} - {\kern 1pt} 0.099 < \tau < 0.72{\kern 1pt} - {\kern 1pt} 0.77$ превосходит циркуляцию около поверхности цилиндра. Этот эффект не наблюдается в несжимаемой жидкости, в которой изменение циркуляции вдоль координаты $r$ – монотонное, а в пределах области ${{G}_{1}}$ циркуляция постоянна. На рис. 5 приведено сравнение $\hat {\gamma }\left( \tau \right)$ для сжимаемого газа при ${{\operatorname{M} }_{1}} = {{F}_{*}} = \Pr = 1$, ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} = - 0.189$ (сплошная кривая) и $\gamma \left( \tau \right) = {{e}^{{ - {{{{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{\tau }^{2}}} 4}} \right. \kern-0em} 4}}}}$ для несжимаемой жидкости (пунктир).

6. Решение задачи при малых числах ${{\operatorname{M} }_{1}}$. При $\lambda \to \infty $, что соответствует малым числам ${{\operatorname{M} }_{1}}$, можно получить решение для $F$ в аналитическом виде. Из соотношения (4.3) и граничного условия на поверхности цилиндра следует, что с точностью до $O\left( {{{\lambda }^{{ - 1}}}} \right)$ в области ${{G}_{1}}\,$

В области ${{G}_{2}}$ по-прежнему выполняется

Асимптотическое сращивание решений (6.1) и (6.2) определяет неизвестные константы ${{\alpha }_{1}}$ и $d$

Аналогичным путем определяется распределение циркуляции. Из (4.27) следует, что в главном приближении

7. Решение задачи при больших числах ${{\operatorname{M} }_{1}}$. В предыдущих пунктах асимптотическое решение задачи при числах ${{\operatorname{M} }_{1}}\sim O(1)$ получено при условии, что $\varepsilon \to 0$. В этом случае и величина ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} \to 0$. Вместе с тем, при реально достижимых больших временах (малых $\varepsilon $) величина ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }}$ может перестать быть пренебрежимо малой, например при $\varepsilon = {{10}^{{ - 4}}}$: ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} \approx - 0.1$.

Анализ результатов при ${{\operatorname{M} }_{1}}\sim O(1)$ указывает на то, что с ростом ${{\operatorname{M} }_{1}}$ величина коэффициента ${{\alpha }_{1}}$ также растет. Поэтому при больших числах ${{\operatorname{M} }_{1}}$ может наступить ситуация, когда коэффициент ${{\alpha }_{1}}{\text{/}}\ln \,\varepsilon $ может перестать быть малой величиной. Определим условия, при котором ${{\alpha }_{1}}{\text{/}}\ln \,\varepsilon $ становится величиной порядка $O(1)$. Для этого рассмотрим решение при $\lambda \ll 1$.

Функции ${{y}_{0}}\left( 1 \right)$ и $y_{0}^{'}(1)$ связаны соотношением (4.14) и поэтому имеют разный порядок малости по параметру $\lambda $. Для определения порядков этих функций проведем численное решение задачи (4.13)–(4.15) при малых $\lambda $. На рис. 6 показано решение этих уравнений при $\lambda = {{10}^{{ - 6}}}$ (сплошная кривая) и $\lambda = {{10}^{{ - 3}}}$ (точки). Видно, что зависимости ${{y}_{0}}\left( {\eta ,\lambda } \right)$ в этих случаях близки друг к другу. В пределе при $\lambda \to 0$ обозначим значение ${{y}_{0}}\left( \eta \right)$ через ${{y}_{{00}}}\left( \eta \right)$. Из численного решения получаются величины, которые имеют порядок $O(1)$: $y_{{00}}^{'}\left( 1 \right) = {{d}_{1}} \approx 1.3641$, ${{y}_{{00}}}\left( \infty \right) = {{d}_{2}} = 0.4450$. Подставляя эти значения в формулу (4.16), получаем

Таким образом, соотношения, полученные в разд. 2–4, справедливы при ${{\operatorname{M} _{1}^{4}} \mathord{\left/ {\vphantom {{\operatorname{M} _{1}^{4}} {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} \ll 1$. Построим решение при ${{\operatorname{M} _{1}^{4}} \mathord{\left/ {\vphantom {{\operatorname{M} _{1}^{4}} {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }}\sim O\left( 1 \right)$.

Так же, как и в случае малых возмущений, в области ${{G}_{2}}$ с точностью до членов порядка $O\left( {M_{1}^{2}{{\varepsilon }^{2}}} \right)$ статическое давление $p = 1$ при $\tau \sim O\left( 1 \right)$ и имеет координатную особенность $p\sim {{\operatorname{M} _{1}^{2}{{\varepsilon }^{2}}} \mathord{\left/ {\vphantom {{\operatorname{M} _{1}^{2}{{\varepsilon }^{2}}} {{{\tau }^{2}}}}} \right. \kern-0em} {{{\tau }^{2}}}}$ при $\tau \to 0$. Плотность, радиальная компонента скорости и функция $F$ подчиняются соотношениям (3.1), (3.2). Асимптотическое поведение решения уравнения (3.2) при $\tau \to 0$ имеет вид

Здесь ${{\alpha }_{0}} \geqslant O\left( 1 \right)$, ${{\tilde {\alpha }}_{1}}\sim O(1)$. Так как функции $F$ и ${v}$ согласно (7.1) зависят от $\tau $ и ${\text{1/}}\ln \varepsilon $, уравнения для их определения в области ${{G}_{2}}$ в главном приближении будут иметь вид

Неизвестные коэффициенты ${{\alpha }_{0}}$ и ${{\tilde {\alpha }}_{1}}$ определяют решение краевой задачи для уравнений (7.2) и должны выбираться из условия $F = 1$ при $\tau \to \infty $ и из сращивания с решением в области ${{G}_{1}}$.

Внешний предел внутреннего разложения для функции $y$ в области ${{G}_{1}}$ определяется из соотношения (7.1). При $\eta \to \infty $

Формула (7.3) указывает на то, что функцию $y\left( \eta \right)$ можно представить в виде асимптотического ряда

Для определения ${{y}_{0}}(\eta )$ можно выписать задачу, совпадающую с (4.13)–(4.15) (рис. 1). Условие сращивания записывается в виде

Краевую задачу (7.2) можно решать, варьируя начальные условия задачи Коши для уравнений (7.2). В качестве начального условия выступает значение $F$, задаваемое функцией (7.1). При этом коэффициенты ${{\alpha }_{0}}$ и ${{\tilde {\alpha }}_{1}}$ связаны соотношением (7.4). Таким образом, варьируя только значение ${{\alpha }_{0}}$ и определяя ${{\tilde {\alpha }}_{1}}$ с помощью (7.4), необходимо найти то значение ${{\alpha }_{0}}$, при котором $F = 1$ при $\tau \to \infty $.

После того, как коэффициенты ${{\alpha }_{0}}$ и ${{\tilde {\alpha }}_{1}}$ найдены, решается задача об определении функции ${{y}_{1}}(\eta )$ в области ${{G}_{1}}$. Алгоритм ее нахождения изложен в разд. 4.

Определение поля температур позволяет решить задачу о нахождении распределения циркуляции в области ${{G}_{2}}$. В главном приближении функция $\gamma $ должна подчиняться уравнению

с граничными условиями $\gamma = A$ при $\tau \to 0$ и $\gamma = 0$ при $\tau \to \infty $.

В области ${{G}_{1}}$ для определения $\gamma $ по-прежнему верна формула (4.2). Величина $A$ выбирается из условия сращивания

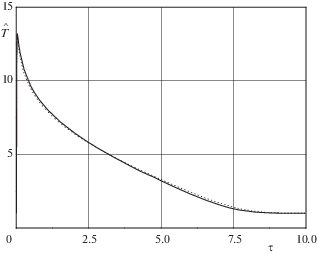
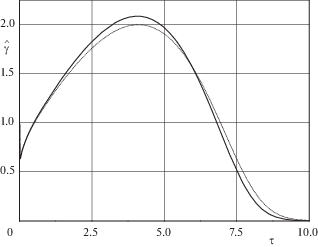
На рис. 7–8 представлено поведение зависимостей $\hat {T}\left( \tau \right) = \sqrt {\hat {F}\left( \tau \right)} $ и $\hat {\gamma }\left( \tau \right)$ (разд. 5), соответствующих случаю ${{M}_{1}} = 7$, ${{F}_{*}} = \Pr = 1$ и ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} = - 0.217$ (сплошные кривые), и численного решения уравнений Навье–Стокса при тех же значениях параметров (пунктир).

8. Численное решение уравнений Навье–Стокса. Асимптотическое решение задачи сравнивается с численным решением уравнений Навье–Стокса (2.1), которое производится методом конечного объема 2-го порядка точности по пространству с разностями против потока и 1-го порядка по времени в круговой области ${{r}_{*}} \leqslant r \leqslant {{10}^{3}}{{r}_{*}}$ на радиально-симметричной сетке с 24 000 ячейками. Число ячеек составляет ${{N}_{\theta }} = 120$ вдоль окружности $r = \operatorname{const} $ и ${{N}_{r}} = 200$ вдоль радиуса; размер ячеек в радиальном направлении равен ${{10}^{{ - 3}}}$ у поверхности цилиндра $r = {{r}_{*}}$ и 20 на внешней границе расчетной области $r = {{10}^{3}}{{r}_{*}}$. На внешней границе ставится граничное условие невозмущенного потока; ошибка ввиду наличия радиального течения с ненулевым значением ${v}$ оказывается приемлемой.

Все расчеты проведены при значениях безразмерных параметров ${{F}_{*}} = 1$, $\Pr = 1$, $\operatorname{Re} = 100$. Наибольший период времени, до которого был проведен расчет, соответствует значениям $\varepsilon = 0.005$, ${1 \mathord{\left/ {\vphantom {1 {\left| {\ln \varepsilon } \right|}}} \right. \kern-0em} {\left| {\ln \varepsilon } \right|}} \approx 0.189$ при ${{\operatorname{M} }_{1}} = 1$; $\varepsilon = 0.01$, ${1 \mathord{\left/ {\vphantom {1 {\left| {\ln \varepsilon } \right|}}} \right. \kern-0em} {\left| {\ln \varepsilon } \right|}} \approx 0.217$ при ${{\operatorname{M} }_{1}} = 7$. Дальнейший расчет в течение обозримого времени не позволяет существенно уменьшить значение малого параметра ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }}$ в разложениях (3.5), (4.12). Шаг по времени $\Delta t$ таков, что ${{{{r}_{*}}} \mathord{\left/ {\vphantom {{{{r}_{*}}} {\sqrt {{{\nu }_{0}}\Delta t} }}} \right. \kern-0em} {\sqrt {{{\nu }_{0}}\Delta t} }} \approx 61.3$ при ${{\operatorname{M} }_{1}} = 1$; ${{{{r}_{*}}} \mathord{\left/ {\vphantom {{{{r}_{*}}} {\sqrt {{{\nu }_{0}}\Delta t} }}} \right. \kern-0em} {\sqrt {{{\nu }_{0}}\Delta t} }} \approx 12.5$ при ${{\operatorname{M} }_{1}} = 7$.

Распределения циркуляции и температуры, полученные из численного решения уравнений Навье–Стокса, подтверждают асимптотическое решение и приведены на рис. 3, 4, 7, 8.

Заключение. Хорошо известна задача о диффузии вихря и обратная задача о создании вихря с помощью вращающегося цилиндра в несжимаемой жидкости. Для данных задач характерен рост линейного размера вязкой области по закону $\sqrt {{{\nu }_{0}}t} $. Распределение циркуляции по радиусу является монотонной функцией, растущей для задачи о диффузии вихря и убывающей для вращающегося цилиндра.

Задача о создании вихря в сжимаемом газе с вязкостью, зависящей от температуры, сходна с аналогичной задачей для случая несжимаемой жидкости размером вязкой области, но кардинально отличается от нее немонотонным распределением циркуляции внутри этой области. На распределение циркуляции, как это следует из уравнений (2.1), влияет не только коэффициент вязкости, но и градиент коэффициента вязкости. Именно благодаря этому влиянию в отличие от несжимаемой жидкости, когда вся завихренность вращающейся жидкости имеет одинаковый знак, в сжимаемом газе имеются режимы, когда завихренность по мере движения вдоль радиуса дважды меняет знак. При одинаковых ${{\nu }_{0}}$ и $t$ и при температуре цилиндра не ниже температуры невозмущенного газа ближние к цилиндру частицы в несжимаемой жидкости будут вращаться быстрее чем в сжимаемом газе, в дальнем поле ситуация будет противоположной (рис. 5). В случае сжимаемого газа с постоянной вязкостью распределение циркуляции будет близким к случаю несжимаемой жидкости.

Решения получены с помощью метода сращиваемых асимптотических разложений на больших временах, когда размер вязкой области намного превосходит радиус цилиндра. Заметим, что в главном приближении решение для температуры и для циркуляции терпит разрыв на стыке областей ${{G}_{1}}$ и ${{G}_{2}}$, т.е. внешний предел внутреннего разложения не равен внутреннему пределу внешнего разложения; данное равенство обеспечивается только в следующих приближениях.

В области ${{G}_{1}}$ температура и циркуляция подчиняются стационарным уравнениям, но граничное условие, обеспечивающее сращивание решения с решением в области ${{G}_{2}}$, нестационарно. Поэтому решение в области ${{G}_{1}}$ будет параметрически зависеть от времени, в пределе $t \to \infty $ выходя на установившийся режим.

Малый параметр задачи ${1 \mathord{\left/ {\vphantom {1 {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }}$ медленно уменьшается с ростом времени. При ${{\operatorname{M} }_{1}}\sim O\left( 1 \right)$ в дальней области задача поддается линеаризации. Но, если ${{\operatorname{M} }_{1}} \gg 1$, то возможна ситуация, когда в дальней области необходимо решать нелинейную задачу обыкновенных дифференциальных уравнений, и это возможно сделать только численным методом. При больших числах ${{\operatorname{M} }_{1}}$ максимум температуры и коэффициент $A$, который отвечает за поведение циркуляции в дальней области, пропорциональны $\operatorname{M} _{1}^{2}$. На рис. 7 для случая ${{\operatorname{M} }_{1}} = 7$ максимум температуры больше температуры поверхности цилиндра в 13 раз. На рис. 8 максимум циркуляции превосходит циркуляцию на поверхности цилиндра всего в 2 раза; можно показать, что он достигнет порядка $\operatorname{M} _{1}^{2}$ только на экспоненциально больших временах, на которых задача в дальней области линейна (${{\operatorname{M} _{1}^{4}} \mathord{\left/ {\vphantom {{\operatorname{M} _{1}^{4}} {\ln \varepsilon }}} \right. \kern-0em} {\ln \varepsilon }} \ll 1$).

Все основные результаты подтверждены численными расчетами уравнений (2.1) для нестационарных осесимметричных течений.

Работа выполнена при финансовой поддержке РФФИ (Проект № 19-01-00163).