Прикладная математика и механика, 2020, T. 84, № 5, стр. 640-649

Контактная задача для упругой пластинки, на границе которой приклеен нелинейно-деформируемый стрингер конечной длины

Н. Н. Шавлакадзе^1, *, О. М. Джохадзе¹, С. С. Харибегашвили¹

¹ Тбилисский государственный университет, Mатематический институт им. А. Размадзе
Тбилиси, Грузия

^* E-mail: nusha1961@yahoo.com

Поступила в редакцию 10.10.2019
После доработки 04.07.2020
Принята к публикации 15.07.2020

DOI: 10.31857/S0032823520050100

Аннотация

Рассматривается задача определения механического поля в однородной полуплоскости, подкрепленной конечным однородным стрингером, материал которого подчиняется нелинейному закону Гука. Контакт между пластинкой и стрингером осуществляется тонким слоем клея. Поставленная задача редуцируется к нелинейному сингулярному интегродифференциальному уравнению. Используя принцип неподвижной точки Шаудера доказывается существование решения этого уравнения. Доказывается единственность решения поставленной задачи. Применяя метод малого параметра нелинейное сингулярное интегродифференциальное уравнение сводится к системе рекуррентных линейных сингулярных интегральных уравнений второго рода.

Ключевые слова: контактная задача, нелинейное сингулярное интегродифференциальное уравнение, принцип Шаудера, метод малого параметра

Введение. В инженерных конструкциях и механизмах, машиностроении и кораблестроении, проектировании летательных аппаратов особенно важное значение имеют задачи подкрепления массивных упругих тел тонкостенными упругими элементами (включениями, стрингерами, накладками), которые относятся к неклассическим гранично-контактным и смешанным задачам.

Были получены [1–4] точные и приближенные решения статических и динамических контактных задач для разных областей, усиленных упругими тонкими накладками как постоянной, так и переменной жесткости, изучено поведение контактных напряжений в концах линии контакта в зависимости от закона изменения геометрических и физических параметров задачи. Библиография различных контактных задач приводится в монографии [1], где рассматриваются плоские контактные задачи о передаче нагрузки от полубесконечного или конечного стрингера (включения) к упругой полуплоскости или плоскости. Задачи сведены к сингулярному интегродифференциальному уравнению Прандтля, получены различные аналитические методы его решения. Рассматривалась [4] контактная задача для анизотропной полуплоскости с упрочняющимися накладками конечной длины, она сводится к решению нелинейного сингулярного интегродифференциального уравнения при определённых граничных условиях. Решались [5–8] контактные задачи для изотропной и ортотропной кусочно-однородной плоскости, а также для клиновидной анизотропной пластины с полубесконечной и конечной накладкой. В работе [9] стрингер конечной длины приклеен к пластинке с тонким однородным слоем клея, который находится в условиях чистого сдвига. Изгибом стрингера пренебрегается, и он находится в условиях одноосного напряженного состояния. Рассмотрены [10–13] различные задачи, касающиеся контактного взаимодействия упругих тел с тонким слоем клея. Изучалась задача [14, 15] об упругой полубесконечной пластине, которая на конечном отрезке своей границы усилена стрингером из линейно-упругого и нелинейно-упругого материала общего вида. В линейном случае найдены асимптотические оценки, точные и приближенные решения полученного интегродифференциального уравнения, а в нелинейном – доказывается существование и единственность решения полученного нелинейного интегродифференциального уравнения, эквивалентного интегральному уравнению типа Гаммерштейна. Нелинейная деформация упругого тела исследуется в [16, 17].

В представленной работе рассматривается задача взаимодействия упругого стрингера к упругой полуплоскости, когда контакт между пластинкой и стрингером осуществляется тонким слоем клея. Доказывается существование и единственность решения полученного нелинейного интегрального уравнения, которое при помощи метода малого параметра сводится к решению системы рекуррентных линейных интегральных уравнений второго рода.

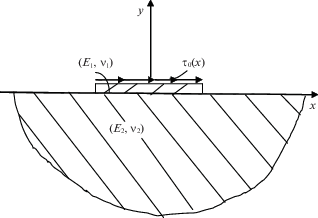
1. Постановка задачи и ее редукция к нелинейному интегральному уравнению. Пусть линейно-упругая бесконечная пластинка (занимающая нижнюю полуплоскость комплексной плоскости) с модулем упругости ${{E}_{2}}$ и коэффициентом Пуассона ${{\nu }_{2}}$ на конечном отрезке $[ - 1,1]$ оси $Ox$ усилена нелинейно-упругим стрингером в виде накладки конечной длины и достаточно малой толщины ${{h}_{1}}$, модулем упругости ${{E}_{1}}$ и коэффициентом Пуассона ${{\nu }_{1}}$, загруженной тангенциальной силой интенсивности ${{\tau }_{0}}(x)$. Контакт между ними осуществляется через тонкий слой клея с модулем упругости ${{E}_{0}}$, коэффициентом Пуассона ${{\nu }_{0}}$ и шириной ${{h}_{0}}$. В условиях плоского напряженного состояния требуется определить касательное контактное напряжение $\tau (x)$, действующего на отрезке соединения стрингера с пластинкой (рис. 1).

Рис. 1.

Геометрия задачи.

Материал стрингера удовлетворяет нелинейному закону Гука

(1.1)

$\varepsilon _{x}^{{(1)}}(x) = \frac{{d{{u}_{1}}(x)}}{{dx}} = \frac{1}{E}g(\sigma _{x}^{{(1)}}(x)),$

где $\varepsilon _{x}^{{(1)}}(x)$ и ${{u}_{1}}(x)$ – деформация и перемещение точек стрингера, соответственно, $\sigma _{x}^{{(1)}}(x)$ – осевое напряжение по направлению оси $Ox$, $E = \frac{{{{E}_{1}}}}{{1 - \nu _{1}^{2}}}$, $\sigma _{x}^{{(1)}}(x)$ = $\frac{1}{{{{h}_{1}}}}\int_{ - 1}^x {[\tau (t) - {{\tau }_{0}}(t)]dt} $, $g:R \to R$ – непрерывная, вообще говоря нелинейная, заданная функция.

Условие равновесия стрингера имеет вид

(1.2)

$\int\limits_{ - 1}^1 {[(\tau (x) - {{\tau }_{0}}(x)} ]dx = 0$

Предполагая, что каждый дифференциальный элемент слоя клея находится в условиях чистого сдвига, будем иметь [9, 10]

(1.3)

${{u}_{1}}(x) - {{u}_{2}}(x,0) = {{k}_{0}}\tau (x),\quad \left| x \right| < 1,\quad {{k}_{0}} = \frac{{2{{h}_{0}}(1 + {{\nu }_{0}})}}{{{{E}_{0}}}},$

где ${{u}_{2}}(x,y)$ – перемещения точек пластинки вдоль оси $Ox$.

В результате интегрирования уравнения (1.1) получим

(1.4)

${{u}_{1}}(x) = \frac{1}{E}\int\limits_{ - 1}^x {g\left( {\frac{1}{{h_{1}^{{}}}}\int\limits_{ - 1}^t {[\tau (s) - {{\tau }_{0}}(s)]ds} } \right)dt + {{u}_{1}}} ( - 1)$

На основе известных результатов (см., например [18]), деформация граничных точек пластинки по оси $Ox$, вызванной распределенными по интервалу $( - 1,1)$ касательными напряжениями интенсивности $\tau (x)$, представляется в виде

(1.5)

${{u}_{2}}(x,0) = - \frac{{(3 - 4{{\nu }_{2}})(1 + {{\nu }_{2}})}}{{4\pi {{E}_{2}}(1 - {{\nu }_{2}})}}\int\limits_{ - 1}^1 {\ln \frac{1}{{\left| {x - t} \right|}}\tau (t)dt + C,} \quad \left| x \right| < 1$

На основании условия контакта (1.3) вдоль линии соединения стрингера с основанием, с учетом (1.4) и (1.5), получим

(1.6)

$\varphi (x) = \frac{1}{{E{{k}_{0}}}}\int\limits_{ - 1}^x {g\left( {\frac{1}{{{{h}_{1}}}}\int\limits_{ - 1}^t {\varphi (s)ds} } \right)dt} + \frac{\lambda }{{\pi {{k}_{0}}}}\int\limits_{ - 1}^1 {\ln \frac{1}{{\left| {x - t} \right|}}} \varphi (t)dt + f(x),\quad \left| x \right| < 1,$

где $\varphi (x) = \tau (x) - {{\tau }_{0}}(x)$,

$\lambda = \frac{{(3 - 4{{\nu }_{2}})(1 + {{\nu }_{2}})}}{{4{{E}_{2}}(1 - {{\nu }_{2}})}},\quad f(x) = \frac{\lambda }{{\pi {{k}_{0}}}}\int\limits_{ - 1}^1 {\ln \frac{1}{{\left| {x - t} \right|}}{{\tau }_{0}}(t)dt + } \frac{{C{\kern 1pt} *}}{{{{k}_{0}}}},\quad C{\kern 1pt} * = {{u}_{1}}( - 1) - C$

В уравнение (1.6) неизвестная постоянная $C{\kern 1pt} *$ определяется из условия (1.2), т.е.

(1.7)

$\int\limits_{ - 1}^1 {\varphi (x)dx} = 0$

С другой стороны, вводя обозначение $\int_{ - 1}^x {\varphi (s)ds = \psi (x)} $, уравнение (1.6) примет вид

(1.8)

${{k}_{0}}\psi {\kern 1pt} ''(x) = \frac{1}{E}g(\psi (x)) - \frac{\lambda }{\pi }\int\limits_{ - 1}^1 {\frac{{\psi {\kern 1pt} '(t)dt}}{{t - x}}} - \frac{\lambda }{\pi }\int\limits_{ - 1}^1 {\frac{{{{\tau }_{0}}(t)dt}}{{t - x}}} ,\quad \left| x \right| < 1$

при условии

(1.9)

$\psi (1) = 0$

Таким образом, поставленная гранично-контактная задача (1.1)–(1.5) эквивалентно редуцирована к решению нелинейного интегрального уравнения (1.6) при условии (1.7) или к нелинейному сингулярному интегродифференциальному уравнению (1.8) при условии (1.9). Относительно функции $f(x)$ будем предполагать, что она принадлежит классу Гёльдера $(H)$ на сегменте [–1, 1]. Решение уравнения (1.6) ищется в классе непрерывных функций в смысле Гёльдера $(H)$ на том же сегменте.

Решение задачи (1.8), (1.9) ищется в классе непрерывных функций на сегменте [–1, 1], первая производная которых ограничена в точках $x = \pm 1$, а вторая производная принадлежит классу $H{\kern 1pt} *$ [18, 19].

2. Существование решения уравнения (1.6). Уравнение (1.6) при условии (1.7) представим в следующем операторном виде

(2.1)

$\varphi = A\varphi ,$

где

(2.2)

$A\varphi : = {{A}_{0}}\varphi - \frac{1}{2}\int\limits_{ - 1}^1 {({{A}_{0}}\varphi )\,dx} ,$

(2.3)

$({{A}_{0}}\varphi )(x): = \frac{1}{{E{{k}_{0}}}}\int\limits_{ - 1}^x {g\left( {\frac{1}{{{{h}_{1}}}}\int\limits_{ - 1}^t {\varphi (s)ds} } \right)} dt + \frac{\lambda }{{\pi {{k}_{0}}}}\int\limits_{ - 1}^1 {\ln \frac{1}{{\left| {x - t} \right|}}} \varphi (t)dt + \frac{\lambda }{{\pi {{k}_{0}}}}\int\limits_{ - 1}^1 {\ln \frac{1}{{\left| {x - t} \right|}}{{\tau }_{0}}(t)dt} $

Пусть

(2.4)

$\left| {g(\xi )} \right| \leqslant {{M}_{1}}{{\left| \xi \right|}^{\alpha }} + {{M}_{2}},\quad \alpha \geqslant 0,\quad \xi \in R,\quad {{M}_{i}} = \operatorname{const} \geqslant 0,\quad i = 1,2$

Из (2.3) с учетом (2.4) будем иметь

(2.5)

$\begin{gathered} \left| {({{A}_{0}}\varphi )(x)} \right| \leqslant \frac{1}{{E{{k}_{0}}}}\int\limits_{ - 1}^x {\left| {g\left( {\frac{1}{{{{h}_{1}}}}\int\limits_{ - 1}^t {\varphi (s)ds} } \right)} \right|} dt + \\ + \;\frac{\lambda }{{\pi {{k}_{0}}}}\int\limits_{ - 1}^1 {\left| {\ln \frac{1}{{\left| {x - t} \right|}}} \right|} \left| {\varphi (t)} \right|dt + \frac{\lambda }{{\pi {{k}_{0}}}}\int\limits_{ - 1}^1 {\left| {\ln \frac{1}{{\left| {x - t} \right|}}} \right|\left| {{{\tau }_{0}}(t)} \right|dt} \leqslant \\ \leqslant \frac{{{{M}_{1}}}}{{E{{k}_{0}}{{h}_{1}}^{\alpha }}}{{\int\limits_{ - 1}^1 {\left| {\int\limits_{ - 1}^t {\varphi (s)ds} } \right|} }^{\alpha }}dt + \frac{{2{{M}_{2}}}}{{E{{k}_{0}}}} + \frac{\lambda }{{\pi {{k}_{0}}}}({{\left\| \varphi \right\|}_{C}} + {{\left\| {{{\tau }_{0}}} \right\|}_{C}})\int\limits_{ - 1}^1 {\left| {\ln \frac{1}{{\left| {x - t} \right|}}} \right|} dt \leqslant \\ \leqslant \frac{{{{2}^{{\alpha + 1}}}{{M}_{1}}}}{{E{{k}_{0}}h_{1}^{\alpha }}}\left\| \varphi \right\|_{C}^{\alpha } + \frac{{2{{M}_{2}}}}{{E{{k}_{0}}}} + \frac{\lambda }{{E{{k}_{0}}}}({{\left\| \varphi \right\|}_{C}} + {{\left\| {{{\tau }_{0}}} \right\|}_{C}})\int\limits_{ - 1}^1 {\left| {\ln \left| {x - t} \right|} \right|} dt \\ \end{gathered} $

Принимая во внимание оценку

$\int\limits_{ - 1}^1 {\left| {\ln \left| {x - t} \right|} \right|} dt = \int\limits_{x - 1}^{x + 1} {\left| {\ln \left| s \right|} \right|} ds \leqslant 2\int\limits_0^2 {\left| {\ln s} \right|} ds = 4\ln 2$

выражение $A\varphi $ из (2.2) с учетом (2.5) оценивается следующим образом

(2.6)

$\left| {(A\varphi )(x)} \right| \leqslant \frac{{{{2}^{{\alpha + 2}}}M_{1}^{{}}}}{{E{{k}_{0}}h_{1}^{\alpha }}}\left\| \varphi \right\|_{C}^{\alpha } + \frac{{4{{M}_{2}}}}{{E{{k}_{0}}}} + \frac{{8\lambda \ln 2}}{{E{{k}_{0}}}}({{\left\| \varphi \right\|}_{C}} + {{\left\| {{{\tau }_{0}}} \right\|}_{C}})$

Рассмотрим неравенство

(2.7)

$a + b{{r}^{\alpha }} \leqslant r$

относительно$r \geqslant 0$, где $a,b = \operatorname{const} > 0$, $\alpha = \operatorname{const} \geqslant 0$

Как известно [20, 21]:

1) если $0 \leqslant \alpha < 1$, то для любых $a$ и $b$ всегда существует $r > 0$, удовлетворяющий неравенству (2.7);

2) если $\alpha = 1$, то b < 1 и неравенство (2.7) имеет решение $r \geqslant \frac{a}{{1 - b}}$;

3) если $\alpha > 1$ и имеет место неравенство $a \leqslant \frac{{\alpha - 1}}{\alpha }{{(\alpha b)}^{{ - {{{(\alpha - 1)}}^{{ - 1}}}}}}$, то тогда существует хотя бы одно положительное решение неравенства (2.7).

Опираясь на эти заключения, связанные с неравенством (2.7), в котором

$a = \frac{{4({{M}_{2}} + 2\lambda \ln 2{{{\left\| {{{\tau }_{0}}} \right\|}}_{C}})}}{\gamma },\quad b = \frac{{{{2}^{{\alpha + 2}}}{{M}_{1}}}}{{\gamma h_{1}^{\alpha }}}$

при условии

(2.8)

$\gamma : = E{{k}_{0}} - 8\lambda \ln 2 > 0$

получим, что в силу (2.6) оператор $A:C([0,1]) \to C([0,1]),$ действующий по формуле (2.2), переводит шар $B(0,r): = \{ \chi \in C([0,1]):{{\left\| \chi \right\|}_{{C([0,1])}}} \leqslant r\} $ в себя:

а) для достаточно большого фиксированного $r$ в случае $0 \leqslant \alpha < 1$

б) для произвольного $r \geqslant \frac{a}{{1 - b}}$ в случае $\alpha = 1$ и $b < 1$, т.е.

$r \geqslant \frac{{4h_{1}^{\alpha }({{M}_{2}} + 2\lambda \ln 2{{{\left\| {{{\tau }_{0}}} \right\|}}_{C}})}}{{\gamma h_{1}^{\alpha } - {{2}^{{\alpha + 2}}}{{M}_{1}}}}$

при

(2.9)

$E > \frac{{8\lambda \ln 2h_{1}^{\alpha } + {{2}^{{\alpha + 2}}}{{M}_{1}}}}{{{{k}_{0}}h_{1}^{\alpha }}}$

в) в случае $\alpha > 1$, при

(2.10)

$E > \max \left\{ {\frac{{4({{M}_{2}} + 2\lambda \ln 2({{{\left\| {{{\tau }_{0}}} \right\|}}_{C}} + 1))}}{{{{k}_{0}}}},{{{\left( {\frac{\alpha }{{\alpha - 1}}} \right)}}^{{\alpha - 1}}}\frac{{{{2}^{{\alpha + 2}}}\alpha {{M}_{1}}}}{{{{k}_{0}}h_{1}^{\alpha }}} + \frac{{8\lambda \ln 2}}{{{{k}_{0}}}}} \right\}$

Поскольку оператор $A:C([0,1]) \to C([0,1])$ является компактным, согласно принципа неподвижной точки Шаудера [21] интегральное уравнение (2.1) имеет хотя бы одно непрерывное решение, которое, опираясь на результаты, изложенные в работе ([19], стр. 175), будет принадлежать классу H.

Замечание 1. Неравенства (2.8)–(2.10), наложенные на жесткость $E$ материала стрингера, показывают естественные условия, выражающие как возможность ее увеличения, так и cуществование широкого возможного спектра значений геометрических и физических параметров материала пластинки, стрингера и клея.

Существование решения интегрального уравнения (1.6) в классе непрерывных на сегменте [–1, 1] функций обеспечивает ограниченность искомых контактных напряжений на концах тонкостенного элемента, в то время, как в условиях жесткого контакта, как известно, контактные напряжения имеют особенность в указанных сингулярных точках.

3. Единственность решения поставленной задачи. Теперь покажем, что если задача (1.1)–(1.6) имеет решение, то оно единственное.

Действительно, предположим, что задача допускает два возможных различных решения $u_{2}^{{(1)}}(x,y)$ и $u_{2}^{{(2)}}(x,y)$. Из соотношений (1.1) и (1.3) получаем

$E\frac{{du_{1}^{{(j)}}(x)}}{{dx}} = g({{\varphi }_{j}}(x));\quad \left| x \right| < 1$

$u_{1}^{{(j)}}(x) - u_{2}^{{(j)}}(x,0) = {{k}_{0}}{{\tau }^{{(j)}}}(x),$

где

${{\varphi }_{j}}(x) = \frac{1}{{{{h}_{1}}}}\int\limits_{ - 1}^x [ {{\tau }^{{(j)}}}(t) - {{\tau }_{0}}(t)]dt;\quad j = 1,2,$

${{\tau }^{{(1)}}}(x)$ и ${{\tau }^{{(2)}}}(x)$ – соответствующие искомые контактные напряжения, а $u_{1}^{{(1)}}(x)$, $u_{1}^{{(2)}}(x)$ – соответствующие перемещения точек стрингера. Разность этих решений $u(x,y) = u_{2}^{{(1)}}(x,y)$ – $u_{2}^{{(2)}}(x,y)$ удовлетворяет основным уравнениям теории упругости при отсутствии внешних сил, а для ее граничного значения имеем

(3.1)

$\begin{gathered} E\frac{{du(x,0)}}{{dx}} + E{{k}_{0}}\frac{{d{{\tau }^{{(0)}}}(x)}}{{dx}} = \frac{1}{{{{h}_{1}}}}\left( {\int\limits_{ - 1}^x {{{\tau }^{0}}(t)dt} } \right)K(x) \\ {{u}_{0}}(x) - u(x,0) = {{k}_{0}}{{\tau }^{0}}(x), \\ \end{gathered} $

где

${{u}_{0}}(x) = u_{1}^{{(1)}}(x) - u_{1}^{{(2)}}(x),\quad {{\tau }^{0}}(t) = {{\tau }^{{(1)}}}(t) - {{\tau }^{{(2)}}}(t)$

$K(x) = \int\limits_0^1 {g{\kern 1pt} '[{{\varphi }_{1}}(x) + \theta ({{\varphi }_{2}}(x) - {{\varphi }_{1}}(x))]d\theta } $

Как известно, согласно формуле Остроградского–Грина имеет место следующее соотношение [18]

(3.2)

$\int\limits_L {({{X}_{n}}u + {{Y}_{n}}{v})dl} = \iint\limits_S {(\lambda {{\theta }^{2}} + 2\mu (e_{{xx}}^{2} + e_{{yy}}^{2} + e_{{zz}}^{2} + 2e_{{xy}}^{2}))dxdy},$

где ${{X}_{n}},\;{{Y}_{n}},\;u,\;{v}$ – компоненты внешних напряжений и смещений на границе $L$ пластинки, соответственно, $\theta = {{e}_{{xx}}} + {{e}_{{yy}}} + {{e}_{{zz}}}$, а ${{e}_{{xx}}}$, ${{e}_{{yy}}}$, ${{e}_{{xy}}}$, ${{e}_{{zz}}}$ – компоненты деформации.

Учитывая (3.1), интеграл в левой части выражения (3.2) имеет вид

(3.3)

$\begin{gathered} \int\limits_L^{} {({{X}_{n}}u + {{Y}_{n}}v)dl} = \int\limits_{ - 1}^1 {{{\tau }^{0}}(x)} u(x,0)dx = \int\limits_{ - 1}^1 {{{\tau }^{0}}(x)[{{u}_{0}}(x) - {{k}_{0}}{{\tau }^{0}}(x)]} dx = \\ = - {{k}_{0}}\int\limits_{ - 1}^1 {[{{\tau }^{0}}(x)} {{]}^{2}}dx + \int\limits_{ - 1}^1 {{{u}_{0}}(x)d\left( {\int\limits_{ - 1}^x {{{\tau }^{0}}(t)dt} } \right)} = - {{k}_{0}}\int\limits_{ - 1}^1 {{{{[{{\tau }^{0}}(x)]}}^{2}}dx} + \left[ {{{u}_{0}}(t)\int\limits_{ - 1}^x {{{\tau }^{0}}(t)dt} } \right]_{{ - 1}}^{1} - \\ - \;\int\limits_{ - 1}^1 {u_{0}^{'}(x)} \left( {\int\limits_{ - 1}^x {{{\tau }^{0}}(t)dt} } \right)dx = - {{k}_{0}}\int\limits_{ - 1}^1 {{{{[{{\tau }^{0}}(x)]}}^{2}}dx - } E{{h}_{1}}\int\limits_{ - 1}^1 {u{{{_{0}^{'}}}^{2}}(x)} \frac{{dx}}{{K(x)}} \\ \end{gathered} $

Так как подынтегральная функция правой части формулы (3.2) представляет собой положительно определенную квадратичную форму, имея в виду (3.3), можно заключить, что если $g{\kern 1pt} ' > 0$, оба решения $u_{2}^{{(1)}}(x,y)$ и $u_{2}^{{(2)}}(x,y)$ дают одинаковые компоненты деформации и напряжения, что означает, задача (1.1)–(1.6) не может иметь более одного решения.

4. Построение решения задачи (1.8), (1.9) при помощи метода малого параметра. Уравнение (1.8) перепишем в виде

(4.1)

${{k}_{0}}\psi {\kern 1pt} '{\kern 1pt} '(x) = \delta g(\psi (x)) - \frac{\lambda }{\pi }\int\limits_{ - 1}^1 {\frac{{\psi {\kern 1pt} '(t)dt}}{{t - x}}} - {{f}_{0}}(x);\quad \left| x \right| < 1,$

где $\delta = \frac{1}{E}$, ${{f}_{0}}(x) = \frac{\lambda }{\pi }\int_{ - 1}^1 {\frac{{{{\tau }_{0}}(t)dt}}{{t - x}}} $.

Будем предполагать, что функции ${{f}_{0}}(x)$ принадлежит классу ${{С}^{1}}[ - 1,1].$

Когда $\delta $ малый параметр, т.е. материал стрингера – жесткий, представим решение уравнения (4.1) в виде ряда по степеням $\delta $:

(4.2)

$\psi (x) = \sum\limits_{k = 0}^\infty {{{\delta }^{k}}{{\psi }_{k}}(x)} = {{\psi }_{0}}(x) + \delta {{\psi }_{1}}(x) + {{\delta }^{2}}{{\psi }_{2}}(x) + {{\delta }^{3}}{{\psi }_{3}}(x) + O({{\delta }^{4}})$

В предположении, что функция $g$ – аналитическая и разлагается в ряд Маклорена: $g(x) = \sum\nolimits_{k = 0}^\infty {\frac{{{{g}^{{(k)}}}(0)}}{{k!}}} {{x}^{k}}$ на всей действительной оси, будем иметь

(4.3)

$g(\psi (x)) = g(0) + \frac{{g{\kern 1pt} '(0)}}{1}\psi (x) + \frac{{g{\kern 1pt} ''(0)}}{{1 \times 2}}{{\psi }^{2}}(x) + \frac{{g{\kern 1pt} '''(0)}}{{1 \times 2 \times 3}}{{\psi }^{3}}(x) + \cdot \cdot \cdot $

Подставляя разложения (4.2) и (4.3) в уравнение (4.1) и приравнивая коэффициенты при одинаковых степенях $\delta $, получим систему рекуррентных уравнений относительно ${{\psi }_{k}}$

(4.4)

${{k}_{0}}\psi _{0}^{{''}}(x) = - \frac{\lambda }{\pi }\int\limits_{ - 1}^1 {\frac{{\psi _{0}^{'}(t)dt}}{{t - x}}} - {{f}_{0}}(x);\quad \left| x \right| < 1\quad {\text{и}}\;{\text{т}}{\text{.д}}.$

при условиях

(4.5)

${{\psi }_{k}}( \pm 1) = 0;\quad k \geqslant 0$

Таким образом, решение уравнения (1.8) при условии (1.9) сводится к решению системы рекуррентных линейных сингулярных интегро-дифференциальных уравнений (4.4) при условиях (4.5). Решения каждого из этих уравнений (относительно функций $\psi _{k}^{'}(x)$, $k \geqslant 0$) с учетом (4.5) представляются в виде ряда ортогональных многочленов Чебышёва [22] в классе функций, ограниченных на обеих концах линии интегрирования. С применением метода ортогональных многочленов уравнения (4.4) при условиях (4.5) сводятся к совокупности бесконечных систем линейных алгебраических уравнений, квазивполне регулярных при любых конечных значениях параметров ${{k}_{0}}$ и λ.

В виде образца рассмотрим первое уравнение из системы (4.4), решение которого будем искать в виде

(4.6)

$\psi _{0}^{'}(x) = \sqrt {1 - {{x}^{2}}} \sum\limits_{k = 1}^\infty {\frac{{{{X}_{k}}}}{k}} {{U}_{{k - 1}}}(x),$

где числа ${{X}_{k}}$ подлежат определению, а ${{U}_{{k - 1}}}(x)$ – ортогональные многочлены Чебышева второго рода, $k = 1,2,...$.

На основе известных соотношений [22] для ортогональных многочленов Чебышёва

(4.7)

$\int\limits_{ - 1}^1 {\frac{{\sqrt {1 - {{t}^{2}}} {{U}_{{k - 1}}}(t)dt}}{{t - x}}} = - \pi {{T}_{k}}(x),\quad \frac{d}{{dx}}\left( {\sqrt {1 - {{x}^{2}}} {{U}_{{k - 1}}}(x)} \right) = - \frac{{k{{T}_{k}}(x)}}{{\sqrt {1 - {{x}^{2}}} }}$

подставляя выражения (4.6) и (4.7) в первое уравнение системы (4.4), умножая обе части полученного равенства на ${{T}_{m}}(x)$ и интегрируя на интервале $( - 1,1)$ получим бесконечную систему линейных алгебраических уравнений

(4.8)

${{X}_{m}} - \frac{{2\lambda }}{\pi }\sum\limits_{k = 1}^\infty {\frac{{{{R}_{{mk}}}}}{k}} {{X}_{k}} = {{f}_{m}};\quad m = 1,2,...{{k}_{0}},$

где

${{R}_{{mk}}} = \int\limits_{ - 1}^1 {{{T}_{m}}} (x){{T}_{k}}(x)dx,\quad {{f}_{m}} = \frac{2}{\pi }\int\limits_{ - 1}^1 {{{f}_{0}}(x){{T}_{m}}} (x)dx,$

а ${{T}_{k}}(x)$ – ортогональные многочлены Чебышёва первого рода.

Исследуем систему (4.8) на регулярность в классе ограниченных последовательностей. Используя известные соотношения для полиномов Чебышёва первого рода получаем

${{R}_{{mk}}} = \left\{ \begin{gathered} 0,\quad m = k + 1,\quad m = k - 1 \hfill \\ - \frac{{{{{( - 1)}}^{{k + m}}} + 1}}{2}\left[ {\frac{1}{{{{{(m + k)}}^{2}} - 1}} + \frac{1}{{{{{(m - k)}}^{2}} - 1}}} \right],\quad m \ne k + 1,\quad m \ne k - 1 \hfill \\ \end{gathered} \right.$

и, соответственно,

(4.9)

${{S}_{m}} = \sum\limits_{k = 1}^\infty {\left| {\frac{{{{R}_{{mk}}}}}{k}} \right| \to 0,\quad } m \to \infty $

а при помощи формулы интегрирования по частям можно показать, что свободный член этой системы ${{f}_{m}}$ стремится к нулю при $m \to \infty $ со скоростью не менее, чем ${{m}^{{ - 1}}}$, т.е.

(4.10)

${{f}_{m}} = O({{m}^{{ - 1}}});\quad m \to \infty $

Таким образом, из (4.9) и (4.10) следует, что система (4.8) квазивполне регулярна для любых положительных значений параметров ${{k}_{0}}$ и $\lambda $ в классе ограниченных последовательностей [23, 24].

В качестве примера рассмотрим случай $g(u) = {{u}^{2}}$. Тогда система рекуррентных уравнений (4.4) принимает вид:

(4.11)

$\begin{gathered} L{{\psi }_{0}}(x) = - {{f}_{0}}(x),\quad L{{\psi }_{1}}(x) = \psi _{0}^{2}(x),\quad L{{\psi }_{2}}(x) = 2{{\psi }_{0}}(x){{\psi }_{1}}(x) \\ \ldots \\ L{{\psi }_{k}}(x) = \sum\limits_{i + j = k - 1} {{{\psi }_{i}}(x){{\psi }_{j}}(x)} ;\quad \left| x \right| < 1, \\ \end{gathered} $

где $L\psi (x) = {{k}_{0}}\psi {\kern 1pt} '{\kern 1pt} '(x) + \frac{\lambda }{\pi }\int_{ - 1}^1 {\frac{{\psi {\kern 1pt} '(t)dt}}{{t - x}}} $

Из системы (4.11) следует, что ${{\left\| {{{\psi }_{n}}} \right\|}_{C}} \leqslant {{4}^{{n - 1}}}\left\| {{{L}^{{ - 1}}}} \right\|_{{{{C}^{1}} \to C}}^{{2n + 1}}\left\| {{{f}_{0}}} \right\|_{{{{C}^{1}}}}^{{n + 1}}$, и ряд (4.2) сходится при условии

(4.12)

$\delta \leqslant \frac{{{{\delta }_{0}}}}{{4{{{\left\| {{{L}^{{ - 1}}}} \right\|}}_{{{{C}^{1}} \to C}}}{{{\left\| {{{f}_{0}}} \right\|}}_{{{{C}^{1}}}}}}},\quad 0 < {{\delta }_{0}} = \operatorname{const} < 1$

Замечание 2. Хорошо известна общая теорема Пуанкаре [25] о разложении решения нелинейных дифференциальных уравнений по степеням малого параметра. Тогда в случае нелинейного сингулярного интегродифференциального уравнения вида (4.1) при конкретных нелинейных функциях $g$, например, для степенных функций, можно получить условие вида (4.12) относительно малого параметра $\delta $, при котором ряд (4.2) сходится. Соответственно, решение уравнения (4.1) при условиях (1.9) можно построить в виде ряда (4.2).

Список литературы

Александров В.М., Мхитарян С.М. Контактные задачи для тел с тонкими покрытиями и прослойками. М.: Наука, 1983. 487 с.
Банцури Р.Д. Контактная задача для анизотропного клина с упругим креплением // Докл. АН СССР. 1975. Т. 222. № 3. С. 568 –571.
Нуллер Б.М. О деформации упругой клиновидной пластинки, подкрепленной стержнем переменной жесткости и об одном методе решения смешанных задач // ПММ. 1976. Т. 40. Вып. 2. С. 306–316.
Саркисян В.С. Некоторые задачи математической теории упругости анизотропного тела. Ереван: ЕГУ, 1983. 534 с.
Shavlakadze N. The contact problems of the mathematical theory of elasticity for plates with an elastic inclusion // Acta Appl. Math. 2007. V. 99. № 1. P. 29–51.
Банцури Р.Д., Шавлакадзе Н.Н. Контактная задача для кусочно-однородной ортотропной пластинки с конечным включением // ПММ. 2011. Т. 75. Вып. 1. С. 133–138.
Shavlakadze N. The solution of system of integral differential equations and its application in the theory of elasticity // ZAMM. 2011. V. 91. № 12. P. 979–992.
Shavlakadze N., Odishelidze N., Criado-Aldeanueva F. The contact problem for a piecewise-homogeneous orthotropic plate with a finite inclusion of variable cross-section // MMS. 2017. V. 22. № 6. P. 1326–1333.
Lubkin J.I., Lewis I.C. Adhesive shear flow for an axially loaded finite stringer bonded to an infinite sheet // Quart. J. Mech. Appl. Math. 1970. № 23. P. 521–533.
Kesari H., Lew A. Adhesive frictionless contact between an elastic isotropic half-space and rigid axi-symetric punch // J. Elasticity. 2011. V. 106. № 2. P. 203–224.
Stan G., Adams G.G. Adhesive contact between a rigid spherical indenter and elastic multi-layer coated substrate.// Intern. J. Solids &Struct. 2016. V. 87. P. 1–10.
Borodich F.M. The Hertz-Type and adhesive contact problem for depth-sensing indentation // Adv. Appl. Mech. 2014. V. 47. P. 225–366.
Selvadurai A.P.S., Katebi A. An Adhesive contact problem for an incompressible non-homogeneous elastic half-space // Acta Mech. 2015. V. 226. № 2. P. 249–265.
Джохадзе О.М., Харибегашвили С.С, Шавлакадзе Н.Н. Приближенные и точные решения сингулярного интегро-дифференциального уравнения, связанного с контактной задачей теории упругости // ПММ. 2018. Т. 82. Вып. 1. С. 114–124.
Джохадзе О.М., Харибегашвили С.С, Шавлакадзе Н.Н. Контактное взаимодействие пластинки с нелинейно-упругим стрингером // Изв. РАН. МТТ. 2019. № 2. С. 101–110.
Nonlinear Elasticity: Theory and Application / Ed. by Fu Y.B., Ogden R.W. Cambridge: Univ. Press, 2001. 525 p.
Luo A.C.J. Nonlinear Deformable-Body, Dynamics. Berlin, Heidelberg: Springer, 2010. P. 161–199.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 707 с.
Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.: Наука, 1968. 511 с.
Краснов М.Л. Интегральные уравнения. М.: Наука, 1975. 302 с.
Треногин В.А. Функциональный анализ. М.: Наука, 1980. 495 с.
Сеге Г. Ортогональные многочлены. М.: Физматлит, 1962. 500 с.
Канторович Л., Крылов В. Приближенные методы высшего анализа. М.; Л.: Физматгиз, 1962. 708 с.
Канторович Л., Акилов Г. Функциональный анализ. М.: Наука, 1977. 741 с.
Голубев В.В. Лекции по аналитической теории дифференциальных уравнении. М.: Изд. технико-теорет. лит., 1950. 436 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал