Прикладная математика и механика, 2020, T. 84, № 6, стр. 733-756

Введение. Изделия из композиционных материалов (КМ) имеют широкое применение [1–7]. Сочетание относительной легкости и высокой прочности КМ наиболее ярко проявляется в тонкостенных элементах конструкций типа пластин и оболочек [4, 8, 9], в которых часто возникает обобщенное плоское напряженное состояние (ПНС) или близкое к нему. Современные тонкостенные композитные изделия могут подвергаться высокоинтенсивному воздействию [3–5, 9], при котором компоненты композиции деформируются неупруго. Моделирование пластического поведения волокнистых пластин и оболочек сейчас находится в стадии становления.

При теоретическом анализе проблемы исчерпания несущей способности композитной конструкции необходима информация о поверхности текучести для армированной среды. Определение поверхности текучести – самостоятельная задача структурной механики композитных сред. Для расчета прочностных свойств волокнистых композитов, с учетом объемного содержания армирующих элементов, первой использована нитяная модель [10], в которой не рассматривается наличие связующей матрицы. Принято во внимание [11] влияние связующего материала в однонаправленно армированном КМ; при этом в волокнах учтены только продольные напряжения – так называемая, модель с одномерным напряженным состоянием в волокнах (МОНСВ), которая была обобщена [12] на случай плоского армирования по произвольным перекрестным направлениям. Структурные соотношения [12] в сочетании с определяющими уравнениями жесткопластического тела для компонентов позволили моделировать предельные состояния тонкостенных конструкций слоисто-волокнистой структур и построить при ПНС предельные кривые и кривые текучести для слоев с разными типами армирования. Были предложены [13] упрощенные условия текучести слоистых элементов при ортогональных направлениях укладки волокон. Напряженное состояние в арматуре здесь также принято одномерным.

Рассмотрены разные аспекты проблемы гомогенизации дисперсно-упрочненных и волокнистых композитных материалов из упругопластически деформируемых компонентов [3, 14–20]. Несущая способность, вычисляемая на основе таких решений, соответствует определению несущей способности по первому предельному состоянию, когда пластическое течение впервые начинается в одном из компонентов. При проектировании композитных изделий, рассчитанных по первому предельному состоянию, несущая способность высокопрочной арматуры используется неэффективно: в ней наибольшее значение интенсивности напряжений намного меньше предела текучести. Используемая в настоящем исследовании жесткопластическая модель, в отличие от приведенных выше моделей, позволяет определить несущую способность без выполнения полного упругопластического пошагового анализа при пропорционально возрастающем нагружении, т.е. без учета истории нагружения, а найденная при этом предельная нагрузка соответствует определению несущей способности элементов по второму предельному состоянию.

Обсуждены [21] вопросы проявления разносопротивляемости материалов, возникновения ее в процессе технологической обработки [22–24] и актуальности проблемы математического моделирования пластического деформирования КМ из таких материалов. Учтена [12, 13] разносопротивляемость арматуры. На основе нитяной структурной модели и теории предельного равновесия получены [25] предельные нагрузки для железобетонных плит. Структурные модели [12] позже были обобщены на случаи, когда все компоненты по разному сопротивляются растяжению–сжатию, и до настоящего времени, наряду с моделью [14], используются для расчетов предельных состояний армированных тонкостенных элементов [26–30].

В рамках МОНСВ волокна не воспринимают нормальные и касательные напряжения в поперечном направлении. Такое допущение в практических расчетах возможно при сильно нарушенном сцеплении между связующим и арматурой, что часто наблюдается при перекрестном армировании [31, 32]. Современные технологии позволяют создавать волокнистые материалы с хорошей адгезией между составляющими композиции, которую при моделировании можно условно считать идеальной. Тогда для выполнения условий полного контакта арматуры со связующим необходимо учитывать сложное напряженное состояние во всех компонентах. Поэтому задача построения поверхностей текучести волокнистых сред при учете сложного напряженного состояния в арматуре является актуальной. Эта проблема исследована [33] в случае, когда жесткопластические материалы компонентов одинаково сопротивляются растяжению и сжатию и подчиняются критерию текучести Треска [23], а волокна расположены по направлениям главных напряжений в композитной среде при ПНС. Было продемонстрировано [33], что возможны такие композиции, для которых некоторые варианты МОНСВ занижают расчетные значения предела текучести в направлениях, ортогональных направлениям волокон, в результате чего недооценивается прочность армированных элементов конструкций.

В настоящей работе рассмотрено построение поверхностей и кривых текучести плоско-перекрестно армированных в произвольных направлениях гибридных композитов при ПНС и учете сложного напряженного состояния во всех компонентах композиции. Принято, что композиция состоит из жесткопластических материалов, имеющих разные свойства на растяжение и сжатие, а их кривые текучести в главных напряжениях при ПНС являются кусочно-линейными [34–36].

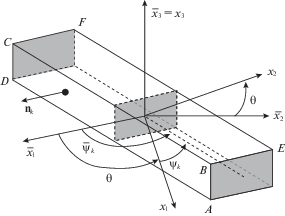
1. Формулировка задачи, основные предположения. В глобальной декартовой прямоугольной системе координат $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$ рассмотрим композитную среду регулярной структуры, армированную K семействами непрерывных прямолинейных волокон по направлениям, параллельным отсчетной плоскости $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}$ (рис. 1, где изображен малый элемент КМ в случае $K = 2$). Для определенности и простоты принимаем, что арматура имеет прямоугольные поперечные сечения, две стороны которых параллельны оси $O{{\bar {x}}_{3}}$, т.е. каждое волокно имеет две вертикальные и две горизонтальные боковые грани. Можно показать [33], что все полученные в настоящем исследовании результаты справедливы для арматуры с произвольной формой сечения (круглой, шестиугольной и др. [37]).

Относительное объемное содержание k-го компонента композиции обозначим ${{\omega }_{k}}$, $0 \leqslant k \leqslant K$, где индекс $k = 0$ соответствует связующему, $k \geqslant 1$ – волокнам k-го семейства. Для ${{\omega }_{k}}$ выполняется условие

Величина ${{\omega }_{k}}$ при $k \geqslant 1$ является плотностью армирования k-м компонентом композиции.

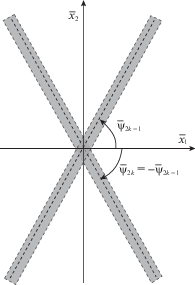
Величины, относящиеся к глобальной системе $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$, будем обозначать чертой сверху. Направление армирования волокнами k-го семейства определяется углом ${{\bar {\psi }}_{k}}$, отсчитываемым от положительного направления оси $O{{\bar {x}}_{1}}$ против часовой стрелки (рис. 2).

Определить действительное распределение напряжений в композитной среде, в которой связующий материал содержит многочисленные цилиндрические включения, сложно даже для однонаправленно армированной линейно-упругой среды [38–42]. Это затруднительно и в рассматриваемом случае жесткопластического деформирования материалов компонентов при произвольном перекрестном армировании. Для построения пригодных в инженерных расчетах кривых и поверхностей текучести рассматриваемой композиции примем гипотезы, схожие с использованными в [33, 39].

1. На макроуровне КМ представляет собой сплошное однородное анизотропное тело. При достаточно густом и равномерном наполнении связующей матрицы армирующими волокнами это допущение вполне приемлемо. К такому выводу приходят все исследователи, изучающие механические свойства дисперсно-армированных сред [38–42].

2. Между волокнами и связующей матрицей реализуется идеальный механический контакт (идеальная адгезия).

3. В пределах репрезентативной ячейки, выделенной из армированной среды на миниуровне, напряжения, деформации и скорости деформаций во всех компонентах и в композиции кусочно-постоянны. Эффекты высших порядков, связанные с изменением полей напряжений, деформаций и их скоростей на микроуровне в малых окрестностях границ контакта арматуры со связующим, не учитываем. Доводы допустимости такого предположения приведены в [33].

4. Усредненные напряжения, деформации и их скорости в композиции определяются усреднением по объему представительного элемента [38, 40]. Согласно предположению 3, они пропорциональны объемному содержанию каждого компонента ${{\omega }_{k}}$, $0 \leqslant k \leqslant K$.

5. В композитной среде реализуется ПНС: ${{\bar {\sigma }}_{{i3}}} = 0$, $i = \overline {1,3} $.

6. Материалы компонентов однородны и изотропны. Их механическое поведение подчиняется ассоциированному закону течения для жесткопластического тела с кусочно-линейными критериями текучести типа Треска (Treska), Йогансена (Johansen) [43], Ху (Нu) [34], Ишлинского–Ивлева [35] и др. [36].

2. Произвольное перекрестное армирование. Вывод соотношений на кривых текучести композиции. В силу предположений 3 и 4 усредненные напряжения ${{\bar {\sigma }}_{{ij}}}$ и скорости деформаций ${{\dot {\bar {\varepsilon }}}_{{ij}}}$ в композиции вычисляются через напряжения $\bar {\sigma }_{{ij}}^{{(k)}}$ и скорости деформаций $\dot {\bar {\varepsilon }}_{{ij}}^{{(k)}}$ в составляющих композиции по формулам:

где точка означает частную производную по времени.

По предположению 2, на поверхностях контакта волокна k-го семейства со связующим материалом для напряжений справедливо (рис. 2) [39]:

Здесь $\bar {n}_{1}^{{(k)}}$, $\bar {n}_{2}^{{(k)}}$ – направляющие косинусы вектора единичной нормали ${{{\mathbf{n}}}_{k}}$ к поверхности ABCD. Равенства (2.2), (2.3) выполняются не только на боковых поверхностях ABCD и BCFE арматуры k-го семейства, но и на противоположных гранях (см. рис. 2), поэтому в равенстве (2.4) указаны два знака ($ \pm $).

Из равенства (2.2) при учете соотношений (2.4) получим

Подставим равенства (2.3) и (2.5) в первое равенство (2.1) при $i = 1{\kern 1pt} - {\kern 1pt} 3$ и $j = 3$. Тогда на основании предположения 5 при учете условия (1.1) имеем

Из равенств (2.6) вытекает, что в рамках используемых предположений во всех материалах композиции также имеет место ПНС.

В силу предположения 5 для построения поверхности текучести армированной среды в трехмерном пространстве усредненных напряжений ${{\bar {\sigma }}_{{11}}}$, ${{\bar {\sigma }}_{{22}}}$ и ${{\bar {\sigma }}_{{12}}}$ следует рассмотреть во всех составляющих композиции все возможные виды напряженного состояния $\bar {\sigma }_{{11}}^{{(k)}}$, $\bar {\sigma }_{{22}}^{{(k)}}$ и $\bar {\sigma }_{{12}}^{{(k)}}$ (см. (2.1) и (2.6)), удовлетворяющие критериям текучести соответствующего компонента композиции (см. предположение 6). Произвольное ПНС может быть задано тремя напряжениями $\bar {\sigma }_{{11}}^{{(k)}}$, $\bar {\sigma }_{{22}}^{{(k)}}$ и $\bar {\sigma }_{{12}}^{{(k)}}$ или двумя главными напряжениями $\sigma _{1}^{{(k)}}$, $\sigma _{2}^{{(k)}}$ и углом ${{\theta }_{k}}$ между направлением главного напряжения $\bar {\sigma }_{1}^{{(k)}}$ ($0 \leqslant k \leqslant K$) и осью $O{{\bar {x}}_{1}}$. Поэтому введем локальную декартову прямоугольную систему координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ ($O{{x}_{3}} = O{{\bar {x}}_{3}}$), которая связана с направлениями главных напряжений в связующем ($k = 0$). Угол между направлением главного напряжения $\sigma _{1}^{{(0)}}$ и осью $O{{\bar {x}}_{1}}$ обозначим $\theta $ (см. рис. 2). В отличие от величин в глобальной системе координат $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$ величины, относящиеся к локальной системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, будем обозначать без черты сверху. В локальной системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ компоненты тензора напряжений в k-м материале композиции обозначим $\sigma _{{11}}^{{(k)}}$, $\sigma _{{22}}^{{(k)}}$ и $\sigma _{{12}}^{{(k)}}$ ($0 \leqslant k \leqslant K$). Для них при $k = 0$ имеют место равенства:

В системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ остаются справедливыми равенства (2.1) и (2.6), где нужно выполнить формальные замены

при учете обозначений (2.7).

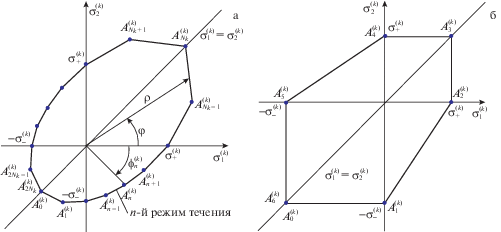
Согласно равенствам (2.6), (2.7) и предположению 6, при ПНС кривая текучести для k-го компонента в главных напряжениях $\sigma _{1}^{{(k)}}$ и $\sigma _{2}^{{(k)}}$ является кусочно-линейной замкнутой линией, выпуклой (в силу выполнения постулата Друккера [34–36]) и симметричной относительно прямой $\sigma _{1}^{{(k)}} = \sigma _{2}^{{(k)}}$, $0 \leqslant k \leqslant K$ (рис. 3). Каждый прямолинейный участок этой линии соответствует определенному режиму пластического течения. В силу симметрии и для удобства изложения считаем, что кривая текучести состоит из четного числа $2{{N}_{k}}$ отрезков. Обозначим угловые точки на линии как $A_{n}^{{(k)}}$ ($0 \leqslant n \leqslant 2{{N}_{k}}$, $0 \leqslant k \leqslant K$), обходя ее против часовой стрелки, начиная от точки, лежащей на прямой $\sigma _{1}^{{(k)}} = \sigma _{2}^{{(k)}}$ в третьем квадранте плоскости $\sigma _{1}^{{(k)}}\sigma _{2}^{{(k)}}$ (см. рис. 3а). Точка $A_{n}^{{(k)}}$ имеет координаты $\left( {s_{{1,n}}^{{(k)}},s_{{2,n}}^{{(k)}}} \right)$. Вершины $A_{0}^{{(k)}}$ и $A_{{2{{N}_{k}}}}^{{(k)}}$ совпадают. В общем случае отрезки $A_{{{{N}_{k}} - 1}}^{{(k)}}A_{{{{N}_{k}} + 1}}^{{(k)}}$ и $A_{{2{{N}_{k}} - 1}}^{{(k)}}A_{1}^{{(k)}}$ могут лежать на одной прямой, например, в случае критерия Ишлинского–Ивлева [35]. Режим, соответствующий отрезку $A_{{n - 1}}^{{(k)}}A_{n}^{{(k)}}$, назовем n-м режимом текучести в k-м компоненте. Для режимов $A_{{n - 1}}^{{(k)}}A_{n}^{{(k)}}$ ($1 \leqslant n \leqslant {{N}_{k}}$), лежащих ниже прямой $\sigma _{1}^{{(k)}} = \sigma _{2}^{{(k)}}$, выполняется

и для режимов $A_{{n - 1}}^{{(k)}}A_{n}^{{(k)}}$ (${{N}_{k}} + 1 \leqslant n \leqslant 2{{N}_{k}}$), лежащих выше прямой $\sigma _{1}^{{(k)}} = \sigma _{2}^{{(k)}}$, будет $\sigma _{1}^{{(k)}} \leqslant \sigma _{2}^{{(k)}}$, а равенство здесь и в (2.9) возможно только в точках $A_{0}^{{(k)}}$ и $A_{{{{N}_{k}}}}^{{(k)}}$. В силу симметрии кривой текучести рассмотрим только вариант (2.9).

На n-м режиме напряжения $\sigma _{1}^{{(k)}}$ и $\sigma _{2}^{{(k)}}$ связаны соотношениями

При ПНС главные напряжения $\sigma _{i}^{{(k)}}$ равны:

где знак перед радикалом выбран с учетом (2.9).

Из (2.10), (2.12) получим, что условие текучести (пластичности) k-го компонента композиции $f_{n}^{{(k)}}$ на n-м режиме имеет вид рациональной функции:

Если n-й режим является горизонтальным или вертикальным (см. отрезки $A_{0}^{{(k)}}A_{1}^{{(k)}}$ и $A_{3}^{{(k)}}A_{4}^{{(k)}}$ или $A_{2}^{{(k)}}A_{3}^{{(k)}}$ и $A_{5}^{{(k)}}A_{6}^{{(k)}}$ на рис. 3 б), то $\Delta _{{2,n}}^{{(k)}} = 0$ или $\Delta _{{1,n}}^{{(k)}} = 0$ (см. (2.11)). Из выражений (2.14) следует $a_{n}^{{(k)}} = 0$ и $d_{n}^{{(k)}} = e_{n}^{{(k)}}$. Тогда функция (2.13) имеет вид

Рассмотрим главные напряжения в связующем материале $\sigma _{1}^{{(0)}}$ и $\sigma _{2}^{{(0)}}$ в полярных координатах $(r,\varphi )$:

Тогда условие текучести для связующего материала примет вид $r = \rho \left( \varphi \right)$ (рис. 3а), а напряжения $\sigma _{1}^{{(0)}}$ и $\sigma _{2}^{{(0)}}$, удовлетворяющие этому условию, можно представить в параметрическом виде:

Для n-го режима кривой текучести из выражений (2.16) и (2.10) при $k = 0$ получим выражение для $\rho \left( \varphi \right)$:

где $\Delta _{{i,n}}^{{(0)}}$ и $\Delta _{n}^{{(0)}}$ определены в (2.11), угол $\phi _{n}^{{(0)}}$ показан на рис. 3а при $k = 0$. Далее напряжения $\sigma _{{ij}}^{{(k)}}$ ($1 \leqslant k \leqslant K$, $i,j = 1,2$) также выразим через параметр $\varphi $.

В силу предположения 2 из условия совпадения напряжений на боковой поверхности арматуры k-го семейства ABCD и ей противоположной (см. рис. 2) при учете (2.7) кроме первого соотношения (2.2) имеем

Здесь ${{\psi }_{k}}\left( \theta \right) = {{\bar {\psi }}_{k}} - \theta $ – угол, задающий направление волокон k-го семейства в локальной системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и отсчитываемый от направления $O{{x}_{1}}$; $n_{1}^{{(k)}}$, $n_{2}^{{(k)}}$ – направляющие косинусы вектора единичной нормали ${{{\mathbf{n}}}_{k}}$ к боковой поверхности ABCD (и ей противоположной), определенные в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$.

Из равенств (2.19) при $n_{1}^{{(k)}} \ne 0$ и $n_{2}^{{(k)}} \ne 0$ получим

Подставим (2.21) в условие текучести (2.13) при $k \geqslant 1$ и получим для $\sigma _{{12}}^{{(k)}}$ квадратное уравнение (при $\,i,\,j = 1,\,2$, $\,i \ne \,j$):

Решения уравнения (2.22) при $A_{n}^{{(k)}} \ne 0$ имеют вид

Знак “$ \pm $” в решении (2.23) выбирается из условия совпадения скоростей деформаций волокна k-го семейства и связующего материала в направлении армирования, которое рассмотрено в разделе 4. При армировании волокнами k-го семейства вдоль направления первого главного напряжения в связующем (${{\psi }_{k}} = {{\bar {\psi }}_{k}} - \theta = 0$) или вдоль направления второго главного напряжения (${{\psi }_{k}} = \pi {\text{/}}2$) при любом выборе знака “$ \pm $” для решения (2.23) выполняется $\sigma _{{12,n}}^{{(k)}} = 0$ ($1 \leqslant n \leqslant {{N}_{k}}$, $1 \leqslant k \leqslant K$).

Для горизонтального или вертикального n-го режима (отрезки $A_{0}^{{(k)}}A_{1}^{{(k)}}$, $A_{3}^{{(k)}}A_{4}^{{(k)}}$, $A_{2}^{{(k)}}A_{3}^{{(k)}}$, $A_{5}^{{(k)}}A_{6}^{{(k)}}$ на рис. 3б из выражений (2.15) и (2.21) имеем ($n_{1}^{{(k)}} \ne 0$ и $n_{2}^{{(k)}} \ne 0$):

Если $n_{i}^{{(k)}} = 0$ и $n_{j}^{{(k)}} = \pm 1$ ($\,i,\,j = 1,\,2$, $\,i \ne \,j$), то из (2.19) следует

а напряжение $\sigma _{{ii}}^{{(k)}}$ для не горизонтального и не вертикального n-го режима определяется из (2.13) при учете (2.25): где $1 \leqslant n \leqslant {{N}_{k}}$, $1 \leqslant k \leqslant K$, $\,i,\,j = 1,\,2$,$\,i \ne \,j$.

Решения уравнения (2.26) имеют вид ($n_{i}^{{(k)}} = 0$, $n_{j}^{{(k)}} = \pm 1$, ($\,i,\,j = 1,\,2$, $\,i \ne \,j$)):

Знак “$ \pm $” в (2.27) выбирается из тех же условий, что и (2.23), которые рассмотрены в разд. 4. Для горизонтального или вертикального n-го режима напряжение $\sigma _{{ii}}^{{(k)}}$ определяется из (2.15), (2.25) ($1 \leqslant n \leqslant {{N}_{k}}$, $1 \leqslant k \leqslant K$, $\,i,\,j = 1,\,2$, $\,i \ne \,j$):

Соотношения (2.23), (2.24) при $n_{1}^{{(k)}} \ne 0$ и $n_{2}^{{(k)}} \ne 0$ и равенства (2.25), (2.27), (2.28) при $n_{i}^{{(k)}} = 0$ и $n_{j}^{{(k)}} = \pm 1$ ($\,i,\,j = 1,\,2$, $\,i \ne \,j$) дают двухпараметрические зависимости для напряжений в арматуре

Усредним напряжения (2.29) (с учетом соотношений (2.7) и (2.16)) по объему представительного элемента композиции (см. (2.1), принимая во внимание (2.8)), тогда получим двухпараметрическую зависимость усредненных напряжений

где правые части известны. В зависимостях (2.30) у напряжений $\sigma _{{ij}}^{{(k)}}$ опущен нижний индекс n (см. (2.23), (2.27) и (2.29)), т.к. подразумевается, что при текущем значении $\varphi $ в равенствах (2.23) и (2.27) не только однозначно выбран знак “$ \pm $”, но и однозначно определен номер n режима пластического течения для k-го компонента.

Соотношения (2.30) задают параметрическую от $(\theta ,\varphi )$ зависимость поверхности текучести рассматриваемой среды в трехмерном пространстве напряжений ${{\sigma }_{{11}}}$, ${{\sigma }_{{22}}}$ и ${{\sigma }_{{12}}}$, определенных в локальной системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. В глобальной системе $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$ усредненные напряжения ${{\bar {\sigma }}_{{11}}}$, ${{\bar {\sigma }}_{{22}}}$ и ${{\bar {\sigma }}_{{12}}}$ связаны с ${{\sigma }_{{11}}}$, ${{\sigma }_{{22}}}$ и ${{\sigma }_{{12}}}$ следующими равенствами, полученными при повороте системы координат на угол $ - \theta $ вокруг оси $O{{\bar {x}}_{3}} = O{{x}_{3}}$ [39] ($0 \leqslant \theta < 2\pi ,0 \leqslant \varphi < 2\pi $):

Искомая поверхность текучести в трехмерном пространстве усредненных напряжений ${{\bar {\sigma }}_{{11}}}$, ${{\bar {\sigma }}_{{22}}}$ и ${{\bar {\sigma }}_{{12}}}$ определяется параметрически из зависимостей (2.30) и (2.31).

3. Случай симметричного армирования. Рассмотрим интересный и практически важный пример, когда в КМ число семейств арматуры четное ($K = 2N$) и для каждого семейства определено парное ему семейство. Волокна парных семейств выполнены из одного материала ($\sigma _{ \pm }^{{(2k - 1)}} = \sigma _{ \pm }^{{(2k)}}$, где $\sigma _{ + }^{{(k)}}$, $\sigma _{ - }^{{(k)}}$ – пределы текучести k-го компонента композиции при растяжении и сжатии), имеют одинаковые плотности армирования (${{\omega }_{{2k - 1}}} = {{\omega }_{{2k}}}$) и расположены симметрично относительно оси $O{{\bar {x}}_{1}}$: ${{\bar {\psi }}_{{2k - 1}}} = - {{\bar {\psi }}_{{2k}}}$, $1 \leqslant k \leqslant N$ (рис. 4). Считаем, что оси $O{{\bar {x}}_{i}}$ ($i = 1,2$) совпадают с направлениями главных напряжений тензора усредненных напряжений в композиции, поэтому вместе с предположением 5 выполняется условие ${{\bar {\sigma }}_{{12}}} \equiv 0$. В силу предположения 1 и симметрии структуры армирования относительно $O{{\bar {x}}_{1}}$ и $O{{\bar {x}}_{2}}$ эти оси совпадают с направлениями главных напряжений в связующей матрице: $O{{\bar {x}}_{i}} = O{{x}_{i}}$ ($i = 1{\kern 1pt} - {\kern 1pt} 3$), т.е. при $k = 0$ кроме (2.6) выполняется равенство $\bar {\sigma }_{{12}}^{{(0)}} \equiv 0$. При этом значение одного из параметров фиксировано: $\theta \equiv 0$ (${{\bar {\psi }}_{k}} = {{\psi }_{k}}$; см. (2.20) и рис. 2), а два первых равенства (2.31) при учете соотношений (2.30) однопараметрически (по $\varphi $) определяют кривую текучести композитной среды в главных усредненных напряжениях в композиции:

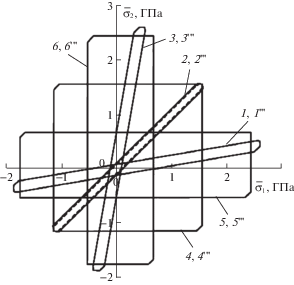
На рис. 5 изображены кривые текучести, рассчитанные в качестве примера для двух металлокомпозиций, состоящих из высокопрочного титанового (сплав Бета-III: $\sigma _{ \pm }^{{(0)}} = \sigma _{{0,2}}^{{(0)}}$ = 1.37 ГПа [45]) или низкопрочного алюминиевого (сплав АДМ: $\sigma _{ \pm }^{{(0)}} = \sigma _{{0,2}}^{{(0)}}$ = = 30 МПа [24]) связующего, армированного двумя ($K = 2$) семействами высокопрочной стальной проволоки марки У8А ($\sigma _{ \pm }^{{(k)}} = \sigma _{{0,2}}^{{(k)}} = 4$ ГПа [24], $k = 1,2$, где $\sigma _{{0,2}}^{{(k)}}$ – условный предел текучести). Для всех компонентов этих композиций $\sigma _{ + }^{{(k)}} = \sigma _{ - }^{{(k)}}$ ($0 \leqslant k \leqslant K$) и справедлив пластический критерий Треска (см. рис. 3б при $\sigma _{ + }^{{(k)}} = \sigma _{ - }^{{(k)}}$).

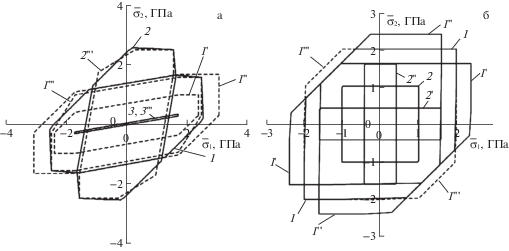
Рассмотрены два варианта симметричного армирования при условии одинакового количества арматуры (см. рис. 4 при $k = 1$):

а) угловое перекрестно-симметричное армирование: ${{\psi }_{2}} = - {{\psi }_{1}}$, ${{\omega }_{1}} = {{\omega }_{2}} = 0.25$;

б) ортогональное армирование вдоль направлений главных напряжений в композиции: ${{\psi }_{1}} = 0$, ${{\psi }_{2}} = \pi {\text{/}}2$, ${{\omega }_{1}} + {{\omega }_{2}} = 0.5$.

На рис. 5а для варианта армирования а) сплошные кривые 1 и 2 рассчитаны для Ti–У8А-композиции, а кривая 3 – для АДМ–У8А-композиции. Кривые 1 и 3 соответствуют углам армирования ${{\psi }_{1}} = - {{\psi }_{2}} = \pi {\text{/}}8$, а кривая 2 – углам ${{\psi }_{1}} = - {{\psi }_{2}} = 3\pi {\text{/}}8$. В случае АДМ–У8А-композиции при таких углах расположения волокон кривая текучести КМ получается зеркальным отражением кривой 3 относительно прямой ${{\bar {\sigma }}_{1}} = {{\bar {\sigma }}_{2}}$ и на рис. 5а не изображена, чтобы его не перегружать. Из сравнения кривых 1 и 2 на рис. 5а видно, что даже при использовании высокопрочного связующего материала (Ti) изменение углов армирования при сохранении общего количества волокон сильно меняет кривую текучести КМ. Зависимость размеров и формы кривой текучести от углов армирования еще ярче проявляется в случае низкопрочного связующего материала, например сплава АДМ (см. кривую 3 на рис. 5а).

На рис. 5б для варианта армирования б) сплошные кривые с номерами 1 рассчитаны для Ti–У8А-композиции, а кривые с номерами 2 – для АДМ–У8А-композиции. Кривые 1 и 2 получены при ${{\omega }_{1}} = {{\omega }_{2}} = 0.25$, кривые 1' и 2' – при ${{\omega }_{1}} = 0.4$ и ${{\omega }_{2}} = 0.1$, а кривые 1'' и 2'' – при ${{\omega }_{1}} = 0.1$ и ${{\omega }_{2}} = 0.4$. Видно, что в при низкопрочном связующем кривые текучести 2, 2' и 2'' по форме близки к прямоугольникам. Из сравнения кривых 1, 1', 1'' и 2, 2', 2'' видно, что при фиксированных углах армирования кривые текучести КМ зависят от изменения плотностей армирования ${{\omega }_{1}}$ и ${{\omega }_{2}}$, причем эта зависимость проявляется тем ярче, чем больше отношение пределов текучести волокон и связующего.

На рис. 6 изображены расчетные предельные кривые для КМ, компоненты которого являются разносопротивляющимися: $\sigma _{ + }^{{(0)}} = 90$ МПа, $\sigma _{ - }^{{(0)}} = 111$ МПа [22] и $\sigma _{ + }^{{(k)}} = 6$ ГПа, $\sigma _{ - }^{{(k)}} = 4.2$ ГПа [24] ($k = 1,2$). Армирование выполнено двумя ($K = 2$) семействами высокопрочных волокон. Такие значения $\sigma _{ \pm }^{{(k)}}$ ($0 \leqslant k \leqslant K$) условно соответствуют эпоксидной смоле и стекловолокнам, изготовленным из расплавленного кварца. Значение $\sigma _{ - }^{{(k)}}$ ($k = 1,2$) для арматуры условно соответствует потере устойчивости в результате сдвиговой деформации [24], поэтому волокна также можно считать разносопротивляющимися растяжению–сжатию. Принято, что предельное состояние составляющих КМ описывается критерием Ху (см. рис. 3б).

На рис. 6 сплошные кривые 1–3 рассчитаны при варианте армирования а), а кривые 4–6 – для варианта армирования б). Кривые 1, 2 и 3 получены при ${{\psi }_{1}} = - {{\psi }_{2}} = \pi {\text{/}}8$, $\pi {\text{/}}4$ и $3\pi {\text{/}}8$ соответственно. Кривая 2 характеризует предельное состояние ортогонально армированной композиции, в которой направления армирования образуют углы $ \pm \pi {\text{/}}4$ с направлениями главных напряжений в композиции. Из сравнения кривых 1–3 видно, что и в случае использования разносопротивляющихся составляющих КМ изменение углов армирования при сохранении общего количества волокон также существенно влияет на размеры и форму предельной кривой композиции.

Кривые 4–6 на рис. 6, как и кривая 2, рассчитаны для ортогонально армированной композиции, когда траектории укладки волокон совпадают с направлениями главных напряжений в КМ (${{\psi }_{1}} = 0$ и ${{\psi }_{2}} = \pi {\text{/}}2$). Кривая 4 определена при ${{\omega }_{1}} = {{\omega }_{2}} = 0.25$, кривая 5 – при ${{\omega }_{1}} = 0.4$ и ${{\omega }_{2}} = 0.1$, а кривая 6 – при ${{\omega }_{1}} = 0.1$ и ${{\omega }_{2}} = 0.4$. Все кривые по форме близки к прямоугольникам. Из сравнения кривых 4–6 также следует, что при фиксированных углах армирования предельная кривая композиции значительно зависит от изменения плотностей армирования ${{\omega }_{1}}$ и ${{\omega }_{2}}$.

Кривые 2 и 4 на рис. 6 демонстрируют, как сильно изменяется предельная кривая ортогонально-армированного КМ при повороте структуры армирования на угол $\pi {\text{/}}4$ (вокруг оси $O{{\bar {x}}_{3}}$) относительно направлений главных напряжений.

Отметим, в случае ${{\psi }_{1}} = - {{\psi }_{2}} = 0$ или ${{\psi }_{1}} = - {{\psi }_{2}} = \pi {\text{/}}2$ (однонаправленное армирование, при котором направления армирования обоих семейств совпадают) предельные кривые, рассчитанные по рассматриваемому методу, совпадают с кривыми, рассчитанными по методике [21].

4. Определение усредненных скоростей деформаций композиции. Из предположения 6 и ассоциированного закона течения, для скоростей деформаций k-го компонента, определенных в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ (рис. 2), имеем:

$\dot {\lambda }_{n}^{{(k)}}$ – неопределенный параметр; $f_{n}^{{(k)}} = 0$ – уравнение поверхности текучести k-го компонента на n-м режиме [46] (см. режим $A_{{n - 1}}^{{(k)}}A_{n}^{{(k)}}$ на рис. 3а).

Применяя для функции текучести $f_{n}^{{(k)}}$ при ПНС выражение (2.13) с учетом (2.7), по формулам (4.1) получим

В силу определения системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ из (2.7), (2.10), (4.1) и (4.2) следует

Согласно гипотезам 2 и 3, скорости деформаций волокна k-го семейства и связующего материала в направлении армирования должны совпадать, поэтому выполняются следующие кинематические соотношения [39]

где при учете соотношений (4.3)

Так как при активном нагружении k-го компонента композиции $\dot {\lambda }_{n}^{{(k)}} > 0$, $0 \leqslant k \leqslant K$ (см. (4.1)), из соотношений (4.4) следует

При выборе знака “$ \pm $” перед радикалами в выражениях (2.23) и (2.27) следует учитывать выполнение условий (4.6) при учете соотношений (4.2), (4.3) и (4.5).

После определения знаков из решений (2.23) и (2.27) при $1 \leqslant n \leqslant {{N}_{k}}$ необходимо однозначно выбрать номер n-го режима текучести в арматуре k-го семейства, который соответствует текущему напряженному состоянию в связующем материале (текущему значению полярного угла $\varphi $ в выражениях (2.16) и (2.17)). Для этого решения (2.23) и (2.27) нужно подставить в выражения (2.12) и определить главные напряжения $\sigma _{{i,n}}^{{(k)}} \equiv \sigma _{i}^{{(k)}}\left( {\sigma _{{11,n}}^{{(k)}},\sigma _{{22,n}}^{{(k)}},\sigma _{{12,n}}^{{(k)}}} \right)$ ($1 \leqslant n \leqslant {{N}_{k}}$) в волокнах k-го семейства ($1 \leqslant k \leqslant K$). С учетом формул (2.10) и (2.11), режим (с номером n) пластического течения арматуры k-го семейства выбирается из условий

где (см. (2.18) и рис. 3а)

По условию (4.7) и соотношениям (4.8) можно однозначно определить номер n режима, который реализуется в арматуре k-го семейства при текущем значении параметра $\varphi $.

Из равенства (4.4) получим

где индекс l выбран в соответствии с условиями (4.7) при учете соотношений (4.8). Согласно выражениям (4.2), (4.3), (4.5), (2.16), (2.17) и (2.29) при учете соотношения ${{\psi }_{k}}\left( \theta \right) = {{\bar {\psi }}_{k}} - \theta $ (см. (2.20) и рис. 2), в выражении (4.9) имеем двухпараметрические представления величин $\xi _{l}^{{(k)}} = \xi _{l}^{{(k)}}\left( {\theta ,\varphi } \right)$ и $\xi _{{k,n}}^{{(0)}} = \xi _{{k,n}}^{{(0)}}\left( {\theta ,\varphi } \right)$.

Используя вторую формулу (2.1) при учете переобозначений (2.8) и соотношений (4.2), (4.3), (4.5) и (4.9), определим усредненные скорости деформаций композитной среды в локальной системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$:

В соотношениях (4.10) и (4.11) опущены нижние индексы n и l (выполнены замены $\dot {\lambda }_{l}^{{(k)}} \to {{\dot {\lambda }}^{{(k)}}}$, $\dot {\lambda }_{n}^{{(0)}} \to {{\dot {\lambda }}^{{(0)}}}$, $\xi _{{k,n}}^{{(0)}} \to \xi _{k}^{{(0)}}$, $\xi _{l}^{{(k)}} \to {{\xi }^{{(k)}}}$, $\xi _{{ij,l}}^{{(k)}} \to \xi _{{ij}}^{{(k)}}$, $\xi _{{ij,n}}^{{(0)}} \to \xi _{{ij}}^{{(0)}}$), так как предполагается, что на основании формул (4.7) и (4.8) уже однозначно определен номер l-го режима в арматуре k-го семейства, соответствующий n-му текущему (по $\varphi $) номеру режима в связующей матрице.

Согласно соотношениям (4.2), (4.5) и (4.11), зависимости (4.10) параметрически ($\theta ,\,\,\varphi $) задают компоненты тензора усредненных скоростей деформаций рассматриваемого КМ, определенные в локальной системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ (см. рис. 2). Для определения компонент усредненных скоростей деформаций композиции в глобальной системе $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$ (${{\dot {\bar {\varepsilon }}}_{{ij}}} = {{\dot {\lambda }}^{{(0)}}}{{\bar {\xi }}_{{ij}}}$, $i,j = 1,2$) нужно применять формулы пересчета, аналогичные (2.31) [39] ($0 \leqslant \theta < 2\pi ,0 \leqslant \varphi < 2\pi $):

5. Обоснование выполнения ассоциированного закона течения для композиции. Чтобы показать выполнение ассоциированного закона течения, нужно доказать справедливость равенств (см. (4.10) и (4.12)) [21, 35]

на гладких участках поверхности текучести композиции $f\left( {{{{\bar {\sigma }}}_{{11}}},{{{\bar {\sigma }}}_{{22}}},{{{\bar {\sigma }}}_{{12}}}} \right) = 0$, задаваемой параметрически соотношениями (2.31) при учете зависимостей (2.30). Величины ${{\bar {\xi }}_{{ij}}}$ в соотношениях (5.1) определяются равенствами (4.12) при учете (4.11). Доказать аналитически справедливость равенств (5.1) авторам пока не удалось.

При выполнении ассоциированного закона течения для композиции, согласно (5.1), вектор $\bar {\xi } = \left\{ {{{{\bar {\xi }}}_{{11}}},{{{\bar {\xi }}}_{{22}}},{{{\bar {\xi }}}_{{12}}}} \right\}$ должен быть ортогонален к гладкому участку поверхности текучести $f = 0$, поэтому обосновать выполнение ассоциированного закона течения для КМ можно путем проверки ортогональности вектора $\bar {\xi }$, вычисленного по формулам (4.11) и (4.12), к гладкому участку поверхности текучести $f = 0$, задаваемой равенствами (2.30) и (2.31). Проверка такой ортогональности выполнена следующим образом.

Вектор $\bar {\xi }$ ортогонален к гладкому участку поверхности $f = 0$, если он на этом участке поверхности ортогонален к координатным линиям, задаваемым параметрами $\theta $ и $\varphi $, т.е. ортогонален к векторам, касательным к этим линиям. Используя формулы (2.31) при учете (2.30), определим частные производные от усредненных напряжений ${{\bar {\sigma }}_{{ij}}}$ по параметрам $\theta $ и $\varphi $:

Векторы ${{\bar {\sigma }}_{\theta }} = \left\{ {\bar {\sigma }_{{11}}^{\theta },\,\,\bar {\sigma }_{{22}}^{\theta },\,\,\bar {\sigma }_{{12}}^{\theta }} \right\}$ и ${{\bar {\sigma }}_{\varphi }} = \left\{ {\bar {\sigma }_{{11}}^{\varphi },\,\,\bar {\sigma }_{{22}}^{\varphi },\,\,\bar {\sigma }_{{12}}^{\varphi }} \right\}$ являются касательными к координатным линиям $\theta $ и $\varphi $ соответственно. Введем величины:

Векторы ${{{\mathbf{\bar {s}}}}_{\theta }} = \left\{ {\bar {s}_{{11}}^{\theta },\bar {s}_{{22}}^{\theta },\bar {s}_{{12}}^{\theta }} \right\}$ и ${{{\mathbf{\bar {s}}}}_{\varphi }} = \left\{ {\bar {s}_{{11}}^{\varphi },\bar {s}_{{22}}^{\varphi },\bar {s}_{{12}}^{\varphi }} \right\}$ имеют единичную длину (см. (5.2) и (5.3)) и являются касательными к координатным линиям $\theta $ и $\varphi $ на гладких участках поверхности текучести композиции ($f = 0$).

Так как параметр ${{\dot {\lambda }}^{{(0)}}}$ является неопределенным, вместо ${{\bar {\xi }}_{{ij}}}$ рассмотрим

Вектор $\bar {\eta } = \left\{ {{{{\bar {\eta }}}_{{11}}},{{{\bar {\eta }}}_{{22}}},{{{\bar {\eta }}}_{{12}}}} \right\}$ имеет единичную длину и при выполнении ассоциированного закона течения для композиции (5.1) ортогонален к гладкому участку поверхности текучести КМ $f = 0$, т.е. ортогонален к векторам ${{{\mathbf{\bar {s}}}}_{\theta }}$ и ${{{\mathbf{\bar {s}}}}_{\varphi }}$. Далее вычислим скалярные произведения

Если ассоциированный закон течения для композиции (5.1) действительно выполняется, то справедливо

Аналитически доказать выполнение равенства (5.6) сложно, но его можно проверить численно. Для этого нужно численно определить производные в (5.2) и величины ${{\Delta }_{\theta }}$ и ${{\Delta }_{\varphi }}$ при учете соотношений (5.3)–(5.5). При выполнении ассоциированного закона течения (5.1), точность выполнения соотношений (5.6) должна быть того же порядка, что и численное определение частных производных в (5.2), так как векторы $\bar {\eta }$, ${{{\mathbf{\bar {s}}}}_{\theta }}$ и ${{{\mathbf{\bar {s}}}}_{\varphi }}$ в (5.5) являются единичными.

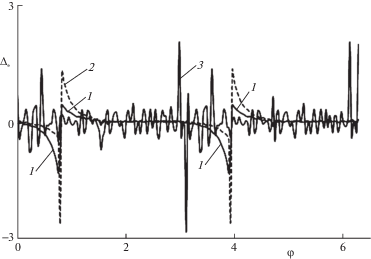
На рис. 7 приведены зависимости ${{\Delta }_{*}}\left( \varphi \right) = {{10}^{4}}{{\Delta }_{\varphi }}\left( \varphi \right)$, соответствующие сплошным кривым текучести на рис. 5а. Номера кривых на этих рисунках совпадают. Принято $\theta \equiv 0$ и на интервале $\varphi \in \left[ {0,\,\,2\pi } \right]$ введена сетка с шагом ${{h}_{\varphi }} = 2\pi {\text{/}}200$ = $3.14 \times {{10}^{{ - 2}}}$. В формулах (5.2) производные $\bar {\sigma }_{{ij}}^{\varphi }$ вычислены конечно-разностными методами на трехточечных шаблонах, т.е. точность определения значений $\bar {\sigma }_{{ij}}^{\varphi }$ имеет порядок $h_{\varphi }^{2} = 9.87 \times {{10}^{{ - 4}}} \approx {{10}^{{ - 3}}}$. В угловых точках кривых 1–3 на рис. 5а для вычисления производных $\bar {\sigma }_{{ij}}^{\varphi }$ использованы скошенные разности. Из рис. 7 видно, что максимальные по модулю значения ${{\Delta }_{\varphi }}$ имеют порядок $h_{\varphi }^{2}$ и пренебрежимо малы по сравнению с единицей.

Определим среднеквадратичные отклонения зависимостей ${{\Delta }_{\varphi }}\left( \varphi \right)$ от нуля

Для кривой 1 на рис. 7 получим ${{\delta }_{\varphi }} = 2.69 \times {{10}^{{ - 5}}}$, для кривой 2 – ${{\delta }_{\varphi }} = 3.63 \times {{10}^{{ - 5}}}$, а для кривой 3 – ${{\delta }_{\varphi }} = 4.24 \times {{10}^{{ - 5}}}$. Интегралы в последней формуле вычислялись по формуле трапеций. Следовательно, во всех рассматриваемых случаях ${{\delta }_{\varphi }}$ равно нулю с рассматриваемой точностью.

Дополнительные расчеты, проведенные для других сплошных кривых текучести на рис. 5б и 6, показали, что функции ${{\Delta }_{\varphi }}\left( \varphi \right)$ для них качественно и количественно сходны с кривыми на рис. 7, а значения ${{\delta }_{\varphi }}$ имеют порядок ${{10}^{{ - 5}}}$. Поэтому можно считать, что в рамках разработанной структурной модели армированной среды ассоциированный закон течения, вообще говоря, выполняется. Значит, для такой композитной среды и для каждого компонента композиции, выполняется постулат Друккера [35, 46], что подтверждает непротиворечивость введенных в данном исследовании исходных гипотез.

В случае симметричного армирования, рассмотренного в разд. 3, при ${{\psi }_{1}} = - {{\psi }_{2}} = 0$ или ${{\psi }_{1}} = - {{\psi }_{2}} = \pi {\text{/}}2$ (однонаправленное армирование) ассоциированный закон течения для композитной среды выполняется строго (см. [21]).

6. Модель с одномерным напряженным состоянием в волокнах. В системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ соотношения МОНСВ при ПНС [12, 30] равны:

Здесь $\omega _{1}^{{(0)}}$ и $\omega _{2}^{{(0)}}$ – коэффициенты; ${{\sigma }_{k}}$ – продольные напряжения в волокнах k-го семейства (в поперечном направлении нормальные и касательные напряжения в арматуре не учитываются); $\sigma _{1}^{{(0)}}$, $\sigma _{2}^{{(0)}}$ – главные напряжения в связующей матрице (см. (2.7)), которые удовлетворяют условию текучести (2.10) ($k = 0$) и параметрически выражаются по формулам (2.16)–(2.18).

В рамках МОНСВ остаются справедливыми соотношения (4.4) и (4.6) при $l = 1,2$, где $\dot {\lambda }_{l}^{{(k)}}\xi _{l}^{{(k)}}$ – продольная скорость деформации волокна k-го семейства (режим $l = 1$ соответствует растяжению арматуры, режим $l = 2$ – сжатию), а $\xi _{{k,n}}^{{(0)}}$ вычисляется по (4.5) и (4.3). Пластическое течение арматуры возможно только при достижении предельных значений ${{\sigma }_{k}} = \pm \sigma _{ \pm }^{{(k)}}$, тогда на основании (4.6) для напряжения в волокнах k-го семейства имеем:

В соотношениях (6.1) коэффициенты $\omega _{1}^{{(0)}}$ и $\omega _{2}^{{(0)}}$ в разных вариантах МОНСВ задаются по-разному. В “мягком” варианте МОНСВ, принято [12]:

При использовании “жесткого” варианта МОНСВ

В работе [30] использовались зависимости вида

Для определения в глобальной системе координат $O{{\bar {x}}_{1}}{{\bar {x}}_{2}}{{\bar {x}}_{3}}$ напряжения, соответствующие соотношениям (6.1), следует применить равенства (2.31).

В рамках МОНСВ структурные соотношения (6.1) при учете равенств (2.31) и (6.2)–(6.5) имеют простой и удобный вид. Определим, является ли значимой ошибка расчета поверхности текучести, которую вносят игнорирование поперечных напряжений в арматуре и выбор параметров $\omega _{1}^{{(0)}}$ и $\omega _{2}^{{(0)}}$ в виде (6.3)–(6.5).

На рис. 5 и 6 для сравнения изображены пунктирные кривые текучести, определенные для соответствующих КМ по формулам (6.1)–(6.5). Пунктирные кривые, номера которых помечены штрихами, рассчитаны при тех же условиях, что и сплошные кривые с теми же номерами, но без штрихов (см. раздел 2). Кривая 1' на рис. 5а соответствует “мягкому” варианту МОНСВ (см. (6.1)–(6.3)); кривая 1'' – “жесткому” варианту МОНСВ (см. (6.1), (6.2) при учете (6.4)). Пунктирные кривые на рис. 5 и 6, номера которых помечены тремя штрихами, получены по формулам (6.1), (6.2) при учете зависимостей вида (6.5).

Сопоставление кривых 1 и 1' на рис. 5а показывает, что “мягкий” вариант МОНСВ при высокопрочном связующем (Ti) приводит к значительному занижению расчетных значений пределов текучести КМ в направлениях, ортогональных (и близких им) к направлениям армирования (например, в направлении напряжения ${{\bar {\sigma }}_{2}}$ на рис. 5а). Сравнение кривых 1 и 1'' на рис. 5а демонстрирует, что в случае высокопрочного связующего расчет по “жесткому” варианту МОНСВ, наоборот, приводит к существенному завышению пределов текучести КМ в направлениях, близких к направлениям армирования (например, в направлении напряжения ${{\bar {\sigma }}_{1}}$ на рис. 5а).

Из сравнения кривых 1, 1''' и 2, 2''' на рис. 5а следует, что вариант МОНСВ [30], лучше всего согласуется со структурной моделью, разработанной в данном исследовании (см. разд. 1 и 2). Так, в самом неблагоприятном случае (при использовании высокопрочного связующего) значения $\max \left| {{{{\bar {\sigma }}}_{1}}} \right|$ и $\max \left| {{{{\bar {\sigma }}}_{2}}} \right|$, определенные по кривым 1, 1''' и 2, 2''' соответственно, отличаются не более чем на 2.4%. Для кривых 1 и 1''' на рис. 5б разница значений $\max \left| {{{{\bar {\sigma }}}_{1}}} \right|$ и $\max \left| {{{{\bar {\sigma }}}_{2}}} \right|$ практически равна нулю.

При малых отношениях пределов текучести связующего и волокон (что часто бывает на практике [22, 24, 37, 44]) различие между расчетными кривыми текучести, определенных на базе МОНСВ и модели, разработанной в данном исследовании, становится малым. Так, кривая 3''' на рис. 5а (АДМ–У8А-композиция) почти совпадает с кривой 3; кривые 1'''–6''' на рис. 6 (стеклопластик) также близки к кривым 1–6 соответственно (максимальное расхождение у кривых 2 и 2'''). Кривые текучести, рассчитанные по формулам (6.1), (6.2) и (6.5) для ортогонально армированных Al–У8А-композиций, близки к кривым 2, 2' и 2'' на рис. 5б, поэтому они не изображены.

Анализ поведения пунктирных кривых на рис. 5 и 6 показывает, что предложенный в [30] вариант МОНСВ (см. (6.1), (6.2) и (6.5)) обоснованно можно применять вместо структурных соотношений данного исследования в инженерных расчетах композитных тонкостенных элементов конструкций.

Заключение. Разработана структурная модель, позволяющая рассчитывать поверхности и кривые текучести для жесткопластических гибридных композитных сред, перекрестно армированных в произвольных направлениях, параллельных некоторой плоскости. Материалы компонентов композиции могут по разному сопротивляться растяжению и сжатию. Пределы текучести материалов компонентов при растяжении могут быть как больше, так и меньше пределов текучести при сжатии. Учтено сложное напряженное состояние в арматуре. Принято, что в плоскости армирования реализуется ПНС в композиции. Показано, что, как следствие этого, в рамках принятых предположений ПНС возникает и во всех компонентах. Пластическое течение в компонентах композиции описывается кусочно-линейными критериями текучести (типа Йогансена, Треска, Ху и др.). Определены усредненные напряжения и скорости деформаций композиции. Перед процедурой усреднения напряжения в компонентах представлены в параметрическом виде. Сформулированы условия однозначного определения границ режима текучести в арматуре, который соответствует напряженному состоянию в связующем материале. Продемонстрировано, что для расчетных кривых (поверхностей) текучести КМ выполняется ассоциированный закон пластического течения. Это позволяет переносить все известные теоремы о предельном состоянии жесткопластических тел и разработанные методы решения соответствующих краевых задач на элементы конструкций, изготовленные из рассматриваемых композиций. Получено, что изменение характера армирования (направлений и плотностей армирования) существенно влияет на размер и форму кривых (поверхностей) текучести композиции. Сравнение кривых текучести КМ, рассчитанных на базе разработанной структурной модели и достаточно простой МОНСВ, показало, что использование варианта МОНСВ, предложенного в [30], позволяет с достаточной для инженерных приложений точностью определять кривые (поверхности) текучести композиции вместо относительно сложных формул, полученных в данной работе. Для композиций, содержащих низкопрочные связующие матрицы, что часто встречается на практике, кривые текучести композиции, рассчитанные по этим теориям, почти не различаются.

Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук на 2017-2020 годы (проект № 23.4.1 – Механика деформирования и разрушения материалов, сред, при механических нагрузках, воздействии физических полей и химически активных сред).