Прикладная математика и механика, 2021, T. 85, № 1, стр. 106-120
О последовательной сменяемости в механизмах производства больших необратимых деформаций
А. С. Бегун 1, *, А. А. Буренин 2, **, Л. В. Ковтанюк 1, ***, А. Н. Прокудин 2, ****
1 Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия
2 Институт машиноведения и металлургии Хабаровского ФИЦ ДВО РАН
Комсомольск-на-Амуре, Россия
* E-mail: ustinova@iacp.dvo.ru
** E-mail: burenin@iacp.dvo.ru
*** E-mail: lk@iacp.dvo.ru
**** E-mail: sunbeam_85@mail.ru
Поступила в редакцию 25.05.2020
После доработки 23.09.2020
Принята к публикации 25.09.2020
Аннотация
Следуя формализму термодинамики обратимая и необратимая составляющие полных деформаций принимаются в качестве термодинамических параметров состояния процесса деформирования. Определения их даются формулированием соответствующих дифференциальных уравнений их изменения (переноса), потоковые слагаемые которых задают взаимовлияние этих термодинамических параметров в процессе деформирования. Источник в уравнении переноса определяется двумя механизмами производства необратимых деформаций: вязким (ползучесть) и пластическим (пластическое течение). Упругопластические границы оказываются местом, где механизм производства необратимых деформаций меняется с вязкого на пластический и при разгрузке наоборот. Необратимые деформации не разделяются на деформации ползучести и деформации пластического течения, только достигнутые первые оказываются начальными значениями для последующего роста вторых в новых условиях пластического течения. При разгрузке смена происходит в обратном порядке. В качестве примера рассмотрена задача о росте необратимых деформаций в условиях вискозиметрического деформирования цилиндрического слоя.
Теория пластического течения материалов [1–4] уже в своем основании, в отличие от деформационной теории пластичности [5, 6], требует разделения полных деформаций на обратимую (упругую) и необратимую (пластическую) составляющие. В опытах полные деформации можно измерить, а их составляющие неизмеримы, потому вводятся гипотетически. Когда деформации принимаются малыми, то аддитивное разделение их на составляющие не встречает возражений. При больших деформациях положение усложняется принципиально. Подобным разделением требуется обеспечить геометрическую непротиворечивость строящейся кинематики, что оказалось непростой задачей. После многочисленных предложений, оказавшихся ошибочными именно по такой причине, был предложен подход [7], обеспечивающий геометрическую безупречность в построении кинематики больших упругопластических деформаций. В основе такого подхода лежит предложение обеспечить взаимно однозначное соответствие каждому деформированному состоянию упругопластического тела другое его состояние, где обратимые деформации отсутствуют совершенно. Достигается последнее состояние снятием усилий с каждого элементарного объема поделенного таким способом тела при дальнейшем предельном переходе при стремлении к бесконечности числа разбиений, когда элементарные объемы стремятся к нулю. Очевидно, что такое предельно разгруженное состояние недостижимо и остается гипотетическим. Более того, возникают сомнения в единственности такого разгруженного состояния. Известно, что разгрузочное состояние в упругопластическом теле может зависеть от пути процесса разгрузки в пространстве напряжений. На таком пути могут возникать повторные (обратные) пластические течения [8] с изменением в уровне и распределении накопленных необратимых деформаций. Следовательно, и предельное разгрузочное состояние может быть различным. Несмотря на обозначенные проблемы, данный подход широко применяется в научной литературе [9–11]. Из большого числа публикаций отметим лишь некоторые [12–17].
В.П. Мясников предложил использовать при создании теории больших деформаций формализм термодинамики [18]. Если уже приходится объявлять в качестве термодинамических параметров состояния упругопластического тела не полные деформации, а их составляющие, то для последних следует записать дифференциальные уравнения их изменения (переноса). Тогда потоковые слагаемые в этих уравнениях обязаны будут указать взаимовлияние обратимых и необратимых деформаций в их изменениях, а источники задать (посредством формулирования для них определяющих законов) причины, заставляющие изменяться такие введенные термодинамические параметры. Возможной конкретизации дифференциальных уравнений переноса для обратимых и необратимых деформаций посвящена публикация [19], подробно воспроизведенная позже в [20]. Данные дифференциальные уравнения следует рассматривать в качестве определения как необратимых, так и обратимых деформаций. Более того с их помощью определяются и скорости изменения таких составляющих полных деформаций, что в иных условиях оказывается самостоятельной задачей как, например, [9], возникающая проблема “выбора” объективной производной именно с целью задания скоростей необратимых деформаций. Введение в математическую модель дифференциальных уравнений переноса обратимых и необратимых деформаций позволило получить решения, включая точные, целого ряда краевых задач теории больших упругопластических и упруговязкопластических деформаций не только при активном нагружении, но и при последующей разгрузке с расчетом остаточных напряжений. Ряд таких решений составили содержание монографии [20]. Из последних публикаций отметим [21–25].
Любой материал необходимо изначально наделен и упругими, и вязкими, и пластическими свойствами. Только с целью упрощения математического аппарата при моделировании конкретных технологических операций некоторыми из таких свойств пренебрегают в зависимости от того, насколько такие свойства проявляются в процессе деформирования. В общем случае упругие и вязкие свойства проявляются непосредственно с началом процесса, а пластические заметны при достижении напряжениями некоторого предельного своего значения. В теории пластического течения полагается, что течение начинается при выходе напряженных состояний на поверхность нагружения (поверхность текучести) в пространстве напряжений. Производство необратимых деформаций задается как вязкими, так и пластическими свойствами деформируемого материала. Следовательно, такие деформации начинают расти непосредственно с началом процесса деформирования за счет проявления вязких свойств материала. Часто данный рост необратимых деформаций называют ползучестью [26]. Как правило, это медленный процесс накопления необратимых деформаций. Но как только напряжения достигают поверхности нагружения начинается более быстрый процесс роста необратимых деформаций, называемый процессом пластического течения. Таким образом упругопластические границы оказываются местом, где меняется механизм производства необратимых деформаций с медленного механизма ползучести на более быстрый механизм пластического течения и наоборот при разгрузке. Деформации ползучести и деформации пластического течения не различаются. Это один и тот же введенный термодинамический параметр, названный необратимыми деформациями. Различие их задается только механизмом их производства при деформировании: либо он задается вязкостью – ползучесть, либо пластичностью – течение.
На упругопластических границах, где механизм производства необратимых деформаций за счет внешнего воздействия на деформируемое тело меняется, необходимо обеспечить непрерывность в росте необратимых деформаций. Это может потребовать согласованности законов ползучести с законами пластического течения, что может оказаться непростой задачей. Примеры решения такой задачи приведены в [22–25], при этом в [22–24] в качестве пластического потенциала выбрано условие пластического течения Треска–Сен-Венана, а в [25] условие Мизеса. В качестве закона ползучести принимается степенной закон Нортона [26]. Здесь укажем еще один пример решения задачи о последовательном накоплении необратимых деформаций со сменой в механизме их производства.
1. Определяющие соотношения. В качестве термодинамических параметров, задающих состояние деформируемого твердого тела, принимаем обратимые ${\mathbf{e}}$ и необратимые ${\mathbf{p}}$ деформации. В соответствии с [19, 20] уравнения их изменения постулируем в форме:
(1.1)
$\begin{gathered} \frac{{D{\mathbf{e}}}}{{Dt}} = {\mathbf{\varepsilon }} - {\mathbf{\gamma }} - \frac{1}{2}\left( {\left( {{\mathbf{\varepsilon }} - {\mathbf{\gamma }} + {\mathbf{z}}} \right) \cdot {\mathbf{e}} + {\mathbf{e}} \cdot \left( {{\mathbf{\gamma }} - {\mathbf{\varepsilon }} - {\mathbf{z}}} \right)} \right) \\ \frac{{D{\mathbf{p}}}}{{Dt}} = {\mathbf{\gamma }} - {\mathbf{p}} \cdot {\mathbf{\gamma }} - {\mathbf{\gamma }} \cdot {\mathbf{p}} \\ \end{gathered} $В уравнениях (1.1) принята система пространственных координат Эйлера и введены обозначения:
(1.2)
$\begin{gathered} {\mathbf{z}} = {{A}^{{ - 1}}}\left( {{{B}^{2}}\left( {{\mathbf{\varepsilon }} \cdot {\mathbf{e}} - {\mathbf{e}} \cdot {\mathbf{\varepsilon }}} \right) + B\left( {{\mathbf{\varepsilon }} \cdot {{{\mathbf{e}}}^{2}} - {{{\mathbf{e}}}^{2}} \cdot {\mathbf{\varepsilon }}} \right) + {\mathbf{e}} \cdot {\mathbf{\varepsilon }} \cdot {{{\mathbf{e}}}^{2}} - {{{\mathbf{e}}}^{2}} \cdot {\mathbf{\varepsilon }} \cdot {\mathbf{e}}} \right) \\ {\mathbf{v}} = \frac{{\partial {\mathbf{u}}}}{{\partial t}} + {\mathbf{v}} \cdot \nabla {\mathbf{u}};\quad {\mathbf{\varepsilon }} = \frac{1}{2}\left( {\nabla {\mathbf{v}} + {{\nabla }^{{\mathbf{T}}}}{\mathbf{v}}} \right) \\ \end{gathered} $Здесь ${\mathbf{u}},{\mathbf{v}}$ – векторы перемещений и скоростей перемещений, ${\mathbf{\tau }}$ – произвольный тензор второго ранга. Последний служит конкретизации объективной производной по времени (первое равенство в системе (1.2)). Только в этом случае уравнения переноса (1.1) оказываются геометрически непротиворечивыми. Заметим, что при равенстве нулю существенно нелинейной части ${\mathbf{z}} = {\mathbf{z}}\left( {{\mathbf{e}},\,{\mathbf{\varepsilon }}} \right)$ тензора поворота, введенная объективная производная совпадает с производной Яумана. С другой стороны, наличие ${\mathbf{z}} \ne 0$ связывает тензоры ${\mathbf{e}}$ и ${\mathbf{p}}$ в их изменениях, задавая взаимовлияние обратимых и необратимых деформаций в процессе деформирования. Тензор ${\mathbf{\gamma }}$ в уравнениях (1.1), являясь источником в уравнении изменения необратимых деформаций, следует называть скоростью производства необратимых деформаций. При ${\mathbf{\gamma }} = 0$ компоненты тензора ${\mathbf{p}}$ изменяются также, как и при жестком движении тела, объективная производная оказывается равной нулю. Именно такое положение позволяет считать тензор ${\mathbf{p}}$ в качестве тензора необратимых деформаций, он может быть неизменен при разгрузке и при деформировании, предваряющем пластическое течение. Как раз такая цель преследовалась ранее [19, 20] при записи дифференциальных уравнений изменений (переноса) для тензоров обратимых ${\mathbf{e}}$ и необратимых ${\mathbf{p}}$ деформаций (1.1) при конкретизации термодинамического подхода к построению теории больших упругопластических деформаций, предлагаемого [18].
Если принять (1.1) в качестве определений для обратимых и необратимых деформаций, то для тензора полных деформаций Альманси следует:
(1.3)
${\mathbf{d}} = {\mathbf{e}} + {\mathbf{p}} - \frac{1}{2}{{{\mathbf{e}}}^{2}} - {\mathbf{e}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{e}} + {\mathbf{e}} \cdot {\mathbf{p}} \cdot {\mathbf{e}}$Согласно (1.3) тензор ${\mathbf{e}}$ оказывается лишь главной линейной частью полного тензора обратимых деформаций ${\mathbf{s}} = {\mathbf{e}} - \frac{1}{2}{{{\mathbf{e}}}^{2}}$. Но именно с помощью данного тензора ${\mathbf{e}}$ удалось записать геометрически безупречное дифференциальное определение тензора обратимых деформаций (1.1).
Введение тензора ${\mathbf{e}}$ служит еще одному обстоятельству. Если принять, как это принято в большинстве публикаций, посвященных созданию численных методов расчетов больших упругопластических деформаций [11, 12], что термодинамический потенциал, являющийся свободной энергией, определяется только консервативной составляющей процесса деформирования, то есть
где $e,s$ – плотности распределения внутренней энергии и энтропии, то следствием закона сохранения энергии можно получить [20] обобщение формулы Мурнагана для среды, где присутствуют и обратимые и необратимые деформации в виде(1.5)
${\mathbf{\sigma }} = \rho \frac{{\partial \psi }}{{\partial \,{\mathbf{e}}}} \cdot \left( {{\mathbf{I}} - {\mathbf{e}}} \right)$При равенстве нулю необратимых деформаций ${\mathbf{p}} \equiv 0$ из соотношений (1.3) и (1.5) следует классическая формула Мурнагана, широко используемая в нелинейной теории упругости
(1.6)
$\sigma = \rho \frac{{\partial \psi }}{{\partial \,{\mathbf{d}}}} \cdot \left( {{\mathbf{I}} - 2{\mathbf{d}}} \right)$Предположение (1.4) о независимости свободной энергии от необратимых деформаций является только гипотезой, но оно существенно упрощает дальнейшие вычисления. Более того, оно распространяет на теорию больших деформаций известное положение классической модели Прандтля–Рейса о том, что упругие деформации задают напряжения в деформируемом материале. Данной гипотезой процесс деформирования разделяется на консервативный, задаваемый термодинамическим потенциалом (в нашем случае свободной энергией (1.4)) и диссипативный, задаваемый определяющими законами, которые должны определить связь источника ${\mathbf{\gamma }}$ в уравнении переноса необратимых деформаций с напряжениями. Изменяющиеся в процессе деформирования напряжения, как следствие внешнего воздействия на материал, являются причиной изменения необратимых деформаций.
Следствием закона сохранения энергии вместе с формулой Мурнагана (1.5) является [20, 23] также уравнение баланса энтропии $s$
(1.7)
$\begin{gathered} \frac{{\partial \left( {\rho s} \right)}}{{\partial t}} = - \operatorname{div} {\kern 1pt} {\mathbf{j}} - {{T}^{{ - 2}}}{\mathbf{q}} \cdot \operatorname{grad} T + {{T}^{{ - 1}}}{\mathbf{\sigma }} \cdot \cdot \;{\mathbf{\gamma }} \\ {\mathbf{j}} = \rho s{\mathbf{v}} + {{T}^{{ - 1}}}{\mathbf{q}} \\ \end{gathered} $Здесь ${\mathbf{q}},{\mathbf{j}}$ – потоки тепла и энтропии. Последние слагаемые правой части задают производство энтропии за счет неравновесного процесса теплопроводности и необратимого деформирования соответственно. В рассматриваемом случае изотермического деформирования важным остается последнее слагаемое в (1.7). Он требует задания определяющего закона, который связывал бы термодинамический поток ${\mathbf{\gamma }}$ с термодинамической силой ${\mathbf{\sigma }}$. Для замыкания математической модели деформирования, таким образом, наряду с уравнением движения (равновесия) следует записать определяющие законы, то есть конкретизировать зависимости $\psi = \psi \left( {\mathbf{e}} \right)$ и ${\mathbf{\gamma }} = {\mathbf{\gamma }}\left( {\mathbf{\sigma }} \right)$. Задание функциональной зависимости $\psi = \psi \left( {\mathbf{e}} \right)$ определяет консервативный (упругий) механизм деформирования. В зависимости от требований ставящейся задачи он может быть любым. В частности, можно принять квадратичную зависимость от двух первый инвариантов ${\mathbf{e}}$ со следованием после дифференцирования в (1.5) или в (1.6) линейных соотношений закона Гука.
При задании определяющего закона ${\mathbf{\gamma }} = {\mathbf{\gamma }}\left( {\mathbf{\sigma }} \right)$ следует учитывать, что производство энтропии в (1.7) задается как за счет вязких свойств деформирования (ползучесть), так и пластических (пластическое течение). Деформации ползучести и пластического течения неразделимы, являясь одновременно необратимыми деформациями. Источник ${\mathbf{\gamma }}$ в уравнении изменения их, являясь скоростью изменения необратимых деформаций, может быть, разным в зависимости от того, происходит ли процесс ползучести или пластического течения. Главное отличие в росте необратимых деформаций за счет вязких свойств деформируемого материала от их роста в условиях пластического течения заключается в том, что процесс ползучести начинается с момента начала процесса нагружения, а пластическое течение только при выходе напряженных состояний на поверхность нагружения, когда выполняются условия пластического течения. При разгрузке наоборот: пластическое течение прекращается, но ползучесть материала продолжается. Следовательно, упругопластические границы оказываются местом, где меняется механизм производства необратимых деформаций с вязкого (ползучесть) на пластический (течение) при активном процессе деформирования и наоборот при разгрузке. Можно положить, что в условиях пластического течения вязкие свойства материала проявляются в форме причины, тормозящей быстрый процесс пластического течения.
Определяющие законы в области пластического течения, в области, предваряющей течение, и в области разгрузки должны быть разными. Важно, однако, чтобы с помощью этих законов возможно было бы обеспечить непрерывность необратимых деформаций на упругопластических границах. В качестве одного из простейших примеров укажем следующий подход. Положим, что первоначально необратимые деформации в теле растут за счет ползучести материала. В качестве закона ползучести примем степенной закон Нортона
(1.8)
${\mathbf{\gamma }} = {{{\mathbf{\varepsilon }}}^{{v}}} = \frac{{\partial V(\Sigma )}}{{\partial {\mathbf{\sigma }}}},\quad V(\Sigma ) = B{{\Sigma }^{n}}$В соотношениях (1.8) ${{{\mathbf{\varepsilon }}}^{{v}}}$ – скорость деформаций ползучести, $B\,,n$ – постоянные материала. В качестве аргумента $\Sigma $ потенциала ползучести при использовании далее классических условий пластического течения удобно принять
(1.10)
$\Sigma = \max \left| {{{\sigma }_{i}} - \sigma } \right|;\quad \sigma = \frac{1}{3}\operatorname{tr} \,{\mathbf{\sigma }}$(1.11)
$\Sigma = \sqrt {\frac{3}{2}} {{\left( {{{{\left( {{{\sigma }_{1}} - \sigma } \right)}}^{2}} + {{{\left( {{{\sigma }_{2}} - \sigma } \right)}}^{2}} + {{{\left( {{{\sigma }_{3}} - \sigma } \right)}}^{2}}} \right)}^{{1/2}}}$В предыдущих соотношениях ${{\sigma }_{i}}$ – главные значения тензора напряжений. Очевидно, что $\Sigma $ принимается в виде (1.9), (1.10), (1.11) при использовании в качестве условия пластического течения условия Треска, условия максимальных приведенных напряжений и условия Мизеса соответственно.
Если принять условия принципа максимума Мизеса [1–4], то пластическое течение отвечает ассоциированному с поверхностью нагружения $f\left( {{\mathbf{\sigma }},{\mathbf{\xi }}} \right)$ = 0 закону течения
(1.12)
${\mathbf{\gamma }} = {\mathbf{\xi }} = \lambda \frac{{\partial f}}{{\partial {\mathbf{\sigma }}}},\quad f\left( {{\mathbf{\sigma }},{\mathbf{\xi }}} \right) = 0,\quad \lambda > 0,\quad {\mathbf{\xi }} = {{{\mathbf{\varepsilon }}}^{p}} - {\mathbf{\varepsilon }}_{0}^{v}$Здесь ${{{\mathbf{\varepsilon }}}^{p}}$ – скорость пластических деформаций; ${\mathbf{\varepsilon }}_{0}^{v}$ – скорость деформаций ползучести в момент прихода в некоторую точку материала упругопластической границы. Данная скорость роста необратимых деформаций оказывается начальным значением для их последующего роста, но уже в условиях пластического течения. Далее, только с целью определенности, в качестве поверхности нагружения $f\left( {{\mathbf{\sigma }},\,{\mathbf{\xi }}} \right) = 0$ будем использовать боковую поверхность наклонной призмы Треска в пространстве главных напряжений с учетом вязкого сопротивления пластическому течению
(1.13)
$\max \left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| = 2k + 2\eta \max \left| {{{\xi }_{k}}} \right|,$Зависимость $\psi = \psi \left( {\mathbf{e}} \right)$, для конкретизации соотношений ставящейся в рассматриваемой конкретной краевой задачи, принимаем в виде
(1.14)
$\begin{gathered} \rho \psi \left( {\mathbf{e}} \right) = W\left( {{{J}_{1}},{{J}_{2}}} \right) = - 2\mu {{J}_{1}} - \mu {{J}_{2}} + bJ_{1}^{2} + \left( {b - \mu } \right){{J}_{1}}{{J}_{2}} - \chi J_{1}^{3} \\ {{J}_{1}} = {\mathbf{I}} \cdot \cdot \;{\mathbf{s}},\quad {{J}_{2}} = {\mathbf{I}} \cdot \cdot \;{{{\mathbf{s}}}^{2}} \\ \end{gathered} $Материал таким способом принимается несжимаемым $\left( {\rho = \operatorname{const} } \right)$. $\mu $ – модуль сдвига, $b,\chi $ – упругие модули более высокого порядка. С учетом принимаемого условия несжимаемости материала соотношение (1.5) следует переписать в виде
(1.15)
${\mathbf{\sigma }} = - p{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{e}}}} \cdot \left( {{\mathbf{I}} - {\mathbf{e}}} \right)$Здесь $p$ – неизвестная добавка в гидростатическое давление. Заметим еще раз, что принятие конкретных зависимостей вида (1.8)–(1.14) никак не ограничивает в принятии любых иных законов упругости, ползучести и пластичности.
2. Постановка задачи. Считаем, что материал, деформационные и прочностные свойства которого подчинены зависимостям предыдущего пункта, заполняет слой между жесткими цилиндрическими поверхностями. В системе цилиндрических координат $r,\;\theta ,\;z$ его размеры ${{r}_{0}} \leqslant r \leqslant R$ позволяют записать граничные условия
(2.1)
$\begin{gathered} \omega \left( {R,t} \right) = {{\omega }_{R}}\left( t \right),\quad \theta \left( {R,t} \right) = {{\theta }_{R}}\left( t \right) = \int\limits_0^t {{{\omega }_{R}}\left( \xi \right)d\xi } \\ \omega \left( {{{r}_{0}},t} \right) = 0,\quad p\left( {r,0} \right) = {{\sigma }_{0}} \\ \end{gathered} $Согласно соотношениям (2.1) на граничных поверхностях слоя $r = {{r}_{0}}$ и $r = R$ выполняется условие жесткого сцепления (прилипания); ${{\omega }_{R}} = {{\omega }_{R}}\left( t \right)$ – задаваемая функция угловой скорости вращения поверхности $r = R$; до момента $t = 0$ времени начала процесса деформирования материал слоя покоится: ${{\sigma }_{0}} = \operatorname{const} $ – задаваемая постоянная. Принимаемая геометрия задачи и условие несжимаемости материала слоя существенно упрощают кинематические зависимости
(2.2)
${{\omega }_{{r\varphi }}} = - {{\varepsilon }_{{r\varphi }}} - \omega ,\quad {{r}_{{\varphi r}}} = \omega + \frac{{2{{\varepsilon }_{{r\varphi }}}\left( {{{e}_{{\varphi \varphi }}} - 1} \right)}}{{{{e}_{{rr}}} + {{e}_{{\varphi \varphi }}} - 2}}$Распределения угловой скорости $\omega = \omega \left( {r,t} \right)$ и угла поворота $\theta = \theta \left( {r,t} \right)$ по слою в каждый момент времени оказываются основными искомыми неизвестными задачи. Полагаем, что вращение поверхности $r = R$ является ускоренным ${{\omega }_{R}} = {{\alpha }^{2}}t$ до некоторого момента времени $t = {{t}_{1}}$, равномерным в промежутке времени ${{t}_{1}} \leqslant t \leqslant {{t}_{2}}$, замедленным ${{\omega }_{R}} = {{\alpha }^{2}}{{t}_{2}} - {{\beta }^{2}}\left( {t - {{t}_{2}}} \right)$ до полной остановки при $t = {{t}_{3}}$.
После интегрирования второго из уравнений равновесия
(2.3)
${{\sigma }_{{rr,r}}} = {{r}^{{ - 1}}}\left( {{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{rr}}}} \right),\quad {{\sigma }_{{r\varphi ,r}}} = - 2{{r}^{{ - 1}}}{{\sigma }_{{r\varphi }}}$(2.4)
${{\sigma }_{{r\varphi }}} = \frac{{c\left( t \right)}}{{{{r}^{2}}}},\quad {{e}_{{r\varphi }}} = \frac{{c\left( t \right)}}{{2\mu {{r}^{2}}}}$Для компонент тензора напряжений, исходя из (1.14) и (1.15), запишем
(2.5)
${{\sigma }_{{rr}}} = - p + 2\left( {b + \mu } \right){{e}_{{rr}}} + 2b{{e}_{{\varphi \varphi }}} + \mu e_{{r\varphi }}^{2}$При записи соотношений (2.5) слагаемые порядка выше второго по ${{e}_{{r\varphi }}}$ опущены. Функция времени $c\left( t \right)$ определяется при выполнении граничных условий (2.1).
Непосредственно с началом деформирования в слое накапливаются необратимые деформации в форме деформаций ползучести. В рассматриваемом случае, следуя (1.8), (1.9), (2.2), (2.4), (2.5), получаем:
(2.6)
$\begin{gathered} \varepsilon _{{r\varphi }}^{v} = Bn{{2}^{{n - 1}}}\frac{{{{c}^{{n - 1}}}\left( t \right)}}{{{{r}^{{2n - 2}}}}},\quad \varepsilon _{{rr}}^{v} = - \varepsilon _{{\varphi \varphi }}^{v} = \frac{{{{e}_{{rr}}} - {{e}_{{\varphi \varphi }}}}}{{{{e}_{{r\varphi }}}}}\frac{{\varepsilon _{{r\varphi }}^{v}}}{2} \\ {{p}_{{r\varphi }}}\left( {r,t} \right) = Bn{{2}^{{n - 1}}}\frac{{{{c}_{1}}\left( t \right)}}{{{{r}^{{2n - 2}}}}},\quad {{c}_{1}}\left( t \right) = \int\limits_0^t {{{c}^{{n - 1}}}\left( \xi \right)d\xi } \\ \end{gathered} $Из зависимостей (2.2) с учетом соотношений (2.4) и (2.6) следует дифференциальное уравнение для $\theta \left( {r,t} \right)$. Разрешая последнее для рассматриваемого момента времени, получим распределение для угла поворота в этот момент времени
(2.7)
$\theta \left( {r,t} \right) = {{\theta }_{R}}\left( t \right) - \frac{{c\left( t \right)}}{{2\mu }}\left( {\frac{1}{{{{r}^{2}}}} - \frac{1}{{{{R}^{2}}}}} \right) - \frac{{Bn{{2}^{{n - 1}}}}}{{n - 1}}{{c}_{1}}\left( t \right)\left( {\frac{1}{{{{r}^{{2n - 2}}}}} - \frac{1}{{{{R}^{{2n - 2}}}}}} \right)$Выполняя граничное условие (2.1) на стенке $r = {{r}_{0}}$, получаем дифференциальное уравнение для $c = c\left( t \right)$
(2.8)
$\frac{{dc}}{{dt}} = \dot {c}\left( t \right) = \frac{{2\mu {{\omega }_{R}}\left( t \right)}}{{r_{0}^{{ - 2}} - {{R}^{{ - 2}}}}} - \frac{{\mu Bn{{2}^{n}}}}{{n - 1}}{{c}^{{n - 1}}}\left( t \right)\frac{{r_{0}^{{2 - 2n}} - {{R}^{{2 - 2n}}}}}{{r_{0}^{{ - 2}} - {{R}^{{ - 2}}}}}$Уравнение (2.8) следует проинтегрировать при условии $с\left( 0 \right) = 0$. С помощью (2.6) из (2.2) исключаются неизвестные до этого компоненты тензора источника необратимых деформаций ${{\gamma }_{{r\varphi }}} = \varepsilon _{{r\varphi }}^{v}$ и ${{\gamma }_{{\varphi \varphi }}} = \varepsilon _{{\varphi \varphi }}^{v}$. Полученная система уравнений замкнута и позволяет рассчитывать изменение напряженных и деформированных состояний, включая рост необратимых деформаций, до той поры пока не выполняется условие пластического течения.
Расчеты показывают, что впервые при условие пластического течения (1.13) выполнится на границе $r = {{r}_{0}}$ слоя в форме ${{\sigma }_{{r\varphi }}} = k$. С этого момента времени от граничной поверхности $r = {{r}_{0}}$, отделяясь, продвигается по слою упругопластическая граница $r = h\left( t \right)$, формируя область пластического течения ${{r}_{0}} \leqslant r \leqslant h\left( t \right)$. В области $h\left( t \right) \leqslant r \leqslant R$ необратимые деформации продолжают свой рост в форме деформаций ползучести. Справедливыми остаются в этой области зависимости (2.4), но в них $c\left( t \right)$ следует заменить на новую неизвестную (требующую своего определения) функцию времени ${{c}_{2}}\left( t \right)$. Аналогично в (2.6) ${{c}_{1}}\left( t \right)$ меняется на ${{c}_{3}}\left( t \right)$ = ${{c}_{1}}\left( {{{t}_{0}}} \right)$ + $\int_{{{t}_{0}}}^t {c_{2}^{{n - 1}}\left( \xi \right)d\xi } $.
В области пластического течения ${{r}_{0}} \leqslant r \leqslant h\left( t \right)$ в соответствии с (1.12) и (1.13) запишем
(2.9)
$\varepsilon _{{r\varphi }}^{p}\left( {r,t} \right) = \frac{1}{\eta }\left[ {\frac{{{{c}_{2}}\left( t \right)}}{{{{r}^{2}}}} - k} \right] + Bn{{2}^{{n - 1}}}{{k}^{{n - 1}}}$Требование непрерывности на упругопластической границе скоростей изменения необратимых деформаций сводится к условию
Из зависимостей (2.2) с учетом соотношений (2.9) следует дифференциальное уравнение для $w\left( {r,t} \right)$, интегрирование которого при условии $w\left( {{{r}_{0}},t} \right) = 0$ приводит к зависимости
(2.11)
$\omega \left( {r,t} \right) = \frac{{{{{\dot {c}}}_{2}}\left( t \right)}}{{2\mu }}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{r}^{2}}}}} \right) + \frac{2}{\eta }\left[ {\frac{{{{c}_{2}}\left( t \right)}}{2}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{r}^{2}}}}} \right) - k\ln \frac{r}{{{{r}_{0}}}}} \right] + Bn{{2}^{n}}{{k}^{{n - 1}}}\ln \frac{r}{{{{r}_{0}}}}$Условие равенства угловых скоростей (2.11) и (2.7) на продвигающейся упругопластической границе $r = h\left( t \right)$ приводит к дифференциальному уравнению для функции $h\left( t \right)$
(2.12)
$\begin{gathered} \dot {h}\left( t \right) = \frac{1}{{h\left( t \right)\left( {r_{0}^{{ - 2}} - {{R}^{{ - 2}}}} \right)}}\left[ {\frac{{\mu {{\omega }_{R}}\left( t \right)}}{k} - \frac{\mu }{\eta }\left( {\frac{{{{h}^{2}}\left( t \right)}}{{r_{0}^{2}}} - 1 - 2\ln \frac{{h\left( t \right)}}{{{{r}_{0}}}}} \right) - } \right. \\ \left. { - \;\frac{{\mu Bn{{2}^{{n - 1}}}{{k}^{{n - 2}}}}}{{n - 1}}\left( {1 - \frac{{{{h}^{{2n - 2}}}\left( t \right)}}{{{{R}^{{2n - 2}}}}}} \right) - \mu Bn{{2}^{n}}{{k}^{{n - 2}}}\ln \frac{{h\left( t \right)}}{{{{r}_{0}}}}} \right], \\ h\left( {{{t}_{0}}} \right) = {{r}_{0}} \\ \end{gathered} $Интегрируя соотношение (2.9), найдем
(2.13)
$\begin{gathered} {{p}_{{r\varphi }}}\left( {r,t} \right) = Bn{{2}^{{n - 1}}}\frac{{{{c}_{3}}\left( {{{t}_{\xi }}\left( r \right)} \right)}}{{{{r}^{{2n - 2}}}}} + \frac{{{{c}_{4}}\left( {r,t} \right)}}{{\eta {{r}^{2}}}} + \left( {Bn{{2}^{{n - 1}}}{{k}^{{n - 1}}} - \frac{k}{\eta }} \right)\left( {t - {{t}_{\xi }}\left( r \right)} \right) \\ {{c}_{4}}\left( {r,t} \right) = \int\limits_{{{t}_{\xi }}\left( r \right)}^t {{{c}_{2}}\left( \xi \right)d\xi } \\ \end{gathered} $Здесь ${{t}_{\xi }}\left( r \right)$ – момент времени, являющийся моментом прихода к точкам материала с координатой $r$ упругопластической границы $r = h\left( t \right)$.
Определив в зависимостях (2.2) компоненту скоростей необратимых деформаций с помощью соотношений (2.6) или (2.9), после некоторых тождественных преобразований запишем
(2.14)
$\begin{gathered} \varepsilon _{{\varphi \varphi }}^{p}\left( {r,t} \right) = - \varepsilon _{{rr}}^{p}\left( {r,t} \right) = \frac{{\varepsilon _{{r\varphi }}^{p}\left( {{{e}_{{\varphi \varphi }}} - {{e}_{{rr}}}} \right)}}{{2{{e}_{{r\varphi }}}}} + \frac{{\bar {\varepsilon }_{{r\varphi }}^{v}}}{2}\left( {\frac{{{{{\bar {e}}}_{{\varphi \varphi }}} - {{{\bar {e}}}_{{rr}}}}}{{{{{\bar {e}}}_{{r\varphi }}}}} - \frac{{{{e}_{{\varphi \varphi }}} - {{e}_{{rr}}}}}{{{{e}_{{r\varphi }}}}}} \right) \\ \frac{{\partial {{p}_{{\varphi \varphi }}}\left( {r,t} \right)}}{{\partial t}} = \left( {\frac{k}{\eta } - \frac{{{{c}_{2}}\left( t \right)}}{{\eta {{r}^{2}}}}} \right)\frac{{{{p}_{{\varphi \varphi }}} - e_{{r\varphi }}^{2}}}{{{{e}_{{r\varphi }}}}} + \left( {\frac{{{{{\dot {c}}}_{2}}\left( t \right)}}{{2\mu {{r}^{2}}}} + \frac{{{{c}_{2}}\left( t \right)}}{{\eta {{r}^{2}}}} - \frac{k}{\eta } + Bn{{2}^{{n - 1}}}{{k}^{{n - 1}}}} \right) \times \\ \times \;\frac{{4{{p}_{{r\varphi }}}\left[ {{{p}_{{\varphi \varphi }}} - \frac{1}{2}e_{{r\varphi }}^{2} - 2{{e}_{{r\varphi }}}{{p}_{{r\varphi }}} + 1} \right]}}{{e_{{r\varphi }}^{2} + 2}} + Bn{{2}^{{n - 1}}}{{k}^{{n - 1}}}\left[ {{{{\bar {e}}}_{{r\varphi }}} + 2{{{\bar {p}}}_{{r\varphi }}} - \frac{{{{{\bar {p}}}_{{\varphi \varphi }}}}}{{{{{\bar {e}}}_{{r\varphi }}}}} - 2{{p}_{{r\varphi }}}} \right] \\ \end{gathered} $Здесь кинематические параметры деформирования являются функциями $r$ и $t$ $({{e}_{{r\varphi }}} = {{e}_{{r\varphi }}}(r,t)$, ${{p}_{{r\varphi }}} = {{p}_{{r\varphi }}}(r,t))$, а в случае, когда же они снабжены чертой сверху – функциями только переменной $r$ $\left( {{{{\bar {e}}}_{{r\varphi }}} = {{{\bar {e}}}_{{r\varphi }}}\left( r \right) = {{{\bar {e}}}_{{r\varphi }}}\left( {r,{{t}_{\xi }}\left( r \right)} \right)} \right)$. Зависимости (2.9)–(2.14) позволяют рассчитать процесс пластического течения в области ${{r}_{0}} \leqslant r \leqslant h\left( t \right)$ и продвижение упругопластической границы $r = h\left( t \right)$. Деформирование в области $h\left( t \right) < r \leqslant R$ подчинено соотношениям (2.2)–(2.8).
Полученные зависимости остаются справедливыми после того как скорость вращения граничной жесткой поверхности $r = R$ становится постоянной ${{\omega }_{R}} = {{\alpha }^{2}}{{t}_{1}}$. Следует только отметить, что развитие области пластического течения замедляется. Заметно уменьшается скорость продвижения $\dot {h}\left( t \right)$ упругопластической границы.
С момента $t = {{t}_{2}}$ вращение замедляется: ${{\omega }_{R}} = {{\alpha }^{2}}{{t}_{2}} - {{\beta }^{2}}\left( {t - {{t}_{2}}} \right)$. Упругопластическая граница $r = m\left( t \right)$ начинает свое движение в обратную сторону. Закон ее продвижения задается тем же дифференциальным уравнением (2.12), где следует заменить $h\left( t \right)$ на $m\left( t \right)$ и принять в качестве начального условия $m\left( {{{t}_{2}}} \right) = {{r}_{m}}$, где ${{r}_{m}}$ – радиус максимального продвижения упругопластической границы. В области $m\left( t \right) \leqslant r \leqslant {{r}_{m}}$, где пластическое течение прекратилось, интегрированием (2.9) находим
(2.15)
$\begin{array}{*{20}{c}} {{{p}_{{r\varphi }}}\left( {r,t} \right) = \frac{{{{c}_{4}}\left( {r,{{t}_{\zeta }}\left( r \right)} \right)}}{{\eta \,{{r}^{2}}}} + \left( {Bn{{2}^{{n - 1}}}{{k}^{{n - 1}}} - \frac{k}{\eta }} \right)\left( {{{t}_{\zeta }}\left( r \right) - {{t}_{\xi }}\left( r \right)} \right) + Bn{{2}^{{n - 1}}}\frac{{{{c}_{5}}\left( {r,t} \right)}}{{{{r}^{{2n - 2}}}}},} \\ {{{c}_{5}}\left( {r,t} \right) = {{c}_{3}}\left( {{{t}_{\xi }}\left( r \right)} \right) + \int\limits_{{{t}_{\zeta }}\left( r \right)}^t {c_{2}^{{n - 1}}\left( \xi \right)d\xi } } \end{array}$В решениях (2.15), как и ранее, ${{t}_{\zeta }}\left( r \right)$ – момент прихода в точку с координатой $r$ упругопластической границы $r = m\left( t \right)$. В момент времени $t = {{t}_{3}}\left( {m\left( {{{t}_{3}}} \right) = {{r}_{0}}} \right)$ область пластического течения исчезает и во всем слое необратимые деформации изменяются в соответствии с законом ползучести.
Напряжения в слое вычисляем в соответствии с (2.3)–(2.5) после того, как компоненты упругих деформаций будут вычислены.
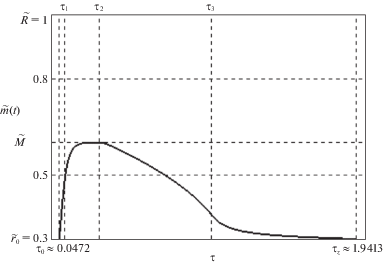
Приведем некоторые результаты расчетов. С этой целью вводились безразмерные переменные: $\tilde {r} = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}$, $\tau = \alpha t$, $\tilde {h}\left( \tau \right) = {{h\left( t \right)} \mathord{\left/ {\vphantom {{h\left( t \right)} R}} \right. \kern-0em} R}$. Постоянные задачи задавались следующими:
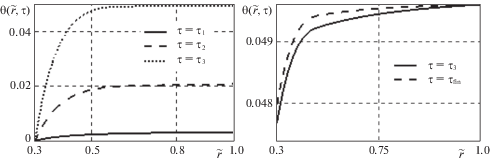
На рис. 1 представлена граница пластической области в своем изменении в течении всего процесса деформирования. На рис. 2 представлена зависимость угла поворота $\theta $ от времени. Величины $\theta \left( {\tilde {r},{{\tau }_{3}}} \right)$ и $\theta \left( {\tilde {r},{{\tau }_{{fin}}}} \right)$ показаны в отдельных графиках поскольку их значения являются достаточно близкими. На рис. 3 и 4 изображено изменение необратимых деформаций со временем на внутренней граничной поверхности $\tilde {r} = {{\tilde {r}}_{0}}$.
Рис. 3.
Необратимые деформации при $\tilde {r} = {{\tilde {r}}_{0}}$ (компоненты ${{p}_{{rr}}}$ и ${{p}_{{\varphi \varphi }}}$).
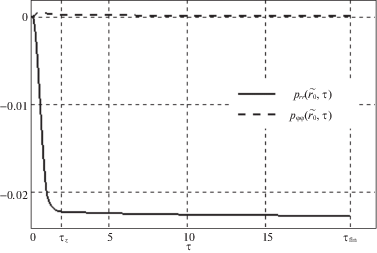
Рис. 4.
Компонента ${{p}_{{r\varphi }}}$ тензора необратимых деформаций при $\tilde {r} = {{\tilde {r}}_{0}}$.
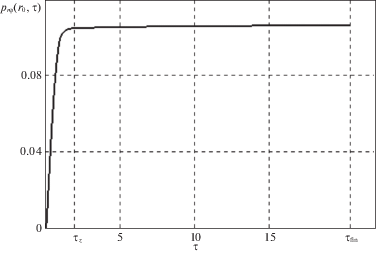
Для сравнения полученных результатов воспользуемся работой [27], в которой аналогичная задача решена с учетом вязких свойств материала только на стадии пластического течения. Установлено, что без учета ползучести материала, пластическое течение начинается раньше, при этом область вязкопластического течения развивается немного дольше. Также учет ползучести материала показывает, что при остановке цилиндра релаксация напряжений занимает на порядок больше времени.
Заключение. Каждый материал изначально наделен и упругими, и вязкими, и пластическими свойствами. Эти свойства по-разному проявляют себя в процессе деформирования. Упругие и вязкие свойства проявляют себя непосредственно с начала процесса, а пластические после достижения напряжениями поверхности текучести в пространстве напряжений. Поскольку и вязкость, и пластичность приводят к производству необратимых деформаций, то необходимо на упругопластических границах учитывать изменения в механизме такого производства. При этом необратимые деформации обязаны быть непрерывными в условиях смены механизма их производства на упругопластических границах. Задача обеспечения данной непрерывности при начале пластического течения на нагружающей упругопластической границе или при его завершении на разгружающей поверхности может оказаться совсем не простой.
Здесь на основе определения обратимой и необратимой составляющих полных деформаций формулированием для них, следуя формализму термодинамики, соответствующих дифференциальных уравнений их изменения (переноса) предпринята попытка постановки данной фундаментальной проблемы современной механики. Необратимые деформации не разделяются на вязкие (деформации ползучести) и пластические. Все различие в них связывается с разным заданием источника в уравнениях переноса. В качестве иллюстрации такого подхода рассмотрен конкретный пример о вискозиметрическом деформировании цилиндрического слоя. Определяющими уравнениями, задающими источники в уравнениях переноса, выбраны простейшие. Вязкие свойства полагаются связанными степенным законом Нортона, а пластические ассоциированы с кусочно-линейной поверхностью, обобщающей условие максимальных касательных напряжений. Подчеркнем, что это только выбор. Препятствий иному выбору не существует, необходимо только, чтобы оставалась возможность обеспечить непрерывность необратимых деформаций на упругопластической границе. Последнее оказывается таким образом фундаментальной задачей феноменологической механики деформируемых тел. Общего решения данной задачи, по-видимому, получить невозможно. Ее разрешением приходится заниматься в каждом конкретном случае при задании конкретных определяющих законов. Рассмотренный пример разрешения такой задачи, кроме самостоятельного значения в качестве новой задачи теории больших деформаций, служит демонстрацией того, что такие задачи могут иметь свое решение.
Авторы посвящают настоящую публикацию светлой памяти своих Учителей Геннадия Ивановича Быковцева и Вениамина Петровича Мясникова.
Список литературы
Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.
Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.
Качанов Л.М. Основы теории пластичности. М.: Наука, 1969. 420 с.
Ивлев Д.Д. Теория идеальной пластичности. М.: Наука, 1966. 232 с.
Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упруго-пластические деформации: теория, алгоритмы, приложения. М.: Наука, 1986. 232 с.
Маркин А.А., Соколова М.Ю. Термомеханика упругопластического деформирования. М.: Физматлит, 2013. 320 с.
Lee E.H. Elastic-plastic deformation at finite strains // J. Appl. Mech. 1969. V. 36. № 1. P. 1–6.
Буренин А.А., Ковтанюк Л.В., Полоник М.В. Возможность повторного пластического течения при общей разгрузке упругопластической среды // Докл. РАН. 2000. Т. 375. № 6. С. 767–769.
Левитас В.И. Большие упругопластические деформации материалов при высоком давлении. Киев: Наукова думка, 1987. 232 с.
Димитриенко Ю.И. Нелинейная механика сплошной среды. М.: Физматлит, 2009. 624 с.
Голованов А.И., Султанов Л.У. Математические модели вычислительной нелинейной механики деформируемых сред. Казань: Изд-во КГУ, 2009. 465 с.
Naghdi P.M. A critical review of the state of finite plasticity // J. Appl. Phys. 1990. V. 41. P. 315–394.
Simo J.C. A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: Part I. Continuum formulation // Comput. Meth. in Appl. Mech.&Engng. 1988. V. 66. № 2. P. 199–219.
Xiao H., Bruhns O.T., Meyers A. A consistent finite elastoplasticity theory combining additive and multiplicative decomposition of the stretching and deformation gradient // Int. J. Plasticity. 2000. V. 16. № 2. P. 143–177.
Pietryga M.R., Reese S., Vladimirov I.N. Anisotropic finite elastoplasticity with nonlinear kinematic and isotropic hardening and application to sheet metal forming // Int. J. Plasticity. 2010. V. 26. № 5. P. 659–687.
Shutov A.V., Ihlemann J. Analysis of some basic approaches to finite strain elasto-plasticity in view of reference change // Int. J. Plasticity. 2014. V. 63. P. 183–197.
Shutov A.V., Larichkin A.Yu., Shutov V.A. Modelling of cyclic creep in the finite strain range using a nested split of the deformation gradient // ZAMM. 2017. V. 97. № 9. P. 1083–1099.
Мясников В.П. Уравнения движения упругопластических материалов при больших деформациях // Вестн. ДВО РАН. 1996. № 4. С. 8–13.
Буренин А.А., Быковцев Г.И., Ковтанюк Л.В. Об одной простой модели для упругопластической среды при конечных деформациях // Докл. РАН. 1996. Т. 347. № 2. С. 199–201.
Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации и упругое последействие. Владивосток: Дальнаука, 2013. 312 с.
Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Неизотермическое движение упруговязкопластических среды в трубе в условиях изменяющегося перепада давления // Докл. РАН. 2015. Т. 464. № 3. С. 284–287.
Бегун А.С., Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации в условиях изменяющихся механизмов их производства и проблема задания пластических потенциалов // Докл. РАН. 2016. Т. 470. № 3. С. 275–278.
Белых С.В., Буренин А.А., Ковтанюк Л.В., Прокудин А.Н. Об учете вязких свойств материалов в теории больших упругопластических деформаций // Чебышевский сб. 2017. Т. 18. № 3(63). С. 108–130.
Prokudin A.N., Firsov S.V. Antiplane strain of hardening elastoviscoplastic medium // J. Siberian Federal Univ. – Math.&Phys. 2018. V. 11. № 4. P. 399–410.
Буренин А.А., Галимзянова К.Н., Ковтанюк Л.В., Панченко Г.Л. О согласовании механизмов роста необратимых деформаций полого шара при всестороннем сжатии // Докл. РАН. 2018. Т. 482. № 4. С. 403–406.
Локощенко А.М. Моделирование процесса ползучести и длительной прочности металлов. М.: МГИУ, 2007. 264 с.
Буренин А.А., Ковтанюк Л.В., Устинова А.С. Об учете упругих свойств неньютоновского материала при его вискозиметрическом течении // ПМТФ. 2008. Т. 49. № 2. С. 143–151.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика