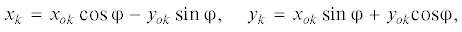Прикладная математика и механика, 2021, T. 85, № 1, стр. 21-43

1. Введение. Тросовые группировки спутников [1–6] это нетрадиционные космические системы, основное преимущество которых состоит в возможности создания протяженных легких конструкций на орбите. Однако вопросы формирования тросовых группировок спутников на орбите, управления их движением еще недостаточно изучены и требуют дальнейшего развития. Важным классом тросовых группировок являются тросовые системы, в состав которых входят наноспутники (НС), обладающие небольшой массой и размером. Так как возможности управления такими системами ограничены, то актуальным представляется разработка достаточно простых алгоритмов управления движением тросовых группировок НС на этапах их развертывания и функционирования. С другой стороны, использование тросов как легких механических связей между спутниками является одним из способов стабилизации движения как системы в целом (гравитационная стабилизация), так и каждого НС в отдельности при его движении вокруг своего центра масс. В последнем случае силы натяжения тросов создают восстанавливающий момент, стабилизирующий угловое движение НС относительно направления троса [7].

При анализе движения орбитальных тросовых группировок чаще всего космические аппараты (КА), входящие в их состав, рассматривались как материальные точки [1–6]. Хотя понятно, что более полное описание движения таких систем должно включать в себя уравнения движения каждого КА вокруг своего центра масс. Детальному анализу движения КА как твердых тел в составе тросовых систем уделялось существенно меньшее внимание. В частности, можно рассматривать [8, 9] влияние колебаний троса со спускаемой капсулой (материальная точка) на свободное движение относительно центра масс базового КА, с которого развертывалась тросовая система. Исследовалось также движение капсулы вокруг центра масс при развертывании тросовой системы [7], причем базовый КА большой массы перемещался по неизменной орбите, и предполагалось, что система управления движением обеспечивает его ориентацию по местной вертикали. Здесь необходимо отметить, что вопросы развертывания и свертывания космических тросовых систем являются наиболее сложными с точки зрения динамики и управления их движением [10–13], что обуславливает постоянное внимание к этому направлению исследований.

2. Описание задачи. В настоящей работе рассматривается задача формирования тросовой группировки, состоящей из трех НС, в положение, близкое к вертикальному. Ставится задача построения достаточно простых программ управления, которые могут быть реализованы без обратной связи. При этом должны выполняться ограничения на силы натяжения тросов для исключения их провисания (они должны быть натянуты, то есть положительны), на скорость выпуска тросов (устройства выпуска тросов работают только на их торможение), на угловое движение НС относительно направления тросов. Оценивается влияние возмущений при разделении НС и их массово-инерционной асимметрии на выполнение рассматриваемых ограничений. Для предварительного упрощенного анализа движения системы построена математическая модель методом Лагранжа, в которой НС рассматриваются как материальные точки. Показано, что в сочетании с этой моделью может быть использовано аналитическое решение [7], полученное методом усреднения, и предназначенное для оценки выполнения ограничений на угловое движение НС. Более полная модель пространственного движения системы записывается в неподвижной геоцентрической системе координат и служит для детального моделирования движения системы, включая процессы разделения НС. Характерной особенностью этой модели является использование кинематических уравнений углового движения НС в форме уравнений Эйлера–Пуассона [14], то есть в этом случае интегрируемыми переменными системы обыкновенных дифференциальных уравнений являются компоненты матрицы перехода от геоцентрической неподвижной к связанным с НС системам координат (матрица направляющих косинусов). Использование рассматриваемых уравнений позволяет избежать особенностей при описании углового движения НС характерных, например, для кинематических уравнений в углах Эйлера. С другой стороны, такая запись кинематических уравнений углового движения для НС позволяет избежать вычисления угловых скоростей вращения тросов относительно неподвижной геоцентрической системы координат при записи кинематических уравнений в углах Эйлера, определенных относительно направления тросов. Предлагаемые программы управления нетрудно распространить на большее число НС в группировке.

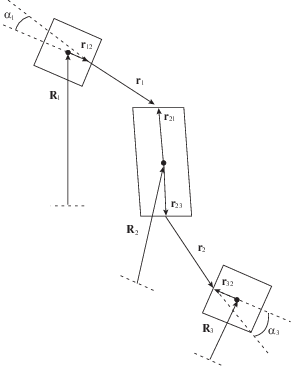
2. Математическая модель движения системы в неподвижной системе координат. Движение системы определяется в геоцентрической системе координат $OXYZ$, где плоскость $OXY$ совпадает с плоскостью экватора, а ось $OX$ направлена в точку весеннего равноденствия. Тогда уравнения движения центров масс НС записываются в виде

где ${{G}_{k}} = - Km{{R}_{k}}{\text{/}}R_{k}^{3}$ – гравитационные силы, $K$ – гравитационный параметр Земли, ${{T}_{k}}$ – силы натяжения тросов, ${{R}_{k}}$ – радиус-вектора центров масс НС. Здесь центральный спутник имеет номер 2 и от него почти одновременно отделяются два НС в противоположных направлениях. Очевидно для концевых НС в системе (2.1) имеем ${{T}_{0}} = {{T}_{3}} = 0$.

Силы натяжения тросов вычисляются следующим образом

где $C = ES$ – жесткость тросов, $E$ – модуль упругости Юнга, $S$ – площадь поперечного сечения тросов, ${{l}_{{1,2}}}$ – недеформированная длина тросов; ${{r}_{1}} = {{R}_{{21}}} - {{R}_{{12}}}$, ${{r}_{2}} = {{R}_{{32}}} - {{R}_{{23}}}$ – радиус-вектора, соединяющие точки крепления тросов; ${{R}_{{12}}} = {{R}_{1}} + {{r}_{{12}}}$, ${{R}_{{21}}} = {{R}_{2}} + {{r}_{{21}}}$, ${{R}_{{23}}} = {{R}_{2}} + {{r}_{{23}}}$, ${{R}_{{32}}} = {{R}_{3}} + {{r}_{{32}}}$ (рис. 1).

Процесс выпуска троса моделируется с помощью динамических уравнений [7]

где коэффициент ${\mu }$ учитывает инерционность механизма управления, ${{F}_{{1,2}}}$ – управляющая (тормозящая) сила в механизме управления, которая изменяется по заданной программе.

При определении углового движения НС относительно направлений тросов используются классические динамическими уравнения Эйлера, записанные в главных связанных системах координат

где $\omega _{x}^{{(k)}},\,\,\omega _{y}^{{(k)}},\,\,\omega _{z}^{{(k)}}$ – угловые скорости НС, $J_{x}^{{(k)}},\,\,\,J_{y}^{{(k)}},\,\,J_{z}^{{(k)}}$ и $M_{x}^{{(k)}},\,\,M_{y}^{{(k)}},\,\,M_{z}^{{(k)}}$ – моменты инерции и моменты сил в главных связанных осях, действующих на каждый НС, $k = \overline {1,3} $.

Кинематические уравнения записываются в форме уравнений Эйлера–Пуассона

где ${{\omega }^{{(k)}}}$ – вектора угловых скоростей НС, ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}}$ – орты главных связанных систем координат, $k = \overline {1,3} $.

При наличии у НС инерционной асимметрии в связанной системе координат, одна из осей которой совпадает с направлением “центр масс – точка крепления троса”, используется пересчет тензоров инерции (2.1), (2.3)–(2.5)

где ${{J}_{k}}$ и ${{I}_{k}}$ – тензоры инерции в главной связанной и связанной системах координат, ${{U}_{k}}$ – матрицы собственных векторов для ${{I}_{k}}$, $\left( * \right)$ – знак транспонирования, ${{M}_{k}}$ и ${{m}_{k}}$ – вектора моментов сил, проекции которых записаны в разных связанных системах координат, $k = 1,2,3$.

Составляющие моментов ${{m}_{k}}$, определенные в главных связанных системах координат, представляют собой суммы

где $m_{{1,2,3}}^{{\left( g \right)}}$ – вектора гравитационных моментов, ${{m}_{{12}}} = {{r}_{{12}}} \times {{T}_{1}}$, ${{m}_{{21}}} = - {{r}_{{21}}} \times {{T}_{1}}$, ${{m}_{{23}}} = {{r}_{{23}}} \times {{T}_{2}}$, ${{m}_{{32}}} = - {{r}_{{32}}} \times {{T}_{2}}$ – моменты от сил натяжения тросов.

Предполагается, что концевые НС это кубы, то есть при почти однородном распределении массы внутри НС их центральный эллипсоид инерции близок к шару. Поэтому, когда концевые НС отделяются от центрального спутника, то на них действует только момент от силы натяжений троса, а гравитационным моментом пренебрегается.

Гравитационный момент, действующий на центральный спутник, определяется стандартным образом [15]

где ${{J}_{2}}$ – тензор инерции НС, $\gamma = {{R}_{2}}{\text{/}}{{R}_{2}}$ – вектор направляющих косинусов в главной связанной системе координат.

При интегрировании уравнений (2.5) должны с заданной погрешностью выполняться условия ортогональности векторов ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}}$ и $\left| {{{e}_{{xk}}}} \right| = \left| {{{e}_{{yk}}}} \right| = \left| {{{e}_{{zk}}}} \right| = 1$. Для этого можно использовать алгоритм коррекции, основанный на минимизации корректирующих добавок при изменении значений компонент векторов ${{e}_{{xk}}},\;{{e}_{{yk}}},\;{{e}_{{zk}}}$ [14], $k = \overline {1,3} $.

Здесь необходимо отметить, что описанная математическая модель движения системы может быть использована в двух вариантах, которые существенно отличаются с точки зрения временных затрат при моделировании. В первом варианте влиянием колебаний концевых тел на натяжения тросов пренебрегается, то есть при расчете сил натяжения полагается ${{r}_{{12}}} = {{r}_{{21}}} = {{r}_{{23}}} = {{r}_{{32}}} = 0$. Во втором варианте приведенные выше уравнения движения используются в полной мере. Как показали результаты моделирования учет колебаний концевых тел при расчете сил натяжения как минимум на порядок увеличивает временные затраты при моделировании. Это объясняется наличием в этом случае высокочастотных продольных колебаний в тросах.

3. Математическая модель движения системы, построенная с помощью метода Лагранжа. Для предварительного анализа движения системы и выбора программы ее развертывания, для получения некоторых аналитических оценок рационально использовать упрощенные уравнения плоского движения системы, в которых механические связи (тросы) нерастяжимы, а НС – материальные точки. Для построения этой модели воспользуемся уравнениями Лагранжа

где ${{T}_{c}}$ и $\Pi $ – кинетическая и потенциальная энергии системы, $q = \left( {{{l}_{1}},{{l}_{2}},{{{\theta }}_{1}},{{{\theta }}_{2}}} \right)$ – вектор обобщенных координат, $\dot {q}$ – соответствующий вектор обобщенных скоростей, $F$ – вектор обобщенных непотенциальных сил. Здесь углы ${{{\theta }}_{1}},{{{\theta }}_{2}}$ определяют положения тросов относительно оси $с{{x}_{o}}$ орбитальной системы координат (рис. 2), связанной с центром масс системы; ${{l}_{1}},\;{{l}_{2}}$ – длины тросов, связывающие центральный спутник с концевыми НС. Орбитальная правая система координат $с{{x}_{o}}{{y}_{o}}{{z}_{o}}$ определяется стандартным образом: ось $с{{x}_{o}}$ направлена по радиус-вектору ${{R}_{с}}$ центра масс, ось $с{{y}_{o}}$ – перпендикулярно ${{R}_{с}}$ в плоскости орбиты в сторону движения центра масс.

При развертывании системы в вектор $F$ (3.1) входят силы натяжения тросов, которые должны изменяться по заданной программе. При записи уравнений движения в форме (3.1), тросы предполагаются нерастяжимыми.

Уравнения (3.1) описывают формирование тросовой системы в плоском случае. Это связано с громоздкостью выражений, описывающих поведение системы в пространственном случае.

Кинетическая и потенциальная энергии системы определяются стандартным образом

где $n = 3$, $\dot {R}_{k}^{2} = \dot {x}_{k}^{2} + \dot {y}_{k}^{2}$, ${{R}_{k}} = \sqrt {x_{k}^{2} + y_{k}^{2}} $, ${{x}_{k}},\;{{y}_{k}}$ – координаты центров масс НС в геоцентрической неподвижной системе координат, связанной с орбитальной плоскостью центра масс системы.

Координаты ${{x}_{k}},\;{{y}_{k}}$ вычисляются из следующих выражений

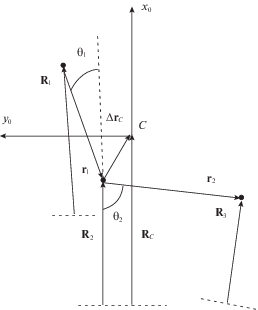
где угол ${\varphi }$ определяет положение орбитальной системы координат относительно геоцентрической неподвижной системы координат.

Чтобы использовать соотношения (3.3) в уравнениях (3.1) величины ${{x}_{{ok}}},\;{{y}_{{ok}}}$ необходимо выразить через обобщенные координаты. Имеют место очевидные векторные соотношения (рис. 2)

где при определении ${{r}_{1}}$ и ${{r}_{2}}$ длиной векторов ${{r}_{{12}}},\;{{r}_{{21}}},\;{{r}_{{23}}},\;{{r}_{{32}}}$ пренебрегается.

Тогда, используя уравнение для положения центра масс системы R_c = = $\sum\nolimits_{k = 1}^n {{{m}_{k}}{{R}_{k}}} {\text{/}}{{m}_{s}}$ и проецируя (3.3) на оси орбитальной системы координат $с{{x}_{o}}{{y}_{o}}$, получим

где ${{m}_{s}}$ – масса системы.

При определении потенциальной энергии системы в гравитационном поле используется обычное допущение о том, что размеры системы много меньше, чем расстояние центра масс системы до притягивающего центра ${{R}_{c}}$. В качестве примера рассмотрим приближенное представление потенциальной энергии для первого НС. Тогда представляя функцию $1{\text{/}}{{R}_{1}}$ в виде ряда по малым параметрам ${{{\varepsilon }}_{{1,2}}}$, получим

где $\Omega $ – угловая скорость движения центра масс системы по орбите,

При записи выражения (3.5) предполагается, что орбита движения центра масс системы круговая и не изменяется за время развертывания системы. Аналогично записываются приближенные выражения для энергий ${{\Pi }_{{2,3}}}$.

Учитывая приближенное представление для составляющих потенциальной энергии системы ${{\Pi }_{{1,2,3}}}$, подставляя соотношения (3.4) в уравнения Лагранжа (3.1) и проводя дифференцирование функций, получим

где ${\ddot {\xi }} = \left( {\begin{array}{*{20}{c}} {{{{\ddot {l}}}_{1}}}&{{{{\ddot {l}}}_{2}}}&{{{{{\ddot {\theta }}}}_{1}}}&{{{{{\ddot {\theta }}}}_{2}}} \end{array}} \right)$ – вектор ускорений для обобщенных координат системы, $A$ и $B$ – известные матрица и вектор, имеющие компоненты здесь ${{\mu }_{1}} = {{m}_{3}}$, ${{\mu }_{2}} = {{m}_{1}}$.

Выпуск тросов осуществляется по заданной программе, что обеспечивается программным изменением сил натяжения тросов, которые зависят от переменных состояния системы. Чаще всего программные силы натяжения ${{T}_{{1,2}}}$ задаются как функции времени, скорости и длины троса [16]. Для системы (3.6) в рассматриваемом случае эти зависимости зададим в виде ${{F}_{{1,2}}} = {{T}_{{1,2}}}\left( {{{l}_{{1,2}}},{{V}_{{1,2}}}} \right)$, ${{F}_{{3,4}}} = 0$. После задания программ выпуска троса система (3.6) может быть проинтегрирована любым численным методом при заданных начальных условиях.

4. Программы выпуска троса. Так как наноспутники характеризуются небольшими массой и размерами, то программы выпуска тросов должны быть по возможности более простыми и не предъявлять больших требований к механизмам управления. Наиболее простой вариант, это чтобы механизмы управления работали только на торможение троса [16] и без обратной связи. Причем программные зависимости ${{T}_{{1,2}}}\left( {{{l}_{{1,2}}},{{V}_{{1,2}}}} \right)$ должны быть построены так, чтобы они обеспечивали формирование системы заданной конфигурации, и при этом выполнялись бы ограничения на ее переменные состояния. В рассматриваемом случае тросовая группировка НС располагается в конечном состоянии вблизи вертикали, а накладываемые ограничения имеют следующий вид: 1) силы натяжения ${{T}_{{1,2}}}\left( {{{l}_{{1,2}}},{{V}_{{1,2}}}} \right) > 0$ (тросы должны быть натянуты); 2) скорости выпуска троса ${{V}_{{1,2}}} > 0$ (механизмы работают только на торможение); 3) при заданной конечной длине между НС ${{l}_{{1,2}}} = {{l}_{{{\text{end}}}}}$ скорости ${{V}_{{1,2}}} \approx 0$.

В связи вышесказанным предлагается следующая программа выпуска тросов

Здесь коэффициент ${{\nu }_{t}}\left( {{{l}_{k}}} \right) > 0$ обеспечивает торможение троса и задается так, чтобы разделить процесс выпуска тросов на два участка: быстрого и медленного развертывания, а именно

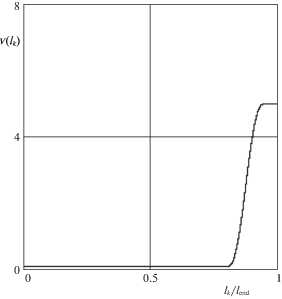
где $k = 1,2$, а функция ${{{\nu }}_{l}}\left( {{{l}_{k}}} \right)$ обеспечивает гладкое соединение участков, где она принимает постоянные значения ${{{\nu }}_{{\min }}}$ и ${{{\nu }}_{{\max }}}$ (${{{\nu }}_{{\max }}} > {{{\nu }}_{{\min }}}$). Соединение участков осуществляется обычным полиномом пятой степени, с помощью которого можно обеспечить непрерывность первых и вторых производных функции (4.2) в точках ${{l}_{k}} = {{l}_{{k1}}}$ и ${{l}_{k}} = {{l}_{{k2}}}$.

Пример изменения функции ${\nu }\left( {{{L}_{k}}} \right)$ в зависимости от относительной величины конечного расстояния между НС ${{l}_{k}}{\text{/}}{{l}_{{{\text{end}}}}}$ при ${{{\nu }}_{{\min }}} = 0.1$, ${{{\nu }}_{{\max }}} = 5$, ${{l}_{{k1}}}{\text{/}}{{l}_{{{\text{end}}}}} = 0.8$, ${{l}_{{k2}}}{\text{/}}{{l}_{{{\text{end}}}}} = 0.95$ приводится на рис. 3. Соотношения (4.1)–(4.2) задают программу выпуска троса, параметрами которой являются величины ${{{\nu }}_{{\min }}},\;{{{\nu }}_{{\max }}},\;{{l}_{{k1}}},\;{{l}_{{k2}}}$. Эти параметры должны быть выбраны так, чтобы при заданной конечной длине троса ${{l}_{{{\text{end}}}}}$ были выполнены перечисленные выше ограничения на переменные состояния процесса развертывания.

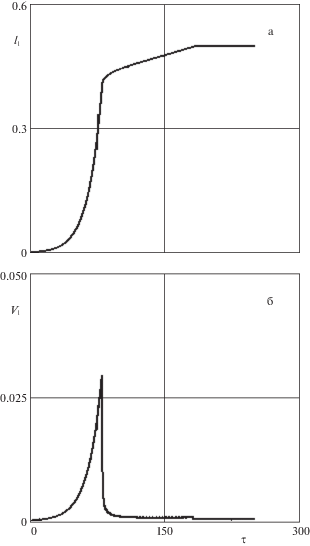
На рис. 4–5 показаны временные зависимости для характеристик процесса выпуска троса для одного из НС при формировании вертикальной тросовой системы, состоящей из трех НС. Зависимости, приведенные на рис. 4, соответствуют программе развертывания троса (4.1)–(4.2) с параметрами, приведенными выше (рис. 3). Другие параметры тросовой системы имеют следующие значения: ${{m}_{{\text{1}}}} = {{m}_{3}} = 2$ кг, ${{m}_{2}} = 12$ кг, ${{l}_{{{\text{end}}}}} = 0.5$ км, высота круговой орбиты 500 км, относительная скорость разделения НС 0.1 м/с, угловая скорость вращения составного спутника до разделения 0.1 с^–1. На рис. 4–5 в качестве независимой переменной используется безразмерное время ${\tau } = \Omega \,t$. При окончании выпуска тросов ${{l}_{{1,2}}} = {{l}_{{{\text{end}}}}}$ их длины фиксируются.

Несмотря на относительную простоту построенной модели, в которой НС представляют собой материальные точки, на основании ее использования все же можно сделать некоторые выводы об особенностях предлагаемой программы развертывания:

1. Вне зависимости от начального положения составного НС относительно вертикали и его начальной угловой скорости (которая может изменяться в достаточно большом диапазоне) по окончании развертывания система совершает колебания относительно вертикали, с некоторой амплитудой, величина которой определяется значениями параметров программы управления.

2. На участке быстрого развертывания (после окончания переходного процесса) все НС располагаются практически на одной линии, если отделение НС осуществляется одновременно, с равными скоростями и НС имеют одинаковые массы. Как показывает анализ уравнений движения (3.6) перемещения НС по прямой, которая составляет постоянный угол с вертикалью (${{{\theta }}_{e}}$), обеспечивается равенством гравитационных моментов и моментов от сил Кориолиса.

3. При переходе на участок медленного торможения скорость выпуска троса уменьшается, что приводит к колебаниям системы относительно вертикали с некоторой амплитудой, величина которой определяется значением угла ${{{\theta }}_{e}}$.

4. Величина угла ${{{\theta }}_{e}}$ определяется значением параметра ${{{\nu }}_{{\min }}}$: при его увеличении амплитуда колебаний системы относительно вертикали уменьшается. Однако это соответственно увеличивает время развертывания системы.

5. Начальная скорость разделения НС может изменяться в достаточно широком диапазоне, что не влияет на выполнение перечисленных выше ограничений, а только изменяет время выпуска троса. Для приведенных исходных данных увеличение скорости разделения НС на один порядок (до $1\,{\text{м/c}}$) уменьшает время выпуска троса приблизительно в 1.5 раза, причем качественно зависимости на рис. 4–5 не изменяются.

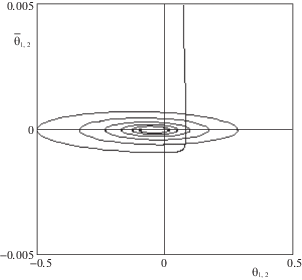
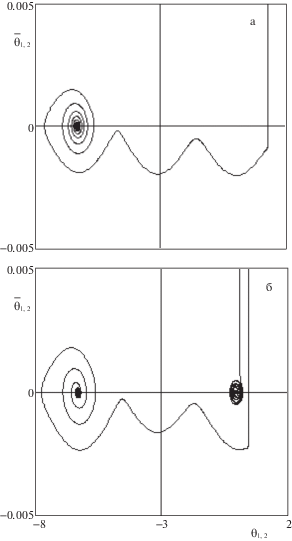
Для последнего вывода (при изменении скорости разделения) необходимо отметить, что фазовый портрет системы на плоскости $\left( {{\theta ,\dot {\theta }}} \right)$ мало изменяется (рис. 6, ${{\theta }_{1}} = {{\theta }_{2}} = \theta $), а для траекторий концевых НС относительно вертикали изменяется лишь масштаб. В качестве примера на рис. 7 показаны траектории концевых тел после разделения НС при изменении скорости разделения от 0.1 м/с (рис. 7, а) до $1\,\;{\text{м/c}}$ (рис. 7, б). Для рис. 7, б масштаб был увеличен в 10 раз. На рис. 7, в показаны полные траектории концевых тел при скорости разделения 0.1 м/с. Время перехода системы из режима вращения в движение вблизи вертикали без вращения является небольшим и зависит от скорости разделения НС почти линейно. При скорости разделения 0.1 м/с время переходного процесс составляет приблизительно 4 с, при скорости 1 м/с – 0.4 с.

Результаты, приведенные на рис. 4–7, относятся к случаю, когда имеется полная симметрия относительно центрального НС (по скорости разделения и ее направлению, по массам ${{m}_{{\text{1}}}} = {{m}_{3}}$). Поэтому траектории концевых НС симметричны и центр масс системы совпадает с центром масс центрального НС. Малая асимметрия по указанным выше характеристикам слабо влияет на приведенные результаты. В качестве примера достаточно большой асимметрии на рис. 7, г показаны траектории концевых тел относительно центрального НС, когда масса нижнего НС в два раза больше массы верхнего НС (${{m}_{{\text{1}}}} = 4$ кг, ${{m}_{3}} = 2$ кг). В этом случае процесс развертывания системы происходит следующим образом, во-первых, нижняя часть тросовой системы с большим по массе НС развертывается быстрее; во-вторых, после окончания развертывания нижней части (когда длина троса фиксируется) имеет место возмущение траектории верхнего НС; в-третьих, изменяется угол ${{{\theta }}_{e}}$ на участке прямолинейного развертывания (для большей нижней концевой массы он меньше). Аналогичное влияние наблюдается, если имеется асимметрия в величине скорости разделения верхнего и нижнего НС. Там, где скорость больше, развертывание этого участка естественно осуществляется быстрее, и далее имеют место те же явления, что и при наличии асимметрии масс.

Влияние направления разделения НС по отношению к вертикали более сложное и может привести к вероятностным явлениям при движении тросовой системы. Даже если начальные углы равны ${{{\theta }}_{1}} = {{{\theta }}_{2}}$, то и в этом случае движение системы может стать не предсказуемым. Было установлено, что существует некоторый диапазон для начальных углов ${{{\theta }}_{{1,2}}}$ такой, что если ${{{\theta }}_{{1,2}}} \notin \left[ { - {{{\theta }}_{{\max }}},{{{\theta }}_{{\max }}}} \right]$, то процесс перехода системы из режима вращения в режим движения вблизи вертикали включает в себя несколько оборотов системы вокруг центра масс системы. Только после этого система выходит на участок прямолинейного движения без вращения. Следовательно, существует некоторая окрестность “седловых” точек ${{{\theta }}_{1}} = {{{\theta }}_{2}} = \pm {\pi /}2$, для которой финальное положение системы (какой НС вверху, а какой внизу) не предсказуемо, так как малое изменение начальных значений углов ${{{\theta }}_{{1,2}}}$ может привести к изменению конечного положения системы. Для исходных данных, соответствующих симметричной системе, и приведенных выше, критический угол ${{{\theta }}_{{\max }}} \approx {\pi /}3$. Переходный процесс, который включает в себя несколько оборотов симметричной системы относительно центра масс, показан на рис. 8, а (начальные углы ${{{\theta }}_{1}} = {{{\theta }}_{2}}$ = 70°). Для симметричной системы критическое значение ${{{\theta }}_{{\max }}}$ при увеличении начальной скорости разделения НС увеличивается, а при увеличении начальной угловой скорости вращения составного НС – уменьшается.

Если отделение НС не симметрично по направлению, то может иметь место запутывание системы, когда один НС начинает вращаться относительно центра масс системы, а другой – нет. Пример такого поведения системы приводится на рис. 8, б, где начальные углы равны ${{{\theta }}_{1}} = 0$, ${{{\theta }}_{2}}$ = 23°.

5. Определение движения спутников относительно центров масс. В общем случае для определения движения НС относительно своих центров масс требуется интегрирование полной системы уравнений (2.1), (2.3)–(2.5) при заданных начальных условиях. В частности, для задания начальных условий кинематических уравнений (2.5) необходимы вычисления матрицы перехода между неподвижной геоцентрической $OXYZ$ и главными связанными системами координат спутников. Для этого используется орбитальная правая система координат, связанная с центром масс $с$ системы $с{{x}_{o}}{{y}_{o}}{{z}_{o}}$ (рис. 2). Матрица перехода между системами координат $OXYZ$ и $с{{x}_{o}}{{y}_{o}}{{z}_{o}}$ определяется стандартным образом [17] с помощью углов $\Omega ,i,u$, где $\Omega $ – долгота восходящего узла, $i$ – наклонение орбиты, $u$ – аргумент широты. Положение тросов относительно системы координат $с{{x}_{o}}{{y}_{o}}{{z}_{o}}$ в пространственном случае определяется двумя углами ${{{\theta }}_{k}}$ и ${{{\beta }}_{k}}$ [7], причем, если ${{{\beta }}_{k}} = 0$, то имеет место плоский случай движения, рассмотренный выше в разд. 3. Угловое положение главных связанных систем координат НС относительно тросов определяется углами Эйлера ${{\psi }_{k}},\;{{\alpha }_{k}},\;{{\varphi }_{k}}$ (соответственно углы прецессии, нутации и собственного вращения). Таким образом, после задания перечисленных выше углов начальные условия для интегрирования кинематических уравнений движения (2.5) для каждого НС определяются из соотношений

где столбцы матрицы $H$есть проекции единичных векторов ${{e}_{x}},\;{{e}_{y}},\;{{e}_{z}}$ на оси геоцентрической неподвижной системы координат $OXYZ$, ${{H}_{{\Omega ,i,u}}}$, ${{H}_{{{\theta ,\beta }}}}$, ${{H}_{{{\psi ,\alpha ,\varphi }}}}$ – матрицы перехода между перечисленными выше системами координат.

В процессе интегрирования системы уравнений (2.1), (2.3)–(2.5) необходимо определять угловое положение НС относительно тросов. Для определения углов, определяющих положение НС относительно тросов, необходимо ввести системы координат, связанные с плоскостями, проходящими через линию, соединяющую точки крепления тросов и их радиус-векторами. Например, пусть точка $a$ это точка крепления троса, соединяющего первый НС со вторым, а ${{R}_{{12}}}$ – ее радиус-вектор в геоцентрической системе координат $OXYZ$. Для этого НС введем правую систему координат $a\,{{x}_{a}}{{y}_{a}}{{z}_{a}}$. Здесь ось $a\,{{x}_{a}}$ направлена к точке крепления троса ко второму НС, ось $a\,{{z}_{a}}$ – по векторному произведению ${{r}_{1}} \times {{R}_{{12}}}$, где ${{r}_{1}} = {{R}_{{21}}} - {{R}_{{12}}}$. Используя известные проекции векторов ${{R}_{{12}}},\;{{R}_{{21}}}$ в геоцентрической системе координат $OXYZ$, можно найти проекции ортов системы координат $a\,{{x}_{a}}{{y}_{a}}{{z}_{a}}$ в той же системе и, таким образом, матрицу перехода между системами координат $a\,{{x}_{a}}{{y}_{a}}{{z}_{a}}$ и $OXYZ$. В этом случае ориентация первого НС относительно вектора ${{r}_{1}}$ (или направления троса) определяется ориентацией связанной с НС системы координат ${{с}_{1}}\,{{x}_{1}}{{y}_{1}}{{z}_{1}}$ относительно системы координат $a\,{{x}_{a}}{{y}_{a}}{{z}_{a}}$. Здесь ось ${{с}_{1}}\,{{x}_{1}}$ связанной системы координат направлена от центра масс НС к точке крепления троса. Очевидно, что угол нутации ${{{\alpha }}_{1}}\,$ для первого НС это угол между осями $a\,{{x}_{a}}$ и ${{с}_{1}}\,{{x}_{1}}$. При этом угол прецессии ${{{\psi }}_{1}}\,$ определяется через проекции единичного вектора оси ${{с}_{1}}\,{{x}_{1}}$ в системе координат $a\,{{x}_{a}}{{y}_{a}}{{z}_{a}}$ следующим образом $\cos {{\psi }_{1}} = e_{{ya1}}^{{}}{\text{/}}\sqrt {e_{{ya1}}^{2} + e_{{za1}}^{2}} $, $\sin {{\psi }_{1}} = {{e}_{{za1}}}{\text{/}}\sqrt {e_{{ya1}}^{2} + e_{{za1}}^{2}} $. Естественно для НС, отличного по крайних НС, определяются две совокупности углов Эйлера по отношению к двум тросам, расположенных по обеим его сторонам.

Следует отметить, что при моделировании движения системы с использованием уравнений (2.1), (2.3)–(2.5) возможны случаи провисания (или ослабления) тросов. Это связано с используемым выражением для определения силы натяжения (2.2), учитывающим односторонность механической связи. В этом случае ориентация НС определяется по отношению к линии, соединяющей точки крепления троса. Естественно, алгоритмы вычисления углов Эйлера не изменяются.

6. Расчет процесса разделения наноспутников. До разделения составной НС, состоящий из нескольких секций, совершает свободное движение по орбите как твердое тело с некоторой угловой скоростью. Очевидно, что в этом случае уравнения движения составного НС представляют собой частный случай уравнений (2.1), (2.3)–(2.5). За расчетный (номинальный) случай принимается случай одновременного отделения двух НС от центрального НС. Если НС отделяются не одновременно, то расчет изменения скоростей НС может быть получен аналогично.

Рассмотрим, например, начальную фазу формирования системы, когда от составного НС отделяются два НС в противоположных направлениях. Пусть разделение НС осуществляется с относительными скоростями ${{V}_{{r1}}}$ и ${{V}_{{r3}}}$. Направление векторов ${{V}_{{r1}}}$ и ${{V}_{{r3}}}$ определяется относительно связанной продольной оси составного НС с помощью углов ${{{\alpha }}_{{s1,3}}}$, ${{{\beta }}_{{s1,3}}}$. В этом случае в связанной системе координат составного НС получим

С использованием закона сохранения импульса вычисляются скорости НС после разделения

где ${{V}_{c}}$ – вектор скорости центра масс составного НС до разделения.

Для определения угловых скоростей НС после разделения используется теорема об изменении кинетического момента твердого тела при ударном воздействии (см., например, [18])

где ${{S}_{{1,3}}}$ – ударные импульсы, действующие на 1 и 3 спутник; $\Delta {{K}_{{1,2,3}}}$ – приращение кинетических моментов НС, $S_{{1,3}}^{'} = - {{S}_{{1,3}}}$.

Импульсы ${{S}_{{1,3}}}$ определяются из выражений

Зная приращения $\Delta {{K}_{{1,2,3}}}$ нетрудно определить изменение угловых скоростей НС после их разделения

где ${{J}_{k}}$ – тензоры инерции спутников.

После разделения ориентация каждого НС соответствует ориентации составного НС до разделения. Приведенный алгоритм вычисления угловых скоростей НС после их разделения учитывает статическую (например, смещение точки крепления троса относительно продольной оси НС) и инерционную (отличие тензора инерции НС от диагонального) асимметрии спутников, что при их наличии приводит к возмущениям углового движения НС.

7. Анализ углового движения спутников в составе развертываемой тросовой системы. Для предварительной оценки углового движения НС можно использовать аналитические формулы, основанные на методе усреднения [7, 19]. Рассматриваемое аналитическое решение соответствует движению твердого тела вокруг неподвижной точки для случая, близкого к случаю Лагранжа, который характеризуется наличием не малого восстанавливающего момента (по сравнению с другими возмущениями) относительно неподвижной точки. Для данной задачи – это момент силы натяжения троса относительно центра масс НС. При применении данного аналитического решения спутники считаются статически и динамически симметричными, но при этом рассматривается пространственное их движение, а ограничения накладываются только на углы нутации спутников, определенные относительно тросов. Ниже показано, что решение может быть применено не только для крайних спутников [7], но и для центрального НС системы. Основное предположение, на котором основывается данное аналитическое решение, это медленное изменение восстанавливающего момента по сравнению с характерной частотой колебаний НС относительно своего центра масс. Аналитическое решение имеет вид [7]

где ${{a}_{{1,2}}}$ – амплитуды колебаний, соответствующие “прямой” и “обратной” прецессиям НС; ${{\omega }_{s}} = \sqrt {T\Delta l{\text{/}}{{J}_{s}}} $ – собственная частота плоских колебаний НС на тросе, $T$ – сила натяжения троса, $\Delta l$ – расстояние между точкой крепления троса и центром масс НС, ${{J}_{s}} = {{J}_{y}} = {{J}_{z}}$ – момент инерции динамически симметричного НС относительно осей связанной системы координат, ${{\bar {J}}_{x}} = {{J}_{x}}{\text{/}}{{J}_{s}}$, ${{a}_{{1,2}}}(0)$ и ${{\omega }_{s}}(0)$ – значения переменных в момент разделения спутников. При использовании формулы (7.1) предполагается, что угловая скорость ${{\omega }_{x}} = {\text{const}}$ (для исключения кручения троса можно использовать специальные шарниры).

Применение решения (7.1) требует вычисления начальных значений ${{a}_{{1,2}}}(0)$, ${{\omega }_{s}}(0)$. Значение частоты ${{\omega }_{s}}(0)$ вычисляется непосредственно по приведенной выше формуле. Начальные значения амплитудных характеристик определяются в пространственном случае после задания начальных угловых скоростей НС в связанной системе координат и углов их ориентации относительно троса: ${{\omega }_{{x,y,z}}}(0)$, ${\alpha }(0),$ ${\psi }(0),$ ${\varphi }(0)$. Причем углы ${\psi },\;{\varphi }$ могут иметь произвольные значения, например, ${\psi }(0) = \,{\varphi }(0) = 0$, что не влияет на определяемые амплитуды колебаний. Тогда [7]

где ${{{\omega }}_{{\alpha }}}\left( 0 \right) = \sqrt {\bar {J}_{x}^{2}\omega _{x}^{2}\left( 0 \right){\text{/}}4 + \omega _{s}^{2}\left( 0 \right)} $, ${{{\omega }}_{{{\text{1,2}}}}}\left( 0 \right) = {{\bar {J}}_{x}}{{\omega }_{x}}\left( 0 \right){\text{/}}2 \pm {{{\omega }}_{{\alpha }}}\left( 0 \right)$.

При использовании аналитического решения (7.1) угол нутации вычисляется следующим образом ${\alpha } = \sqrt {a_{1}^{2} + a_{2}^{2} + {{a}_{1}}{{a}_{2}}\cos \left( {{{{\psi }}_{1}} - {{{\psi }}_{2}}} \right)} $, где ${{{\psi }}_{{1,2}}}$ – фазы колебаний. Отсюда получается оценка для максимального и минимального угла нутации

Аналитическое решение может быть использовано совместно с любой из описанных моделей движения (2.3)–(2.5) или (3.6), достаточно задать программу изменения сил натяжения тросов.

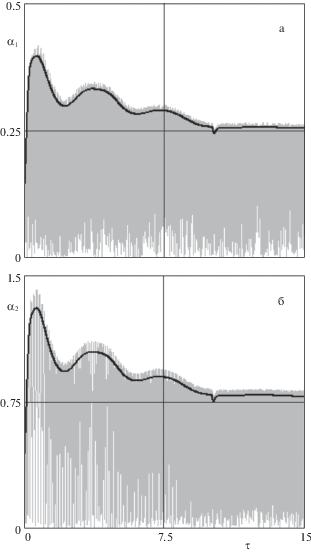
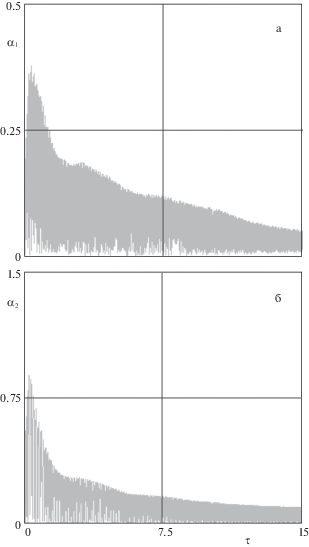
Применение аналитического решения показало, что оно может быть использовано для предварительной оценки амплитуд колебаний НС относительно направления троса при достаточно малых начальных угловых скоростях НС, которые возникают при их разделении. Это связано с тем, что увеличение угловых скоростей приводит соответственно к увеличению амплитуд колебаний НС, то есть к не малым углам нутации, а это являлось одним из допущений, которое использовалось при получении аналитического решения. Результаты моделирования показали, что приведенное аналитическое решение можно использовать, если углы нутации не превышают приблизительно 1.2 радиана. Кроме того, было установлено, что аналитическое решение с достаточной точностью описывает только решения, которые получаются, если при использовании математической модели (2.1)–(2.4) полагается ${{r}_{{12}}} = {{r}_{{21}}} = {{r}_{{23}}} = {{r}_{{32}}} = 0$, то есть не учитывается влияние колебаний концевых тел на силы натяжения в тросах. С другой стороны, аналитическое решение с достаточной точностью правильно оценивает максимум амплитуды для угла нутации, который достигается после разделения НС. При дальнейшем движении системы более точный учет колебаний концевых тел во всех случаях (авторам не удалось найти опровержения этого утверждения) вело к уменьшению амплитуд колебаний НС относительно направления тросов.

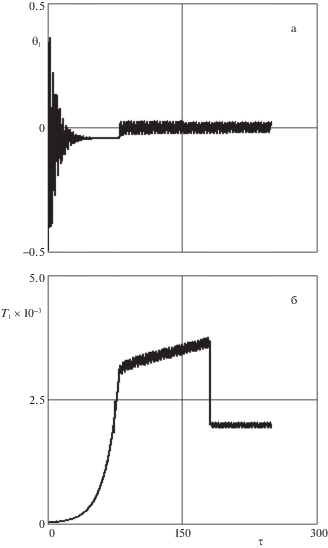
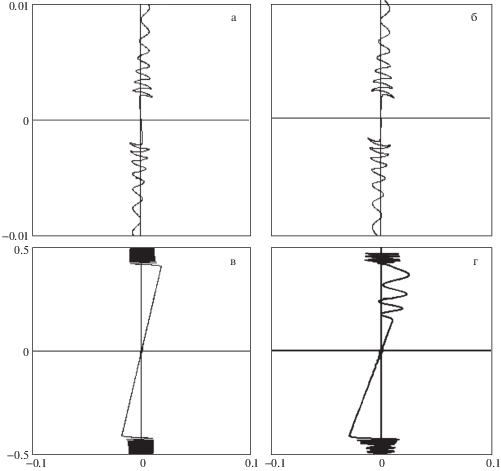
Приведенные выводы иллюстрируются зависимостями, представленными на рис. 9–10, где рис. 9, а и рис. 10, а характеризуют движение крайнего НС, а рис. 9, б и рис. 10, б – центрального НС. Рис. 9 относится к случаю, когда не полностью учитывается взаимодействие между колебаниями концевых тел и тросом, а на рис. 10 в полной мере учитывается это взаимодействие. На рис. 9 также показаны (жирными линиями) амплитудные характеристики углов нутации, полученные с помощью аналитического решения (7.3). Как следует из приведенных результатов моделирования имеет место интересный эффект стабилизации движения НС за счет взаимодействия колебаний твердых тел и троса. Причем такая стабилизация более ярко выражена для центрального НС, который имеет связь с тросами с обеих сторон. Понятно, что такой довольно сложный эффект не описывается аналитическим решением. Рис. 9–10 построены при некотором произвольном распределении угловых скоростей в момент разделения: ${{\omega }_{x}}\left( 0 \right) = 0.1$ с^–1, ${{\omega }_{y}}\left( 0 \right) = - 0.1$ с^–1, ${{\omega }_{z}}\left( 0 \right) = 0.1$ с^–1, то есть соответствуют пространственному случаю движения НС. Крайние НС представляют собой кубы с ребром $0.1\;{\text{м}}$, центральный спутник – прямоугольный параллелепипед ($0.1 \times 0.1 \times 0.6$ м). Здесь следует отметить, что очень значимым фактором, который влияет на амплитудные характеристики углового движения НС является величина относительных скоростей их отделения от центрального спутника ${{V}_{{r1,3}}}$. С увеличением величины этих скоростей максимальные углы нутации НС по крайней мере для симметричных НС уменьшаются. Однако это имеет свои пределы, во-первых, всегда имеются технические ограничения, во-вторых, переходный процесс в вертикальной плоскости растягивается (рис. 7, а, б), что в конечном итоге приводит к увеличению амплитуд колебаний всей системы относительно вертикали в конечном состоянии.

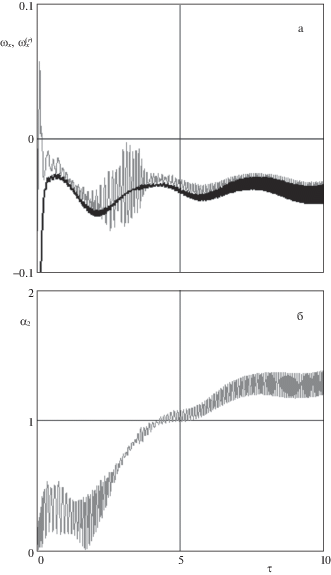
Влияние массово-инерционной асимметрии на движение НС относительно центра масс имеет два источника, во-первых, при разделении НС действие ударных импульсов приводит к дополнительным возмущениям для угловых скоростей (6.3), (6.5); во-вторых, имеют место периодические возмущения для углов нутации в процессе развертывания системы. В последнем случае возможны два характерных варианта изменения амплитудных характеристик при колебаниях НС относительно тросов. Это связано с тем, что задача анализа колебаний НС относительно тросов близка к задаче о движения волчка Лагранжа с малой асимметрией вокруг неподвижной точки [20–22]. Поэтому в рассматриваемой системе также возможны проявления резонансных эффектов. Если реализуются нерезонансные случаи движения, то хотя это ведет к некоторому увеличению амплитуд колебаний углов нутации НС за счет наличия периодических возмущений, но это увеличение не является катастрофическим. Положение изменяется, если траектория системы проходит через резонансные области. В этом случае возможны случаи, когда в течение некоторого времени в силу действующих возмущений система “застревает” в резонансной области, то есть реализуется “захват” в резонанс. Тогда увеличение углов нутации может быть большим, что может привести к запутыванию или ослаблению тросов. Такой вариант поведения системы показан на рис. 11, где угловая скорость ${{\omega }_{x}}$ центрального НС пересекает резонансную кривую [20, 22] (ее отрицательную ветвь, которая показана жирной линией) $\omega _{x}^{{\left( r \right)}}\left( {\tau } \right)$ = = $ \pm {{\omega }_{s}}\left( {\tau } \right)\sqrt {\cos {{{\alpha }}_{2}}} {\text{/}}\sqrt {1 - J_{x}^{{(2)}}{\text{/}}J_{s}^{{(2)}}} $, где $J_{s}^{{(2)}} = \left( {J_{y}^{{(2)}} + J_{z}^{{(2)}}} \right){\text{/}}2$. Центральный НС имеет статическую асимметрию, которая характеризуется смещением его центра масс относительно продольной оси, связанной с ним системы координат ${{y}_{2}}{\text{/}}{{r}_{{23}}} = 0.01$, ${{z}_{2}}{\text{/}}{{r}_{{23}}} = - 0.01$, и динамическую асимметрию – $\left( {J_{z}^{{(2)}} - J_{y}^{{(2)}}} \right){\text{/}}J_{s}^{{(2)}} = 0.1$. Конечно, рассматриваемые режимы движения НС требуют более подробного и полного изучения, так как, например, необходимо учитывать трение в специальных шарнирах, которые исключают скручивание тросов.

Заключение. На основании проведенного анализа процесса развертывания на орбите тросовой группировки, состоящей из трех НС, можно сделать следующие выводы:

1. Предложенная программа развертывания тросовой системы при надлежащем выборе параметров обеспечивает приведение системы в состояние, близкое к вертикальному, с учетом выполнения задаваемых ограничений, в частности, на угловое движение НС.

2. Показано, что при разделении НС в направлении, близком к горизонтальному, переход системы из вращательного режима в движение вблизи вертикали может происходить после нескольких оборотов системы относительно центра масс.

3. Максимальные углы нутации НС почти всегда имеют место сразу после их разделения на начальном участке развертывания системы.

4. С увеличением относительных скоростей разделения НС амплитуды углов нутации уменьшаются, однако это приводит к увеличению амплитуд колебаний всей системы относительно вертикали после окончания ее развертывания.

5. С помощью численного моделирования установлено, что аналитическое решение, полученное ранее для вычисления амплитудных характеристик в задачах движения твердого тела, близких к случаю Лагранжа, во всех рассмотренных случаях дает верхнюю оценку для амплитуд колебаний углов нутации симметричных НС в данной задаче.

6. Взаимное влияние колебаний НС относительно центров масс и колебаний сил натяжения, как показали численные результаты, приводит к уменьшению углов нутации НС, определенных относительно направления тросов.

7. Наличие статической и динамической асимметрий НС может привести к резонансным эффектам при движении НС относительно центра масс (“захватам” в резонанс), что ведет к быстрому увеличению углов нутации НС в процессе развертывания системы.

Работа выполнена при поддержке гранта РФФИ 21-51-53002.