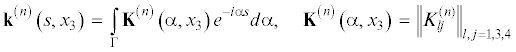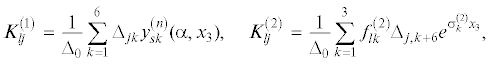Прикладная математика и механика, 2021, T. 85, № 3, стр. 309-320

О динамике неоднородной преднапряженной электроупругой среды в условиях воздействия внешнего электрического поля

Т. И. Белянкова^1, *, В. В. Калинчук^1, **

¹ Южный научный центр РАН
Ростов-на-Дону, Россия

^* E-mail: tbelen415@mail.ru
^** E-mail: vkalin415@mail.ru

Поступила в редакцию 03.02.2021
После доработки 25.02.2021
Принята к публикации 12.03.2021

DOI: 10.31857/S003282352103005X

Аннотация

Развивается метод исследования волн Релея на поверхности неоднородной предварительно напряженной электроупругой среды, находящейся под воздействием внешнего электростатического поля. Среда представляет собой однородное полупространство с неоднородным покрытием, выполненным из функционально градиентного материала. Полупространство и покрытие в естественном состоянии (ЕС) представляют собой пьезоэлектрики класса 6 мм, оси симметрии которых совпадают и ориентированы по нормали к поверхности среды. Начально-деформированное состояние (НДС) покрытия вызвано действием начальных механических усилий и внешнего электростатического поля. Методами операционного исчисления краевая задача о колебаниях среды сведена к системе обыкновенных дифференциальных уравнений с переменными коэффициентами, которая, в свою очередь, сведена к системе задач Коши с начальными условиями. Использование численных методов позволяет построить интегральное представление, описывающее движение произвольной точки среды, а также дисперсионное уравнение, решение которого определяет основные характеристики поверхностных акустических волн. Метод позволяет исследовать влияние свойств покрытия, градиентности и локализации неоднородности, вида начального напряженного состояния и величины начальных напряжений, внешнего электростатического поля на параметры распространения релеевcких волн в широком диапазоне изменения параметров.

Ключевые слова: пьезоэлектрическая структура, подложка, покрытие, начальные напряжения, внешнее электростатическое поле, функционально градиентный пьезоэлектрический материал (ФГПМ), волны Релея

1. Введение. Особенности технологии получения новых типов сегнетоэлектрических структур из кристаллических пленок или керамики с переменными свойствами приводят к появлению деформаций, существенно изменяющих физические свойства исходных материалов. Это обуславливает необходимость усовершенствования заложенных [1–5] фундаментальных основ создания акустоэлектронных устройств. В работах [6–8] проведена последовательная линеаризация и построены линеаризованные определяющие соотношения динамики однородных или слоисто-неоднородных предварительно напряженных электро- [6, 7] и электротермоупругих [8] сред при наличии внешних электрических полей. Влияние электростатического поля на особенности распространения акустических волн в кристаллических пластинах рассмотрено в статьях [5, 9]. В работе [10] на примере структур “пьезоэлектрический кристалл/изотропная подложка” и “изотропный слой/пьезоэлектрическая подложка” исследовано влияние электростатического поля на параметры дисперсии и анизотропию распространения волн Релея и Лява. Особенности распространения сдвиговых волн в слоистых преднапряженных средах рассмотрены в [11–15]. Изучено влияние начальных напряжений на скорости распространения волн Лява и Гуляева–Блюштейна [11–14]. Исследованы процессы распространения волн в функционально градиентных пьезоактивных средах специального типа, параметры которых допускают построение аналитического решения [15–18]. Более общая модель неоднородного покрытия рассмотрена в работах [19–23]. Покрытие представляет собой либо слой, выполненный из ФГПМ [19, 20, 23], либо пакет неоднородных слоев [21, 22]. В этих работах исследованы особенности распространения sh-волн в зависимости от физических свойств покрытия, в частности, характера, интенсивности и области локализации неоднородности. Процесс распространения релеевских волн в функционально градиентных средах в отсутствие начальных напряжений исследовался в [24]. Изучено влияние коэффициентов градиентности изменения упругих и электрических модулей на изменение скорости волн Релея. В работе [25] исследованы дисперсионные соотношения для поверхностных акустических волн Лява, распространяющихся в трехслойном изотропном упругом полупространстве. Установлены свойства структуры среды, при которых выполняются условия существования волны Лява. В статье [26] исследованы нелинейные уравнения, описывающие поведение упругих пьезоэлектриков в электромагнитном поле при учете процессов релаксации диэлектрической поляризации. Получены дисперсионные уравнения, вычислены скорости и декременты затухания таких волн. В работе [27] проведен цикл исследований по применению поверхностных акустических волн (ПАВ) для неразрушающей диагностики слоистых сред. Исследовано дисперсионное уравнение для многослойного композита, контактирующего с анизотропным полупространством. Показано, что изменение физических параметров и геометрии любого из внутренних слоев приводит к изменению характера дисперсионных кривых. В работе [28] предложен полуаналитический подход к исследованию многослойных структур из однородных слоев, позволяющий эффективно исследовать задачи дифракции, энергетические характеристики и направленность излучения волн, возбуждаемых в многослойной среде поверхностными пьезоактуаторами. В настоящей работе развит метод исследования особенностей распространения ПАВ в сегнетоэлектрической гетероструктуре с предварительно напряженным покрытием, выполненным из ФГПМ и находящимся под воздействием внешнего электростатического поля. Метод позволяет изучать влияние свойств покрытия, градиентности неоднородности и ее локализации, вида начального напряженного состояния и величины начальных напряжений, ориентации и напряженности внешнего электростатического поля на основные характеристики волн Релея в широком диапазоне изменения параметров.

2. Постановка задачи. Рассматривается задача об установившихся гармонических колебаниях сегнетоэлектрической гетероструктуры, представляющей собой неоднородное пьезоактивное покрытие $0 \leqslant {{x}_{3}} \leqslant H$ на пьезоэлектрической подложке ${{x}_{3}} \leqslant 0$, $\left| {{{x}_{1}}} \right|$, $\left| {{{x}_{2}}} \right| \leqslant \infty $. Поверхность среды предполагается свободной от напряжений, свойства покрытия описываются функциями

(2.1)

${{\rho }^{{\left( 1 \right)}}} = \rho _{0}^{{}}f_{\rho }^{{\left( 1 \right)}}\left( {{{x}_{3}}} \right),\quad c_{{ij}}^{{\left( 1 \right)}} = c_{{ij}}^{0}f_{c}^{{\left( 1 \right)}}\left( {{{x}_{3}}} \right),\quad e_{{ij}}^{{\left( 1 \right)}} = e_{{ij}}^{0}f_{e}^{{\left( 1 \right)}}\left( {{{x}_{3}}} \right),\quad \varepsilon _{{ij}}^{{\left( 1 \right)}} = \varepsilon _{{ij}}^{0}f_{\varepsilon }^{{\left( 1 \right)}}\left( {{{x}_{3}}} \right)$

${{\rho }_{0}}$, $с_{{ij}}^{0}$, $e_{{ij}}^{0}$, $\varepsilon _{{ij}}^{0}$ – соответственно плотность, упругие, пьезоэлектрические и диэлектрические модули материала подложки класса 6 мм с осью симметрии, направленной вдоль оси ${{x}_{3}}$. НДС покрытия однородно и наводится за счет действия механических напряжений и электростатического поля [6–8]:

(2.2)

${\mathbf{R}} = {\mathbf{r}} \cdot {\mathbf{\Lambda ,}}\quad {\mathbf{G}} = {\mathbf{\Lambda }} \cdot {{{\mathbf{\Lambda }}}^{{\mathbf{T}}}}{\mathbf{,}}\quad {\mathbf{\Lambda }} = {{\delta }_{{ij}}}{{{v}}_{i}}{{{\mathbf{r}}}_{i}}{{{\mathbf{r}}}_{j}},\quad {{\varphi }_{0}} = - {{{\mathbf{E}}}_{0}} \cdot {\mathbf{R}},\quad {{{v}}_{i}} = {\text{const}}$

Здесь ${\mathbf{R}}$, r – радиус-векторы точки среды в НДС и в естественном состоянии (ЕС) соответственно, ${{{v}}_{i}} = 1 + {{\delta }_{i}}$, ${{\delta }_{i}}$ – главные относительные удлинения, ${{\delta }_{{ij}}}$ – символ Кронекера, ${{\varphi }_{0}}$ – электрический потенциал, ${{{\mathbf{E}}}_{0}}$ – напряженность начального внешнего электростатического поля.

Полагаем, что колебания среды вызваны действием удаленного источника и удовлетворяют условиям ($k = 1,3,4$, $s = 1,2,3$, $n = 1,2$)

(2.3)

${{u}_{k}}^{{\left( n \right)}} = {{u}_{k}}^{{\left( n \right)}}({{x}_{1}},{{x}_{3}}),\quad \partial {\text{/}}\partial {{x}_{2}} = 0,\quad {{u}_{2}}^{{\left( n \right)}} = u_{s}^{{\left( 0 \right)}} = 0$

Верхний индекс n = 0, 1, 2 отвечает соответственно вакууму, покрытию и полупространству. Ниже использованы безразмерные параметры [21–23]: $l{\kern 1pt} ' = l{\text{/}}H$, $\rho {\kern 1pt} {{'}^{{\left( n \right)}}} = {{\rho }^{{\left( n \right)}}}{\text{/}}{{\rho }^{{\left( 2 \right)}}}$, 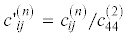, , 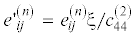, 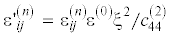$\varphi {\kern 1pt} {{'}^{{\left( n \right)}}} = {{\varphi }^{{\left( n \right)}}}{\text{/}}\left( {\xi H} \right)$, $E_{k}^{'} = {{{{E}_{k}}} \mathord{\left/ {\vphantom {{{{E}_{k}}} \xi }} \right. \kern-0em} \xi }$; ${{\varepsilon }^{{\left( 0 \right)}}}$ – диэлектрическая проницаемость вакуума, $\xi = {{10}^{{10}}}$ В/м, ${{\kappa }_{2}} = \omega H{\text{/}}V_{S}^{{\left( 2 \right)}}$ и ${{\kappa }_{{2e}}}\, = \,\omega H{\text{/}}V_{{Se}}^{{\left( 2 \right)}}$ – безразмерные частоты, $V_{{Se}}^{{\left( 2 \right)}}$ = $\sqrt {{\text{(}}c_{{44}}^{{\left( 2 \right)}} + {{{(e_{{15}}^{{\left( 2 \right)}})}}^{2}}{\text{/}}\varepsilon _{{11}}^{{\left( 2 \right)}}{\text{)/}}{{\rho }^{{\left( 2 \right)}}}} $ и $V_{S}^{{\left( 2 \right)}}\, = \,\sqrt {c_{{44}}^{{\left( 2 \right)}}{\text{/}}{{\rho }^{{\left( 2 \right)}}}} $ – скорости объемных сдвиговых волн с учетом и без учета пьезоэлектрических свойств среды. Далее штрихи опущены.

Задача о движении составной преднапряженной электроупругой среды описывается уравнениями [6–8] (${{{\mathbf{\Theta }}}^{{\left( n \right)}}} = {{{\mathbf{\Pi }}}^{{\left( n \right)}}} + {{{\mathbf{m}}}^{{\left( n \right)}}}$)

(2.4)

${{\nabla }_{0}} \cdot {{{\mathbf{\Theta }}}^{{\left( n \right)}}} = \rho _{0}^{{\left( n \right)}}{{{\mathbf{\ddot {u}}}}^{{{\mathbf{e}}\left( n \right)}}},\quad {{\nabla }_{0}} \cdot {{{\mathbf{d}}}^{{\left( n \right)}}} = 0;\quad n = {\text{ }}1,2$

Для вакуума справедливо

(2.5)

$\Delta {{\varphi }^{{\left( 0 \right)}}} = 0$

Граничные условия на поверхности среды ${{x}_{3}} = H$:

отсутствие напряжений

(2.6)

${\mathbf{n}} \cdot {{{\mathbf{\Theta }}}^{{\left( 1 \right)}}} = 0$

случай электрически свободной поверхности

(2.7)

${\mathbf{n}} \cdot {{{\mathbf{d}}}^{{(1)}}} = {\mathbf{n}} \cdot {{{\mathbf{d}}}^{{(0)}}},\quad {{\varphi }^{{(1)}}} = {{\varphi }^{{\left( 0 \right)}}}$

случай короткозамкнутой (металлизированной и заземленной) поверхности

(2.8)

${{\varphi }^{{(1)}}} = 0$

На границе раздела сред ${{x}_{3}} = 0$ предполагается выполнение условий

(2.9)

${{{\mathbf{u}}}^{{\mathbf{e}}}}^{{(1)}} = {{{\mathbf{u}}}^{{\mathbf{e}}}}^{{(2)}},\quad {\mathbf{n}} \cdot {{{\mathbf{\Theta }}}^{{(1)}}} = {\mathbf{n}} \cdot {{{\mathbf{\Theta }}}^{{(2)}}},\quad {\mathbf{n}} \cdot {{{\mathbf{d}}}^{{(1)}}} = {\mathbf{n}} \cdot {{{\mathbf{d}}}^{{(2)}}}$

На бесконечности

(2.10)

${{\left. {{{{\mathbf{u}}}^{{\mathbf{e}}}}^{{(2)}}} \right|}_{{{{x}_{3}} \to - \infty }}} \to 0,\quad {{\left. {{{\varphi }^{{(0)}}}} \right|}_{{{{x}_{3}} \to \infty }}} \to 0$

Здесь ${{\nabla }_{0}}$ – оператор Гамильтона, ${{{\mathbf{u}}}^{{\mathbf{e}}}}^{{(n)}} = \{ u_{1}^{{(n)}},u_{3}^{{(n)}},u_{4}^{{(n)}} = {{\varphi }^{{\left( n \right)}}}\} $ – расширенный вектор перемещений, ${{\varphi }^{{\left( n \right)}}}$ – электрический потенциал, ${\mathbf{n}}$ – вектор внешней нормали к поверхности структуры в системе координат, связанной с ЕС, $\rho _{0}^{{(n)}}$ – плотность материала n-й составляющей структуры в ЕС, $\Delta $ – оператор Лапласа. Компоненты линеаризованных тензора напряжений Пиолы ${{{\mathbf{\Pi }}}^{{\left( n \right)}}}$, электрического тензора Пиолы–Максвелла ${{{\mathbf{m}}}^{{\left( n \right)}}}$ и “материального” вектора индукции ${{{\mathbf{d}}}^{{\left( n \right)}}}$ представляются в виде [6–8] ($k,l,s,p = 1,2,3$, $n = 1,2$):

(2.11)

$\begin{gathered} \Theta _{{lk}}^{{\left( n \right)}} = \Pi _{{lk}}^{{\left( n \right)}} + m_{{lk}}^{{\left( n \right)}},\quad \Pi _{{lk}}^{{\left( n \right)}} = c_{{lksp}}^{{\left( n \right)*}}u_{{s,p}}^{{\left( n \right)}} + e_{{lkp}}^{{\left( n \right)*}}\varphi _{{,p}}^{{\left( n \right)}} \\ m_{{lk}}^{{\left( n \right)}} = \zeta _{{lksp}}^{{\left( n \right)*}}u_{{s,p}}^{{\left( n \right)}} + \psi _{{lkp}}^{{\left( n \right)*}}\varphi _{{,p}}^{{\left( n \right)}},\quad d_{l}^{{\left( n \right)}} = g_{{lsp}}^{{\left( n \right)*}}u_{{s,p}}^{{\left( n \right)}} - \eta _{{lp}}^{{\left( n \right)*}}\varphi _{{,p}}^{{\left( n \right)}} \\ \end{gathered} $

Далее для удобства используем представление тензора напряжений и вектора индукции в виде:

(2.12)

$\Theta _{{lk}}^{{\left( n \right)}} = \theta _{{lksp}}^{{\left( n \right)}}u_{{s,p}}^{{\left( n \right)}} + \theta _{{lk4p}}^{{\left( n \right)}}\varphi _{{,p}}^{{\left( n \right)}},\quad d_{l}^{{\left( n \right)}} = \theta _{{l4sp}}^{{\left( n \right)}}u_{{s,p}}^{{\left( n \right)}} + \theta _{{l44p}}^{{\left( n \right)}}\varphi _{{,p}}^{{\left( n \right)}},$

где

(2.13)

$\begin{gathered} \theta _{{lksp}}^{{\left( n \right)}} = c_{{lksp}}^{{\left( n \right)*}} + M_{{lksp}}^{{\left( n \right)}},\quad \theta _{{lk4p}}^{{\left( n \right)}} = e_{{lkp}}^{{\left( n \right)*}} + M_{{lk4p}}^{{\left( n \right)}} \\ \theta _{{l4sp}}^{{\left( n \right)}} = e_{{lsp}}^{{\left( n \right)*}} + M_{{l4sp}}^{{\left( n \right)}},\quad \theta _{{l44p}}^{{\left( n \right)}} = - \eta _{{lp}}^{{\left( n \right)*}} \\ M_{{lksp}}^{{\left( n \right)}} = \zeta _{{lksp}}^{{\left( n \right)*}},\quad M_{{lk4p}}^{{\left( n \right)}} = \psi _{{lkp}}^{{\left( n \right)*}},\quad M_{{l4sp}}^{{\left( n \right)}} = \psi _{{lsp}}^{{\left( n \right)*}};\quad k,l,s,p = 1,2,3 \\ \end{gathered} $

Вид коэффициентов $c_{{lksp}}^{{\left( 1 \right)*}}$, $e_{{lsp}}^{{\left( 1 \right)*}}$, $\zeta _{{lksp}}^{{\left( 1 \right)*}}$, $\psi _{{lkp}}^{{\left( 1 \right)*}}$, $\eta _{{lp}}^{{\left( 1 \right)*}}$ и $g_{{lsp}}^{{\left( 1 \right)*}} = e_{{lsp}}^{{\left( 1 \right)*}} + \psi _{{lsp}}^{{\left( 1 \right)*}}$ для общего случая преднапряженного покрытия приведен в работах [7, 8]. Следует отметить, что коэффициенты $c_{{lksp}}^{{\left( 1 \right)*}}$, $e_{{lsp}}^{{\left( 1 \right)*}}$ и $\eta _{{lp}}^{{\left( 1 \right)*}}$ являются функциями ${{x}_{3}}$, компоненты $M_{{lksp}}^{{\left( 1 \right)}}$ не зависят от ${{x}_{3}}$ и определены направлением и величиной напряженности начального электростатического поля. В общем случае компоненты $\theta _{{lksp}}^{{\left( 1 \right)}}$ и $M_{{lksp}}^{{\left( 1 \right)}}$ зависят от характера и величины наведенных начальных деформаций. Для однородного материала подложки в ЕС выполняются соотношения

$c_{{lksp}}^{{\left( 2 \right)*}} = c_{{lksp}}^{{\left( 2 \right)}},\quad e_{{lsp}}^{{\left( 2 \right)*}} = g_{{lsp}}^{{\left( 2 \right)*}} = e_{{lsp}}^{{\left( 2 \right)}},\quad \eta _{{lp}}^{{\left( 2 \right)*}} = \varepsilon _{{lp}}^{{\left( 2 \right)}} = {{\varepsilon }_{0}}{{\delta }_{{lp}}} + \beta _{{lp}}^{{\left( 2 \right)}},\quad M_{{lksp}}^{{\left( 2 \right)}} = 0$

С учетом зависимостей (2.1), (2.3) и представлений (2.11)–(2.13) краевая задача (2.4)–(2.10) о колебаниях электроупругой среды с предварительно напряженным неоднородным покрытием принимает вид [19–21, 23]:

для неоднородного покрытия $0 \leqslant {{x}_{3}} \leqslant H$

${\mathbf{L}}_{{11}}^{{(1)}}[u_{1}^{{(1)}}] + {\mathbf{L}}_{{12}}^{{(1)}}[u_{3}^{{(1)}}] + {{\theta }^{{(1)}}}u_{{3,13}}^{{(1)}} + {\mathbf{L}}_{{13}}^{{(1)}}[u_{4}^{{(1)}}] + {{\psi }^{{(1)}}}u_{{4,13}}^{{(1)}} + \theta _{{3113,3}}^{{(1)}}u_{{1,3}}^{{(1)}} + \theta _{{1313,3}}^{{(1)}}u_{{3,1}}^{{(1)}} + \theta _{{3141,3}}^{{(1)}}u_{{4,1}}^{{(1)}} = 0$

(2.14)

${\mathbf{L}}_{{12}}^{{(1)}}[u_{1}^{{(1)}}] + {{\theta }^{{(1)}}}u_{{1,13}}^{{(1)}} + {\mathbf{L}}_{{22}}^{{(1)}}[u_{3}^{{(1)}}] + {\mathbf{L}}_{{23}}^{{(1)}}[u_{4}^{{(1)}}] + \theta _{{1133,3}}^{{(1)}}u_{{1,1}}^{{(1)}} + \theta _{{3333,3}}^{{(1)}}u_{{3,3}}^{{(1)}} + \theta _{{3343,3}}^{{(1)}}u_{{4,3}}^{{(1)}} = 0$

${\mathbf{L}}_{{13}}^{{(1)}}[u_{1}^{{(1)}}] + {{\psi }^{{(1)}}}u_{{1,13}}^{{(1)}} + {\mathbf{L}}_{{23}}^{{(1)}}[u_{3}^{{(1)}}] + {\mathbf{L}}_{{33}}^{{(1)}}[u_{4}^{{(1)}}] + \theta _{{1143,3}}^{{(1)}}u_{{1,1}}^{{(1)}} + \theta _{{3343,3}}^{{(1)}}u_{{3,3}}^{{(1)}} + \theta _{{3443,3}}^{{(1)}}u_{{4,3}}^{{(1)}} = 0$

для подложки ${{x}_{3}} \leqslant 0$

(2.15)

$\begin{gathered} {\mathbf{L}}_{1}^{{(2)}}[u_{1}^{{(2)}}] + {{\theta }^{{(2)}}}u_{{3,13}}^{{(2)}} + {{\psi }^{{(2)}}}u_{{4,13}}^{{(2)}} = 0 \\ {{\theta }^{{(2)}}}u_{{1,13}}^{{(2)}} + {\mathbf{L}}_{2}^{{(2)}}[u_{3}^{{(2)}}] + {\mathbf{L}}_{3}^{{(2)}}[u_{4}^{{(2)}}] = 0 \\ {{\psi }^{{(2)}}}u_{{1,13}}^{{(2)}} + {\mathbf{L}}_{3}^{{(2)}}[u_{3}^{{(2)}}] + {\mathbf{L}}_{4}^{{(2)}}[u_{4}^{{(2)}}] = 0 \\ \end{gathered} $

для вакуума ${{x}_{3}} > H$

(2.16)

$\sum\limits_{k = 1,3} {u_{{4,kk}}^{{\left( 0 \right)}}} = 0$

Граничные условия на поверхности ${{x}_{3}} = H$

(2.17)

$\begin{gathered} \Theta _{{31}}^{{(1)}} = M_{{3133}}^{{(1)}}u_{{3,3}}^{{(1)}} + \theta _{{3113}}^{{(1)}}u_{{1,3}}^{{(1)}} + \theta _{{1313}}^{{(1)}}u_{{3,1}}^{{(1)}} + \theta _{{3141}}^{{(1)}}u_{{4,1}}^{{(1)}} + M_{{3143}}^{{(1)}}u_{{4,3}}^{{(1)}} = 0 \\ \Theta _{{33}}^{{(1)}} = \theta _{{1133}}^{{(1)}}u_{{1,1}}^{{(1)}} + \theta _{{3333}}^{{(1)}}u_{{3,3}}^{{(1)}} + M_{{3313}}^{{(1)}}u_{{1,3}}^{{(1)}} + M_{{3341}}^{{(1)}}u_{{4,1}}^{{(1)}} + \theta _{{3343}}^{{(1)}}u_{{4,3}}^{{(1)}} = 0 \\ \end{gathered} $

случай электрически свободной поверхности

(2.18)

$\begin{gathered} d_{3}^{{(1)}} = \theta _{{1143}}^{{(1)}}u_{{1,1}}^{{(1)}} + \theta _{{3343}}^{{(1)}}u_{{3,3}}^{{(1)}} + M_{{3413}}^{{(1)}}u_{{1,3}}^{{(1)}} + M_{{3431}}^{{(1)}}u_{{3,1}}^{{(1)}} + \theta _{{3443}}^{{(1)}}u_{{4,3}}^{{(1)}} \\ d_{3}^{{(0)}} = d_{3}^{{(1)}},\quad u_{4}^{{(0)}} = u_{4}^{{(1)}} \\ \end{gathered} $

случай короткозамкнутой (металлизированной и заземленной) поверхности

(2.19)

$u_{4}^{{(1)}} = 0$

Граничные условия на поверхности ${{x}_{3}} = 0$

(2.20)

$\Theta _{{31}}^{{(1)}} = \Theta _{{31}}^{{(2)}},\quad \Theta _{{33}}^{{(1)}} = \Theta _{{33}}^{{(2)}},\quad d_{3}^{{(1)}} = d_{3}^{{(2)}},\quad u_{1}^{{(1)}} = u_{1}^{{(2)}},\quad u_{3}^{{(1)}} = u_{3}^{{(2)}},\quad u_{4}^{{(1)}} = u_{4}^{{(2)}}$

Условие на бесконечности

(2.21)

${{\left. {u_{1}^{{(2)}},u_{3}^{{(2)}},u_{4}^{{(2)}}} \right|}_{{{{x}_{2}} \to - \infty }}} \to 0,\quad {{\left. {u_{4}^{{(0)}}} \right|}_{{{{x}_{2}} \to \infty }}} \to 0$

В уравнениях (2.13) и (2.14) использованы обозначения

${\mathbf{L}}_{{11}}^{{\left( 1 \right)}} = \theta _{{1111}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \theta _{{3113}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}} + {{\rho }^{{\left( 1 \right)}}}\kappa _{2}^{2},\quad {\mathbf{L}}_{{12}}^{{\left( 1 \right)}} = M_{{1131}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + M_{{3133}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}$

${\mathbf{L}}_{{13}}^{{\left( 1 \right)}} = M_{{1141}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + M_{{3143}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}},\quad {\mathbf{L}}_{{22}}^{{\left( 1 \right)}} = \theta _{{1331}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \theta _{{3333}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}} + {{\rho }^{{\left( 1 \right)}}}\kappa _{2}^{2}$

(2.22)

${\mathbf{L}}_{{23}}^{{\left( 1 \right)}} = \theta _{{1341}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \theta _{{3343}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}},\quad {\mathbf{L}}_{{33}}^{{\left( 1 \right)}} = \theta _{{1441}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \theta _{{3443}}^{{\left( 1 \right)}}\frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}}$

${\mathbf{L}}_{1}^{{\left( 2 \right)}} = {\mathbf{L}}_{{11}}^{{\left( 2 \right)}},\quad {\mathbf{L}}_{2}^{{\left( 2 \right)}} = {\mathbf{L}}_{{22}}^{{\left( 2 \right)}},\quad {\mathbf{L}}_{3}^{{\left( 2 \right)}} = {\mathbf{L}}_{{23}}^{{\left( 2 \right)}},\quad {\mathbf{L}}_{4}^{{\left( 2 \right)}} = {\mathbf{L}}_{{33}}^{{\left( 2 \right)}}$

${{\theta }^{{\left( n \right)}}} = \theta _{{1133}}^{{\left( n \right)}} + \theta _{{1313}}^{{\left( n \right)}},\quad {{\psi }^{{\left( n \right)}}} = \theta _{{1143}}^{{\left( n \right)}} + \theta _{{3141}}^{{\left( n \right)}}$

Участвующие в представлениях (2.14)–(2.22) коэффициенты в рамках предположений (2.2) с учетом свойств материала имеют вид

$\theta _{{1111}}^{{\left( 1 \right)}} = c_{{11}}^{{\left( 1 \right)}}{v}_{1}^{2} + {{P}_{{11}}} - {{\varepsilon }_{0}}\frac{{{{{v}}_{2}}{{{v}}_{3}}}}{{{{{v}}_{1}}}}E_{1}^{2},\quad \theta _{{3333}}^{{\left( 1 \right)}} = c_{{33}}^{{\left( 1 \right)}}{v}_{3}^{2} + {{P}_{{33}}} - {{\varepsilon }_{0}}\frac{{{{{v}}_{1}}{{{v}}_{2}}}}{{{{{v}}_{3}}}}E_{3}^{2}$

$\theta _{{1133}}^{{\left( 1 \right)}} = \theta _{{3311}}^{{\left( 1 \right)}} = c_{{13}}^{{\left( 1 \right)}}{{{v}}_{1}}{{{v}}_{3}} + \frac{1}{2}{{\varepsilon }_{0}}{{{v}}_{2}}{{M}_{{13}}},\quad \theta _{{1313}}^{{\left( 1 \right)}} = \theta _{{3131}}^{{\left( 1 \right)}} = c_{{44}}^{{\left( 1 \right)}}{{{v}}_{1}}{{{v}}_{3}} - \frac{1}{2}{{\varepsilon }_{0}}{{{v}}_{2}}{{M}_{{13}}}$

$\theta _{{1331}}^{{\left( 1 \right)}} = c_{{44}}^{{\left( 1 \right)}}{v}_{3}^{2} + {{P}_{{11}}} - {{\varepsilon }_{0}}\frac{{{{{v}}_{2}}{{{v}}_{3}}}}{{{{{v}}_{1}}}}E_{3}^{2},\quad \theta _{{3113}}^{{\left( 1 \right)}} = c_{{44}}^{{\left( 1 \right)}}{v}_{1}^{2} + {{P}_{{33}}} - {{\varepsilon }_{0}}\frac{{{{{v}}_{1}}{{{v}}_{2}}}}{{{{{v}}_{3}}}}E_{1}^{2}$

$\theta _{{1143}}^{{\left( 1 \right)}} = \theta _{{3411}}^{{\left( 1 \right)}} = e_{{31}}^{{\left( 1 \right)}}{{{v}}_{1}} + {{\varepsilon }_{0}}{{{v}}_{2}}{{E}_{3}},\quad \theta _{{3343}}^{{\left( 1 \right)}} = e_{{33}}^{{\left( 1 \right)}}{{{v}}_{3}} - {{\varepsilon }_{0}}{{E}_{3}}{{{v}}_{1}}{{{v}}_{2}}{\text{/}}{{{v}}_{3}}$

$\theta _{{1341}}^{{\left( 1 \right)}} = \theta _{{1431}}^{{\left( 1 \right)}} = e_{{15}}^{{\left( 1 \right)}}{{{v}}_{3}} - {{\varepsilon }_{0}}{{E}_{3}}{{{v}}_{2}}{{{v}}_{3}}{\text{/}}{{{v}}_{1}},\quad \theta _{{3141}}^{{\left( 1 \right)}} = \theta _{{1413}}^{{\left( 1 \right)}} = e_{{15}}^{{\left( 1 \right)}}{{{v}}_{1}} - {{\varepsilon }_{0}}{{{v}}_{2}}{{E}_{3}}$

$M_{{1131}}^{{\left( 1 \right)}} = M_{{1311}}^{{\left( 1 \right)}} = - {{\varepsilon }_{0}}\frac{{{{{v}}_{2}}{{{v}}_{3}}}}{{{{{v}}_{1}}}}{{E}_{1}}{{E}_{3}},\quad M_{{1141}}^{{\left( 1 \right)}} = M_{{1411}}^{{\left( 1 \right)}} = - {{\varepsilon }_{0}}\frac{{{{{v}}_{2}}{{{v}}_{3}}}}{{{{{v}}_{1}}}}{{E}_{1}}$

$M_{{3313}}^{{\left( 1 \right)}} = M_{{3133}}^{{\left( 1 \right)}} = - {{\varepsilon }_{0}}\frac{{{{{v}}_{1}}{{{v}}_{2}}}}{{{{{v}}_{3}}}}{{E}_{1}}{{E}_{3}},\quad M_{{3341}}^{{\left( 1 \right)}} = M_{{1433}}^{{\left( 1 \right)}} = {{\varepsilon }_{0}}{{{v}}_{2}}{{E}_{1}}$

$M_{{1343}}^{{\left( 1 \right)}} = M_{{3431}}^{{\left( 1 \right)}} = - {{\varepsilon }_{0}}{{{v}}_{2}}{{E}_{1}},\quad M_{{3143}}^{{\left( 1 \right)}} = M_{{3413}}^{{\left( 1 \right)}} = - {{\varepsilon }_{0}}{{E}_{1}}{{{v}}_{1}}{{{v}}_{2}}{\text{/}}{{{v}}_{3}}$

${{M}_{{13}}} = E_{1}^{2} + E_{3}^{2} - E_{2}^{2},\quad {{E}_{i}} = {{W}_{i}}{\text{/}}{{{v}}_{i}}$

Здесь ${{P}_{{ii}}}$ и ${{W}_{i}}$ – компоненты тензора Кирхгофа, определяющие действие начальных механических напряжений, и компоненты вектора напряженности начального электростатического поля в системе координат, связанной с ЕС.

Далее рассматриваются две важные для изучения особенностей процесса распространения волн Релея задачи:

задача I – “открытый случай”. Задача описывается системой уравнений движения (2.14)–(2.16), (2.22) с граничными условиями (2.17), (2.18), (2.20) и (2.21);

задача II – “короткозамкнутый случай”. Поверхность среды металлизирована и заземлена. Задача описывается уравнениями движения (2.14), (2.15), (2.22) с граничными условиями (2.17), (2.19)–(2.21).

3. Решение задач. Решение задач I и II строится в пространстве образов Фурье ($\alpha $ – параметр преобразования по координате ${{x}_{1}}$):

(3.1)

$U_{p}^{{\left( 1 \right)}}\left( {\alpha ,{{x}_{3}}} \right) = \sum\limits_{k = 1}^6 {c_{k}^{{\left( 1 \right)}}y_{{sk}}^{{\left( 1 \right)}}\left( {\alpha ,{{x}_{3}}} \right)} ;\quad p = 1,3,4,\quad s = 4,5,6$

(3.2)

$U_{p}^{{(2)}}(\alpha ,{{x}_{3}}) = \sum\limits_{k = 1}^3 {f_{{pk}}^{{(2)}}c_{k}^{{\left( 2 \right)}}{{e}^{{\sigma _{k}^{{(2)}}{{x}_{3}}}}}} ,\quad U_{4}^{{\left( 0 \right)}}(\alpha ,{{x}_{3}}) = c_{1}^{{\left( 0 \right)}}{{e}^{{ - \alpha {{x}_{3}}}}}$

Функции $y_{{sk}}^{{\left( 1 \right)}}\left( {\alpha ,{{x}_{3}}} \right)$ в представлении (3.1) являются линейно независимыми решениями задачи Коши с начальными условиями $y_{{sk}}^{{\left( 1 \right)}}\left( {\alpha ,\,0} \right) = {{\delta }_{{sk}}}$ для уравнения

(3.3)

${{{\mathbf{Y}}}^{{\left( 1 \right)'}}} = {{{\mathbf{R}}}^{{\left( 1 \right)}}}\left( {\alpha ,{{x}_{3}}} \right){{{\mathbf{Y}}}^{{\left( 1 \right)}}}$

(3.4)

${{{\mathbf{Y}}}^{{\left( 1 \right)}}} = \left( {\begin{array}{*{20}{c}} {{\mathbf{Y}}_{{\mathbf{\Sigma }}}^{1}} \\ {{\mathbf{Y}}_{{\mathbf{u}}}^{1}} \end{array}} \right),\quad {\mathbf{Y}}_{{\mathbf{\Sigma }}}^{1} = {{\{ \Theta _{{31}}^{{F\left( 1 \right)}},\Theta _{{33}}^{{F\left( 1 \right)}},D_{3}^{{F\left( 1 \right)}}\} }^{T}},\quad {\mathbf{Y}}_{{\mathbf{u}}}^{1} = {{\{ U_{1}^{{\left( 1 \right)}},U_{3}^{{\left( 1 \right)}},U_{4}^{{\left( 1 \right)}}\} }^{T}}$

Здесь $\Theta _{{31}}^{{F\left( n \right)}}$, $\Theta _{{33}}^{{F\left( n \right)}}$, $D_{3}^{{F\left( n \right)}}$, $U_{k}^{{\left( n \right)}}$ – трансформанты Фурье компонент тензора напряжений, вектора индукции (2.12), (2.13) и расширенного вектора смещений; ${{\delta }_{{kp}}}$ – символ Кронекера. Элементы матрицы ${{{\mathbf{R}}}^{{\left( 1 \right)}}}\left( {\alpha ,{{x}_{3}}} \right)$ = $\left\| {{{R}_{{ij}}}} \right\|_{{i,j = 1}}^{6}$ имеют вид:

${{R}_{{11}}} = i\alpha {{g}_{{12}}}{\text{/}}{{g}_{0}},\quad {{R}_{{12}}} = - i\alpha {{g}_{{11}}}{\text{/}}{{g}_{0}},\quad {{R}_{{13}}} = i\alpha {{g}_{{13}}}{\text{/}}{{g}_{0}}$

${{R}_{{14}}} = - {{\alpha }^{2}}({{(\theta _{{1133}}^{{\left( 1 \right)}})}^{2}}{{r}_{0}} + {{(\theta _{{1143}}^{{\left( 1 \right)}})}^{2}}{{r}_{5}} - 2\theta _{{1133}}^{{\left( 1 \right)}}\theta _{{1143}}^{{\left( 1 \right)}}{{r}_{1}}){\text{/}}{{g}_{0}} + {{P}_{1}}$

${{R}_{{15}}} = {{\alpha }^{2}}{\text{(}}M_{{3341}}^{{\left( 1 \right)}}{{g}_{{13}}} - \theta _{{3131}}^{{\left( 1 \right)}}{{g}_{{12}}} + M_{{1131}}^{{\left( 1 \right)}}{{g}_{0}}{\text{)/}}{{g}_{0}}$

${{R}_{{16}}} = {{\alpha }^{2}}{\text{(}}M_{{3341}}^{{\left( 1 \right)}}{{g}_{{11}}} - \theta _{{3141}}^{{\left( 1 \right)}}{{g}_{{12}}} + M_{{1141}}^{{\left( 1 \right)}}{{g}_{0}}{\text{)/}}{{g}_{0}}$

${{R}_{{21}}} = - i\alpha {{g}_{{22}}}{\text{/}}{{g}_{0}},\quad {{R}_{{22}}} = i\alpha {{g}_{{21}}}{\text{/}}{{g}_{0}},\quad {{R}_{{23}}} = - i\alpha {{g}_{{23}}}{\text{/}}{{g}_{0}},\quad {{R}_{{24}}} = {{R}_{{15}}}$

${{R}_{{25}}} = - {{\alpha }^{2}}({{(M_{{3341}}^{{\left( 1 \right)}})}^{2}}{{r}_{5}} + {{(\theta _{{3131}}^{{\left( 1 \right)}})}^{2}}{{r}_{3}} - 2M_{{3341}}^{{\left( 1 \right)}}\theta _{{3131}}^{{\left( 1 \right)}}{{r}_{4}}){\text{/}}{{g}_{0}} + {{P}_{2}}$

${{R}_{{26}}} = - {{\alpha }^{2}}(M_{{3341}}^{{\left( 1 \right)}}{{g}_{{21}}} - \theta _{{3141}}^{{\left( 1 \right)}}{{g}_{{23}}} - \theta _{{1431}}^{{\left( 1 \right)}}{{g}_{0}}){\text{/}}{{g}_{0}}$

${{R}_{{31}}} = - i\alpha {{g}_{{32}}}{\text{/}}{{g}_{0}},\quad {{R}_{{32}}} = i\alpha {{g}_{{31}}}{\text{/}}{{g}_{0}},\quad {{R}_{{33}}} = - i\alpha {{g}_{{33}}}{\text{/}}{{g}_{0}}$

${{R}_{{34}}} = {{R}_{{16}}},\quad {{R}_{{35}}} = {{R}_{{26}}}$

${{R}_{{36}}} = - {{\alpha }^{2}}({{(M_{{3341}}^{{\left( 1 \right)}})}^{2}}{{r}_{0}} + {{(\theta _{{3141}}^{{\left( 1 \right)}})}^{2}}{{r}_{3}} - 2M_{{3341}}^{{\left( 1 \right)}}\theta _{{3141}}^{{\left( 1 \right)}}{{r}_{2}} - \theta _{{1441}}^{{\left( 1 \right)}}{{g}_{0}}){\text{/}}{{g}_{0}}$

(3.5)

${{R}_{{41}}} = {{r}_{3}}{\text{/}}{{g}_{0}},\quad {{R}_{{42}}} = - {{r}_{2}}{\text{/}}{{g}_{0}},\quad {{R}_{{43}}} = {{r}_{4}}{\text{/}}{{g}_{0}},\quad {{R}_{{44}}} = {{R}_{{11}}},\quad {{R}_{{45}}} = {{R}_{{21}}},\quad {{R}_{{46}}} = {{R}_{{31}}}$

${{R}_{{51}}} = {{R}_{{42}}},\quad {{R}_{{52}}} = {{r}_{0}}{\text{/}}{{g}_{0}},\quad {{R}_{{53}}} = - {{r}_{1}}{\text{/}}{{g}_{0}},\quad {{R}_{{54}}} = {{R}_{{12}}},\quad {{R}_{{55}}} = {{R}_{{22}}},\quad {{R}_{{56}}} = {{R}_{{32}}}$

${{R}_{{61}}} = {{R}_{{43}}},\quad {{R}_{{62}}} = {{R}_{{53}}},\quad {{R}_{{63}}} = {{r}_{5}}{\text{/}}{{g}_{0}},\quad {{R}_{{64}}} = {{R}_{{13}}},\quad {{R}_{{65}}} = {{R}_{{23}}},\quad {{R}_{{66}}} = {{R}_{{33}}}$

${{g}_{0}} = \theta _{{3333}}^{{\left( 1 \right)}}{{r}_{0}} - M_{{3313}}^{{\left( 1 \right)}}{{r}_{2}} - \theta _{{3343}}^{{\left( 1 \right)}}{{r}_{1}},\quad {{r}_{0}} = {{(M_{{3143}}^{{\left( 1 \right)}})}^{2}} - \theta _{{3113}}^{{\left( 1 \right)}}\theta _{{3443}}^{{\left( 1 \right)}}$

${{r}_{1}} = M_{{3313}}^{{\left( 1 \right)}}M_{{3143}}^{{\left( 1 \right)}} - \theta _{{3113}}^{{\left( 1 \right)}}\theta _{{3343}}^{{\left( 1 \right)}},\quad {{r}_{2}} = \theta _{{3343}}^{{\left( 1 \right)}}M_{{3143}}^{{\left( 1 \right)}} - M_{{3313}}^{{\left( 1 \right)}}\theta _{{3443}}^{{\left( 1 \right)}}$

${{r}_{3}} = {{(\theta _{{3343}}^{{\left( 1 \right)}})}^{2}} - \theta _{{3333}}^{{\left( 1 \right)}}\theta _{{3443}}^{{\left( 1 \right)}},\quad {{r}_{4}} = \theta _{{3333}}^{{\left( 1 \right)}}M_{{3143}}^{{\left( 1 \right)}} - M_{{3313}}^{{\left( 1 \right)}}\theta _{{3343}}^{{\left( 1 \right)}}$

${{r}_{5}} = {{(M_{{3313}}^{{\left( 1 \right)}})}^{2}} - \theta _{{3113}}^{{\left( 1 \right)}}\theta _{{3333}}^{{\left( 1 \right)}},\quad {{g}_{{11}}} = (\theta _{{1143}}^{{\left( 1 \right)}}{{r}_{1}} - \theta _{{1133}}^{{\left( 1 \right)}}{{r}_{0}}),\quad {{g}_{{12}}} = (\theta _{{1143}}^{{\left( 1 \right)}}{{r}_{4}} - \theta _{{1133}}^{{\left( 1 \right)}}{{r}_{2}})$

${{g}_{{13}}} = (\theta _{{1143}}^{{\left( 1 \right)}}{{r}_{5}} - \theta _{{1133}}^{{\left( 1 \right)}}{{r}_{1}}),\quad {{g}_{{21}}} = (M_{{3341}}^{{\left( 1 \right)}}{{r}_{1}} - \theta _{{3131}}^{{\left( 1 \right)}}{{r}_{2}}),\quad {{g}_{{22}}} = (M_{{3341}}^{{\left( 1 \right)}}{{r}_{4}} - \theta _{{3131}}^{{\left( 1 \right)}}{{r}_{3}})$

${{g}_{{23}}} = (M_{{3341}}^{{\left( 1 \right)}}{{r}_{5}} - \theta _{{3131}}^{{\left( 1 \right)}}{{r}_{4}}),\quad {{g}_{{31}}} = (M_{{3341}}^{{\left( 1 \right)}}{{r}_{0}} - \theta _{{3141}}^{{\left( 1 \right)}}{{r}_{2}}),\quad {{g}_{{32}}} = (M_{{3341}}^{{\left( 1 \right)}}{{r}_{2}} - \theta _{{3141}}^{{\left( 1 \right)}}{{r}_{3}})$

${{g}_{{33}}} = (M_{{3341}}^{{\left( 1 \right)}}{{r}_{1}} - \theta _{{3141}}^{{\left( 1 \right)}}{{r}_{4}}),\quad {{P}_{1}} = {{\alpha }^{2}}\theta _{{1111}}^{{\left( 1 \right)}} - {{\rho }^{{\left( 1 \right)}}}\kappa _{2}^{2},\quad {{P}_{2}} = {{\alpha }^{2}}\theta _{{1331}}^{{\left( 1 \right)}} - {{\rho }^{{\left( 1 \right)}}}\kappa _{2}^{2}$

Уравнение (3.3) с обозначениями (3.4), (3.5) представляет собой систему обыкновенных дифференциальных уравнений (ОДУ) с переменными коэффициентами, линейно независимые решения которой строятся на основе численного решения набора задач Коши с начальными условиями при фиксированных значениях параметра $\alpha $. Для решения систем ОДУ могут быть использованы различные численные методы. Участвующие в представлении (3.2) величины $\sigma _{k}^{{\left( 2 \right)}}$ удовлетворяют уравнению

(3.6)

$\begin{gathered} \det {\mathbf{R}}_{\sigma }^{{\left( 2 \right)}}\left( \sigma \right) = 0 \\ {\mathbf{R}}_{\sigma }^{{\left( 2 \right)}}\left( s \right) = \left( {\begin{array}{*{20}{c}} {c_{{44}}^{{\left( 2 \right)}}{{s}^{2}} - {{P}_{1}}}&{ - i\alpha {{\theta }^{{\left( 2 \right)}}}s}&{ - i\alpha {{\psi }^{{\left( 2 \right)}}}s} \\ { - i\alpha {{\theta }^{{\left( 2 \right)}}}s}&{c_{{33}}^{{\left( 2 \right)}}{{s}^{2}} - {{P}_{2}}}&{e_{{33}}^{{\left( 2 \right)}}{{s}^{2}} - e_{{15}}^{{\left( 2 \right)}}{{\alpha }^{2}}} \\ { - i\alpha {{\psi }^{{\left( 2 \right)}}}s}&{e_{{33}}^{{\left( 2 \right)}}{{s}^{2}} - e_{{15}}^{{\left( 2 \right)}}{{\alpha }^{2}}}&{ - \varepsilon _{{33}}^{{\left( 2 \right)}}{{s}^{2}} + \varepsilon _{{11}}^{{\left( 2 \right)}}{{\alpha }^{2}}} \end{array}} \right) \\ \end{gathered} $

Коэффициенты $f_{{pk}}^{{\left( 2 \right)}}$ определяются из однородной системы линейных уравнений (3.6) с матрицей ${\mathbf{R}}_{\sigma }^{{\left( 2 \right)}}(\sigma _{k}^{{\left( 2 \right)}})$. При подстановке представлений (3.1) и (3.2) в граничные условия для вычисления неизвестных коэффициентов $c_{k}^{{\left( n \right)}}$ получается однородная система линейных алгебраических уравнений с матрицей [15–17, 22]

(3.7)

${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{B}}}^{{\left( 1 \right)}}}\left( H \right)}&{{{{\mathbf{G}}}^{{\left( 1 \right)}}}} \\ {{{{\mathbf{A}}}^{{\left( 1 \right)}}}\left( 0 \right)}&{{{{\mathbf{B}}}^{{\left( 2 \right)}}}\left( 0 \right)} \end{array}} \right)$

Размеры матрицы ${\mathbf{A}}$ (3.7) и матриц ее составляющих определяются типом задачи и граничными условиями. Матрица ${{{\mathbf{A}}}^{{\left( 1 \right)}}}\left( 0 \right)$ в силу принятых начальных условий задачи Коши, как для задачи I, так и для задачи II является единичной ${{{\mathbf{A}}}^{{\left( 1 \right)}}}\left( 0 \right) = {\mathbf{E}}$. Для задачи I матрица ${\mathbf{A}}$ имеет размерность $10 \times 10$, ее составляющие в соответствии с граничными условиями (2.17), (2.18), (2.20) и (2.21) представляются в виде

(3.8)

${{{\mathbf{B}}}^{{\left( 1 \right)}}}\left( H \right) = \left\| {B_{{ij}}^{{\left( 1 \right)}}} \right\|_{{i = 1,j = 1}}^{{4,6}},\quad {{{\mathbf{B}}}^{{\left( 2 \right)}}}\left( 0 \right) = \left\| {B_{{ij}}^{{\left( 2 \right)}}} \right\|_{{i = 1,j = 1}}^{{6,4}},\quad {{{\mathbf{G}}}^{{\left( 1 \right)}}} = \left\| {{{G}_{{ij}}}} \right\|_{{i,j = 1}}^{4},$

где

$B_{{ij}}^{{\left( 1 \right)}} = {{\gamma }_{i}}y_{{ij}}^{{\left( 1 \right)}},\quad {{\gamma }_{1}} = {{\gamma }_{2}} = 1,\quad {{\gamma }_{3}} = {{\gamma }_{4}} = {{e}^{{\alpha H}}};\quad i = 1,..4,\quad j = 1,..,6$

${{G}_{{34}}} = - {{\varepsilon }_{0}}\alpha ,\quad {{G}_{{44}}} = - 1,\quad {{G}_{{ij}}} = 0;\quad i = 1,2,3,\quad j = 1,2,\quad B_{{j4}}^{{\left( 2 \right)}} = 0;\quad j = 1,..,6$

$B_{{1k}}^{{\left( 2 \right)}} = c_{{44}}^{{(2)}}\sigma _{k}^{{\left( 2 \right)}}f_{{1k}}^{{\left( 2 \right)}} - i\alpha c_{{44}}^{{(2)}}f_{{3k}}^{{\left( 2 \right)}} - i\alpha e_{{15}}^{{\left( 2 \right)}}f_{{4k}}^{{\left( 2 \right)}}$

$B_{{2k}}^{{\left( 2 \right)}} = - i\alpha c_{{13}}^{{(2)}}f_{{1k}}^{{\left( 2 \right)}} + c_{{33}}^{{(2)}}\sigma _{k}^{{\left( 2 \right)}}f_{{3k}}^{{\left( 2 \right)}} + e_{{33}}^{{\left( 2 \right)}}\sigma _{k}^{{\left( 2 \right)}}f_{{4k}}^{{\left( 2 \right)}}$

$B_{{3k}}^{{\left( 2 \right)}} = - i\alpha e_{{31}}^{{(2)}}f_{{1k}}^{{\left( 2 \right)}} + e_{{33}}^{{(2)}}\sigma _{k}^{{\left( 2 \right)}}f_{{3k}}^{{\left( 2 \right)}} - \varepsilon _{{33}}^{{\left( 2 \right)}}\sigma _{k}^{{\left( 2 \right)}}f_{{4k}}^{{\left( 2 \right)}}$

$B_{{ik}}^{{\left( 2 \right)}} = - f_{{pk}}^{{\left( 2 \right)}};\quad i = 4,5,6,\quad p = 1,3,4,\quad k = 1,2,3$

Для задачи II матрица ${\mathbf{A}}$ имеет размерность $9 \times 9$, ${{{\mathbf{G}}}^{{\left( 1 \right)}}}$ – нулевая матрица размерности $3 \times 3$, матрицы ${{{\mathbf{B}}}^{{\left( 1 \right)}}}\left( H \right)$ и ${{{\mathbf{B}}}^{{\left( 2 \right)}}}\left( 0 \right)$ получаются путем вычеркивания 3-й строки и 4-го нулевого столбца в представлениях (3.8) соответствующих матриц задачи I, в матрице ${{{\mathbf{B}}}^{{\left( 1 \right)}}}\left( H \right)$ коэффициент ${{\gamma }_{i}} = 1$.

Применяя к выражениям (3.1) и (3.2) обратное преобразование Фурье получаем решение краевой задачи (2.4)–(2.10). В более общем случае при рассмотрении динамических задач о гармонических колебаниях пьезоэлектрической структуры с функционально градиентным преднапряженным покрытием, вызванных действием заданной на интервале [–а; а] поверхностной нагрузки q(х₁), решение задачи имеет вид [29]:

(3.9)

${{{\mathbf{u}}}^{{\left( n \right)}}}({{x}_{1}},{{x}_{3}}) = \frac{1}{{2\pi }}\int\limits_{ - a}^a {{{{\mathbf{k}}}^{{\left( n \right)}}}\left( {{{x}_{1}} - \xi ,{{x}_{3}}} \right){\mathbf{q}}\left( \xi \right)d\xi } $

с символом ядра

(3.10)

Контур $\Gamma $ в представлении (3.10) проходит в области аналитичности подынтегральной функции и выбирается в соответствии с правилами, указанными в работе [29]. Компоненты матрицы-функции ${{{\mathbf{K}}}^{{\left( n \right)}}}\left( {\alpha ,{{x}_{3}}} \right)$ в выражении (3.10) имеют вид ($l,j = 1,3,4$, $s = 4,5,6$):

(3.11)

${{\Delta }_{0}}$, ${{\Delta }_{{ns}}}$ – определитель и алгебраическое дополнение элемента ns матрицы ${\mathbf{A}}$ (3.6). Выражения (3.10) и (3.11) являются определяющими элементами в интегральном представлении перемещения произвольной точки среды (3.9). Основные характеристики волнового процесса определяются дисперсионным уравнением

(3.12)

$det{\mathbf{A}} = 0$

Решение уравнения (3.12) позволяет исследовать влияние свойств покрытия, градиентности неоднородности и ее локализации, вида начального напряженного состояния и величины начальных напряжений, внешнего электростатического поля на параметры распространения релеевских волн в широком диапазоне изменения параметров. Центральным моментом в процессе исследования является численное построение определителя матрицы А на основе решения уравнения (3.3), которое представляет собой систему обыкновенных дифференциальных уравнений (ОДУ) с переменными коэффициентами. Ее линейно независимые решения строятся на основе численного решения набора задач Коши с начальными условиями при фиксированных значениях параметра $\alpha $. Для решения систем ОДУ традиционно привлекаются различные численные методы [21–23]. Одним из наиболее распространенных является классический метод Рунге–Кутты четвёртого порядка. Однако при исследовании ПАВ целесообразно применять методы более высокого порядка повышенной точности. Высокую эффективность продемонстрировал метод Рунге–Кутты пятого порядка в модификации Мерсона (в литературе используют название Рунге–Кутты–Мерсона или Кутты–Мерсона), который позволяет сочетать хорошую точность и высокую скорость вычислений. Преимуществом метода является автоматическое изменение шага в ходе решения систем дифференциальных уравнений, что обеспечивает уменьшение общего числа шагов в несколько раз и уменьшает вероятность неустойчивости численного алгоритма.

Заключение. Развит метод исследования особенностей распространения волн Релея на поверхности сегнетоэлектрической гетероструктуры, представляющей собой однородную пьезоэлектрическую подложку с неоднородным предварительно напряженным покрытием из ФГПМ, свойства которого изменяются по заданному закону. В основе метода лежит сведение краевой задачи для системы уравнений в частных производных с переменными коэффициентами к системе начальных задач Коши, решение которой строится численно с помощью метода Рунге–Кутты пятого порядка в модификации Мерсона. Метод позволяет изучать влияние свойств покрытия, градиентности и локализации неоднородности, вида начального напряженного состояния и величины начальных напряжений, внешнего электростатического поля на основные характеристики релеевского волнового поля в широком диапазоне изменения параметров.

Работа выполнена в рамках реализации госзадания Южного научного центра РАН, номер госрегистрации 01201354242 при частичной финансовой поддержке Российского фонда фундаментальных исследований, проекты 19-08-01051, 19-01-00719.

Список литературы

Mason W.P. Physical Acoustics and the Properties of Solids. Princeton (N.J.): Van Nostrand, 1958. 402 p.
Dieulesaint E., Royer D. On des Elastiques Dans Les Solides. Application au traitement du signal. Paris: Ed. Masson, 1974. 407 p.
Matthews H. (ed.) Surface Wave Filters. Design, Construction and Use. New York: John Wiley & Sons, 1977. 521 p.
Biryukov S.V., Gulyaev Y.V., Krylov V.V. et al. Surface Acoustic Waves in Inhomogeneous Media. New York: Springer, 1995. 287 p.
Александров К.С., Сорокин Б.П., Бурков С.И. Эффективные пьезоэлектрические кристаллы для акустоэлектроники, пьезотехники и сенсоров. Т. 2. Новосибирск: Изд-во СО РАН, 2008. 429 с.
Калинчук В.В., Белянкова Т.И. Динамические контактные задачи для предварительно напряженных электроупругих тел. М.: Физматлит, 2006. 272 с.
Евдокимова О.В., Белянкова Т.И., Калинчук В.В. Уравнения динамики преднапряженной пьезоактивной среды при наличии внешнего электростатического поля // Вестн. Южного науч. центра РАН. 2007. Т.3. № 4. С. 19–25.
Белянкова Т.И., Калинчук В.В., Шейдаков Д.Н. Уравнения динамики преднапряженной электротермоупругой среды // Вестн. Южного науч. центра РАН. 2011. Т. 7. № 2. С. 5–14.
Бурков С.И., Золотова О.П., Сорокин Б.П. и др. Влияние внешнего электрического поля на характеристики волны Лэмба в пьезоэлектрической пластине // Акустич. ж. 2010. Т. 56. № 5. С. 606–612.
Burkov S.I., Zolotova O.P., Sorokin B.P. Influence of bias electric field on elastic waves propagation in piezoelectric layered structures // Ultrasonics. 2013. V. 53. № 6. P. 1059–1064.
Liu H., Wang Z.K., Wang T.J. Effect of initial stress on the propagation behavior of Love waves in a layered piezoelectric structure // Int. J. Eng.Sci. 2001. V. 38. P. 37–51.
Jin F., Wang Z., Wang T. The Bleustein–Gulyaev (B–G) wave in a piezoelectric layered half-space // Int. J. Eng. Sci. 2001. V. 39. P. 1271–1285.
Liu H., Kuang Z.B., Cai Z.M. Propagation of Bleustein–Gulyaev waves in a prestressed layered piezoelectric structure // Ultrasonics. 2003. V. 41. P. 397–405
Qian Z., Jin F., Wang Z. et al. Love waves propagation in a piezoelectric layered structure with initial stresses // Acta Mech. 2004. V. 171. P. 41–57.
Collet B., Destrade M., Maugin G.A. Bleustein–Gulyaev waves in some functionally graded materials // Europ. J. Mech. A/Solids. 2006. V. 25. P. 695–706.
Cao X., Jin F., Wang Z. et al. Bleustein–Gulyaev waves in a functionally graded piezoelectric material layered structure // Sci. China Ser. G-Phys. Mech. Astron. 2009. V. 52. P. 613–625.
Qian Z., Jin F., Wang Z. et al. Transverse surface waves on a piezoelectric material carrying a functionally graded layer of finite thickness // Int. J. Engng. Sci. 2007. V. 45. P. 455–466.
Qian Z.-H., Jin F., Lu T. et al. Effect of initial stress on Love waves in a piezoelectric structure carrying a functionally graded material layer // Ultrasonics. 2010. V. 50. P. 84–90.
Belyankova T.I., Kalinchuk V.V. Propagation of SH-waves in piezoelectric structures with functionally graded coating from different materials // IOP J. Phys. Conf. Ser. 2019. V. 1260. P. 112005.
Калинчук В.В., Белянкова Т.И. Динамика поверхности неоднородных сред. М.: Физматлит, 2009. 312 с.
Belyankova T.I., Kalinchuk V.V., Tukodova O.M. Peculiarities of the surface SH – waves propagation in the weakly inhomogeneous pre-stressed piezoelectric structures // Springer Proc. in Phys. 2016. V. 175. P. 413–429.
Belyankova T.I., Kalinchuk V.V. Surface sh-waves in pre-stressed piezoelectrics with functionally graded coating // PNRPU Mech. Bull. 2016. V. 3. P. 7–27.
Belyankova T.I., Kalinchuk V.V. Shear horizontal waves in piezoelectric structures with a functionally graded coating // Mech. Adv. Mater.&Struct. 2019. https://doi.org/10.1080/15376494.2019.1578006
Ben Salah I., Njeh A., Ben Ghozlen M.H. A theoretical study of the propagation of Rayleigh waves in a functionally graded piezoelectric material (FGPM) // Ultrasonics. 2012. V. 52. № 2. P. 306–314
Капцов А.В., Кузнецов С.В. Волны Лява в трехслойном упругом полупространстве // ПММ. 2015. Т. 79. В. 7. С. 550–557.
Желнорович В.А. Поверхностные волны Релея и Блюстейна–Гуляева в упругих пьезоэлектриках при наличии релаксации диэлектрической поляризации // ПММ. 2015. Т. 79. В. 2. С. 273–285.
Гольдштейн Р.В., Кузнецов С.В. Поверхностные акустические волны в диагностике слоистых сред. Чувствительность волн к вариации свойств отдельных слоев // ПММ. Т. 77. В. 4. 2013. С. 74–82.
Глушков Е.В., Глушкова Н.В., Кривонос А.С. Возбуждение и распространение упругих волн в многослойных анизотропных композитах // ПММ. Т. 74. В. 5. 2010. С. 419–432.
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979. 320 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал