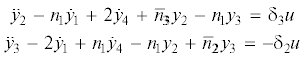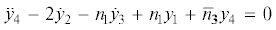Прикладная математика и механика, 2021, T. 85, № 4, стр. 436-453

1. Введение. Электродинамическое взаимодействие спутника с магнитным полем Земли оказывает существенное влияние на динамику вращательного движения спутника вокруг центра масс и может быть использовано как для пассивной, так и для активной стабилизации. Особый интерес для этих задач представляют стационарные движения спутника (положения относительного равновесия и регулярные прецессии) при его движении по круговой орбите. Устойчивость этих стационарных движений в гравитационном поле подробно исследована в [1–9]. Влияние гравитационных, магнитных и аэродинамических моментов на устойчивость стационарных движений рассмотрено в [10–13]. Характер устойчивости не является асимптотическим, и вопрос о стабилизации этих движений тем или иным способом представляет практический интерес. Одним из таких способов является стабилизация при помощи магнитных систем, принцип действия которых основан на взаимодействии собственного магнитного момента спутника с внешним магнитным полем. Особенно много публикаций посвящено вопросам стабилизации положения относительного равновесия спутника. Обзор работ этого направления содержится в [14–19].

Работ, в которых рассматривается стабилизация вращательных движений динамически симметричного спутника при помощи магнитных моментов немного. В [20, 21] рассматривается задача стабилизации при помощи магнитных и лоренцевых моментов программного движения спутника, при котором ось симметрии расположена вдоль местной вертикали или отклонена от нее на некоторый фиксированный угол, а сам спутник совершает медленное движение вокруг этой оси. Предполагается, что орбита – круговая экваториальная. Аналогичная задача рассматривается в [22]. Стабилизация при помощи магнитных моментов движения симметричного спутника вокруг оси, ортогональной плоскости круговой орбиты, рассмотрена в [23, 24].

Особенностью рассматриваемой задачи является то, что линеаризованные модели исследуемых задач представляют линейные нестационарные системы (ЛНС), так как управляющий момент является функцией геомагнитного поля, которое изменяется во время движения спутника по орбите вокруг Земли. Здесь, как и в большинстве работ этого направления, предполагается, что это изменение носит периодический характер, если орбита спутника – круговая. (Как отмечено в [18], это предположение вполне оправдано). Поэтому математическая модель рассматриваемых задач представляет собой систему дифференциальных уравнений с периодическими коэффициентами. Это обстоятельство вносит существенные трудности как в изучение управляемости системы, так и в разработку эффективных алгоритмов стабилизации.

Цель предлагаемой статьи – представить строгий аналитический подход к изучению рассматриваемой задачи стабилизации регулярных прецессий симметричного спутника при помощи магнитных моментов. Этот подход, заключающийся в приведении исходной нестационарной системы к стационарной системе большей размерности, был развит для ЛНС определенного класса и ранее применялся для решения ряда прикладных задач [25–29], в том числе для задачи стабилизации относительного равновесия спутника при использовании магнитных моментов [19, 30] и при использовании моментов лоренцевых сил [31].

Свойство приводимости системы к стационарной эффективно используется как при анализе управляемости, так и при построении алгоритмов стабилизации. При наличии свойства управляемости приведенной стационарной системы для нее строится оптимальный алгоритм стабилизации, основанный на LQR-методе на бесконечном интервале времени, который позволяет построить управление в виде обратной связи с постоянными коэффициентами, обеспечивающее асимптотическую устойчивость стационарной системы. Построенное стабилизирующее управление вводится в исходную нестационарную систему при помощи дополнительных переменных и соответствующего ограниченного преобразования, при этом коэффициенты обратной связи оказываются переменными. Исходная система, замкнутая таким управлением, также асимптотически устойчива.

Следует подчеркнуть, что выбор коэффициентов обратной связи, имеющий важное и принципиальное значение, при указанном подходе хорошо алгоритмизован и состоит из определения коэффициентов для стационарной системы при помощи стандартной процедуры LQR (при этом требуется задать лишь параметры функционалов) и преобразования к исходным переменным, которое строится конструктивным способом.

В работе получены линеаризованные уравнения управляемого движения для каждого типа прецессии при использовании магнитных моментов. Полученные нестационарные системы, относящиеся к классу приводимых систем, преобразуются к стационарным системам большей размерности, чем исходная система. Проведен анализ управляемости как для полученных стационарных систем, так и для исходных нестационарных систем. Для приведенных стационарных систем предложены оптимальные алгоритмы стабилизации, основанные на LQR-методе. Построенные управления при помощи конструктивного преобразования вводятся в исходные нестационарные системы. Работоспособность и эффективность предложенных алгоритмов подтверждается математическим моделированием.

2. Постановка задачи. Рассматривается движение динамически симметричного спутника около центра масс в гравитационном и магнитном полях Земли. Предполагается, что центр масс спутника движется по круговой орбите.

2.1. Системы координат и уравнения движения. Используются две правые системы координат:

$OXYZ$ – орбитальная система координат с началом в центре масс спутника: ось $OZ$ направлена по радиус-вектору центра масс относительно притягивающего центра (центра Земли); $OY$ – по нормали к плоскости орбиты, $OX$ дополняет систему до правой тройки;

$Oxyz$ – полусвязная система координат (не участвующая в собственном вращении): ось $Oz$ направлена по оси симметрии спутника. Переход от системы $OXYZ$ к системе $Oxyz$ осуществляется двумя поворотами. Первый поворот на угол $\alpha $ вокруг оси $OX$ приводит к системе координат $Ox{\kern 1pt} '{\kern 1pt} y{\kern 1pt} '{\kern 1pt} z{\kern 1pt} '$. Второй поворот на угол $\beta $ вокруг оси $Oy{\kern 1pt} '$ приводит к системе $Oxyz$. Положение оси симметрии спутника задается двумя углами $\alpha ,\beta $. Третий угол $\varphi $ – угол собственного вращения. Ориентация системы $Oxyz$ относительно орбитальной системы координат $OXYZ$ определяется таблицей направляющих косинусов [32]

Здесь ${{{\mathbf{e}}}_{\tau }},{{{\mathbf{e}}}_{n}},{{{\mathbf{e}}}_{r}}$ – единичные векторы по направлениям касательной, нормали и радиус-вектора орбитальной системы координат.

Компоненты абсолютной угловой скорости спутника ${\mathbf{\omega }} = {{{\mathbf{\omega }}}_{c}} + \dot {\varphi }{\mathbf{k}}$ (${\mathbf{k}}$ – единичный вектор оси симметрии, ${{{\mathbf{\omega }}}_{c}}$ – угловая скорость системы координат $Oxyz$) в проекциях на оси $Oxyz$ имеют вид

где ${{\omega }_{o}}$ – угловая скорость орбитального движения.

Динамические уравнения движения спутника около центра масс имеют вид [5]

Здесь $J = \operatorname{diag} ({{J}_{1}},{{J}_{1}},{{J}_{3}}),$ $({{J}_{1}} \ne {{J}_{3}})$, ${{J}_{j}}$ – главные центральные моменты инерции спутника, ${{{\mathbf{M}}}_{g}} = 3\omega _{0}^{2}({{{\mathbf{e}}}_{r}} \times J{{{\mathbf{e}}}_{r}})$ – гравитационный момент, ${\mathbf{M}}$ – управляющий момент, который создается за счет взаимодействия собственного дипольного момента, формируемого магнитными катушками, с магнитным полем Земли: ${\mathbf{M}} = {\mathbf{m}} \times {\mathbf{b}}(t)$, ${\mathbf{m}} = {{(\begin{array}{*{20}{c}} {{{m}_{1}}}&{{{m}_{2}}}&{{{m}_{3}}} \end{array})}^{{\text{T}}}}$ – магнитный дипольный момент спутника, ${\mathbf{b}}(t)$ – вектор индукции геомагнитного поля, которое описывается прямым магнитным диполем в орбитальной системе координат [33]

где ${{b}_{1}} = \sin I\cos {{\omega }_{0}}t$, ${{b}_{2}} = - \cos I$, ${{b}_{3}} = 2\sin I\cos {{\omega }_{0}}t$, $I$ – угол наклона плоскости орбиты спутника к плоскости экватора; ${{\mu }_{E}}$ – постоянная магнитного поля Земли, $R$ – радиус орбиты центра масс спутника.

В полусвязной системе координат вектор индукции имеет вид

где

Далее будем считать, что собственный магнитный момент направлен по оси симметрии спутника, т.е. ${\mathbf{m}} = {{(\begin{array}{*{20}{c}} 0&0&m \end{array})}^{{\text{T}}}}$.

Компоненты гравитационного ${{{\mathbf{M}}}_{g}}$ и управляющего момента ${\mathbf{M}}$ в системе координат $Oxyz$ имеют вид

Уравнения движения (2.2) с учетом полученных выражений для моментов представляются в виде

Здесь ${{r}_{0}} = \dot {a}\operatorname{s} \beta + \dot {\varphi } - {{\omega }_{0}}{\text{s}}\alpha {\text{c}}\beta = {\text{const}}$. Для краткости записи введены обозначения

Переходя в уравнениях (2.3) к безразмерным переменным, вводя обозначения $\tau = {{\omega }_{0}}t$, ${{\mu }_{0}} = \frac{{{{\mu }_{E}}}}{{{{R}^{3}}\omega _{0}^{2}{{J}_{1}}}}$, $a = \frac{{{{r}_{0}}}}{{{{\omega }_{0}}}}$, $b = \frac{{{{J}_{3}}}}{{{{J}_{1}}}}$ и при этом, сохраняя старые обозначения для дифференцирования по $\tau $, получим

2.2. Стационарные движения. В отсутствии управляющих моментов ($m = 0$) уравнения (2.4) допускают стационарные решения (регулярные прецессии)

Уравнения стационарных движений

имеют известные решения, которые называют [4, 5] цилиндрической, гиперболоидальной и конической прецессиями:

1) ${\text{c}}{{\alpha }_{0}} = 0$, ${\text{s}}{{\beta }_{0}} = 0$ $\left( {{{\alpha }_{0}} = \frac{\pi }{2},{{\beta }_{0}} = 0} \right)$ ось симметрии перпендикулярна плоскости орбиты;

2) ${\text{c}}{{\alpha }_{0}} = 0$, $\left( {{{\alpha }_{0}} = \frac{\pi }{2}} \right)$, ${\text{c}}{{\beta }_{0}} = - ab$ ось симметрии перпендикулярна радиус-вектору;

3) ${\text{s}}{{\alpha }_{0}} = \frac{{ab}}{{3b - 4}}$, ${\text{s}}{{\beta }_{0}} = 0$ $({{\beta }_{0}} = 0)$ ось симметрии перпендикулярна касательной к орбите.

3. Стабилизация стационарных движений. Требуется построить управление, обеспечивающее асимптотическую устойчивость стационарных движений, основываясь на линеаризованных для каждого стационарного движения уравнениях, которые являются нестационарными. Управляющий момент следует формировать в виде обратной связи по компонентам вектора состояния $\alpha ,\beta ,\dot {\alpha },\dot {\beta }$.

Заметим, что при линеаризации уравнений в окрестности стационарных движений, очевидно, линеаризуются выражения для управляющих моментов.

В соответствии с указанным во введении подходом к исследованию такого типа задач для каждого стационарного движения рассматриваются линеаризованные уравнения возмущенного движения. Эти уравнения приводятся к стационарным системам большего порядка. Управляемость в рассматриваемых задачах можно исследовать как исходя из нестационарных систем, так и анализируя приведенные стационарные системы. Исследование управляемости стационарной системы необходимо для построения корректных алгоритмов стабилизации, основанных на этих системах. Как уже указывалось, стационарная система является избыточной по отношению к исходной нестационарной системе. Если стационарная система управляема, то управляема и исходная система. Однако неуправляемость стационарной системы может и не повлечь неуправляемость исходной системы. Управляемость стационарных систем можно исследовать, выявляя условия существования в системе линейных интегралов, не зависящих от управления. А затем можно проверить управляемость исходных нестационарных систем в полученных критических случаях.

3.1. Линеаризация. Преобразование к стационарным системам. Управляемость. Цилиндрическая прецессия $\left( {{{\alpha }_{0}} = \frac{\pi }{2},{{\beta }_{0}} = 0} \right)$. В возмущенном движении положим

Линеаризованные уравнения управляемого движения имеют вид

Здесь ${{k}_{1}} = 2 + ab$, ${{k}_{2}} = 4 + ab - 3b$, ${{k}_{3}} = 1 + ab$, $u = {{\mu }_{0}}m$

Согласно [25], введем новые переменные ${{y}_{j}}$ $(j = 1, \ldots 4)$ по формулам

Дважды дифференцируя эти соотношения, подставляя их в систему (3.1) и приравнивая коэффициенты при функциях $\cos \tau $, $\sin \tau $, получим стационарную систему

Здесь ${{\bar {k}}_{2}} = {{k}_{2}} + 1$, ${{\bar {k}}_{3}} = {{k}_{3}} + 1$.

На экваториальной орбите ($\sin I = 0$) система (3.1), очевидно, неуправляема.

Как известно [34], необходимым и достаточным условием управляемости стационарной системы второго порядка

является условие

Достаточные условия неуправляемости можно получить, если стационарная система (3.3) имеет линейный интеграл, не зависящий от управления. Определим условия наличия такого интеграла.

Умножим первое и четвертое уравнения системы (3.3) на постоянные величины ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ соответственно и сложим. Полученное соотношение не должно содержать слагаемых, зависящих от ${{y}_{1}},{{y}_{4}}$, т.е. должно выполняться:

Отсюда

Величины ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ не равны нулю, если

Возможны два случая: 1) $ab = - 2$ и 2) $b = 1$.

При выполнении указанных условий линейный интеграл имеет вид

Если умножить второе уравнение системы (3.3) на 2 и сложить с третьим, то новых условий существования интегралов не появится.

Условия (3.4) являются достаточными условиями неуправляемости стационарной системы (3.3). Используя критерий Красовского [34] можно показать, что исходная нестационарная система (3.1) неуправляема, если выполняются оба условия (3.4), т.е. при $b = 1$, $a = - 2$. Это означает, что система неуправляема при $\Omega = - {{\omega }_{0}}$, т.е. угловая скорость собственного вращения равна и противоположна по знаку орбитальной угловой скорости.

Гиперболоидальная прецессия. $\left( {{{\alpha }_{0}} = \frac{\pi }{2},{{\beta }_{0}} \ne 0,\frac{\pi }{2}} \right)$

В возмущенном движении положим

В этом случае линеаризованные уравнения управляемого движения имеют вид

Здесь $k = 3(b - 1)$, ${{d}_{1}} = - 2\frac{{{\text{s}}I}}{{{\text{c}}{{\beta }_{0}}}}$, ${{d}_{2}} = \operatorname{s} I{\text{c}}{{\beta }_{0}}$, ${{d}_{3}} = {\text{c}}I{\text{s}}{{\beta }_{0}}$

Согласно [25], введем новые переменные ${{y}_{j}}$ $(j = 1, \ldots ,6)$ по формулам

Новые переменные удовлетворяют стационарной системе

Рассмотрим управляемость нестационарной системы (3.5) и стационарной системы (3.7), (3.8). Если орбита экваториальная, то система (3.5) становится стационарной, и ее условие неуправляемости $\sin {{\beta }_{0}} = 0$, т.е. $\bar {\Omega } = \frac{\Omega }{{{{\omega }_{0}}}} = \pm \frac{{b - 1}}{b}$. В частности, при $b = 1$ собственное вращение спутника отсутствует.

Если орбита полярная ($\cos I = 0$), то ${{d}_{3}} = 0$, и вводить переменные ${{y}_{5}},{{y}_{6}}$ не требуется. Если $\cos I \ne 0$, то система (3.7) неуправляема, если $b = 1$. Это же условие является достаточным условием неуправляемости системы (3.7), так как в этом случае система (3.7) имеет линейный интеграл, не зависящий от управления

Пусть $\sin I \ne 0$. Используя двойственную к системе (3.4) систему с наблюдением, можно показать, что при $b = 1$ она наблюдаема и, следовательно, в силу принципа двойственности исходная нестационарная система (3.5) управляема.

Коническая прецессия ($\alpha = {{\alpha }_{0}}$, ${{\beta }_{0}} = 0$)

В возмущенном движении положим

В этом случае линеаризованные уравнения управляемого движения имеют вид

Здесь

Как и выше, согласно [25], по формулам (3.6) введем новые переменные ${{y}_{j}}$ $(j = 1, \ldots ,6)$, которые в данном случае удовлетворяют стационарной системе

Здесь , ${{\bar {n}}_{3}} = {{n}_{3}} - 1$.

На экваториальной орбите система (3.9) становится стационарной. Необходимые и достаточные условия ее неуправляемости имеют вид

Система (3.10) является неуправляемой, если 1) $b = 1$; 2) $b = 2{\text{/}}3$; 3) $\operatorname{s} {{\alpha }_{0}} = 0$, т.е. $a = {{r}_{0}}{\text{/}}{{\omega }_{0}} = 0$, откуда следует ${{r}_{0}} = \Omega - {{\omega }_{0}}{\text{s}}{{\alpha }_{0}} = 0$, т.е. $\Omega = 0$, что означает, что собственное вращение отсутствует (коническая прецессия переходит в относительное равновесие, при котором ось симметрии спутника расположена по радиус-вектору (${{\alpha }_{0}} = 0$)).

Определим условия существования в системе (3.10) линейных интегралов, не зависящих от управления. Так же, как и для случая цилиндрической прецессии, умножив первое и четвертое уравнения системы (3.10) на постоянные величины ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ и складывая, получим соотношение, которое при выполнении условий

не зависит от переменных ${{y}_{j}}$. Условие $n_{1}^{2} - {{\bar {n}}_{2}}{{\bar {n}}_{3}} = 0$ существования неравных нулю величин ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ в данном случае имеет вид

Итак, в системе (3.10) существует линейный интеграл, не зависящий от управления, в следующих случаях

Умножив второе уравнение системы (3.10) на ${{\delta }_{2}}$, а третье на ${{\delta }_{3}}$ и сложив их, получим выражение, которое при выполнении условий

не зависит от переменных ${{y}_{2}},{{y}_{3}}$. Условия существования решения этой системы приводят к выражениям $b = 2{\text{/}}3$; ${{{\text{c}}}^{2}}{{\alpha }_{0}} = 1{\text{/}}2$, которые совпадают с выражениями 2) и 3) условий (3.12). Таким образом, новых условий существования интегралов в системе (3.15) не возникает.

Если орбита полярная, то ${{\delta }_{1}} = 0$, то переменные ${{y}_{5}},{{y}_{6}}$ не требуется вводить.

Используя критерий Красовского [35], можно показать, что на полярной орбите при выполнении условий $b = 2{\text{/}}3$ и ${{s}^{2}}{{\alpha }_{0}} = 1{\text{/}}2$ исходная нестационарная система (3.9) является неуправляемой. Если же орбита не является полярной, то при этих условиях система управляема.

4. Построение стабилизирующего управления

4.1. Способ построения алгоритма стабилизации. Поведение вектора $x = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{2}}} \end{array}} \right]}^{{\text{T}}}}$ исходной системы описывается нестационарными системами (3.1), (3.5) и (3.9) соответственно для каждого варианта прецессий. Для построения алгоритмов стабилизации эти системы должны быть представлены в форме Коши

Для цилиндрической прецессии

Для гиперболоидальной прецессии

Для конической прецессии

Одна из основных идей предлагаемого метода состоит в использовании построенных стационарных систем для выбора стабилизирующего управления. Это алгоритмизированный, устойчивый в работе способ удобный для применения (см. [19, 29–31]).

Задача стабилизации состоит в том, чтобы построить управление, обеспечивающее при $\tau \to \infty $ стремление к нулю компонент вектора состояния $Y$ системы, полученной из указанных стационарных систем

(Заметим, что в рассматриваемых случаях $n = 4,6$).

Предполагается, что пара ${{A}_{y}},{{B}_{y}}$ управляема.

Матрицу коэффициентов управления можно выбрать из условия минимума квадратичного функционала

где $Q$ – неотрицательно определенная постоянная матрица соответствующей размерности, $\gamma > 0$. Оптимальное управление имеет вид [36]

Матрица $P$ размерности $2n \times 2n$ является решением дифференциального матричного уравнения Риккати. Система стационарна и управляема, поэтому это уравнение имеет положительно определенное стационарное решение, совпадающее с единственным решением алгебраического уравнения Риккати

Синтезированное на основе расширенной стационарной системы управляющее воздействие является функцией переменных $Y(\tau )$ стационарной системы более высокого порядка, чем исходная нестационарная система.

Для введения управления непосредственно в исходную систему следует выразить вектор $Y(2n \times 1)$ ($n = 4,6$) через вектор $x(2 \times 1)$ исходной системы, дополненный некоторым вектором $x{\kern 1pt} '(N \times 1)$ ($N = 2,4$), и их производные.

Вектор $\xi = \left[ {\begin{array}{*{20}{c}} x \\ {x{\kern 1pt} '} \end{array}} \right]$ и вектор $y$ связаны соотношением

Матрица $F(\tau )$ определена согласно формулам (3.2) и (3.4) соответственно для $n = 2$ и $n = 6$.

Дополнительный вектор $x{\kern 1pt} '$ вводится таким образом, чтобы квадратные матрицы ${{T}_{y}}$ и ${{\dot {T}}_{y}}$ были невырожденными.

Введем вектор $\eta = \left[ {\begin{array}{*{20}{c}} \xi \\ {\dot {\xi }} \end{array}} \right]$. Вектора $Y$ и $\eta $ связаны преобразованием

Тогда управление (4.4) может быть записано в виде

Уравнения для дополнительного вектора $X{\kern 1pt} ' = \left[ {\begin{array}{*{20}{c}} {x{\kern 1pt} '} \\ {\dot {x}{\kern 1pt} '} \end{array}} \right]$ имеют вид

Матрицы $A{\kern 1pt} ',B{\kern 1pt} '(\tau )$ для конкретных случаев выписаны ниже.

Расширенная нестационарная система для построения алгоритма стабилизации состоит из исходной системы (4.1) и системы (4.9), где управление формируется согласно (4.8) с учетом формул (4.6).

Решения этой расширенной нестационарной системы, замкнутой управлением (4.8) стремятся к нулю при $\tau \to \infty $, в силу выбора матрицы ${{K}_{Y}}$, так как компоненты вектора $\xi $ связаны с компонентами вектора $y$ ограниченным преобразованием (4.6).

4.2. Алгоритм стабилизации регулярных прецессий. Оптимальные стабилизирующие управления строятся для соответствующих стационарных систем.

Для случая цилиндрической прецессии: система стационарных уравнений (4.2), соответствующая системе (3.3), имеет 8-й порядок. Матрицы расширенной нестационарной системы (4.1), (4.9) имеют вид

Матрицы $F,P$ преобразования (4.7) $T(\tau )$ имеют вид:

Для случая гиперболоидальной прецессии система стационарных уравнений (4.2), соответствующая системе (3.7), (3.8), имеет 12-й порядок. Матрицы расширенной нестационарной системы (4.1), (4.9) в этом случае имеют вид

Матрицы $F,D$ преобразования (4.6) $T(\tau )$ для случаев гиперболоидальной и конической прецессий имеют вид:

Для конической прецессии стационарная система уравнений (4.2), соответствующая системе (3.10), (3.11), имеет также 12-й порядок. Матрицы систем (4.1), (4.9) в случае конической прецессии имеют вид

Таким образом, алгоритм стабилизации нестационарных систем для указанных случаев прецессий состоит из 3-х этапов: 1) нахождение постоянных коэффициентов управления ${{K}_{Y}}$ для решения задачи оптимальной стабилизации соответствующей стационарной системы (на основе алгебраического уравнения Риккати); 2) построение управления в виде (4.8) с помощью невырожденных преобразований $T(\tau )$ и 3) решения расширенной нестационарной системы, содержащей исходную нестационарную систему (4.1) и уравнения для вспомогательных переменных (4.9).

5. Моделирование. Цель приведенных ниже результатов моделирования – показать принципиальную применимость предложенных алгоритмов и продемонстрировать их работоспособность.

Моделирование проводилось при помощи стандартного пакета Wolfram mathematica v11.0. Коэффициенты управления выбирались при помощи стандартной программы LQR для стационарных систем (4.2).

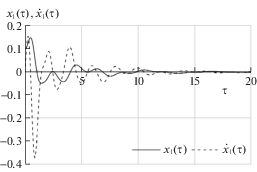
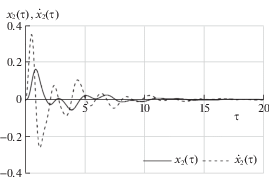
Наклон орбиты движения спутника $I = \pi {\text{/}}6$. Начальные отклонения по углам ${{x}_{1}}(0) = {{x}_{2}}(0) = 0.1$; по скоростям ${{\dot {x}}_{1}}(0) = {{\dot {x}}_{2}}(0) = 0.0$.

Параметр спутника $b = 0.5$; параметр $a = \pm 10.0$ для цилиндрической прецессии, $a = 1.0$ для гиперболической и конической прецессий

Параметры функционала (4.3): $Q = 100.0 \cdot {{E}_{k}}$ $(k = 8,12);$ $\gamma = 1$.

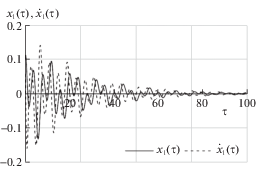
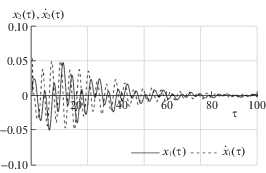
На рис. 1–4 представлено поведение переменных ${{x}_{1}}(\tau ),{{\dot {x}}_{1}}(\tau )$ и ${{x}_{2}}(\tau ),{{\dot {x}}_{2}}(\tau )$ для случая цилиндрической прецессии.

На рис. 5 и 6 представлено поведение переменных ${{x}_{1}}(\tau ),{{\dot {x}}_{1}}(\tau )$ и ${{x}_{2}}(\tau ),{{\dot {x}}_{2}}(\tau )$ для случая гиперболоидальной прецессии.

На рисунках 7 и 8 представлено поведение переменных ${{x}_{1}}(\tau ),{{\dot {x}}_{1}}(\tau )$ и ${{x}_{2}}(\tau ),{{\dot {x}}_{2}}(\tau )$ для случая конической прецессии.

Таким образом, представленные результаты моделирования подтверждают работоспособность предложенных алгоритмов стабилизации спутника в окрестности регулярных прецессий.

Заключение. Представлен строгий аналитический подход к изучению задачи стабилизации регулярных прецессий симметричного спутника при помощи магнитных моментов. Линеаризованные системы уравнений движений являются линейными нестационарными системами, приводимыми к стационарным. Для трех типов регулярных прецессий эти системы приведены к стационарным системам большей размерности. В каждом случае исследована управляемость. Алгоритмы оптимальной стабилизации построены для полученных стационарных систем системы при помощи стандартной процедуры LQR. Указаны преобразования, позволяющие вводить управления в исходные нестационарные системы. Работоспособность и эффективность предложенных алгоритмов подтверждена результатами математического моделирования.