Прикладная математика и механика, 2021, T. 85, № 4, стр. 454-460

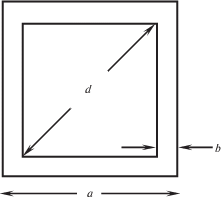
1. Введение. Описана [1] конструкция, состоящая из трех одинаковых плоских квадратных рам, имеющих форму, показанную на рис. 1. Диагональ $d$ внутреннего квадрата равна стороне $a$ внешнего квадрата. В терминах ширины $b$ полос, из которых сделаны рамы, это условие имеет вид $(a - 2b)\sqrt 2 = a$, или

При таком условии контакта рама 1 может быть вставлена наполовину в раму 3, как показано на рис. 2. В этом положении рама 1 может свободно поворачиваться вокруг линии, соединяющей две точки контакта.

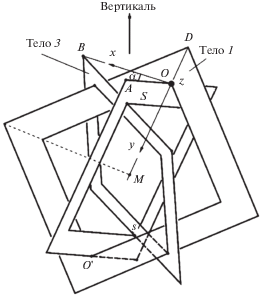
При надлежащем выборе угла $\alpha $ между двумя рамами рама 2 может быть вставлена так, чтобы одним и тем же образом каждая рама была охвачена другой и содержала в себе следующую раму. Это показано на рис. 3 (перед установкой из рамы 2 временно должна быть демонтирована одна из сторон, так что рама принимает вид буквы $U$). Полученная конструкция с одинаковыми углами $\alpha $ между каждой парой рам является жесткой. В разд. 2 показано, что сборка возможна с однозначно определенным углом $\alpha $. В разд. 3 исследуются конструкции с неплоскими рамами.

2. Вычисление ${\mathbf{\alpha }}$. Пусть с рамой 1 связана декартова система координат $x,y,z$, показанная на рис. 3. Ось $y$ направлена вдоль диагонали, ось $z$ – перпендикулярно раме. Ось $x$ проходит через точку $B$. В точке $S$ пересекаются прямые $MA$ и $BC$. рис. 4

Векторы $\overrightarrow {OM} $, $\overrightarrow {OA} $, $\overrightarrow {OB} $, $\overrightarrow {OD} $, $\overrightarrow {OC} $ имеют координаты: $\overrightarrow {OM} $ = $\frac{a}{2}(0,1,0)$, $\overrightarrow {OA} $ = = $\frac{a}{2}(cos\alpha ,1,sin\alpha )$, $\overrightarrow {OB} $ = $\frac{a}{2}(1,0,0)$, $\overrightarrow {OD} = \frac{a}{2}(0$, $1 - \sqrt 2 $, 0), $\overrightarrow {OC} = \frac{a}{2}( - cos\alpha $, $1 - cos\alpha $, $\sqrt 2 sin\alpha )$.

Прямые $MA$ и $BC$ запишем в параметрической форме:

Точка пересечения S определяется уравнениями ${{\lambda }_{1}}cosa$ = $1 - {{\lambda }_{2}}(1 + cos\alpha )$, $1 - {{\lambda }_{1}}$ = = ${{\lambda }_{2}}(1 - cos\alpha )$, ${{\lambda }_{1}} = {{\lambda }_{2}}\sqrt 2 $, которые дают

Это доказывает, что три рамы могут быть собраны в единственно определенную конфигурацию. Треугольник $(ABD)$ равносторонний, поскольку векторы

имеют равные длины.

Произведение $\overrightarrow {AB} \times \overrightarrow {BD} $ определяет единичный вектор $\vec {n}$, перпендикулярный к плоскости треугольника (вертикаль на рис. 3): $\vec {n}$ = $(1{\text{/}}\sqrt 3 )\left[ {\sqrt {\sqrt 2 - 1} ,\sqrt {\sqrt 2 - 1} ,\sqrt 2 - 1} \right]$. Угол между $\vec {n}$ и $\overrightarrow {MA} $, $\overrightarrow {MB} $, $\overrightarrow {MD} $ равен $arccos\left[ {3{\text{/}}\sqrt {\sqrt 2 - 1} } \right]$. Отражения точек $A$, $B$ и $D$ относительно центра $M$ являются вершинами углов другого равностороннего треугольника с той же нормалью $\vec {n}$. В направлении, противоположном вектору $\vec {n}$, эти два треугольника видны повернутыми на 30° друг относительно друга.

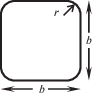
3. Неплоские квадратные рамы. Конструкция, изображенная на рис. 3, может быть собрана с тем же углом $\alpha $ между парами рам, если плоские полосы, из которых сделаны рамы заменить профильными трубами с поперечным сечением, показанным на рис. 5. Ширина $b$ и радиус $r$ – свободные параметры. Исследование включает частные случаи $r = 0$ (квадратное сечение) и $2r = b$ (круглое поперечное сечение). Как и раньше, длина стороны внешнего квадрата обозначается $a$. Угол $\alpha $ отсчитывается в средних плоскостях рам. Сборка конструкции возможна, если условие контакта (1.1) заменить условием контакта по параметрам $a$, $b$ и $r$.

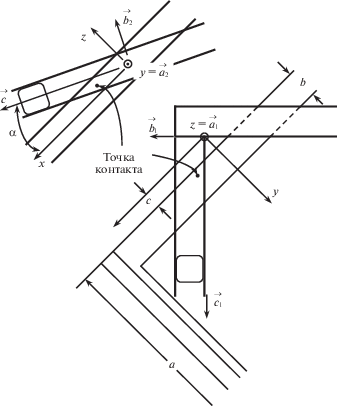
Плоскость $x,y$ на рис. 3, теперь расположена в средней плоскости рамы 1. Вблизи начала координат $O$ одна сторона рамы 2 находится в контакте с рамой 1 в двух точках на противоположных плоскостях рамы 1. Всего существует двенадцать точек контакта.

Из соображений симметрии условие контакта можно получить, исследуя единственную точку контакта. На рис. 6 точка контакта показана в двух проекциях около начала координат в области $x,y,z > 0$. Вспомогательная величина $c$ связана с $a$ и $b$ уравнением $a + 2c = (a - 2b)\sqrt 2 $, или

В точке контакта поверхности представляют собой круглые цилиндры радиуса r. В обозначениях, показанных на рис. 7, оба цилиндра имеют параметрическое представление

${{P}_{i}}$ – произвольно выбранная точка на оси цилиндра. ${{\vec {a}}_{i}}$, ${{\overrightarrow b }_{i}}$ и ${{\vec {c}}_{i}}$ – взаимно перпендикулярные единичные векторы, а ${{\varphi }_{i}}$, ${{\lambda }_{i}}$ – координаты. Единичные нормальные векторы в точке ${{\varphi }_{i}},{{\lambda }_{i}}$ равны ${{\vec {n}}_{i}}$ = ${{\vec {a}}_{i}}cos{{\varphi }_{i}}$ + ${{\overrightarrow b }_{i}}sin{{\varphi }_{i}}$ $(i = 1,2)$.

Цилиндры находятся в контакте, если (а) ${{\vec {z}}_{2}} = {{\vec {z}}_{1}}$ и (б) ${{\vec {n}}_{2}} = - {{\vec {n}}_{1}}$. Условие (б) записывается так:

С учетом этого соотношения условие (а) принимает вид

Для цилиндров на рис. 6 векторы ${{\vec {a}}_{i}}$, ${{\overrightarrow b }_{i}}$, ${{\vec {c}}_{i}}$ и ${{\overrightarrow P }_{i}}$ $(i = 1,2)$ имеют следующие $x,y,z$ – координаты:

Отсюда с помощью уравнений (3.2), (3.3) получаем

Из этих шести уравнений для ${{\varphi }_{1}}$, ${{\lambda }_{1}}$, ${{\varphi }_{2}}$, ${{\lambda }_{2}}$ и $c$ только пять являются линейно независимыми, поскольку левая и правая части уравнения (3.2) являются единичными векторами. Сумма уравнений (3.4) и (3.5) дает

Знак минус в выражении для $sin{{\varphi }_{2}}$ выбран с учетом, что $\pi < {{\varphi }_{2}} < 3\pi {\text{/}}2$ (см. рис. 6).

Из уравнений (3.4) и (3.6) следует, что

Уравнения (3.7)–(3.9) линейны по ${{\lambda }_{1}}$, ${{\lambda }_{2}}$ и $c$. Решение для $c$ имеет вид

После подстановки в выражения (3.10), (3.11) и (2.1) значений величин $sin{{\varphi }_{1}}$, $cos{{\varphi }_{1}}$, $sin\alpha $ и $cos\alpha $ найдем, что

Подстановка в равенство (3.1) дает требуемое условие контакта

Фото на рис. 7 демонстрирует модели, выполненные из алюминия и дерева с круглым и квадратным сечением соответственно.

Уравнение (3.12) показывает, что параметр $a$ очень чувствителен к изменениям параметра $r$. Следствием этого является обстоятельство, что жесткая конструкция квадратного сечения с полосами практически невозможна. В результате малейшего износа острой кромки (углов квадрата) длина $a$, выбранная в предположении $r = 0$, оказывается слишком большой. Следствием этого является подвижность конструкции, в результате которой в точках, где требуется контакт, возникают большие зазоры. С другой стороны, если величина $a$ слишком мала, сборка конструкции невозможна. Коммерчески доступны трубы круглого сечения высокоточных размеров.

В 2004 г. стальная конструкция из труб диаметром $2r = 40.5$ см была установлена в городе 26406 Витмунд в Остфрисланде, а в 2006 г. конструкция из труб, изготовленных из нержавеющей стали, диаметром $2r = 30$ см – в кампусе Технологического института Карлсруэ (Эта статья была написана в 1992 году. Она ранее не публиковалась, по требованиям сохранения коммерческой тайны). Эти конструкции получили название ТРИАДА. Обе, а точнее их тени, можно увидеть, увеличив масштаб в известном приложении Google Earth (На сайте http://itm-serv.itm.uni-karlsruhe.de/ITM/Personal/Wittenburg/TRIADE/start.html имеется фотография монумента и анимация “Триада – виртуальный тур”).

4. Нереализуемая конструкция. Представьте себе трехмерное пространство, заполненное решеткой из кубов. Каждая грань, общая для двух кубов, есть рама с параметрами $a$, $b$ и $r$, которые удовлетворяют соотношению (3.12). Теперь представьте, что на всех трех гранях конструкции, исследуемой в разд. 3, возведена заполняющая пространство решетка из кубов. Можно ли собрать эту конструкцию без натяга полос? Ответ отрицательный. На каждой из трех рам только в одну ее сторону можно вставить куб.