Прикладная математика и механика, 2021, T. 85, № 5, стр. 635-663
Аэротермобаллистика дробящихся метеороидов в атмосфере Земли
1 Научно-исследовательский институт механики МГУ им. М.В. Ломоносова
Москва, Россия
* E-mail: tirskiy@imec.msu.ru
Поступила в редакцию 20.01.2021
После доработки 14.06.2021
Принята к публикации 01.07.2021
Аннотация
Проведено численное и аналитическое решение полных уравнений физической теории метеоров (ФТМ, уравнения торможения, уравнения энергии и угла наклона траектории) метеороида как единого тела. Методом последовательных приближений получены выражения для безразмерных скорости и массы с учетом переменности угла наклона траектории метеороида. На их основе в аналитическом виде получено выражение для скоростного напора и погонной (на единицу пути) кинетической энергии, как для единого тела, так и дробящегося тела. Показано, что для единого тела формулы скорости и массы зависят от одного эффективного параметра.
Создана модель прогрессивного равновесного дробления (ПРД), с помощью которой исключается из уравнения торможения масса тела. В статье рассмотрена созданная с использованием гипотезы Вэйбулла [1] модель ПРД под действием аэродинамического сопротивления. Проведено усовершенствование этой модели с учетом задержки в образовании отдельных фрагментов в виду наличия конечной скорости их расхождения.
Приведена полная система уравнений ФТМ, содержащая действие силы тяжести, реактивную силу и влияние подъемной силы на угол отклонения траектории. Эта полная система уравнений решена численно и оказалось, что для типичных метеороидов больше 1 кг результаты не зависят от учета дополнительных членов, связанных с учетом силы тяжести, реактивной силы и влияния подъемной силы на угол наклона траектории.
Обнаруженный максимум погонной кинетической энергии на высоте примерно 10 км приводит к терминальному (тепловому) взрыву в воздухе крупных метеороидов [2].
1. Прочность разрушения метеороидов. Случаи дробления метеороидов при полете в атмосфере – достаточно давно установленный в метеорной физике факт [3–5]. Дробление многократно наблюдалось как визуально, так и фотографически, а также рядом других методов. Примерами тому являются Челябинский метеорит (2013) [6], Витимский болид (Восточная Сибирь, 2002) и многие десятки других. Пршибрам был первым метеоритом, падение которого было зафиксировано фотографическими способами на станциях наблюдения в Чехии [7]. Около 6-ти килограмм осколков было собрано на поле около 15 × 1 км2. Три метеорита были почти полностью покрыты “корой плавления”. Фрагменты Пршибрама представляют собой обычные хондриты, его масса оценивалась примерно в 700–5000 кг. Метеорит Lost-City был сфотографирован в полете и сетью Prairie (США) в 1970 году [8]. Найдено четыре фрагмента массой 17 кг. Lost-City – обычный хондрит. Все найденные фрагменты метеорита были полностью покрыты корой плавления. Это говорит о том, что фрагментация в основном прекратилась до прекращения абляции. Начальная масса Lost-City составляла около 163 кг. В полете было обнаружено десять точек фрагментации. Вся масса выделялась в виде пыли. Метеорит Innisfree стал третьим падением, для которого точные орбитальные данные были записаны камерой Network [9]. Девять фрагментов метеорита составляли массу 4.58 кг. Метеорит Peekskill упал в 1992 году. Яркий огненный шар, продолжавшийся более сорока секунд, был записан пятнадцатью видеокамерами случайных свидетелей. Метеорит был полностью покрыт корой плавления [10]. Обширная фрагментация начиналась на высоте около 41.5 км. Было найдено около 70 фрагментов разного размера. Была зафиксирована вспышка на высоте 36.2 км. Скоростной напор оценивается как 0.7–1 МПа. Начальная масса Peekskill оценивалась в 10 т. Также известны метеорит Моравки [11], метеорит Нойшванштайн, метеорит Park Forest [12, 13], метеорит Bunburra Rockhole [14], метеорит Almahata Sitta [15], метеорит Есенице [16], метеорит Гримсби [17]. Данные о вышеперечисленных метеоритах можно найти в соответствующих ссылках [18]. Мелкие тела тормозятся и сгорают на больших высотах. Примерно половина больших тел (>1 м) разрушается (дробится) в полете, не долетая до земли. Разрушение сопровождается вспышками – резкими свечениями в полете по нескольку раз. После дробления на мелкие осколки 0.01–0.04 мм через одну секунду происходит их быстрое и яркое сгорание – вспышка [3]. Например, у Челябинского метеорита наблюдалось 3–4 вспышки [6]. Важно отметить, что дробление метеорных тел в полете проявляется в разных видах, в частности, в форме квазинепрерывного поверхностного дробления (пиролиза), (см. далее) когда под действием поверхностных касательных и нормальных аэродинамических сил, ослабления за счет возможного пиролиза и выдува летучих компонентов, дефектов, плавления, трещин, термонапряжений поверхность метеороида эродирует – происходит отделение и унос твердых частиц и отдельных фрагментов разных размеров и капель, которые догорают в ударном слое.
В другом крайнем случае тело может распадаться на несколько крупных отдельных фрагментов (так называемая gross-фрагментация) [19], которые продолжают свое движение независимо друг от друга или же происходит дезинтеграция всего объема тела, которое далее распадается на множество мелких фрагментов. Необходимо также подчеркнуть, что в той или иной форме “дроблению подвержены любые метеорные тела, крупные и мелкие, железные или каменные, а тем более тела “кометной природы” [20, 21].
До сих пор остается открытым вопрос о построении адекватной математической модели этого явления.
Особенно это касается так называемого “air blast” – взрывного воздушного разрушения крупных (Челябинского, Тунгусского) метеоритов. При этой модели разрушения в атмосфере на высоте 5–10 км достигается максимум потери кинетической энергии метеороида, которая уходит в кинетическую энергию атмосферы с образованием воздушной ударной волны и потоком за ней нагретого до очень высоких температур пара (до нескольких десятков тысяч градусов заполненного очень мелкими частицами). Так, образовавшаяся взрывоподобная ударная волна от Тунгусского метеорита повалила лес на площади порядка 2000 км2. Это явление называется “air blast” и оно сопровождается образованием ярко светящихся шаров.
По-видимому, одной из первых работ, в которых упоминается дробление метеороидов в полете, является работа Яккиа [22], рассматривающая проблему лишь качественно. В ранних работах по разрушению метеороидов преимущественно изучались кривые блеска (свечения), т.е. вспышки метеоров [23, 24]. В работе [24] были качественно рассмотрены различные типы дробления и их влияние на фотометрические кривые. Дробление в виде облака мелких фрагментов (пыли) сопровождается далее (через одну–две секунды) после выдува с поверхности вспышкой, ярким свечением [3]. Если выделение мелких частиц не происходит с поверхности обтекаемого тела, то вспышка отсутствует. Вспышку часто называют взрывом [25]. Однако под взрывом, согласно Большой российской энциклопедии, понимается выделение энергии за очень короткий промежуток времени. При этом образуется ударная волна, которая не наблюдается при вспышке.
Оригинальная модель взрывного лавинообразного разрушения развивалась в работах Покровского (1996). Однако анализ прочности и действующих на тело аэродинамических нагрузок в первых работах не проводился. Обзор этих и других ранних работ, содержит лишь качественное рассмотрение моделей дробления [5] и [26].
Дальнейшее развитие моделей фрагментации (их математическое моделирование) можно условно разбить на два направления: ПРД на все более мелкие осколки и взрывоподобное разрушение с образованием связного конгломерата осколков с квазистатистическими свойствами (рой мелких осколков). В первой группе пионерской работой была работа Ю.И. Фадеенко (1967), идея которой была использована и далее развита в дальнейшем [27–30]. Модель последовательного разрушения осколков на две половины исследована в работе [31], аналогичная модель развита в [32]. Относительно недавно предложена модель сплющивающегося метеороида [33], когда рой осколков, объединенных одной головной ударной волной, сжимается в продольном направлении и расширяется в поперечном. Ряд работ по взаимодействию крупных метеороидов с атмосферой были посвящены Тунгусскому метеориту. Автор статьи не касается Тунгусского метеорита, так как эта тема требует специального рассмотрения [34]. Второй, так называемый, гидродинамический подход развивался также в работах Ю.И. Фадеенко (1967) и особенно С.С. Григоряна (1976, 1979), группы Коробейникова [35–38], Хиллса и Годы [39], Чайбы и коллег [40], группы Немчинова [26, 41], хотя конкретные математические модели, использовавшиеся этими авторами, были различны.
Сначала обсудим принципиальные аспекты аэродинамического нагружения и разрушения тела в атмосфере. Рассмотрим движение метеороида, считая его не подверженным аэродинамическому нагреванию, но испытывающим торможение и деформацию за счет перегрузки, т.е. за счет увеличивающегося “веса” в собственной системе координат. Деформация происходит за счет массовых сил инерции, которые уравновешиваются аэродинамическими поверхностными силами с наветренной (обращенной в обратную сторону движения) стороны и малыми поверхностными силами с подветренной (обращенной в сторону движения) стороны. В реальных условиях эта модель (в пренебрежении аэродинамическим нагреванием) хорошо описывает взаимодействие с атмосферой достаточно крупных тел (R > 10 см), что впервые было показано [42] с помощью количественных оценок, уравнений гидродинамики, которые несколько другим способом воспроизводятся ниже. Действительно, толщина прогрева поверхностного слоя, слабо зависящая от физико-химических процессов, протекающих на поверхности метеороида (диссоциация, ионизация, возбуждение, внутренних степеней свободы, а также плавление, испарение, горение), т.е. аэродинамическая тепловая эрозия (прогрев) оценивается по порядку величины выражением $\Delta (t)$ ~ ~ $\sqrt {\lambda t} $ = $0.1\sqrt t $ см, $\left[ t \right] = с$, где $\lambda \approx {{10}^{{ - 2}}}$ см2/с – коэффициент теплопроводности. Время воздействия аэродинамического нагрева до достижения максимальных перегрузок, которая составляет величину по времени порядка $h{\text{/}}{{V}_{e}}\sin \theta $ ~ 1 с (h – шкала высот по давлению, равная примерно 7 км, θ – угол наклона траектории к горизонту, Ve – скорость входа тела в атмосферу). За это время метеороид прогревается не более чем на 1–2 мм (для железных метеороидов.. $\Delta \sim 0.3\sqrt t $ < 3–4 мм. Другими словами перепад температуры в 2200/3000 K (начало интенсивного испарения в приповерхностном слое метеороида ограничено весьма тонким слоем в несколько миллиметров). Следовательно, для достаточно больших метеороидов, рассматриваемых в данной работе, аэродинамический нагрев не может изменить исходных механических свойств основной массы тела. Термонапряжения, возникающие в приповерхностном слое, т.е. в области большого перепада температур, не могут существенно повлиять на напряженное состояние основной его массы. Поэтому рассмотрение модели холодного деформирующего тела и в итоге разрушающегося метеороида представляет практический интерес.
Как показывают наблюдения, механическое разрушение метеороидов размером более 10 см происходит на высотах ниже 50 км [43]. При этом воздействии атмосферы на метеороиды сводится в основном к нормальному давлению (касательные силы–силы трения на этих высотах пренебрежимо малы из-за достаточно малых чисел Рейнольдса). Давление на поверхности выпуклого тела, например, шара, будем определять по закону Ньютона.
(1.1)
$P = \nu \rho {{\nu }^{2}}{{\cos }^{2}}\varphi ,\quad 0 \leqslant \varphi \leqslant \pi {\text{/2}}\quad \left( {{\text{наветренная сторона сферы}}} \right),$(1.2)
$P = 0,\quad \pi {\text{/2}} \leqslant \varphi \leqslant \pi \quad \left( {{\text{подветренная сторона сферы}}} \right){\text{,}}$За счет поверхностных (нормальных и касательных) аэродинамических сил тело тормозится, поэтому возникают непрерывно распределенные по объему массовые силы инерции (отличны от нуля все компоненты тензора напряжений). Максимальная величина этих сил зависит от квадрата скорости входа (скоростного напора), шкалы высот, угла входа. При метеорных скоростях они достигают нескольких тысяч земных ускорений g (возьмем для примера ${{V}_{e}}$ = 43 км/c перегрузка в атмосфере Земли будет равна 5000g). Формула для перегрузки приведена далее в тексте. Пример перегрузки при 43 км/с взят для того, чтобы представить ее возможное максимальное значение. Под действием скоростного напора метеороид сдавливается и начинает деформироваться. Деформация будет зависеть от времени (высоты). В работах [45, 46] было показано, что напряженное состояние можно считать квазистационарным для больших тел размером $D < 0.1H$ ($H$ ~ 7–10 км), т.е. $D$ < 700 м для атмосферы Земли. Для атмосферы Юпитера (Н = 25–90 км) условие квазистационарного нагружения будет выполняться при D < 2–3 км. Следовательно, как для Тунгусского тела [38] ($D$ = 60 м), так и для кометы Шумейкеров–Леви 9 [47] ($D$ = 1 км), условие квазистационарного нагружения выполняется с большим запасом.
Нерегулярность формы реального метеороида, создающая локальную концентрацию повышенных напряжений и отрыв отдельных небольших частей (например, за счет напряжений при изгибе) не меняет общей качественной картины напряженного состояния основной массы метеороида, которое в силу линейности классических уравнений теории упругости будет пропорционально скоростному напору $\rho {{{v}}^{2}}$. Концентрация максимальных напряжений в угловых точках проявляется в начале дробления метеороида, примерно до появления десяти осколков [37]. Задача о напряженном состоянии упругого тела (шара) хорошо известная по теории упругости. Для шара эта задача теории упругости решается аналитически в виде рядов по полиномам Лежандра, что позволяет детально определить деформацию и поле упругих напряжений в метеороиде в любой момент времени (на любой высоте), пропорционально скоростному напору $\rho {{{v}}^{2}}$ [48]. Из точного решения этой задачи о напряженном состоянии для шара [49, 50] следует, что растягивающие напряжения ${{\sigma }_{\operatorname{e} }}$ максимальны на поверхности шара на его тыльной (подветренной) стороне в точке, противоположной передней лобовой (критической) точке. Интенсивная касательная (скалывающая) компонента напряжений ${{\sigma }_{\tau }}$ максимальна внутри шара на окружности при $\varphi = 60^\circ $ на расстоянии 0.25–0.35 радиуса от центра в зависимости от коэффициента Пуассона материала метеороида. Зависимость ${{({{\sigma }_{\operatorname{e} }})}_{{\max }}}$ и ${{({{\sigma }_{\tau }})}_{{\max }}}$ от этого коэффициента слабая, и с достаточной для оценок точностью можно положить ${{({{\sigma }_{\operatorname{e} }})}_{{\max }}}$ = $0.365\rho {{{v}}^{2}}$, ${{({{\sigma }_{\tau }})}_{{\max }}}$ = $0.265\rho {{{v}}^{2}}$. Напряженное состояние метеороида будет зависеть от соотношения между его характерной прочностью на сжатие, которая достигается в лобовой точке, характерными прочностями на растяжение и на сдвиг, которые также могут быть достигнутыми с ростом скоростного напора, монотонно увеличивающегося на траектории входа до своего максимального значения и далее монотонно уменьшающегося. У большинства материалов при комнатной температуре предел прочности на сдвиг $\sigma _{\tau }^{*}$ ниже предела прочности на растяжение σp. Для хрупких материалов (или материалов при низкой температуре) это соотношение будет обратным, т.е. $\sigma _{e}^{*} < \sigma _{\tau }^{*}$. Поэтому условие начала разрушения можно написать в общем виде, не останавливаясь на каком-либо конкретном начале разрушения
где κ = 3–4, $\sigma {\kern 1pt} *$ – некая условная прочность, фигурирующая в какой-либо теории разрушения. После достижения на траектории условия разрушения (1.3) начинается раскалывание метеороида на части – его фрагментация (дробление). Если условие (1.3) на траектории не достигается, например, для достаточно прочного метеороида, то последний проходит атмосферу и сталкивается с поверхностью планеты, образуя на суше кратер, а на воде – гравитационные волны (цунами для очень больших тел) [42, 51]. Хотя не все метеороиды дробятся, статистика показывает, что половина из них падает на землю раздробленными частями [3]. Более того, было обнаружено, что процентное содержание числа дробящихся в полете метеороидов резко увеличивается с увеличением их внеатмосферной массы [18]. Увеличение массы метеороида ведет к большому погружению в атмосфере и к увеличению максимального скоростного напора до достижения максимального значения, т.е. к большей вероятности его фрагментации по сравнению с метеороидом меньшей начальной массы.Для трех болидов зарегистрированных астрономическими сетями, разрушение происходило в момент, когда скоростной напор составлял от 10 до 100 атмосфер. Оба эти предела больше, чем напряжения разрушения. Приведенные данные [28, 52] убедительно свидетельствуют, что прочность метеороидов в полете существенно меньше прочности метеоритов на земле. Данные по изменению скорости с высотой разрушения материала Пршибрам, Лост-Сити и Иннисфри [28, 52] показывают, что скоростной напор нигде не достигал пределов прочности их фрагментов. Более того, разница между скоростным напором, при котором начиналось дробление метеорита Пршибрам и прочностью на разрыв достигала не менее 200 атм, а разница с прочностью сжатия была не менее 1000 атм (естественно, последняя выше на разность этих величин). Аналогичная картина наблюдалась и для других каменных метеороидов.
Столь большую разницу между аэродинамическими нагрузками, приводящими к разрушению каменных метеороидов и прочностью их метеоритов, можно отнести только за счет их первоначальной (до разрушения) неоднородности. Прочность структурно неоднородных тел дает феноменологическая статистическая теория прочности, предложенная Вейбуллом еще в конце 30-х годов [1]. Согласно этой теории, вероятность разрушения при наличии этих дефектов увеличивается с увеличением объема нагруженного материала, т.е. прочность неоднородного тела уменьшается с увеличением его размера. Другими словами, при возрастании нагрузки тело разрушается по этим дефектам с образованием фрагментов большей прочности, чем исходное тело. Вероятностное рассмотрение этого эффекта проводит к степенной зависимости предела прочности осколков дробящегося тела (тела с дефектами) от их размеров (массы)
(1.4)
$\sigma * = {{\sigma }_{e}}{{\left( {\frac{{{{M}_{{{{e}_{*}}}}}}}{{{{M}_{f}}}}} \right)}^{\alpha }},$Параметры метеорита Лост-Сити были выбраны в качестве модельного примера в работе [29]. При этом полагалось $\alpha = 0$, что соответствует мгновенному раздроблению тела, независимо от его размера, а прочность тела считалась прямо пропорциональной числу образующихся фрагментов. Такая зависимость, для начального этапа разрушения тела [27] пригодна до тех пор, пока число фрагментов невелико (не более 10), т.е. на начальном этапе разрушения. Однако, решения, полученные в [29], применялись на всей траектории, вплоть до окончания дробления. Таким образом, предложенная модель оказалась пригодной для описания образования нескольких фрагментов метеорита Лост-Сити, но применимость ее для моделирования дробления Челябинского тела или Сихоте-Алинского метеорита, сопровождавшегося образованием многочисленных мелких осколков, остается под вопросом. В рамках формулы (1.4) при $\alpha = 0$ метеороид разрушается на фрагменты неопределяемых размеров и далее он движется, как можно схематизировать, в гидродинамическом режиме в виде роя, содержащего широкий и непрерывный спектр масс осколков, взаимодействующих с атмосферой как большая “капля несжимаемой жидкости”, движущаяся в атмосфере с большой скоростью. Эта модель впервые была предложена и качественно разработана для разрушения крупных тел при их входе в атмосферу в работах [49, 50].
Согласно идее Григоряна, после того, как давление на лобовой поверхности тела достигает разрушающих величин, по телу с большой скоростью (3–5 км/с) начинает перемещаться фронт разрушения, а раздробленная масса растекается в боковые стороны (тело расплющивается). Причем, уравнение растекания облака раздробленных осколков (расплющивания большой капли [55], см. далее) большой капли существенно зависит от положения внешней границы раздробленной массы относительно начального радиуса тела. Границей между двумя режимами является точка (высота), соответствующая движению начального размера тела в направлении, перпендикулярном направлению полета за счет сжатия облака раздробленного тела. К этому моменту весь метеороид раздроблен, а распределение давлений на поверхности дробленой массы на боковой части имеет минимум, так что растекание приводит к сжатию объема с дробленой массой в продольном направлении и к ее расширению в поперечном. В результате краевые части тела под действием скоростного напора встречного потока будут отгибаться назад, придавая всему жидкому объему форму медузы. Рассматривая движение подобного образования, Григорян оценил высоту, на которой скорость тела упадет до величин порядка скорости звука. Здесь баллистическая головная ударная волна перестает получать подпитку от тела и происходит его повышенное торможение и полный распад с передачей всей кинетической энергии окружающему газу. Данный процесс, полученный качественным анализом, представляет собой квазимгновенный взрыв. Здесь рассуждение Григоряна трудно воспринимаются с точки зрения газовой динамики.
Следует отметить, что гидродинамический режим после мгновенного дробления тела ($\alpha = 0$) рассмотрен ранее [50]. Вместо большой “капли” он рассматривал движение жидкого тела в виде кумулятивной струи до ее полного исчезновения.
Эти рассуждения о деформации большой капли (размером примерно 50–60 м для Тунгусского метеорита) идеальной несжимаемой жидкости противоречат реальной картине, ее деформации. Вследствие развития неустойчивостей Рэлея–Тейлора и Кельвина–Гельмгольца на границах (капли), а также уноса массы, раздробленное тело принимает различную форму, которую заранее невозможно точно определить. В некоторых случаях тело стремится принять коническую форму и легче выдерживает полет сквозь атмосферу, в других оно распадается и принимает форму тора. Эти результаты были получены прямым численным решением уравнений Эйлера при помощи свободного лагранжева-эйлерова метода (ALE method) со специальным способом маркировки границы тела [26]. При скорости входа 20 км/с 200-метровое ледяное тело теряет перед падением кинетическую энергию, но увеличивает свой радиус и уменьшает свою среднюю плотность. Несмотря на разрушение, единая головная баллистическая ударная волна охватывает тело.
Идея распространения фронта дробления по телу фигурирует также в работе [35]. Однако, в модели этих авторов дробление тела начинается изнутри под действием касательных напряжений и распространяется к периферийным участкам метеороида до полного дробления всего тела. Напряжения в твердом теле рассматривались в рамках решения уравнений теории термоупругости. Распределение температуры внутри тела и ее влияние на напряженное состояние тела, учитывавшиеся Коробейниковым и его коллегами, как было показано выше, незначительно для крупных тел, но может быть существенным для более мелких. Условием окончания дробления считался момент, когда объем разрушенной области тела достигал определенной, заранее выбранной доли общего объема. Далее в газодинамической постановке рядом авторов решалась задача о разлете осколков разрушенного тела, который рассматривался условно как взрыв по модели распада произвольного сферического взрыва. Модель газодинамического взрыва обычно не пригодна для модели метеорного взрыва под воздействием сжатых и горячих паров разрушенного метеороида.
2. Модель ПРД. При построении количественной теории дробления (фрагментации) метеороида будем предполагать, что метеороид с массой $М$ непрерывно дробиться на N частей дробленой массы: ${{М}_{f}} = М{\text{/}}N$, прочность которых далее будет зависеть от их массы ${{М}_{f}}$ по закону $\sigma {\kern 1pt} *$ = ${{\sigma }_{e}}{{\left( {{{M}_{e}}{\text{/}}{{M}_{f}}} \right)}^{\alpha }}$. После начала разрушения скоростной напор в каждый момент будет определять число разных фрагментов, если подчинить его равновесному условию при соответствующих значениях масштабного фактора $\alpha $
(2.1)
$\rho {{V}^{2}} = \sigma {\kern 1pt} *{\kern 1pt} (N) \equiv k{{\sigma }_{e}}{{\left( {\frac{{{{M}_{{{{e}_{*}}}}}}}{M}N} \right)}^{\alpha }} = k{{\sigma }_{e}}{{\left( {\frac{{{{M}_{{{{e}_{*}}}}}}}{{{{M}_{f}}}}} \right)}^{\alpha }},$Из (2.1) с учетом условия начала разрушения
(2.2)
${{\rho }_{*}}V_{*}^{2} = k{{\sigma }_{e}}{{\left( {\frac{{{{M}_{{{{e}_{*}}}}}}}{{{{M}_{*}}}}} \right)}^{\alpha }} \equiv \sigma {\kern 1pt} *$Тем самым число осколков $N$ на траектории дробящегося метеороида определится через $V$ и $M$ роя осколков, которые находятся из решения уравнений ФТМ
(2.3)
$N = \frac{M}{{{{M}_{*}}}}{{\left( {\frac{{\rho {{V}^{2}}}}{{{{\rho }_{*}}V_{*}^{2}}}} \right)}^{{1/\alpha }}}$При ${{V}_{e}} = {{V}_{*}}$, $\rho {{V}^{2}} = {{\rho }_{*}}V_{*}^{2}$, $N = 1$, где ${{M}_{*}}$ и Ме – масса метеороида к моменту начала дробления и его внеатмосферная масса, ${{\rho }_{*}}$, ${{V}_{*}}$ – плотность (высота) атмосферы и скорость метеорного тела в момент начала разрушения. Так как метеороид подвергается аэродинамической эрозии еще до начала появления дробления, то ${{M}_{*}}$ < Ме.
В режиме дробящегося тела эффективная площадь миделя роя осколков S увеличивается и будет тем самым зависеть от числа фрагментов N. Примем далее для тела произвольной формы (феноменологическое соотношение для S) $S = f{{\left( {M{\text{/}}\delta } \right)}^{{2/3}}}$, ( f – форм-фактор, δ – плотность метеороида), если тело меняется подобно себе. Если тело массы М дробится каждый раз на $N = M{\text{/}}{{M}_{f}}$ частей, которые не перекрываются (успели разойтись), то из условия сохранения массы для эффективной площади миделя S такого роя осколков можно получить равенство
(2.4)
$S = f{{\left( {\frac{М}{\delta }} \right)}^{{\frac{2}{3}}}}{{N}^{{\frac{1}{3}}}} = {{S}_{*}}{{\left( {\frac{М}{{{{М}_{*}}}}} \right)}^{{\frac{2}{3}}}}{{N}^{{\frac{1}{3}}}},\quad f = \frac{1}{N}\sum\limits_{k = 1}^N {{{f}_{k}}} ,\quad {{S}_{*}} = f{{\left( {\frac{{{{М}_{*}}}}{\delta }} \right)}^{{\frac{2}{3}}}}$В этом выражении форм-фактор f предполагается средним между N форм-факторами ${{f}_{i}}$ отдельных фрагментов, ${{S}_{*}}$ – площадь миделева сечения к моменту начала дробления. Площадь миделя одного осколка равна
При дроблении размер осколков ${{R}_{i}}$ уменьшается. Действительно, если для единого тела и одного фрагмента обозначить радиусы соответственно $R$ = $\sqrt {S{\text{/}}\pi } $ = $\sqrt {f{\text{/}}\pi } {{\left( {M{\text{/}}\delta } \right)}^{{1/3}}}$ и
(2.5)
${{R}_{i}} = \sqrt {\frac{{{{f}_{i}}}}{f}} \sqrt {\frac{f}{\pi }} {{\left( {\frac{M}{\delta }} \right)}^{{1/3}}}{{N}^{{ - 1/3}}} = \sqrt {\frac{{{{f}_{i}}}}{f}} R{{N}^{{ - 1/3}}},$Если осколки перекрываются (не успевают разойтись), то степень N в выше полученных выше формулах для $S$ и ${{R}_{i}}$ будет меньше 1/3. Поэтому замена 1/3 на меньший коэффициент в приведенном решении может в какой-то мере служить оценкой учета эффекта перекрытия (экранирования) осколков между собой в процессе дробления.
Понятно, что предположение дробления на равные осколки при заданном скоростном напоре на каждом этапе дробления на всем режиме разрушения метеороида, но с размерами частей, зависящими от скорости их роя, является дополнительным результатом, особенно для железных или не очень крупных метеороидов, которые разрушаются примерно при одинаковых значениях скоростного напора и дробятся примерно на равные части. Однако дробление на равные фрагменты следует здесь понимать в среднем статистическом смысле. С другой стороны, все части с одинаковой прочностью подвергаются одному и тому же давлению, поэтому они примерно разделяются на части одинакового размера на каждом этапе дробления. Размер частей уменьшается с ростом скорости метеороида. Так как все части на каждой стадии разрушения подвергаются одному и тому же скоростному напору, то их размер будет близок друг к другу. Для простоты получения дальнейших решений мы оставим степень 1/3 и не будем учитывать это обстоятельство (перекрытие площади осколков).
Движение такого тела рассматривалось в работе [44]. Точка на траектории с плотностью ${{\rho }_{*}}$, где начинается дробление, будет определяться из условия (2.2). Для изотермической атмосферы плотность газа и высота начала дробления с учетом (2.2) будут определяться, соответственно, из выражений [44]:
Далее с высоты ${{z}_{*}}$ будет двигаться рой раздробленных осколков с прогрессивно увеличивающимся их числом по мере приближения их к поверхности планеты. Уравнение движения роя дробящихся и теряющих массу за счет аэродинамической эрозии осколков, в каждый момент будет совпадать с уравнением движения единого тела, но с переменной площадью миделя, определяемой выражением (2.4). Здесь под скоростью понимается средняя скорость осколков или скорость роя осколков. Эту модель будем называть моделью ПРД. При переменном значении параметра уноса массы $\sigma = {{C}_{H}}{\text{/}}\left( {Q{{C}_{D}}} \right)$ (${{C}_{H}}$ – коэффициент теплопередачи, Q – эффективная теплота уноса массы, ${{С}_{D}} = 1$ – коэффициент сопротивления) она допускает только численное решение в случае изотермической атмосферы. Модель ПРД может быть усовершенствована, если учесть некоторое запаздывание в образовании отдельно летящих фрагментов после удовлетворения равновесного условия разрушения. Это запаздывание определяется временем расхождения фрагментов. Относительная скорость поперечного движения их центров масс может быть аппроксимирована выражением [44], которое запишем в виде, вытекающем из равенства скоростных напоров в лобовой и боковой точках жидкой капли $\delta {{\left( {ds{\text{/}}dt} \right)}^{2}}$ = ${{K}^{2}}\rho {{V}^{2}}$ ($s$ – площадь миделевого сечения) в виде
Это выражение впервые было получено в работе [46] из рассмотрения фрагментации жидкой капли – раздробленного тела. Переходя в этом уравнении к дифференцированию по независимой переменной $\rho $, получим дифференциальное уравнение с разделяющимися переменными
где θ – угол наклона траектории к горизонту.Интегрируя это уравнение от значений, определяющих равновесной моделью разрушения до искомых поправочных, получим
(2.7)
${{s}_{N}} - {{s}_{{{{N}_{\rho }}}}} \equiv \Delta {{S}_{N}}\frac{{2Kh}}{{\sin \theta }}\frac{{{{\rho }_{{{{N}_{\rho }}}}}}}{\delta }\left( {\sqrt {\frac{\rho }{{{{\rho }_{{{{N}_{\rho }}}}}}}} - 1} \right) = \frac{{2Kh}}{{\sin \theta }}\sqrt {\frac{{{{\rho }_{{{{N}_{\rho }}}}}}}{\delta }} \left( {\frac{{\Delta {{z}_{N}}}}{{\exp \left( {2h} \right)}} - 1} \right),$Известно, что фрагменты можно считать летящими независимо друг от друга, если расстояние между ними порядка их размеров. Если размер исходного тела обозначить через D, размер каждого из N фрагментов будет равен ${{D}_{N}} = D{\text{/}}{{N}^{{1/3}}}$.
Путь, проходимый центрами масс фрагментов от момента, когда их N штук до момента, когда их будет L штук
В частности,
Полагая, что количество фрагментов каждый раз увеличивается на единицу, т.е. в момент выполнения равновесного условия образование N фрагментов имеется N – 1 летящих независимо фрагментов, будет иметь $\Delta {{S}_{N}}$ = $\Delta {{s}_{{N - 1,N}}}$. Из (2.7) найдем поправку к значению высоты образования N фрагментов, даваемой моделью ПРД.
Высота, на которой N фрагментов можно считать летящими независимо, определяется следующей величиной
(2.8)
${{z}_{N}} = {{z}_{{{{N}_{p}}}}} - 2h\ln \left( {\sqrt {\frac{\delta }{{{{\rho }_{{{{N}_{p}}}}}}}} \frac{{\left( {2N - 1} \right){{D}_{N}} - \left( {2N - 3} \right){{D}_{{N - 1}}}}}{{2Kh}}\sin \theta + 1} \right)$Если на высоте ${{z}_{N}}$ выполняется условие образования N + 1 фрагмента модели ПPД, то значение ${{z}_{{N + 1}}}$ следует отсчитывать от ${{z}_{N}}$. В противном случае надо определить высоту $\Delta {{z}_{{N + 1,\rho }}}$. Иногда может реализоваться ситуация, когда скоростной напор возрастает столь быстро, что для всех N условие образования следующего числа фрагментов выполняется раньше, чем они успевают разойтись. В этом случае поправочные высоты для любого N можно выразить через высоту первой фрагментации (когда N = 2), определяемую в равновесной модели. В этом случае путь, проходимый центром масс N-го фрагмента, выразится в виде $\Delta {{s}_{N}}$ = $(2N - 1){{D}_{N}}$ – D.
А положение высоты N фрагментов определяется как
(2.9)
${{z}_{N}} = {{z}_{{{{2}_{\rho }}}}} - 2h\ln \left( {\frac{{\left[ {\left( {2N - 1} \right){{D}_{N}} - D} \right]\sin \theta }}{{2Kh}}\sqrt {\frac{\delta }{{{{\rho }_{{{{2}_{p}}}}}}}} + 1} \right)$При выполнении условий применимости формулы (2.9) расчет можно вести и по формуле (2.8), хотя это менее удобно, т.к. она имеет “пошаговый” характер, в то время как формула (2.9) позволит определять ${{z}_{N}}$ непрерывным образом для любого N.
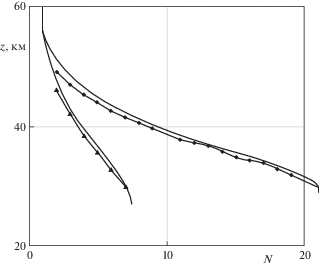
Зависимость количества образующихся фрагментов от высоты с учетом поправок на их расхождение. Модель ПРД может быть усовершенствована, если учесть запаздывание образования фрагментов после равновесного образования фрагментов. На рис. 1 для входных параметров болида Бенешов приведен пример расчета (формула (2.8)) поправок к высоте образования фрагментов (кривые зависимостей количества образовавшихся фрагментов от высоты соответствуют разным значениям параметра $\alpha $: ромбики – α = 0.95, треугольники – α = 1.62). При этом зависимости числа образующихся фрагментов от высоты получены с учетом поправок на их расхождение. Большие значения α взяты потому, что они соответствуют сравнительно малому числу образующихся осколков, при увеличении масштабного фактора α число осколков существенно уменьшается. Так, например, менее, чем двукратное уменьшение величины $\alpha $ влечет более, чем трехкратное увеличение числа образующихся фрагментов.
Рис. 1.
Зависимость количества образующихся фрагментов от высоты с учетом поправок на их расхождение:
 – α = 0.95; $\blacktriangle $ – α = 1.62.
– α = 0.95; $\blacktriangle $ – α = 1.62.
В заключение этого раздела приведем полную систему уравнений ФТМ включающую силу тяжести, реактивную силу (уравнение Мещерского) и подъемную силу (угол атаки – наклон траектории метеороида – $\theta $). Уравнение движения (уравнение Ньютона) связывает величину $d\ln V{\text{/}}d\bar {Z}$ с реактивной силой уноса массы.
(2.10)
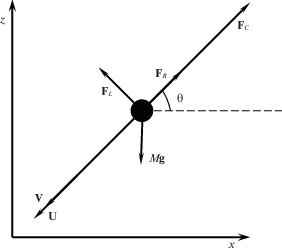
$\begin{gathered} \frac{{d\ln V}}{{d\bar {Z}}} = \frac{1}{2}\frac{{\bar {\rho }}}{{{{{\bar {M}}}^{{1/3}}}\sin \theta }} - \frac{{gh}}{{{{V}^{2}}}} + \frac{{U - V}}{V}\frac{{d\ln M}}{{d\bar {Z}}};\quad \bar {Z} = \frac{Z}{h},\quad \bar {\rho } = \frac{\rho }{{{{\rho }_{m}}}} \\ \frac{{d{{M}^{{1/3}}}}}{{d\bar {Z}}} = \frac{1}{6}\frac{{\bar {\rho }}}{{\sin \theta }}\sigma {{V}^{2}};\quad \sigma {{V}^{2}} = \frac{1}{6}\frac{{{{C}_{H}}}}{{Q{{C}_{D}}}}{{V}^{2}} = \frac{1}{6}\frac{{{{C}_{H}}}}{{Q{{C}_{D}}}} \\ \frac{{d{{{\sin }}^{2}}\theta }}{{dZ}} = \left[ {2\left( {\left( {\frac{h}{{{{R}_{ \otimes }} + Z}} - \frac{{gh}}{{{{V}^{2}}}}} \right) + \frac{{\bar {\rho }K}}{{{{{\bar {M}}}^{{1/3}}}\cos \theta }}} \right)} \right]{{\cos }^{2}}\theta ;\quad K = \frac{{{{C}_{L}}}}{{{{C}_{D}}}}, \\ \end{gathered} $Рис. 2.
Силовая схема движения метеороида. ${{{\mathbf{F}}}_{C}}$ – сила сопротивления, ${{{\mathbf{F}}}_{R}}$ – реактивная сила, $M{\mathbf{g}}$ – сила тяжести, направленная вертикально вниз, ${{{\mathbf{F}}}_{L}}$ – подъемная сила, действующая под прямым углом на траекторию метеороида, ${\mathbf{V}}$ – скорость метеороида.
Система уравнений (2.10) – второй закон Ньютона, учитывающий силу тяжести и реактивную силу уноса массы (силу Мещерского), влияющую в том числе на угол траектории метеороида, отличается от классической системы уравнений ФТМ. Далее система уравнений (2.10) будет записана через независимую переменную $\rho $. Используя формулу преобразования ${d \mathord{\left/ {\vphantom {d {dz}}} \right. \kern-0em} {dz}}$ = ${d \mathord{\left/ {\vphantom {d {d\rho }}} \right. \kern-0em} {d\rho }}$ – ${\rho \mathord{\left/ {\vphantom {\rho h}} \right. \kern-0em} h}$, получим систему уравнений с независимой переменной $\rho $ без учета силы тяжести, реактивной силы и члена изменения угла наклона:
(2.11)
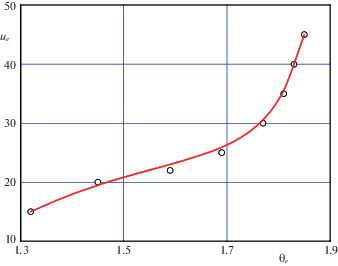
$\begin{gathered} \frac{{d\ln \bar {V}}}{{d\bar {\rho }}} = - \frac{1}{{2{{{\bar {M}}}^{{1/3}}}\sin \theta }} + \frac{{gh}}{{{{V}^{2}}}} \\ \frac{{d{{{\bar {M}}}^{{1/3}}}}}{{d\bar {\rho }}} = - u;\quad u = \frac{1}{6}\sigma {{V}^{2}} \\ \end{gathered} $Будем решать систему (2.11) методом последовательных приближений. В качестве нулевого приближения для скорости возьмем ${{\bar {V}}^{{(0)}}} = 1$. Тогда уравнение для $\bar {M}$ будет, $d{{\bar {M}}^{{1/3}}}{\text{/}}d\bar {\rho } = - {{u}_{e}}$, решение которого даст первое приближение для $\bar {M}$: ${{\bar {M}}^{{1/3}}} = 1 - {{u}_{e}}\bar {\rho }$, где $\bar {\rho } = \rho {\text{/}}\left( {{{\rho }_{m}}\sin \theta } \right)$. На рис. 3 приведена зависимость параметра ${{u}_{e}}$ от угла ${{\theta }_{e}}$ входа метеороида в атмосферу.
Рис. 3.
Зависимость параметра задачи ${{u}_{e}} = \frac{1}{6}\sigma V_{e}^{2}$ в зависимости от угла θe входа метеороида в атмосферу.
Первое приближение для скорости найдется из уравнения
Подставив это решение в уравнение для $\bar {M}$, получим
Решение для V и M сравнивалось с численным решением полной системы (2.10) при переменном параметре уноса массы $\sigma $. Параметр ${{u}_{e}}$ был подобран методом наименьших квадратов таким образом, чтобы полученное решение для скорости и массы совпадало с численным решением, полученным при переменном $\sigma $. На рис. 4 приведены профиль скорости и массы для тела, движущегося под углом 20° при Q = 5 км2/c2. Оказалось, что значение эффективного параметра ${{u}_{e}}$ разное для скорости и массы. Для скорости ${{u}_{e}}$ равняется 1.45, для массы ${{u}_{e}}$ равняется 1.7. На рис. 5 приведено изменение скорости и массы с высотой.
Рис. 4.
Профили скорости, массы и угла наклона траектории. Сплошной линией обозначено аналитическое решение $\sigma $, кружочками – численное решение (при переменном σ).
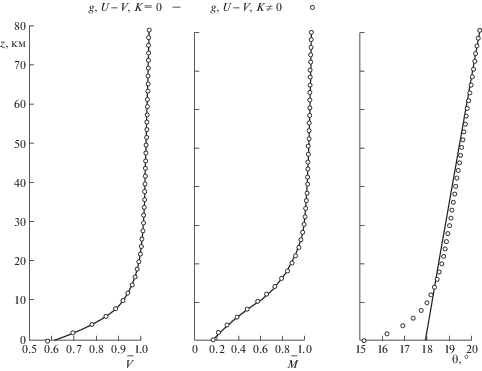
Рис. 5.
Изменение скорости (а) и массы (б) с высотой: 1 – численное решение с учетом дробления; 2 – численное решение без дробления; 3 – классическое аналитическое решение при $\sigma $ = const.
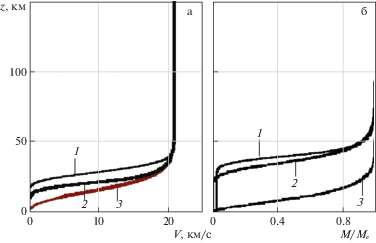
Получены численные решения для скорости и массы и угла $\theta $ для двух случаев. Первый случай, когда сила тяжести, реактивная сила и влияние угла траектории к горизонту учитывается, а во втором случае эти величины не учитываются. Для метеороидов от 1 до 109 кг при скоростях до 30 км/с кривые для $\bar {V}$ и $\bar {M}$ совпадают. Это означает что для типичных метеороидов и скоростей отброшенные члены в уравнении: сила тяжести, реактивная сила и влияние на угол траектории подъемной силы практически не влияют, поэтому в такой постановке, как правило, решается большинство задач ФТМ. Используя полученное аналитическое решение, могут быть получены явные выражения для скоростного напора и кинетической энергии метеороида.
3. Баллистика дробящегося метеороида. Под действием сил инерции (или, другими словами, увеличение “веса” в собственной системе координат) космические тела, движущиеся в атмосфере планеты, испытывают дробление. В данной работе будем количественно рассматривать следующий сценарий этого процесса.
Первый этап. Вход в атмосферу тела с заданными коэффициентами сопротивления и теплопередачи как единого тела до момента начала разрушения.
Второй этап. Дальнейшее торможение тела с потерей массы (абляцией), а также с учетом дробления на фрагменты (части) при выполнении равновесного условия разрушения.
Третий этап. Падение осколков на землю с учетом силы тяжести и уноса массы.
Критерием перехода от первого этапа ко второму будет служить условие начала разрушения. При решении системы уравнений (3.1) (см. ниже) ФТМ оно используется как начальное условие. Результатом решения являются значения всех параметров в момент начала разрушения. Эти величины, в свою очередь, служат начальными значениями при решении уравнений второго этапа, которое сводится к решению следующей системы уравнений баллистики дробящегося тела:
(3.1)
$\begin{gathered} Q\frac{{dM}}{{dt}} = - \frac{1}{2}{{C}_{H}}S\rho {{V}^{3}} \\ \frac{{dz}}{{dt}} = - V\sin \theta \\ \end{gathered} $Система уравнений (3.1) отличается от системы уравнений для единого тела тем, что площадь миделя $S$ здесь пропорциональна числу осколков в степени 1/3. Величины со звездочкой ${{\rho }_{*}}$, ${{V}_{*}}$, ${{M}_{*}}$ относятся к высоте (плотности) начала дробления. Система (3.1) описывает движение дробящихся осколков и отличается от системы уравнений единого (не дробящегося) тела тем, что площадь миделевого сечения теперь зависит от числа осколков, которое в свою очередь связано со скоростным напором и общей массой роя осколков $M$ (выражение для $N$). Рассмотрим сначала баллистику для случая изотермической атмосферы, когда шкала высот атмосферы по плотности h и шкала высот атмосферы по давлению H постоянны и равны между собой. Из наблюдений полетов достаточно крупных метеороидов (Пршибрам, 1959; Lost-City, 1970; Пикскилл, 1972; Иннисфри, 1977, рис. 1) и других метеороидов видно, что они начинают дробиться, не успев существенно затормозиться, т.е. ${{V}_{*}} \approx {{V}_{e}}$. Этот эффект неоднократно обсуждался в литературе (см., например, [4, 22, 29]). Причем в двух последних упомянутых работах не совсем корректно говорится, что дробление предшествует торможению и уносу массы. Дело в том, что и унос массы, и торможение происходят с самого начала входа метеороида в атмосферу, но к моменту начала разрушения их относительные величины оказываются незначительными по сравнению с самими массой $M$ и скоростью $V$. По-видимому, процитированные работы следует понимать в том смысле, что торможением и уносом массы до начала фрагментации метеороида можно пренебречь ввиду их относительной малости. Строго в этом можно убедиться с помощью решения задачи баллистики для достаточно крупных метеороидов с учетом эффекта уноса массы.
Таким образом, при расчетах можно считать, что скорость метеороида до начала разрушения не меняется, т.е. к началу разрушения скорость метеороида равна скорости входа метеороида в атмосферу (${{V}_{*}} \approx {{V}_{e}}$). Массу также для достаточно больших тел можно либо полагать постоянной, либо рассчитать по формуле для уноса массы единого тела.
Рассмотрим баллистику (уравнения) роя осколков в рамках модели ПРД. Первое уравнение (уравнение торможения) системы (3.1) при переходе к новой независимой переменной $\tilde {\rho } = \rho {\text{/}}{{\rho }_{*}}$ (высоте) принимает вид с учетом исключения массы из условия равновесного дробления:
(3.2)
$\frac{{d\tilde {V}}}{{d\tilde {\rho }}} = - \frac{{{{{\bar {\rho }}}_{*}}}}{2}\tilde {V}{{\left( {\tilde {\rho }{{{\tilde {V}}}^{2}}} \right)}^{{1/3\alpha }}},\quad \tilde {V} = \frac{V}{{{{V}_{*}}}},\quad {{\bar {\rho }}_{*}} = \frac{{{{\rho }_{*}}}}{{{{\rho }_{{{{m}_{*}}}}}}}$Получим это уравнение из исходного уравнения торможения (3.1) с использованием граничного (начального) условия РПД:
Откуда получаем искомое фундаментальное оригинальное уравнение торможения, справедливое после начала дробления (для дробящегося тела)
(3.3)
$\frac{{d\tilde {V}}}{{d\tilde {\rho }}} = - \frac{1}{2}{{\bar {\rho }}_{*}}\tilde {V}{{\left( {\frac{{\rho {{V}^{2}}}}{{{{\rho }_{*}}V_{*}^{2}}}} \right)}^{{1/3\alpha }}},\quad \tilde {\rho } = \frac{\rho }{{{{\rho }_{*}}}},\quad {{\bar {\rho }}_{*}} = \frac{{{{\rho }_{*}}}}{{{{\rho }_{{{{m}_{*}}}}}}},\quad \tilde {V} = \frac{V}{{{{V}_{*}}}},$Важно отметить, что в полученное уравнение торможения (3.3) или (3.2) дробящегося тела не вошла масса роя осколков благодаря использованию условия равновесного дробления, связывающего массу роя осколков М со скоростным напором. Ранее [44] в режиме движения единого тела масса тела М исключалась из уравнения торможения с использованием уравнения энергии и тем самым получалось уравнение, содержащее переменный параметр уноса массы $\sigma $. В случае баллистики дробящегося тела параметр $\sigma $ в уравнение торможения не входит, т.к. масса тела исключалась с помощью условия равновесного дробления, которое параметр $\sigma $ не содержит.
Интегрируя уравнение (3.3) для изотермической атмосферы ($f = 1.21$, $h = 7$ км, ${{C}_{D}} = 1$), начиная от высоты начала дробления с плотностью воздуха ${{\rho }_{*}}$ = 2.01 × 10–6 г/см3 получим решение уравнения для скорости $V$ в аналитическом виде, зависящем от масштабного фактора α:
(3.4)
$V = {{V}_{*}}{{\left[ {1 + \frac{{{{{\bar {\rho }}}_{*}}}}{{1 + 3\alpha }}\left( {{{{\tilde {\rho }}}^{{1 + \frac{1}{{3\alpha }}}}} - 1} \right)} \right]}^{{ - \frac{{3\alpha }}{2}}}},\quad \tilde {\rho } = \rho {\text{/}}{{\rho }_{*}},\quad {{\bar {\rho }}_{*}} = {{\rho }_{*}}{\text{/}}{{\rho }_{m}}$При α → ∞ это решение переходит в решение для единого абсолютно твердого тела (идеального не дробящегося метеороида):
Разрушение, начавшееся на высоте с плотностью ${{\rho }_{*}}$, будет продолжаться, если плотность ${{\rho }_{*}}$ достигается до высоты появления соответствующего максимального скоростного напора единого тела, т.е. при выполнении условия ${{\bar {\rho }}_{*}}$ < ${{\bar {\rho }}_{m}}$.
При выполнении этого условия лавинное разрушение осколков, движущихся со скоростью, меньшей скорости единого тела будет продолжаться до тех пор, пока скоростной напор не достигнет максимального значения. Этот максимум, вычисляемый с помощью (3.4), будет достигаться на высоте с относительной плотностью ${{\tilde {\rho }}_{ \times }}$, равной
(3.5)
${{\tilde {\rho }}_{ \times }} = \frac{{{{\rho }_{ \times }}}}{{{{\rho }_{*}}}} = \frac{{{{{\tilde {\rho }}}_{*}}}}{{{{{\tilde {\rho }}}_{*}}}}{{\left[ {1 + n\left( {1 - {{{\bar {\rho }}}_{*}}} \right)} \right]}^{{\tfrac{1}{{n + 1}}}}};\quad n = {\text{1/}}\left( {3\alpha } \right)$(3.6)
${{\rho }_{ \times }}V_{ \times }^{2} = {{\rho }_{*}}V_{*}^{2}\rho _{*}^{{\frac{1}{{n + 1}}}}{{\left[ {1 + n\left( {1 - {{{\bar {\rho }}}_{*}}} \right)} \right]}^{{ - \frac{1}{{n(n + 1)}}}}}$Скорость на этой высоте будет равна
(3.7)
${{V}_{ \times }} = {{V}_{*}}{{\left[ {1 + n(1 - {{{\bar {\rho }}}_{*}})} \right]}^{{ - 1/2n}}}$При α → ∞ (n → 0) из (3.7) получаем ${{\tilde {\rho }}_{ \times }} \to {{\rho }_{ \times }}{\text{/}}{{\rho }_{*}}$ (${{\rho }_{ \times }} = {{\rho }_{m}}$), ${{\rho }_{ \times }}V_{ \times }^{2}$ → ${{\rho }_{m}}V_{m}^{2}$, как и должно быть для единого тела.
Таким образом, лавинное (последовательное) разрушение метеороида будет происходить в интервале высот, соответствующем интервалу плотности ${{\rho }_{*}}$ < ρ < ρ×.
Из уравнения (3.4), используя (3.1) для величины торможения ($ - \dot {V}$), получаем
(3.8)
$j \equiv - \dot {V} = \frac{{{{\rho }_{*}}V_{*}^{2}}}{{2{{\beta }_{*}}}}{{\left( {\frac{{{{\rho }_{*}}{{V}^{2}}}}{{{{\rho }_{*}}V_{*}^{2}}}} \right)}^{{1 + n}}};\,\,\,\,{{\beta }_{*}} = \frac{m}{{{{C}_{D}}}} = \frac{{{{M}_{*}}}}{{{{S}_{*}}{{C}_{D}}}}$Отсюда видно, что максимальная перегрузка $\dot {V}$ будет достигаться при той же безразмерной плотности ${{\bar {\rho }}_{*}}$, что и максимальный скоростной напор. Подставляя (3.6) в (3.8), найдем
(3.9)
${{j}_{{\max }}} = \frac{{{{\rho }_{*}}V_{*}^{2}}}{{2{{\beta }_{*}}}}\frac{1}{{{{{\bar {\rho }}}_{*}}\left[ {1 + n\left( {1 - {{{\bar {\rho }}}_{*}}} \right)} \right]_{{\max }}^{{1/n}}}}$При α → ∞ (n → 0) из (3.8) получаем максимальную перегрузку для единого тела. Из (3.9) также следует, что при ${{\bar {\rho }}_{*}} < 1$ (условие появления и продолжения дробления) для любого α = 1/(3n) перегрузки будут больше, чем для единого тела. Следовательно, рой осколков будет тормозиться сильнее, чем единое тело той же массы, влетающее в атмосферу с той же скоростью. Этот очевидный эффект более сильного торможения роя осколков по сравнению с торможением единого тела будет проявляться тем сильнее, чем меньше ${{\bar {\rho }}_{*}}$, т.е. чем выше начнет дробиться тело, тем меньше будет прочность на разрушение влетающего в атмосферу тела.
Из (3.1) находим максимальное число фрагментов в конце разрушения метеороида
Здесь следует брать целую часть от N×, округляя его в сторону ближайшего целого числа.
Выше М× – суммарная масса роя осколков на высоте прекращения дробления метеороида. Найдем М×. Если считать, что как единое тело до дробления, так и осколки имеют одинаковое значение параметра уноса массы σ, то интеграл массы (3.10) будет описывать потерю массы метеороида на всей траектории, включая и этап дробления, за исключением последней фазы полета, когда унос массы за счет аэродинамической эрозии прекращается. Это происходит, когда скорость метеороида падает примерно до величин порядка 2–4 км/с, что вытекает из уравнения для скорости и массы записанного для дробящегося тела (3.1). На основании первых двух уравнений системы (3.1) получаем интеграл массы
(3.10)
${{М}_{ \times }} = {{М}_{{е \times }}}\exp \left[ {\frac{\sigma }{2}\left( {V_{ \times }^{2} - V_{{e \times }}^{2}} \right)} \right]\quad {\text{или}}\quad {{М}_{ \times }} = {{М}_{*}}\exp \left[ {\frac{\sigma }{2}\left( {V_{ \times }^{2} - V_{*}^{2}} \right)} \right]$Площадь эффективного миделя (для всего роя осколков) в конце дробления будет равна
(3.11)
${{S}_{ \times }} = {{S}_{*}}\frac{{{{М}_{ \times }}}}{{{{М}_{*}}}}{{\left( {\frac{{{{\rho }_{ \times }}V_{ \times }^{2}}}{{{{\rho }_{*}}V_{*}^{2}}}} \right)}^{{\frac{1}{{3\alpha }}}}} = {{S}_{*}}{{\left( {\frac{{{{M}_{ \times }}}}{{{{M}_{*}}}}} \right)}^{{\frac{2}{3}}}}N_{ \times }^{{1/3}} = {{S}_{*}}\frac{{{{М}_{ \times }}}}{{{{М}_{*}}}}{{\left\{ {\bar {\rho }_{*}^{n}\left[ {1 + n\left( {1 - {{{\bar {\rho }}}_{*}}} \right)} \right]} \right\}}^{{ - \frac{1}{{1 + n}}}}}$Средний минимальный размер фрагмента “метеоритного дождя” и их масса в рамках рассматриваемой модели дробления будут равны.
Оценим количественно полученные параметры “метеоритного дождя”. Примем СD = 1.6, СН = 0.01, Q = 5 × 1010 эрг/г, Vе = 20 км/с (метеороид Пршибрам). Тогда $\sigma V_{e}^{2}$ = = ${{C}_{H}}V_{e}^{2}{\text{/}}\left( {Q{{C}_{D}}} \right)$ = 0.5. Для М×/Ме из (3.10) получаем ${{M}_{ \times }}{\text{/}}{{M}_{e}}$ = $\exp \left\{ { - 0.25\left[ {1 - {{{\left( {{{V}_{ \times }}{\text{/}}{{V}_{e}}} \right)}}^{2}}} \right]} \right\}$. На фотографиях полета метеороида Пршибрам видно, что окончание дробления наступило при V× ≈ 10 км/с [1]. Тогда М× = 0.83Ме, т.е. суммарная масса метеороида к моменту окончания его дробления уменьшилась всего на 17%. На самом деле величина параметра уноса массы $\sigma $ может быть существенно больше, $\sigma $ ≈ 0.02–0.03 с2/км2, так как $\sigma $ напрямую зависит от коэффициента радиационной теплопередачи, который сильно меняется со скоростью метеороида [44]. Тогда уменьшение массы к моменту окончания дробления оценивается десятками процентов.
Итак, внеатмосферная масса крупного метеороида к моменту окончания дробления может уменьшаться существенно больше, чем наполовину. Таким образом, возможность пренебрежения уносом массы рассмотренной модели динамики роя осколков является оправданной только для достаточно малых коэффициентов теплопередачи CH и больших значений эффективной теплоты уноса массы Q.
Если далее принять h = 7 км, СD = 1.6, D = 10 м, sinθ = sin45° = 0.71, δ = 3.5 г/см3, то параметр взаимодействия к моменту начала дробления будет равен
Если тело начинает дробиться, скажем, на высоте z = 50 км (${{\rho }_{*}}$ = 0.98 × 10–6 г/см3), то ${{\bar {\rho }}_{*}} = 3.04 \times {{10}^{{ - 4}}}$. Значение этого параметра является определяющим при нахождении числа осколков, их размеров и массы. В силу малости ${{\bar {\rho }}_{*}}$ из (3.9) получаем для максимального числа осколков очень простую приближенную формулу
Таким образом, при увеличении масштабного фактора α в два раза число осколков уменьшается при фиксированном значении параметра взаимодействия ${{\bar {\rho }}_{*}}$ более чем в 25 раз. Чем больше значение α, тем материал метеороида неоднороднее, следовательно, он дробится на меньшее число частей. С другой стороны, уменьшение α соответствует переходу к более однородному материалу и его дроблению на большее число осколков. В пределе при α → 0 развиваемая в этой работе модель прогрессивного дробления переходит в модель мгновенного разрушения тела до весьма малых (мелких) осколков, и динамику такого разрушенного тела дальше можно описывать по модели работы [49], т.е. как единого тела несжимаемой жидкости, подверженного неустойчивостям Рэлея–Тейлора и Кельвина–Гельмгольца.
Начиная с высоты с плотностью ρ×, скоростной напор будет монотонно убывать, и рой осколков без увеличения их числа, но с уносом массы (согласно рассматриваемой модели) будет продолжать двигаться к поверхности планеты, если, конечно, он не достиг ее раньше, чем плотность окружающей атмосферы стала равной ρ×.
Интеграл массы (3.10) для текущей массы M можно записать в виде
Отсюда следует, что при больших скоростях (Ve = 30–35 км/с) масса тела становится весьма малой, близкой к нулю. Отсюда видно, что параметр напрямую определяет уменьшение массы тела.
То есть масса существенно уменьшается. Уменьшение будет тем больше, чем больше начальная скорость тела и коэффициент теплопередачи CH.
Из решения и других параметров дробящегося тела, рассмотренных в этом разделе следует, что модель ПРД является весьма содержательной, охватывающей дробящиеся и не дробящиеся тела.
4. Баллистика дробящегося метеороида в неизотермической атмосфере. Рассмотрим далее более реальный процесс – баллистику дробящегося метеороида с учетом уноса массы в неизотермической (произвольной) атмосфере (с переменной температурой по высоте).
Уравнение движения с учетом неизотермичности атмосферы и переменности коэффициента сопротивления CD в случае его переменности и шкалы высот по плотности h запишется в виде:
(4.1)
${{\tilde {V}}^{{ - \left( {1 + \frac{2}{{3\alpha }}} \right)}}}\frac{{d\tilde {V}}}{{dt}} = - \frac{{{{{\bar {\rho }}}_{*}}}}{2}\tilde {h}{{\tilde {C}}_{D}}{{\tilde {\rho }}^{{\frac{1}{{3\alpha }}}}}\frac{{d\tilde {\rho }}}{{dt}},$(4.2)
$\tilde {V} = {{\left( {1 + \frac{{{{{\bar {\rho }}}_{*}}}}{{3\alpha }}I} \right)}^{{ - \frac{{3\alpha }}{2}}}}$(4.3)
${\rm I}(\tilde {\rho }) = \int {\tilde {h}{{{\tilde {C}}}_{D}}{{{\tilde {\rho }}}^{{\frac{1}{{3\alpha }}}}}d\tilde {\rho } \approx \frac{{3\alpha }}{{1 + 3\alpha }}\left( {{{{\tilde {\rho }}}^{{\frac{1}{{3\alpha }} + 1}}} - 1} \right)} $Здесь выражение для I, полученное при постоянных $h$ и ${{C}_{D}}$ ($\bar {h} = 7$ км, ${{\bar {C}}_{D}} = 1$), может быть полезно для получения оценок.
Число фрагментов N в переменных $\tilde {\rho }$, $\tilde {V}$ будет находиться из выражения
(4.4)
$N = \frac{M}{{{{M}_{*}}}}{{\left( {\tilde {\rho }{{{\tilde {V}}}^{2}}} \right)}^{{1/\alpha }}},\quad \frac{M}{{{{M}_{*}}}} = \exp \left[ {\frac{{\sigma V_{*}^{2}}}{2}\left( {{{{\tilde {V}}}^{2}} - 1} \right)} \right]$Лавинообразно разрушенный метеороид, который представляет собой уже рой осколков, движущийся со скоростью (4.2), будет продолжать разрушаться до тех пор, пока число осколков, вычисленное по формуле (4.4), не достигнет максимального значения. Вычислим сначала N× = Nmax, считая М слабо меняющейся функцией. Тогда из условия $\frac{{d(\rho {{V}^{2}})}}{{d\rho }}$ = $V_{*}^{2}\frac{{d\left( {\tilde {\rho }{{{\tilde {V}}}^{2}}} \right)}}{{d\tilde {\rho }}}$ = 0 найдем безразмерную плотность атмосферы ${{\tilde {\rho }}_{ \times }} = {{\rho }_{ \times }}{\text{/}}{{\rho }_{*}}$, при которой достигается максимум скоростного напора ρV2. Это значение для неизотермической атмосферы при переменном коэффициенте сопротивления и переменной шкале атмосферы по плотности $h$ будет определяться неявно
(4.5)
${{\bar {\rho }}_{*}}\left[ {\tilde {h}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {C}}}_{D}}\left( {{{{\tilde {\rho }}}_{ \times }}} \right)\tilde {\rho }_{ \times }^{{1 + \frac{1}{{3\alpha }}}} - \frac{1}{{3\alpha }}{\rm I}\left( {{{{\tilde {\rho }}}_{ \times }}} \right)} \right] = 1$Если воспользоваться приближенным выражением (4.3) для ${\rm I}\left( {{{{\tilde {\rho }}}_{ \times }}} \right)$, то получим ${{\tilde {\rho }}_{ \times }}$ в явном виде, совпадающим c выражением (3.5).
Максимальный скоростной напор будет равен
(4.6)
$\begin{gathered} {{\left( {\tilde {\rho }{{{\tilde {V}}}^{2}}} \right)}_{{\max }}} = \left( {\frac{{{{\rho }_{ \times }}V_{ \times }^{2}}}{{{{\rho }_{*}}V_{*}^{2}}}} \right) = {{\left[ {\tilde {h}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {C}}}_{D}}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {\rho }}}_{ \times }}{{{\bar {\rho }}}_{*}}} \right]}^{{ - 3\alpha }}} \approx \\ \approx \bar {\rho }_{*}^{{ - \frac{{3\alpha }}{{1 + 3\alpha }}}}{{\left[ {1 + \frac{1}{{3\alpha }}(1 - {{{\bar {\rho }}}_{*}})} \right]}^{{ - \frac{{9{{\alpha }^{2}}}}{{1 + 3\alpha }}}}} \approx \bar {\rho }_{*}^{{ - \frac{{3\alpha }}{{1 + 3\alpha }}}}{{\left( {\frac{{3\alpha }}{{1 + 3\alpha }}} \right)}^{{\frac{{9{{\alpha }^{2}}}}{{1 + 3\alpha }}}}} \\ \end{gathered} $Второе выражение в (4.6) получено при постоянных h и CD, третье выражение – при дополнительном предположении ${{\bar {\rho }}_{*}} \ll 1$.
Максимальное число осколков согласно формуле (4.4) при упрощающем предположении М ≈ const в процессе прогрессивного дробления будет равно
(4.7)
$\begin{gathered} {{N}_{{\max }}} = {{N}_{ \times }} = \frac{{{{M}_{ \times }}}}{{{{M}_{*}}}}{{\left[ {\tilde {h}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {C}}}_{D}}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {\rho }}}_{ \times }}{{{\bar {\rho }}}_{*}}} \right]}^{{ - 1}}} \approx \\ \approx \frac{{{{M}_{ \times }}}}{{{{M}_{*}}}}\bar {\rho }_{*}^{{ - \frac{3}{{1 + 3\alpha }}}}{{\left[ {1 + \frac{1}{{3\alpha }}(1 - {{{\bar {\rho }}}_{*}})} \right]}^{{ - \frac{{9\alpha }}{{1 + 3\alpha }}}}} \approx \frac{{{{M}_{ \times }}}}{{{{M}_{*}}}}\bar {\rho }_{*}^{{ - \frac{3}{{1 + 3\alpha }}}}{{\left( {\frac{{3\alpha }}{{1 + 3\alpha }}} \right)}^{{\frac{{9\alpha }}{{1 + 3\alpha }}}}} \\ \end{gathered} $Размер и масса отдельных фрагментов при этом будут равны
(4.8)
$\begin{gathered} {{R}_{{\min }}} = \sqrt {\frac{S}{\pi }} = \sqrt {\frac{{{{M}_{ \times }}}}{{\pi {{m}_{*}}}}{{{\left( {{{{\tilde {\rho }}}_{ \times }}\tilde {V}_{ \times }^{2}} \right)}}^{{1/3\alpha }}}} = \sqrt {\frac{{{{M}_{ \times }}}}{{\pi {{m}_{*}}}}} {{\left[ {\tilde {h}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {C}}}_{D}}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {\rho }}}_{ \times }}{{{\bar {\rho }}}_{*}}} \right]}^{{ - 1/2}}} \approx \\ \approx \sqrt {\frac{{{{M}_{ \times }}}}{{\pi {{m}_{*}}}}} \bar {\rho }_{*}^{{ - \frac{1}{{2(1 + 3\alpha )}}}}{{\left[ {1 + \frac{1}{{3\alpha }}(1 - {{{\bar {\rho }}}_{*}})} \right]}^{{ - \frac{{3\alpha }}{{2(1 + 3\alpha )}}}}} \approx \sqrt {\frac{{{{M}_{ \times }}}}{{\pi {{m}_{*}}}}} \bar {\rho }_{*}^{{ - \frac{1}{{2(1 + 3\alpha )}}}}{{\left( {\frac{{3\alpha }}{{1 + 3\alpha }}} \right)}^{{\frac{{3\alpha }}{{2(1 + 3\alpha )}}}}} \\ \end{gathered} $(4.9)
$\begin{gathered} {{М}_{{\min }}} = \frac{{{{M}_{ \times }}}}{{{{N}_{ \times }}}} = {{M}_{*}}{{\left[ {\tilde {h}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {C}}}_{D}}\left( {{{{\tilde {\rho }}}_{ \times }}} \right){{{\tilde {\rho }}}_{ \times }}{{{\bar {\rho }}}_{*}}} \right]}^{3}} \approx \\ \approx {{M}_{*}}\bar {\rho }_{*}^{{\frac{3}{{1 + 3\alpha }}}}{{\left[ {1 + \frac{1}{{3\alpha }}(1 - {{{\bar {\rho }}}_{*}})} \right]}^{{\frac{{9\alpha }}{{1 + 3\alpha }}}}} \approx {{M}_{*}}\bar {\rho }_{*}^{{\frac{3}{{1 + 3\alpha }}}}{{\left( {\frac{{1 + 3\alpha }}{{3\alpha }}} \right)}^{{\frac{{9\alpha }}{{1 + 3\alpha }}}}} \\ \end{gathered} $Таким образом, отличие результатов настоящего раздела от соответствующих результатов, полученных в предыдущем разделе для изотермической атмосферы при СD = const и $h = \operatorname{const} $, состоит в появлении функции $\tilde {h}\left( {\tilde {\rho }} \right){{\tilde {C}}_{D}}\left( {\tilde {\rho }} \right)$ и интеграла (4.3), зависящего от этой функции, которая должна быть затабулирована для получения оценки влияния неизотермичности атмосферы и переменности коэффициентов ${{C}_{D}}$ и $h$ на характерные параметры баллистики прогрессивно дробящегося метеороида. Однако в силу экспоненциального нарастания скоростного напора с уменьшением высоты полета дробящегося метеороида главный вклад в характерные значения параметров баллистики роя осколков будет давать значение определяющего параметра ${{\bar {\rho }}_{*}}$, равное отношению заметенной поперечным сечением метеороида массы газа к моменту начала дробления, умноженной на коэффициент сопротивления, к массе метеороида в момент начала дробления. Этот параметр может меняться на порядки в зависимости от размера, скорости и прочности метеороида и, как правило, ${{\bar {\rho }}_{*}} \ll 1$.
Еще раз отметим, что при предположении постоянства на траектории метеороида параметра уноса массы σ и параметра изменения формы $f = 1.21$, входящего в феноменологическое определение S* по формуле(2.4), выражение для массы (3.10) остается справедливым при любом механизме дробления метеороида и зависит только от интенсивности аэродинамической эрозии. При σ = const это означает, что как единое тело до начала дробления, так и совокупность его фрагментов в процессе дробления теряют массу одинаковым образом. Предположение σ = const является основным в ФТМ [3], хотя на самом деле параметр σ меняется примерно в диапазоне 0.02 < $\sigma $ < 0.03 c2/км2 для известных автору метеороидов [3, 47]. Переменность параметра σ приводит к необходимости численного решения задачи с учетом переменности ${{C}_{H}}$, $Q$ и ${{C}_{D}}$ на траектории входа метеороида в атмосферу. Однако в разд. 2 был введен эффективный параметр ue, который учитывает переменность параметра $\sigma $ и дает возможность при этом получать аналитические решения близкие к численным.
В данной работе получено численное решение задачи в рамках модели ПРД с учетом переменности коэффициентов. В равновесной модели предполагается, что число осколков увеличивается непрерывно и коэффициенты, фигурирующие в уравнениях, меняются мгновенно с изменением размеров осколков. Исходная прочность тела и масштабный фактор $\alpha $ были заданы таким образом, чтобы высота начала и окончания дробления совпадала с наблюдениями [56].
Для сравнения интенсивности уноса массы в модели дробящегося и единого тела построена кривая изменения массы единого метеороида так же при переменных коэффициентах. Как видно, наличие фрагментации ведет к более быстрой потере массы при прочих равных условиях.
5. Заключительная (третья) стадия движения раздробленного метеороида. Процесс дробления метеороида происходит, как правило, в довольно небольшом диапазоне высот, так что после его окончания рой осколков движется с космической скоростью в нескольких километров от поверхности планеты. Поскольку в развиваемой модели разрушения считается, что если образуются близкие по массе фрагменты для каждой скорости, то достаточно следить за движением одного. Оно описывается той же системой уравнений, что и движение единого тела (3.1), (3.2). На последнем этапе дробления происходит интенсивное торможение, и возникает необходимость учета силы тяжести. Уравнение торможения в этом случае принимает вид
и система (3.1), (3.2) дополняется уравнением изменения угла наклона траектории к плоскости горизонта.6. Применение модели ПРД к определению высоты свечения Челябинского метеорита. Модель ПРД применима к количественному объяснению баллистики (скорости и массы) как единого, так и дробящегося тела. В этих задачах подбор масштабного фактора α дает разную модель разрушения. Так, при α → 0 тело дробится на мелкие части с образованием жидкого объема (модель С.С. Григоряна). При α → ∞ (gross фрагментация) тело не дробится или дробится на крупные части (Сeplecha). По модели ПРД моделируются скорость, масса, плотность метеорита и не моделируется высота начала дробления метеорита, которая для большинства тел находится на высоте примерно 45–50 км. Именно на этот диапазон скоростей указывает работа [2]. Однако, в данной статье построена аналитическая теория испарения метеоритов, из которой устанавливается связь между высотой вспышки и высотой дробления метеорита. По этой теории по наблюдаемой высоте вспышки возможно определение высоты начала дробления. По результатам этой теории предлагается оригинальный метод определения высоты дробления в зависимости от высоты вспышки.
6.1. Математическая постановка задачи о свечении метеоритов. В литературе по данной тематике под светимостью (свечением) понимается скорость уменьшения кинетической энергии метеорита за единицу времени
(6.1)
$\frac{I}{{{{\tau }_{0}}}} = - {{V}^{n}}\frac{d}{{dt}}\left( {\frac{{M{{V}^{2}}}}{2}} \right) = - {{V}^{n}}\left( {\frac{{dM}}{{dt}}\frac{{{{V}^{2}}}}{2} + MV\frac{{dV}}{{dt}}} \right)$Используя выражения для dV/dt и $dM{\text{/}}dt$ из уравнений баллистики единого и дробящегося метеороида (см. разд. 3), получим
(6.2)
$\frac{I}{{{{\tau }_{0}}}} = {{V}^{n}}K\rho {{M}^{{2/3}}}\left( {\frac{1}{2}{{V}^{{5 + n}}}\sigma + {{V}^{{3 + n}}}} \right),$(6.3)
$\frac{1}{M}\frac{{dM}}{{d\rho }} = \sigma {{V}^{2}}\frac{{d\ln V}}{{d\rho }},\quad \rho \frac{{d\ln V}}{{d\rho }} = - \frac{{a{{{\tilde {\rho }}}^{{1/\left( {3\alpha + 1} \right)}}}}}{{1 - a + a{{{\tilde {\rho }}}^{{1/\left( {3\alpha + 1} \right)}}}}} = \frac{x}{{1 + x}},$Тогда в итоге получаем
(6.4)
$\begin{gathered} \frac{{F\left( \rho \right)}}{{{{M}^{{\frac{2}{3}}}}{{V}^{{3 + n}}}}} = \frac{{\sigma {{V}^{2}}}}{2}\left[ {1 - \frac{{\frac{2}{3}\sigma V_{e}^{2} + \left( {5 + n} \right){{{\left( {1 + x} \right)}}^{{3\alpha }}}}}{{{{{\left( {1 + x} \right)}}^{{3\alpha }}}}}\frac{x}{{1 + x}}} \right] + 1 - \\ - \;\frac{{\frac{2}{3}\sigma V_{e}^{2} + \left( {3 + n} \right){{{\left( {1 + x} \right)}}^{{3\alpha }}}}}{{{{{\left( {1 + x} \right)}}^{{3\alpha }}}}}\frac{x}{{1 + x}} = 0 \\ \end{gathered} $Первое слагаемое этого выражения связано со свечением метеороида от уноса массы. Второе слагаемое связано со свечением от торможения (уменьшения скорости).
Это алгебраическое трансцендентное нелинейное уравнение (6.4) для определения x от α, которое может быть решено численно во всем диапазоне α от 0 до 1.
6.2. Определение высоты максимального свечения. Имея этот результат, можно вычислить плотность (высоту) максимального свечения. Для этого необходимо решить уравнение
Из полученной в статье теории ПРД следует, что высота свечения существенно зависит от высоты дробления, которая была принята здесь равной 50 км (это типичная высота дробления многих метеоритов) (${{\rho }_{*}} = 0.98 \times {{10}^{{ - 6}}}$). Кроме этого, данная модель свечения дает при α = 0 модель идеальной несжимаемой жидкости [49] и при α → 0 – модель gross фрагментации (Сeplecha, 2005).
Заключение. Статья посвящена численным и аналитическим решениям уравнений аэротермобалистики единого и дробящегося тела. В рамках модели прогрессивно равновесного дробления появляется возможность управления числом осколков от 0 до большого их числа с помощью масштабного фактора α (0 < α < ∞). При малых α тело дробится на бесконечно большое число осколков, и в этом случае раздробленное тело моделируется большой каплей несжимаемой жидкости [49], которая неустойчива (неустойчивость Рэлея – Тейлора раздробленного тела, имеющего непредсказуемую форму и неустойчивость Кельвина–Гельмгольца за счет испарения с поверхности). В другом крайнем случае, при больших масштабных факторах α, тело фактически не дробится. Таким образом, модель ПРД существенно расширяет возможность моделирования различных видов дробления метеороидов. Предложен и развит метод последовательных приближений для получения аналитических решений основных уравнений ФТМ. Полученные решения для скорости и массы единого тела по первому приближению сравнены с численным решением и дают хорошее совпадение. С использованием этого решения находятся простые аналитические выражения для скоростного напора и погонной кинетической энергии метеороида. Найдена точная аналитическая формула для скорости дробящегося тела. Полученная модель прогрессивно равновесного дробления метеороида под действием аэродинамического сопротивления усовершенствована так, чтобы учесть задержки в образовании отдельных фрагментов ввиду наличия конечной скорости их расхождения. В статье приведена полная система уравнений аэротермобалистики, включающая в себя силу тяжести, реактивную силу испарения и подъемную силу, действующую на траекторию метеороида. Эта полная система решена численно. Показано, что для типичных метеороидов от 1 кг и больше решение этой полной системы совпадает с решением без учета этих дополнительных сил.
Список литературы
Weibull W. A statistical theory of the strength of materials // Proc. Roy. Swedish Inst. Engng. Res. 1939. № 151.
Tirskiy G.A., Khanukaeva D.Y. The modeling of bolide terminal explosions // Earth, Moon&Planets. 2004. V. 95. № 1–4. P. 513–520.
Бронштэн В.А. Физика метеорных явлений. M.: Наука, 1981. 416 с.
Бронштэн В.А. Абляция метеороидов // Метеорные исследования. 1983. №8. С. 38–50.
Бронштэн В.А. О динамике разрушения крупных метеороидов // Космич. исслед. 1985. Т. 23. № 5. С. 797–799.
Емельяненко В.В., Попова О.П., Чугай Н.Н. и др. Астрономические и физические аспекты челябинского события 15 февраля 2013 г. // Астрон. вестн. Исслед. солнечной системы. 2013. Т. 47. № 4. С. 262–262.
Ceplecha Z. Multiple fall of Pribram meteorites photographed. 1. Double-station photographs of the fireball and their relations to the found meteorites // Bull. Astron. Inst. Czechosl. 1961. V. 12. P. 21.
McCrosky R.E., Posen A., Schwartz G., Shao C.-Y. Lost City meteorite – its recovery and a comparison with other fireballs // J. Geophys. Res. 1971. V. 76. P. 4090–4108.
Halliday I., Griffin A.A., Blackwell A.T. The Innisfree meteorite fall: A photographic analysis of fragmentation, dynamics and luminosity // Meteoritics. 1981. V. 16(2). P. 153–170.
Brown P., Ceplecha Z., Hawkes R. et al. The orbit and atmospheric trajectory of the Peekskill meteorite from video records // Nature. 1994. V. 367. P. 624–626.
Borovicka J., Spurný P., Kalenda P., Tagliaferri E. The Morávka meteorite fall: 1. Description of the events and determination of the fireball trajectory and orbit from video records // Meteor.&Planet. Sci. 2003. V. 38. № 7. P. 975–987.
Brown P., Pack D., Edwards W.N. et al. The orbit, atmospheric dynamics, and initial mass of the Park Forest meteorite // Meteor.&Planet. Sci. 2004. V. 39. P. 1781–1796.
Simon S.B., Grossman L., Clayton R.N. et al. The fall, recovery, and classification of the Park Forest meteorite // Meteor.&Planet. Sci. 2004. V. 39. P. 625–634.
Spurný P., Bland Ph.A. et al. The Bunburra Rockhole meteorite fall in SW Australia: fireball trajectory, luminosity, dynamics, orbit, and impact position from photographic and photoelectric records // Meteor.&Planet. Sci. 2012. V. 47. № 2. P. 163–185.
Jenniskens P., Shaddad M.H. et al. The impact and recovery of asteroid 2008 TC3 // Nature. 2009. V. 458. P. 485–488.
Spurný P., Borovička J. et al. Analysis of instrumental observations of the Jesenice meteorite fall on April 9, 2009 // Meteor.&Planet. Sci. 2010. V. 45. № 8. P. 1392–1407.
Brown P.G., McCausland P.J.A. et al. The fall of the Grimsby meteorite-I: Fireball dynamics and orbit from radar, video, and infrasound records // Meteorit.&Planet. Sci. 2011. V. 46. № 3. P. 339–363.
Popova O., Borovicka J. et al. Very low strengths of interplanetary meteoroids and small asteroids // Meteorit.&Planet. Sci. 2011. V. 46. № 10. P. 1525–1550.
Ceplecha Z., Revelle D.O. Fragmentation model of meteoroid motion, mass loss, and radiation in the atmosphere // Meteorit.&Planet. Sci. 2005. V. 40. № 1. P. 35–54.
Бронштэн В.А. Применение теории Григоряна к расчету дробления гигантских метеороидов // Астрон. вестник. 1994. Т. 28. № 2. С. 118–124.
Бронштэн В.А. Дробление и разрушение крупных метеорных тел в атмосфере // Астрон. вестн. 1995. Т. 29. № 5. С. 450–458.
Jacchia L.G. The physical theory of meteors. VIII. Fragmentation as cause of the faint meteor anomaly // Astrophys. J. 1955. V. 121. P. 521.
Левин Б.Ю., Симоненко А.Н. Параметры фрагментации метеоров // Астрон. ж. 1967. Т. 44. № 3. С. 630–637.
Симоненко А.Н. Размеры частиц, отделяющихся от метеорных тел во время вспышек // Кометы и метеоры. 1967. № 15. С. 34–44.
Фортов В.Е., Султанов В.Г., Шутов А.В. Взрыв Челябинского суперболида в атмосфере Земли: рядовое событие или уникальное стечение обстоятельств? // Геохимия. 2013. № 7. С. 609–609.
Svetsov V.V., Nemtchinov I.V., Teterev A.V. Disintegration of large meteoroids in Earth’s atmosphere: theoretical models // Icarus. 1995. V. 116. № 1. P. 131–153.
Baldwin B., Sheaffer Y. Ablation and breakup of large meteoroids during atmospheric entry // J. Geophys. Res. 1971. V. 76. № 19. P. 4653–4668.
Цветков В.И., Скрипник А.Я. Атмосферное дробление метеоритов с точки зрения механической прочности // Астрон. вестн. 1991. Т. 25. № 3. С. 364–371.
Стулов В.П. Аналитическая модель последовательного дробления и абляции метеорного тела в атмосфере // Астрон. вестн. 1998. Т. 32. № 5. С. 455–458.
Немчинов И.В., Попова О.П. Анализ Сихотэ-Алинского события 1947 г. и его сравнение с явлением 1 февраля 1994 г. // Астрон. вестн. 1997. Т. 31. С. 458–471.
Иванов А.Г., Рыжанский В.А. Фрагментация малого небесного тела при его взаимодействии с атмосферой // Докл. АН. 1997. Т. 353. № 3. С. 334–337.
Стулов В.П., Титова Л.Ю. Модель фрагментации метеороида в атмосфере // Докл. АН. 2001. Т. 376. № 1. С. 53–54.
Brykina I.G., Bragin M.D. On models of meteoroid disruption into the cloud of fragments // Planet.&Space Sci. 2020. V. 187. P. 104942.
Шуршалов Л.В. Взрыв в полете // Изв. АН СССР. МЖГ. 1984. № 5. С. 126–129.
Коробейников В.П., Чушкин П.И., Шуршалов Л.В. О гидродинамических эффектах при полете и взрыве в атмосфере Земли крупных метеоритных тел // Метеоритика. 1973. Вып. 3. С. 73–89.
Коробейников В.П. Математическое моделирование катастрофических явлений природы // Знание. 1986. № 1. 48 с.
Коробейников В.П., Чушкин П.И., Шуршалов Л.В. Комплексное моделирование полета и взрыва в атмосфере метеорного тела // Астрон. вестн. 1991. Т. 25. № 3. С. 61–75.
Korobeinikov V.P., Shurshalov L.V., Vlasov V.I., Semenov I.V. A complex modeling of the Tunguska catastrophe // Planet Space Sci. 1998. V. 46. № 213. P. 231–244.
Hills J.A., Goda M.P. The fragmentation of small asteroids in the atmosphere // Astron. J. 1993. V. 5. № 3. P. 1114–1144.
Chyba C.F., Thomas P.J., Zahnle K.J. The 1908 Tunguska explosion: Atmospheric disruption of a stony asteroid // Nature. 1993. V. 361. P. 40–44.
Немчинов И.В., Попова О.П., Тетерев А.В. Внедрение крупных метеороидов в атмосферу: теория и наблюдения (Обзор) // ИФЖ. 1999. Т. 72. № 6. С. 1233–1265.
Artem'eva N.A., Shuvalov V.V. Interaction of shock waves during the passage of a disrupted meteoroid through the atmosphere // Shock Waves. 1996. № 5. P. 359–367.
Khanukaeva D.Y., Tirskiy G.A. A model of single and fragmenting meteoroid interaction with isothermal and non-isothermal atmosphere // Earth Moon Planet. 2004. V. 95. P. 395–402.
Брагин М.Д., Тирский Г.А. Аналитическое решение уравнений физической теории метеоров для недробящегося тела с уносом массы в неизотермической атмосфере // ПМТФ. 2019. Т. 60. № 5. С. 13–18.
Лунев В.В. Гиперзвуковая аэродинамика: М.: Машиностроение, 1975. 327 с.
Григорян С.С. О движении и разрушении метеоритов в атмосферах планет // Космич. исслед. 1979. Т. 17. № 6. С. 875–893.
Фортов В.Е., Гнедин Ю.Н., Иванов М.Ф. и др. Столкновение кометы Шумейкеров–Леви 9 с Юпитером: что мы увидели // УФН. 1996. Т. 166. С. 391–422.
Тирский Г.А., Ханукаева Д.Ю. Баллистика единого метеорного тела с учетом уноса массы в неизотермической атмосфере // Космич. исслед. 2007. Т. 45. № 6. С. 476–485.
Егорова Л.А. Напряженно-деформированное состояние и разрушение метеороида при движении в атмосфере // ПММ. 2011. Т. 75. № 3. С. 513–518.
Фадеенко Ю.И. Разрушение метеорных тел в атмосфере // Физика горения и взрыва. 1967. Т. 3. № 2. С. 278–280.
Nemtchinov I.V., Popova O.P., Shuvalov V.V., Svetsov V.V. Radiation emitted during the flight of asteroids and comets through the atmosphere // Planet.&Space Sci. 1994. V. 42. № 6. P. 491–506.
Медведев Р.В. Определение механических и тепловых свойств метеоритов Кунашак и Еленовка // Метеоритика. 1974. № 33. С. 100–104.
Болотин В.В. Статистические методы в строительной механике. М.: Госстройиздат, 1961. 264 с.
Брыкина И.Г., Брагин М.Д., Егорова Л.А. О моделях фрагментации метеороидов в атмосфере // Физ.-хим. кинетика в газовой динамике. 2019. Т. 20, № 2. Эл. журнал. http://chemphys.edu.ru/issues/2019-20-2/articles/822
Тирский Г.А., Брыкина И.Г., Жлуктов С.В. Численно-аналитический метод решения уравнений физической теории метеоров при переменном параметре абляции // Вестн. Моск. ун-та. Сер. 1. Матем., мех., 2020, № 6. С. 48–53.
Ceplecha Z., Borovička J., Elford W.G. et al. Meteor Phenomena and Bodies // Space Sci. Rev. 1998. V. 84. P. 327–471.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


