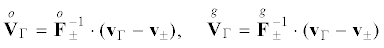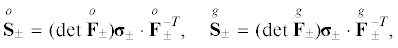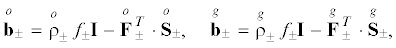Прикладная математика и механика, 2022, T. 86, № 4, стр. 571-583

1. Введение. Механика конфигурационных сил активно развивается с конца 80-х–начала 90-х гг. ХХ века как одно из направлений механики деформируемого твердого тела, позволяющее естественным образом включить в рассмотрение эволюцию неоднородностей различной природы – от движения локализованных дефектов и роста трещины до развития областей новой фазы, распространения фронтов химических реакций и роста биологических тканей в условиях воздействия механических напряжений (см., напр., [1–10]). Общим для этих процессов является то, что они не могут быть сведены к перемещению материальных точек под действием механических сил, как в механике Ньютона, но приводят к изменению конфигурации тела вследствие движения дефектов и границ относительно материальных точек, то есть в “пространстве материала” [3].

Ниже дается краткий обзор механики конфигурационных сил применительно к математическому описанию распространения межфазных границ и фронтов химических реакций с акцентом на описание конфигураций, порождаемых превращениями. Обсуждаются кинематические условия и балансовые соотношения на межфазной границе. Затем записывается выражение для диссипации энергии вследствие распространения межфазной границы или фронта химической реакции. Это дает возможность формулировки дополнительных определяющих соотношений – кинетических уравнений, определяющих скорость межфазной границы или фронта реакции. Детали постановок и решения задач описания фазовых переходов и химических реакций под напряжением не рассматриваются (см. библиографию и примеры решения краевых задач с межфазными границами и фронтами химических реакций [11–17]); обсуждается только общий вывод кинетического уравнения, связанного с фундаментальными законами и вторым законом термодинамики безотносительно реологических моделей деформируемого тела.

Пусть тело в актуальной (деформированной) конфигурации ${v} = {{{v}}_{ - }} \cup {{{v}}_{ + }}$ в момент времени $t$ разделено на части, занимающие области пространства ${{{v}}_{ - }}$ и ${{{v}}_{ + }}$ с границей раздела $\Gamma $ и состоящие из материалов “–” и “+” соответственно. Такое разделение может иметь:

− конструкционное происхождение как, например, в случае дисперсно-упрочненных композитных материалов, состоящих из матрицы и включений другого материала;

− технологическое происхождение, когда включения возникают на стадии получения материала;

− в силу физических причин: при определенных термомеханических и/или других физических воздействиях в теле возникают и развиваются области новой фазы как, например, при мартенситных превращениях в сплавах с эффектом памяти формы;

− в силу химических причин как, например, при формировании диоксида кремния в полупроводниках или литизации кремния в литий-ионных батареях.

Перечисление причин появления областей нового материала отражает существование двух типов границ – связанных на всех этапах деформирования с одними и теми же материальными точками тела и движущихся только вместе с этими точками, и границ, перемещающихся по точкам тела.

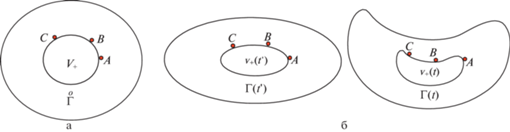
Первый тип границ имеет место, например, в теле с включением (рис. 1). Во все моменты времени, то есть во всех актуальных конфигурациях, области ${{{v}}_{ + }}$ заполнены одними и теми же материальными точками материала “+”, а области ${{{v}}_{ - }}$ – одними и теми же материальными точками материала “–”. Граница раздела областей деформируется вместе с телом и в разные моменты времени проходит через разные точки пространства, но остается связанной с одними и теми же материальными точками (A, B, C на рис. 1). Границы $\Gamma (t{\kern 1pt} ')$ и $\Gamma (t)$ имеют один и тот же прообраз $\mathop \Gamma \limits^o $ в отсчетной конфигурации. Такие границы называют материальными.

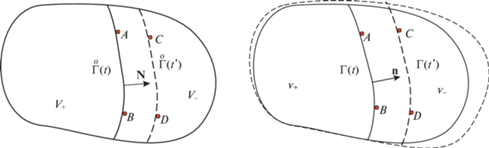
Второй тип границ наблюдается в материалах, претерпевающих фазовые или химические превращения. В этом случае при развитии области ${{{v}}_{ + }}$ превращенного материала граница $\Gamma (t)$ перемещается вследствие относительного перемещения точек тела, то есть деформаций, а также вследствие превращения одного материала в другой (рис. 2).

В разные моменты времени $t$ и $t{\kern 1pt} '$ граница проходит через разные материальные точки A, B и C, D. Положениям границы $\Gamma (t)$ и $\Gamma (t{\kern 1pt} ')$ в актуальной конфигурации соответствуют разные прообразы $\mathop \Gamma \limits^o (t)$ и $\mathop \Gamma \limits^o (t{\kern 1pt} ')$ в отсчетной конфигурации, то есть разные исходные составные тела $V = {{V}_{ - }} \cup {{V}_{ + }}$. Граница распространяется относительно отсчетной конфигурации. Причину распространения такой границы, то есть причину изменения отсчетной конфигурации называют конфигурационной силой.

В ньютоновой механике сила вводится как причина изменения состояния движения материальной точки – изменения ее скорости. Движение межфазных границ происходит по термодинамическим причинам. Формально конфигурационная сила, движущая дефект или границу, может быть получена как величина, сопряженная скорости границы в выражении для диссипации энергии. Мотивация такого определения следует из того, что в термодинамике необратимых процессов показано, что формула производства энтропии имеет вид билинейной формы [18]

образованной термодинамическими силами ${{X}_{\alpha }}$ и потоками ${{J}_{\alpha }}$, порождаемыми этими силами. Это, в свою очередь, позволяет формулировать кинетические уравнения в виде зависимостей термодинамических потоков от сил:

Тогда конфигурационная сила может быть определена как термодинамическая сила, сопряженная скорости изменения параметра, характеризующего конфигурацию тела.

Отметим также механические аналогии. Потенциальная сила может рассматриваться как множитель при скорости перемещения в выражении скорости изменения потенциальной энергии, а сила трения как множитель при скорости в выражении диссипации вследствие трения.

Термодинамический подход, согласно которому термодинамические силы являются функциями термодинамических потоков, будем использовать при формулировке кинетических уравнений в виде зависимостей скорости распространения фронта фазового или химического превращения от конфигурационной силы. При этом внешние воздействия, в том числе механические, влияют на скорость границы через конфигурационную силу.

2. Конфигурации двухфазных тел. Рассмотрим фазовое или локализованное на фронте реакции химическое превращение, сопровождающееся собственной деформацией превращения и, возможно, изменением реологических свойств материала.

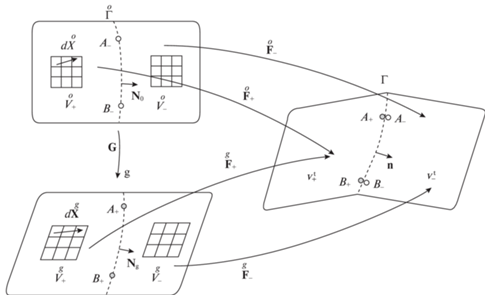
Пусть ${v} = {{{v}}_{ + }} \cup {{{v}}_{ - }}$ – актуальная конфигурация тела в момент времени $t$, где область ${{{v}}_{ - }}$ занята материалом в фазовом состоянии “–”, а область ${{{v}}_{ + }}$ материалом в фазовом состоянии “+”, $\Gamma (t)$ – межфазная граница, разделяющая области ${{{v}}_{ + }}$ и ${{{v}}_{ - }}$ (рис. 3).

Полагаем, что определены свободные от напряжений конфигурации тела $\mathop V\limits^o $ и $\mathop V\limits^g $ в фазовых состояниях “–” и “+”, соответственно (натуральные состояния). Линейные элементы $d{\kern 1pt} \mathop {\mathbf{X}}\limits^o $ и $d{\kern 1pt} \mathop X\limits^g $ конфигураций $\mathop V\limits^o $ и $\mathop V\limits^g $ связаны тензором $G$, задающим деформацию превращения:

Тензор G характеризует изменение геометрии решетки в результате фазового превращения кристаллического тела [19], или объемное расширение в результате химической реакции. Направление главных осей G, вообще говоря, зависит от напряженного состояния двухфазной конфигурации и тогда подлежит определению. Возможен также набор тензоров G, определяемый группой симметрии материала и соответствующий вариантам новой фазы (вариантам мартенсита и двойникованию в случае мартенситных фазовых переходов). Отметим, что в случае фазовых переходов под напряжением одно из натуральных состояний может быть метастабильным (соответствующим локальному, но не глобальному минимуму энергии) или гипотетическим, когда, например, новая фаза может существовать только в напряженном состоянии, то есть при наложении на G дополнительных деформаций. Далее рассматриваются границы для заданного тензора превращения G.

Если тензор G задан, то актуальной конфигурации ${v} = {{{v}}_{ - }} \cup {{{v}}_{ + }}$ могут быть поставлены в соответствие две отсчетные конфигурации: конфигурация $\mathop V\limits^o = {{\mathop V\limits^o }_{ - }}\; \cup {{\mathop V\limits^o }_{ + }}$, образованная материалом в натуральном фазовом состоянии “–” с границей $\mathop \Gamma \limits^o (t)$, проходящей через те же материальные точки фазы “–”, что и граница $\Gamma (t)$ в актуальной конфигурации A_– (точки ${{A}_{ - }}$, ${{B}_{ - }}$ на рис. 3), и отсчетная конфигурация $\mathop V\limits^g = {{\mathop V\limits^g }_{ + }}\; \cup {{\mathop V\limits^g }_{ - }}$, образованная натуральным фазовым состоянием “+” с границей $\Gamma (t)$, проходящей через те же материальные точки фазы “+”, что и $\Gamma (t)$ (точки ${{A}_{ + }}$, ${{B}_{ + }}$).

Положение материальных точек фазы “–” в актуальной ${v}$ и отсчетной $\mathop V\limits^o $ конфигурациях определяется векторами ${{x}_{ - }} \in {{{v}}_{ - }}$ и ${{\mathop X\limits^o }_{ - }} \in {{\mathop V\limits^o }_{ - }}$, соответственно. Положение точек фазы “+” в актуальной конфигурации и отсчетной $\mathop V\limits^g $ конфигурации определяется векторами ${{x}_{ + }} \in {{{v}}_{ + }}$ и ${{\mathop X\limits^g }_{ + }} \in {{\mathop V\limits^g }_{ + }}$. Отображения

задают деформацию материала в фазовых состояниях “–” и “+” из соответствующих натуральных состояний. Градиенты деформаций ${{\mathop {\mathbf{F}}\limits^o }_{ - }} = \mathop \nabla \limits^o {\mathbf{x}}_{ - }^{T}$ и ${{\mathop F\limits^g }_{ + }} = \mathop \nabla \limits^g {\mathbf{x}}_{ + }^{T}$, где $\mathop \nabla \limits^o $ и $\mathop \nabla \limits^g $ – набла-операторы, заданные в базисах отсчетных $\mathop V\limits^o $ и $\mathop V\limits^g $ конфигураций (в декартовых координатах $\mathop {{{F}_{{ij}}}}\limits^o = \partial {{x}_{i}}{\text{/}}\partial {\kern 1pt} {{\mathop X\limits^o }_{j}}$, $\mathop {{{F}_{{ij}}}}\limits^g = \partial {{x}_{i}}{\text{/}}\partial {\kern 1pt} {{\mathop X\limits^g }_{j}}$, где ${{x}_{i}}$, ${{\mathop X\limits^o }_{j}}$ и ${{\mathop X\limits^g }_{j}}$ – декартовы координаты материальной точки в актуальной ${{{v}}^{t}}$ и отсчетных $\mathop V\limits^o $ и $\mathop V\limits^g $ конфигурациях), связывают линейные элементы $d{{x}_{ \pm }} \in {v}_{ \pm }^{t}$ актуальной конфигурации с линейными элементами $d{{\mathop X\limits^o }_{ - }} \in {{\mathop V\limits^o }_{ - }}$ и $d{\kern 1pt} {{\mathop X\limits^g }_{ + }} \in {{\mathop V\limits^g }_{ + }}$ отсчетных конфигураций:

Отметим, что естественным представлением определяющих соотношений материалов фаз является задание зависимостей напряжений именно от градиентов деформации ${{\mathop F\limits^o }_{ - }}$ и ${{\mathop F\limits^g }_{ + }}$. Но так как деформации в актуальной конфигурации могут определяться относительно любой конфигурации, для обеих фаз может быть выбрана единая отсчетная конфигурация, соответствующая натуральному состоянию одной из фаз, например, фазы “–”. Тогда ${{x}_{ + }} = {{\mathop x\limits^o }_{ + }}({{\mathop X\limits^o }_{ + }},t)$, где ${{\mathop X\limits^o }_{ + }} \in {{\mathop V\limits^o }_{ + }}$ – положение прообраза превращенной точки в натуральном фазовом состоянии “–”, а градиент деформации ${{\mathop F\limits^o }_{ + }} = {{\mathop F\limits^g }_{ + }}\; \cdot G$ связывает линейный элемент $d{{x}_{ + }} \in {{{v}}_{ + }}$ в фазовом состоянии “+” с его прообразом $d{\kern 1pt} {{\mathop X\limits^o }_{ + }} \in {{\mathop V\limits^o }_{ + }}$ в фазовом состоянии “–” (до деформирования и фазового превращения): $d{{x}_{ + }} = {{\mathop F\limits^o }_{ + }}\; \cdot d{\kern 1pt} {{\mathop X\limits^o }_{ + }}$

Скорости точек в фазовых состояниях “–” и “+” определяются соотношениями

Полагаем, что на межфазной границе сохраняется непрерывность поля перемещений, то есть рассматривается когерентная граница. Из непрерывности перемещений следуют кинематические условия совместности первого и второго рола (см., напр., [20]):

где ${{N}_{0}}$ и ${{N}_{g}}$ – нормали к прообразам межфазной границы $\mathop \Gamma \limits^o $ и $\mathop \Gamma \limits^g $ в отсчетных конфигурациях “–” и “+”, внешние к областям ${{\mathop V\limits^o }_{ + }}$ и ${{\mathop V\limits^g }_{ + }}$, соответственно, $\mathop a\limits^o $ и $a$ – векторы амплитуды скачка, ${{\mathop V\limits^o }_{\Gamma }}$ и ${{\mathop V\limits^g }_{\Gamma }}$ – скорости прообразов межфазной границы $\mathop \Gamma \limits^o $ и $\mathop \Gamma \limits^g $, ${{W}_{0}} = {{\mathop V\limits^o }_{\Gamma }}\; \cdot {{N}_{0}}$, ${{W}_{g}} = {{\mathop V\limits^g }_{\Gamma }}\; \cdot {{N}_{g}}$ – нормальные составляющие скорости межфазной границы, двойные скобки обозначают скачок величин на межфазной границе: $[\varphi ] = {{\varphi }_{ + }} - {{\varphi }_{ - }}$.

Первое условие означает, что скачок градиента деформаций имеет вид диады, образованной вектором нормали к прообразу межфазной границы в отсчетной конфигурации и некоторым вектором, называемым вектором амплитуды скачка. В силу второго условия скачок скорости материальных точек на межфазной границе подстраивается под скорость границы так, чтобы сохранялась сплошность материала. Отметим, что условия непрерывности на границе наиболее простым образом выглядят при записи в терминах отсчетных конфигураций.

Скорость границы в актуальной конфигурации ${{v}_{\Gamma }}$ связана со скоростями прообразов границы ${{\mathop V\limits^o }_{\Gamma }}$ и ${{\mathop V\limits^g }_{\Gamma }}$ относительно отсчетных конфигураций формулами

3. Кинетика межфазных границ, тензор напряжений Эшелби. Из балансов массы, импульса и энергии и второго закон термодинамики, записанного в виде неравенства Клаузиуса–Дюгема с учетом теоремы переноса Рейнольдса для тела с распространяющейся внутренней границей следуют соотношения для скачков на движущейся межфазной границе (см., напр., [21, 22]), которые запишем относительно обеих отсчетных конфигураций:

где $\mathop S\limits^o $ и $\mathop S\limits^g $ – тензоры напряжений Пиолы–Кирхгофа, определенные относительно $\mathop V\limits^o $ и $\mathop V\limits^g $ конфигураций: если ${{\sigma }_{ \pm }}$ – тензоры напряжений Коши, то $\mathop h\limits^o $ и $\mathop h\limits^g $ – векторы теплового потока, определенные относительно $\mathop V\limits^o $ и $\mathop V\limits^g $ конфигураций, u и s – массовые плотности внутренней энергии и энтропии, T – температура, $[\mathop \rho \limits^o ] = {{\mathop \rho \limits^o }_{ + }}\; - {{\mathop \rho \limits^o }_{ - }}$, $[\mathop \rho \limits^g ] = {{\mathop \rho \limits^g }_{ + }}\; - {{\mathop \rho \limits^g }_{ - }}$, ${{\mathop \rho \limits^o }_{ - }}$ и ${{\mathop \rho \limits^g }_{ + }}$ – плотности материала в ненапряженных фазовых состояниях “–” и “+”; ${{\mathop \rho \limits^g }_{ - }}$ и ${{\mathop \rho \limits^o }_{ + }}$ – плотности материала в фазовых состояниях “–” и “+”, пересчитанные как масса фазы “+” на единицу объема фазового состояния “–” и масса фазы “–” на единицу объема фазового состояния “+”. Если порция фазы “–” $d{{m}_{ - }}$ превращается в порцию фазы “+” $d{{m}_{ + }}$, то где согласно (2.1)

Из (3.7), (3.8) следует, что

где введено обозначение ${{g}^{3}} = \det G$. В случае фазового перехода $d{{m}_{ + }} = d{{m}_{ - }}$. Тогда из (3.7) следует, что ${{\mathop \rho \limits^o }_{ + }} = {{\mathop \rho \limits^o }_{ - }}$, ${{\mathop \rho \limits^g }_{ - }} = {{\mathop \rho \limits^g }_{ + }}$, что согласуется с балансом массы в виде (3.8). На распространяющейся межфазной границе $[\mathop \rho \limits^o ] = 0$, $[\mathop \rho \limits^g ] = 0$.

Полагаем, что температура непрерывна. Тогда, исключив $\left[ {{{{\mathbf{h}}}_{0}}{\text{/}}T} \right]$ из (3.5) с помощью (3.3), (3.4) и (3.2), получим выражение для диссипации энергии вследствие распространения межфазной границы (см., напр., [21–23]):

где – тензоры энергии-импульса Эшелби [24, 25], которые называют также тензорами напряжений Эшелби, определенные относительно конфигураций $\mathop V\limits^o $ и $\mathop V\limits^g $, $f = u - Ts$ – массовая плотность свободной энергии Гельмгольца, $I$ – единичный тензор, $\mathop C\limits^o = \mathop F\limits^o {{{\kern 1pt} }^{T}}\; \cdot \mathop F\limits^o $, $\mathop C\limits^g = \mathop F\limits^g {{{\kern 1pt} }^{T}}\; \cdot \mathop F\limits^g $.

В квазистатике диссипация определяется нормальной компонентой тензора Эшелби:

Для нелинейно упругих фаз первая формула (3.13) была получена в [26]. Независимо было показано, что необходимым условием минимума энергии Гиббса двухфазного упругого тела является непрерывность нормальной компоненты тензора Эшелби на равновесной межфазной границе [27, 28] (см. также [29]), аналогично непрерывности скалярного химического потенциала. Это привело к заключению о тензорности химического потенциала в случае деформируемого твердого тела и рассмотрении тензора Эшелби как тензора химического потенциала, скачок нормальной компоненты которого является конфигурационной силой, определяющей скорость границы согласно кинетическому уравнению вида

так что $[{{\mathop b\limits^o }_{{NN}}}]\mathop W\limits^o \leqslant 0$. В приближении линейной термодинамики $\mathop W\limits^o = - k[{{\mathop b\limits^o }_{{NN}}}]$, где кинетический коэффициент $k > 0$. Это кинетическое уравнение использовалось при решении задач описания межфазных границ, в том числе при численном моделировании распространения границ (см., напр., [6, 7, 30–33]), при моделировании межфазных границ в пластинах-оболочках [34, 35], для анализа кинетической устойчивости межфазных границ [36] и при исследовании гистерезисных явлений при прямом и обратном фазовых превращениях [37].

4. Кинетика и блокирование фронтов химических реакций. Рассматривалась химическая реакция между деформируемым твердым и диффундирующим компонентами, локализованная на фронте реакции, разделяющим исходное вещество и деформируемый продукт реакции. Реакция имеет вид

где ${{B}_{ - }}$, ${{B}_{*}}$ и ${{B}_{ + }}$ – химические формулы исходного твердого и диффундирующего компонентов и продукта реакции, ${{n}_{ - }}$, ${{n}_{*}}$ и ${{n}_{ + }}$ – стехиометрические коэффициенты.

Реакция поддерживается диффузией компонента ${{B}_{*}}$ к фронту реакции и сопровождается объемной деформацией превращения и изменением реологических свойств материала. Примерами таких реакций являются окисление и литизация кремния, сопровождающиеся большим объемным расширением и превращением упругого материала в вязкоупругий (см., напр., [38–40], а также библиографию [41]).

Далее следуем работам [13, 41–43], не останавливаясь на деталях. Полагаем, что тензор деформации превращения – шаровой. Тогда из химической формулы реакции следует, что

где ${{M}_{ \pm }}$ – молярные массы твердых компонент реакции, ${{\mathop \rho \limits^o }_{ - }}$ и ${{\mathop \rho \limits^g }_{ + }}$ – плотности твердых компонентов реакции в их натуральных состояниях (ср. с (3.8), (3.9)). В этом случае $d{{m}_{ + }} \ne d{{m}_{ - }}$. Фазовому превращению соответствует ${{M}_{ + }} = {{M}_{ - }} = M$, ${{n}_{ + }} = {{n}_{ - }}$.

Для открытой системы с диффузией и химической реакцией, как и в случае фазового превращения, были записаны балансовые соотношения и неравенство Клаузиуса–Дюгема. В результате были получены выражения поверхностной плотности диссипации энергии на фронтах реакции в отсчетных конфигурациях твердых компонентов реакции:

где $\mathop \omega \limits^o (N)$ и $\mathop \omega \limits^g (N)$ – скорости реакции на ориентированных площадках с нормалью $N$, ${{A}_{{NN}}}$ – нормальная компонента тензора химического сродства. В квазистатическом приближении где тензоры химического потенциала твердых компонентов равны тензорам Эшелби, деленным на плотности материала: ${{\mu }_{*}}$ – химический потенциал диффундирующего компонента, зависит от концентрации диффундирующего компонента. Сравнив (4.3) с классическим выражением $A = - \sum {{{n}_{k}}{{M}_{k}}{{\mu }_{k}}} $, появляющимся в формуле для диссипации энергии $D = A\omega $ в случае реакций в газах и жидкостях в виде множителя при скорости реакции [44], видим обоснованность термина тензор химического сродства.

Тензорность сродства, как и тензорность химического потенциала, может быть объяснена тем, что в деформируемом теле равновесие фаз и химические реакции связаны с ориентированными площадками. На тензорность сродства также указывалось в [45, 46].

Скорости фронта связаны со скоростями реакции соотношениями

Подставив нормальную компоненту тензора сродства в известное кинетическое уравнение, определяющее скорость реакции от скалярного сродства [18], получим

где $\mathop c\limits^o $ – концентрация диффундирующего компонента относительно отсчетной конфигурации исходного вещества, ${{k}_{*}}$ – константа скорости реакции. Аналогичная формула может быть записана для конфигурации продукта реакции.

Из (4.5), (4.6) видно, что нормальная компонента тензора химического сродства является конфигурационной силой, определяющей кинетику фронта реакции. Напряженно-деформированное состояние влияет на скорость фронта через сродство. Согласно (4.6) напряжения могут ускорять, замедлять и блокировать реакцию, см., напр., [13, 15, 16]. Фронт реакции может распространяться только если ${{A}_{{NN}}} \geqslant 0$. Если ${{A}_{{NN}}} < 0$ $\forall N$, то фронт не может распространяться ни в каких направлениях. Это приводит к понятию запретных зон в пространстве деформаций или напряжений, образованных деформациями (напряжениями), при которых распространение фронта прямой реакции невозможно, и которые в случае упругих компонентов реакции строятся аналогично введенным ранее зонам фазовых переходов [12]. Примеры построения запретных зон [47, 48] отражают конкурирующее влияние химических энергий (энергий компонентов в натуральном состоянии) и энергии деформаций на возможность протекания реакции.

Заключение. Концепция конфигурационных сил была кратко представлена для случая фазовых и химических превращений, локализованных на фронте превращения. Вместе с тем возможны нелокализованные превращения, когда в каждом характерном объеме присутствуют в определенной пропорции обе фазы или исходный материал и продукт химической реакции. При этом возникают вопросы о моделировании объемных превращений, о реализации различных типов превращений и об условиях перехода от объемных к локализованным превращениям и обратно. Поскольку объемные превращения также изменяют отсчетную конфигурацию, механика конфигурационных сил и здесь может найти эффективное применение.

Автор благодарен Н.Ф. Морозову за многолетнюю плодотворную поддержку исследований в области механики материалов, претерпевающих фазовые или химические превращения. Часть результатов, полученных нами совместно, нашла отражение и в этой статье.

Работа выполнена за счет гранта № 19-19-00552-П Российского научного фонда.