Прикладная математика и механика, 2022, T. 86, № 4, стр. 551-570

1. Введение. Учет в полной мере геометрических и физических особенностей фаз при аналитическом моделировании распространения поля по гетерогенной среде остается нерешенной проблемой. Одной из подзадач в рамках данной проблемы является определение условий на несущую фазу и на существенное изменение свойств анализируемой неоднородной системы (структурный фазовый переход) при существенно различных физических свойствах фаз на всем интервале объемных концентраций. Это имеет отношение, например, к переходу в коллоидах, суспензиях и гранулированных средах к макроскопически связному распространению поля упругости (вязкоупругости) по дисперсной фазе, при котором происходит существенное изменение поведения системы [1].

Начиная с работ Релея [2], Максвелла [3], Эйнштейна [4], к настоящему моменту создан ряд континуальных подходов по моделированию гетерогенных сред: метод условных моментов [5, 6], вариационный метод [7–10], метод самосогласованного поля [10–14] и подход Эшелби [10, 15] в рамках него, ряд статистических методов, базирующихся на функции Грина [6, 16, 17], сингулярное и обобщенное сингулярное приближение [10], гипотеза сильной изотропии [10, 18], теория смесей [19], анализ периодических сред [20], модель Понте Кастанеды, Уиллиса [21], модель Мори, Танаки [22], гомогенизированная модель [23]. Широкий математический аппарат, содержащийся в представленных подходах, по большей части направлен на получение из исходных уравнений осредненных с входящими в них эффективными коэффициентами переноса, отображающими континуальное “размазывание” истинной среды. При этом границы разделов фаз либо не учитываются (соответственно и размеры), либо их учет производится с введением упрощений (например, рассмотрение периодической структуры или введение феноменологических коэффициентов). Подход теории смесей [19] позволяет получить осредненные уравнения для каждой из фаз, учитывая конфигурацию внутренних границ, но при этом в рамках данного подхода отсутствует алгоритм поиска эффективных коэффициентов переноса.

В работе [24] для анализа упругих свойств гетерогенной среды использован математический формализм обобщенной производной, который наличием сингулярной составляющей отображает поведение полей на внутренних границах неоднородной среды, разделяющих фазы с разными физическими свойствами. На основе формализма обобщенной производной и пространственного осреднения в [24] получена пространственная теорема осреднения [19], являющаяся фундаментом теории смесей. Для получения эффективных коэффициентов в данной работе использован метод условных моментов, базирующийся на формализме функций Грина, условном осреднении и преобразовании Фурье. Модифицированный обобщенными производными оператор в исходной модели линейной теории упругости приводит к функции Грина, учитывающей микроструктурные особенности гетерогенной среды. В результате чего итоговые эффективные коэффициенты упругости интегрально отображают микроструктуру системы.

В настоящей работе проводится обобщение эффективных коэффициентов линейной теории упругости работы [24] на случай распространения поля упругости в пространстве заданной размерности. Данный механизм подразумевает эффективное число внутренних степеней свободы, определяющих распространение поля упругости по гетерогенной среде (определенной геометрической структуры, сформированной из фаз с разными физическими свойствами). В работе проводится анализ полученных эффективных коэффициентов переноса в частных случаях на всем интервале объемной концентрации при существенно различающихся упругих свойствах фаз.

2. Постановка задачи. Исследуем стационарное распределение упругого поля в микронеоднородной двухфазной среде. Структуру среды считаем обладающей статистически однородными и изотропными свойствами и заполняющей все пространство. В качестве исходной модели используем стационарную изотропную модель линейной теории упругости в форме

где параметр $n$ характеризует размерность исследуемого пространства. Исследуемые поля напряжений ${{\sigma }_{{ij}}}$, деформаций ${{\varepsilon }_{{\alpha \beta }}}$ и смещений ${{u}_{\alpha }}$, а также тензор упругости ${{\lambda }_{{ij\alpha \beta }}}$, содержащий объемный $K$ и сдвиговый $\mu $ упругие модули системы, рассматриваются в пространстве размерности $n$. Тензор ${{\lambda }_{{ij\alpha \beta }}}$ имеет такой вид, чтобы девиаторная составляющая, характеризуемая сдвиговым модулем $\mu $, имела нулевой след, и объемный модуль $K$ определялся шаровой составляющей. При этом учитываем соотношения для символов Кронекера ${{\delta }_{{ij}}}$, ${{\delta }_{{ij}}}{{\delta }_{{ij}}} = n$.

Координатами в модели (2.1) выступают микроточки, в каждой из которых находится одна из фаз со своими физическими свойствами. Значения модулей $K$ и $\mu $ при этом зависят от фазы, находящейся в точке. Аналогично и значения исследуемых полей ${{u}_{\alpha }}$, ${{\varepsilon }_{{\alpha \beta }}}$ и ${{\sigma }_{{ij}}}$ зависят от фазы, находящейся в микроточке.

Для учета микроструктурных особенностей фаз (физических и геометрических) по аналогии с работой [24] используем формализм обобщенной производной

где помимо обычной составляющей производной содержится сингулярная составляющая, которая выражается в подынтегральных выражениях конфигурацией дельта-функций на поверхностях разрыва ${{S}_{k}}$, т.е. согласно формуле (2.1) каждой точке ${\mathbf{x}}$ поверхности разрыва соответствует своя дельта-функция $\delta \left( {{\mathbf{r}} - {\mathbf{x}}} \right)$. Запись ${{\left[ {{{u}_{i}}} \right]}_{{\mathbf{x}}}}$ = = ${{u}_{i}}\left( {{\mathbf{x}} + {\mathbf{0}}} \right)$ – ${{u}_{i}}\left( {{\mathbf{x}} - {\mathbf{0}}} \right)$ характеризует скачок смещений фаз на границах разрыва ${{S}_{k}}$. В системе уравнений (2.1) обычные производные заменяются на обобщенные (2.2). При этой модификации в исходных дифференциальных уравнениях появляется составляющая, отображающая поведение поля на внутренних границах, и физическая суть анализируемых уравнений (закон сохранения и закон Гука) не нарушается [24].

Систему (2.1) следует дополнить граничными условиями на бесконечно удаленной границе и на конфигурации внутренних границ [24].

3. Получение эффективных коэффициентов в пространстве заданной размерности методом условных моментов. На основе метода условных моментов [5] получим из исходной модели (2.1) осредненный закон Гука ${{\sigma }_{{ij}}} = \left\langle {\lambda _{{ij\alpha \beta }}^{*}} \right\rangle \left\langle {{{\varepsilon }_{{\alpha \beta }}}} \right\rangle $, содержащий в эффективном тензоре упругости $\lambda _{{ij\alpha \beta }}^{*}$ искомые эффективные коэффициенты $K{\kern 1pt} *$, $\mu {\kern 1pt} *$. Тензор $\lambda _{{ij\alpha \beta }}^{*}$ структурно аналогичен тензору ${{\lambda }_{{ij\alpha \beta }}}$ с точностью до замен $K \to K{\kern 1pt} *$, $\mu \to \mu {\kern 1pt} *$. Посредством символов Кронекера ${{\delta }_{{ij}}}$, (${{\delta }_{{ij}}}{{\delta }_{{ij}}} = n$), и тензоров ${{\lambda }_{{ij\alpha \beta }}}$ и $\lambda _{{ij\alpha \beta }}^{*}$ информация о размерности пространства $n$ отображена в исходной модели (2.1) и возникает в ходе ее преобразований.

Итоговое выражение по вычислению эффективных коэффициентов упругости в методе условных моментов [5] имеет вид

где

В полученных формулах $\varphi \left( {\mathbf{r}} \right)$ – корреляционная функция геометрии структуры, ${{c}_{1}}$, ${{c}_{2}}$ – объемные концентрации фаз, $\left\langle {{{G}_{{ip}}}} \right\rangle $ – осредненная тензорная функция Грина, $2{{\partial }_{{(j}}}\left\langle {{{G}_{{i)p}}}} \right\rangle $ = ${{\partial }_{j}}\left\langle {{{G}_{{ip}}}} \right\rangle $ + ${{\partial }_{i}}\left\langle {{{G}_{{jp}}}} \right\rangle $. Для нахождения $\lambda _{{jk\alpha \beta }}^{*}$ следует вычислить интегралы ${{R}_{{ijpq}}}$, содержащие вторые производные от тензорной функции Грина. Исходя из этого, саму тензорную функцию Грина находить не нужно, имеют смысл лишь сингулярные составляющие от действия на нее вторых производных. Выражение на осредненный тензор Грина [24] имеет вид

где член ${{T}_{{ip}}}\left( {\mathbf{r}} \right)$ характеризует источник, осредненно учитывающий микроструктурные особенности системы. Точки ${{{\mathbf{x}}}_{k}}$ и функции ${{\rho }_{k}}$ отражают геометрические свойства структуры и физические свойства фаз ${{K}_{1}}$, ${{\mu }_{1}}$, ${{K}_{2}}$, ${{\mu }_{2}}$.

Представленное уравнение для источника направлено выразить переходный слой. Если производные рассматриваются не в обобщенном смысле, то источник имеет вид как в работе [5]: ${{T}_{{ip}}}\left( {\mathbf{r}} \right) = {{\delta }_{{ip}}}\delta \left( {\mathbf{r}} \right)$ и учет сингулярной составляющей от действия вторых производных на функцию Грина ${{\partial }_{q}}{{\partial }_{{(j}}}\left\langle {{{G}_{{i)p}}}} \right\rangle \left( {\mathbf{r}} \right)$ ∝ $\delta \left( {\mathbf{r}} \right)$ приведет при этом к потере информации о микроструктуре системы $\varphi \left( {\mathbf{0}} \right) = 1$ при вычислении интегралов ${{R}_{{ijpq}}}\left( {\mathbf{0}} \right)$.

Преобразуем функцию Грина (3.2) к Фурье-пространству, используя источник в виде ${{T}_{{ip}}}\left( {\mathbf{r}} \right) = {{\delta }_{{ip}}}\delta \left( {\mathbf{r}} \right)$, а затем обобщим его на случай источника в общем виде (3.2). Имеем выражение для образа функцию Грина

где ${{a}_{i}} = {{k}_{i}}{\text{/}}k$, ${{k}_{i}}$ – координаты в Фурье-образе. Выполнение обратного преобразования Фурье от (3.3) приводит к выражению где $J\left( {\mathbf{r}} \right)$ и $H\left( {\mathbf{r}} \right)$ фундаментальные функции для изотропного случая, содержащие информацию о размерности пространства (для случая размерности $n = 3$ с точностью до констант это функции ${\text{1/}}r$ и $r$ соответственно). Продифференцируем дважды полученное выражение (3.4):

Для нахождения эффективных коэффициентов нужно знать действие вторых производных на функцию $\left\langle {{{G}_{{ip}}}} \right\rangle \left( {\mathbf{r}} \right)$, что эквивалентно знанию функций ${{\partial }_{k}}{{\partial }_{q}}J\left( {\mathbf{r}} \right)$ и ${{\partial }_{i}}{{\partial }_{p}}{{\partial }_{k}}{{\partial }_{q}}H\left( {\mathbf{r}} \right)$. В силу изотропии сингулярные составляющие слагаемых ${{\partial }_{k}}{{\partial }_{q}}J$, ${{\partial }_{i}}{{\partial }_{p}}{{\partial }_{k}}{{\partial }_{q}}H$ принимают вид

где $A$ и $B$ неизвестные параметры, не зависящие от упругих параметров в силу сопоставления выражений (3.4) и (3.5). Оба параметра находятся подстановкой (3.5)–(3.6) в (3.2) при ${{T}_{{ip}}}\left( {\mathbf{r}} \right) = {{\delta }_{{ip}}}\delta \left( {\mathbf{r}} \right)$ и с использованием соотношения ${{\delta }_{{ip}}}{{\delta }_{{ip}}} = n$, что приводит к равенству

С учетом независимости $A$ и $B$ от упругих параметров, выделяются два уравнения, решение которых принимает вид $A = \frac{1}{n}$, $B = - \frac{1}{{{{n}^{2}} + 2n}}$.

При источнике из уравнения (3.2) выражение (3.3) для $\left\langle {{{G}_{{ip}}}} \right\rangle \left( {\mathbf{k}} \right)$ будет пропорционально члену $M = \int {\sum\nolimits_l {{{\rho }_{l}}\delta } } \left( {{\mathbf{r}} - {{{\mathbf{x}}}_{l}}} \right){{e}^{{ - i{\mathbf{kr}}}}}d{\mathbf{r}}$ (вместо $\int {\delta \left( {\mathbf{r}} \right)} {{e}^{{ - i{\mathbf{kr}}}}}d{\mathbf{r}} = 1$). При обратном преобразовании Фурье функции $\left\langle {{{G}_{{ip}}}} \right\rangle \left( {\mathbf{k}} \right)$ вместо функций $J\left( {\mathbf{r}} \right)$ и $H\left( {\mathbf{r}} \right)$ будут присутствовать суммы функций $\sum\nolimits_k {{{\rho }_{k}}J} \left( {{\mathbf{r}} - {{{\mathbf{x}}}_{k}}} \right)$ и $\sum\nolimits_k {{{\rho }_{k}}H} \left( {{\mathbf{r}} - {{{\mathbf{x}}}_{k}}} \right)$. Действие вторых производных на функцию $\left\langle {{{G}_{{ip}}}} \right\rangle \left( {\mathbf{r}} \right)$ при этом приведет к пропорциональности $\sum\nolimits_l {{{\rho }_{l}}\delta } \left( {{\mathbf{r}} - {{{\mathbf{x}}}_{l}}} \right)$, не меняющей коэффициенты в (3.5) , что с учетом вида уравнения (3.2) не изменит результат для параметров $A$ и $B$.

Зная значение тензорной функции ${{\partial }_{k}}{{\partial }_{q}}\left\langle {{{G}_{{ip}}}} \right\rangle \left( {\mathbf{r}} \right)$, вычислим интегралы ${{R}_{{jkpq}}}\left( 0 \right)$. Имеем равенство

где, как и в работе [24], использовано обозначение

Случай ${{T}_{{ip}}}\left( {\mathbf{r}} \right) = {{\delta }_{{ip}}}\delta \left( {\mathbf{r}} \right)$ приводит к $\gamma = 1$ и не отображает внутренние границы фаз. Отметим, что если внутренние границы фаз приводят суммарно к нулевому вкладу, то тогда также следует результат $\gamma = 1$.

Подставляя найденное выражение для ${{R}_{{jkpq}}}$ в формулу по вычислению эффективных коэффициентов (3.1), приведем итоговый результат в виде

4. Сопоставление с существующими подходами. При $\gamma = 1$ и $n = 3$ полученные эффективные коэффициенты эквивалентны результату в рамках метода самосогласованного поля [10–14] и подходу Эшелби [10, 15]. В рамках данной модели не учитывается переходный слой между включением и матрицей, обладающей искомыми эффективными свойствами (эффективными свойствами учитывается коллективное взаимодействие), что имеет отношение к пренебрежению границами раздела фаз. В случае $\gamma = 1$ внутренние границы раздела фаз не учитываются, т.е. отсутствует введение формализма обобщенной производной [24]. Если в (3.8) положить $\gamma = 1$ и $n = 3$, то следует результат, полученный на основе гипотезы сильной изотропии [10, 18]. В данном методе поле упругости в пределах каждого компонента сразу полагается однородным, что также не учитывает внутренние границы раздела фаз. Метод условных моментов [5, 6], вариационный метод [7–10], ряд статистических методов, базирующихся на функции Грина [6, 16, 17], обобщенное сингулярное приближение [10] содержат разный математический аппарат, но объединены гипотезой о теле сравнения. Если параметры тела сравнения ${{K}_{c}},~{{\mu }_{c}}$ положить равными искомым эффективным параметрам ${{K}_{c}} = K{\kern 1pt} *$, ${{\mu }_{c}} = \mu {\kern 1pt} *$, то полученный результат также будет эквивалентен формулам (3.8) при $\gamma = 1$ и $n = 3$. В вариационном методе при равенстве ${{K}_{c}} = K{\kern 1pt} *$, ${{\mu }_{c}} = \mu {\kern 1pt} *$ получаются эффективные коэффициенты, а не вилка Хашина–Штрикмана.

5. Анализ эффективных коэффициентов. Проведем анализ эффективных коэффициентов в частном случае при $\gamma = 1$, $n = 3$. Исследуемые параметры $\mu {\kern 1pt} *$, $K{\kern 1pt} *$ в формулах (3.8) являются неявными и взаимозависимыми, но сводятся к уравнению четвертой степени на функцию $\mu {\kern 1pt} *$

Проанализируем случай с фазой, обладающей нулевыми упругими параметрами фазы μ₁, ${{K}_{1}} = 0$, т.е. “пустое” пространство. При этом имеем ${{a}_{4}} = 0$ и ${{a}_{5}} = 0$. Последующее деление уравнения (5.1) на ${{\left( {\mu {\kern 1pt} *} \right)}^{2}} \ne 0$ приводит к решению квадратного уравнения

Выражение (5.2) описывает поведение системы при концентрации твердой фазы ${{c}_{2}} > 0.5$. Решением уравнения (5.1) при концентрации ${{c}_{2}} < 0.5$ является $\mu * = 0$. Эффективный объемный модуль $K{\kern 1pt} *$ также обращается в нуль при ${{c}_{2}} < 0.5$. Точка ${{c}_{2}} = 0.5$ является предельной (переходной) объемной концентрацией. В силу уравнения (5.1) при концентрации ${{c}_{2}} > 0.5$ твердая фаза является связной $\mu *\sim {{\mu }_{2}}$, $K*\sim {{K}_{2}}$, а при концентрации ${{c}_{1}} > 0.5$ связной является фаза “пустого” пространства $\mu * = K* = 0$, т.е. при концентрации ${{c}_{2}} < 0.5$ связная проводимость поля упругости отсутствует. Используемое понятие связности определяет несущую фазу, т.е. характеризует возможность макроскопической передачи поля упругости по структуре определенной фазой. На интервале ${{c}_{2}} > 0.5$ твердая фаза является несущей и определяет передачу поля упругости по структуре, а на интервале ${{c}_{2}} < 0.5$ несущей фазой является “пустое” пространство. Описанную ситуацию иллюстрирует рис. 1.

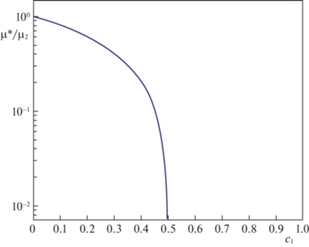
Физической интерпретацией системы с ${{K}_{1}}$, ${{\mu }_{1}} = 0$ может выступать пористый каркас. При концентрации ${{c}_{2}} < 0.5$ формирующая каркас твердая фаза “неустойчива” к макроскопически связанному распространению упругого поля $K* = \mu * = 0$, исходя из чего каркас не существует (рис. 1). Тогда при концентрации ${{c}_{2}} = 0.5$ согласно проведенному анализу при $\gamma = 1$ и $n = 3$ происходит перколяция поля упругости по твердой фазе в структуре.

Характерное поведение эффективного модуля сдвига при ненулевых, но достаточно малых упругих коэффициентах фазы “пустого” пространства ${{K}_{1}}$, ${{\mu }_{1}} \ll {{K}_{2}}$, ${{\mu }_{2}}$ представлено на рис. 2. Фазой 1 в данном случае может являться газ, жидкость, твердая фаза с существенно меньшими параметрами.

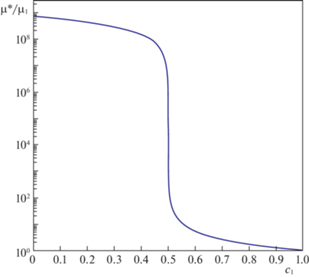
При наличии у фазы 1 ненулевых, но относительно малых коэффициентов упругости ${{K}_{1}}$, ${{\mu }_{1}} \ll {{K}_{2}}$, ${{\mu }_{2}}$ на интервале ${{c}_{2}} > 0.5$ с точностью до отношения упругих характеристик фаз ${{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, ${{K}_{1}}{\text{/}}{{K}_{2}}$, ${{\mu }_{1}}{\text{/}}{{K}_{2}}$, ${{K}_{1}}{\text{/}}{{\mu }_{2}} \ll 1$ эффективный модуль сдвига определяется выражением (5.2). При концентрации ${{c}_{1}} > 0.5$ эффективный модуль сдвига определяется выражением

которое является следствием квадратного уравнения, полученного из уравнения (5.1) делением последнего на ${{\mu }_{2}}{{K}_{2}}$ и отбрасыванием малых слагаемых ${{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, ${{K}_{1}}{\text{/}}{{K}_{2}}$, ${{\mu }_{1}}{\text{/}}{{K}_{2}}$, ${{K}_{1}}{\text{/}}{{\mu }_{2}}$ с учетом свойственной интервалу ${{c}_{1}} > 0.5$ пропорциональности $\mu *\sim {{\mu }_{1}}$, ${{K}_{1}}$. При увеличении относительной разности упругих коэффициентов фаз ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$ эффективные коэффициенты $\mu {\kern 1pt} *$, $K{\kern 1pt} *$ по обе стороны от критической концентрации ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} = 0.5$ стремятся к асимптотическим формулам (5.2), (5.3). Устремляя ненулевые ${{K}_{1}}$, ${{\mu }_{1}}$ к нулю при ${{c}_{2}} < 0.5$ исходя из выражения (5.3) следует значение $\mu * = 0$. Аналогично для K*. Согласно выражениям (5.2) и (5.3) на интервале ${{c}_{2}} > 0.5$ несущей фазой является твердая $\mu {\kern 1pt} *$, $K*\sim {{\mu }_{2}}$, ${{K}_{2}}$, а на интервале ${{c}_{1}} > 0.5$ несущей фазой является фаза “пустого” пространства $\mu {\kern 1pt} *$, $K*\sim {{\mu }_{1}}$, ${{K}_{1}}$. В окрестности точки ${{c}_{{{\text{2crit}}}}} = 0.5$ происходит резкое увеличение эффективных упругих свойств от $\mu {\kern 1pt} *$, $K*\sim {{\mu }_{1}}$, ${{K}_{1}}$ до $\mu {\kern 1pt} *$, $K*\sim {{\mu }_{2}}$, ${{K}_{2}}$ (проанализируем это детальнее ниже). То есть при концентрации ${{c}_{2}} = {{c}_{{{\text{2crit}}}}}$ = 0.5 начинает происходить макроскопически связанное распространение исследуемого поля упругости по твердой фазе в структуре (эффект перколяции). Переход между несущими фазами в точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} = 0.5$ интерпретируем как структурный фазовый переход. Соответствующее переходное поведение иллюстрирует рис. 2.

Исследовав поведение эффективного сдвигового модуля $\mu {\kern 1pt} *$ по обе стороны от критической точки, проанализируем его поведение непосредственно в области перехода ${{c}_{2}}\sim {{c}_{{{\text{2crit}}}}}$. Значение $\mu {\kern 1pt} *$ в области перехода оценим как ${{\mu }_{1}} \ll \mu * \ll {{\mu }_{2}}$. При этом считаем, что ${{K}_{1}}\sim {{\mu }_{1}} \ll {{K}_{2}}\sim {{\mu }_{2}}$. Базируясь на исходном выражении (5.1), проведем оценки слагаемых:

Основываясь на представленных оценках, выделим выражения одного порядка: ${{\left( {{{\mu }_{2}}} \right)}^{2}}{{\mu }_{1}}\mu {\kern 1pt} *$ ~ $\left( {{{c}_{1}} - {{c}_{2}}} \right){{\left( {{{\mu }_{2}}\mu {\kern 1pt} *} \right)}^{2}}$ ~ ${{\mu }_{2}}{{\left( {\mu {\kern 1pt} *} \right)}^{3}}$. Малость остальных отброшенных слагаемых подтвердится далее. С учетом проведенных оценок выражение (5.1) сводится к виду

где с учетом рассмотрения переходной области ${{c}_{2}}\sim {{c}_{{{\text{2crit}}}}}$ коэффициенты ${{b}_{i}}\sim 1$ (точный вид этих коэффициентов можно выписать, но это не представляет концептуальной необходимости). Выпишем решение данного уравнения

Второе решение не является физическим. Проведем исследование выражения (5.5) путем разложения подкоренного выражения при различных соотношениях параметров:

При соотношении $\left( {{{c}_{1}} - {{c}_{2}}} \right) \ll \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ учтены первые три основные слагаемые (при необходимости ряд можно продолжить). Для соотношений $\left| {{{c}_{1}} - {{c}_{2}}} \right| \gg \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ учтены только соответствующие основные слагаемые. Величина $\sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ выражает характерный масштаб переходной области. В связи с этим введем параметр $\varepsilon \sim \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $, выражающий ε-окрестность критической точки и возникающий как следствие конечного отношения упругих параметров фаз ${{\mu }_{1}}{\text{/}}{{\mu }_{2}}$ (а также отношений $~{{K}_{1}}{\text{/}}{{K}_{2}}$, ${{\mu }_{1}}{\text{/}}{{K}_{2}}$, ${{K}_{1}}{\text{/}}{{\mu }_{2}}$). Исходя из проведенной оценки (5.6) видно, что в критической точке $\mu *\sim \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $. И при переходе через критическую точку эффективный модуль $\mu {\kern 1pt} *$ совершает существенный рост от значения $\mu * \ll \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $, до значения $\mu * \gg \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $. В приведенных соотношениях (5.4)–(5.6) с учетом равенства ${{c}_{1}} + {{c}_{2}} = 1$ разность $\left( {{{c}_{1}} - {{c}_{2}}} \right)$ можно заменить на $\left( {{{c}_{{{\text{2crit}}}}} - {{c}_{2}}} \right)$ с точностью до коэффициента ${{\left( {{{c}_{{{\text{2crit}}}}}} \right)}^{{ - 1}}} = 2$. Следует отметить, что согласно (5.6) по разные стороны от критической точки имеют место разные асимптотики, меняющиеся от $\mu *\sim {{\mu }_{1}}{{\left( {{{c}_{{{\text{2crit}}}}} - {{c}_{2}}} \right)}^{{ - 1}}}$ до $\mu *\sim {{\mu }_{2}}{{\left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right)}^{1}}$. Эти же асимптотики предсказываются асимптотическими выражениями (5.3) и (5.2) соответственно. Это достигается с учетом сопоставления членов в выражении (5.3) и разложением по малому параметру $\left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right)$ в выражении (5.2). Исходя из сравнения асимптотических выражений (5.2) и (5.3) в предельных точках ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} + \varepsilon $ и ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} - \varepsilon $ также следует полученный результат для $\varepsilon \sim \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ и $\mu *\sim \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $. Что касается правильности оценки слагаемых в исходном выражении (5.1) при анализе переходной области, то выделенные слагаемые в уравнении (5.4) при $\left( {{{c}_{1}} - {{c}_{2}}} \right)\sim \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ и $\mu *\sim \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $ имеют порядок $\sim {\kern 1pt} {{\mu }_{2}}{{\left( {{{\mu }_{1}}{{\mu }_{2}}} \right)}^{{3/2}}}$, что существенно больше отброшенных слагаемых. При соотношениях $1 \gg \left( {{{c}_{1}} - {{c}_{2}}} \right) \gg \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ и ${{\mu }_{1}} \ll \mu * \ll \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $ используемое выражение (5.4) также имеет место, но в силу малости в нем можно сразу отбросить слагаемое $\sim {\kern 1pt} {{\mu }_{2}}{{\left( {\mu {\kern 1pt} *} \right)}^{3}}$, что приведет к полученному для данных соотношений результату в (5.6). При соотношениях $1 \gg \left( {{{c}_{2}} - {{c}_{1}}} \right) \gg \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $ и ${{\mu }_{2}} \gg \mu * \gg \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $ в выражении (5.4) в силу малости следует отбросить слагаемое $\sim {\kern 1pt} {{\left( {{{\mu }_{2}}} \right)}^{2}}{{\mu }_{1}}\mu {\kern 1pt} *$, что также приводит к соответствующему результату в (5.6).

Анализируемые эффективные коэффициенты (3.8) являются непрерывными функциями объемной концентрации ${{c}_{2}}$. Полученная ε-окрестность критической точки ${{c}_{{{\text{2crit}}}}}$ характеризует резкое изменение эффективных коэффициентов, но данное поведение не является скачком по определению. $\varepsilon $-окрестность критической точки, которую определяет асимптотическое решение (5.5), можно рассматривать как сшивку различных асимптотических решений (5.2) и (5.3) по обе стороны от нее. При этом асимптотические решения (5.2), (5.3) и (5.5) являются следствиями одного уравнения (5.1).

Проведем исследование структурного фазового перехода с учетом полученных результатов. Начнем со случая, в котором фаза “пустого” пространства имеет ненулевые параметры упругости ${{K}_{1}}$, ${{\mu }_{1}} \ll {{K}_{2}}$, ${{\mu }_{2}}$. Анализируемые эффективные коэффициенты упругости определяют обусловленную полем упругости внутреннюю энергию $\frac{1}{2}\int {\lambda _{{ij\alpha \beta }}^{*}{{\varepsilon }_{{ij}}}{{\varepsilon }_{{\alpha \beta }}}d{\mathbf{r}}} $ в системе. Из приведенного исследования эффективных коэффициентов $K{\kern 1pt} *$, μ* следует наличие критической точки ${{c}_{{{\text{2crit}}}}}$ и соответствующей ей переходной области, характеризующейся масштабом $\varepsilon \sim \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} \ll 1$. При переходе через ε-окрестность критической точки происходит резкое (скачкообразное) изменение эффективных модулей, что эквивалентно существенному изменению внутренней энергии. Выше, с позиции асимптотических выражений (5.2) и (5.3) говорилось про изменение эффективных модулей от $K{\kern 1pt} *$, $\mu *\sim {{K}_{1}}$, ${{\mu }_{1}}$ к $K*,\mu *\sim {{K}_{2}}$, ${{\mu }_{2}} \gg {{K}_{1}}$, ${{\mu }_{1}}$. Но с учетом проведенного анализа переходной области корректнее сказать, что с одной стороны от ε-окрестности критической точки при ${{c}_{2}} < {{c}_{{{\text{2crit}}}}}$ имеет место ${{K}_{1}},{{\mu }_{1}} \ll K{\kern 1pt} *$, $\mu * \ll \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $, а с другой стороны при ${{c}_{2}} > {{c}_{{{\text{2crit}}}}}$ имеет место $\sqrt {{{\mu }_{1}}{{\mu }_{2}}} \ll K{\kern 1pt} *$, $\mu * \ll {{K}_{2}},{{\mu }_{2}}$. При этом следует отметить, что в пределе $\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}} \to \infty $ масштаб ε-окрестности устремляется к нулю $\varepsilon \sim \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} \to 0$ и в точке ${{c}_{{{\text{2crit}}}}}$ следует говорить о разрыве эффективных коэффициентов $K{\kern 1pt} *$, $\mu {\kern 1pt} *$. Здесь сразу следует отметить, что случай $\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}} \to \infty $ отличается от случая ${{\mu }_{1}} = 0$ тем, что в последнем разрыва эффективных коэффициентов не происходит (см. рис. 1). С этой точки зрения изменение отклика в структуре на распространяющееся поле упругости следует интерпретировать как фазовый переход первого рода, имеющий отношение к смене агрегатного состояния. Параметром, определяющим скачкообразное поведение, является объемная концентрация ${{c}_{2}}$, в линейном упругом рассмотрении представляющая собой вероятность нахождения определенной фазы в макроточке.

Исследуем структурный фазовый переход системы при наличии у фазы (“пустого” пространства) нулевых коэффициентов упругости ${{K}_{1}},{{\mu }_{1}} = 0$. В точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} = 0.5$ эффективные упругие параметры $K{\kern 1pt} *$, $\mu {\kern 1pt} *$ либо равны нулю, либо находятся в окрестности нуля, стремясь к нулю при ${{c}_{2}} \to {{c}_{{{\text{2crit}}}}}$. Рассмотрим поведение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ при подходе к критической точке с двух сторон. В точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} - \varepsilon $, где $\varepsilon \to + 0$ поведение эффективных коэффициентов определяется значением $K* = \mu * = 0$, т.е. производная $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}} = 0$. При этом в точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} + \varepsilon $ производная $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}} \ne 0$ и подходит к критической точке оси абсцисс под некоторым углом $\pi {\text{/}}2 < \beta < \pi $, что следует из выражения (5.2). Анализ системы с параметрами ${{K}_{1}} = {{\mu }_{1}} = 0$ отображает предельный случай, при котором параметр $\varepsilon $ можно устремить к нулю (что согласуется с полученной при рассмотрении случая ${{K}_{1}},{{\mu }_{1}} \ne 0$ оценкой $\varepsilon \sim \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} = 0$). Таким образом, в точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}}$ производная $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ терпит разрыв, связанный со сменой функциональной зависимости эффективных коэффициентов по обе стороны перехода. Поведение эффективных коэффициентов в критической точке при ${{K}_{1}},{{\mu }_{1}} = 0$ соответствует фазовому переходу второго рода. Рис. 1 иллюстрирует это поведение. Говоря о фазовых переходах второго рода, следует иметь ввиду параметр порядка. В рассматриваемом случае параметром порядка является объемная концентрация сфер ${{c}_{2}}$ (${{c}_{1}} + {{c}_{2}} = 1$), она же является вероятностью нахождения твердой фазы в структуре. При параметре порядка ${{c}_{2}} = 1$ система полностью упорядочена. Фазовые переходы второго рода также связывают с изменением симметрии в среде (см. теорию Ландау). Вероятной интерпретацией структурного изменения в точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}}$ является переход твердой фазы к упорядоченному состоянию, при котором твердая фаза начинает занимать узлы симметричной “кристаллической” решетки.

Рассмотрим поведение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ при ненулевых параметрах ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$. Исследуем вначале поведение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ по обе стороны вдали от критической концентрации. Соответствующее поведение следует из дифференцирования полученных асимптотических выражений (5.2) и (5.3), имеющих разную функциональную зависимость. Рассмотрим вспомогательный член $\frac{1}{{{{\mu }_{1}}}}\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$. При концентрации ${{c}_{2}} > {{c}_{{{\text{2crit}}}}}$ поведение этого члена исходя из выражения (5.2) оценивается как $\frac{1}{{{{\mu }_{1}}}}\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}\sim \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}$ (также полагаем ${{K}_{1}}\sim {{\mu }_{1}}$ $ \ll $ ${{K}_{2}}\sim {{\mu }_{2}}$). А при концентрации ${{c}_{2}} < {{c}_{{{\text{2crit}}}}}$ исходя из выражения (5.3) поведение этого члена оценивается как $\frac{1}{{{{\mu }_{1}}}}\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}\sim 1$. Проанализируем теперь поведение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ при подходе к критической точке. Используя выражение (5.6), найдем соответствующие асимптотики

Таким образом, в области критической точки значение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$, нормированной на ${{\mu }_{1}}$, существенно меняется от $\sim {\kern 1pt} {{\left( {{{c}_{1}} - {{c}_{2}}} \right)}^{{ - 2}}} \ll \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}$ до $\sim {\kern 1pt} \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}$. В рамках асимптотической формулы (5.2) поведение вспомогательного члена при подходе к критической точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} + \varepsilon $ не поменялось $\frac{1}{{{{\mu }_{1}}}}\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}\sim \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}$. В то время как поведение асимптотической формулы (5.3) при подходе к критической точке ${{c}_{2}} = {{c}_{{{\text{2crit}}}}} - \varepsilon $ существенно изменилось: $\frac{1}{{{{\mu }_{1}}}}\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}\sim \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}} \gg 1$. При увеличении концентрации ${{c}_{2}}$ относительно значения ${{c}_{2}} = {{c}_{{{\text{2crit}}}}}$ значение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ не испытывает существенного изменения, в то время как на интервале ${{c}_{{{\text{2crit}}}}} - \varepsilon $ < ${{c}_{2}} < {{c}_{{{\text{2crit}}}}}$ происходит ее скачкообразное изменение (вдали от критической точки ${{c}_{2}} < {{c}_{{{\text{2crit}}}}}$ поведение члена $\frac{1}{{{{\mu }_{1}}}}\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}\sim 1$ согласно выражению (5.3)). Данное поведение также можно описать оценочной записью

в которой значение эффективного модуля $\mu {\kern 1pt} *$ изменилось от $\mu *\sim \alpha {{\mu }_{1}}$, где 1 < < $\alpha \ll {{\left( {{{\mu }_{2}}{\text{/}}{{\mu }_{1}}} \right)}^{{1/2}}}$ до значения $\mu *\sim \sqrt {{{\mu }_{1}}{{\mu }_{2}}} $ на интервале масштаба $\varepsilon \sim {{\left( {{{\mu }_{1}}{\text{/}}{{\mu }_{2}}} \right)}^{{1/2}}}$. На рис. 3 отражено поведение модуля производной эффективного сдвигового коэффициента $\left| {\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{1}}}}} \right|$, нормированного на модуль ${{\mu }_{1}}$ в зависимости от концентрации фазы ${{c}_{1}}$ при ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$.

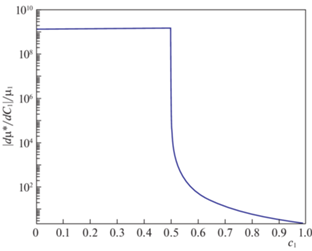
Исходя из проведенного анализа выражения (5.5) (следствие функциональной зависимости (5.1)) производная $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ в случае ${{\mu }_{1}},~{{K}_{1}} \ll {{K}_{2}},~{{\mu }_{2}}$ испытывает скачкообразное изменение в переходной области критической точки ${{c}_{{{\text{2crit}}}}}$. Отличие от разрыва производной, имеющего место в предельном случае ${{K}_{1}} = {{\mu }_{1}} = 0$, заключается в наличии у переходной области малой, но конечной окрестности критической точки $\varepsilon \sim {{\left( {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} \right)}^{{1/2}}}$, обусловленной ненулевыми параметрами ${{K}_{1}},{{\mu }_{1}}$ в выражении (5.1). При устремлении отношений ${{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, ${{K}_{1}}{\text{/}}{{K}_{2}}$, ${{\mu }_{1}}{\text{/}}{{K}_{2}}$, ${{K}_{1}}{\text{/}}{{\mu }_{2}}$ к нулю масштаб ε-окрестности критической точки устремляется к нулю и в пределе имеет место разрыв производной как и в предельном случае ${{K}_{1}} = {{\mu }_{1}} = 0$. Анализ поведения эффективных модулей $\mu {\kern 1pt} *$, $K{\kern 1pt} *$ при ${{K}_{1}} = {{\mu }_{1}} = 0$ указывает на фазовый переход второго рода. Поведение эффективных модулей в случае ${{\mu }_{1}},{{K}_{1}} \ll {{K}_{2}},{{\mu }_{2}}$ с точностью до ε-окрестности критической точки также указывает на фазовый переход второго рода.

Покажем, что поведение производных $\frac{{{{d}^{l}}\mu {\kern 1pt} *}}{{dc_{2}^{l}}}$ при $l > 1$ в окрестности критической точки отличается от случаев $l = 0$ и $l = 1$. Начнем со случая $l = 2$. Взяв вторую производную в выражении (5.5), получим выражения

которые предсказывают δ-образный всплеск в $\varepsilon $-окрестности критической точки. Действительно, по обе стороны от критической точки $\left| {{{c}_{2}} - {{c}_{1}}} \right| \gg {{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{{1/2}}}$ имеет место оценка $\sim {\kern 1pt} {{\left| {{{c}_{2}} - {{c}_{1}}} \right|}^{{ - 3}}} \ll {{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{{3/2}}}$, которая существенно меньше оценки $\sim {\kern 1pt} {{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{{3/2}}}$ при $\left( {{{c}_{1}} - {{c}_{2}}} \right) \ll \sqrt {\frac{{{{\mu }_{1}}}}{{{{\mu }_{2}}}}} $. Рис. 4 отражает предсказанное поведение производной $\frac{{{{d}^{2}}\mu {\kern 1pt} *}}{{dc_{2}^{2}}}$.

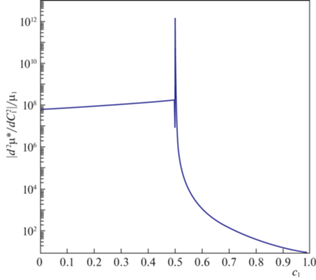
Отметим также, что асимптотическим выражением (5.3) в окрестности точки ${{c}_{2}} < {{c}_{{{\text{2crit}}}}} - \varepsilon $ для вспомогательного члена предсказывается оценка $\frac{1}{{{{\mu }_{1}}}}\frac{{{{d}^{2}}\mu {\kern 1pt} *}}{{dc_{2}^{2}}}$ ~ ${{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{{3/2}}}$. В свою очередь из асимптотического выражения (5.2) на интервале ${{c}_{2}} > {{c}_{{{\text{2crit}}}}} + \varepsilon $ следует оценка $\sim {\kern 1pt} {{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{1}}$. На рис. 4 видно падение значения члена $\frac{1}{{{{\mu }_{1}}}}\frac{{{{d}^{2}}\mu {\kern 1pt} *}}{{dc_{2}^{2}}}$ вблизи критической точки ${{c}_{2}} \approx {{c}_{{{\text{2crit}}}}}$, ${{c}_{2}} > {{c}_{{{\text{2crit}}}}}$. Соответствующее падение является следствием того, что при увеличении ${{c}_{2}}$ асимптотика $\sim {\kern 1pt} {{\left( {{{c}_{2}} - {{c}_{1}}} \right)}^{{ - 3}}}$ меняется на асимптотику $\sim {\kern 1pt} {{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{1}}$, причем на рассматриваемом интервале “падения” оказывается справедливым неравенство ${{\left( {{{c}_{2}} - {{c}_{1}}} \right)}^{{ - 3}}}$ < ${{\left( {\frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}} \right)}^{1}}$.

Наличие δ-образного поведения в $\varepsilon $-окрестности критической точки имеет место и для производных более высших порядков. Данные всплески имеют отношение к δ-функции и ее производным. В предельном случае ${{K}_{1}} = {{\mu }_{1}} = 0$ производная $\frac{{{{d}^{l}}\mu {\kern 1pt} *}}{{dc_{2}^{l}}}$ содержит δ-функции и производные от них вплоть до порядка $l - 2$, $l \geqslant 2$, которые сосредоточены в критической точке (масштаб $\varepsilon $-окрестности при ${{K}_{1}} = {{\mu }_{1}} = 0$ равен нулю). Для доказательства этого утверждения заметим, что эффективный сдвиговый модуль при ${{K}_{1}} = {{\mu }_{1}} = 0$ представим в виде $\mu * = \tilde {\mu }{\kern 1pt} *{\kern 1pt} \theta \left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right)$, где $\tilde {\mu }{\kern 1pt} *$ определяется выражением (5.2), а функция $\theta \left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right)$ является функцией Хевисайда ($\theta \left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right) = 1$ при ${{c}_{2}} > {{c}_{{{\text{2crit}}}}}$ и $\theta \left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right) = 0$ при ${{c}_{2}} < {{c}_{{{\text{2crit}}}}}$). Дифференцирование такого эффективного сдвигового модуля по ${{c}_{2}}$ приводит к выражению $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ = $\frac{{d\tilde {\mu }{\kern 1pt} *}}{{d{{c}_{2}}}}\theta \left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right)$. Член с δ-функцией, появляющийся при дифференцировании $\theta \left( {{{c}_{2}} - {{c}_{{{\text{2crit}}}}}} \right)$, исчезает вследствие $\tilde {\mu }{\kern 1pt} *{\kern 1pt} \left( {{{c}_{2}} = {{c}_{{{\text{2crit}}}}}} \right) = 0$. Такое поведение производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ свойственно фазовым переходам второго рода. Для производной $\frac{{{{d}^{2}}\mu {\kern 1pt} *}}{{dc_{2}^{2}}}$ имеет место выражение

которое предсказывает δ-образное поведение в критической точке $\left( {\frac{{d\tilde {\mu }{\kern 1pt} *}}{{d{{c}_{2}}}}\left( {{{c}_{2}} = {{c}_{{{\text{2crit}}}}}} \right) \ne 0} \right)$. Из представленного выражения видно, что производные более высших порядков содержат δ-функцию и ее производные (коэффициенты перед ними не обращаются в нуль). В случае малых, но конечных ${{K}_{1}},{{\mu }_{1}}$, появляющийся в окрестности критической точки δ-образный всплеск при рассмотрении производных $\frac{{{{d}^{l}}\mu {\kern 1pt} *}}{{dc_{2}^{l}}}$, $l \geqslant 2$ имеет приближенное отношение к $\delta $-функции и ее производным порядка $l - 2$, $l \geqslant 2$. Соответствующее приближенное отношение является следствием того, что точное представление через θ-функцию эффективного модуля μ* при ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$ отсутствует. Первая производная $l = 1$ эффективного модуля μ* в рассмотренном предельном случае ${{K}_{1}} = {{\mu }_{1}} = 0$ не содержит δ-функции, что имеет отношение к отсутствию $\delta $-образного скачка первой производной эффективного модуля μ* в случае ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$. То есть выражение (5.1) для эффективного модуля μ* устроено таким образом, что в случае ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$ его скачкообразное поведение в переходной области не приводит к $\delta $-образному всплеску его первой производной в этой ε-окрестности критической точки, такому, которое проявляется для производных более высшего порядка. В отличие от производных порядка $l > 1$ эффективный модуль $\mu {\kern 1pt} *{\kern 1pt} \left( {{{c}_{2}}} \right)$ и его первая производная $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}\left( {{{c}_{2}}} \right)$ демонстрируют непрерывный рост при увеличении ${{c}_{2}}$, что согласуется с полученными асимптотическими выражениями (5.2), (5.3) и (5.5). Отличие поведения производной эффективного модуля $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ от самого модуля μ* в переходной области заключается в изменении скачкообразного поведения: наклон производной $\frac{{d\mu {\kern 1pt} *}}{{d{{c}_{2}}}}$ становится более сингулярным относительно модуля μ*, исходя из выражений (5.7) и (5.8) отношение соответствующих наклонов

Исходя из представленного анализа при конечном отношении параметров упругости фаз ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$ полученные эффективные коэффициенты $K*,\mu {\kern 1pt} *$ характеризуются не только существенным изменением своих значений в малой ε-окрестности критической точки ${{c}_{{{\text{2crit}}}}}$, но и резким изменением в поведении первых производных от соответствующих эффективных коэффициентов в этой $\varepsilon $-окрестности. Найденная информация о фазовом переходе как первого рода, так и второго отражает нетривиальное поведение эффективных коэффициентов в случае ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$. Наличие малой, но ненулевой ε-окрестности при анализе эффективных коэффициентов возникает как следствие конечного отношения упругих параметров фаз и отображает переходное состояние в поведении структуры.

Для описания структурного фазового перехода следует также дать качественное пояснение механизма контакта между разными элементарными структурными элементами (частицами) одной фазы. Используем при этом позицию обобщенной производной (2.2). Применение формулы (2.2) к уравнениям (2.1), приводит к дифференциальным уравнениям на смещение

отображающим распространение поля в гетерогенной среде в целом с учетом внутренних границ. Одно из появившихся сингулярных слагаемых, содержащее в поверхностном интеграле член ${{\left[ {{{\lambda }_{{ij\alpha \beta }}}{{\partial }_{\beta }}{{u}_{\alpha }}} \right]}_{{\mathbf{x}}}}$, занулилось вследствие равенства напряжений на границах раздела фаз. При рассмотрении контактов одной фазы слагаемое ${{\left[ {{{\lambda }_{{ij\alpha \beta }}}{{u}_{\alpha }}} \right]}_{{\mathbf{x}}}}$ отлично от нуля если тангенциальные смещения разных элементов одной фазы различаются на границе раздела. Равенство соответствующих тангенциальных смещений может интерпретироваться как образование жесткой связи (кластеризация, слипание). В рассматриваемом случае $\gamma = 1$ данные члены равны нулю и описанный механизм выполняется.

Проведем анализ эффективных коэффициентов (3.8) при заданном $n$ и $\gamma = 1$. В данном случае также получается уравнение четвертой степени на μ*, но с другими коэффициентами ${{a}_{i}}\left( {{{c}_{2}},n} \right)$. Отличие при этом заключается в значении критической объемной концентрации ${{c}_{{{\text{2crit}}}}}$. Исходя из представленных выкладок следует, что значение ${{c}_{{{\text{2crit}}}}}$ одинаково как для фазы “пустого” пространства с ${{K}_{1}},{{\mu }_{1}} = 0$, так и для случая ${{K}_{1}},{{\mu }_{1}} \ne 0$, ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$. Однако удобнее находить ${{c}_{{{\text{2crit}}}}}$ для случая ${{K}_{1}},{{\mu }_{1}} = 0$ приравниванием к нулю коэффициента ${{a}_{3}}\left( {{{c}_{2}},n,{{n}_{0}}} \right) = 0$ в полученном уравнении четвертой степени на μ*. Для произвольной эффективной размерности $n$ условие на критическую концентрацию имеет вид

При $n = 3$ имеем полученное значение ${{c}_{{{\text{2crit}}}}} = 0.5$. При $n = 2$ следует ${{c}_{{{\text{2crit}}}}} = {\text{2/3}}$, $n = 1$ дает ${{c}_{{{\text{2crit}}}}} = 1$.

При произвольном $n$ и $\gamma = 1$ изложенные аспекты, связанные с несущей фазой и структурным фазовым переходом, сохранятся с точностью до значения ${{c}_{{{\text{2crit}}}}}$.

Эффективные коэффициенты (3.8) отображают необходимость увеличения концентрации проводящей фазы для связного распространения поля по ней в гетерогенной среде при уменьшении размерности рассматриваемого пространства, в котором распространяется поле. То есть при меньшем числе внутренних связей нужна большая концентрация проводящей фазы.

Обобщение эффективных коэффициентов на случай некоторой размерности пространства делается также с целью отображения эффективного числа внутренних степеней свободы при распространении поля по гетерогенной среде с существенно различающимися физическими свойствами фаз на всем интервале концентраций.

На основе проделанного анализа приведем качественное сопоставление с экспериментальными данными.

Согласно проведенному в работе [25] молекулярно-динамическому моделированию значение концентрации ${{c}_{2}} = 0.5$ входит в диапазон концентраций, описывающих фазовый переход первого рода между жидкостью и твердой фазой. В основе моделирования использована модель жестких твердых сфер. Автор статьи [1] интерпретирует значение 0.494 как “наибольшую случайную плотность” среди монодисперсных сфер, как точку затвердевания “freezing point”. Соответствующая структурная особенность проявляется в экспериментах с коллоидами [26]. Обратим здесь внимание на то, что автор статьи [1] связывает точку затвердевания с наибольшей плотностью случайно распределенных сфер. Продолжая эту мысль, укажем, что приближение концентрации фазы сфер к критической, вероятно, дает вклад одновременно как в изменение сопротивления нагрузке (вызванное процессом “затвердевания”), так и в упорядоченность структуры. Под вкладом в упорядоченность понимается структурное изменение в среде, которая изначально представляла собой стохастически распределенную структуру. Выше было показано, что случаю ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$ соответствует структурный фазовый переход, имеющий признаки фазовых переходов первого и второго рода. Фактически, данный структурный фазовый переход отображает изменение сопротивления нагрузке и вклад в упорядоченность структуры (структурное изменение).

В работе [1] исследуется случайная плотная упаковка сфер, которая представляется как состояние гранулированной среды, соответствующее структурному фазовому переходу, проявляющему признаки фазовых переходов первого и второго рода. При этом значение объемной концентрации монодисперсных сфер ${{c}_{{{\text{2crit}}}}}$ = 0.6366 ± 0.0005, что реализуется по протоколу “вертикального встряхивания”. В работе [1] также приводятся другие предельные значения объемной концентрации сфер, например, ${{c}_{{{\text{2crit}}}}} \approx 0.6$. Такое же значение присутствует в работе [27] при исследовании суспензий. Данные значения следуют из выражения (5.9) при $n < 3$, что интерпретируем уменьшением эффективного числа внутренних степеней свободы при распространении поля по гетерогенной среде.

Полученные эффективные коэффициенты способны согласовываться с экспериментом не только вблизи критических значений. Например, в работе [28] исследуется модуль Юнга композитного материала, состоящего из резины и эпоксидной смолы. Из эксперимента и используемой авторами клеточной модели при малых концентрациях эпоксидной смолы следует выражение для модуля Юнга системы $E* = {{E}_{1}}$ + + $\frac{5}{2}{{E}_{1}}{{c}_{2}}$. Это же выражение следует из полученных коэффициентов (3.8) при условиях $\gamma = 1$ и $n = 3$, ${{K}_{1}},{{\mu }_{1}} \ll {{K}_{2}},{{\mu }_{2}}$, ${{K}_{1}} \gg {{\mu }_{1}}$, соответствующих исследуемой системе и с учетом ${{c}_{2}} \ll 1$. В работе [28] предельная концентрация также ограничена значением ${{c}_{2}} = 0.5$. Формулы (3.8) при $\gamma = 1$ и $n = 3$ хорошо описывают пористые системы при малой концентрации пористости [6].

Заключение. Произведено обобщение эффективных коэффициентов линейной теории упругости для пространства заданной размерности при учете формализма обобщенной производной. Представлено сравнение полученных эффективных коэффициентов с результатами существующих подходов. Обобщение эффективных коэффициентов направлено отобразить специфику распространения поля по гетерогенной среде с существенно различающимися физическими свойствами фаз на всем диапазоне объемных концентраций. Из анализа эффективных коэффициентов, примененного для гетерогенных сред с существенно различающимися свойствами фаз, предсказано наличие несущей фазы и структурного фазового перехода (перколяции). Структурный фазовый переход отображает переход фазы от несвязного распространения поля по системе к макроскопически связному и имеет признаки фазовых переходов первого и второго рода. Полученные результаты имеют согласование с имеющимися данными по коллоидам, гранулированным средам и суспензиям.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-31-90090.