Прикладная математика и механика, 2022, T. 86, № 4, стр. 584-594

Влияние анизотропии материала на взаимодействие трещины со свободной границей

А. В. Савиковский^1, *, А. С. Семенов^1, **, М. Л. Качанов^{1, 2, 3, ***}

¹ Санкт-Петербургский политехнический университет Петра Великого
Санкт-Петербург, Россия

² Университет Тафтса
Массачусетс, Медфорд, США

³ Нижегородский государственный университет им. Лобачевского
Нижний Новгород, Россия

^* E-mail: savikovskii.artem@yandex.ru
^** E-mail: semenov.artem@googlemail.com
^*** E-mail: Mark.Kachanov@tufts.edu

Поступила в редакцию 15.03.2022
После доработки 11.05.2022
Принята к публикации 15.05.2022

EDN: HAAPYL
DOI: 10.31857/S0032823522040129

Полный текст (PDF)

Аннотация

Рассматривается взаимодействие одиночной прямолинейной трещины со свободной границей анизотропной упругой пластины конечных размеров. Показано, что при приближении вершины трещины к границе пластины возрастает влияние упругой анизотропии материала на значения коэффициентов интенсивности напряжений. Исследовано влияние степени анизотропии упругих свойств материала и ориентации трещины (моды разрушения) на этот эффект.

Ключевые слова: анизотропный материал, коэффициент интенсивности напряжений, трещина, линейно-упругая механика разрушения, формализм Лехницкого, конечно-элементное моделирование

1. Введение. Определение коэффициентов интенсивности напряжений (КИН) играет ключевую роль при исследовании условий распространения трещин в хрупких материалах. В то время как задача определения КИН детально изучена для изотропных упругих сред с трещиной [1, 2], она является значительно более трудоемкой и менее исследованной для анизотропных тел. В случае бесконечной упругой пластины, обладающей произвольной анизотропией упругих свойств и содержащей прямолинейную трещину, произвольно ориентированную по отношению к осям анизотропии материала, метод анализа был разработан Лехницким [3] для более общего случая эллиптической полости. В работе Си, Пэриса и Ирвина [4] для бесконечной анизотропной пластины с трещиной при произвольно ориентированном по отношению к трещине одноосном растяжении установлено отсутствие зависимости значений КИН от упругих констант и, как следствие этого, совпадение значений КИН для анизотропного и изотропного материала, определяемых выражениями [4]:

(1.1)

${{K}_{{\text{I}}}} = \sigma \sqrt {\pi a} {{\sin }^{2}}\varphi ,\quad {{K}_{{{\text{II}}}}} = \sigma \sqrt {\pi a} \sin \varphi \cos \varphi ,$

где $\sigma $ – растягивающее напряжение, a – полудлина трещины, $\varphi $ – угол между направлением действия одноосного растягивающего напряжения и направлением трещины.

Однако для пластин конечных размеров, представляющих непосредственный интерес для приложений, значения КИН зависят от упругих констант и, в частности, от степени анизотропии материала. В литературе имеются лишь несколько численных результатов для КИН трещин в анизотропных пластинах конечных размеров (см., например, [5]– [9]). В статье [6] рассчитывались КИН для ортотропной пластины конечных размеров, но влияние расстояния от трещины до края на значение КИН не исследовалось. В статье [7] приводится исследование влияния ориентации трещины на значение КИН для анизотропной пластины конечных размеров. В статье [8] вычисляются КИН для боковой трещины в анизотропной пластине конечных размеров и исследуется влияние ориентации осей материала на значение КИН. Также в этой статье приводятся значения КИН для центральной трещины в анизотропной пластине конечных размеров и исследуется влияние ориентации осей анизотропного материала и расстояния от вершины трещины до края, но для компактного образца, и не исследуется степень влияния анизотропии. В статье [9] исследуется влияние расстояния от вершины трещины до края образца на значение КИН для изотропного и анизотропного материалов, но анализ выполняется только для цилиндрического образца и не исследуется влияние степени анизотропии. Также исследовалось влияние ориентации трещины на значение КИН для анизотропного материала. Неисследованным остается важный вопрос о влиянии степени анизотропии на взаимодействие трещины с границами тела.

Упомянутые факторы детально исследуются в настоящей работе на примере трещины в упругой анизотропной пластине конечных размеров. Целью является исследование влияния ориентации трещины и степени анизотропии материала на взаимодействие трещины с границей, оцениваемое по величине отношения КИН для анизотропного и изотропного материалов.

2. Постановка задачи. Рассматривается квадратная анизотропная упругая пластина, содержащая внутреннюю одиночную прямолинейную трещину (рис. 1). Исследуются два варианта ориентации трещины по отношению к пластине. Рассматривается одноосное растяжение пластины в вертикальном направлении. Задача решается в 2-мерной постановке в предположении плоского напряженного состояния (решение данной задачи с учетом потери плоской формы получено в [10]). Оси анизотропии упругих свойств параллельны краям пластины. Исследование эффектов влияния степени анизотропии материала и ориентации трещины осуществляется на основе многовариантных вычислительных экспериментов при различных значениях размера “перемычки” a – расстояния между вершиной трещины и границей пластины. Расчет КИН проводился методом конечных элементов, с использованием конечно-элементного программного комплекса PANTOCRATOR [11], который обладает способностью автоматизированных вычислений КИН для изотропных и анизотропных материалов на основе различных методов. В процессе выполнения расчетов варьировались степень анизотропии, ориентация трещины по отношению к осям анизотропии материала и расстояние от вершины трещины до края пластины.

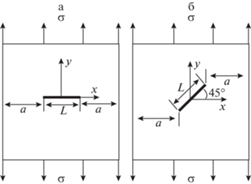
Рис. 1.

Варианты ориентации прямолинейной трещины в квадратной анизотропной пластине: а) горизонтальная трещина (φ = 0°), б) наклонная трещина (φ = 45°).

3. Методы определения КИН. Асимптотические выражения для перемещений в окрестности вершины трещины в общем трехмерном случае при наличии трех мод разрушения (ненулевые ${{K}_{{\text{I}}}}$, ${{K}_{{{\text{II}}}}}$, ${{K}_{{{\text{III}}}}}$) для изотропного материала определяются соотношениями [12]:

${{u}_{x}}(r,\alpha ) = \frac{{{{K}_{{\text{I}}}}}}{G}\sqrt {\frac{r}{{2\pi }}} \cos \frac{\alpha }{2}\left( {\frac{{\kappa - 1}}{2} + {{{\sin }}^{2}}\frac{\alpha }{2}} \right) + \frac{{{{K}_{{{\text{II}}}}}}}{G}\sqrt {\frac{r}{{2\pi }}} \sin \frac{\alpha }{2}\left( {\frac{{\kappa + 1}}{2} + {{{\cos }}^{2}}\frac{\alpha }{2}} \right)$

(3.1)

${{u}_{y}}(r,\varphi ) = \frac{{{{K}_{{\text{I}}}}}}{G}\sqrt {\frac{r}{{2\pi }}} \sin \frac{\alpha }{2}\left( {\frac{{\kappa + 1}}{2} - {{{\cos }}^{2}}\frac{\alpha }{2}} \right) + \frac{{{{K}_{{{\text{II}}}}}}}{G}\sqrt {\frac{r}{{2\pi }}} \cos \frac{\alpha }{2}\left( {\frac{{\kappa - 1}}{2} + {{{\sin }}^{2}}\frac{\alpha }{2}} \right)$

${{u}_{z}}(r,\alpha ) = \frac{{{{K}_{{{\text{III}}}}}}}{G}\sqrt {\frac{r}{{2\pi }}} \sin \frac{\alpha }{2},$

где ${{u}_{x}}(r,\alpha )$, ${{u}_{y}}(r,\alpha )$, ${{u}_{z}}(r,\alpha )$ – осевые перемещения в системе координат трещины, ${{K}_{{\text{I}}}}$, ${{K}_{{{\text{II}}}}}$, ${{K}_{{{\text{III}}}}}$ – КИН для I, II и III мод разрушения, $\kappa = \left( {3 - \nu } \right){\text{/}}\left( {1 + \nu } \right)$ в случае ПНС, G – модуль сдвига, r – расстояние до рассматриваемой точки от вершины трещины, α – угол между направлением на точку и осью трещины, $\nu $ – коэффициент Пуассона.

Асимптотические выражения для перемещений около вершины трещины в общем трехмерном случае для анизотропного материала, полученные с использованием формализма Лехницкого, имеют следующий вид [4, 6, 13]:

$\begin{gathered} {{u}_{x}}(r,\alpha ) = \frac{{{{K}_{{\text{I}}}}\sqrt {2r} }}{{\sqrt \pi }}\operatorname{Re} \left( {\frac{1}{{\mu _{1}^{'} - \mu _{2}^{'}}}\left( {\mu _{1}^{'}{{p}_{2}}\sqrt {\cos \alpha + \mu _{2}^{'}\sin \alpha } - \mu _{2}^{'}{{p}_{1}}\sqrt {\cos \alpha + \mu _{1}^{'}\sin \alpha } } \right)} \right) + \\ + \;\frac{{{{K}_{{{\text{II}}}}}\sqrt {2r} }}{{\sqrt \pi }}\operatorname{Re} \left( {\frac{1}{{\mu _{1}^{'} - \mu _{2}^{'}}}\left( {{{p}_{2}}\sqrt {\cos \alpha + \mu _{2}^{'}\sin \alpha } - {{p}_{1}}\sqrt {\cos \alpha + \mu _{1}^{'}\sin \alpha } } \right)} \right) \\ \end{gathered} $

(3.2)

${{u}_{y}}(r,\alpha ) = \frac{{{{K}_{{\text{I}}}}\sqrt {2r} }}{{\sqrt \pi }}\operatorname{Re} \left( {\frac{1}{{\mu _{1}^{'} - \mu _{2}^{'}}}\left( {\mu _{1}^{'}{{q}_{2}}\sqrt {\cos \alpha + \mu _{2}^{'}\sin \alpha } - \mu _{2}^{'}{{q}_{1}}\sqrt {\cos \alpha + \mu _{1}^{'}\sin \alpha } } \right)} \right) + $

$\begin{gathered} + \;\frac{{{{K}_{{{\text{II}}}}}\sqrt {2r} }}{{\sqrt \pi }}\operatorname{Re} \left( {\frac{1}{{\mu _{1}^{'} - \mu _{2}^{'}}}\left( {{{q}_{2}}\sqrt {\cos \alpha + \mu _{2}^{'}\sin \alpha } - {{q}_{1}}\sqrt {\cos \alpha + \mu _{1}^{'}\sin \alpha } } \right)} \right) \\ {{u}_{z}}(r,\alpha ) = \frac{{{{K}_{{{\text{III}}}}}\sqrt {2r} }}{{\sqrt \pi }}\operatorname{Re} \left( {\frac{{\sqrt {\cos \alpha + \mu _{3}^{'}\sin \alpha } }}{{{{c}_{{45}}} + {{\mu }_{3}}{{c}_{{44}}}}}} \right), \\ \end{gathered} $

где $\mu _{1}^{'}$ и $\mu _{2}^{'}$ – комплекснозначные корни уравнения четвертой степени (комплексные параметры анизотропного материала [3]).

(3.3)

$S_{{11}}^{'}{{\mu }^{4}} - 2S_{{16}}^{'}{{\mu }^{3}} + (2S_{{12}}^{'} + S_{{66}}^{'}){{\mu }^{2}} - 2S_{{26}}^{'}\mu + S_{{22}}^{'} = 0$

с положительной мнимой частью, $S_{{ij}}^{'}$ – элементы матрицы упругой податливости материала при использовании обозначений Фойгта в системе координат трещины, ${{p}_{i}} = S_{{11}}^{'}\mu _{i}^{{'2}}$ + $S_{{12}}^{'} - S_{{16}}^{'}\mu _{i}^{'}$, ${{q}_{i}} = S_{{12}}^{'}\mu _{i}^{'}$ + $\frac{{S_{{22}}^{'}}}{{\mu _{i}^{'}}} - S_{{26}}^{'}$, $\mu _{3}^{'}$ – корень уравнения $С_{{44}}^{'}{{\mu }^{2}} - 2С_{{45}}^{'}\mu $ + + $С_{{55}}^{'} = 0$ с положительной мнимой частью, $С_{{ij}}^{'}$ – константы матрицы упругих модулей материала в системе координат трещины ($[{\mathbf{С}}] = {{[{\mathbf{S}}]}^{{ - 1}}}$).

В случае изотропного материала перемещения связаны с КИНами формулами (3.1). Чтобы найти перемещения на свободных берегах трещины, подставим α = π в уравнение (3.1) и выразим КИН через перемещения для изотропного материала:

(3.4)

${{K}_{{\text{I}}}} = {{u}_{y}}(r,\pi )\sqrt {\frac{{2\pi }}{r}} \frac{{2G}}{{1 + \kappa }},\quad {{K}_{{{\text{II}}}}} = {{u}_{x}}(r,\pi )\sqrt {\frac{{2\pi }}{r}} \frac{{2G}}{{1 + \kappa }},\quad {{K}_{{{\text{III}}}}} = {{u}_{z}}(r,\pi )\sqrt {\frac{{2\pi }}{r}} G$

В случае анизотропного материала результатом подстановки α = π в (3.2), получаем выражения:

(3.5)

$\left\{ {\mathbf{u}} \right\} = \sqrt {\frac{{2r}}{\pi }} [{\mathbf{B}}] \cdot \left\{ {\mathbf{K}} \right\},$

где

$\left\{ {\mathbf{u}} \right\}\, = \,\left\{ {\begin{array}{*{20}{c}} {{{u}_{x}}(r,\pi )} \\ {{{u}_{y}}(r,\pi )} \\ {{{u}_{z}}(r,\pi )} \end{array}} \right\},\quad \left\{ {\mathbf{K}} \right\}\, = \,\left\{ {\begin{array}{*{20}{c}} {{{K}_{I}}} \\ {{{K}_{{II}}}} \\ {{{K}_{{III}}}} \end{array}} \right\},\quad \left[ {\mathbf{B}} \right]\, = \,\left( {\begin{array}{*{20}{c}} {\operatorname{Re} \left( {\frac{{\mu _{1}^{'}{{p}_{2}} - \mu _{2}^{'}{{p}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&{\operatorname{Re} \left( {\frac{{{{p}_{2}} - {{p}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&0 \\ {\operatorname{Re} \left( {\frac{{\mu _{1}^{'}{{q}_{2}} - \mu _{2}^{'}{{q}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&{\operatorname{Re} \left( {\frac{{{{q}_{2}} - {{q}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&0 \\ 0&0&{\frac{1}{{\sqrt {С_{{44}}^{'}С_{{55}}^{'} - С_{{45}}^{{'2}}} }}} \end{array}} \right)$

– матрица 3 × 3 взаимного влияния трех компонент вектора относительного смещения берегов трещины на три коэффициента интенсивности напряжений.

Результат обращения (3.5) позволяет вычислить КИН через перемещения берегов трещины в случае анизотропного материала [9, 14]:

(3.6)

$\{ {\mathbf{K}}\} = \sqrt {\frac{\pi }{{2r}}} {{[{\mathbf{B}}]}^{{ - 1}}}\{ {\mathbf{u}}\} ,$

где

(3.7)

$\begin{gathered} {{[{\mathbf{B}}]}^{{ - 1}}} = \left( {\begin{array}{*{20}{c}} {\frac{1}{{\det [{\mathbf{D}}]}}\operatorname{Re} \left( {\frac{{\mu _{1}^{'}{{p}_{2}} - \mu _{2}^{'}{{p}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&{\frac{1}{{\det [{\mathbf{D}}]}}\operatorname{Re} \left( { - \frac{{{{p}_{2}} - {{p}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&0 \\ {\frac{1}{{\det [{\mathbf{D}}]}}\operatorname{Re} \left( { - \frac{{\mu _{1}^{'}{{q}_{2}} - \mu _{2}^{'}{{q}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&{\frac{1}{{\det [{\mathbf{D}}]}}\operatorname{Re} \left( {\frac{{{{q}_{2}} - {{q}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&0 \\ 0&0&{\sqrt {С_{{44}}^{'}С_{{55}}^{'} - С_{{45}}^{{'2}}} } \end{array}} \right) \\ \det [{\mathbf{D}}] = \left| {\begin{array}{*{20}{c}} {\operatorname{Re} \left( {\frac{{\mu _{1}^{'}{{p}_{2}} - \mu _{2}^{'}{{p}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&{\operatorname{Re} \left( {\frac{{{{p}_{2}} - {{p}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)} \\ {\operatorname{Re} \left( {\frac{{\mu _{1}^{'}{{q}_{2}} - \mu _{2}^{'}{{q}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)}&{\operatorname{Re} \left( {\frac{{{{q}_{2}} - {{q}_{1}}}}{{\mu _{1}^{'} - \mu _{2}^{'}}}i} \right)} \end{array}} \right| \\ \end{gathered} $

Стоит отметить, что если система координат трещины не совпадает с осями анизотропии материала, то константы матрицы податливости и жесткости должны быть преобразованы в систему координат трещины и корни $\mu _{2}^{'}$, $\mu _{2}^{'}$ должны находиться из уравнения 4 степени с константами податливости в системе координат трещины. В случае поворота системы координат матрица перехода от одной системы координат к другой при повороте в плоскости на угол φ имеет вид: $Q = \left( {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \sin \varphi }&0 \\ {\sin \varphi }&{\cos \varphi }&0 \\ 0&0&1 \end{array}} \right)$ и формула преобразования элементов тензора податливости и жесткости 4 ранга из старой в новую систему координат имеет следующий вид:

(3.8)

$\begin{gathered} S_{{ijkl}}^{'} = {{Q}_{{im}}}{{Q}_{{jn}}}{{Q}_{{ko}}}{{Q}_{{lp}}}{{S}_{{mnop}}} \\ C_{{ijkl}}^{'} = {{Q}_{{im}}}{{Q}_{{jn}}}{{Q}_{{ko}}}{{Q}_{{lp}}}{{C}_{{mnop}}}, \\ \end{gathered} $

где ${{S}_{{mnop}}}$ – элементы тензора податливости в исходной системе координат, $S_{{ijkl}}^{'}$ – элементы тензора податливости в повернутой системе координат (трещины); ${{C}_{{mnop}}}$ – элементы тензора упругих модулей в исходной системе координат, $C_{{ijkl}}^{'}$ – элементы тензора упругих модулей в повернутой системе координат (трещины). При использовании формул (3.4) и (3.6) перемещения также нужно преобразовать из глобальной системы координат в систему координат, связанную с трещиной. Данные формулы были запрограммированы в конечно-элементном комплексе PANTOCRATOR [11].

При проведении расчетов относительное расстояние a/L от вершины трещины до границы варьировалось в пределах [1; 10.5], где L – длина трещины (a – абсолютное расстояние от вершины трещины до границы пластины), и принимало дискретные значения: a/L = 1, 2, 4, 6, 8, 10.5. Анизотропия предполагалась кубического типа, для описания которой необходимо задать 3 независимых упругих модуля. Отклонение от изотропии характеризовалось параметром ρ:

(3.9)

$\rho = \frac{E}{{2G}} - \nu ,$

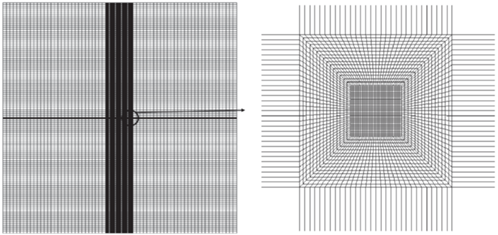
который для изотропного материала принимает значение $\rho = 1$. В расчетах для материала с кубической симметрией использовались значения $\rho = - 0.25$, $\rho = 5$ и $\rho = 10$. При проведении расчетов варьировалось значение G при фиксированных значениях упругих модулей E и $\nu $.

При выборе геометрических размеров пластины для задач с горизонтальной и наклонной трещиной обеспечивалось условие влияния на трещину близости только боковых границ, в то время как влиянием верхней и нижней границ можно было бы пренебречь в силу их значительного удаления от вершины трещины. На рис. 2 представлена конечно-элементная модель для задачи с горизонтальной трещиной для случая a = 4L. Число степеней свободы составляет 185 000. В расчетах использовались восьмиузловые изопараметрические конечные элементы с квадратичной аппроксимацией перемещений в пределах одного конечного элемента. В целях валидации полученных результатов проводилось сравнение полученного конечно-элементного решения для случая a = 10.5L с аналитическим решением для бесконечной пластины и производилось исследование практической сходимости численного решения на различных вложенных сетках для данной задачи на примере изотропного материала. При уменьшении числа степеней свободы в 2 раза результат меняется менее, чем на 1%.

Рис. 2.

Конечно-элементная модель пластины с горизонтальной трещиной (a = 4L, φ = 0°).

Для других размеров перемычки a конечно-элементная сетка вокруг вершины трещины не менялась, а менялись только размеры пластины. Разбиение увеличенных областей производилось пропорционально длине. Области оставались квадратными.

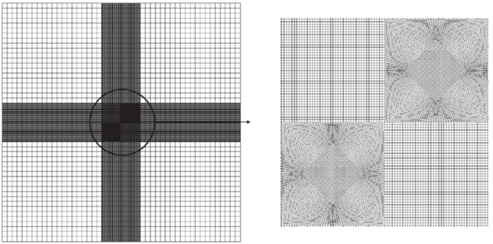
На рис. 3 показана конечно-элементная модель для задачи с наклонной трещиной для случая a = 4L, φ = 45°. Число степеней свободы составляет 126 000.

Рис. 3.

Конечно-элементная модель пластины с наклонной трещиной (a = 4L, φ = 45°).

Также проводилось исследование практической сходимости решения для данной конечно-элементной модели на примере изотропного материала. При уменьшении числа степеней свободы в 2 раза результат тоже меняется менее, чем на 1%.

В случае наклонной трещины расстояние от вершины трещины до верхнего края также оставалось равным расстоянию до верхней границы. При дальнейшем увеличении a область оставалась квадратной. Конечно-элементные модели фиксировались слева по оси x для исключения твердотельных перемещений.

В задаче с горизонтальной трещиной анализировалось влияние параметров ρ и a/L на ${{K}_{{\text{I}}}}$. В задаче с наклонной трещиной исследовалось влияние параметров ρ, a/L и φ на ${{K}_{{\text{I}}}}$ и ${{K}_{{{\text{II}}}}}$.

4. Результаты расчетов. На рис. 4 показана зависимость ${{K}_{{\text{I}}}}$ от размера перемычки a для задачи с горизонтальной трещиной (рис. 1а) для различных степеней отклонения кубической симметрии от изотропии ρ (3.10).

Рис. 4.

Зависимость нормированного значения ${{K}_{{\text{I}}}}$ от расстояния до края анизотропной пластины a для горизонтальной трещины φ = 0° (нормировано по отношению к значению ${{K}_{{\text{I}}}}$ для изотропного материала).

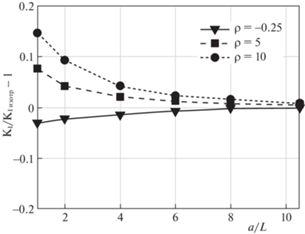
При значительном удалении трещины от края пластины (a/L > 8) наблюдается совпадение (с точностью до 1%) значений ${{K}_{{\text{I}}}}$ для анизотропных материалов с различной степенью анизотропии с прогнозом для изотропного материала. При приближении вершины трещины к границе (уменьшении отношения a/L) наблюдается прогрессирующий рост отличия прогнозов изотропного и анизотропного материалов. Приближение трещины к границе пластины пробуждает влияние анизотропии упругих свойств на КИН. При ρ > 1 (G > G_{изотроп}) наблюдается увеличение ${{K}_{I}}$ для анизотропного материала в сравнении с изотропным, а при ρ < 1 (G < G_{изотроп}) наблюдается уменьшение ${{K}_{{\text{I}}}}$ для анизотропного материала в сравнении с изотропным случаем.

На рис. 5 показана зависимость ${{K}_{{\text{I}}}}$ от a для задачи с наклонной трещиной (рис. 1б) для различных степеней отклонения кубической симметрии от изотропии ρ, определяемых уравнением (3.9).

Рис. 5.

Зависимость нормированного значения ${{K}_{{\text{I}}}}$ от расстояния до края анизотропной пластины a для наклонной трещины φ = 45° (нормировано по отношению к значению ${{K}_{{\text{I}}}}$ для изотропного материала).

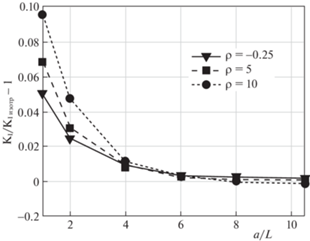
Аналогично случаю горизонтальной трещины при значительном удалении наклонной трещины от края пластины (a/L > 8) наблюдается совпадение (с точностью до 1%) значений ${{K}_{{\text{I}}}}$ для анизотропных материалов с прогнозом для изотропного материала. Аналогично при приближении вершины наклонной трещины к границе пластины (уменьшении отношения a/L) наблюдается прогрессирующий рост отличия прогнозов изотропного и анизотропного материалов. В рассматриваемом случае наклонной трещины также наблюдается эффект усиления влияния анизотропии упругих свойств на КИН при приближении трещины к границе пластины. В отличии от случая горизонтальной трещины и при ρ > 1 (G > G_{изотроп}), и при ρ < 1 (G < G_{изотроп}) для наклонной трещины наблюдается увеличение ${{K}_{{\text{I}}}}$ для анизотропного материала в сравнении с изотропным случаем.

На рис. 6 показана зависимость ${{K}_{{{\text{II}}}}}$ от размера перемычки a для задачи с наклонной трещиной для степеней отклонения кубической симметрии от изотропии ρ.

Рис. 6.

Зависимость нормированного значения ${{K}_{{{\text{II}}}}}$ от расстояния до края анизотропной пластины для наклонной трещины φ = 45° (нормировано по отношению к значению ${{K}_{{{\text{II}}}}}$ для изотропного материала).

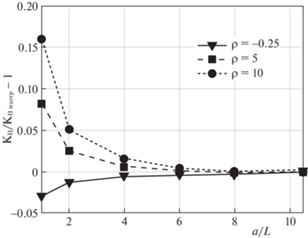
Для ${{K}_{{{\text{II}}}}}$ при значительном удалении наклонной трещины от края пластины (a/L > 8) также наблюдается совпадение (с точностью до 1%) значений КИН для анизотропных и изотропных материалов. При приближении вершины наклонной трещины к границе пластины (уменьшении отношения a/L) наблюдается прогрессирующий рост отличия ${{K}_{{{\text{II}}}}}$ для изотропного и анизотропного материалов. При ρ > 1 (G > G_{изотроп}) наблюдается увеличение ${{K}_{{II}}}$ для анизотропного материала в сравнении с изотропным, а при ρ < 1 (G < G_{изотроп}) наблюдается уменьшение ${{K}_{{II}}}$ для анизотропного материала в сравнении с изотропным случаем.

При удалении трещины от границы эффект влияния анизотропии исчезает. КИН для изотропного и анизотропного материалов для бесконечной пластины совпадают [4]. В таблице 1 представлены результаты сравнения отличий численных решений для КИН при максимальном моделируемом удалении a = 10.5L от аналитического решения (1.1) для бесконечной пластины [4] для всех рассмотренных вариантов ориентации трещины и значений параметра степени анизотропии $\rho = - 0.25$, $\rho = 5$ и $\rho = 10$.

Таблица 1.

Отличие расчетных КИН при a/L = 10.5 от аналитического решения (1.1) для бесконечной пластины

	$\rho = - 0.25$	$\rho = 5$	$\rho = 10$
Погрешность для K_I в задаче с горизонтальной трещиной	0.8%	0.5%	0.08%
Погрешность для K_I в задаче с наклонной трещиной	0.2%	0.4%	0.5%
Погрешность для K_II в задаче с наклонной трещиной	0.5%	0.5%	0.4%

Во всех случаях погрешность вычисления КИН по сравнению с аналитическим решением составляет меньше 1%.

Заключение. На основе проведенных вычислительных экспериментов установлен эффект возрастания влияния анизотропии упругих свойств на значения КИН при приближении вершины трещины к границе пластины. При значительном удалении вершины трещины от края пластины (a/L > 8) КИН для анизотропного материала (с точностью до 2%) совпадает с КИН для изотропного материала. При меньших расстояниях (a/L < 8) анизотропию материала рекомендуется учитывать.

Результаты конечно-элементного моделирования показали, что для трещин различных ориентаций (различных мод разрушения) с уменьшением расстояния между вершиной трещины и границей пластины наблюдается прогрессирующее усиление влияния анизотропии материала на значения КИН. Отличия в прогнозах КИН для изотропного материала и материала с кубической симметрией превышают 15% для рассматриваемых в расчетах констант материала и случаев нагружения.

Эффект возрастания влияния анизотропии упругих свойств на значения КИН при приближении трещины к границе пластины усиливается с ростом степени анизотропии.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № 0784-2020-0027).

Список литературы

Мураками Ю., Аоки С., Хасебе Н. и др. Справочник по коэффициентам интенсивности напряжений. В 2-х тт. Т. 1. М.: Мир, 1990. 488 с.
Морозов Н.Ф. Математические вопросы теории трещин. М.: Наука. ГРФМЛ, 1984. 174 с.
Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 416 с.
Sih G.C., Paris P.C., Irwin G.R. On cracks in rectilinearly anisotropic bodies // Int. J. Fracture Mech. 1965. № 1. P. 189–203.
Kachanov M., Shafiro B., Tsukrov I. Handbook of Elasticity Solutions. Boston: Springer, 2003. 330 p.
Banks-Sills L., Hershkovitz I., Wawrzynek P.A. et al. Methods for calculating stress intensity factors in anisotropic materials: Part I – z = 0 is a symmetric plane // Engng. Fracture Mech. 2005. V. 72. P. 2328–2358.
Yu H., Kuna M. Interaction integral method for computation of crack parameters K-T – a review // Eng. Fract. Mech. 2021. № 249. P. 107722.
Ozkan U., Nied H.F., Kaya A.C. Fracture analysis of anisotropic materials using enriched crack tip elements // Engng. Fracture Mech. 2010. V. 77. P. 1191–1202.
Ranjan S., Arakere N.K. A Fracture-mechanics-based methodology for fatigue life prediction of single crystal nickel-based superalloys // J. Eng. Gas Turbines Power. 2008. V. 130.
Морозов Н.Ф., Семенов Б.Н., Товстик П.Е. Об оценке уровня работоспособности растягиваемой пластины, ослабленной поперечной трещиной // Вестн. СПбГУ. Математика. Механика. Астрономия. 2019. Т. 6(64). С. 338–346.
Семенов А.С. PANTOCRATOR – конечно-элементный программный комплекс, ориентированный на решение нелинейных задач механики // Тр. V-й Межд. конф. “Научно-технические проблемы прогнозирования надежности и долговечности конструкций”. СПб.: СПбГПУ, 2003. С. 466–480.
Качанов Л.М. Основы механики разрушения. М.: Наука. 1974. С. 223–226.
Judt P.O., Ricoeur A., Linek G. Crack path prediction in rolled aluminum plates with fracture toughness orthotropy and experimental validation // Engng. Fracture Mech. 2015. V. 138. P. 33–48.
Семенов А.С., Семенов С.Г., Гецов Л.Б. Методы расчетного определения скорости роста трещин усталости, ползучести и термоусталости в поли- и монокристаллических лопатках ГТУ // Пробл. прочн. 2015. № 2. С. 61–87.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал