Прикладная математика и механика, 2022, T. 86, № 5, стр. 741-752
Автомодельные несимметричные течения вязкого газа в клине
М. А. Брутян 1, 2, *, У. Г. Ибрагимов 2, **
1 Центральный аэрогидродинамический институт им. Н.Е. Жуковского
Жуковский, Россия
2 Московский физико-технический институт
Долгопрудный, Россия
* E-mail: murad.brutyan@tsagi.ru
** E-mail: umar.ibragimov@phystech.edu
Поступила в редакцию 29.03.2022
После доработки 01.07.2022
Принята к публикации 05.07.2022
- EDN: SNSQPS
- DOI: 10.31857/S003282352205006X
Аннотация
Рассматривается течение вязкого сжимаемого газа, истекающего из вершины плоского клина. Показано, что несимметричное автомодельное течение возможно и реализуется при задании специальных граничных условий на температуру стенок канала. Для случая малых дозвуковых скоростей течений газа при постоянной, но различной температуре стенок клина, найдено асимптотическое решение. В общем случае полученная система обыкновенных дифференциальных уравнений решается численно.
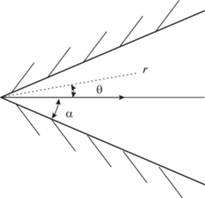
1. Введение. Известное точное решение Джеффри–Гамеля уравнений Навье–Стокса для случая течения вязкой несжимаемой жидкости описывает автомодельное течение в плоском клиновидном диффузоре от источника/стока, расположенного в вершине клина [1, 2]. В случае конфузорного течения (сток), решение существует при любых числах Рейнольдса $\operatorname{Re} $, произвольном угле раствора клина $2\alpha < \pi $ и является симметричным относительно плоскости θ = 0, рис. 1. В случае диффузорного течения профиль скорости в поперечном направлении, при достижении некоторого критического числа $\operatorname{Re} = {{\operatorname{Re} }_{{\max }}}$, оказывается немонотонным. При увеличении числа $\operatorname{Re} > {{\operatorname{Re} }_{{\max }}}$ возникают области возвратного течения, и профиль скорости может стать несимметричным. При дальнейшем увеличении $\operatorname{Re} $ возникает симметричное решение с одним минимумом и двумя максимумами скорости. Во всех этих решениях имеются чередующиеся области вытекающей и втекающей жидкости. При $\operatorname{Re} \to \infty $ наблюдается увеличение числа локальных минимумов и максимумов, поэтому определенного предельного решения не существует, что, по всей видимости, связано с тем, что при увеличении $\operatorname{Re} $ стационарное диффузорное течение описанного типа вскоре после достижения некоторого критического значения делается неустойчивым и в действительности возникает нестационарное турбулентное движение [3].
Для несжимаемых течений в работе [4] дано описание широкого класса известных и новых точных решений уравнений Навье–Стокса, в частности известного решения Джеффри–Гамеля для течения вязкой несжимаемой жидкости в плоском диффузоре.
Вопросам возможности построения автомодельных течений типа Джеффри–Гамеля для течения вязкого сжимаемого газа посвящены работы [5–13]. В [5] рассмотрена задача о течении вязкого газа в коническом диффузоре с граничными условиями проскальзывания на стенках. В [6, 7] также рассмотрена задача о течении газа в коническом диффузоре с наличием внутри потока внутреннего объемного источника/стока энергии. Другие автомодельные осесимметричные решения уравнений Навье–Стокса для течений вязкого газа получены в работах [8, 9].
В работах [10, 11] рассмотрен класс автомодельных решений для течения газа в плоском клине. При этом в [10] рассмотрено течение газа твердых сфер и максвелловских молекул, для которых коэффициент динамической вязкости $\eta \sim {{T}^{{0.5}}}$ и $\eta \sim T$ соответственно. В работе [11] найдено аналитическое решение для произвольной степенной зависимости коэффициентов переноса от температуры $\eta \sim {{T}^{k}}$ (закон Фроста). В работе [12] рассмотрено аналогичное автомодельное течение вязкого сжимаемого газа от струи (источника импульса), истекающей в область между двумя расходящимися стенками. Точное решение уравнений Навье–Стокса для течений Куэтта и Пуазейля горячего газа с коэффициентом вязкости, зависящим от температуры по закону Сазерленда, получено в работах [13, 14].
В недавней работе [15] установлено, что автомодельное решение существует и для течения вязкого газа, у которого коэффициенты переноса зависят от температуры произвольным образом, $\eta = \eta (T)$. Во всех выше перечисленных работах, посвященных автомодельным течениям вязкого газа, рассмотрены исключительно симметричные режимы течения.
В настоящей работе аналитически и численно изучается возможность построения автомодельных несимметричных решений типа Джеффри–Гамеля для течений вязкого сжимаемого теплопроводного газа в плоском диффузоре.
2. Автомодельные течения типа Джеффри–Гамеля. Рассмотрим течение вязкого газа, истекающего из вершины плоского клина при различной температуре стенок $T_{w}^{ + }$ и $T_{w}^{ - }$, рис. 1.
Уравнения Навье–Стокса в полярных координатах (r, θ) (рис. 1), записанные в безразмерных переменных, имеют вид [16]:
(2.2)
$\rho u\frac{{\partial u}}{{\partial r}} = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{rr}}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{r\theta }}}}}{{\partial \theta }} - \frac{{{{\sigma }_{{\theta \theta }}}}}{r}} \right]$(2.3)
$0 = - \frac{1}{r}\frac{{\partial p}}{{\partial \theta }} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{r\theta }}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{\theta \theta }}}}}{{\partial \theta }} + \frac{{{{\sigma }_{{r\theta }}}}}{r}} \right]$(2.4)
$\begin{gathered} \frac{{\rho u}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}}}\frac{{\partial T}}{{\partial r}} = u\frac{{\partial p}}{{\partial r}} + \frac{{\nabla \cdot \left( {\varkappa \nabla T} \right)}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr {{{\operatorname{Re} }}_{0}}}} + \\ + \;\frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {2\eta \left( {\varepsilon _{{rr}}^{2} + \varepsilon _{{\theta \theta }}^{2}} \right) + 4\eta \varepsilon _{{r\theta }}^{2} - \frac{2}{3}\eta {{{\left( {\nabla \cdot {\mathbf{V}}} \right)}}^{2}}} \right] \\ \end{gathered} $Течение предполагается радиальным, ${\mathbf{V}} = (u,\,0)$. Компоненты тензора вязких напряжений ${\mathbf{\sigma }}$ и тензора скоростей деформации ${\mathbf{\varepsilon }}$ имеют вид:
В уравнениях (2.1)–(2.4) безразмерные переменные связанны с размерными газодинамическими параметрами, помеченными звездочкой, следующим образом:
В уравнении энергии (2.4) учтены члены, отвечающие за диссипацию энергии вследствие влияния вязкости. Как будет показано ниже, при умеренных числах ${{{\text{M}}}_{0}}$ число Рейнольдса в автомодельном решении оказывается небольшим, т.е. вязкость и диссипация энергии оказывает влияние на все поле течения внутри клина.
Автомодельное решение уравнений (2.1)–(2.4) ищем в виде:
(2.5)
$u = \frac{{u(\theta )}}{{{{r}^{m}}}},\quad \rho = {{r}^{{m - 1}}}\rho (\theta ),\quad p = \frac{{p(\theta )}}{{{{r}^{{m + 1}}}}},\quad T = \frac{{T(\theta )}}{{{{r}^{{2m}}}}},\quad \eta = {{\left( {\frac{{T(\theta )}}{{{{r}^{{2m}}}}}} \right)}^{k}},\quad \varkappa = {{\left( {\frac{{T(\theta )}}{{{{r}^{{2m}}}}}} \right)}^{k}}$Показатель m назовем параметром автомодельности. Как было показано ранее в работах [9–11], для существования плоских автомодельных решений необходимо выполнение следующего условия:
Вопрос существования автомодельных решений при k = 0 и различных значениях m в зависимости от определяющих параметров задачи для случая симметричных плоских течений исследован в работе [9]. Течения газа при m ≠ 0 оказываются более сложными для исследования. Решение в этом случае сводится к анализу системы нелинейных дифференциальных уравнений с заранее неизвестным параметром автомодельности $m$, который должен определяться в процессе численного решения задачи.
В настоящей работе рассматривается иной случай, а именно $k \ne 0$, $m = 0$. В [15] установлено, что в этом случае автомодельное решение может быть построено при произвольной зависимости коэффициентов переноса от температуры. Ниже при изучении несимметричных решений для определенности предполагается степенная зависимость, $\eta \sim {{T}^{k}}$.
3. Автомодельное течение газа в клине при различной температуре стенок. Для получения несимметричных решений температуру стенок клина будем считать различной, но постоянной. Подставляя (2.5) в (2.1)–(2.4) легко убедиться, что уравнение неразрывности (2.1) выполняется автоматически, а уравнения (2.2)–(2.4) можно переписать в виде следующей системы обыкновенных дифференциальных уравнений (ОДУ):
(3.1)
${{\operatorname{Re} }_{0}}p - \frac{4}{3}u\eta + \frac{d}{{d\theta }}\left( {\eta \frac{{du}}{{d\theta }}} \right) = 0$(3.2)
${{\operatorname{Re} }_{0}}\frac{{dp}}{{d\theta }} = \eta \frac{{du}}{{d\theta }} + \frac{4}{3}\frac{d}{{d\theta }}\left( {\eta u} \right)$(3.3)
${{\operatorname{Re} }_{0}}up = \frac{1}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr }}\frac{d}{{d\theta }}\left( {\eta \frac{{dT}}{{d\theta }}} \right) + \eta \left[ {\frac{4}{3}{{u}^{2}} + {{{\left( {\frac{{du}}{{d\theta }}} \right)}}^{2}}} \right]$Из условия нормировки для параметров течения на оси клина при $\theta = 0$ имеем:
Продифференцируем уравнение (3.1) один раз по $\theta $ и вычтем из (3.2). В результате получим следующее уравнение:
Используя условия нормировки (3.4) находим связь между константой $a$ и числами ${{{\text{M}}}_{0}}$ и ${{\operatorname{Re} }_{0}}$:
Подставим (3.5) и (3.6) в уравнение энергии (3.3) и проинтегрируем один раз по $\theta $. В результате получим следующее выражение:
(3.7)
$\frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + \eta u\frac{{du}}{{d\theta }} = Q,$Используя полученное выражение (3.7) можно определить удельный тепловой поток через стенки канала в азимутальном направлении:
(3.8)
${{\left. {q_{\theta }^{*} = - \frac{{\kappa {\text{*}}}}{{r{\text{*}}}}\frac{{dT{\text{*}}}}{{d\theta }}} \right|}_{{\theta = \pm \alpha }}}$Введем безразмерный тепловой поток ${{q}_{\theta }} = q_{\theta }^{*}{{r}_{0}}{\text{/}}{{\kappa }_{0}}{{T}_{0}}$ и перепишем (3.8) в следующей форме:
Тогда используя (3.7) и учитывая, что в безразмерных переменных $\eta = \kappa $, получаем:
где ${{{\mathbf{e}}}_{\theta }}$ – единичный вектор в азимутальном направлении. Из полученного соотношения (3.9) видно, что константа Q пропорциональна величине теплового потока через стенки клина. Из (3.9) также следует, что абсолютная величина теплового потока через нижнюю и верхнюю стенки клина одинакова. При этом если $Q > 0$, то к верхней стенке подводится тепло, а от нижней стенки тепло отводится.Равенство по модулю величин тепловых потоков через стенки клина объясняется тем, что в автомодельном течении поток энергии в радиальном направлении отсутствует, так как при $m = 0$ температура, как это следует из (2.5), не зависит от $r$, $T = T(\theta )$. Таким образом, в полученном решении перенос тепловой энергии наблюдается только в азимутальном направлении. Заметим, что поскольку в азимутальном направлении отсутствует перенос иного вида энергии, то равенство тепловых потоков обусловлено законом сохранения энергии.
4. Аналитическое решение для случая малых дозвуковых скоростей течения газа в клине. Введем безразмерный параметр $\chi = {\text{M}}_{0}^{2}\Pr \left( {\gamma - 1} \right)$ и рассмотрим предельный случай $\chi \ll 1$, соответствующий малым дозвуковым скоростям течения газа в клине. Очевидно, что решение задачи зависит от величины теплового потока Q. Для получения наглядного результата по влиянию разницы температур стенок клина на симметрию решения, рассмотрим случай сильного теплового потока, $Q\sim {\text{1/}}\chi \gg 1$.
Решение уравнений (3.5), (3.7) будем искать в виде степенных рядов по малому параметру $\chi $
Далее будем предполагать, что производные $du{\text{/}}d\theta $ и $dT{\text{/}}d\theta $ ограничены всюду в области течения. Тогда в нулевом приближении получаем следующую систему уравнений:
где ${\rm X} = Q\chi \sim O(1)$. При заданной зависимости ${{\eta }^{0}} = {{\eta }^{0}}\left( {{{T}^{0}}} \right)$ решение уравнения (4.2) с учетом условий нормировки (3.4) принимает вид:(4.3)
${\rm N}\left( {{{T}^{0}}} \right) = \theta {\rm X},\quad {\rm N}\left( {{{T}^{0}}} \right) = \int\limits_1^{{{T}^{0}}} {{{\eta }^{0}}\left( T \right)dT} $Откуда видно, что температура $T_{w}^{ + }$, $T_{w}^{ - }$ на стенках клина, полуугол раствора $\alpha $ и тепловой поток ${\rm X}$ в нулевом приближении связаны соотношениями:
Из уравнений (4.1) и (4.2) с учетом соотношений (4.3) получаем следующее дифференциальное уравнение:
Значения констант $a$ и $b$ определяются из граничных условий прилипания скорости на стенках клина. Используя значения температур на стенках $T_{w}^{ + }$, $T_{w}^{ - }$ данные условия можно записать в виде:
Рассмотрим случай степенной зависимости ${{\eta }^{0}} = {{\left( {{{T}^{0}}} \right)}^{k}}$. Тогда интеграл (4.3) принимает вид:
(4.4)
${{T}^{0}} = {{\left( {1 + \left( {k + 1} \right){\rm X}\theta } \right)}^{{^{{\frac{1}{{k + 1}}}}}}}$Используя данное выражение можно найти решение уравнения (4.1) в квадратурах:
(4.5)
${{u}^{0}}(\theta ) = a\int\limits_0^\theta {\frac{{\sin \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } + b\int\limits_0^\theta {\frac{{\cos \Theta }}{{{{{\left( {1 + \left( {k + 1} \right){\rm X}\Theta } \right)}}^{{\frac{k}{{k + 1}}}}}}}d\Theta } + 1$Здесь учтены условия нормировки (4.3). Константы a и b определяются из следующих соотношений:
В частном случае модели газа сверхтвердых частиц ($k = 0$) решения (4.4), (4.5) принимают простую форму:
(4.6)
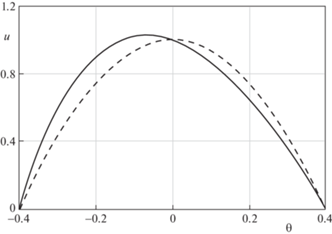
${{T}^{0}} = 1 + {\rm X}\theta ,\quad {{u}^{0}} = \frac{{\cos \alpha - \cos \theta }}{{\cos \alpha - 1}},$Сравнение симметричного (4.6) и несимметричного профиля скорости в нулевом приближении для течения одноатомного газа максвелловских молекул ($k = 1$) [21] в клине с углом полураствора $\alpha = 0.4$ рад при ${\rm X} = 1$ показано на рис. 2.
Рис. 2.
Сравнение автомодельных решений; сплошная линия – несимметричный профиль скорости, штриховая линия – симметричный профиль скорости.
5. Численное исследование несимметричных решений при различных числах Маха течения газа на оси клина. При произвольном числе Маха система уравнений (3.5), (3.7) не поддается аналитическому рассмотрению, поэтому для получения решений требуется численное исследование задачи. Для удобства и простоты процедуры численного расчета вместо решения краевой задачи с заданными параметрами (угол $\alpha $, температура стенок $T_{w}^{ + }$, $T_{w}^{ - }$ и числа ${{{\text{M}}}_{0}}$, ${{\operatorname{Re} }_{0}}$), решается задача Коши с начальными условиями на оси клина для скорости $u(0) = 1$ и температуры $T(0) = 1$ в областях $\theta > 0$ и $\theta < 0$; при этом значения чисел ${{{\text{M}}}_{0}}$, ${\text{R}}{{{\text{e}}}_{0}}$ и Q считаются заданными. В ходе численного интегрирования угол раствора клина $2\alpha $ находится из условия равенства нулю скорости на стенках канала: $u(\theta _{w}^{ + }) = u(\theta _{w}^{ - }) = 0$, $2\alpha = \theta _{w}^{ + } - \theta _{w}^{ - }$, где $\theta _{w}^{ + }$, $\theta _{w}^{ - }$ – значение азимутальной координаты на верхней и нижней стенках соответственно. Температура стенок определяется в результате численного интегрирования при заданном значении теплового потока Q, $T_{w}^{ \pm } = T(\theta _{w}^{ \pm })$.
Ниже приведены результаты численных расчетов для течения одноатомного гелия $\gamma = 5{\text{/}}3$, $\Pr = 2{\text{/}}3$ при $k = 1$. Сравнение профилей скорости и температуры при ${{{\text{M}}}_{0}} = 1.5$, ${{\operatorname{Re} }_{0}} = 1000$ для $Q = 8$ в несимметричном случае и $Q = 0$ в симметричном случае, представлено на рис. 3 и рис. 4. Отметим, что заметное отличие от симметрии течения проявляется при достаточно большом перепаде температур на стенках канала.
Рис. 3.
Профили скорости; сплошная линия – симметричный профиль, штриховая линия – несимметричный профиль.
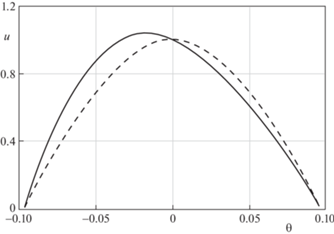
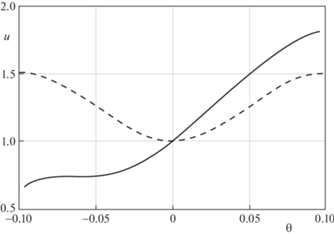
Рис. 4.
Профили температуры; сплошная линия – симметричный профиль, штриховая линия – несимметричный профиль.
На основании проведенных систематических расчетов можно сделать вывод, что автомодельное несимметричное течение существует лишь в ограниченном диапазоне значений Q. Оказывается, что при некотором предельном значении ${{Q}_{{\max }}}$ температура на одной из стенок клина обращается в ноль. Зависимость величины Xmax = = ${{Q}_{{\max }}}{\text{M}}_{0}^{2}\Pr (\gamma - 1)$, которая пропорциональна безразмерному тепловому потоку через стенки клина, от числа Маха на оси ${{{\text{M}}}_{0}}$ показана на рис. 5 при различных углах раствора клина $2\alpha = 0.2$ рад, $2\alpha = 0.4$ рад и $2\alpha = 0.6$ рад.
Рис. 5.
Зависимость ${{{\rm X}}_{{\max }}}$ от ${{{\text{M}}}_{0}}$; 1 – $\alpha \approx 0.1$ рад, 2 – $\alpha \approx 0.2$ рад, 3 – $\alpha \approx 0.3$ рад.
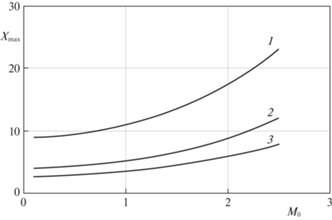
Как видно из данного рисунка, при увеличении ${{{\text{M}}}_{0}}$ максимально возможный тепловой поток увеличивается. Это объясняется тем, что по мере увеличения ${{{\text{M}}}_{0}}$ температура на одной из стенок канала увеличивается, а следовательно растет перепад температур. При увеличении угла раствора клина перепад температур уменьшается.
Заключение. В рамках уравнений Навье–Стокса установлена возможность построения несимметричных точных решений типа Джеффри–Гамеля для течения вязкого сжимаемого газа в плоском клине. Для степенной зависимости коэффициентов переноса от температуры показано, что несимметричное автомодельное течение реализуется при различной температуре нижней и верхней стенок клина. В полученном решении перенос тепловой энергии имеет место только в азимутальном направлении, причем суммарный тепловой поток через стенки клина оказывается равным нулю. Для случая малых дозвуковых скоростей течений газа найдено аналитическое решение.
Полученное решение имеет весьма специальный вид: скорость течения оказывается радиальной и постоянной на линиях тока θ = const, температура также постоянна на линиях тока, а плотность и давление убывают обратно пропорционально расстоянию от вершины клина. Подобное поведение решения наблюдалось ранее в работах [10, 11, 15] при построении автомодельных решений стационарных уравнений Навье–Стокса вязкого теплопроводного газа для источника массы и в работе [12] для источника импульса.
Известно [22], что автомодельные решения описывают не только поведение физических систем в некоторых частных условиях, но и промежуточно-асимптотическое поведение решений более широких классов задач в той области, где эти решения перестают зависеть от деталей начальных и (или) граничных условий, но система еще далека от предельного состояния. Это означает, что полученное решение описывает не только физически нереализуемое поле течения от точечного источника, истекающего в бесконечное пространство. Оно описывает также и реальное поле течения, возникающее в конечной области размером $D$, если истечение с заданным расходом происходит не из точки, а из конечной области $d \ll D$. При этом автомодельное решение будет справедливым на расстояниях много больших $d$, и вместе с тем, много меньших $D$.
Список литературы
Jeffery G.B.L. The two-dimensional steady motion of a viscous fluid // The London, Edinburgh&Dublin Phil. Mag.&J. of Sci. 1915. V. 29.172. P. 455–465.
Hamel G. Spiralförmige Bewegungen zäher Flüssigkeiten // Jahresbericht der Deutschen Mathematiker-Vereinigung. 1917. V. 25. P. 34–60.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 735 с.
Аристов С.Н., Князев Д.В., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных // Теорет. основы хим. технол. 2009. Т. 43. № 5. С. 547–566.
Williams J.C. III. Conical nozzle flow with velocity slip and temperature jump // AIAA J. 1967. V. 5. № 12. P. 2128–2134.
Williams J.C. III. Diabatic internal source flow // Appl. Sci. Res. 1967. V. 17. P. 407–421.
Williams J.C. III. Conical nozzle flow of a viscous compressible gas with energy extraction // Appl. Sci. Res. 1968. V. 19. P. 285–301.
Брутян М.А., Ибрагимов У.Г. Автомодельные течения вязкого газа, истекающего из вершины конуса // Уч. зап. ЦАГИ. 2018. Т. XLIX. № 3. С. 26–35.
Брутян М.А., Ибрагимов У.Г. Влияние параметра автомодельности на критические характеристики сжимаемого течения типа Гамеля // Тр. МАИ. 2018. Вып. 100. http://trudymai.ru/published.php?ID=93319
Быркин А.П. Об одном точном решении уравнений Навье–Стокса для сжимаемого газа // ПММ. 1969. Т. 33. № 1. С. 152–157.
Брутян М.А. Автомодельные решения типа Джеффери–Гамеля для течения вязкого сжимаемого газа // Уч. зап. ЦАГИ. 2017. Т. XLVIII. № 6. С. 13–22.
Брутян М.А., Крапивский П.Л. Точные решения стационарных уравнений Навье–Стокса вязкого теплопроводного газа для плоской струи из линейного источника // ПММ. 2018. Т. 82. № 5. С. 644–656.
Голубкин В.Н., Сизых Г.Б. О сжимаемом течении Куэтта // Уч. зап. ЦАГИ. 2018. Вып. 49. № 1. С. 27–38.
Хорин А.Н., Конюхова А.А. Течение Куэтта горячего вязкого газа // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Вып. 24. № 2. С. 365–378.
Брутян М.А., Ибрагимов У.Г. Автомодельные течения вязкого газа в плоском канале при произвольной зависимости коэффициентов переноса от температуры // ПММ. 2021. Т. 85. № 6. С. 755–764.
Probstein R.F., Kemp N.H. Viscous aerodynamic characteristics in hypersonic rarefied gas flow // J. Aerosp. Sci. 1960. V. 27. № 3. P. 174–192.
Ферцигер Дж., Капер Г. Математическая теория процессов переноса в газах. М.: Мир, 1976.
Ernst M.N. Nonlinear model-Boltzmann equations and exact solutions // Phys. Rev. 1981. V. 78. № 1. P. 1–171.
Ernst M.N. Exact solutions of nonlinear Boltzmann equation // J. Stat. Phys. 1984. V. 34. № 516. P. 1001–1017.
Бобылев А.В. Точные решения нелинейного уравнения Больцмана и теория релаксации максвелловского газа // ТМФ. 1984. Т. 60. № 2. С. 280–310.
Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Наука, Гл. ред. физ.-мат. лит., 1979. Т. 10.
Баренблатт Г.И. Подобие, автомодельность, промежуточная асимптотика. Л.: Гидрометеоиздат, 1982. 255 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика