Прикладная математика и механика, 2022, T. 86, № 5, стр. 724-740
Моделирование истечения сыпучего тела из емкости с учетом эффекта сцепления со стенкой
Т. Р. Аманбаев 1, 2, *, С. Д. Энтони 3, **
1 Южно-Казахстанский государственный университет им. М. Ауэзова
Шымкент, Казахстан
2 Институт математики и математического моделирования
Алматы, Казахстан
3 Школа химической и технологической инженерии, Университет Лидса
LS2 9JT Лидс, Великобритания
* E-mail: tulegen_amanbaev@mail.ru
** E-mail: s.j.antony@leeds.ac.uk
Поступила в редакцию 08.11.2021
После доработки 26.05.2022
Принята к публикации 10.06.2022
- EDN: EQFUNM
- DOI: 10.31857/S0032823522050022
Аннотация
В рамках подхода, основанного на уравнении вязкой жидкости как непрерывной среды (НС), изучен процесс истечения сыпучей среды под действием силы тяжести из объема между двумя пластинами, наклоненными друг к другу под некоторым углом. На границе с твердой стенкой принимается условие частичного скольжения (или сцепления), описываемое с помощью некоторого коэффициента, который меняется от 0 до 1. В двумерной постановке найдено распределение скорости движения среды внутри емкости. Проанализировано влияние изменения коэффициента скольжения на характер течения сыпучей среды. Проведено сравнение подхода НС, и подхода, основанного на описании гранулированной среды как дискретных слоев (ДС). Приведены формулы для скорости и расхода сыпучего тела на выходе из емкости. Проанализированы зависимости указанных параметров от коэффициента внутреннего трения и угла раствора между пластинами.
1. Введение. В настоящее время в порошковой технологии нашли широкое применение аппараты дозирования, сушки, смешения и т.п. гранулированных сред [1–3]. Для дальнейшего усовершенствования этих устройств необходимо создание математических моделей процессов, происходящих в них [4, 5]. Для описания течения сыпучей среды используются различные подходы, основными из которых являются дискретный и непрерывный подходы. В дискретном подходе изучается поведение каждой индивидуальной частицы сыпучей среды в отдельности. Здесь воспользуемся непрерывным подходом, где гранулированная среда рассматривается как непрерывная (сплошная) среда. Обычно движение плотного слоя сыпучей среды условно разделяют на два режима: квазистатический, соответствующий малым скоростям сдвига, который описывается в рамках теории предельного равновесия [6], и инерционный, отвечающий большим скоростям сдвига [7]. При инерционном режиме движения внутренние напряжения в среде возникают вследствие переноса импульса гранулами, аналогично тому, как это происходит при хаотическом движении молекул в жидкости. Описание этого режима течения основывается, как правило, на законах сохранения массы и импульса. Существуют также методы описания движения сыпучей среды, основанные на ее дискретном представлении [8–11].
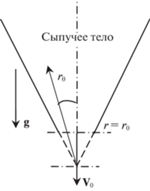
2. Постановка и решение задачи в рамках подхода НС. Рассмотрим процесс истечения несвязной (эффект когезии не учитывается) гранулированной среды под действием силы тяжести из объема между наклоненными друг к другу под некоторым углом двух плоскостей через нижнее выпускное отверстие (рис. 1). При этом допустим, что высота сыпучего тела намного больше, а частицы намного меньше размеров выпускного отверстия. Для описания этого процесса воспользуемся уравнениями движения НС как вязкой несжимаемой жидкости (уравнения Навье–Стокса), записанными в цилиндрической системе координат r, θ, z (ось z направлена перпендикулярно к плоскости рис. 1). Рассмотрим стационарный процесс движения НС вдоль радиальной координаты. Таким образом, имеем
(2.1)
$\frac{\partial }{{\partial t}} \equiv 0,\quad \frac{\partial }{{\partial z}} \equiv 0,\quad \rho = {\text{const}},\quad {{{v}}_{\theta }} = 0,\quad {{{v}}_{z}} = 0,\quad {{{v}}_{r}} = {v}(r,\theta ),$(2.2)
${v}\frac{{\partial {v}}}{{\partial r}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial r}} + \eta \left( {\frac{{{{\partial }^{2}}{v}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {v}}}{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{v}}}{{\partial {{\theta }^{2}}}} - \frac{{v}}{{{{r}^{2}}}}} \right) + {{F}_{r}}$(2.3)
$0 = - \frac{1}{{\rho r}}\frac{{\partial p}}{{\partial \theta }} + \eta \left( {\frac{2}{{{{r}^{2}}}}\frac{{\partial {v}}}{{\partial \theta }}} \right) + {{F}_{\theta }}$Здесь p, η – давление и “кинематическая вязкость” (которая в ходе дальнейших преобразований выпадает из уравнений) среды, $g$ – ускорение силы тяжести, ${{F}_{r}}$, ${{F}_{\theta }}$ – компоненты вектора силы тяжести по координатам r, $\theta $ соответственно. Уравнения (2.2), (2.3) это уравнения сохранения импульса, уравнение (2.4) – уравнение несжимаемости. Из (2.4) сразу следует
где $\psi \left( \theta \right)$ – неизвестная функция. Далее пренебрежем нелинейным членом в левой части уравнения (2.2), считая, что в основной зоне емкости скорость течения достаточно мала. Кроме того, исключим давление из уравнений. Для этого уравнение (2.2) продифференцируем по $\theta $, а уравнение (2.3) после умножения обеих его частей на r – по r, и вычтем полученные уравнения друг из друга. В результате придем к уравнению, где отсутствуют давление и сила тяжести (считается, что $\eta $ ≠ 0)Приравнивая нулю выражение внутри круглых скобок, и учитывая соотношение (2.5) получим линейное обыкновенное дифференциальное уравнение относительно функции $\psi $
Общее решение уравнения (2.6) имеет вид
где C1, C2, C3 – постоянные интегрирования. Из соображений симметричности движения среды относительно плоскости $\theta $ = 0 сразу вытекает, что постоянная C3 должна быть равна нулю: C3 = 0. Остальные неизвестные постоянные определяются из граничных условий на стенках и условия постоянства расхода среды.Учитывая то обстоятельство, что скорость на стенке не может быть больше (из-за трения) скорости на плоскости симметрии, граничное условие на стенках емкости поставим в форме
где $\alpha $ – угол раствора между плоскостями. Граничные условия (2.7) учитывают эффект частичного сцепления сыпучей среды с поверхностью стенок, где Λ есть коэффициент скольжения, зависящий от физико-механических свойств поверхности стенок (шероховатости и др.) и гранулированного материала. Очевидно, 0 ≤ Λ ≤ 1, при этом, если Λ = 1, то имеет место полное скольжение (скорость на стенке совпадает со скоростью на плоскости симметрии), а в случае Λ = 0 реализуется полное сцепление (прилипание). Отметим, что величина ${v}\left( {r,0} \right)$ в правой части (2.7) представляет собой скорость среды на плоскости симметрии на расстоянии r от вершины угла. Так что коэффициент Λ показывает, насколько меньше скорость на стенке по сравнению со скоростью на плоскости симметрии.Следует заметить, что граничное условие на твердой стенке, устанавливающее эффект сцепления, может быть задан и по-другому [4]. Анализ показал, что при задании граничного условия как в [4] решение поставленной задачи при определенных углах раствора становится бесконечным. Кроме того, коэффициент, введенный в [4], и характеризующий эффект частичного скольжения, меняется от нуля до бесконечности, что создает некоторые неудобства по определению значений данного коэффициента. В связи с этим принятие в настоящей работе условия на границе в виде (2.7) с коэффициентом скольжения, меняющимся от нуля до единицы, можно считать вполне целесообразным. К тому же так введенный коэффициент легко измерить экспериментально. Обычно для жидкости на твердой границе ставится условие прилипания (полного сцепления), а в случае сыпучей среды граничное условие допускает скольжение с некоторой скоростью, характеризуемой свойствами контактирующих материалов.
Очевидно, через любое сечение r = const проходит (в 1 с) одинаковое количество сыпучего материала (полный расход) ${{Q}_{ - }}$ (м2/с)
(2.8)
${{Q}_{ - }} = \int\limits_{ - \alpha /2}^{\alpha /2} {{v}(r,\theta )rd\theta } = {\text{const}} < 0$Используя граничное условие на одной из стенок, например, при θ = α/2, (второе условие при этом выполняется автоматически из-за симметричности движения) и условие (2.8) находим функцию $\psi $, подставляя которую в (2.5) получим распределение скорости внутри рассматриваемого объема
(2.9)
$\begin{gathered} {v}(r,\theta ) = - \frac{Q}{{{\rm A}r}}\left[ {1 - (1 - \Lambda )\frac{{{{{\sin }}^{2}}\theta }}{{{{{\sin }}^{2}}\frac{\alpha }{2}}}} \right] \\ {\rm A} = \alpha - (1 - \Lambda )\frac{{\alpha - \sin \alpha }}{{1 - \cos \alpha }},\quad - {\kern 1pt} \frac{\alpha }{2} \leqslant \theta \leqslant \frac{\alpha }{2},\quad Q = - {{Q}_{ - }} > 0,\quad \alpha \ne 0 \\ \end{gathered} $В частном случае Λ = 1 имеем Α = $\alpha $. Анализ показал, что при приближении $\alpha $ к нулю величина Α также стремится к нулю (возникающая при этом неопределенность типа 0/0 во втором слагаемом в выражении для Α легко раскрывается разложением в ряд тригонометрических функций). Очевидно, при $\alpha \ne 0$ параметр Α всегда меньше $\alpha $. Для малых углов раствора с точностью до второго порядка малости по $\alpha $ имеет место следующее асимптотическое представление:
При крайнем значении Λ = 1 асимптотическая формула (2.10) дает Α = $\alpha $, что совпадает с вышеприведенной основной формулой для Α (с учетом условия Λ = 1). Более подробная картина поведения зависимости Α от $\alpha $ при разных коэффициентах скольжения Λ показана на рис. 2, где видно, что с ростом $\alpha $ и Λ величина Α также увеличивается. Причем асимптотическая формула (2.10) довольно хорошо описывает зависимость Α($\alpha $) для не очень больших $\alpha $.
Рис. 2.
Зависимость параметра ${\text{A}}$ от $\alpha $ (рад) при разных значениях коэффициента скольжения: 1 – Λ = 0, 2 – Λ = 0.25, 3 – Λ = 0.5, 4 – Λ = 0.75, 5 – Λ = 1. Штриховые линии – асимптотическая формула (2.10).

На плоскости симметрии ($\theta $ = 0) из (2.9) следует
так что скорость на линии симметрии зависит от координаты r, угла раствора $\alpha $, коэффициента скольжения Λ и расхода $Q$. Из (2.11) следует, что в случае одного и того же расхода усиление эффекта сцепления (соответствует уменьшению коэффициента Λ, и как следствие согласно рис. 2, уменьшению Α) приводит к увеличению (по модулю) скорости ${{{v}}_{s}}$. С учетом формулы (2.11) решение (2.9) примет вид(2.12)
${v}(r,\theta ) = {{{v}}_{s}}(r)\left[ {1 - (1 - \Lambda )\frac{{{{{\sin }}^{2}}\theta }}{{{{{\sin }}^{2}}\frac{\alpha }{2}}}} \right]$3. Анализ влияния коэффициента скольжения. Проанализируем некоторые частные случаи, соответствующие характерным значениям коэффициента скольжения. В случае полного сцепления Λ = 0 (т.е. при отсутствии скольжения) из (2.12) вытекает
Из решения (2.9) видно, что в случае полного скольжения (Λ = 1) скорость среды не зависит от угловой координаты θ и имеет равномерное распределение для любого r
При этом очевидно, что в данном случае (т.е. когда Λ = 1) ${{{v}}^{{(1)}}} = {{{v}}_{s}}$. В этом случае скорость имеет потенциал $\Phi = - \left( {Q{\text{/}}\alpha } \right)\ln r$, соответствующий находящемуся на вершине угла плоскому стоку интенсивности $Q$, в то время как движение среды в общем случае, описываемое уравнением (2.9) не является потенциальным. Таким образом, наличие сцепления со стенкой нарушает свойство потенциальности течения сыпучей среды.
Интересно сравнить распределения скоростей среды при наличии (Λ < 1) и отсутствии (Λ = 1) сцепления со стенкой. С этой целью рассмотрим отношение ${v}{\text{/}}{{{v}}^{{(1)}}}$
Видно, что данное соотношение характеризуется величиной $\kappa = {{{v}}_{s}}{\text{/}}{{{v}}^{{(1)}}}$, поэтому имеет смысл подробно проанализировать зависимость $\kappa $ от определяющих параметров $\alpha $ и Λ. Отношение характерных скоростей $\kappa $ при одном и том же расходе $Q$ запишется в форме
(3.1)
$\kappa = \frac{{{{{v}}_{s}}}}{{{{{v}}^{{(1)}}}}} = \frac{\alpha }{{\rm A}} = {{\left[ {1 - (1 - \Lambda )\frac{{\alpha - \sin \alpha }}{{\alpha (1 - \cos \alpha )}}} \right]}^{{ - 1}}}$Формула (3.1) показывает, насколько скорость на линии симметрии при наличии сцепления со стенкой ${{{v}}_{s}}$ отличается от скорости при полном скольжении среды ${{{v}}^{{(1)}}}$. Поскольку величина Α всегда меньше или равна α (см. выше), то имеет место соотношение $\kappa $ ≥ 1 (или ${{{v}}_{s}}$ ≥ ${{{v}}^{{(1)}}}$). В предельном случае полного сцепления (Λ = 0) имеем
В этом случае $\kappa $ принимает свое максимальное значение. Очевидно, при Λ = 1 величина $\kappa $ = 1. Разлагая тригонометрические функции в формуле (3.1) в ряды, и пренебрегая в этих рядах членами выше пятого порядка малости, получим приближенное выражение, пригодное для расчета величины κ при малых углах раствора $\alpha \ll 1$
(3.2)
$\kappa = \frac{3}{{2 + \Lambda }}\left[ {1 - \frac{1}{4}\left( {\frac{1}{3} - \frac{\gamma }{{2 + \Lambda }}} \right){{\alpha }^{2}}} \right],\quad \gamma = 1 - \frac{1}{5}(1 - \Lambda )$Из (3.2) вытекает соотношение для случая, когда $\alpha $ → 0
Отсюда, в частности, следует, что при движении сыпучей среды между параллельными плоскостями скорость на плоскости симметрии в крайних ситуациях полного сцепления и полного скольжения различается в 1.5 раза (в предположении одинакового расхода).
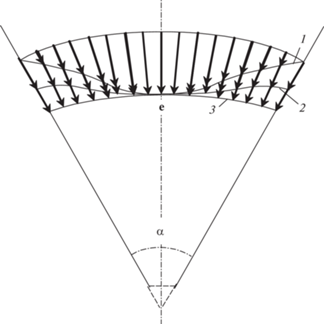
Эпюры безразмерной скорости ${\mathbf{v}}{\text{/}}{{{v}}_{s}}$ при $\alpha = \pi {\text{/}}3$ и различных значениях коэффициента скольжения Λ представлены на рис. 3. Видно, что с ростом Λ профиль скорости среды стремится к равномерному распределению. Следует иметь в виду, что профили скорости на рис. 3 соответствуют разным расходам, поскольку в данном случае величина ${{{v}}_{s}}$ фиксирована, и поэтому при изменении Λ меняется также и $Q$ (от которых зависит ${{{v}}_{s}}$).
Рис. 3.
Эпюры безразмерной скорости ${\mathbf{v}}{\text{/}}{{{v}}_{s}}$ в случае $\alpha = \pi {\text{/}}3$ при разных коэффициентах скольжения. Профили: 1 – Λ = 0, 2 – Λ = 0.5, 3 – Λ = 1, e – единичный вектор.
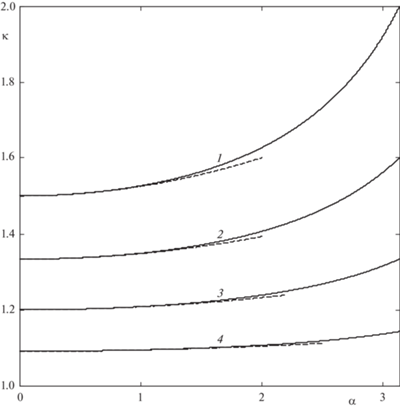
На рис. 4 показан график зависимости $\kappa $ от $\alpha $, откуда видно, что при увеличении угла раствора $\alpha $ величина $\kappa $ растет, тогда как с увеличением коэффициента Λ оно, наоборот, уменьшается. Необходимо подчеркнуть, что при значениях Λ, близких к единице, а также при не очень больших углах раствора $\alpha $ указанное отношение скоростей меняется достаточно слабо. Следует иметь в виду, что значение величины $\kappa $, соответствующее нулевому углу раствора достигается в пределе при $\alpha $ → 0. Заметим, что приближенная формула (3.2) хорошо аппроксимирует исходную зависимость.
Рис. 4.
Зависимость $\kappa = {{{v}}_{s}}{\text{/}}{{{v}}^{{(1)}}}$ от $\alpha $ (рад) при разных значениях коэффициента скольжения: 1 – Λ = 0, 2 – Λ = 0.25, 3 – Λ = 0.5, 4 – Λ = 0.75. Штриховые линии – расчеты по приближенной формуле (3.2).
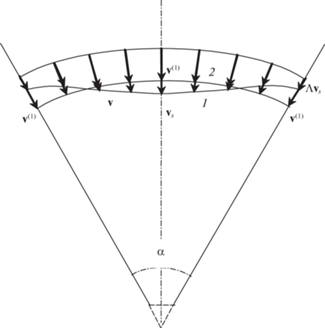
Особенности взаимосвязи между скоростями ${{{v}}_{s}}$ и ${{{v}}^{{(1)}}}$ наглядно демонстрирует диаграмма, приведенная на рис. 5, где эпюры скоростей построены для угла раствора $\alpha = \pi {\text{/}}3$. Поскольку расход сыпучей среды один и тот же, то площади, охваченные профилями скоростей ${\mathbf{v}}$ и ${{{\mathbf{v}}}^{{(1)}}}$ должны быть одинаковыми.
Рис. 5.
Эпюры скорости в случаях частичного ${\mathbf{v}}$ и полного ${{{\mathbf{v}}}^{{(1)}}}$ скольжения при одинаковом расходе сыпучего материала (для $\alpha = \pi {\text{/}}3$). Профили: 1 – Λ = 0.25, 2 – Λ = 1.
4. Средняя скорость истечения. Также можно определить среднюю скорость на расстоянии r от вершины угла
(4.1)
${{{v}}_{a}}(r) = \frac{1}{{\alpha r}}\int\limits_{ - \alpha /2}^{\alpha /2} {{v}(r,\theta )rd\theta } = - \frac{Q}{{\alpha r}}$Интересно, что как видно из (4.1), при заданном $Q$ средняя скорость не зависит от Λ и для одного и того же расхода $Q$ совпадает со скоростью среды при полном скольжении. Причем она обладает таким же потенциалом $\Phi = - \left( {Q{\text{/}}\alpha } \right)\ln r$, соответствующим находящемуся на вершине угла $\alpha $ плоскому стоку интенсивности $Q$, в то время как движение среды в общем случае, описываемое уравнением (2.9), как отмечено выше, не является потенциальным. Таким образом, в соотношениях ${{{v}}_{s}}{\text{/}}{{{v}}^{{(1)}}}$ и ${v}{\text{/}}{{{v}}^{{(1)}}}$ скорость ${{{v}}^{{(1)}}}$ вполне можно заменить на ${{{v}}_{a}}$.
Введем некоторую характерную скорость $V$ по формуле $V = Q{\text{/}}\alpha $, которую можно трактовать как среднюю скорость истечения сыпучего тела через выпускное отверстие шириной $a$, поскольку величина $aV$ дает расход среды. Тогда используя формулу для $V$ решение (2.9) можно переписать в другой форме
(4.2)
${v}(r,\theta ) = - \frac{{aV}}{{{\rm A}r}}\left[ {1 - (1 - \Lambda )\frac{{{{{\sin }}^{2}}\theta }}{{{{{\sin }}^{2}}\frac{\alpha }{2}}}} \right]$Для сравнения запишем выражение для скорости среды на линии симметрии ($\theta $ = 0)
и для средней скорости (совпадающей со скоростью при полном скольжении)Формулы (4.2)–(4.4) позволяют рассчитать распределение скорости среды внутри емкости через характерную скорость на выходе $V$. Указанные формулы физически правильно описывают поведение зависимостей скоростей ${v}$, ${{{v}}_{s}}$, ${{{v}}_{a}}$ от ширины выходной щели $a$: они с увеличением $a$ растут.
Для сравнения далее рассмотрим другой подход для моделирования истечения сыпучего груза из емкости, основанный на представлении гранулированной среды как дискретных слоев (ДС).
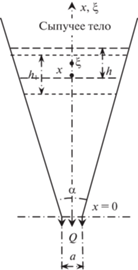
5. Моделирование истечения сыпучего тела с использованием ДС. Для приближенного описания сформулированной выше задачи об истечении сыпучего тела из бункера может быть использована точка зрения Лагранжа к изучению движения среды. Пусть среда истекает с интенсивностью $Q$ > 0 и пусть эффект сцепления сыпучего тела со стенкой отсутствует (Λ = 1). В начальный момент времени $t = {{t}_{0}}$ выбираем любой элементарный объем среды высотой $h$ (рис. 6), которую назовем “крупной частицей” или элементарным “дискретным слоем” (ДС) [12]. В качестве лагранжевой координаты примем начальную координату центра ДС, так что
За время $t - {{t}_{0}}$ первоначальный слой высотой $h$ перейдет в новое положение с высотой ${{h}_{1}}$. Для несжимаемой среды площадь элементарного слоя будет постоянной. Учитывая это условие вместе с геометрическими размерами емкости можно получить следующие соотношения для разработки расчетных схем с целью последующего анализа истечения сыпучей среды из бункера
Скорость дискретного элемента выражается как
(5.2)
$u = \frac{{dx}}{{dt}} = - \frac{1}{2}\frac{{hQ}}{{{{h}_{1}}{{h}_{{11}}}{{h}_{{12}}}}}\left( {\xi \operatorname{tg} \frac{\alpha }{2} + \frac{a}{2}} \right)$Из формул (5.1) и (5.2) устремляя $h$ к нулю $h$ → 0 можно получить закон движения среды (после раскрытия неопределенности $h{\text{/}}{{h}_{1}}$)
(5.3)
$x = \left[ { - \frac{a}{2} + \sqrt {{{{\left( {\frac{a}{2} + \xi \operatorname{tg} \frac{\alpha }{2}} \right)}}^{2}} - Q(t - {{t}_{0}})\operatorname{tg} \frac{\alpha }{2}} } \right]\operatorname{ctg} \frac{\alpha }{2},$(5.4)
$u = - \frac{1}{2}\frac{Q}{{\sqrt {{{{\left( {\frac{a}{2} + \xi \operatorname{tg} \frac{\alpha }{2}} \right)}}^{2}} - Q(t - {{t}_{0}})\operatorname{tg} \frac{\alpha }{2}} }}$Из (5.3) следует выражение для времени, в течение которого частица с начальной координатой $\xi $ достигнет выпускного отверстия ($x$ = 0)
Видно, что зависимость характерного времени ${{t}_{\xi }}$ от начальной координаты частицы $\xi $ подчиняется квадратичному закону. Причем величина ${{t}_{\xi }}$ обратно пропорциональна расходу $Q$, что согласуется с физическими соображениями: чем больше расход среды, тем меньше время истечения.
Комбинируя формулы (5.3) и (5.4) получаем распределение скорости среды вдоль оси $x$
Далее для удобства переходим к координате $y$ (вместо $x$), начало которой откладывается, аналогично r, от линии пересечения рассматриваемых плоскостей
Тогда (5.5) перепишется в виде
(5.6)
$u = - \frac{Q}{{2y}}\operatorname{ctg} \frac{\alpha }{2},\quad y \geqslant \frac{a}{2}\operatorname{ctg} \frac{\alpha }{2}$Здесь расход $Q$ аналогично предыдущему разделу можно представить в виде $Q = aV$. Напомним, что в подходе ДС используется только закон сохранения массы без привлечения закона сохранения импульсов (в этом заключается простота подхода ДС).
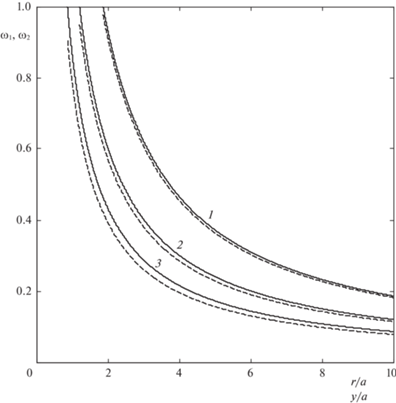
На рис. 7 проводится сравнение безразмерных скоростей, вычисленных по разным формулам (2.17) и (5.6), соответствующим разным подходам описания истечения сыпучей среды. Видно, что оба рассмотренных здесь подхода дают значения скорости, незначительно отличающиеся друг от друга, хотя с увеличением угла раствора различие между ними растет.
Рис. 7.
Распределения безразмерной скорости в радиальном направлении при разных значениях угла раствора: 1 – $\alpha = \pi {\text{/}}6$, 2 – $\alpha = \pi {\text{/}}4$, 3 – $\alpha = \pi {\text{/}}3$. Сплошные кривые – средняя скорость в рамках модели НС ${{\omega }_{1}} = - {{{v}}_{a}}{\text{/}}V$ (зависит от $r{\text{/}}a$), штриховые кривые – скорость в рамках подхода ДС ${{\omega }_{2}} = - u{\text{/}}V$ (зависит от $y{\text{/}}a$).
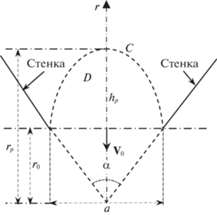
6. Расчет скорости и расхода сыпучего тела на выходе из емкости. Таким образом, как следует из предыдущих разделов, распределение скорости внутри емкости зависит от расхода $Q$ сыпучего материала через нижнее выпускное отверстие. В связи с этим для полного описания приведенных выше моделей, необходимо указать способ определения расхода. Для расчета расхода разработаны различные подходы [13–17]. Далее укажем на один из способов определения установившейся скорости гранулированного потока ${{V}_{0}}$ и расхода $Q$ на выходе из емкости. Для этого воспользуемся структурно-механической моделью истечения сыпучей среды, изложенной в [17]. Здесь остановимся на ключевых моментах данной модели. Вкратце, траектории зерен внутри бункера разделены на разные зоны. В данном случае цель состоит в том, чтобы сосредоточить внимание на скорости потока зерна на выходе из бункера. Поэтому здесь рассматривается описание зоны выходного потока $D$, ограниченной параболой (рис. 8). В этой зоне гранулированные частицы сталкиваются с другими частицами непрерывно в хаотическом движении [16–18]. Следовательно, сыпучая среда в этой зоне находится в свободнодисперсном состоянии и, согласно [7, 18] ее движение описывается уравнениями непрерывной среды. С помощью круга Мора можно показать, что для несвязного сыпучего тела граница между динамическим сводом $C$ и зоной обрушения $D$ представляет собой параболу [19] (рис. 8), высота которой ${{h}_{p}}$ зависит от параметров внутреннего трения среды и определяется по формуле
Здесь $f$, $\varphi $ – коэффициент и угол внутреннего трения в сыпучей среде.
Используя на линии симметрии уравнение Бернулли в [17] получены следующие формулы для скорости истечения на линии симметрии и расхода среды на выходе
(6.1)
${{V}_{0}} = {{\left[ {\frac{{2g({{r}_{p}} - {{r}_{0}})}}{{1 + \zeta - {{{\left( {{{r}_{0}}{\text{/}}{{r}_{p}}} \right)}}^{2}}}}} \right]}^{{1/2}}} = {{\left( {\frac{{2g{{h}_{p}}}}{{1 + \zeta - B}}} \right)}^{{1/2}}} = {{\left( {\frac{{agK}}{{1 + \zeta - B}}} \right)}^{{1/2}}}$(6.2)
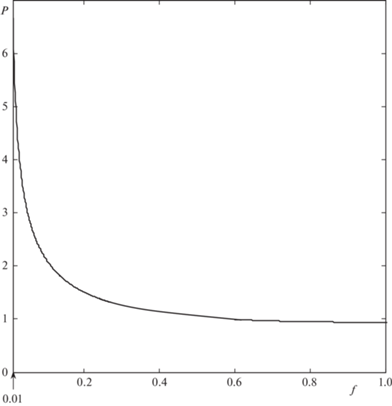
$\begin{gathered} Q = \frac{2}{3}{{a}^{{3/2}}}{{\left( {\frac{{gK}}{{1 + \zeta }}} \right)}^{{1/2}}}\frac{{1 - 8{{\beta }^{{3/2}}}}}{{1 - 4\beta }} \\ \beta = \frac{\lambda }{2}\frac{{\lambda - 1}}{{\lambda + 1}},\quad \lambda = \frac{{\sqrt {1 + {{f}^{2}}} }}{f} \geqslant 1,\quad B = {{\left( {1 + K\operatorname{tg} \frac{\alpha }{2}} \right)}^{{ - 2}}} \leqslant 1,\quad K = \frac{1}{2}\left( {f + \sqrt {1 + {{f}^{2}}} } \right), \\ \end{gathered} $На рис. 9 показана зависимость безразмерной скорости истечения среды на линии симметрии $W$ от угла раствора $\alpha $ при разных углах внутреннего трения сыпучего тела $\varphi $, соответствующих некоторым характерным сыпучим средам (песок, цемент и др.). С увеличением $\alpha $ безразмерная скорость $W$ сначала резко падает, затем меняется достаточно плавно. Причем различие скоростей истечения разных сред с ростом $\alpha $ постепенно увеличивается. Зависимость безразмерного расхода от коэффициента внутреннего трения $f$ представлена на рис. 10. Видно, что безразмерный расход P с ростом $f$ быстро уменьшается.
Рис. 9.
Зависимость безразмерной скорости на выходе $W$ от угла раствора $\alpha $ (рад) при разных значениях угла внутреннего трения сыпучей среды $\varphi $: 1 – $\varphi = 15^\circ $ (песок и др.), 2 – $\varphi = 50^\circ $ (цемент и др.).
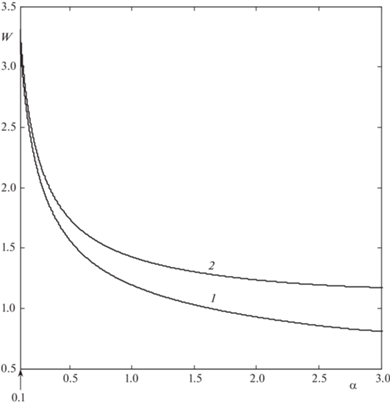
Рис. 10.
Зависимость безразмерного расхода $P$ от коэффициента внутреннего трения сыпучего тела $f$.
Таким образом, зная расход сыпучей среды из емкости нетрудно рассчитать распределение скорости внутри объема сыпучего тела (в частности, в зависимости от коэффициента скольжения, коэффициента внутреннего трения сыпучей среды и т.п.) по формулам из предыдущих разделов.
Заключение. В рамках модели непрерывной среды изучено распределение скорости сыпучего тела при истечении из емкости с учетом эффекта сцепления со стенками. Проанализировано влияние коэффициента скольжения, характеризующего степень сцепления со стенкой, на течение гранулированной среды. Проведено сравнение скорости движения сыпучей среды при разных подходах, а именно, в рамках непрерывной среды и дискретных слоев, которое показало, что оба эти подхода дают примерно одинаковые результаты. Данное обстоятельство позволяет утверждать, что для описания характеристик течения сыпучей среды в емкости наряду с моделью, основанной на подходе непрерывной среды, вполне можно использовать в пределах допустимой погрешности простую геометрическую модель, базирующуюся на представлении сыпучей среды как дискретных слоев.
Список литературы
Макаров Ю.И. Аппараты для смешения сыпучих материалов. М.: Машиностроение, 1973. 216 с.
Росляк А.Т., Бирюков Ю.А., Пачин В.Н. Пневматические методы и аппараты порошковой технологии. Томск: Изд-во Томского ун-та, 1990. 272 с.
Першина С.В., Каталымов А.В., Однолько В.Г., Першин В.Ф. Весовое дозирование зернистых материалов. М.: Машиностроение, 2009. 164 с.
Шваб А.В., Марценко А.А., Марценко М.С. Моделирование гидродинамики высококонцентрированной гранулированной среды в смесительном бункере // Вестн. Томского гос. ун-та. Сер. Математика, механика. 2013. № 4. С. 126–132.
Шваб А.В., Марценко М.С., Рыжих Ю.Н. Моделирование гидродинамики и процесса усреднения высококонцентрированной гранулированной среды в аппаратах порошковой технологии // Инж.-физ. ж. 2011. Т. 84. № 4. С. 676–682.
Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2003. 704 с.
Механика гранулированных сред. Теория быстрых движений / Под ред. Ишлинского А.Ю. М.: Мир, 1985. 280 с.
Клишин С.В., Лавриков С.В., Ревуженко А.Ф. Численное моделирование выпуска раздробленного материала методами дискретных элементов и клеточных автоматов // Геодинамика и напряженное состояние недр Земли. 2013. С. 208–215.
Kruggel-Emden H., Simsek E., Rickelt S. et al. Review and extension of normal force models of the Discrete Element Method // Powder Technol. 2007. V. 171. № 3. P. 157–173.
Losert W., Bocquet L., Lubensky T.C., Gollub J.P. Particle dynamics in sheared granular matter // Phys. Rev. Lett. 2000. V. 85. № 7. P. 1428–1431.
Ojha R.P., Lemieux P.-A., Dixon P.K. et al. Statistical mechanics of a gas-fluidized particle // Nature. 2004. V. 427. P. 521–523.
Antony S.J., Arowosola B., Richter L., Amanbayev T., Barakat T. Flow behavior of grains through the dosing station of spacecraft under low-gravity environments // J. Aerospace Engng. 2017. V. 30. № 6. 04017078.
Каталымов А.В., Лукьянов П.И. Теоретическое определение расхода сыпучего материала при свободном истечении из отверстия // Теор. основы химич. технол. 1976. Т. 10. № 1. С. 162–164.
Генералов М.Б. Истечение сыпучих материалов из аппаратов // Теор. основы химич. технол. 1985. Т. 19. № 1. С. 53–58.
Лукьянов П.И. Аппараты с движущимся зернистым слоем. М.: Машиностроение, 1974. 184 с.
Богомягких В.А., Несмиян А.Ю. Функционирование бункеров максимального расхода в условиях сводообразующего истечения зерновых материалов. Зерноград: Азово-Черном. инж. ин-т ФГБОУ ВПО ДГАУ, 2015. 179 с.
Кирия Р.В. Описание процесса истечения сыпучего груза из бункера с помощью структурно-механических моделей // Системные технол. 2009. № 3 (62). С. 3–19.
Кирия Р.В. Кинетический подход к выводу уравнений движения сыпучих сред // Вестн. Днепропетр. гос. унив. Сер. Механика. 1999. № 2. С. 143–150.
Зенков Р.Л. Механика насыпных грузов. М.: Машиностроение, 1964. 251 с.
Штеренлихт Д.В. Гидравлика. М.: Энергоатомиздат, 1984. 639 с.
Кирия Р.В. О коэффициенте внутренних потерь при движении сыпучей среды по элементам перегрузочных узлов ленточных конвейеров // Геотехн. мех. 2003. № 41. С. 159–167.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика