1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 5, 2022

Прикладная математика и механика, 2022, T. 86, № 5, стр. 666-684

О движении осесимметричного твердого тела, опирающегося на горизонтальную площадку, в условиях ортотропного динамически согласованного трения

Н. Н. Дмитриев 1, *

1 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

* E-mail: dn7@rambler.ru

Поступила в редакцию 19.05.2022
После доработки 19.07.2022
Принята к публикации 20.07.2022

Полный текст (PDF)

Аннотация

Анизотропия силы трения оказывает влияние на траекторию движения материальной точки, на кинематические характеристики твердых тел и на процессы, происходящие в области контакта пары трения. Известно также, что при движении твердых тел по плоскости плотность нормальной реакции может зависеть от скорости центра масс тела и его угловой скорости. Одновременному учету указанных явлений на динамику тела, опирающегося на круговую или кольцевую область, посвящена данная работа.

Ключевые слова: анизотропное трение, ортотропное трение, согласованное трение

1. Введение. Изучается движение твердого тела по горизонтальной плоскости. При расположении центра масс тела над плоскостью скольжения при движении происходит перераспределение плотности нормальных напряжений. С этим явлением связано понятие динамически согласованного трения, согласно которому при движении твердого тела с плоским основанием предполагается, что угловая скорость тела перпендикулярна плоскости опоры и должны выполняться общие теоремы динамики, записанные относительно осей, проходящих через центр масс тела [1, 11]. Этот подход получил свое развитие в публикациях [6–8, 18].

Но в упомянутых выше работах предполагалось, что сила трения во всех точках контакта обладает изотропными свойствами. Однако, во многих экспериментальных и теоретических работах показано, что сила трения может обладать анизотропными свойствами. Анизотропное трение возникает из-за неоднородности материала трущихся поверхностей, ориентированных следов механической обработки, износа поверхностей трения, кристаллической структуры материалов пары трения и многих других причин. В [2, 3] вводится тензор трения, через который описывается анизотропное трение, дается доказательство характерных свойств силы анизотропного трения и тензора трения.

В данном исследовании рассматривается влияние ортотропного трения на динамику движения тела при учете концепции динамически согласованного трения. При этом будет выбрана линейная модель ортотропного трения [2, 3].

2. Динамически согласованная модель контактных напряжений при ортотропном трении. Пусть контакт твердого тела с горизонтальной плоскостью происходит по площадке $S$. С этой площадкой свяжем систему координат $C\xi \eta \zeta $ так, что ось $C\zeta $ перпендикулярна плоскости скольжения. С плоскостью, по которой скользит тело, свяжем неподвижную систему координат $Oxyz$, причем ось $Oz$ перпендикулярна плоскости. Будем полагать, что плотность давления $p(\xi ,\,\eta )$ можно представить в виде [1, 11]:

(2.1)
$p(\xi ,\eta ) = {{p}_{0}} + {{p}_{1}}\xi + {{p}_{2}}\eta $

Кроме того, оси $Ox$ и $Oy$ направлены так, что тензор коэффициентов трения имеет вид:

(2.2)
$\mathcal{F} = \left( {\begin{array}{*{20}{c}} {{{f}_{x}}}&0 \\ 0&{{{f}_{y}}} \end{array}} \right)$

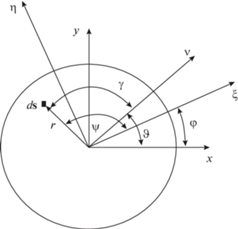
При сделанных допущениях, сила трения, действующая на элементарную площадку, выражается формулой (см. рис. 1a)

(2.3)
$dT = - p(\xi ,\eta )\mathcal{F}\frac{v}{{v}}d\xi d\eta ,$
где
(2.4)
$\begin{gathered} v = {{{v}}_{x}}(\xi ,\eta )i + {{{v}}_{y}}(\xi ,\eta )j,\quad \omega = \dot {\varphi } \\ {{{v}}_{x}} = {{{v}}_{0}}\cos \vartheta - \omega \left( {\xi \sin \varphi + \eta \cos \varphi } \right),\quad {{{v}}_{y}} = {{{v}}_{0}}\sin \vartheta + \omega \left( {\xi \cos \varphi - \eta \sin \varphi } \right) \\ \end{gathered} $
${{v}_{0}} = {{{v}}_{0}}\cos \vartheta i + {{{v}}_{0}}\sin \vartheta j$ – вектор скорости точки $C$, ${\mathbf{\omega }} = \omega k$ – угловая скорость тела, $i$, $j$, $k$ – орты системы координат $Cxyz$.

Рис. 1.

Область контакта и системы координат. (a) Взаимное расположение осей подвижной и неподвижной систем координат; (б) Проекции силы трения на оси $C\xi $ и $C\eta $, действующей на площадку $ds$.

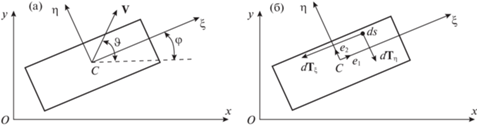
Проекции элементарной силы $dT$ и момента этой силы относительно оси $C\zeta $ записываются следующим образом

$d{{T}_{x}} = - p(\xi ,\eta ){{f}_{x}}\frac{{{{{v}}_{0}}\cos \vartheta - \omega \left( {\xi \sin \varphi + \eta \cos \varphi } \right)}}{{v}}d\xi d\eta $
$d{{T}_{y}} = - p(\xi ,\eta ){{f}_{y}}\frac{{{{{v}}_{0}}\sin \vartheta + \omega \left( {\xi \cos \varphi - \eta \sin \varphi } \right)}}{{v}}d\xi d\eta $
(2.5)
$\begin{gathered} d{{M}_{T}} = - \frac{{p(\xi ,\eta )}}{{v}}\left[ {{{f}_{x}}\left( {{{{v}}_{0}}\left( {\xi \sin \left( {\vartheta - \varphi } \right) - \eta \cos \left( {\vartheta - \varphi } \right)} \right) + \omega \left( {{{\xi }^{2}} + {{\eta }^{2}}} \right)} \right)} \right. + \\ \left. { + \;\mu \left( {{{{v}}_{0}}\left( {\xi \cos \varphi \sin \vartheta - \eta \sin \varphi \sin \vartheta } \right) + \omega {{{\left( {\xi \cos \varphi - \eta \sin \varphi } \right)}}^{2}}} \right)} \right]d\xi d\eta \\ \end{gathered} $
${v} = \sqrt {{v}_{0}^{2} + {{\omega }^{2}}\left( {{{\xi }^{2}} + {{\eta }^{2}}} \right) + 2{{{v}}_{0}}\omega \left( {\xi \sin \left( {\vartheta - \varphi } \right) - \eta \cos \left( {\vartheta - \varphi } \right)} \right)} $
$\mu = {{f}_{y}} - {{f}_{x}}$

Обозначим через $C{\kern 1pt} '$ точку, соответствующую центру масс твердого тела. Будем считать, что проекция точки $C{\kern 1pt} '$ на плоскость скольжения совпадает с точкой $C$ – началом, выбранной ранее системы координат $C\xi \eta \zeta $, и оси $C{\kern 1pt} '{\kern 1pt} \xi {\kern 1pt} '$, $C{\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '$, $C{\kern 1pt} '{\kern 1pt} \zeta {\kern 1pt} '$ – главные оси инерции тела, причем оси систем $C\xi \eta \zeta $ и $C{\kern 1pt} '{\kern 1pt} \xi {\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '{\kern 1pt} \zeta {\kern 1pt} '$ параллельны. Так как в представленном исследовании рассматриваются осесимметричные тела, то такие допущения можно считать обоснованными. Если таких допущений сделать нельзя, то нижеприведенные рассуждения усложняются в связи с необходимостью учитывать взаимную ориентацию систем $C\xi \eta \zeta $ и $C{\kern 1pt} '{\kern 1pt} \xi {\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '{\kern 1pt} \zeta {\kern 1pt} '$.

Вектор $dT$ можно представить в виде

(2.6)
$\begin{gathered} dT = d{{T}_{x}}i + d{{T}_{y}}j = d{{T}_{\xi }}{{e}_{{\text{1}}}} + d{{T}_{\eta }}{{e}_{{\text{2}}}} \\ {{e}_{{\text{1}}}} = \cos \varphi i + \sin \varphi j,\quad {{e}_{2}} = - \sin \varphi i + \cos \varphi j \\ \end{gathered} $
${{e}_{{\text{1}}}}$, ${{e}_{{\text{2}}}}$ – орты осей $C\xi $ и $C\eta $, $i$, $j$ – орты осей $Ox$ и $Oy$ соответственно (см. рис. 1б)). На рис. 1б) векторы $d{{T}_{\xi }}$ и $d{{T}_{\eta }}$ изображены условно. Направление вектора $dT$ зависит от направления скорости элементарной площадки $ds$ в плоскости $Oxy$ в соответствии с формулами (2.5).

Для того, чтобы тело не опрокидывалось сумма моментов от силы трения и от реакции опорной плоскости относительно осей $C{\kern 1pt} '{\kern 1pt} \xi {\kern 1pt} '$ и $C{\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '$ должны равняться нулю (см. рис. 1б и рис. 2):

(2.7)
$\begin{gathered} {{M}_{{C'\xi '}}} = \iint\limits_S {\left[ {p\left( {\xi ,\eta } \right) \cdot \eta + d{\text{T}} \cdot {{{\text{e}}}_{2}} \cdot h} \right]}d\xi d\eta = 0 \\ {{M}_{{C'\eta '}}} = \iint\limits_S {\left[ { - p\left( {\xi ,\eta } \right) \cdot \xi - d{\text{T}} \cdot {{{\text{e}}}_{1}} \cdot h} \right]}d\xi d\eta = 0 \\ \end{gathered} $
Рис. 2.

Местоположение центра масс относительно опорной плоскости и силы, создающие момент вокруг него (${\mathbf{T}}$ – сила трения, ${\mathbf{N}}$ – равнодействующая реакции опоры на тело).

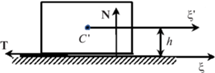
Кроме того, величина нормальной реакции опорной плоскости должна равняться весу твердого тела:

(2.8)
$\iint\limits_S {p\left( {\xi ,\eta } \right)}d\xi d\eta = mg$

Для определения коэффициентов ${{p}_{0}}$, ${{p}_{1}}$ и ${{p}_{2}}$ стоящих в формуле (2.1) перепишем выражения (2.7) в виде

(2.9)
$\begin{gathered} {{M}_{{c'\xi '}}} = \iint\limits_S {\left\{ {\left( {{{p}_{0}} + {{p}_{1}}\xi + {{p}_{2}}\eta } \right)} \right.}\eta + \frac{h}{{v}}\left[ {{{p}_{0}}\left( {{{{v}}_{0}}{{\kappa }_{1}} + \xi \omega {{\kappa }_{2}} + \eta \omega {{\kappa }_{3}}} \right) + } \right. \\ \left. { + \;{{p}_{1}}\left( {{{{v}}_{0}}\xi {{\kappa }_{1}} + {{\xi }^{2}}\omega {{\kappa }_{2}} + \xi \eta \omega {{\kappa }_{3}}} \right) + {{p}_{2}}\left( {{{{v}}_{0}}\eta {{\kappa }_{1}} + \xi \eta \omega {{\kappa }_{2}} + {{\eta }^{2}}\omega {{\kappa }_{3}}} \right)} \right\}d\xi d\eta \\ {{M}_{{c'\eta '}}} = - \iint\limits_S {\left\{ {\left( {{{p}_{0}} + {{p}_{1}}\xi + {{p}_{2}}\eta } \right)} \right.}\xi - \frac{h}{v}\left[ {{{p}_{0}}\left( {{{{v}}_{0}}{{\kappa }_{4}} + \xi \omega {{\kappa }_{5}} + \eta \omega {{\kappa }_{6}}} \right) + } \right. \\ \left. { + \;{{p}_{1}}\left( {{{{v}}_{0}}\xi {{\kappa }_{4}} + {{\xi }^{2}}\omega {{\kappa }_{5}} + \xi \eta \omega {{\kappa }_{6}}} \right) + {{p}_{2}}\left( {{{{v}}_{0}}\eta {{\kappa }_{4}} + \xi \eta \omega {{\kappa }_{5}} + {{\eta }^{2}}\omega {{\kappa }_{6}}} \right)} \right\}d\xi d\eta , \\ \end{gathered} $
где
(2.10)
$\begin{gathered} {{\kappa }_{1}} = - {{f}_{x}}\sin \left( {\vartheta - \varphi } \right) - \mu \sin \vartheta \cos \varphi ,\quad {{\kappa }_{2}} = - \left( {{{f}_{x}} + \mu {{{\cos }}^{2}}\varphi } \right),\quad {{\kappa }_{3}} = \mu \sin \varphi \cos \varphi \\ {{\kappa }_{4}} = {{f}_{x}}\cos \left( {\vartheta - \varphi } \right) + \mu \sin \vartheta \cos \varphi ,\quad {{\kappa }_{5}} = \mu \sin \varphi \cos \varphi ,\quad {{\kappa }_{6}} = - \left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\varphi } \right), \\ \end{gathered} $
а ${v}$ и $\mu $ выписаны в (2.5).

Для дальнейших рассуждений необходимо определиться с областью контакта твердого тела с плоскостью.

3. Опора на круг радиуса ${\text{R}}$. Пусть тело опирается на плоскость круговой площадкой радиуса $R$. Тогда декартовые координаты, введенные выше, можно заменить на полярные $r$ и $\psi $ (рис. 3):

(3.1)
$\xi = r\cos \psi ,\quad \eta = r\sin \psi ;\quad r \in \left[ {0,\;R} \right],\quad \psi \in \left[ {0,\;2\pi } \right)$
Рис. 3.

Связь декартовой системы координат $Cxy$ с полярной системой.

В этом случае проекции на оси $Ox$ и $Oy$ скорости элементарной площадки и величина этой скорости, в соответствии с формулами (2.4) и (2.5) переписываются следующим образом

(3.2)
$\begin{gathered} {{{v}}_{x}} = {{{v}}_{0}}\cos \vartheta - \omega r\sin \left( {\psi + \varphi } \right) \\ {{{v}}_{y}} = {{{v}}_{0}}\sin \vartheta + \omega r\cos \left( {\psi + \varphi } \right) \\ {v} = \sqrt {{v}_{0}^{2} + {{\omega }^{2}}{{r}^{2}} - 2{{{v}}_{0}}\omega r\sin \gamma } ;\quad \gamma = \psi - \vartheta + \varphi \\ \end{gathered} $

Из соотношения (2.8) имеем

(3.3)
$\int\limits_0^R {\int\limits_0^{2\pi } {\left( {{{p}_{0}} + {{p}_{1}}r\cos \psi + {{p}_{2}}r\sin \psi } \right)} } rdrd\psi = mg$
и после интегрирования
${{p}_{0}}\pi {{R}^{2}} = mg,$
откуда

(3.4)
${{p}_{0}} = \frac{{mg}}{{\pi {{R}^{2}}}}$

Отметим два частных случая: ${{{v}}_{0}} = 0$, $\omega > 0$ и ${{{v}}_{0}} > 0$, $\omega = 0$.

Из формул (2.9), (3.2) и условия (2.7) при ${{{v}}_{0}} = 0$, $\omega > 0$ следует, что ${{p}_{1}} = {{p}_{2}} = 0$, т.е. при чистом вращении плотность давления распределена равномерно

(3.5)
$p = {{p}_{0}} = \frac{{mg}}{{\pi {{R}^{2}}}}$

При ${{{v}}_{0}} > 0$, $\omega = 0$ условие (2.7) позволяет определить ${{p}_{1}}$ и ${{p}_{2}}$:

(3.6)
${{p}_{1}} = \frac{{4h{{p}_{0}}{{\kappa }_{4}}}}{{{{R}^{2}}}},\quad {{p}_{2}} = - \frac{{4h{{p}_{0}}{{\kappa }_{1}}}}{{{{R}^{2}}}}$
и, следовательно,

(3.7)
$p = {{p}_{0}}\left( {1 + \frac{{4hr}}{{{{R}^{2}}}}\left( {{{\kappa }_{4}}\cos \psi - {{\kappa }_{1}}\sin \psi } \right)} \right)$

Подстановка ${{\kappa }_{1}}$ и ${{\kappa }_{4}}$ из (2.10) в это выражение позволяет записать два эквивалентных соотношения

(3.8)
$p = {{p}_{0}}\left[ {1 + \frac{{4hr}}{{{{R}^{2}}}}\sqrt {f_{x}^{2}{{{\cos }}^{2}}\vartheta + f_{y}^{2}{{{\sin }}^{2}}\vartheta } \cos \left( {\psi + \alpha } \right)} \right],\quad \alpha = {\text{arctg}}\frac{{{{\kappa }_{1}}}}{{{{\kappa }_{4}}}}$
(3.9)
$p = {{p}_{0}}\left[ {1 + \frac{{4hr}}{{{{R}^{2}}}}\left( {{{f}_{x}}\cos \gamma + \mu \sin \vartheta \sin \left( {\psi + \varphi } \right)} \right)} \right]$

Так как рассматривается безотрывное скольжение, то должно быть выполнено условие $p\left( {r,\,\psi } \right) \geqslant 0$ при любых $\psi \in \left[ {0,\;2\pi } \right)$, $r \in \left[ {0,\;R} \right]$, и, следовательно, имеет место неравенство, которое должно выполняться в случае безотрывного скольжения

$R \geqslant 4h\sqrt {f_{x}^{2}{{{\cos }}^{2}}\vartheta + f_{y}^{2}{{{\sin }}^{2}}\vartheta } $

При изотропном трении (${{f}_{x}} = {{f}_{y}}$, $\mu = 0$) получаем известную формулу [10, 11]

$R \geqslant 4h{{f}_{x}}$

Далее полагаем, без ущерба для общности, что выполнены условия ${{{v}}_{0}} > 0$, $\omega > 0$.

Введем величину $\beta = {{{v}}_{0}}{\text{/}}\omega $ и безразмерные переменные по формулам:

${{{v}}_{0}} = {{{v}}_{{0*}}}\sqrt {\frac{{Rg}}{\pi }} ,\quad \omega = {{\omega }_{*}}\sqrt {\frac{g}{{\pi R}}} ,\quad \beta = {{\beta }_{*}}R,\quad t = {{t}_{*}}\sqrt {\frac{{R\pi }}{g}} $
${{p}_{0}} = {{p}_{{0*}}}\frac{{mg}}{{\pi {{R}^{2}}}},\quad {{p}_{\ell }} = {{p}_{{\ell *}}}\frac{{mg}}{{\pi {{R}^{3}}}};\quad \ell = 1,2$
(3.10)
$h = {{h}_{*}}R\pi ,\quad r = {{r}_{*}}R$
${{M}_{\xi }} = {{M}_{{\xi *}}}mgR,\quad {{M}_{\eta }} = {{M}_{{\eta *}}}mgR$
${{T}_{x}} = {{T}_{{x*}}}mg,\quad {{T}_{y}} = {{T}_{{y*}}}mg,\quad {{M}_{T}} = {{M}_{{T*}}}mgR$

Тогда безразмерные моменты относительно осей $C{\kern 1pt} '{\kern 1pt} \xi {\kern 1pt} '$ и $C{\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '$ записываются в виде (звездочки далее не пишем)

${{M}_{{C'\xi '}}} = \frac{1}{4}{{p}_{2}} + h\iint\limits_S {\left\{ {{{p}_{0}}\left[ {\beta {{\kappa }_{1}}r + {{r}^{2}}\left( {{{f}_{{01\xi }}}\cos \gamma + {{f}_{{02\xi }}}\sin \gamma } \right)} \right]} \right.} + $
(3.11)
$ + \;{{p}_{1}}\left[ {\beta {{\kappa }_{1}}{{r}^{2}}\cos \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{10\xi }}} + {{f}_{{11\xi }}}\sin \gamma \cos \gamma + {{f}_{{12\xi }}}{{{\cos }}^{2}}\gamma } \right)} \right] + $
$\left. { + \;{{p}_{2}}\left[ {\beta {{\kappa }_{1}}{{r}^{2}}\sin \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{20\xi }}} + {{f}_{{21\xi }}}\sin \gamma \cos \gamma + {{f}_{{22\xi }}}{{{\cos }}^{2}}\gamma } \right)} \right]} \right\}\frac{{drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}$
${{M}_{{C'\eta '}}} = - \frac{1}{4}{{p}_{1}} + h\iint\limits_S {\left\{ {{{p}_{0}}\left[ {\beta {{\kappa }_{4}}r + {{r}^{2}}\left( {{{f}_{{01\eta }}}\cos \gamma + {{f}_{{02\eta }}}\sin \gamma } \right)} \right]} \right.} + $
(3.12)
$ + \;{{p}_{1}}\left[ {\beta {{\kappa }_{4}}{{r}^{2}}\cos \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{10\eta }}} + {{f}_{{11\eta }}}\sin \gamma \cos \gamma + {{f}_{{12\eta }}}{{{\cos }}^{2}}\gamma } \right)} \right] + $
$\left. { + \;{{p}_{2}}\left[ {\beta {{\kappa }_{4}}{{r}^{2}}\sin \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{20\eta }}} + {{f}_{{21\eta }}}\sin \gamma \cos \gamma + {{f}_{{22\eta }}}{{{\cos }}^{2}}\gamma } \right)} \right]} \right\}\frac{{drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }},$
где $\lambda = \vartheta - \varphi $,

(3.13)
$\begin{gathered} {{f}_{{01\xi }}} = {{\kappa }_{2}}\cos \lambda + {{\kappa }_{3}}\sin \lambda ,\quad {{f}_{{02\xi }}} = - {{\kappa }_{1}}\sin \lambda + {{\kappa }_{3}}\cos \lambda \\ {{f}_{{10\xi }}} = {{\kappa }_{2}}{{\sin }^{2}}\lambda - {{\kappa }_{3}}\sin \lambda \cos \lambda ,\quad {{f}_{{11\xi }}} = - {{\kappa }_{2}}\sin 2\lambda + {{\kappa }_{3}}\cos 2\lambda \\ {{f}_{{12\xi }}} = {{\kappa }_{2}}\cos 2\lambda + {{\kappa }_{3}}\sin 2\lambda ,\quad {{f}_{{20\xi }}} = {{\kappa }_{3}}{{\cos }^{2}}\lambda - {{\kappa }_{2}}\sin \lambda \cos \lambda \\ {{f}_{{21\xi }}} = {{\kappa }_{2}}\cos 2\lambda + {{\kappa }_{3}}\sin 2\lambda ,\quad {{f}_{{22\xi }}} = {{\kappa }_{3}}\sin 2\lambda - {{\kappa }_{3}}\cos 2\lambda \\ \end{gathered} $

Коэффициенты ${{f}_{{ij\eta }}}$ получаются из (3.13) путем замены ${{\kappa }_{2}}$ на ${{\kappa }_{5}}$ и ${{\kappa }_{3}}$ на ${{\kappa }_{6}}$.

В выражениях (3.11) и (3.12) присутствуют интегралы

${{I}_{1}} = \iint {\frac{{rdrd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }},\quad }{{I}_{2}} = \iint {\frac{{{{r}^{2}}\cos \gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}}$
(3.14)
${{I}_{3}} = \iint {\frac{{{{r}^{2}}\sin \gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }},\quad }{{I}_{4}} = \iint {\frac{{{{r}^{3}}drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}}$
${{I}_{5}} = \iint {\frac{{{{r}^{3}}\sin \gamma \cos \gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }},\quad }{{I}_{6}} = \iint {\frac{{{{r}^{3}}{{{\cos }}^{2}}\lambda drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}},$
в которых интегрирование производится по круговой области контакта тела с плоскостью. Подынтегральные функции в (3.11) и (3.12) непрерывны по переменной $\gamma $ и интегрирование в (3.14) происходит в пределах $r \in \left[ {0,1} \right]$, $\gamma \in \left[ { - \lambda ,2\pi - \lambda } \right)$. Интегралы (3.14) приводятся к следующим соотношениям

${{I}_{2}} = {{I}_{5}} = 0$
${{I}_{1}} = \left\{ \begin{gathered} 4\beta \left[ {{\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) - \left( {1 - {{\beta }^{{ - 2}}}} \right){\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta > 1 \hfill \\ 4{\text{E}}\left( \beta \right);\quad \beta \leqslant 1 \hfill \\ \end{gathered} \right.$
(3.15)
${{I}_{3}} = \left\{ \begin{gathered} \frac{{4{{\beta }^{2}}}}{3}\left[ {\left( {2 - {{\beta }^{{ - 2}}}} \right){\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) - 2\left( {1 - {{\beta }^{{ - 2}}}} \right){\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta > 1 \hfill \\ \frac{{4{{\beta }^{{ - 1}}}}}{3}\left[ {\left( {1 - {{\beta }^{2}}} \right){\text{K}}\left( \beta \right) + \left( {2{{\beta }^{2}} - 1} \right){\text{E}}\left( \beta \right)} \right];\quad \beta \leqslant 1 \hfill \\ \end{gathered} \right.$
${{I}_{4}} = \left\{ \begin{gathered} \frac{{4{{\beta }^{3}}}}{9}\left[ {\left( {4 + {{\beta }^{{ - 2}}}} \right){\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) - \left( {1 - {{\beta }^{{ - 2}}}} \right)\left( {4 + 3{{\beta }^{{ - 2}}}} \right){\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta > 1 \hfill \\ \frac{4}{9}\left[ {2\left( {1 - {{\beta }^{2}}} \right){\text{K}}\left( \beta \right) + \left( {1 + 4{{\beta }^{2}}} \right){\text{E}}\left( \beta \right)} \right];\quad \beta \leqslant 1 \hfill \\ \end{gathered} \right.$
${{I}_{6}} = \left\{ \begin{gathered} \frac{{4{{\beta }^{3}}}}{{45}}\left[ {\left( {3{{\beta }^{{ - 4}}} + 7{{\beta }^{{ - 2}}} - 2} \right){\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) + \left( {6{{\beta }^{{ - 4}}} - 8{{\beta }^{{ - 2}}} + 2} \right){\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta > 1 \hfill \\ - \frac{{4{{\beta }^{{ - 2}}}}}{{45}}\left[ {\left( {1 - {{\beta }^{2}}} \right)\left( {3 + {{\beta }^{2}}} \right){\text{K}}\left( \beta \right) + \left( {2{{\beta }^{4}} - 7{{\beta }^{2}} - 3} \right){\text{E}}\left( \beta \right)} \right];\quad \beta \leqslant 1 \hfill \\ \end{gathered} \right.$

Здесь ${\text{K}}\left( \beta \right)$, ${\text{E}}\left( \beta \right)$ – полные эллиптические интегралы первого и второго рода соответственно.

Условия неопрокидывания тела (2.7) и выражения для безразмерных моментов (3.11), (3.12) позволяют записать систему уравнений для определения безразмерных величин ${{p}_{1}}$ и ${{p}_{2}}$:

(3.16)
$\begin{gathered} {{a}_{{11}}}{{p}_{1}} + {{a}_{{12}}}{{p}_{2}} = {{b}_{1}} \\ {{a}_{{21}}}{{p}_{1}} + {{a}_{{22}}}{{p}_{2}} = {{b}_{2}}, \\ \end{gathered} $
где

${{a}_{{11}}} = h\left[ {\beta {{\kappa }_{1}}\left( {{{I}_{2}}\cos \lambda - {{I}_{3}}\sin \lambda } \right) + {{f}_{{10\xi }}}{{I}_{4}} + {{f}_{{11\xi }}}{{I}_{5}} + {{f}_{{12\xi }}}{{I}_{6}}} \right]$
${{a}_{{12}}} = \frac{1}{4} + h\left[ {\beta {{\kappa }_{1}}\left( {{{I}_{3}}\cos \lambda + {{I}_{2}}\sin \lambda } \right) + {{f}_{{20\xi }}}{{I}_{4}} + {{f}_{{21\xi }}}{{I}_{5}} + {{f}_{{22\xi }}}{{I}_{6}}} \right]$
(3.17)
$\begin{gathered} {{b}_{1}} = - h{{p}_{0}}\left( {\beta {{\kappa }_{1}}{{I}_{1}} + {{f}_{{01\xi }}}{{I}_{2}} + {{f}_{{02\xi }}}{{I}_{3}}} \right) \\ {{a}_{{21}}} = - \frac{1}{4} + h\left[ {\beta {{\kappa }_{4}}\left( {{{I}_{2}}\cos \lambda - {{I}_{3}}\sin \lambda } \right) + {{f}_{{10\eta }}}{{I}_{4}} + {{f}_{{11\eta }}}{{I}_{5}} + {{f}_{{12\eta }}}{{I}_{6}}} \right] \\ \end{gathered} $
${{a}_{{22}}} = h\left[ {\beta {{\kappa }_{4}}\left( {{{I}_{3}}\cos \lambda + {{I}_{2}}\sin \lambda } \right) + {{f}_{{20\eta }}}{{I}_{4}} + {{f}_{{21\eta }}}{{I}_{5}} + {{f}_{{22\eta }}}{{I}_{6}}} \right]$
${{b}_{2}} = - h{{p}_{0}}\left( {\beta {{\kappa }_{4}}{{I}_{1}} + {{f}_{{01\eta }}}{{I}_{2}} + {{f}_{{02\eta }}}{{I}_{3}}} \right)$

Так как коэффициенты ${{a}_{{ij}}}$ и ${{b}_{i}}$ в (3.17) зависят от $\beta $, направления скорости центра масс относительно неподвижных осей, которое задается углом $\vartheta $ и компонент тензора трения, то и ${{p}_{1}}$ и ${{p}_{2}}$ являются функциями этих параметров.

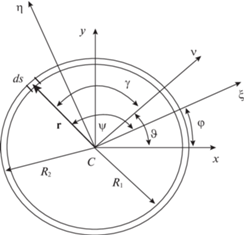
4. Распределение давления при опоре твердого тела на тонкую кольцевую область. Рассмотрим второй классический случай опоры твердого тела на горизонтальную плоскость, а именно, опоры на кольцевую область [4, 5, 9, 11, 12, 18]. В этом случае область контакта тела с плоскостью задается полярными координатами (3.1), где $r \in \left[ {{{R}_{1}},{{R}_{2}}} \right]$, $\psi \in \left[ {0,2\pi } \right)$. При этом будем полагать, что кольцо области контакта тонкое (${{R}_{1}} \to {{R}_{2}}$) (см. рис. 4).

Рис. 4.

Связь декартовой системы координат $Cxy$ с полярной системой для кольцевой области в случае опоры на кольцо.

Для определения ${{p}_{0}}$, ${{p}_{1}}$, ${{p}_{2}}$ вначале проинтегрируем соотношение (2.8) по области контакта. В результате получаем

(4.1)
${{p}_{0}} = \frac{{mg}}{{\pi \left( {R_{2}^{2} - R_{1}^{2}} \right)}}$

Из соотношений (2.9) при переходе к полярным координатам и интегрировании по кольцевой области получим

(4.2)
$\begin{gathered} {{M}_{{C'\xi '}}} = \frac{{{{p}_{2}}\pi \left( {R_{2}^{4} - R_{1}^{4}} \right)}}{4} + h\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\int\limits_0^{2\pi } {\left\{ {{{p}_{0}}\left[ {\beta {{\kappa }_{1}}r + {{r}^{2}}\left( {{{f}_{{01\xi }}}\cos \gamma + {{f}_{{02\xi }}}\sin \gamma } \right)} \right]} \right.} } + \\ + \;{{p}_{1}}\left[ {\beta {{\kappa }_{1}}{{r}^{2}}\cos \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{10\xi }}} + {{f}_{{11\xi }}}\sin \gamma \cos \gamma + {{f}_{{12\xi }}}{{{\cos }}^{2}}\gamma } \right)} \right] + \\ \left. { + \;{{p}_{2}}\left[ {\beta {{\kappa }_{1}}{{r}^{2}}\sin \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{20\xi }}} + {{f}_{{21\xi }}}\sin \gamma \cos \gamma + {{f}_{{22\xi }}}{{{\cos }}^{2}}\gamma } \right)} \right]} \right\}\frac{{drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }} \\ \end{gathered} $
(4.3)
$\begin{gathered} {{M}_{{C'\eta '}}} = - \frac{{{{p}_{1}}\pi \left( {R_{2}^{4} - R_{1}^{4}} \right)}}{4} + h\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\int\limits_0^{2\pi } {\left\{ {{{p}_{0}}\left[ {\beta {{\kappa }_{4}}r + {{r}^{2}}\left( {{{f}_{{01\eta }}}\cos \gamma + {{f}_{{02\eta }}}\sin \gamma } \right)} \right]} \right.} } + \\ + \;{{p}_{1}}\left[ {\beta {{\kappa }_{4}}{{r}^{2}}\cos \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{10\eta }}} + {{f}_{{11\eta }}}\sin \gamma \cos \gamma + {{f}_{{12\eta }}}{{{\cos }}^{2}}\gamma } \right)} \right] + \\ \left. { + \;{{p}_{2}}\left[ {\beta {{\kappa }_{4}}{{r}^{2}}\sin \left( {\gamma + \lambda } \right) + {{r}^{3}}\left( {{{f}_{{20\eta }}} + {{f}_{{21\eta }}}\sin \gamma \cos \gamma + {{f}_{{22\eta }}}{{{\cos }}^{2}}\gamma } \right)} \right]} \right\}\frac{{drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }} \\ \end{gathered} $

В выражениях (4.2) и (4.3) осуществим переход к безразмерным переменным по формулам (3.10), в которых $R$ заменим на ${{R}_{2}}$ и

(4.4)
${{p}_{0}} = \frac{{mg}}{{\pi \left( {R_{2}^{2} - R_{1}^{2}} \right)}}{{p}_{{0*}}},\quad {{p}_{\ell }} = \frac{{mg}}{{\pi \left( {R_{2}^{2} - R_{1}^{2}} \right){{R}_{2}}}}{{p}_{{\ell *}}};\quad \ell = 1,2$

Кроме того, интегрирование по переменной $r$ осуществляем аналогично тому как это было сделано в [4, 5] при стремлении ${{R}_{1}} \to {{R}_{2}}$. В результате безразмерные моменты относительно осей $C{\kern 1pt} '{\kern 1pt} \xi {\kern 1pt} '$ и $C{\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '$ приводятся к виду

${{M}_{{C'\xi '}}} = \frac{{{{p}_{2}}}}{2} + \frac{h}{2}\int\limits_0^{2\pi } {\left\{ {{{p}_{0}}\left[ {\beta {{\kappa }_{1}} + {{f}_{{01\xi }}}\cos \gamma + {{f}_{{02\xi }}}\sin \gamma } \right]} \right.} + $
$ + \;{{p}_{1}}\left[ {\beta {{\kappa }_{1}}\cos \left( {\gamma + \lambda } \right) + {{f}_{{10\xi }}} + {{f}_{{11\xi }}}\sin \gamma \cos \gamma + {{f}_{{12\xi }}}{{{\cos }}^{2}}\gamma } \right] + $
(4.5)
$\begin{gathered} \left. { + \;{{p}_{2}}\left[ {\beta {{\kappa }_{1}}\sin \left( {\gamma + \lambda } \right) + {{f}_{{20\xi }}} + {{f}_{{21\xi }}}\sin \gamma \cos \gamma + {{f}_{{22\xi }}}{{{\cos }}^{2}}\gamma } \right]} \right\}\frac{{d\gamma }}{{\sqrt {{{\beta }^{2}} + 1 - 2\beta \sin \gamma } }} \\ {{M}_{{C'\eta '}}} = - \frac{{{{p}_{1}}}}{2} + \frac{h}{2}\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\int\limits_0^{2\pi } {\left\{ {{{p}_{0}}\left[ {\beta {{\kappa }_{4}} + {{f}_{{01\eta }}}\cos \gamma + {{f}_{{02\eta }}}\sin \gamma } \right]} \right.} } + \\ \end{gathered} $
$ + \;{{p}_{1}}\left[ {\beta {{\kappa }_{4}}\cos \left( {\gamma + \lambda } \right) + {{f}_{{10\eta }}} + {{f}_{{11\eta }}}\sin \gamma \cos \gamma + {{f}_{{12\eta }}}{{{\cos }}^{2}}\gamma } \right] + $
$\left. { + \;{{p}_{2}}\left[ {\beta {{\kappa }_{4}}\sin \left( {\gamma + \lambda } \right) + {{f}_{{20\eta }}} + {{f}_{{21\eta }}}\sin \gamma \cos \gamma + {{f}_{{22\eta }}}{{{\cos }}^{2}}\gamma } \right]} \right\}\frac{{d\gamma }}{{\sqrt {{{\beta }^{2}} + 1 - 2\beta \sin \gamma } }}$

Введем обозначения для интегралов

${{I}_{{1R}}} = \int\limits_0^{2\pi } {\frac{{d\gamma }}{{\sqrt {1 + {{\beta }^{2}} - 2\beta \sin \gamma } }}} ,\quad {{I}_{{2R}}} = \int\limits_0^{2\pi } {\frac{{\cos \gamma d\gamma }}{{\sqrt {1 + {{\beta }^{2}} - 2\beta \sin \gamma } }}} $
(4.6)
${{I}_{{3R}}} = \int\limits_0^{2\pi } {\frac{{\sin \gamma d\gamma }}{{\sqrt {1 + {{\beta }^{2}} - 2\beta \sin \gamma } }}} ,\quad {{I}_{{4R}}} = \int\limits_0^{2\pi } {\frac{{\sin \gamma \cos \gamma d\gamma }}{{\sqrt {1 + {{\beta }^{2}} - 2\beta \sin \gamma } }}} $
${{I}_{{5R}}} = \int\limits_0^{2\pi } {\frac{{{{{\cos }}^{2}}\gamma d\gamma }}{{\sqrt {1 + {{\beta }^{2}} - 2\beta \sin \gamma } }}} ,$
которые выражаются через полные эллиптические интегралы первого и второго рода

${{I}_{{2R}}} = {{I}_{{4R}}} = 0$
(4.7)
$\begin{gathered} {{I}_{{1R}}} = \left\{ {\begin{array}{*{20}{c}} {4{\text{K}}\left( \beta \right);\quad \beta < 1} \\ {\frac{4}{\beta }{\text{K}}\left( {{{\beta }^{{ - 1}}}} \right);\quad \beta \geqslant 1} \end{array}} \right. \\ {{I}_{{3R}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{4}{\beta }\left[ {{\text{K}}\left( \beta \right) - {\text{E}}\left( \beta \right)} \right];\quad \beta < 1} \\ { - 4\left[ {{\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) - {\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta \geqslant 1} \end{array}} \right. \\ \end{gathered} $
${{I}_{{5R}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{4}{{3{{\beta }^{2}}}}\left[ { - \left( {1 - {{\beta }^{2}}} \right){\text{K}}\left( \beta \right) + \left( {1 + {{\beta }^{2}}} \right){\text{E}}\left( \beta \right)} \right];\quad \beta < 1} \\ {\frac{{4\beta }}{3}\left[ {\left( {1 + {{\beta }^{{ - 2}}}} \right){\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) - \left( {1 - {{\beta }^{{ - 2}}}} \right){\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta \geqslant 1} \end{array}} \right.$

В итоге, для определения безразмерных значений ${{p}_{1}}$ и ${{p}_{2}}$ получаем систему уравнений

(4.8)
$\begin{gathered} {{p}_{1}}h\left( { - \beta {{\kappa }_{1}}\sin \lambda {{I}_{{3R}}} + {{f}_{{10\xi }}}{{I}_{{1R}}} + {{f}_{{12\xi }}}{{I}_{{5R}}}} \right) + \\ + \;{{p}_{2}}\left[ {1 + h\left( {\beta {{\kappa }_{1}}\cos \lambda {{I}_{{3R}}} + {{f}_{{20\xi }}}{{I}_{{1R}}} + {{f}_{{22\xi }}}{{I}_{{5R}}}} \right)} \right] = - h{{p}_{0}}\left( {\beta {{\kappa }_{1}}{{I}_{{1R}}} + {{f}_{{02\xi }}}{{I}_{{3R}}}} \right) \\ {{p}_{1}}\left[ { - 1 + h\left( { - \beta {{\kappa }_{4}}\sin \lambda {{I}_{{3R}}} + {{f}_{{10\eta }}}{{I}_{{1R}}} + {{f}_{{12\eta }}}{{I}_{{5R}}}} \right)} \right] + \\ + \;{{p}_{2}}h\left( {\beta {{\kappa }_{4}}\cos \lambda {{I}_{{3R}}} + {{f}_{{20\eta }}}{{I}_{{1R}}} + {{f}_{{22\eta }}}{{I}_{{5R}}}} \right) = - h{{p}_{0}}\left( {\beta {{\kappa }_{4}}{{I}_{{1R}}} + {{f}_{{02\eta }}}{{I}_{{3R}}}} \right), \\ \end{gathered} $
которая может быть упрощена при совмещении системы координат $C\xi \eta \zeta $ с естественным трехгранником ($\lambda = 0$).

Итак, получены системы уравнений, из которых определяются коэффициенты стоящие в формуле распределения плотности давления (2.1). При этом, в отличии от классических работ, рассматривается случай ортотропного трения контакта тела с плоскостью. Это обстоятельство позволяет отметить, что распределение давления зависит от направления скорости центра масс тела, параметра $\beta $ и компонентов тензора трения. Далее, изучим движение твердого тела, опирающегося на круговую и тонкую кольцевую площадки.

5. Сила трения и момент трения. Опора на круговую область. Из первых двух соотношений (2.5) получаем выражения для проекций элементарной силы трения:

$d{{T}_{x}} = - {{f}_{x}}\left[ {{{p}_{0}}{{{v}}_{0}}\cos \vartheta + \xi \left( {{{p}_{1}}{{{v}}_{0}}\cos \vartheta - {{p}_{0}}\omega \sin \varphi } \right)} \right. + \eta \left( {{{p}_{2}}{{{v}}_{0}}\cos \vartheta - {{p}_{0}}\omega \cos \varphi } \right) - $
$\left. { - \;{{\xi }^{2}}{{p}_{1}}\omega \sin \varphi - {{\eta }^{2}}{{p}_{2}}\omega \cos \varphi - \xi \eta \omega \left( {{{p}_{1}}\cos \varphi + {{p}_{2}}\sin \varphi } \right)} \right]\frac{{d\xi d\eta }}{{v}}$
(5.1)
$d{{T}_{y}} = - {{f}_{y}}\left[ {{{p}_{0}}{{{v}}_{0}}\sin \vartheta + \xi \left( {{{p}_{1}}{{{v}}_{0}}\sin \vartheta + {{p}_{0}}\omega \cos \varphi } \right)} \right. + \eta \left( {{{p}_{2}}{{{v}}_{0}}\sin \vartheta - {{p}_{0}}\omega \sin \varphi } \right) + $
$\left. { + \;{{\xi }^{2}}{{p}_{1}}\omega \cos \varphi - {{\eta }^{2}}{{p}_{2}}\omega \sin \varphi + \xi \eta \omega \left( { - {{p}_{1}}\sin \varphi + {{p}_{2}}\cos \varphi } \right)} \right]\frac{{d\xi d\eta }}{{v}}$
${v} = \sqrt {{v}_{0}^{2} + {{\omega }^{2}}\left( {{{\xi }^{2}} + {{\eta }^{2}}} \right) + 2{{{v}}_{0}}\omega \left( {\xi \sin \left( {\vartheta - \varphi } \right) - \eta \cos \left( {\vartheta - \varphi } \right)} \right)} ,$
в которых для круговой площадки контакта перейдем к безразмерным переменным по формулам (3.10), к полярным координатам (3.1) и проинтегрируем в предположении, что ось $С\xi $ направлена вдоль вектора скорости точки $С$ ($\lambda = \vartheta - \varphi = 0$). В итоге получаем проекции силы трения на оси неподвижной системы координат $Oxyz$:
(5.2)
$\begin{gathered} {{T}_{x}} = - \frac{{{{f}_{x}}}}{\pi }\left[ {\left( {{{p}_{0}}\beta {{I}_{1}} - {{p}_{2}}{{I}_{4}} + \left( {{{p}_{2}}\beta - {{p}_{0}}} \right){{I}_{3}}} \right)\cos \vartheta + \left( {{{p}_{2}}\cos \vartheta - {{p}_{1}}\sin \vartheta } \right){{I}_{6}}} \right] \\ {{T}_{y}} = - \frac{{{{f}_{y}}}}{\pi }\left[ {\left( {{{p}_{0}}\beta {{I}_{1}} - {{p}_{2}}{{I}_{4}} + \left( {{{p}_{2}}\beta - {{p}_{0}}} \right){{I}_{3}}} \right)\sin \vartheta + \left( {{{p}_{2}}\sin \vartheta + {{p}_{1}}\cos \vartheta } \right){{I}_{6}}} \right], \\ \end{gathered} $
и, следовательно, на оси естественного трехгранника проекции силы трения будут иметь вид

(5.3)
$\begin{gathered} {{T}_{\tau }} = {{T}_{x}}\cos \vartheta + {{T}_{y}}\sin \vartheta = - \frac{1}{\pi }\left[ {\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)} \right.\left( {{{p}_{0}}\beta {{I}_{1}} - {{p}_{2}}{{I}_{4}} + \left( {{{p}_{2}}\beta - {{p}_{0}}} \right){{I}_{3}}} \right) + \\ + \;\left. {\left( {{{p}_{1}}\mu \sin \vartheta \cos \vartheta + {{p}_{2}}\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)} \right){{I}_{6}}} \right] \\ {{T}_{n}} = - {{T}_{x}}\sin \vartheta + {{T}_{y}}\cos \vartheta = - \frac{1}{\pi }\left[ {\mu \sin \tau \cos \vartheta \left( {p_{0}^{{}}\beta {{I}_{1}} - {{p}_{2}}{{I}_{4}} + \left( {{{p}_{2}}\beta - {{p}_{0}}} \right){{I}_{3}}} \right)} \right. + \\ + \left. {\left( {{{p}_{1}}\left( {{{f}_{x}} + \mu {{{\cos }}^{2}}\vartheta } \right) + {{p}_{2}}\mu \sin \vartheta \cos \vartheta } \right){{I}_{6}}} \right] \\ \end{gathered} $

Момент от силы трения, действующий на элементарную площадку, относительно оси $C\zeta $ определен в (2.5). После перехода к полярным координатам и безразмерным величинам по формулам (3.10), и совмещении подвижной системы координат $C\xi \eta \zeta $ с естественным трехгранником получаем выражение для безразмерного элементарного момента

$d{{M}_{T}} = - \left\{ {{{p}_{0}}\left[ {{{r}^{3}}\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) - {{r}^{2}}\beta \sin \gamma \left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)} \right.} \right. + $
$ + \left. {\;{{r}^{2}}\mu \beta \cos \gamma \sin \vartheta \cos \vartheta + {{r}^{3}}\mu {{{\cos }}^{2}}\gamma \cos 2\vartheta - {{r}^{3}}\mu \sin \gamma \cos \gamma \sin 2\vartheta } \right] + $
$ + \;{{p}_{1}}\left[ { - {{r}^{3}}\beta \sin \gamma \cos \gamma \left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + {{r}^{4}}\cos \gamma \left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)} \right. + $
$ + \;\left. {{{r}^{3}}\mu \beta {{{\cos }}^{2}}\gamma \sin \vartheta \cos \vartheta + {{r}^{4}}\mu {{{\cos }}^{3}}\gamma \cos 2\vartheta - {{r}^{4}}\mu \sin \gamma {{{\cos }}^{2}}\gamma \sin 2\vartheta } \right] + $
$ + \;{{p}_{2}}\left[ { - {{r}^{3}}\beta {{{\sin }}^{2}}\gamma \left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + {{r}^{4}}\sin \gamma \left( {{{f}_{x}} + \mu {{{\cos }}^{2}}\vartheta } \right)} \right. + $
$ + \;{{r}^{3}}\mu \beta \sin \gamma \cos \gamma \sin \vartheta \cos \vartheta + {{r}^{4}}\mu {{\cos }^{3}}\gamma \sin 2\vartheta + $
(5.4)
$ + \;\left. {\left. {{{r}^{4}}\mu \sin \gamma {{{\cos }}^{2}}\gamma \cos 2\vartheta - {{r}^{4}}\mu \cos \gamma \sin 2\vartheta } \right]} \right\}\frac{{drd\lambda }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}$

После интегрирования по области круга получаем выражение для момента трения относительно оси $C\zeta $:

${{M}_{T}} = - \left\{ {{{p}_{0}}[\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)} \right.\left( {{{I}_{4}} - \beta {{I}_{3}}} \right) + \mu \beta {{I}_{2}}\sin \vartheta \cos \vartheta + $
$\left. { + \;\mu \left( {{{I}_{6}}\cos 2\vartheta - {{I}_{5}}\sin 2\vartheta } \right)} \right] + $
$\begin{gathered} + \,{{p}_{1}}\left[ {\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)\left( { - \beta {{I}_{5}} + {{I}_{8}}} \right) + \mu \beta {{I}_{6}}\sin \vartheta \cos \vartheta - } \right. \\ - \left. {\mu \left( {{{I}_{{10}}}\cos 2\vartheta + {{I}_{9}}\sin 2\vartheta } \right)} \right] + \\ \end{gathered} $
$ + \;{{p}_{2}}\left[ {\beta \left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)\left( { - {{I}_{4}} + {{I}_{6}}} \right) + \left( {{{f}_{x}} + \mu {{{\cos }}^{2}}\vartheta } \right){{I}_{7}} + } \right.$
(5.5)
$\left. {\left. { + \;\mu \beta {{I}_{5}}\sin \vartheta \cos \vartheta + \mu \left( {\left( {{{I}_{{10}}} - {{I}_{8}}} \right)\sin 2\vartheta + {{I}_{9}}\cos 2\vartheta } \right)} \right]} \right\}$

Здесь к интегралам (3.14) добавляются следующие:

(5.6)
$\begin{gathered} {{I}_{7}} = \iint {\frac{{{{r}^{4}}\sin \gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}},\quad {{I}_{8}} = \iint {\frac{{{{r}^{4}}\cos \gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}} \\ {{I}_{9}} = \iint {\frac{{{{r}^{4}}\sin \gamma {{{\cos }}^{2}}\gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}},\quad {{I}_{{10}}} = \iint {\frac{{{{r}^{4}}{{{\cos }}^{3}}\gamma drd\gamma }}{{\sqrt {{{\beta }^{2}} + {{r}^{2}} - 2\beta r\sin \gamma } }}}, \\ \end{gathered} $
которые при интегрировании по круговой области записываются в виде

${{I}_{8}} = {{I}_{{10}}} = 0$
(5.7)
${{I}_{7}} = \left\{ {\begin{array}{*{20}{l}} {4{{\beta }^{4}}\left[ {\frac{{16 + 4{{\beta }^{{ - 2}}} - 9{{\beta }^{{ - 4}}}}}{{45}}{\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) - \frac{4}{{45}}\left( {1 - {{\beta }^{{ - 2}}}} \right)\left( {4 + 3{{\beta }^{{ - 2}}}} \right){\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta > 1} \\ {\frac{4}{{225\beta }}\left[ {\left( {1 - {{\beta }^{2}}} \right)\left( {45 + 40{{\beta }^{2}}} \right){\text{K}}\left( \beta \right) + \left( {80{{\beta }^{4}} + 20{{\beta }^{2}} - 45} \right){\text{E}}\left( \beta \right)} \right];\quad \beta \leqslant 1} \end{array}} \right.$
${{I}_{9}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{4{{\beta }^{4}}}}{{15}}\left[ {\frac{{6{{\beta }^{{ - 6}}} - 9{{\beta }^{{ - 4}}} + 19{{\beta }^{{ - 2}}} - 8}}{{21}}{\text{E}}\left( {{{\beta }^{{ - 1}}}} \right) + \frac{{\left( {1 - {{\beta }^{{ - 2}}}} \right)\left( {8 - 15{{\beta }^{{ - 2}}} + 3{{\beta }^{{ - 4}}}} \right)}}{{21}}{\text{K}}\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta > 1} \\ { - \frac{{4\left[ {\left( {8{{\beta }^{6}} - 19{{\beta }^{4}} + 9{{\beta }^{2}} - 6} \right){\text{E}}\left( \beta \right) + 2\left( {1 - {{\beta }^{2}}} \right)\left( {2{{\beta }^{4}} - 3{{\beta }^{2}} + 3} \right){\text{K}}\left( \beta \right)} \right]}}{{315{{\beta }^{3}}}};\quad \beta \leqslant 1} \end{array}} \right.$

6. Опора твердого тела на тонкую кольцевую область. Определение проекций силы трения и момента трения, действующих на твердое тело в рассматриваемом случае, происходит путем интегрирования выражений (5.1) и (5.4) по кольцевой области:

(6.1)
$\begin{gathered} {{T}_{x}} = - \frac{{{{f}_{x}}}}{{2\pi }}\left[ {\left( {{{I}_{{1R}}}\left( {{{p}_{0}}\beta - {{p}_{2}}} \right) + {{I}_{{3R}}}\left( {{{p}_{2}}\beta - {{p}_{0}}} \right)} \right)\cos \vartheta + {{I}_{{5R}}}\left( {{{p}_{2}}\cos \vartheta - {{p}_{1}}\sin \vartheta } \right)} \right] \\ {{T}_{y}} = - \frac{{{{f}_{y}}}}{{2\pi }}\left[ {\left( {{{I}_{{1R}}}\left( {{{p}_{0}}\beta - {{p}_{2}}} \right) + {{I}_{{3R}}}\left( {{{p}_{2}}\beta - {{p}_{0}}} \right)} \right)\sin \vartheta + {{I}_{{5R}}}\left( {{{p}_{2}}\sin \vartheta + {{p}_{1}}\cos \vartheta } \right)} \right] \\ {{M}_{T}} = - \frac{1}{{2\pi }}\left\{ {{{p}_{0}}\left[ {\left( {{{I}_{{1R}}} - \beta {{I}_{{3R}}}} \right)\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + {{I}_{{5R}}}\mu \cos 2\vartheta } \right]} \right. + \\ + \;{{p}_{1}}\left[ {{{I}_{{5R}}}\beta \mu \sin \vartheta \cos \vartheta - \mu {{I}_{{7R}}}\sin 2\vartheta } \right] + \\ + \left. {\;{{p}_{2}}\left[ {\beta \left( { - {{I}_{{1R}}} + {{I}_{{5R}}}} \right)\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + {{I}_{{3R}}}\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + \mu {{I}_{{7R}}}\cos 2\vartheta } \right]} \right\} \\ \end{gathered} $

Здесь

(6.2)
$\begin{gathered} {{I}_{{7R}}} = \int\limits_0^{2\pi } {\frac{{\sin \gamma {{{\cos }}^{2}}\gamma d\gamma }}{{\sqrt {1 + {{\beta }^{2}} - 2\beta \sin \gamma } }}} = \\ = \;\left\{ {\begin{array}{*{20}{l}} {\frac{4}{{15{{\beta }^{3}}}}\left[ {2\left( {1 - {{\beta }^{2}} + {{\beta }^{4}}} \right)E\left( \beta \right) - \left( {{{\beta }^{4}} - 3{{\beta }^{2}} + 2} \right)K\left( \beta \right)} \right];\quad \beta < 1} \\ {\frac{4}{{15{{\beta }^{2}}}}\left[ {2\left( {1 - {{\beta }^{2}} + {{\beta }^{4}}} \right)E\left( {{{\beta }^{{ - 1}}}} \right) + \left( { - 2{{\beta }^{4}} + 3{{\beta }^{2}} - 1} \right)K\left( {{{\beta }^{{ - 1}}}} \right)} \right];\quad \beta \geqslant 1} \end{array}} \right. \\ \end{gathered} $

Проекции на тангенциальную и нормальную оси естественного трехгранника силы трения имеют вид:

(6.3)
$\begin{gathered} {{T}_{\tau }} = - \frac{1}{{2\pi }}\left\{ {\left[ {{{I}_{{1R}}}\left( {{{p}_{0}}\beta - {{p}_{2}}} \right) + {{I}_{{3R}}}\left( {{{p}_{2}}\beta - {{p}_{0}}} \right)} \right]} \right.\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + \\ + \;\left. {{{I}_{{5R}}}\left[ {{{p}_{2}}\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right) + \mu {{p}_{1}}\sin \vartheta \cos \vartheta } \right]} \right\} \\ {{T}_{n}} = - \frac{1}{{2\pi }}\left\{ {\left[ {{{I}_{{1R}}}\left( {{{p}_{0}}\beta - {{p}_{2}}} \right) + {{I}_{{3R}}}\left( {{{p}_{2}}\beta - {{p}_{0}}} \right)} \right]} \right.\mu \sin \vartheta \cos \vartheta + \\ + \;\left. {{{I}_{{5R}}}\left[ {{{p}_{2}}\mu \sin \vartheta \cos \vartheta + {{p}_{1}}\left( {{{f}_{x}} + \mu {{{\cos }}^{2}}\vartheta } \right)} \right]} \right\} \\ \end{gathered} $

7. Уравнения движения и их анализ. Уравнения движения тела по горизонтальной плоскости в проекциях на оси естественного трехгранника записываются в виде

(7.1)
$\begin{gathered} m{\dot {v}} = {{T}_{\tau }}\left( {{{p}_{0}},{{p}_{1}},{{p}_{2}},\beta ,\vartheta } \right) \\ m{v}\dot {\vartheta } = {{T}_{n}}\left( {{{p}_{0}},{{p}_{1}},{{p}_{2}},\beta ,\vartheta } \right) \\ I\dot {\omega } = {{M}_{T}}\left( {{{p}_{0}},{{p}_{1}},{{p}_{2}},\beta ,\vartheta } \right), \\ \end{gathered} $
где ${{T}_{\tau }}$ и ${{T}_{n}}$ определены формулами (5.3) и (6.3), а ${{M}_{T}}$ – (5.5) и (6.1) соответственно для опоры на круг и тонкую кольцевую область. Отметим, что ${{T}_{\tau }}\left( {{{p}_{0}},{{p}_{1}},{{p}_{2}},\beta ,\vartheta } \right) \leqslant 0$, ${{M}_{T}}\left( {{{p}_{0}},{{p}_{1}},{{p}_{2}},\beta ,\vartheta } \right) \leqslant 0$ при любых значениях $\beta $ и $\vartheta $, ${{f}_{x}}$, $\mu $, а величина ${{T}_{n}}$ при соответствующих параметрах, может принимать как положительные, так и отрицательные значения. Покажем это для случая опоры на кольцевую область. Величина ${{T}_{n}}$ в соответствии с соотношением (6.3) переписывается в виде

(7.2)
$\begin{gathered} {{T}_{n}} = - \frac{1}{{2\pi }}\left\{ {_{{}}^{{}}\mu \left[ {{{p}_{0}}\left( {{{I}_{{1R}}}\beta - {{I}_{{3R}}}} \right) + {{p}_{2}}\left( {{{I}_{{3R}}}\beta - {{I}_{{1R}}}} \right)} \right]\sin \vartheta \cos \vartheta } \right. + \\ + \;\left. {{{I}_{{5R}}}\left[ {{{p}_{1}}\left( {{{f}_{x}} + \mu {{{\cos }}^{2}}\vartheta } \right) + \mu {{p}_{2}}\sin \vartheta \cos \vartheta } \right]} \right\} \\ \end{gathered} $

Решим уравнение ${{T}_{n}}\left( {\vartheta ,\;\beta } \right) = 0$ относительно переменной $\vartheta $. Из формул (4.8) при $\lambda = 0$ ($\varphi = \vartheta $) следуют соотношения

${{p}_{1}} = \frac{{{{\Delta }_{1}}}}{\Delta },\quad {{p}_{2}} = \frac{{{{\Delta }_{2}}}}{\Delta }$
${{\Delta }_{1}} = {{p}_{0}}\left( {\beta {{I}_{{1R}}} - {{I}_{{3R}}}} \right)h\left( {{{f}_{x}} + \mu {{{\sin }}^{2}}\vartheta } \right)$
(7.3)
${{\Delta }_{2}} = {{p}_{0}}\left( {\beta {{I}_{{1R}}} - {{I}_{{3R}}}} \right)h\left( {\mu \sin \vartheta \cos \vartheta + h{{I}_{{5R}}}{{f}_{x}}{{f}_{y}}} \right)$
$\Delta = a + b\sin \vartheta \cos \vartheta $
$a = 1 - {{h}^{2}}{{I}_{{5R}}}{{f}_{x}}{{f}_{y}}\left( {\beta {{I}_{{3R}}} - {{I}_{{1R}}} + {{I}_{{5R}}}} \right),\quad b = - h\mu \left( {\beta {{I}_{{3R}}} - {{I}_{{1R}}} + 2{{I}_{{5R}}}} \right),$
после подстановки которых в выражение для ${{T}_{n}}$ в (7.2) получаем

(7.4)
$\begin{gathered} {{T}_{n}} = - \frac{{{{p}_{0}}\left( {{{I}_{{1R}}}\beta - {{I}_{{3R}}}} \right)}}{{8\pi \left( {a + b\sin \vartheta \cos \vartheta } \right)}}\left\{ {{{{\sin }}^{2}}2\vartheta \left[ {\mu b + {{\mu }^{2}}h\left( {1 + {{I}_{{5R}}}} \right) + {{I}_{{5R}}}{{\mu }^{2}}h} \right]} \right. + \\ + \left. {\;\sin 2\vartheta \left[ {2\mu a + 2\mu {{h}^{2}}{{f}_{x}}{{f}_{y}}{{I}_{{5R}}}\left( {1 + {{I}_{{5R}}}} \right)} \right] + 4{{I}_{{5R}}}h{{f}_{x}}{{f}_{y}}} \right\} \\ \end{gathered} $

Откуда при $\mu = 0$ (изотропное трение) будем иметь

(7.5)
${{T}_{n}} = - \frac{{{{p}_{0}}\left( {{{I}_{{1R}}}\beta - {{I}_{{3R}}}} \right)}}{{2\pi a}}{{I}_{{5R}}}h{{f}_{x}}^{2} < 0,$
что означает поворот вектора скорости центра масс по часовой стрелке, если смотреть вдоль вектора скорости. Данный факт отмечен в работах [9, 11].

При увеличении коэффициента $\mu = {{f}_{y}} - {{f}_{x}} > 0$ уравнение ${{T}_{n}}\left( {\vartheta ,\beta } \right) = 0$ может приобрести корни $\vartheta \left( \beta \right)$. Для их определения выражения, стоящие в фигурных скобках в (7.4) приравняем нулю и рассмотрим его как квадратное уравнение относительно $\sin 2\vartheta $. Решение этого уравнения дается соотношениями

(7.6)
$\begin{gathered} \sin 2\vartheta = \frac{{ - 2\left[ {\mu a + \mu {{h}^{2}}{{f}_{x}}{{f}_{y}}{{I}_{{5R}}}\left( {1 + {{I}_{{5R}}}} \right)} \right] \pm \sqrt D }}{{2\left[ {\mu b + {{\mu }^{2}}h\left( {1 + 2{{I}_{{5R}}}} \right)} \right]}} \\ D = 4{{\left[ {\mu a + \mu {{h}^{2}}{{f}_{x}}{{f}_{y}}{{I}_{{5R}}}\left( {1 + {{I}_{{5R}}}} \right)} \right]}^{2}} - 16{{I}_{{5R}}}h{{f}_{x}}{{f}_{y}}\left[ {\mu b + {{\mu }^{2}}h\left( {1 + 2{{I}_{{5R}}}} \right)} \right] \\ \end{gathered} $

Для существования решения (7.6) необходимо чтобы дискриминант $D$ был неотрицательный и абсолютная величина $\sin 2\vartheta $ не превосходила единицу.

Решение системы уравнений (7.1) методом Рунге–Кутта с различными начальными условиями и изучение финальных характеристик движения показывают, что величина угла $\vartheta $ стремится к решению (7.6), при соответствующем финальном значении ${{\beta }_{*}}$. И, кроме того, в момент остановки выполняются соотношения

(7.7)
$\begin{gathered} {{\beta }_{*}} - \Phi \left( {{{\beta }_{*}},{{\vartheta }_{*}}} \right) = 0;\quad \Phi \left( {{{\beta }_{*}},{{\vartheta }_{*}}} \right) = \frac{{{{I}_{*}}{{T}_{\tau }}\left( {{{\beta }_{*}},{{\vartheta }_{*}}} \right)}}{{{{M}_{T}}\left( {{{\beta }_{*}},{{\vartheta }_{*}}} \right)}} \\ \tilde {\Phi }\left( {{{\delta }_{*}},{{\vartheta }_{*}}} \right) - {{\delta }_{*}} = 0;\quad \tilde {\Phi }\left( {{{\delta }_{*}},{{\vartheta }_{*}}} \right) = \frac{{{{M}_{T}}\left( {{{\delta }_{*}},{{\vartheta }_{*}}} \right)}}{{{{I}_{*}}{{T}_{\tau }}\left( {{{\delta }_{*}},{{\vartheta }_{*}}} \right)}} \\ {{\delta }_{*}} = \beta _{*}^{{ - 1}} \\ \end{gathered} $

Обсуждение этих условий представлено в [4, 5].

Замечание. Если в начальный момент угловая скорость рассматриваемых тел равна нулю, то при движении по инерции момент от сил трения будет равен нулю до полной остановки, иными словами, тело будет двигаться как материальная точка в соответствии с уравнениями

$\ddot {x} = - g{{f}_{x}}\cos \vartheta ,\quad \ddot {y} = - g{{f}_{y}}\sin \vartheta ,\quad \ddot {\varphi } = 0$

Аналогичная ситуация наблюдается в случае, когда начальная скорость центра масс равна нулю, но имеется угловая скорость не равная нулю. При таких начальных условиях движение будет чисто вращательным до полной остановки. Момент сил трения в этом случае равен

${{M}_{T}} = - \frac{1}{3}{{p}_{0}}\left( {R_{2}^{3} - R_{1}^{3}} \right)\pi \left( {{{f}_{x}} + {{f}_{y}}} \right) < 0,$
и уравнения движения записываются в виде

$\ddot {x} = 0,\quad \ddot {y} = 0,\quad J\ddot {\varphi } = {{M}_{T}}$

Следует еще отметить, что уравнения (7.7) имеют решения по ${{\beta }_{*}}$ (${{\delta }_{*}} = \beta _{*}^{{ - 1}}$) отличные от нулевого или бесконечно большого при определенных значениях момента инерции. Это было показано для случаев распределения давления по законам Герца, Буссинеска и равномерного распределения давления [12, 14–17]. В рассматриваемой задаче такая зависимость тоже прослеживается.

Подчеркнем, что при численном решении системы уравнений (7.1) и определении финальных характеристик движения тела по инерции при отсутствии решения уравнения ${{T}_{n}}\left( {\vartheta ,\beta } \right) = 0$ угол $\vartheta $ стремится к бесконечности. Очевидно, что в действительности это не происходит и следует иметь критерий остановки численного решения. В публикации [13] отмечено, что при скоростях меньше некоторого значения происходит адгезионное схватывание. Опираясь на этот факт, можно задаться малой величиной $\varepsilon $ и при условии ${v} < \varepsilon $, $\omega < \varepsilon $ остановить процедуру численного решения системы уравнений (7.1), так как при таких скоростях меняется физический процесс в зоне контакта и происходит остановка твердого тела.

В табл. 1 и 2 представлены финальные значения величин ${{\vartheta }_{*}}$ и ${{\beta }_{*}}$ для случая скольжения по инерции цилиндра, опирающегося на круговое основание (${{J}_{*}} = 1{\text{/}}2$) и полого цилиндра, опирающегося на тонкую кольцевую область (${{R}_{1}} \to {{R}_{2}}$, ${{J}_{*}} = 1$). Для сопоставления указанных финальных величин для этих тел было введено предположение, что центр масс тел располагается на одинаковой высоте ($h = 0$, $h = 0.5{{h}_{*}}$, $h = {{h}_{*}}$, ${{h}_{*}} = \frac{1}{{4\pi {{f}_{{y\max }}}}}$, ${{f}_{x}} = 0.42$, ${{f}_{{y\max }}} = {{f}_{x}} + {{\mu }_{{\max }}}$ = 0.84).

Таблица 1.

Кинематические параметры, характеризующие момент остановки цилиндра, опирающегося на круговую площадку при учете согласованного ортотропного трения с учетом его высоты

$\mu $ $h = 0$ $h = 0.5{{h}_{*}}$ $h = {{h}_{*}}$ $\mu $ $h = 0$ $h = 0.5{{h}_{*}}$ $h = {{h}_{*}}$
0.00 $\begin{gathered} \vartheta = {{\vartheta }_{0}} \hfill \\ \beta = 0.653 \hfill \\ \end{gathered} $ – – 0.21 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.928 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.186 \hfill \\ {{\vartheta }_{2}} = 2.955 \hfill \\ \beta = 0.905 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.439 \hfill \\ {{\vartheta }_{2}} = 2.703 \hfill \\ \beta = 0.823 \hfill \\ \end{gathered} $
0.03 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.697 \hfill \\ \end{gathered} $ – – 0.24 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.967 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.165 \hfill \\ {{\vartheta }_{2}} = 2.976 \hfill \\ \beta = 0.944 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.377 \hfill \\ {{\vartheta }_{2}} = 2.765 \hfill \\ \beta = 0.869 \hfill \\ \end{gathered} $
0.06 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.739 \hfill \\ \end{gathered} $ – – 0.27 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.014 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.148 \hfill \\ {{\vartheta }_{2}} = 2.993 \hfill \\ \beta = 0.985 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.333 \hfill \\ {{\vartheta }_{2}} = 2.809 \hfill \\ \beta = 0.911 \hfill \\ \end{gathered} $
0.09 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.778 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.437 \hfill \\ {{\vartheta }_{2}} = 2.704 \hfill \\ \beta = 0.734 \hfill \\ \end{gathered} $ – 0.30 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.089 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.133 \hfill \\ {{\vartheta }_{2}} = 3.009 \hfill \\ \beta = 1.043 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.299 \hfill \\ {{\vartheta }_{2}} = 2.843 \hfill \\ \beta = 0.952 \hfill \\ \end{gathered} $
0.12 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.816 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.316 \hfill \\ {{\vartheta }_{2}} = 2.825 \hfill \\ \beta = 0.785 \hfill \\ \end{gathered} $ – 0.33 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.211 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.117 \hfill \\ {{\vartheta }_{2}} = 3.024 \hfill \\ \beta = 1.138 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.271 \hfill \\ {{\vartheta }_{2}} = 2.871 \hfill \\ \beta = 0.996 \hfill \\ \end{gathered} $
0.15 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.854 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.254 \hfill \\ {{\vartheta }_{2}} = 2.888 \hfill \\ \beta = 0.827 \hfill \\ \end{gathered} $ – 0.36 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.428 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.099 \hfill \\ {{\vartheta }_{2}} = 3.042 \hfill \\ \beta = 1.297 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.243 \hfill \\ {{\vartheta }_{2}} = 2.899 \hfill \\ \beta = 1.065 \hfill \\ \end{gathered} $
0.18 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 0.890 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.214 \hfill \\ {{\vartheta }_{2}} = 2.927 \hfill \\ \beta = 0.867 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.545 \hfill \\ {{\vartheta }_{2}} = 2.597 \hfill \\ \beta = 0.764 \hfill \\ \end{gathered} $ 0.39 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.944 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.078 \hfill \\ {{\vartheta }_{2}} = 3.064 \hfill \\ \beta = 1.620 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.212 \hfill \\ {{\vartheta }_{2}} = 2.930 \hfill \\ \beta = 1.180 \hfill \\ \end{gathered} $
Таблица 2.

Кинематические параметры, характеризующие момент остановки твердого тела, опирающегося на тонкую кольцевую площадку при учете согласованного ортотропного трения

$\mu $ $h = 0$ $h = 0.5{{h}_{*}}$ $h = {{h}_{*}}$ $\mu $ $h = 0$ $h = 0.5{{h}_{*}}$ $h = {{h}_{*}}$
0.00 $\begin{gathered} \vartheta = {{\vartheta }_{0}} \hfill \\ \beta = 1.000 \hfill \\ \end{gathered} $ – – 0.21 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.192 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.146 \hfill \\ {{\vartheta }_{2}} = 2.996 \hfill \\ \beta = 1.172 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.318 \hfill \\ {{\vartheta }_{2}} = 2.823 \hfill \\ \beta = 1.118 \hfill \\ \end{gathered} $
0.03 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.010 \hfill \\ \end{gathered} $ – – 0.24 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.257 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.128 \hfill \\ {{\vartheta }_{2}} = 3.013 \hfill \\ \beta = 1.233 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.278 \hfill \\ {{\vartheta }_{2}} = 2.863 \hfill \\ \beta = 1.167 \hfill \\ \end{gathered} $
0.06 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.026 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.499 \hfill \\ {{\vartheta }_{2}} = 2.639 \hfill \\ \beta = 1.011 \hfill \\ \end{gathered} $ – 0.27 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.344 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.113 \hfill \\ {{\vartheta }_{2}} = 3.029 \hfill \\ \beta = 1.313 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.245 \hfill \\ {{\vartheta }_{2}} = 2.896 \hfill \\ \beta = 1.230 \hfill \\ \end{gathered} $
0.09 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.046 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.316 \hfill \\ {{\vartheta }_{2}} = 2.896 \hfill \\ \beta = 1.033 \hfill \\ \end{gathered} $ – 0.30 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.466 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.099 \hfill \\ {{\vartheta }_{2}} = 3.043 \hfill \\ \beta = 1.424 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.217 \hfill \\ {{\vartheta }_{2}} = 2.925 \hfill \\ \beta = 1.314 \hfill \\ \end{gathered} $
0.12 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.071 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.240 \hfill \\ {{\vartheta }_{2}} = 2.901 \hfill \\ \beta = 1.058 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.612 \hfill \\ {{\vartheta }_{2}} = 2.518 \hfill \\ \beta = 1.014 \hfill \\ \end{gathered} $ 0.33 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.651 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.085 \hfill \\ {{\vartheta }_{2}} = 3.056 \hfill \\ \beta = 1.588 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.190 \hfill \\ {{\vartheta }_{2}} = 2.952 \hfill \\ \beta = 1.432 \hfill \\ \end{gathered} $
0.15 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.102 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.197 \hfill \\ {{\vartheta }_{2}} = 2.945 \hfill \\ \beta = 1.088 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.453 \hfill \\ {{\vartheta }_{2}} = 2.689 \hfill \\ \beta = 1.045 \hfill \\ \end{gathered} $ 0.36 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.971 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.070 \hfill \\ {{\vartheta }_{2}} = 3.071 \hfill \\ \beta = 1.863 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.162 \hfill \\ {{\vartheta }_{2}} = 2.979 \hfill \\ \beta = 1.613 \hfill \\ \end{gathered} $
0.18 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 1.142 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.167 \hfill \\ {{\vartheta }_{2}} = 2.974 \hfill \\ \beta = 1.125 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.371 \hfill \\ {{\vartheta }_{2}} = 2.770 \hfill \\ \beta = 1.079 \hfill \\ \end{gathered} $ 0.39 $\begin{gathered} {{\vartheta }_{1}} = 0 \hfill \\ {{\vartheta }_{2}} = \pi \hfill \\ \beta = 2.717 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.052 \hfill \\ {{\vartheta }_{2}} = 3.090 \hfill \\ \beta = 2.455 \hfill \\ \end{gathered} $ $\begin{gathered} {{\vartheta }_{1}} = - 0.131 \hfill \\ {{\vartheta }_{2}} = 3.010 \hfill \\ \beta = 1.931 \hfill \\ \end{gathered} $

В табл. 1 и 2 имеются незаполненные ячейки. Это означает, что при параметрах $\mu $ и $h$, которые соответствуют этим ячейкам решение системы (7.7) отсутствует. Отметим, что нет решения и при значениях $\mu > 0.42$. Это означает, что финальное движение при данных параметрах характеризуется отсутствием решения уравнения ${{T}_{n}}({{\vartheta }_{*}},{{\beta }_{*}}) = 0$ и стремлением безразмерной величины ${{\beta }_{*}} = {{{v}}_{*}}{\text{/}}{{\omega }_{*}}$ к нулю или бесконечности.

Важной особенностью движения при динамически согласованном трении является искривление траектории центра масс. На рис. 5 изображена траектория центра масс цилиндра в случае $h = 0.5{{h}_{*}}$ и $\mu $ равных 0, 0.21 и 0.42. На рис. 6 тоже, но при $h = {{h}_{*}}$. Траектория центра масс тонкостенного полого цилиндра при тех же параметрах $h$ и $\mu $ представлены на рис. 7 и рис. 8. Начальные условия во всех случаях были одинаковыми: $t = 0$, ${{{v}}_{0}} = 0.1$, ${{\vartheta }_{0}} = 0$, ${{\omega }_{0}} = 1$.

Рис. 5.

Траектории центра масс цилиндра, опирающегося на круг основания при $h = 0.5{{h}_{*}}$.

Рис. 6.

Траектории центра масс цилиндра, опирающегося на круг основания при $h = {{h}_{*}}$.

Рис. 7.

Траектории центра масс полого цилиндра, опирающегося на окружность основания при $h = 0.5{{h}_{*}}$.

Рис. 8.

Траектории центра масс полого цилиндра, опирающегося на окружность основания при $h = {{h}_{*}}$.

Численные расчеты представленные в табл. 1 и 2, а так же работа [5] показывают, что при $h = 0$ непосредственно перед остановкой центр масс пластины, имеющей форму круга или тонкого кольца, при равномерном распределении давления имеет скорость направленную параллельно оси, вдоль которой коэффициент трения минимален. В случае учета расстояния от плоскости скольжения до центра масс тела качественный и количественный результат меняется. При некоторых значениях параметра $\mu $ решения системы (7.7) и уравнения ${{T}_{n}}\left( {\vartheta ,\beta } \right) = 0$ нет, формально угол $\vartheta $ при численном решении системы (7.1) стремится к бесконечности. Если решение (7.7) имеется, то финальное движение характеризуется искривлением траектории в сторону противоположную угловой скорости, как и в случае изотропного трения. То есть эффект учета расположения центра масс над плоскостью превосходит эффект, который возникает от ортотропности трения. Но при увеличении параметра $\mu $ влияние этих эффектов могут стать сопоставимыми, из представленных таблиц видно, что при увеличении параметра $\mu $ вектор скорости на финальном участке становится ближе к оси, вдоль которой коэффициент трения меньше.

Заключение. Подведем некоторые итоги.

1. При изучении движения твердого тела по инерции при наличии сил трения скорость центра масс и угловая скорость должны обратиться в ноль. Поэтому следует выработать условие, при котором численные расчеты следует остановить. Это важно, когда уравнение ${{T}_{n}}\left( {{{\vartheta }_{*}},{{\beta }_{*}}} \right) = 0$ не имеет решений, так как в этом случае величина $\vartheta $ будет стремиться к бесконечности.

2. Введенная в работе величина $\beta = {{{v}}_{0}}{\text{/}}\omega $ соответствует расстоянию от центра масс до мгновенной оси вращения. При финальном движении эта характеристика может иметь конечное значение, равняться нулю или стремиться к бесконечности. Прослеживается зависимость величины $\beta $ от величины $\mu = {{f}_{y}} - {{f}_{x}} \geqslant 0$ и от расстояния от центра масс до плоскости $h$, по которой происходит скольжение. На данный момент не удалось получить утверждения, связывающие компоненты тензора трения, момент инерции тела, величину $h$ и значение $\beta $, как это было сделано в [14–17].

3. Если начальная скорость направлена вдоль оси $Oy$ (${{f}_{y}} > {{f}_{x}}$), то сочетание согласованного трения и ортотропного трения, приводит к увеличению отклонения центра масс вправо, если смотреть вдоль вектора начальной скорости. В случае, когда начальная скорость направлена вдоль оси $Ox$, происходит уменьшение отклонения центра масс вправо, вызываемого учетом расстояния от центра масс до плоскости скольжения вследствие влияния сил ортотропного трения. В [5] было отмечено, что движение вдоль главной оси, соответствующей наибольшему коэффициенту трения при ортотропном трении, является неустойчивым главным направлением скольжения. Одновременный учет концепции согласованного трения и закона ортотропного трения усиливает неустойчивость движения вдоль оси $Oy$.

4. Движение при динамически согласованном изотропном трении изучалось в работах [11, 18, 19]. В них были сформулированы утверждения отражающие качественные особенности движения симметричных тел. Изучение движения при согласованном ортотропном трении требует изменения формулировок утверждений, сделанных в этих публикациях. В частности, появляется зависимость от направления скорости на финальном участке движения тела по инерции. Особым случаем является опора тела на несколько точек [20]. При таком контакте тела с плоскостью финальное движение может быть вращением вокруг оси, проходящей через точку опоры, быть поступательным или может существовать предельное положение мгновенной оси вращения. При этом все эти варианты зависят от ориентации опор по отношению к главным осям скольжения. В данном направлении предполагаются дальнейшие исследования.

5. Результаты, полученные в работе, могут быть применены при исследовании динамики систем, в которых контакт с плоскостью происходит по круговой или кольцевой площадке или совокупности таких площадок.

В ходе подготовки данной статьи автор обсуждал результаты со своим учителем Товстиком Петром Евгеньевичем. Его точные и доброжелательные замечания учтены при подготовке данной публикации. К огромному сожалению Петра Евгеньевича не стало в декабре 2020 года. Данную статью посвящаю большому ученому, моему наставнику Товстику Петру Евгеньевичу.

Список литературы

  1. Иванов А.П. Динамически совместная модель контактных напряжений при плоском движении твердого тела // ПММ. Т. 73. Вып. 2. 2009. С. 189–203.

  2. Александрович А.И., Векшин В.С., Потапов И.Н. Тензор коэффициентов трения анизотропных поверхностей // Трение и износ. 1985. Т. 4. № 6. С. 996–1004.

  3. Zmitrowicz A. Mathematical descriptions of anisotropic friction // Int. J. Solids&Struct. 1989. № 25(8). P. 837–862. https://doi.org/10.1016/0020-7683(89)90034-6

  4. Ишлинский А.Ю., Соколов Б.Н., Черноусько Ф.Л. О движении плоских тел при наличии сухого трения // Изв. АН СССР. МТТ. 1981. № 4. С. 17–28.

  5. Дмитриев Н.Н. Движение диска и кольца по плоскости с анизотропным трением // Трение и износ. 2002. Т. 23. № 1. С. 10–15.

  6. Русинова А.М. О динамике однородной шайбы на наклонной плоскости с трением // ПММ. 2013. Т. 77. Вып. 4. С. 538–544.

  7. Русинова А.М. О динамике шайбы на наклонной плоскости при несимметричном распределении нормальных напряжений // ПММ. Механика. 2015. Т. 79. Вып. 6. С. 768–777.

  8. Зобова А.А. Обзор моделей распределенного сухого трения // ПММ. 2016. Т. 80. Вып. 2. С. 194–206.

  9. Иванов А.П., Шувалов Н.Д. О движении тяжелого тела с кольцевым основанием по горизонтальной плоскости и загадках керлинга // Нелин. дин. 2011. Т. 7. № 3. С. 521–530.

  10. Мак-Миллан В.Д. Динамика твердого тела. М.: Иностр. лит., 1951. 468 с.

  11. Иванов А.П. Основы теории систем с трением. М.; Ижевск: Регул. и хаотич. дин., 2011. 302 с.

  12. Розенблат Г.М. Динамические системы с трением. М.; Ижевск: Регул. и хаотич. Дин., 2006. 204 с.

  13. Веттегрень В.И., Савицкий А.В., Ляшков А.И., Мамалимов Р.И. Зависимость коэффициента трения одномерно армированного волокнистого композита от свойств матрицы // Письма в ЖТФ. 2008. Т. 34. Вып. 19. С. 79–85.

  14. Дмитриев Н.Н. Скольжение твердого тела, опирающегося на круговую площадку, по горизонтальной плоскости с ортотропным трением. Ч. I. Равномерное распределение нагрузки // Трение и износ. 2009. Т. 30. № 4. С. 317–326.

  15. Дмитриев Н.Н. Скольжение твердого тела, опирающегося на круговую площадку, по горизонтальной плоскости с ортотропным трением. Ч. II. Распределение давления по закону Буссинеска // Трение и износ. 2009. Т. 30. № 5. С. 429–439.

  16. Дмитриев Н.Н. Скольжение твердого тела, опирающегося на круговую площадку, по горизонтальной плоскости с ортотропным трением. Ч. III. Распределение давления по закону Герца // Трение и износ. 2010. Т. 31. № 4. С. 342–352.

  17. Дмитриев Н.Н. Движение твердых тел, опирающихся на тонкую кольцевую область, по горизонтальной плоскости с ортотропным трением// Вестн. СПб. ун-та. Сер. 1. 2011. Вып. 4. С. 109–117.

  18. Ердакова Н.Н., Мамаев И.С. Динамика тела с осесимметричным основанием, скользящего по шероховатой плоскости // Нелин. дин. 2013. Т. 9. № 3. С. 521–545.

  19. Сальникова Т.В., Трещев Д.В., Галлямов С.Р. Движение свободной шайбы по шероховатой горизонтальной плоскости // Нелин. дин. 2012. Т. 8. № 1. С. 83–101.

  20. Розенблат Г.М. О движении тела, опирающегося на шероховатую горизонтальную плоскость тремя точками // Докл. РАН. 2017. Т. 476. № 1. С. 35–38.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал