Прикладная математика и механика, 2022, T. 86, № 5, стр. 654-665
Равновесие упругого тела с закругленными кромками на упругом наклонном полупространстве
А. А. Зобова 1, *, И. Г. Горячева 1, 2, **
1 МГУ им. М.В. Ломоносова
Москва, Россия
2 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: alexandra.zobova@math.msu.ru
** E-mail: goryache@ipmnet.ru
Поступила в редакцию 15.06.2022
После доработки 15.07.2022
Принята к публикации 25.07.2022
- EDN: KFZHFQ
- DOI: 10.31857/S0032823522050137
Аннотация
Рассмотрена задача о равновесии упругого тела с плоским основанием и закругленными кромками на наклоненном полупространстве из того же материала в поле силы тяжести. Получены уравнения, определяющие границы области контактного взаимодействия и подобластей частичного проскальзывания и сцепления на ней. Изучено влияние механических и геометрических характеристик взаимодействующих тел и коэффициента трения на структуру области контактного взаимодействия и угол поворота тела вследствие деформаций. Построены графики распределений нормальных и касательных напряжений в области контактного взаимодействия в зависимости от угла наклона основания и расположения центра масс упругого тела. Определено условие его скольжения по основанию.
1. Введение. Задача о равновесии тела на деформируемом основании является классической задачей теории упругости [1–4]. Основное внимание при ее исследовании уделяется таким вопросам, как определение областей контактного взаимодействия, сближения взаимодействующих тел, а также распределения напряжений в деформируемом материале при заданных независимых друг от друга прижимной и касательной нагрузках и моменте. В теоретической механике в подобных задачах определяются возможные положения равновесия систем тел под действием некоторой заданной внешней силы, чаще всего, силы тяжести. При этом вопрос определения компонент реакции, т.е. прижимной и касательной нагрузки и момента, обеспечивающих равновесие, для систем с сухим трением представляет значительную сложность [6, 7]. В связи с этим модели контактного взаимодействия между телами значительно упрощаются. Так, например, при решении задачи о равновесии системы тел в [8] контакт между телами сложной формы предполагается сосредоточенным в трех точках, а трение между телами задается классическим законом Кулона–Амонтона.
В представленной работе подходы теории упругости и теоретической механики объединяются при исследовании равновесия тела на наклонной плоскости с сухим трением. Эта задача является составной частью многих практических задач: например, в динамике мобильных роботов (например, [9, 10]), в том числе при движении в сложной среде с препятствиями [11], задачах о движении гранулированных сред [12], при экспериментальном определении параметров взаимодействия объектов в различных условиях [13, 14].
Рассматривается равновесие упругого цилиндрического тела на наклоненном полупространстве из того же материала в поле силы тяжести. Предполагается, что контактирующая поверхность тела состоит из плоского участка и закругленных кромок. Вследствие деформируемости контактирующих тел и действия силы тяжести упругое тело поворачивается на некоторый угол, и в области контактного взаимодействия возникает несимметричное распределение нормальных $p$ и касательных напряжений $q$, которое определяется решением статической задачи теории упругости [4, 15], учитывающим существование подобластей скольжения и сцепления поверхностей в области их контакта. В отличие от [4, 15], прижимающая и касательная внешние силы, действующие на тело, не являются независимыми величинами, а суть проекции силы тяжести и зависят от угла наклона полупространства к горизонту; при этом момент силы тяжести определяется как положением центра масс в теле, так и его поворотом вследствие упругих деформаций.
Целью исследования является изучение условий равновесия тела в зависимости от механических характеристик материалов взаимодействующих тел, расположения центра масс лежащего на наклонном основании тела, ширины его плоского участка, коэффициента трения и угла наклона к горизонту поверхности основания. Представлены постановка задачи (разд. 2), распределения контактных напряжений и уравнения, определяющие границы контактной области и угол наклона упругого тела (разд. 3), анализ влияния наклона основания и коэффициента трения на расположение подобластей сцепления и проскальзывания в области контактного взаимодействия (разд. 4), зависимость угла наклона упругого тела, лежащего на наклоненном основании, от его геометрических, массово-инерционных и механических характеристик (разд. 5).
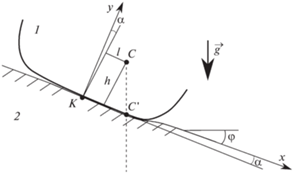
2. Постановка задачи. Рассмотрим (рис. 1) задачу о равновесии в поле силы тяжести тела 1 на полупространстве 2 из одного и того же линейно упругого материала с модулем Юнга $E$ и коэффициентом Пуассона $\nu $. Недеформированная граница $Oxz$ полупространства составляет угол $\varphi $ с горизонтом. Тело предполагается бесконечно протяженным в направлении оси $Oz$, перпендикулярной к плоскости чертежа; обозначим $m$ – его массу на единицу длины в этом направлении.
С недеформированной границей основания свяжем систему отсчета $Kxyz$, ось $Ky$ перпендикулярна основанию, плоскость $Kxy$ перпендикулярна образующей тела. Пусть точка $K$ является серединой плоской части основания тела, ширину которой обозначим $2c$, радиусы кривизны кромок равны $R$ (в точках $x = \pm c$). Наклон тела к основанию, возникающий в результате действия на него силы тяжести и деформации контактирующих тел, обозначим $\alpha $. Этот угол, как и границы области контактного взаимодействия $x \in [ - a,b]$ заранее неизвестны и определяются решением контактной задачи. Обозначим $\gamma = \operatorname{tg} \alpha $, тогда форма наклоненного индентора описывается функцией:
(2.1)
$f(x) = \left( \begin{gathered} \frac{{{{{(x + c)}}^{2}}}}{{2R}} - \gamma x,\quad - {\kern 1pt} a \leqslant x \leqslant - c \hfill \\ - \gamma x,\quad - {\kern 1pt} c \leqslant x \leqslant c \hfill \\ \frac{{{{{(x - c)}}^{2}}}}{{2R}} - \gamma x,\quad c \leqslant x \leqslant b \hfill \\ \end{gathered} \right.$Замечание. Заметим, что форма наклоненного тела на скруглениях описывается указанной функцией лишь для малых углов $\alpha $, таких что $\operatorname{tg} \alpha \simeq sin\alpha \simeq \alpha $, $cos\alpha \simeq 1$.
Сделаем следующие предположения о касательных напряжениях на деформированной границе двух тел, которая состоит из подобластей сцепления и проскальзывания точек взаимодействующих поверхностей [3, 4]:
• В области скольжения ${{\Omega }_{s}}$ направление касательных сил противоположно направлению относительного проскальзывания, т.е.
где $\mu $ – коэффициент трения, $s(x) = ({{u}_{{x1}}}(x) - {{u}_{{x2}}}(x) - {{\delta }_{x}})$ – относительное проскальзывание частиц материала, ${{u}_{{xi}}}(x)$ – смещение границы каждого тела ($i = 1,2$) в результате их упругого деформирования вдоль оси $Kx$, ${{\delta }_{x}} = {\text{const}}$ – относительное смещение в направлении оси $Kx$ фиксированных точек тел, расположенных на некотором удалении от области контакта. Заметим, что величина этого смещения не оказывает влияние на распределение нормальных и касательных напряжений в области контактного взаимодействия.• В области сцепления ${{\Omega }_{a}}$ относительное проскальзывание $s(x)$ равно нулю, т.е.
и выполняется равенствоДоказано [4], что возможна только одна зона сцепления внутри области контактного взаимодействия, т.е. ${{\Omega }_{a}} = [{{d}_{1}},{{d}_{2}}]$, ${{\Omega }_{s}} = \left[ { - a,{{d}_{1}}} \right) \cup \left( {{{d}_{2}},b} \right]$. Суммарная реакция, действующая на тело со стороны основания, равна
Момент касательных напряжений относительно точки $K$ равен нулю, а момент нормальных напряжений направлен вдоль оси $Kz$ и равен
Составим уравнения равновесия тела. Пренебрегая перераспределением массы из-за деформации тела при контакте с основанием, будем считать, что действие силы тяжести в каждом вертикальном сечении сводится к одной силе $m\vec {g}$, приложенной в центре масс $C$, который находится на высоте $h$ от плоской части основания и смещен на расстояние $l$ от оси симметрии (рис. 1). Проекции силы тяжести на оси $Ox$ и $Oy$ соответственно равны $mgsin\varphi $ и $ - mgcos\varphi $, а величина момента силы тяжести относительно точки $K$ зависит от угла наклона тела и равна $mg(lcos(\varphi + \alpha ) + hsin(\varphi + \alpha ))$. Окончательно, условия равновесия тела имеют вид:
(2.7)
${{{M}_{K}} = \int\limits_{ - a}^b x p(x)dx = mg(lcos(\varphi + \alpha ) + hsin(\varphi + \alpha ))}$Это система уравнений относительно функций $p(x)$ и $q(x)$ и угла поворота тела $\alpha $ совместно с граничными условиями (2.2)–(2.4) для определения контактных напряжений служит для расчета как контактных напряжений, так и угла поворота тела при заданных точке приложения и величине силы тяжести.
3. Распределение нормальных и касательных напряжений. Обезразмерим величины, имеющие размерность длины, выбрав радиус скругления кромок тела в качестве масштаба:
Параметр $P{\text{*}}$ задает соотношение между весом тела, радиусом скругления и упругими модулями материала.
Вследствие равенства упругих модулей тела и основания, уравнения, определяющие распределения нормальных $p(x)$ и касательных $q(x)$ контактных напряжений, разделяются. Согласно решению Мусхелишвили [2], распределение нормальных напряжений определяется формулой:
(3.2)
$\frac{{p(x)}}{{E{\text{*}}}} = - \frac{{\sqrt {(x + a)(b - x)} }}{{2\pi }}\int\limits_{ - a}^b {\frac{{h{\text{'}}(t)dt}}{{(t - x)\sqrt {(t + a)(b - t)} }}} ;\quad x \in [ - a,b],$(3.3)
$h{\kern 1pt} '(x) = - f{\kern 1pt} '(x) = \left( \begin{gathered} - (x + c) + \gamma ,\quad - {\kern 1pt} a \leqslant x \leqslant - c \hfill \\ \gamma ,\quad - {\kern 1pt} c \leqslant x \leqslant c \hfill \\ - (x - c) + \gamma ,\quad c \leqslant x \leqslant b \hfill \\ \end{gathered} \right.$Границы области контактного взаимодействия $a$, $b$ и тангенс угла наклона $\gamma $ плоской части тела определяются из следующих уравнений, являющихся следствиями уравнений равновесия (2.5), (2.7) и условия сходимости интеграла (3.2):
(3.4)
$\int\limits_{ - a}^b {\frac{{th{\kern 1pt} '(t)dt}}{{\sqrt {(t + a)(b - t)} }}} = - 2P{\kern 1pt} *{\kern 1pt} \cos \varphi $(3.5)
$\frac{1}{{E{\kern 1pt} *}}\int\limits_{ - a}^b {tp} (t)dt = P{\kern 1pt} *{\kern 1pt} (l\cos (\varphi + \alpha ) + h\sin (\varphi + \alpha ))$Распределение касательных напряжений, удовлетворяющее граничным условиям (2.2) и (2.4) в областях скольжения ${{\Omega }_{s}}$ и сцепления ${{\Omega }_{a}}$, имеет вид [4]:
Функция $q{\kern 1pt} *{\kern 1pt} (x)$ определяется соотношением [4]
(3.7)
$\frac{{q{\kern 1pt} *{\kern 1pt} (x)}}{{E{\kern 1pt} *}} = - \frac{{\mu \sqrt {({{d}_{2}} - x)(x - {{d}_{1}})} }}{{2\pi }}\int\limits_{{{d}_{1}}}^{{{d}_{2}}} {\frac{{h{\kern 1pt} '(t)dt}}{{(t - x)\sqrt {({{d}_{2}} - t)(t - {{d}_{1}})} }}} ;\quad x \in \left[ {{{d}_{1}},{{d}_{2}}} \right],$(3.8)
$\int\limits_{{{d}_{1}}}^{{{d}_{2}}} {\frac{{h{\text{'}}(t)dt}}{{\sqrt {({{d}_{2}} - t)(t - {{d}_{1}})} }}} = 0$(3.9)
$\mu \int\limits_{{{d}_{1}}}^{{{d}_{2}}} {\sqrt {\frac{{{{d}_{2}} - t}}{{t - {{d}_{1}}}}} } h{\text{'}}(t)dt = 2P{\text{*}}(\mu cos\varphi - sin\varphi )$Последнее уравнение есть следствие уравнения равновесия (2.6).
Таким образом, решение задачи о равновесии упругого тела на наклонном основании сводится к последовательному решению системы (3.4)–(3.6) относительно $a$, $b$ и $\gamma = \operatorname{tg} \alpha $ и затем системы (3.8)–(3.9) относительно ${{d}_{1}}$ и ${{d}_{2}}$. Параметрами первой системы являются величины $P{\text{*}}$, угол наклона опорного полупространства $\varphi $, ширина плоской части $c$ и положение центра масс ($l$, $h$); во второй системе к параметрам добавляется коэффициент трения $\mu $.
Решение указанных систем проводилось численно с помощью библиотеки численных методов GNU Scientific Library. Заметим, что в [4] приведены точные аналитические выражения для распределения давлений (3.2) и касательных напряжений (3.7) для заданной функции (3.3), а также конечные уравнения на параметры распределений, равносильные (3.4)–(3.6) и (3.8)–(3.9). Эти выражения использовались для проверки точности численных расчетов, но так как в настоящей работе решение системы уравнений проводилось численно, то для получения результатов использовались указанные выше универсальные интегральные формулы. Это не ухудшало существенно скорости и точности получения результатов.
4. Влияние угла наклона основания и коэффициента трения на структуру области контактного взаимодействия. При расчетах в качестве базовых были выбраны следующие численные значения безразмерных параметров:
Значение для $P{\text{*}}$ выбрано на основании значений плотности $\rho $ и модулей упругости $E$, $\nu $ для некоторого типа резины ($\rho = 1100$ кг/м3, $E = 23$ МПа, $\nu = 0.5$).
На рис. 2 приведена зависимость границ области контактного взаимодействия $ - a$ и $b$ и границ области сцепления ${{d}_{1}}$ и ${{d}_{2}}$ от угла наклона основания для трех значений коэффициента трения $\mu = 0.1$, $\mu = 0.2$, $\mu = 0.3$.
Рис. 2.
Зависимость границ области контактного взаимодействия $\left[ { - a,b} \right]$ (кривые 1 и 2) и области сцепления от угла $\varphi $ для коэффициентов трения $\mu = 0.1$ (кривые 3, пунктир и сплошная), 0.2 (кривые 4), 0.3 (кривые 5). Тонкая линия 6 – координата вертикальной проекции центра масс тела на основание.
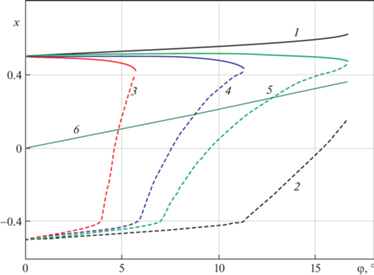
Коэффициент трения не влияет на ширину и положение области контактного взаимодействия. Кроме того, ясно, что при симметричном расположении центра масс ($l = 0$) структура контактной области симметрична для положительных и отрицательных углов наклона $\varphi $, поэтому далее рассматривается только случай $\varphi \geqslant 0$. Для указанных выше параметров при $\varphi < 12^\circ $ тело опирается как на плоскую часть, так и на оба скругления. При $\varphi > 12^\circ $ контакт происходит по плоской части и правому краю тела (т.е. $a < c$).
Расчеты показывают, что если контактная область распространяется на оба (рис. 3, a,б) или один (рис. 3, в) скругленный край, то распределение давлений имеет максимум (один или два) на соответствующем участке контактной области. Давление минимально на плоской части контактирующей поверхности упругого тела. Распределение касательных напряжений в областях проскальзывания показано на рис. 3 красными линиями. При увеличении угла наклона основания величины максимальных контактных напряжений возрастают.
Рис. 3.
Распределение нормированных нормальных $\mu p(x){\text{/}}E{\text{*}}$ (черная сплошная линия 1) и касательных $q(x){\text{/}}E{\text{*}}$ напряжений (красная штриховая линия 2) при $\varphi = 5^\circ $ (а), 10° (б), 16° (в), коэффициент трения $\mu = 0.3$.
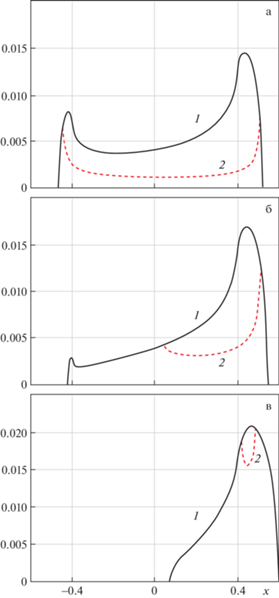
Коэффициент трения $\mu $ влияет на расположение и ширину областей проскальзывания и сцепления материалов. Область сцепления ${{\Omega }_{a}}$ всегда единственна и находится внутри контактной области, причем для малых углов распространяется на плоскую часть и оба скругления, т.е. ${{d}_{1}} < - c$, ${{d}_{2}} > c$ (рис. 3, a), на плоскую часть и правое скругление, т.е. $ - c < {{d}_{1}} < c$, ${{d}_{2}} > c$ (рис. 3, б), только на скругление, т.е. $c < {{d}_{1}} < {{d}_{2}}$ (рис. 3, в).
Максимальное значение угла наклона основания, при котором область сцепления существует и соответственно выполнено условие равновесия (3.5), определяется неравенством [4]
откуда следует (см. (2.5), (2.6))При выполнении этого условия существует единственное решение системы уравнений (3.8)–(3.9). При критическом угле наклона основания $\varphi * = \operatorname{arctg} \mu $ область сцепления вырождается в одну точку ${{d}_{1}} = {{d}_{2}}$.
Замечание. Поворот тела на угол $\alpha $ не влияет на условие равновесия (4.1), означающее отсутствие скольжения. Это связано с тем, что в линейной теории упругости вследствие предположения о малости деформаций как опоры, так и самого тела давление $p(x)$ и касательное напряжение $q(x)$ относят к недеформированной границе основания – т.е. оси $Kx$, поэтому касательные напряжения должны уравновешивать только касательную составляющую силы тяжести $Q = mgsin\varphi $ (не зависящую от $\alpha $), а их момент относительно точки $K$ равен нулю. Вообще говоря, при учете изменения наклона элементарных площадок в контактной области результирующая касательных напряжений $Q$ не параллельна оси $Kx$, а их момент окажется ненулевым. Тогда модифицированные уравнения, соответствующие (3.4)–(3.6) и (3.8)–(3.9), не будут разделяться, а критический угол $\varphi {\text{*}}$, помимо коэффициента трения $\mu $, будет зависеть от остальных параметров задачи. Однако эти эффекты малы и в настоящей работе не учитываются.
5. Зависимость наклона тела от параметров задачи. Наклон тела $\alpha $ определяется как углом наклона упругого основания $\varphi $, так и другими параметрами задачи.
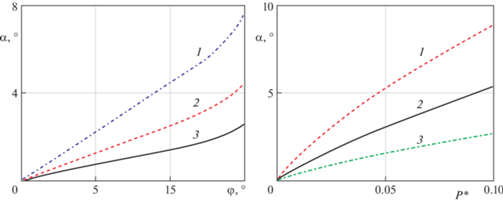
При расположении центра масс на оси симметрии тела ($l = 0$) на горизонтальном основании ($\varphi = 0$) тело не наклоняется: $\alpha = 0$. На рис. 4, слева, приведена зависимость наклона тела $\alpha $ от угла $\varphi $ при разных значениях параметра $P{\text{*}}$. Правая часть рис. 4 показывает зависимость $\alpha $ от $P{\text{*}}$ при фиксированных углах наклона основания $\varphi $. Напомним, см. (3.1), что параметр $P{\text{*}}$ увеличивается при увеличении веса тела, либо при уменьшении жесткости материала $E{\text{*}}$, либо при уменьшении радиуса скругления $R$ (и одновременном пропорциональном уменьшении остальных параметров, имеющих размерность длины). Видно, что чем больше угол наклона основания $\varphi $, тем больше угол наклона $\alpha $, причем, чем больше безразмерный параметр $P{\text{*}}$, тем более выражен этот эффект. При этом в пределе при нулевом значении $P{\text{*}}$ (при нулевом весе тела $mg = 0$ или абсолютно жестком материале $E* = + \infty $) тело не поворачивается $\alpha = 0$ даже при ненулевых углах наклона основания $\varphi \ne 0$ (рис. 4, справа).
Рис. 4.
Слева: зависимость угла наклона тела $\alpha $ от угла наклона основания $\varphi $. Кривая 1: $P* = 8 \times {{10}^{{ - 2}}}$, 2: $P* = 4 \times {{10}^{{ - 2}}}$, 3: $P* = 2 \times {{10}^{{ - 2}}}$. Справа: зависимость угла наклона тела $\alpha $ от параметра $P{\text{*}}$. Кривая 1: $\varphi = 15^\circ $, 2: $\varphi = 10^\circ $, 3: $\varphi = 5^\circ $.
Кроме того, наклон тела существенно зависит от координат ($l$, $h$) центра масс тела. Как было указано выше, влияние деформаций в области контактного взаимодействия на относительное положение центра масс внутри тела пренебрежимо мало, поэтому величины $l$ и $h$ считаются постоянными. Момент массовой силы тяжести, действующей на тело, вычисляется как момент сосредоточенной силы, равной $mg$ и приложенной к центру масс. Координата вертикальной проекции центра масс тела (см. рис. 1) для малых углов $\alpha $ может быть вычислена по формуле:
Условие положительности давлений $p(x) > 0$ внутри области контакта и условие равновесия (3.6) влечет неравенство $ - a < {{x}_{{C'}}} < b$, т.е. центр масс должен проектироваться внутрь области контактного взаимодействия. На рис. 2 положение проекции центра масс внутри области контактного взаимодействия отмечено тонкой линией (приведен случай симметричного расположения центра масс $l = 0$).
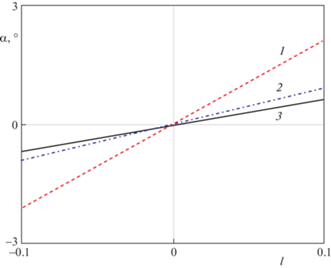
Если центр масс расположен несимметрично $l \ne 0$, то наклон тела возникает и на горизонтальном основании $\varphi = 0$. Так как наклон определяется величиной момента силы тяжести (см. (2.7)), то чем больше параметры $l$ и $h$, тем больше наклон $\alpha $. При уменьшении ширины $c$ плоской части тела, угол наклона также увеличивается. Эти утверждения подтверждаются результатами расчета угла наклона $\alpha $ для $\varphi = 0$ при изменении параметра $l$ при значениях $h = 1.2,\;3.5$ и $c = 0.2,\;0.4$ (рис. 5). Заметим, что при отрицательных значениях смещения центра масс $l < 0$, угол наклона тела на горизонтальном основании отрицателен $\alpha < 0$. (Для приведенных расчетов значение параметра $P* = 2 \times {{10}^{{ - 2}}}$, зависящего от механических параметров материала, не менялось.)
Рис. 5.
Зависимость угла наклона тела $\alpha $ от сдвига $l$ центра масс от оси симметрии для $\varphi = 0$. Значения параметров: 1 – $h = 1.2$, $c = 0.4$; 2 – $h = 3.5$, $c = 0.4$; 3 – $h = 1.2$, $c = 0.2$.
Аналогичный эффект наблюдается и при наклоне основания: при увеличении $\varphi $ угол наклона тела $\alpha $ тем больше, чем больше высота $h$ и смещение центра масс $l$ и чем меньше ширина плоской части $c$ (рис. 6). Две приведенные на этом рисунке кривые ($l = 0.05$, $l = 0.1$) имеют вертикальные касательные при $\varphi = 15.23^\circ $ и $\varphi = 13.35^\circ $: это означает, что указанные углы являются предельными, для которых равновесие тела возможно. Для больших углов проекция центра масс ${{x}_{{C'}}}$ выходит из области контакта и происходит переворот тела через переднюю кромку (см. рис. 7, представлены зависимости границ области контактного взаимодействия и подобластей сцепления и скольжения для несимметричного случая при $l = 0.1$, ср. с симметричным случаем, показанным на рис. 2).
Рис. 6.
Зависимость угла наклона тела $\alpha $ от угла наклона основания $\varphi $. Кривая 1 – $l = 0.1$; 2 – $l = 0.05$; 3 – $l = 0$; 4 – $h = 0.1$; 5: $h = 0.1$, $c = 0.8$.
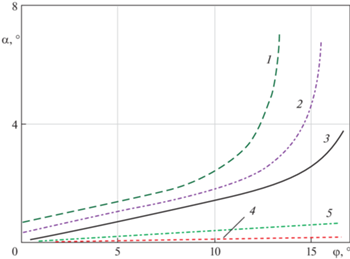
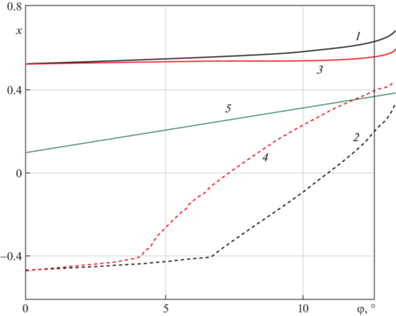
Рис. 7.
Зависимость границ контакта (кривая 1: $b$, кривая 2: $ - a$) и зоны сцепления (кривая 3: ${{d}_{1}}$, кривая 4: ${{d}_{2}}$) от $\varphi $ при $h = 1.2$, $c = 0.4$, $l = 0.1$. Кривая 5: вертикальная проекция центра масс ${{x}_{{C'}}}$.
Заключение. Проведено исследование условий равновесия упругого тела, представляющего собой бесконечный цилиндр, контактирующая поверхность которого имеет плоское основание и закругленные кромки, на наклоненном упругом полупространстве из того же материала.
Показано, что в условиях покоя и деформируемости контактирующих тел область контакта состоит из подобластей сцепления и относительного проскальзывания, размеры которых, а также угол поворота основания упругого тела относительно поверхности полупространства, зависят от упругих характеристик взаимодействующих тел, геометрии контактирующей поверхности упругого тела, положения его центра масс и величины коэффициента трения.
Проведен анализ структуры области контактного взаимодействия и участка сцепления на ней, а также угла поворота упругого тела относительно основания от угла наклона основания, веса тела и механических характеристик материала, положения центра масс упругого тела и коэффициента трения.
Несмотря на то, что в рамках рассмотренной модели условие равновесия упругого тела на наклоненном упругом основании совпадает с условием равновесия жестких тел (критический угол $\varphi {\text{*}}$, при котором начинается скольжение тела, определяется соотношением $\varphi * = \operatorname{arctg} \mu $, где $\mu $ – коэффициент трения), проведенное исследование позволяет провести оценку размера области сцепления в зависимости от наклона упругого основания, а также от формы, механических характеристик и положения центра масс лежащего на нем тела.
Анализ решения контактной задачи выполнен по теме государственного задания (№ госрегистрации AAAA-A20-120011690132-4).
Список литературы
Hertz H. Über die Berührung fester elastischer Körper // J. Reine und angew. Mathematik. 1882. № 92. S. 156–171.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 708 с.
Галин Л.А. Контактные задачи теории упругости и вязкоупругости. М.: Наука, 1980. 304 с.
Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.
Аппель П. Теоретическая механика. Т. 1. М.: Физматлит, 1960. 505 с.
Джеллет Д.Х. Трактат по теории трения. М.; Ижевск: 2009. 264 с.
Иванов А.П. Основы теории систем с трением. М.: Ижевск: 2011. 304 с.
Иванов А.П. О равновесии “балансирующих камней” // ПММ. 2018. Т. 82. Вып. 5. С. 592–598.
Bolotnik N., Schorr P., Zeidis I., Zimmermann K. Periodic locomotion of a two-body crawling system along a straight line on a rough inclined plane // ZAMM-J. Appl. Math.&Mech. 2018. T. 98. № 11. P. 1930–1946.
Bolotnik N.N., Figurina T.Y. Control of a system of two interacting bodies on a rough inclined plane // 15th Int. Conf. Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy’s Conference). IEEE, 2020. P. 1–4.
Golubev Y.F., Koryanov V.V. Overcoming obstacles in the form of a stack of rough cylinders by an insectomorphic robot // J. Comput. Syst. Sci. Int. 2022. V. 61. P. 253–269.
Russell A.S., Johnson C.G., Edwards A.N., Viroulet S., Rocha F.M., Gray J.M.N.T. Retrogressive failure of a static granular layer on an inclined plane // J. Fluid Mech. 2019. V. 869. P. 313–340.
Carbone L., Gourc J.P., Carrubba P., Pavanello P., Moraci N. Dry friction behaviour of a geosynthetic interface using inclined plane and shaking table tests // Geotextiles and Geomembranes. 2015. V. 43. № 4. P. 293–306.
Sudoł E., Szewczak E., Małek M. Comparative analysis of slip resistance test methods for granite floors // Materials. 2021. V. 14. № 5. P. 1108.
Goryacheva I.G., Murthy H., Farris T.N. Contact problem with partial slip for the inclined punch with rounded edges // Int. J. Fatigue. 2002. V. 24. № 11. P. 1191–1201.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика