1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 5, 2022

Прикладная математика и механика, 2022, T. 86, № 5, стр. 685-694

К вопросу о контакте волнистого цилиндра и упругой полуплоскости

И. Ю. Цуканов 1, *

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: ivan.yu.tsukanov@gmail.com

Поступила в редакцию 29.06.2022
После доработки 19.07.2022
Принята к публикации 20.07.2022

Полный текст (PDF)

Аннотация

На основе решения плоских контактных задач для одной и двух зон контакта исследовано влияние геометрии волнистого цилиндра на длину фактической области контакта при внедрении его в упругую полуплоскость. Получены аналитические выражения для определения границ двух зон контакта и полной нагрузки при произвольной функции зазора между поверхностями. Установлена связь между границами зоны контакта и фиктивной зоны отрицательных (растягивающих) контактных напряжений, возникающей при использовании решения для односвязной области. Показано, что волнистость поверхности цилиндра оказывает значительное влияние на зависимость длины фактической области контакта от нагрузки. Выявлено немонотонное поведение этой зависимости при переходе от двухсвязной области контакта к односвязной.

Ключевые слова: контактная задача, волнистый цилиндр, упругий контакт, неровности поверхности

Микрогеометрия поверхностей оказывает существенное влияние на условия их контактного взаимодействия, от которого, в свою очередь, зависят функциональные свойства подвижных и неподвижных сопряжений. Когда одно или оба контактирующих тела изготовлены из упругих материалов с низким модулем упругости зазор между ними может быть весьма мал даже при невысоких приложенных давлениях. Вследствие наличия нескольких масштабных уровней неровностей, связанных как с погрешностями изготовления деталей (например, волнистость и шероховатость), так и с наличием искусственно созданной текстуры, их взаимовлияние может приводить к смене режима взаимодействия неровностей, что не всегда возможно учесть в рамках континуальных (например, модель нелинейного слоя [1]) и иерархических (например, фрактальных [2]) моделей в механике контакта тел с многоуровневым микрорельефом. Влияние масштабных уровней неровностей особенно проявляется в поведении фактической площади касания соприкасающихся тел с ростом приложенной нагрузки, что важно для создания текстур поверхностей с управляемыми адгезионными свойствами [3].

Эффекты, связанные с взаимовлиянием масштабных уровней неровностей при контактном взаимодействии, хорошо иллюстрирует задача о контакте волнистого цилиндра и упругой полуплоскости. Численно-аналитическое решение для очень малых амплитуд волнистости получено в работе [4] в виде ряда Фурье. Численное моделирование данной задачи при конкретных геометрических параметрах проведено в работах [5, 6] с помощью итерационного метода решения интегрального уравнения контактной задачи и в [7] методом граничных элементов. В недавней работе [8] разработан алгоритм решения задач дискретного контакта для семейства штампов и упругой полосы, в том числе для штампа, близкого по форме к волнистому цилиндру.

В работе [7] показано, что на основные контактные характеристики – зависимость длины фактической области контакта от нагрузки и максимальное контактное давление – оказывает существенное влияние геометрия в месте начального касания волнистого цилиндра и полуплоскости. В данной работе на основе решения задач механики контактного взаимодействия проведен анализ влияния двух вариантов геометрии в месте начального касания волнистого цилиндра и полуплоскости на фактическую область контакта.

1. Постановка задач и допущения. Рассмотрим контакт волнистого упругого цилиндра и упругой полуплоскости (рис. 1) в момент их начального касания. Функция профиля поверхности цилиндра определяется следующим выражением:

(1.1)
$f(x) = \frac{{{{x}^{2}}}}{{2R}} + \Delta \cos \left( {nx + \psi } \right) + {{C}_{0}},$
где $R$ – радиус цилиндра; Δ, $n$ – амплитуда и частота волнистости; $\psi $ – фаза, в данной работе рассмотрены случаи $\psi = 0$ (рис. 1, а) и $\psi = \pi $ (рис. 1, б); С0 – константа, определяющая отсутствие зазора в зоне касания.

Рис. 1.

Схема контакта волнистого цилиндра и упругой полуплоскости при $\psi = 0$ (а) и $\psi = \pi $ (б).

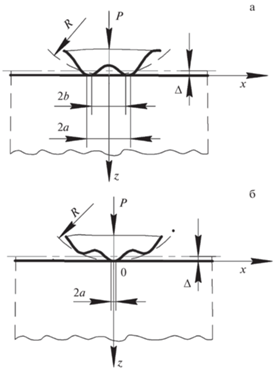
Задача рассматривается в рамках линейной теории упругости для полубесконечных тел в плоской постановке. При этом считается, что в направлении оси $y$ контактирующие тела имеют неограниченную длину (плоское деформированное состояние).

В качестве допущений примем, что амплитуда $\Delta $ существенно меньше периода волнистости $\lambda = 2\pi {\text{/}}n$, который, в свою очередь, значительно меньше радиуса $R$ цилиндра. Влиянием сил трения и межмолекулярных сил на распределение контактных напряжений в задаче пренебрегается.

2. Определение зависимости длины фактической области контакта от нагрузки. Рассмотрим случай $\psi = 0$ (см. рис. 1, а). Изначально в контакт вступают две неровности, положение которых зависит от геометрических параметров цилиндра и волнистости. Начало координат расположим в центре впадины между неровностями.

Запишем интегральное уравнение контактной задачи [9]:

(2.1)
$h{\kern 1pt} '(x) = \frac{2}{{\pi E{\kern 1pt} *}}\int\limits_L {\frac{{p(\xi )d\xi }}{{x - \xi }}} ,$
где функция зазора $h\left( x \right) = \delta - f\left( x \right)$, $\delta $ – величина сближения двух тел; $L$ – множество зон контакта, в данном случае $L = {{L}_{1}} \cup {{L}_{2}}$, ${{L}_{1}} = \left[ { - a, - b} \right]$, ${{L}_{2}} = \left[ {b,a} \right]$, $E{\text{*}}$ – приведенный модуль упругости материалов контактирующих тел:
(2.2)
$\frac{1}{{E{\text{*}}}} = \frac{{1 - \nu _{1}^{2}}}{{{{E}_{1}}}} + \frac{{1 - \nu _{2}^{2}}}{{{{E}_{2}}}},$
где ${{E}_{1}}$, ${{E}_{2}}$ и ${{\nu }_{1}}$, ${{\nu }_{2}}$ – модули Юнга и коэффициенты Пуассона материалов контактирующих тел, соответственно.

Решение уравнения (2.1) для двух зон контакта с неизвестными границами имеет следующий вид [10]:

(2.3)
$p(x) = \frac{{E{\text{*}}\sqrt {\left( {{{x}^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{x}^{2}}} \right)} }}{{2\pi }}\int\limits_L {\frac{{h{\kern 1pt} '(\xi )d\xi }}{{\sqrt {\left( {{{\xi }^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{\xi }^{2}}} \right)} \left( {\xi - x} \right)}}} ;\quad \forall x \in L$

При этом граничные точки ($a$ и $b$), в которых контактное давление $p\left( x \right)$ обращается в нуль, связаны условием согласованности [10]:

(2.4)
$\int\limits_b^a {\frac{{h{\kern 1pt} '(\xi )d\xi }}{{\sqrt {\left( {{{\xi }^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{\xi }^{2}}} \right)} }} = 0} $

Вычисление сингулярного интеграла в (2.3) для биквадратной функции зазора $h\left( x \right)$ получено в [11], однако для произвольного вида данной функции оно может быть затруднительно.

Для практических приложений наиболее важно определение зависимости длины фактической области контакта от приложенной нагрузки $P$, которая находится из уравнения равновесия

(2.5)
$P = \int\limits_L {p(x)dx} $

С использованием (2.3), (2.5) и равенства Рисса для повторных интегралов с одним сингулярным интегралом [12] при удовлетворении функцией $h{\kern 1pt} '(x)$ условия Гёльдера имеем

(2.6)
$P = \frac{{E{\text{*}}}}{{2\pi }}\int\limits_L {\frac{{h{\kern 1pt} '(\xi )}}{{\sqrt {\left( {{{\xi }^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{\xi }^{2}}} \right)} }}\int\limits_L {\frac{{\sqrt {\left( {{{x}^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{x}^{2}}} \right)} }}{{\xi - x}}} dxd\xi } ;\quad \forall x \in L$

Вычисление внутреннего интеграла в (2.6) дает выражение для полной нагрузки.

(2.7)
$P = \frac{{E{\text{*}}}}{2}\int\limits_b^a {\frac{{\left( {2{{\xi }^{2}} - {{a}^{2}} - {{b}^{2}}} \right)h{\kern 1pt} '(\xi )d\xi }}{{\sqrt {\left( {{{\xi }^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{\xi }^{2}}} \right)} }}} $

Интеграл в (2.7) не является сингулярным, что позволяет вычислить его стандартными численными методами. Выражения (2.4) и (2.7) образуют систему уравнений для определения граничных точек областей контакта при заданной нагрузке.

С использованием допущения $\Delta \ll 2\pi {\text{/}}n$ функция (1.1), описывающая форму волнистого цилиндра, может быть с достаточной точностью представлена рядом Тейлора 6-й степени. Тогда производная функции зазора $h{\text{'}}(x)$ будет иметь вид:

(2.8)
$h{\text{'}}(x) = - {{A}_{1}}{{x}^{5}} + {{A}_{2}}{{x}^{3}} + {{A}_{3}}x,$
где ${{A}_{1}} = \frac{{\Delta {{n}^{6}}}}{{120}}$; ${{A}_{2}} = \frac{{\Delta {{n}^{4}}}}{6}$; ${{A}_{3}} = \frac{1}{R} - \Delta {{n}^{2}}$.

Вычисляя интеграл в (2.4) при $a > b$ получим следующее уравнение:

(2.9)
$\int\limits_b^a {\frac{{\left( { - {{A}_{1}}{{x}^{5}} + {{A}_{2}}{{x}^{3}} + {{A}_{3}}x} \right)d\xi }}{{\sqrt {\left( {{{\xi }^{2}} - {{b}^{2}}} \right)\left( {{{a}^{2}} - {{\xi }^{2}}} \right)} }}} = \frac{{ - \pi {{A}_{1}}}}{{16}}\left( {4{{a}^{4}} + 2{{a}^{2}}{{b}^{2}} + 3{{b}^{4}}} \right) + \frac{{\pi {{A}_{2}}}}{4}\left( {{{a}^{2}} + {{b}^{2}}} \right) + \frac{{\pi {{A}_{3}}}}{2}$

Приравнивая выражение (2.9) к нулю для выполнения условия согласованности, получим уравнение связи концов области контакта $a$ и $b$.

(2.10)
$ - {{A}_{1}}\left( {\frac{3}{{16}}{{a}^{4}} + \frac{1}{8}{{a}^{2}}{{b}^{2}} + \frac{3}{{16}}{{b}^{4}}} \right) + {{A}_{2}}\frac{1}{4}\left( {{{a}^{2}} + {{b}^{2}}} \right) + {{A}_{3}}\frac{1}{2} = 0$

При $a > b > 0$ решение уравнения (2.10) относительно $b$ имеет вид:

(2.11)
$b = \frac{{\sqrt 3 }}{3}\sqrt {\frac{{2{{A}_{2}}}}{{{{A}_{1}}}} - \frac{2}{{{{A}_{1}}}}\sqrt {2{{A}_{1}}{{A}_{2}}{{a}^{2}} - 2A_{1}^{2}{{a}^{4}} + 6{{A}_{3}}{{A}_{1}} + A_{2}^{2}} - {{a}^{2}}} $

В условиях полного контакта на отрезке $x \in \left[ { - a,a} \right]$ выражение для полной нагрузки, обеспечивающей “закрытие” зазора между неровностями определяется как [13]

(2.12)
${{P}_{f}} = E{\kern 1pt} *{\kern 1pt} \int\limits_0^a {\frac{{\xi h{\kern 1pt} '(\xi )d\xi }}{{\sqrt {\left( {{{a}^{2}} - {{\xi }^{2}}} \right)} }}} $

Подставляя выражение (2.8) в (2.12) и вычисляя интегралы, получим:

(2.13)
${{P}_{f}}(a) = \frac{{\pi E{\text{*}}}}{4}\left( { - {{A}_{1}}\frac{{5{{a}^{6}}}}{8} + {{A}_{2}}\frac{{3{{a}^{4}}}}{4} + {{A}_{3}}{{a}^{2}}} \right)$

Так как задача симметрична относительно начала координат, то для определения контактного давления применим метод [14, 15] и определим производную нормальной силы Pf:

(2.14)
$P_{f}^{'}(a) = \frac{{\pi E{\text{*}}}}{{16}}\left( { - 15{{A}_{1}}{{a}^{5}} + 12{{A}_{2}}{{a}^{3}} + 8{{A}_{3}}a} \right),$

тогда распределение контактного давления определяется как [14, 15]:

(2.15)
${{p}_{f}}(x) = \frac{1}{\pi }\int\limits_x^a {\frac{{P_{f}^{'}(s)ds}}{{\sqrt {{{s}^{2}} - {{x}^{2}}} }}} = \frac{{E{\text{*}}}}{{16}}\int\limits_x^a {\frac{{\left( { - 15{{A}_{1}}{{s}^{5}} + 12{{A}_{2}}{{s}^{3}} + 8{{A}_{3}}s} \right)ds}}{{\sqrt {{{s}^{2}} - {{x}^{2}}} }}} $

Вычисляя интеграл в (2.15), получим:

(2.16)
${{p}_{f}}(x) = E{\kern 1pt} *{\kern 1pt} \sqrt {{{a}^{2}} - {{x}^{2}}} \left( { - {{A}_{1}}\left( {\frac{3}{{16}}{{a}^{4}} + \frac{1}{4}{{a}^{2}}{{x}^{2}} + \frac{1}{2}{{x}^{4}}} \right) + \frac{1}{4}{{A}_{2}}\left( {{{a}^{2}} + 2{{x}^{2}}} \right) + \frac{1}{2}{{A}_{3}}} \right)$

С уменьшением внешней нагрузки контакт становится неполным, и при использовании формулы (2.16) появляются зоны с отрицательным давлением. Решение задачи для распределения давлений в таком случае сводится к вычислению сингулярного интеграла (2.6), например, с использованием соотношений для многочленов Чебышева на двух симметричных интервалах [11].

Представляет интерес взаимосвязь фактических границ зоны контакта и фиктивной зоны отрицательных (растягивающих) контактных напряжений, появляющихся при использовании формулы (2.16) для полного контакта на отрезке $x \in \left[ { - a,a} \right]$. Граница этой фиктивной зоны определяется из условия ${{p}_{f}}\left( {{{x}_{0}}} \right) = 0$. Сомножитель, содержащий радикал, в зависимости (2.16) не равен нулю при $x < a$, следовательно

(2.17)
$ - {{A}_{1}}\left( {\frac{3}{{16}}{{a}^{4}} + \frac{1}{4}{{a}^{2}}x_{0}^{2} + \frac{1}{2}x_{0}^{4}} \right) + \frac{1}{4}{{A}_{2}}\left( {{{a}^{2}} + 2x_{0}^{2}} \right) + \frac{1}{2}{{A}_{3}} = 0$

Уравнения (2.17) и (2.10) для определения величины x0 и границы зоны контакта $b$ являются уравнениями 4-й степени с одинаковым количеством членов. При малых значениях ${{x}_{0}}$ можно пренебречь компонентом при ${{x}_{0}}$ в 4-й степени. Тогда уравнение (2.17) приводится к виду

(2.18)
$\left( { - {{A}_{1}}\frac{1}{2}{{a}^{2}} + {{A}_{2}}} \right){{x}_{0}}^{2} = {{A}_{1}}\frac{3}{8}{{a}^{4}} - \frac{1}{2}{{A}_{2}}{{a}^{2}} - {{A}_{3}}$

Аналогично, при отбрасывании компонента при $b$ в четвертой степени для (2.10) имеем

(2.19)
$\left( { - {{A}_{1}}\frac{1}{2}{{a}^{2}} + {{A}_{2}}} \right)\frac{{{{b}^{2}}}}{2} = {{A}_{1}}\frac{3}{8}{{a}^{4}} - {{A}_{2}}\frac{1}{2}{{a}^{2}} - {{A}_{3}}$

Из уравнений (2.18) и (2.19) напрямую следует, что при малых размерах области, в которой контакт отсутствует ($x \in \left[ { - b,b} \right]$), соотношение между фактической $b$ и фиктивной ${{x}_{0}}$ границами зоны контакта равно

(2.20)
$\frac{b}{{{{x}_{0}}}} = \sqrt 2 $

Выражение (2.20) в точности совпадает с соотношением, полученным в работе [16], при рассмотрении случая почти полного контакта как сжимаемой трещины под воздействием некоторого параболического давления, которым аппроксимируется распределение давления вблизи центра зоны, в которой контакт отсутствует.

В работе [17] выдвинуто предположение и показано на конкретных примерах, что исключение небольшой области с фиктивными растягивающими контактными напряжениями (в которой контакт отсутствует) путем представления ее сжимаемой трещиной не приводит к изменению полной нагрузки на контактирующие тела. Этот вывод справедлив для распределения фиктивных контактных напряжений, представимых степенным рядом [17]. С учетом условия согласованности (2.4), при $b \to 0$ подынтегральные выражения в формулах (2.12) и (2.7) совпадают. Кроме того, анализируя выражения (2.10) и (2.17) при $b = {{x}_{0}} = 0$, становится ясно, что граница области контакта $a$, при которой реализуется односвязная область контакта, одинакова для указанных выражений.

Длина фактической области контакта будет определяться следующим выражением

(2.21)
${{L}_{r}} = {\text{2}}(a{\text{ }}--{\text{ }}b){\text{ }} \approx 2\left( {a - \sqrt 2 {{x}_{0}}} \right)$

При достижении полного контакта, при котором две зоны контакта сливаются ($b = 0$), из (2.10) следует выражение для длины фактической области контакта $L_{r}^{*}$:

(2.22)
$L_{r}^{*} = \frac{{\sqrt 3 }}{3}\sqrt {\frac{{2{{A}_{2}}}}{{{{A}_{1}}}} - \frac{{2\sqrt {6{{A}_{1}}{{A}_{3}} + A_{2}^{2}} }}{{{{A}_{1}}}}} $

Описанные результаты относятся к случаю начального контакта тел при двух подобластях контакта. После слияния подобластей контакта в рамках приведенных допущений область контакта становится односвязной для $\psi = 0$. В случае $\psi = \pi $ область контакта изначально состоит только из одного отрезка ($L = \left[ { - a,a} \right]$, см. рис. 1, б).

Для односвязной области контакта допустимо применение принципа суперпозиции, и контактное давление можно выразить как сумму двух составляющих:

(2.23)
$p(x) = {{p}_{h}}(x) + {{p}_{w}}(x),$
где ${{p}_{h}}\left( x \right)$ – герцевское давление, соответствующее, параболической компоненте функции зазора $h\left( x \right)$ [13]; ${{p}_{w}}\left( x \right)$ – давление, соответствующее гармонической компоненте. Решение интегрального уравнения (2.1) для $L = \left[ { - a,a} \right]$ и гармонической функции зазора получено в [18] в виде ряда по многочленам Чебышева 2-го рода. Таким образом, контактное давление будет иметь вид:
(2.24)
$p(x) = \frac{{E{\kern 1pt} *}}{{2R}}\sqrt {{{a}^{2}} - {{x}^{2}}} \mp \frac{{E{\kern 1pt} *{\kern 1pt} \Delta n}}{a}\sqrt {{{a}^{2}} - {{x}^{2}}} \sum\limits_{{\text{ }}k = 0}^\infty {{{{( - 1)}}^{k}}{{{\text{J}}}_{{2k + 1}}}(an){{U}_{{2j}}}\left( {\frac{x}{a}} \right)} ,$
где знак минус берется при $\psi = 0$, а знак плюс – при $\psi = \pi $; ${{\operatorname{J} }_{k}}\left( x \right)$ – Функция Бесселя 1-го рода целого порядка $k$; ${{U}_{k}}\left( x \right)$ – многочлен Чебышева 2-го рода.

Полная нагрузка для односвязной области контакта определяется интегрированием уравнения равновесия (2.5):

(2.25)
$P = \int\limits_{ - a}^a {p(x)dx} = \frac{{\pi E{\kern 1pt} *{\kern 1pt} {{a}^{2}}}}{{4R}} \mp \frac{{\pi E{\kern 1pt} *{\kern 1pt} \Delta an}}{2}{{{\text{J}}}_{1}}\left( {an} \right),$
а длина фактической области контакта ${{L}_{r}} = 2a$.

3. Результаты и их обсуждение. Зависимости полной нагрузки, обезразмеренные на нагрузку, при внедрении гладкого цилиндра [19] ${{P}_{h}} = \pi {{a}^{2}}E{\kern 1pt} *{\kern 1pt} {\text{/}}4R$, от длины фактической области контакта приведены на рис. 2.

Рис. 2.

Зависимость безразмерной нагрузки $P$ от длины фактической области контакта ${{L}_{r}}$: сплошные линии – точное решение; штриховые линии – расчет на основе (2.13) и (2.20); 1 – R/Δ = 1300, $n = 9$; 2 – $R{\text{/}}\Delta = 1600$, $n = 11$.

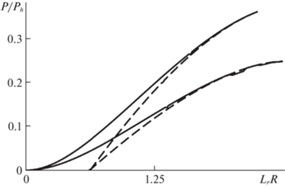
Из рис. 2 видно, что в области высоких нагрузок точное и приближенное решение удовлетворительно совпадают. На графике зависимости нагрузки от длины области контакта выделяется наличие трех участков: двух нелинейных (при малых и больших нагрузках соответственно) и линейный переходный участок. Такое же поведение кривой характерно для периодической задачи о контакте синусоидальной волнистости и полуплоскости [13, 19]. С ростом частоты и амплитуды волнистости длина фактической области контакта уменьшается, но характер кривых остается прежним.

На рис. 3 показаны графики длины фактической области контакта в зависимости от приложенной нагрузки при $R{\text{/}}\Delta = 1300$, $n = 9$ и различном значении фазы $\psi $.

Рис. 3.

Зависимости длины фактической области контакта от приложенной нагрузки при $\psi = 0$ (кривая 1); $\psi = \pi $ (кривая 2) и для гладкого цилиндра (кривая 3); символом “×” обозначена точка перехода от двухсвязной области контакта к односвязной.

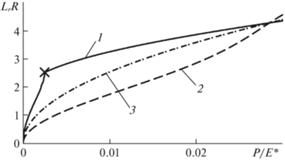
Из рис. 3 видно, что фаза гармоники волнистости оказывает значительное влияние на поведение длины фактической области контакта для небольших нагрузок. Это связано с различием, как в количестве областей контакта, так и в производной функции зазора $h\left( x \right)$. Кривая для гладкого цилиндра находится между кривыми для $\psi = 0$ и $\psi = \pi $, и при определенном значении нагрузки они пересекаются, что связано с осциллирующим поведением функции $P\left( a \right)$ при полном контакте на отрезке $x \in \left[ { - a,a} \right]$. Переход от двухсвязной области контакта к односвязной характеризуется немонотонным изменением зависимости длины фактической области контакта от нагрузки. Такое поведение согласуется с численными результатами для многоуровневой волнистой поверхности [20] и показывает, что наличие таких переходных участков кривой длины фактической области контакта характеризует изменение связности контактной области.

Анализируя полученные результаты можно заключить, что если достижим полный контакт на конкретном масштабном уровне неровностей, то два механизма образования фактической области контакта – возрастание размеров отдельных пятен контакта и увеличение их количества – могут конкурировать друг с другом. Это приводит к нестабильности поведения контактных и фрикционных характеристик с ростом нагрузки. С ростом амплитуды и частоты волнистости полный контакт на отрезке $x \in \left[ { - a,a} \right]$ становится недостижимым, и взаимодействие поверхностей будет осуществляться только на вершинах неровностей.

Заключение. Полученные решения контактной задачи для волнистого цилиндра, контактирующего с упругой полуплоскостью, позволили проанализировать различие в поведении длины фактической области контакта с ростом приложенной нагрузки в условиях односвязной и двухсвязной областей контакта, возникающих при различной фазе волнистости. Установлено, что геометрия начального касания оказывает влияние на размер длины фактической области контакта при фиксированной нагрузке. С ростом частоты и амплитуды волнистости длина фактической области контакта для двухсвязной области уменьшается, но характер ее зависимости от нагрузки не меняется и идентичен случаю периодической задачи о контакте синусоидальной волнистости и полуплоскости. На кривой выделяется наличие трех участков: двух нелинейных (при малых и больших нагрузках соответственно) и линейный переходный участок. Переход от двухсвязной области контакта к односвязной характеризуется немонотонным изменением зависимости длины фактической области контакта от нагрузки, что может отразиться на поведении других контактных и фрикционных характеристик. Это необходимо учитывать при создании микротекстурированных поверхностей, работающих в паре с упругими низкомодульными материалами.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-01-00400.

Список литературы

  1. Горячева И.Г. Расчет контактных характеристик с учетом параметров макро- и микрогеометрии поверхностей // Трение и износ. 1999. Т. 20. № 3. С. 239–248.

  2. Borodich F.M. Fractal Contact Mechanics. Encyclopedia of Tribology. 2013. P. 1249–1258.

  3. Goryacheva I., Makhovskaya Yu. Discrete Contact Mechanics with Applications in Tribology. Elsevier, 2022. 209 p.

  4. Guduru P.R. Detachment of a rigid solid from an elastic wavy surface: Theory // J. Mech. Phys. Solids. 2007. V. 55. P. 445–472.

  5. Chekina O.G., Keer L.M. A new approach to calculation of contact characteristics // ASME J. Tribol. 1999. V. 121. № 1. P. 20–27.

  6. Sundaram N., Farris T.N. Multiple contacts of similar elastic materials // J. Appl. Mech. T-ASME. 2009. V. 131. № 2. P. 1–12.

  7. Seabra J., Berthe D. Influence of surface waviness and roughness on the normal pressure distribution in the hertzian contact // J. Tribology. 1987. V. 109. № 3. P. 462–469.

  8. Бобылев А.А. Алгоритм решения задач дискретного контакта для упругой полосы // ПММ. 2022 Т. 86. Вып. 3. С. 404–423.

  9. Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Изд-во АН СССР, 1933. 382 с.

  10. Ghanati P., Adibnazari S. Two-dimensional symmetric double contacts of elastically similar materials // Proc. Inst. Mech. Eng. Pt. C J. Mechan. Eng. Sci. 2015. V. 230. № 10. P. 1626–1633.

  11. Gladwell G.M.L. Contact Problems in the Classical Theory of Elasticity. Dordrecht: Springer, 1980. 736 p.

  12. Хведелидзе Б.В. Метод интегралов типа Коши в разрывных граничных задачах теории голоморфных функций одной комплексной переменной // Итоги науки и техн. Сер. Соврем. пробл. мат. 1975. Т. 7. С. 5–162.

  13. Штаерман И.Я. Контактная задача теории упругости. Л.: Гостехтеоретиздат, 1949. 270 с.

  14. Александров В.М., Коваленко Е.В. Задачи механики сплошных сред со смешанными граничными условиями. М.: Наука, 1986. 336 с.

  15. Barber J.R. Contact Mechanics. Cham: Springer Int. Publ., 2018. 592 p.

  16. Manners W., Greenwood J.A. Some observations on Persson’s diffusion theory of elastic contact // Wear. 2006. V. 261. № 5–6. P. 600–610.

  17. Greenwood J.A. On the almost-complete contact of elastic rough surfaces: The removal of tensile patches // Int. J. Solids Struct. 2015. V. 56–57. P. 258–264.

  18. Tsukanov I.Y. Partial contact of a rigid multisinusoidal wavy surface with an elastic half-plane // Adv. Tribol. 2018. V. 2018. P. 1–8.

  19. Джонсон К. Механика контактного взаимодействия. М.: Мир, 1989. 510 с.

  20. Paggi M., Reinoso J. A variational approach with embedded roughness for adhesive contact problems // Mech. Adv. Mater. 2018. V. 2018. P. 1731–1747.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал