Прикладная математика и механика, 2022, T. 86, № 5, стр. 695-709

1. Введение. При решении задачи о действии на пластины простейших подвижных нагрузок – сосредоточенных и распределенных сил, при постоянных и переменных скоростях движения, применяются интегральные преобразования Фурье и Лапласа [1–4], для грузов находят применения численные решения интегральных уравнений относительно динамических реакций при построении рекуррентных соотношений [5, 6]. В случае действия равномерно распределенной инерционной нагрузки, при переменной скорости движения, путем изменения ее ступенями в работе [7] используется специальное разделение переменных. Методы расчета на действие простейшей инерционной подвижной нагрузки на прямоугольные пластины, как и для стержней, распадаются на два основных подхода. В первом случае используются обобщенные координаты при разложении прогиба по собственным формам балки или пластины и задача сводится к решению системы обыкновенных дифференциальных уравнений с переменными коэффициентами [8, 9]. Во втором случае, после расчленения системы “балка–груз” или “пластина–груз”, задача сводится к решению интегрального уравнения относительно динамической реакции груза [5, 6]. В [8, 9] увеличение числа удерживаемых форм приводит к увеличению порядка системы уравнений, в [5, 6] возникают трудности при решении интегральных уравнений, связанные с условной устойчивостью шаговых процедур. В статье для прямоугольных пластин на упругом основании предлагается метод – “узловых ускорений”, объединяющий между собой указанные подходы и ликвидирующий указанные у них недостатки, так как доступно учитывает любое необходимое число форм в разложении прогиба, и имеет, как и в методе интегральных уравнений [5, 6], разрешающую систему уравнений с минимальным числом неизвестных, при использовании безусловно-устойчивой схемы интегрирования, предложенной в [10]. Отметим, что метод “узловых ускорений” применяется и для стержневых систем [11–14]. Колебания пластин при действии подвижной инерционной нагрузки исследуются, привлекая метод конечных элементов (МКЭ) в [15–18], как для простейшей силовой нагрузки при косоугольных пластинах [15], так и с привлечением комплексов, например, ABAQUS и LS-DYNA [16–18]. Используя конечноэлементную базу этих комплексов, в [16–18] реализуется, в том числе, аналог первого подхода к решению задачи на подвижную нагрузку, с привлечением набора собственных форм конструкции. В [17] решение задачи “груз–балка” или “груз–плита”, путем введения линейного элемента между движущимся грузом и проезжей частью, сводится к решению системы линейных уравнений с привлечением результатов вычисления форм колебаний конструкции, используя при этом метод Ньюмарка. Другой подход, с привлечением LS-DYNA, реализуемый в [18], сводится к изучению действия сложной подвижной инерционной нагрузки на конструкции при применении метода динамической релаксации (DYNAMIC RELAXATION). Заметим, что метод “узловых ускорений”, предлагаемый для пластин, реализуется и в случае движения инерционной нагрузки в [14] при конечноэлементной дискретизации коробчатой конструкции пролетного строения моста.

1. Числовая процедура, используемая для решения задачи. Применяемый метод для решения задачи о действии подвижной нагрузки на пластину использует шаговую процедуру [10]. Рассмотрим предварительно решение задачи для осциллятора. Рассмотрим шаговую процедуру для решения уравнения (1.1)

Проведем временную дискретизацию с шагом, где $\Delta {{t}_{j}} = {{t}_{{j + 1}}} - {{t}_{j}}$, ($j = 0,1,2, \ldots $)

Преобразуем первое уравнение (1.2), используя замену

и выражения ${{\dot {x}}_{{j + 1}}}$ и ${{x}_{{j + 1}}}$ из второго и третьего уравнений (1.2). В итоге получаем шаговую процедуру где ${{\tilde {\tilde {a}}}_{j}} = {{\left\{ {1 + \left( {{{\omega }^{2}}{\text{/}}{{\alpha }_{2}}} \right)\left( {\mu \Delta {{t}_{j}} + \Delta t_{j}^{2}{\text{/}}{{\alpha }_{3}}} \right)} \right\}}^{{ - 1}}}$, ${{\alpha }_{1}} = {{\alpha }_{2}} = {{\alpha }_{3}} = 2$

Схема (1.4), при обозначении $\beta = - {{\omega }^{2}}{{\tilde {\tilde {a}}}_{j}}$, имеет вид

Для безусловно-устойчивой процедуры требуется выполнение условия ρ(A) = $\max \left| {{{\lambda }_{i}}} \right| \leqslant 1$, $i = 1,2,3$, при любом $\Delta {{t}_{j}}$, где $\rho $ – спектральный радиус оператора аппроксимации ${\mathbf{A}}$ и ${{\lambda }_{i}}$ – корни характеристического уравнения $\left\| {{\mathbf{A}} - \lambda {\mathbf{E}}} \right\| = 0$ [19]. Для процедуры (1.4), раскрывая определитель по первой строке и делая замену $Z = 1 - \lambda + \beta \Delta {{t}^{2}}{\text{/}}2$, имеем уравнение $ - \lambda \left[ {{{Z}^{2}} - \mu \Delta {{t}^{2}}{{\omega }^{2}}{{{\tilde {\tilde {a}}}}_{j}}Z + \Delta {{t}^{2}}{{\omega }^{2}}{{{\tilde {\tilde {a}}}}_{j}}^{2}} \right]$ = 0. Решая квадратное уравнение относительно переменной $Z$, определяем ${{\lambda }_{{1,2}}}$ и $\left| {{{\lambda }_{{1,2}}}} \right|$

Для проверки условия $\max \left| {{{\lambda }_{i}}} \right| \leqslant 1$ рассматривается выполнение при $h = (\mu \omega {\text{/}}2) > 1$ и $h = (\mu \omega {\text{/}}2) < 1$, когда корни ${{\lambda }_{{1,2}}}$ действительные и, соответственно, комплексные. Из простейшей оценки неравенств, следует, что $\rho ({\mathbf{A}}) < 1$ при $\mu \ne 0$ и $\rho ({\mathbf{A}}) = 1$ при $\mu = 0$ для любых значений $\Delta {{t}_{j}}$. Отметим, что если положить в (1.4) $\mu = 0$, ${{\dot {x}}_{j}} = {{x}_{j}} = 0$ и $\tilde {P}(t) = P = \operatorname{const} $, то при $\Delta {{t}_{j}} \to \infty $, ${{\ddot {x}}_{{j + 1/2}}} \to 0$, ${{\dot {x}}_{{j + 1}}} \to 0$, ${{x}_{{j + 1}}} = 2{{x}_{C}}$, где ${{x}_{C}}$ – статический прогиб осциллятора под действием силы $P$.

Применяемая процедура (1.4) совпадает с методом постоянного среднего ускорения, но с измененным начальным ускорением. Метод Ньюмарка [20], при $\delta $ = 0.5, $\beta $ = = 0.25, совпадает с предложенным С.П. Тимошенко в [21] методом постоянного среднего ускорения. Процедура (1.4) имеет характеристики погрешности интегрирования такие же, как у метода Ньюмарка, при $\delta $ = 0.5, $\beta $ = 0.25, при этом, она приводит только к минимальному увеличению периода численного решения без снижения амплитуды [19].

Процедура (1.4), сохраняя указанные характеристики, находит применение к решению методом прямого интегрирования систем уравнений

где ${\mathbf{M}}$, ${\mathbf{C}}$ и ${\mathbf{K}}$ – матрицы масс, демпфирования и жесткости, соответственно; ${\mathbf{R}}$ – вектор внешних узловых нагрузок; ${\mathbf{\ddot {U}}}$, ${\mathbf{\dot {U}}}$, ${\mathbf{U}}$ – векторы узловых ускорений, скоростей и перемещений узловых точек транспортной системы или узловых смещений ансамбля конечных элементов. Для решения (1.7) имеем процедуру где ${{{\mathbf{\tilde {\tilde {B}}}}}_{j}} = {\mathbf{M}} + {\mathbf{C}}(\Delta {{t}_{j}}{\text{/}}{{\alpha }_{2}}) + {\mathbf{K}}\Delta t_{j}^{2}{\text{/}}\tilde {\beta }$, при ${{\alpha }_{1}} = {{\alpha }_{2}} = {{\alpha }_{3}} = 2$, $\tilde {\beta } = {{\alpha }_{2}}{{\alpha }_{3}}$ = 4.

2. Общие формулы и тестовые примеры. Обратимся с начала к решению классической задачи о движении груза по пластине с переменной скоростью, а затем перейдем к случаю более сложной нагрузки. Используем, далее, безусловно-устойчивую шаговую процедуру по времени (1.8) и метод учета действия безмассовой и инерционной подвижной нагрузки, применяемый для расчета стержневых систем, и предложенных ранее в [10, 11]. Будем рассматривать случаи равнопеременного движения подвижной нагрузки по конструкциям.

Дифференциальное уравнение колебаний прямоугольной пластины при движении по ней груза весом $P$ и массой $M$ имеет вид

Здесь $D$ – цилиндрическая жесткость; $\Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}$, ${{\tilde {\mu }}_{1}}$ – коэффициент, учитывающий диссипацию энергии, $q{\kern 1pt} *{\kern 1pt} \left( {x,y,t} \right)$ – прогиб пластины, $R_{{o1}}^{{}}(s(t),t)$ – давление груза на пластину, $x$ и $y$ – координаты по ширине и длине пластины (рис. 1), $\delta \left( {y - s(t)} \right)$ – дельта-функция, $s(t) = {{s}_{0}} + {{{v}}_{0}}t + w{{t}^{2}}{\text{/}}2$ – закон движения груза по пластине, ${{s}_{0}}$ и ${{{v}}_{0}}$ – начальное положение и скорость груза при приземлении на плиту, ${v} = {{{v}}_{0}} + wt$ и $w$ – скорость и ускорение движения груза, $m$ – погонная масса пластины, $b$ и $\ell $ – ширина и длина пластины, $k{\kern 1pt} *$ – коэффициент постели.

Прогиб свободно опертой пластины на упругом основании в момент ${{t}_{{j + 1}}}$ при движении по ней сосредоточенной силы ${{R}_{{}}} = \delta \left( {x - 0.5b} \right)\delta \left( {y - s(t)} \right)$ × ${{R}_{{o1}}}$, используя шаговую процедуру (1.4), предложенную в [10], можно записать в виде

Здесь $q_{{kij}}^{{}}$ – обобщенные координаты пластины, ${{\tilde {\omega }}_{{ik}}}$ – круговая частота колебаний, $\sigma $ – коэффициент Пуассона, $h$ – толщина пластины, $E$ – модуль упругости.

Полагая ${{\ddot {q}}_{{1j + 1/2}}} = {{d}^{2}}q{\kern 1pt} *{\kern 1pt} \left( {s(t),t} \right){\text{/}}d{{t}^{2}}$, при $t = {{t}_{{j + 1/2}}}$, запишем полное вертикальное ускорение точки контакта груза [1] при постоянной координате его движения ${{x}_{c}} = \operatorname{const} $ (рис. 1) в виде

Используя (2.2) и (2.3), имеем на шаге [t_j, t_j + 1]

Здесь ${{D}_{1}}$ и ${{D}_{O}}$ – функции, сгруппированные и выделенные из (2.4).

Обозначим через $\varepsilon ({{R}_{{}}}) = \tilde {\alpha }{{R}^{{2/3}}}$ контактное сближение груза и пластины. Уравнение динамического равновесия груза в момент контакта ${{t}_{{j + 1/2}}}$ имеют вид

где ${{q}_{1}}$ – смещение точки контакта груза на пластине, $q_{2}^{{}}$ – вертикальное смещение центра масс груза.

Представим выражение контактной силы на шаге $[{{t}_{j}},{{t}_{{j + 1}}}]$ в виде

Для линеаризации полученного уравнения, учитывая (2.8), используем выражение, для приращения, например, функции $f(x,y)$ двух переменных в точке ${{x}_{o}}$, ${{y}_{o}}$ в форме

Преобразуем выражение (2.6) к виду

В итоге, имеем на шаге [t_j, t_j + 1]

где ${{L}_{{j + 1/2}}} = \tilde {k}\left( {{{q}_{{2j}}} - {{q}_{{1j}}}} \right) - {{\tilde {k}}_{1}}{{\left( {{{q}_{{2j}}} - {{q}_{{1j}}}} \right)}^{{3/2}}} + {{P}_{{j + 1/2}}}$.

Объединяя в систему (2.10) и (2.4) на шаге [t_j, t_j + 1], имеем

Здесь ${\mathbf{\bar {q}}} = [{{q}_{1}},{{q}_{2}}]{\kern 1pt} '$, ${\mathbf{A}} = [{{a}_{{ik}}}]$, ${\mathbf{B}} = [{{b}_{i}}]$, $i,k = 1,2$, $j = 0,1,2,3, \ldots $

На шаге [t_j, t_j + 1] выражение ${{{\mathbf{\ddot {\bar {q}}}}}_{{j + 1/2}}}$ из (2.11), используя (2.6) и (2.2), позволяет вычислять начальные условия для следующего шага интегрирования, используя, на каждом шаге, условия совместности деформаций в точке контакта груза и пластины.

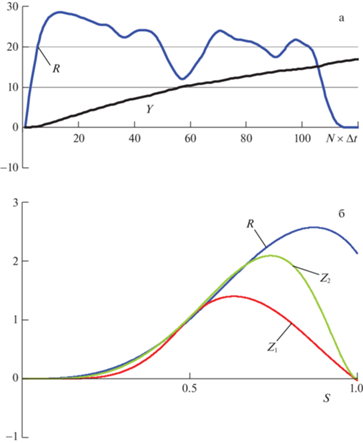
На первом этапе проведем тестирование алгоритма для учета нелинейной упругости при сближении груза и пластины при ударе, будем для тестирования использовать пример, представленный в [5]. Рассмотрим удар при падении с высоты ${{h}_{0}}$ = 0.26 м груза весом $P$ = 14.7 × 9.8 Н в центр квадратной, стальной, свободно опертой пластины при $b$ = 0.6 м, $h$ = 0.012 м. Процедура (2.3)–(2.11) реализовывалась, полагая при $t$ = 0, $s = {{s}_{0}} = 0.3$ м, ${{{v}}_{0}} = w$ = 0 и ${{q}_{1}}$ = ${{\dot {q}}_{1}} = {{q}_{2}} = 0$, ${{\dot {q}}_{2}} = \sqrt {2g{{h}_{0}}} $. Коэффициент ${{k}_{1}}$ определялся по формуле (для случая одинакового материала у соударяющихся тел) ${{k}_{1}} = 2E\sqrt r {\text{/}}(3(1$ – – σ²)) [5], где $r$ = 0.07141 м. На рис. 2а представлены изменения контактной силы $R$ [кН] и смещение пластины под грузом ${{q}_{1}} = Y \times {{10}^{{ - 4}}}$ [м] в зависимости от времени $t = N \times \Delta {{t}_{j}}$, где $N$ – число шагов при интегрировании системы (2.11), при $\Delta {{t}_{j}} = 0.1057 \times {{10}^{{ - 4}}}$ с. Следует отметить, что результаты, представленные на рис. 2а, практически совпадают с результатами из ([5], с. 715, рис. 19.13). Вторая тестовая задача связана с равнопеременным движением груза по свободно опертой по контору пластине с параметрами [6]

где ${{\mu }_{1}} = \ell {\text{/}}b$, ${{{v}}_{c}} = \left( {{{{v}}_{0}} + {{{v}}_{1}}} \right){\text{/}}2$, ${{{v}}_{0}}$ и ${{{v}}_{1}}$ – скорости, соответственно, въезда и схода груза с плиты. Шаговая процедура (2.3)–(2.11) реализована при $\beta = 1$, $\alpha = 1{\text{/}}2$, ${{{v}}_{1}}{\text{/}}{{{v}}_{0}} = 2{\text{/}}3$, ${{x}_{c}} = b{\text{/}}2$ и параметрах для пластины из [6] $\ell $ = 2 м, $b$ = 1 м, $h$ = 0.02 м, $E$ = 2.06 × × 10⁸ кН/м², $\sigma = 0.3$, $\rho $ = 7.85 кг/м³ и для груза при $E$ = 8.83 × 10³ кН/м², $\sigma = 0.42$, вычисляя ${{k}_{1}}$, для случая вдавливания шара с радиусом $r = $0.5 м в пластину. На рис. 2б представлен характер изменения динамических коэффициентов при замедленном движении груза: $R = {{P}_{D}}{\text{/}}P$, ${{P}_{D}}$ – давление под грузом; ${{Z}_{1}} = {{Z}_{D}}{\text{/}}{{Z}_{0}}$, ${{Z}_{D}}$ – динамический прогиб пластины при $y = \ell {\text{/}}2$ и ${{Z}_{0}} = {{\alpha }_{1}}P{{b}^{2}}{\text{/}}D$ – статический прогиб пластины при действии в том же месте силы P [6]; ${{Z}_{2}} = {{Z}_{D}}{\text{/}}{{Z}_{0}}$, ${{Z}_{D}}$ – динамический прогиб под грузом при $y = S(t)$. Следует отметить, что результаты, представленные на рис. 2б, для изменения динамического коэффициента для прогиба в середине пластины – ${{Z}_{1}}$ близки к результатам из ([6], с. 105, рис. 57), где для указанной пластины и въезжающего груза контакт по Герцу моделируется через распределенную по эллиптической поверхности нагрузку с использованием численного интегрирования и построения рекуррентных соотношений для определения динамического взаимодействия. Отметим, что динамические коэффициенты для давления в [6] не представлены.

3. Метод решения уравнений для системы “самолет–посадочная полоса”. Алгоритм (2.3)–(2.11) легко реализуется в случае движения системы грузов по плите. Выражения вида (2.5) при движении $N$ грузов формируют систему $N$ линейных, алгебраических уравнений

Здесь ${\mathbf{A}}$, ${\mathbf{B}}$ – матрица и вектор (порядок равен числу грузов), ${\mathbf{E}}$ – единичная матрица, ${{{\mathbf{R}}}_{{ok}}} = \left[ {{{R}_{{Oi}}}} \right]$ ($i = 1, \ldots N)$ – вектор динамических давлениям грузов на плиту, ${{{\mathbf{\ddot {q}}}}_{K}}$ – вектор вертикальных ускорений точек контактов движущихся грузов.

Рассмотрим механическую систему в виде пластины на упругом основании, свободно опертой по контуру, и самолета в момент пробега (заключительного этапа посадки самолета). Движение самолета на пробеге считается равнозамедленным с некоторым средним ускорением –$w$. На этапе пробега самолет кроме непрерывно уменьшающихся аэродинамических сил Y и F (рис. 3), т.е. подъемной силы – Y и силы лобового сопротивления – F, включающей составляющую от тормозных парашютов, действует сила трения колес об аэродромное покрытие ${{F}_{{Tp}}}$ = $\sum\nolimits_{i = 1}^3 {{{F}_{{i,Tp}}}} $ = $\sum\nolimits_{i = 1}^3 {f \times {{R}_{{i,}}}} $. Уравнение движения самолета при пробеге можно записать в виде [22, 23] $(G{\text{/}}g)w = F + {{F}_{m}}$, где $G$ – вес самолета при посадке; $f$ – коэффициент трения. При математическом моделировании посадки следует учесть этапы посадки, предшествующие пробегу, т.е. этап выдерживания, при котором Y = G (снижение происходит до высоты 0.25–0.3 м) и этап парашютирования, малый по времени, при Y < G [22, 23], путем ввода подвижной системы координат, в которой рассматриваются вертикальные смещения самолета в момент пробега.

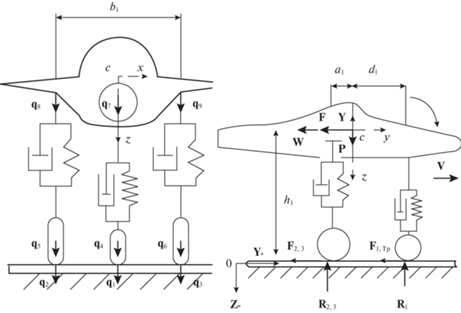
Будем далее обозначать модель самолета через $\left\{ {{{e}_{h}}} \right\}$ $h = 1, \ldots ,4$, представляя ее, как систему жестких тел ${{e}_{h}}$, состоящую из корпуса и трех связанных с ним линейными упруго-вязкими связями колес шасси, имеющих нелинейные связи с пластиной (рис. 3). Будем считать, что начальные условия у $\left\{ {{{e}_{h}}} \right\}$ нулевые, а параметры, определяющие положение $\left\{ {{{e}_{h}}} \right\}$ в системе ${{O}_{*}}{{X}_{*}}{{Y}_{*}}{{Z}_{*}}$, движущейся вдоль плиты поступательно, со скоростью ${v}$, имеют нулевые значения до момента касания колес самолета плиты, при этом в момент контакта $\left\{ {{{e}_{h}}} \right\}$ с плитой считается, что подъемная сила $Y = 0$ (рис. 3). Положение в пространстве корпуса подвижной нагрузки на этапе пробега $\left\{ {{{e}_{h}}} \right\}$ определяется параметрами: ${{q}_{C}}$ – вертикальным смещением центра масс корпуса и малыми поворотами ${{\varphi }_{x}}$ и ${{\varphi }_{y}}$ относительно горизонтальных осей $ox$ и $oy$ (рис. 3). В качестве обобщенных координат ${{q}_{i}}$ ($i$ = 1, …, 9) будем рассматривать вертикальные смещения узловых точек, соединяющих элементы $\left\{ {{{e}_{h}}} \right\}$ через связи (рис. 3).

Для составления системы дифференциальных уравнений движения $\left\{ {{{e}_{h}}} \right\}$ применяется метод кинетостатики. Используя метод расчленения для $\left\{ {{{e}_{h}}} \right\}$, имеем

где ${{\alpha }_{i}} = {{q}_{i}} - {{q}_{{i + 3}}}$, ${{T}_{i}} = {{c}_{{i + 3}}}({{q}_{{i + 3}}} - {{q}_{{i + 6}}})$, ${{q}_{C}} = \left( {\frac{1}{2}{{a}_{1}}({{q}_{8}} + {{q}_{9}}) + {{d}_{1}}{{q}_{7}}} \right){\text{/}}({{a}_{1}} + {{d}_{1}})$.

Здесь ${{m}_{i}}$ – массы колес шасси при $i = 1,2,3$ и кузова ${{m}_{4}} = {{M}^{{(куз)}}}$, ${{c}_{{i + 3}}}$ – жесткости линейных связей, моделирующих упругость шасси, $\mu $ – коэффициенты, учитывающие затухания в линейных связях, ${{J}_{x}}$, ${{J}_{y}}$ – моменты инерции относительно осей, проходящих через центр масс кузова, ${{M}^{{(ин)}}}$ = ${{F}_{{Tp}}} \times {{h}_{1}}$ = $({{M}^{{(куз)}}}w - F) \times {{h}_{1}}$ – инерционный момент (рис. 3), ${{a}_{1}}$, ${{b}_{1}}$, ${{c}_{1}}$, ${{d}_{1}}$, ${{h}_{1}}$ – конструктивные размеры $\left\{ {{{e}_{h}}} \right\}$, ${{k}_{i}}$ – коэффициент характеризующий нелинейные связи, в соответствии с (2.8).

После дискретизации по времени системы уравнений (3.2), используя шаговую процедуру (1.8) из [10] и линеаризацию уравнений в соответствии с (2.8)–(2.11), имеем на шаге [t_j, t_j + 1] систему линейных уравнений

Здесь ${{{\mathbf{\bar {q}}}}_{c}} = [{{q}_{1}}, \ldots {{q}_{9}}]{\kern 1pt} ' = [\bar {q}_{1}^{o},{{\bar {q}}_{2}}]{\kern 1pt} '$ – вектор независимых обобщенных координат, определяющих $\left\{ {{{e}_{h}}} \right\}$ в системе ${{O}_{*}}{{X}_{*}}{{Y}_{*}}{{Z}_{*}}$ (рис. 3), где ${\mathbf{\bar {q}}}_{1}^{o} = [{{q}_{1}},{{q}_{2}},{{q}_{3}}]{\kern 1pt} '$ – вертикальные смещения точек контакта колес с пластиной на упругом основании, при движении $\left\{ {{{e}_{h}}} \right\}$ в режиме торможения, ${{{\mathbf{M}}}_{*}}$, ${{{\mathbf{C}}}_{*}}$, ${{{\mathbf{K}}}_{*}}$ матрицы масс, демпфирования и жесткости для $\left\{ {{{e}_{h}}} \right\}$, ${{{\mathbf{P}}}_{{\mathbf{1}}}}$ – вектор, учитывающий весовые характеристики, инерционный момент и элементы дискретизации при линеаризации системы (3.1) на шаге [t_j, t_j + 1], ${{\Pi }_{*}}$ – матрица соединения векторов ${{{\mathbf{\bar {R}}}}_{*}}$ и ${{{\mathbf{R}}}_{*}}$, где ${{{\mathbf{\bar {R}}}}_{*}} = [{{R}_{1}},{{R}_{2}},{{R}_{3}}]{\kern 1pt} '$ – вектор реакций $\left\{ {{{e}_{h}}} \right\}$ в точках контакта с проезжей частью.

Представим систему (3.3), в соответствии с (1.8), на шаге [t_j, t_j + 1] в виде

Будем считать, что посадка $\left\{ {{{e}_{h}}} \right\}$, при решении задачи происходит на три колеса одновременно (аварийный, но один из возможных вариантов), хотя методика, имея в основе шаговую процедуру, не накладывает ограничений на вид посадки, при этом торможение $\left\{ {{{e}_{h}}} \right\}$ происходит при усредненном постоянном значении сил F и Y = 0 (рис. 3). При движении $\left\{ {{{e}_{h}}} \right\}$ по пластине требуем выполнение условий неразрывности перемещений и скоростей ${{{\mathbf{\bar {q}}}}_{{ok}}} = {\mathbf{\bar {q}}}_{1}^{^\circ }$, ${\mathbf{\dot {\bar {q}}}}_{K}^{{}} = {\mathbf{\dot {\bar {q}}}}_{1}^{^\circ }$ и условий равновесия в движущихся узлах (в точках контакта колес с пластиной)

Выделим из (3.4) подсистему уравнений, отвечающих в левой части подвектору ${\mathbf{\ddot {\bar {q}}}}_{{1j + 1/2}}^{o}$, и выразим далее эту подсистему относительно вектора динамических давлений, представив ее в виде

Подставим в (3.6) векторы ${{{\mathbf{\bar {R}}}}_{{ok}}}$ и ${{{\mathbf{\bar {R}}}}_{*}}$, соответственно, из (3.1) и (3.7), в итоге имеем разрешающую систему уравнений на шаге [t_j, t_j + 1]

где ${\mathbf{D}}$, ${{{\mathbf{D}}}^{o}}$ – матрица и вектор, характеризующие на шаге [t_j, t_j + 1] движение самолета по посадочной полосе.

Проследим ход решения всей задачи при j = 0, 1, 2, … На шаге [t_j, t_j + 1] при начальных условиях задачи в момент t_j определяется, применяя (3.8), вектор ${{{\mathbf{\ddot {\bar {q}}}}}_{{K\,j + 1/2}}}$, далее, используя (3.4), (3.5) и (2.2), вычисляются поля смещений, давлений, скоростей и ускорений для системы $\left\{ {{{e}_{h}}} \right\}$ в момент t_j + 1. Далее процесс повторяется.

4. Результаты численного моделирования. Шаговая процедура (3.8) реализована для $\left\{ {{{e}_{h}}} \right\}$ и пластины с параметрами $\ell $ = 130 м, $b$ = 40 м, Е₁ = 0.23 × 10⁸ кН/м², h = 0.18 м, m = 0.36 т/м², $\sigma $₁ = 0.18, $k* = 120 \times {{10}^{3}}$ кН/м³, $n_{1}^{{}}$ = 240 и $n_{2}^{{}}$ = 640. Для системы $\left\{ {{{e}_{h}}} \right\}$ (рис. 3) условно выбраны параметры: ${{b}_{1}}$ = 3 м, ${{a}_{1}} + {{d}_{1}}$ = 7 м, $h{}_{1}$ = 2.5 м, ${{J}_{x}}$ = 397 т м², ${{J}_{y}}$ = 53.5 т м², ${{m}_{1}}$ = 0.15 т, ${{m}_{2}}$ = ${{m}_{3}}$ = 0.25 т, ${{m}_{4}}$ = 22.0 т, ${{c}_{i}}$ = 800 кН/м, $\mu $ = 6 кНс/м, ${{P}_{1}}$ = 63.6 кН, ${{P}_{2}} = {{P}_{3}}$ = 71.65 кН, $\tilde {\alpha } = {{[9{{({{\vartheta }_{1}} + {{\vartheta }_{2}})}^{2}}{\text{/}}256r]}^{{1/3}}}$, где ${{\vartheta }_{i}} = 4(1 - \sigma _{i}^{2}){\text{/}}{{E}_{i}}$ $(i = 1,2)$, ${{E}_{2}}$ = 8.83 × × 10³ кН/м², ${{\sigma }_{2}}$ = 0.42, $r$ = 0.5 м [6, 22, 23].

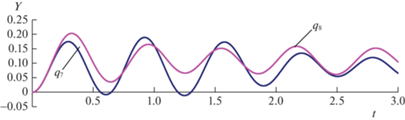
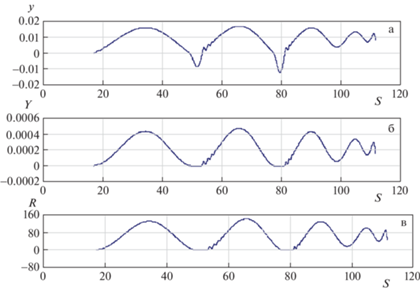
Посадка самолета происходит со скоростью ${{{v}}_{o}}$ = 63 м/с, а торможение с ускорением $w$ = –21 м/с², при этом время движения ${{t}_{{{дв}}}}$ = 3 с, с использованием тормозных парашютов. Интегрирование системы дифференциальных уравнений (3.8) происходит при $\Delta {{t}_{j}} = 0.00025$ с и числе шагов $N$ = 12 000. При посадке $\left\{ {{{e}_{h}}} \right\}$ считается, что касание носового колеса пластины происходит при нулевой вертикальной скорости на расстоянии $s{}_{o}$ = 17 м от края пластины, при ${{x}_{c}}$ = 20 м (рис. 2). Тормозной путь системы $\left\{ {{{e}_{h}}} \right\}$ до остановки составляет 94.5 м. На рис. 4(а, б, в), в режиме торможения $\left\{ {{{e}_{h}}} \right\}$, представлены в зависимости от s[м] = ${{s}_{0}} + {{{v}}_{0}}t + w{{t}^{2}}{\text{/}}2$, при тестовом соответствии между графиками: 1) вертикальное смещение у $\left\{ {{{e}_{h}}} \right\}$ носового (первого) колеса $Y = {{q}_{4}}$ [м] (рис. 4, а), при движении его с отскоком в зоне $s$ = 50–52 м; 2) вертикальное смещение плиты $Y = {{q}_{1}}$ [м] (рис. 4, б) под первым колесом; 3) динамическое давление $\left\{ {{{e}_{h}}} \right\}$ на плиту под первым колесом $R = {{R}_{1}}$ [кН] (рис. 4, в). Отметим, что при реализации шаговой процедуры $R = {{R}_{1}}$ = 0 в момент отскоков колеса. На рис. 5 представлены, в зависимости от времени t [с] вертикальные смещения узлов корпуса самолета $Y({\text{м)}} = {{q}_{7}}$ и $Y({\text{м)}} = {{q}_{8}}$ (рис. 3) при его движении с торможением по пластине на упругом основании. Следует отметить, что изменения динамических давлений ${{R}_{1}}$ и ${{R}_{2}}$ происходят, соответственно, относительно значений статических давлений ${{P}_{1}}$ и ${{P}_{2}}$ колес на пластину.

Остановимся еще на одном этапе исследования колебаний пластин при пробеге летательного аппарата по аэродромной полосе. К этому этапу относятся задачи, связанные с распространением волн деформаций в аэродромном покрытии. При решении волновых задач для протяженных пластин и стержней на упругом основании используются как интегральные преобразования при движении силовой нагрузки [1, 4], так и, для конструкций конечных размеров, наборы собственных форм сооружения. Применение численных методов позволяет, при этом, отслеживать процесс движения, в частности, сдвиговых волн от внезапной нагрузки, например, для балки Тимошенко на дискретных упруго-инерционных опорах в [24]. В пластинах и стержнях на упругом основании с учетом затуханий распространяются волны с сильной дисперсией [25]. Отметим, что высокоскоростные режимы движения могут вызывать дополнительные эффекты, что требует определенных оценок. Используем комбинированный подход. Для оценки появления резонансных решений приведем решение задачи о движении сосредоточенной силы $P$ по пластине на упругом основании, в виде бесконечной полосы свободно опертой по краям. Решение уравнения (2.1) при правой части $P\delta (x - {{x}_{c}})\delta (\zeta )$ и ${{\tilde {\mu }}_{1}}$ = 0 ищется в виде $q{\kern 1pt} *{\kern 1pt} (x,\zeta )$ = $\sum\nolimits_{n = 1,}^\infty {{{f}_{n}}(\zeta )} \sin \left( {{{\omega }_{n}}x} \right)$, ($\zeta = y - {v}t$, ${{\omega }_{n}} = \pi n{\text{/}}b$, ${{x}_{c}} = b{\text{/}}2$). Прогиб $q{\kern 1pt} *{\kern 1pt} (x,y - {v}t)$ части бегущей волны у пластины перед силой, при $\zeta = y - {v}t \geqslant 0$, имеет вид

где $\alpha = \sqrt {\frac{{\tilde {b} - \tilde {a}{{{v}}^{2}}}}{2}} $, $\beta = \sqrt {\frac{{\tilde {b} + \tilde {a}{{{v}}^{2}}}}{2}} $, $\tilde {a} = - \frac{{\omega _{n}^{2}}}{{{{{v}}^{2}}}} + \frac{m}{{2D}}$, $\tilde {b} = \sqrt {\omega _{n}^{4} + \frac{{k{\kern 1pt} *}}{D}} $, здесь $\zeta $ – абсцисса текущего сечения пластины отсчитываемого от подвижного начала координат, совмещенного с движущейся силой $P$.

В знаменателе (4.1), при $x = {{x}_{c}}$ и $\zeta $ = 0, находится выражение $\tilde {b} - \tilde {a}{{{v}}^{2}}$, определяющее серию критических скоростей движения силы по бесконечной полосе, моделируемой пластиной на упругом винклеровском основании.

В итоге при $n = 1,3,5$

Отметим, что в соответствии с (4.2) можно оценить диапазон появления критических скоростей при движении нагрузки в зависимости от параметров плиты и основания. В статье, при выбранных параметрах $D$, $m$, $k{\kern 1pt} *$, $b$, посадочная скорость самолета лежит вне зоны появления критических скоростей.

Заключение. Предложенный метод позволяет исследовать, используя шаговую процедуру, предложенную в [10] и метод узловых ускорений из [11], действие подвижной инерционной нагрузки при движении с переменной скоростью, по пластинам при различных граничных условиях, используя соответствующие фундаментальные функции [5]. В задачах автомобильного и авиационного транспорта метод позволяет исследовать поведение системы “инерционная подвижная нагрузка – техническое покрытие, моделируемое плитой на упругом основании” при различных скоростях движения нагрузки и неровностях поверхности, и определять напряженно-деформируемое состояние пластины и динамические давления колес в режимах торможения или разгона $\left\{ {{{e}_{h}}} \right\}$.