Прикладная математика и механика, 2022, T. 86, № 5, стр. 710-723
Приближенная теория распространения звука в ограниченной вязкоупругой среде с цилиндрическими каналами
Л. И. Казаков *
* E-mail: lev-kazakov@rambler.ru
Поступила в редакцию 15.04.2022
После доработки 20.06.2022
Принята к публикации 20.06.2022
- EDN: KWLIBY
- DOI: 10.31857/S0032823522050113
Аннотация
Выполнен расчет акустических характеристик цилиндрической вязкоупругой трубки конечной длины с радиально закрепленной внешней поверхностью, замещающей шестигранную элементарную ячейку отрезка микронеоднородной среды с цилиндрическими каналами. Применены принцип наименьшего действия и гипотеза плоских сечений. Найдено дисперсионное уравнение для продольных звуковых волн в трубке, совпадающее с приближениями точного дисперсионного уравнения и имеющее типичную для микронеоднородных резонансных сред форму. Из подходящей аппроксимации результатов известных измерений приведенной входной проводимости “полубесконечных” образцов найдена частотная зависимость комплексного модуля сдвига применявшейся резины.
1. Введение. Акустические свойства искусственной упругой среды с цилиндрическими каналами, центры которых совпадают с узлами правильной треугольной сетки, можно найти, решая осесимметричную задачу о распространении упругих волн вдоль трубки с радиально-закрепленной внешней цилиндрической поверхностью, которая приближенно заменяет шестигранную поверхность, окружающую канал.
Идея создания и первый приближенный расчет такой среды принадлежат Г.Д. Малюжинцу. В работе В.В. Тютекина [1] дана точная теория распространения осесимметричных упругих волн в безграничном волноводе типа “трубка”. Дальнейшие исследования этих вопросов изложены в работе А.Е. Вовк [2]. Получено точное решение для частного случая “трубки” конечного размера в работе [3].
Теория Г.Д. Малюжинца основана на применении принципа наименьшего действия Гамильтона–Остроградского и гипотезы плоских сечений и в этом отношении подобна расчету А. Лява ([4], § 278, с. 446) для продольных волн в стержне, учитывающему поправку Рэлея ([5], § 157, с. 273) на инерцию поперечного движения.
2. Вывод уравнения движения. Изложенная ниже приближенная теория также базируется на принципе наименьшего действия и гипотезе плоских сечений, которая состоит в предположении, что осевые смещения частиц ${{U}_{z}}$ во времени $t$ не зависят от радиуса r, т.е. любое поперечное сечение трубки остается при движении плоским:
Радиальные смещения зададим, следуя Г.Д. Малюжинцу, в виде
где $A = \operatorname{const} $, значение которой определим позже, ${{r}_{1}}$ – внешний радиус трубки, штрих над $f(z,t)$ означает производную по координате $z$.Отличными от нуля компонентами тензоров деформаций и напряжений для осесимметричного случая будут ([6], с. 13, 23):
(2.3)
$\begin{gathered} {{U}_{z}}_{z} = \frac{{\partial {{U}_{z}}}}{{\partial z}} = f{\kern 1pt} '(z,t),\quad {{U}_{{rr}}} = \frac{{\partial {{U}_{r}}}}{{\partial r}},\quad {{U}_{{\phi \phi }}} = \frac{{{{U}_{r}}}}{r},\quad {{U}_{{rz}}} = \frac{1}{2}\frac{{\partial {{U}_{r}}}}{{\partial z}} \\ {{\sigma }_{{rz}}} = 2\mu {{U}_{{rz}}} = \mu A\frac{{r_{1}^{2} - {{r}^{2}}}}{{2r}}f{\kern 1pt} ''(z,t) \\ \end{gathered} $(2.4)
${{\sigma }_{{\alpha \alpha }}} = \lambda \operatorname{div} \vec {U} + 2\mu {{U}_{{\alpha \alpha }}},\quad \alpha \alpha = rr,\phi \phi ,zz,$Заданная форма смещений (2.1), (2.2) удовлетворяет требуемым граничным условиям на внешней поверхности трубки
На свободной внутренней поверхности трубки радиуса ${{r}_{0}}$ должны выполняться условия
(2.7)
${{\sigma }_{{rr}}}(z,{{r}_{0}}) = \left[ {\lambda \left( {1 - A} \right) - \mu A\left( {1 + \frac{1}{\varepsilon }} \right)} \right]f{\kern 1pt} '(z,t) = 0,$(2.8)
$A = {{A}_{0}} = {{\left( {1 + \mu \frac{{1 + \varepsilon }}{{\lambda \varepsilon }}} \right)}^{{ - 1}}},$Найдем кинетическую $T$ и упругую $E$ энергии отрезка трубки длиною $h$ по формулам:
Вычисления дадут:
(2.9)
$E(t) = \frac{{\pi \mu r_{1}^{2}}}{2}\int\limits_0^h {\left\{ {D\left( {A,\varepsilon } \right){{{\left[ {f{\kern 1pt} '(z,t)} \right]}}^{2}} + {{\xi }^{2}}{{A}^{2}}r_{0}^{2}b(\varepsilon ){{{\left[ {f{\kern 1pt} ''(z,t)} \right]}}^{2}}} \right\}} dz$(2.10)
$T(t) = \frac{{\pi \rho r_{1}^{2}}}{2}\int\limits_0^h {\left\{ {{{A}^{2}}r_{0}^{2}b(\varepsilon ){{{\left[ {\frac{{\partial f{\kern 1pt} '(z,t)}}{{\partial t}}} \right]}}^{2}} + (1 - \varepsilon ){{{\left[ {\frac{{\partial f(z,t)}}{{\partial t}}} \right]}}^{2}}} \right\}dz,} $Применим к решению задачи, которая состоит теперь в отыскании функции $f(z,t)$, принцип наименьшего действия Гамильтона–Остроградского
(2.11)
$\delta \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left( {T - E + W} \right)dt} = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left( {\delta T - \delta E + \delta W} \right)dt} = 0,$(2.12)
$\begin{gathered} \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\int\limits_0^h {\left( {{{f}^{{IV}}} - \frac{\rho }{\mu }\frac{{{{\partial }^{2}}f{\kern 1pt} ''}}{{\partial {{t}^{2}}}} - \frac{{D(A,\varepsilon )}}{{{{A}^{2}}r_{0}^{2}b(\varepsilon )}}f{\kern 1pt} ''\; + \frac{{\rho (1 - \varepsilon )}}{{\mu {{A}^{2}}r_{0}^{2}b(\varepsilon )}}\frac{{{{\partial }^{2}}f}}{{\partial {{t}^{2}}}}} \right)} } \delta fdzdt - \\ - \;\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\left\{ {\left[ {\left( {f{\kern 1pt} '''\; - \frac{{D(A,\varepsilon )}}{{{{A}^{2}}r_{0}^{2}b(\varepsilon )}}f{\kern 1pt} '\; - \frac{\rho }{\mu }\frac{{{{\partial }^{2}}f{\kern 1pt} '}}{{\partial {{t}^{2}}}}} \right)\delta f - f{\kern 1pt} ''{\kern 1pt} \delta f{\kern 1pt} '} \right]_{0}^{h} + \frac{{\delta W}}{{\pi \mu r_{1}^{2}{{A}^{2}}{{r}_{0}}^{2}b(\varepsilon )}}} \right\}dt = 0} \\ \end{gathered} $Вариация работы внешних сил $\delta W$ есть линейная форма от вариаций $\delta f = \delta {{U}_{z}}$ и $\delta f{\kern 1pt} '\sim \delta {{U}_{r}}$, взятых при $z = 0$ и $z = h$. В силу произвольности всех вариаций в выражении (2.12) каждый интеграл в отдельности должен обращаться в нуль. Тогда первый интеграл дает уравнение движения
(2.13)
${{f}^{{IV}}} - \frac{\rho }{\mu }\frac{{{{\partial }^{2}}f{\kern 1pt} ''}}{{\partial {{t}^{2}}}} - \frac{{D(A,\varepsilon )}}{{{{A}^{2}}r_{0}^{2}b(\varepsilon )}}f{\kern 1pt} ''\; + \frac{{\rho (1 - \varepsilon )}}{{\mu {{A}^{2}}r_{0}^{2}b(\varepsilon )}}\frac{{{{\partial }^{2}}f}}{{\partial {{t}^{2}}}} = 0,$Будем считать, что к торцевым сечениям трубки примыкают тонкие жесткие пластинки. Через них на трубку можно воздействовать извне только давлениями $P(0,t)$ и $P(h,t)$, работа которых запишется в виде
откудаРассмотрим два крайних варианта крепления таких пластинок на торцах трубки: без трения (“скользкая” пластинка) и жесткое крепление, или сцепление. В первом случае обращаются в нуль касательные напряжения ${{\sigma }_{{rz}}}$ между пластинкой и трубкой, т.е. в соответствии с формулой (2.3) должно выполняться граничное условие
В случае сцепления запрещены радиальные смещения в торцевом сечении трубки, что на основании формулы (2.2) дает граничное условие
Соответствующие динамические граничные условия найдем из выражения (2.12) с учетом (2.14):
для “скользкой” пластинки:
(2.17)
$f{\kern 1pt} '''({{z}_{0}},t) - \frac{{D(A,\varepsilon )}}{{{{A}^{2}}r_{0}^{2}b(\varepsilon )}}f{\kern 1pt} '({{z}_{0}},t) - \frac{\rho }{\mu }\frac{{{{\partial }^{2}}f{\kern 1pt} '({{z}_{0}},t)}}{{\partial {{t}^{2}}}} = \frac{{P({{z}_{0}},t)}}{{\mu {{A}^{2}}r_{0}^{2}b(\varepsilon )}}$для случая сцепления:
(2.18)
$f{\kern 1pt} '''({{z}_{0}},t) = \frac{{P({{z}_{0}},t)}}{{\mu {{A}^{2}}r_{0}^{2}b(\varepsilon )}}$При гармонических колебаниях, когда временна́я зависимость величин задана сокращаемым множителем ${{e}^{{ - i\omega t}}}$, где $i$ – мнимая единица, $\omega $ – круговая частота, уравнение движения (2.13) и динамические граничные условия (2.17), (2.18) для комплексных амплитуд запишем в виде
(2.19)
$f{\kern 1pt} '''({{z}_{0}}) + \left( {{{k}^{2}} - {{\kappa }^{2}}} \right)f{\kern 1pt} '({{z}_{0}}) = \frac{{{{k}^{2}}{{\kappa }^{2}}P({{z}_{0}})}}{{{{\omega }^{2}}\rho (1 - \varepsilon )}}$(2.20)
$\left( {{{k}^{2}} - {{\kappa }^{2}}} \right) = \frac{{{{\omega }^{2}}\rho }}{\mu } - \frac{{D(A,\varepsilon )}}{{{{A}^{2}}r_{0}^{2}b(\varepsilon )}}$(2.21)
${{k}^{2}}{{\kappa }^{2}} = \frac{{{{\omega }^{2}}\rho (1 - \varepsilon )}}{{\mu {{A}^{2}}r_{0}^{2}b(\varepsilon )}}$Введя дифференциальный оператор $\nabla \equiv d{\text{/}}dz$, уравнение (2.19) можно записать в виде
Общее решение этого уравнения может быть представлено суммой решений волновых уравнений
(2.22)
$f(z) = {{A}_{1}}\operatorname{sh} \kappa z + {{A}_{2}}\operatorname{ch} \kappa z + {{A}_{3}}\sin kz + {{A}_{4}}\cos kz,$3. Дисперсионное уравнение. Пока остается неопределенной постоянная $A$. Ее можно связать с волновым числом $k$ следующим образом. Возьмем точное уравнение в цилиндрических координатах для аксиальной составляющей смещения при осесимметричных движениях ([6], с. 126, (22.6))
Усредним его по площади сечения трубки $\pi \left( {r_{1}^{2} - r_{0}^{2}} \right)$ и, используя граничные условия (2.5) и (2.6), найдем:
Исключив из уравнений (2.20), (2.21), (3.1) $\kappa $ и $A$, найдем
(3.2)
$\frac{1}{{({{n}^{2}} - 1)\left( {1 - \frac{1}{{2\alpha }}{{n}^{2}}} \right)}}\left[ {{{n}^{2}} - \frac{{1 + \left( {2\alpha - 1} \right)\varepsilon }}{{1 + \left( {3 - \frac{2}{\alpha }} \right)\varepsilon }}} \right] = {{\Omega }^{2}},$(3.4)
${{\Omega }^{2}} = \frac{{2\alpha \varepsilon b(\varepsilon )}}{{a(\varepsilon )}}{{({{k}_{l}}{{r}_{1}})}^{2}} = \frac{{{{\omega }^{2}}\rho r_{1}^{2}\varepsilon b(\varepsilon )}}{{\mu a(\varepsilon )}}$(3.5)
$a(\varepsilon ) = \frac{{1 - \varepsilon }}{\varepsilon }\left[ {1 + \left( {3 - \frac{2}{\alpha }} \right)\varepsilon } \right]$Постоянную $A$ найдем из формул (3.1)–(3.3):
Из формул (2.8), (3.6) и (3.2) при $\Omega \to 0$, получим:
что означает выполнение граничного условия (2.7) в квазистатическом случае.Выражение (3.2) является приближенным дисперсионным уравнением для определения $k = n{{k}_{l}}$. Тогда получаем, что при $\Omega \to 0$
Для вязкоупругих материалов (например, резин) модуль сдвига при гармонических колебаниях является комплексной функцией частоты:
где $\mu (\omega )$ – модуль сдвига, $\eta (\omega )$ – коэффициент сдвиговых потерь, величина которого обычно лежит в пределах $\eta (\omega ) = 0.1 \ldots 1.0$. Первый коэффициент Ламе $\lambda $ на звуковых и ультразвуковых частотах можно считать вещественной постоянной, причем $\lambda \gg \left| {\mu {\kern 1pt} *{\kern 1pt} (\omega )} \right|$. В связи с этим волновое число ${{k}_{l}}$, а также $a(\varepsilon )$ (3.5) будем с малой ошибкой полагать вещественными. Для вязкоупругих материалов допустим, чтоТогда дисперсионное уравнение (3.2) запишется в виде:
(3.9)
${{n}^{{ * 2}}} = \frac{{\Omega _{1}^{{*2}} - {{\Omega }^{{ * 2}}}}}{{1 - {{\Omega }^{{ * 2}}}}};\quad \Omega _{1}^{{*2}} = \frac{{1 + \left( {2\alpha {\kern 1pt} * - 1} \right)\varepsilon }}{{1 + \left( {3 - \frac{2}{{\alpha {\kern 1pt} *}}} \right)\varepsilon }},$(3.10)
$\alpha * = \frac{\alpha }{{1 - i\eta }},\quad \left| {\alpha {\text{*}}} \right| \gg 1,\quad {{\Omega }^{{ * 2}}} = \frac{{{{\Omega }^{2}}}}{{1 - i\eta }}$Точное дисперсионное уравнение получено в работе [1]:
(3.11)
$(1 - {{n}^{2}})\left[ {{{n}^{2}}\Phi (U) - \alpha } \right] + {{(\alpha - {{n}^{2}})}^{2}}\Phi (V) = 0,$(3.12)
$\Phi (x) = \sqrt \varepsilon x\frac{{{{J}_{1}}(x){{N}_{0}}\left( {\sqrt \varepsilon x} \right) - {{N}_{1}}(x){{J}_{0}}\left( {\sqrt \varepsilon x} \right)}}{{{{J}_{1}}(x){{N}_{1}}\left( {\sqrt \varepsilon x} \right) - {{N}_{1}}(x){{J}_{1}}\left( {\sqrt \varepsilon x} \right)}}$Выражение (3.9) следует из (3.11) в качестве низкочастотного приближения при $\left| U \right|$, $\left| V \right| \ll 1$. Используя в (3.12) представления цилиндрических функций рядами при $\left| x \right| \ll 1$ ([8], с. 415, 428), получим
(3.13)
$\Phi (x) = - \frac{{2\varepsilon }}{{1 - \varepsilon }}\frac{{1 + \frac{{{{x}^{2}}}}{4}\left( {1 + \ln \varepsilon - \varepsilon } \right) + \ldots }}{{1 - \frac{{{{x}^{2}}}}{8}\frac{{1 + 2\varepsilon \ln \varepsilon - {{\varepsilon }^{2}}}}{{1 - \varepsilon }} + \ldots }} = - \frac{{2\varepsilon }}{{1 - \varepsilon }}\left( {1 - \frac{{\varepsilon b(\varepsilon )}}{{1 - \varepsilon }}{{x}^{2}} + \ldots } \right)$Ограничившись только выписанными здесь членами в разложениях для функций $\Phi (U)$ и $\Phi (V)$ и подставив последние в уравнение (3.11), получим в точности формулу (3.9) [7]. При таком выводе она справедлива для вязкоупругих материалов, лишь когда
Фактически формула (3.9) была получена таким способом уже в работе [1] в качестве квазистатического приближения с рэлеевской поправкой.
В наиболее интересных случаях применения (для звукопоглощения), когда справедливы допущения: (3.8), $\left| {n{\kern 1pt} *} \right|\sim 1$, ${{k}_{l}}{{r}_{1}} \leqslant 1$, $\sqrt {2\varepsilon {\text{/}}\alpha } \ll 1$, $\varepsilon \ll 0.25$, можно считать, что $\left| U \right| \gg 1$, $\left| V \right| \ll 1$. Используя в формуле (3.12) для $\Phi (U)$ асимптотические представления цилиндрических функций [8, с. 449], а для $\Phi (V)$ – приближение (3.13), найдем:
(3.15)
$\Phi (V) \approx - \frac{{2\varepsilon }}{{1 - \varepsilon }}\left( {1 - \frac{{{{{({{k}_{l}}{{r}_{1}})}}^{2}}\varepsilon b(\varepsilon )}}{{1 - \varepsilon }}\left( {1 - {{n}^{2}}} \right)} \right)$Подставив (3.14), (3.15) в (3.11), при принятых допущениях снова придем к формуле (3.9) [7].
Учитывая (3.3)–(3.5), (3.10), представим зависимость (3.9) в виде
(3.16)
${{n}^{{ * 2}}} = {{(n{\kern 1pt} '\; + in{\kern 1pt} '')}^{2}} = s* = s{\kern 1pt} '\; + is{\kern 1pt} '' = 1 + \frac{{2\varepsilon \alpha }}{{(1 + 3\varepsilon )\left( {1 - {{\Omega }^{2}} - i\eta } \right)}},$(3.17)
$s{\kern 1pt} ' = {{n}^{{'2}}} - {{n}^{{''2}}} = 1 + \frac{{2\varepsilon \alpha }}{{1 + 3\varepsilon }}\frac{{1 - {{\Omega }^{2}}}}{{{{{\left( {1 - {{\Omega }^{2}}} \right)}}^{2}} + {{\eta }^{2}}}}$(3.18)
$s{\kern 1pt} '' = 2n{\kern 1pt} '{\kern 1pt} n{\kern 1pt} '' = \frac{{2\varepsilon \alpha }}{{1 + 3\varepsilon }}\frac{\eta }{{{{{\left( {1 - {{\Omega }^{2}}} \right)}}^{2}} + {{\eta }^{2}}}}$Величину $s{\kern 1pt} *$ можно назвать приведенной комплексной сжимаемостью перфорированной каналами среды [1]. Формула (3.16) подобна выражению для квадрата комплексного показателя преломления в теории дисперсии и абсорбции электромагнитных волн в разреженной среде, содержащей осцилляторы одного сорта, т.е. имеет обычный лоренцевский вид ([9], с. 56, (32.27)), ([10], § 156, с. 556). При этом $s{\kern 1pt} *$ является аналогом комплексной диэлектрической проницаемости такой среды, и поэтому $s{\kern 1pt} '$ и $s{\kern 1pt} ''$ должны быть связаны дисперсионными соотношениями Крамерса–Кронига ([11], § 82, с. 389, [12]).
На рис. 1 построены зависимости от ${{k}_{l}}{{r}_{1}}$ функций $s{\kern 1pt} '$ (3.17) и $s{\kern 1pt} ''$ (3.18) при $\alpha = 800$, $\eta = 1$, $\varepsilon = {{0.05}^{2}}$. Точками показаны значения этих величин для нулевой квазипродольной волны, вычисленные по точной теории в работе [2]. Видно хорошее совпадение. При $s{\kern 1pt} ' < 0$ мнимая часть $k{\kern 1pt} ''$ волнового числа $k* = {{k}_{l}}n{\kern 1pt} *$ превышает вещественную часть $k{\kern 1pt} '$. Из формулы (3.17) следует, что это возможно лишь при
в диапазоне частот, границы которого определяет соотношениеРис. 1.
Компоненты функции $s{\text{*}}(x)$ (3.16), $x = {{k}_{l}}{{r}_{1}}$ при $\alpha = 800$, $\eta = 1.0$, $\varepsilon = {{0.05}^{2}}$. $\operatorname{Re} \left( {s{\text{*}}(x)} \right)$: $\bigcirc $ – данные [2], $\rlap{--} $ – по формуле (3.17); $\operatorname{Im} \left( {s{\text{*}}(x)} \right)$: $ \bullet $ – данные [2], - - - - – по формуле (3.18).
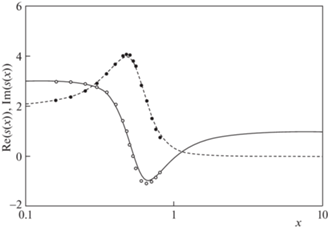
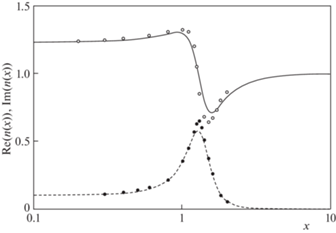
Рисунок 2 демонстрирует степень совпадения расчетных приближенных значений $n{\kern 1pt} '({{k}_{l}}{{r}_{1}})$ и $n{\kern 1pt} ''({{k}_{l}}{{r}_{1}})$ с точными из работы [2] при $\alpha = 125$, $\eta = 0.5$, $\varepsilon = {{0.05}^{2}}$. Условие (3.19) здесь не выполняется и поэтому везде $n{\kern 1pt} ' > n{\kern 1pt} ''$, т.е. эффект нераспространения отсутствует.
Рис. 2.
Компоненты показателя преломления $n{\text{*}}(x)$ при $\alpha = 125$, $\eta = 0.5$, $\varepsilon = {{0.05}^{2}}$: $\operatorname{Re} \left( {n{\text{*}}(x)} \right)$: $\bigcirc $ – из работы [2], $\rlap{--} $ – по формуле (3.16); $\operatorname{Im} \left( {n{\text{*}}(x)} \right)$: $ \bullet $ – из работы [2], - - - - – по формуле (3.16).
Из формулы (3.16) с учетом (3.3)–(3.5), (3.10) найдем выражение для волнового числа:
(3.20)
${{k}^{{ * 2}}} = k_{l}^{2} + \frac{1}{{1 - \frac{{{{\omega }^{2}}\mu ({{\omega }_{p}})}}{{\omega _{p}^{2}\mu (\omega )}} - i\eta }} \cdot \frac{{{{\omega }^{2}}\rho \varepsilon }}{{(1 + 3\varepsilon )\mu (\omega )}},$При $\sqrt \varepsilon \leqslant 0.3$ достаточно хороша приближенная формула $\sqrt {b(\varepsilon ){\text{/}}a(\varepsilon )} $ = $\frac{1}{2}\sqrt {\ln \frac{1}{\varepsilon } - 1.5} $. Для заданного значения ${{r}_{1}}$ собственная частота канала минимальна при $\varepsilon = {{\varepsilon }_{0}}$ = 0.11 и слабо зависит от ${{r}_{0}}$ в широком диапазоне относительно больших значений $\varepsilon $, возрастая до бесконечности как при $\varepsilon \to 0$, так и при $\varepsilon \to 1$. Такое же значение ${{\omega }_{p}}$ получено в теории Г.Д. Малюжинца. Значение параметра ${{k}_{t}}{{r}_{0}}$ на резонансе: ${{({{k}_{t}}{{r}_{0}})}_{p}} = \sqrt {a(\varepsilon ){\text{/}}b(\varepsilon )} $.
Эффективные комплексные параметры дисперсных микронеоднородных сред – волновое число $\tilde {\kappa }$, сжимаемость $\tilde {k}$, плотность $\tilde {\rho }$ – связаны соотношением ${{\tilde {\kappa }}^{2}} = {{\omega }^{2}}\tilde {k}\tilde {\rho }$. Некоторые такие среды обладают резонансными свойствами, например, вода с газовыми пузырьками ([14], с. 379), резина с полостями, резина с твердыми включениями [15, 16]. В двух первых случаях за резонансные свойства отвечает комплексная сжимаемость $\tilde {k}$, тогда как $\tilde {\rho }$ – величина вещественная. В последнем случае наоборот: сжимаемость $\tilde {k}$ вещественна (при учете только вязких потерь), а резонансные свойства среды обусловлены ее комплексной плотностью $\tilde {\rho }$. Для таких сред, если они малоконцентрированные и монодисперсные, квадраты волновых чисел ${{\tilde {\kappa }}^{2}}$ выражаются такими же формулами, как (3.20).
Для вязкоупругих материалов согласно (3.6) и (3.10)
Поэтому при заданной форме движений (2.1), (2.2) для распространяющейся волны $\left( {\partial {\text{/}}\partial z \to ik{\kern 1pt} *} \right)$, используя зависимость (3.16), найдем:
Отсюда видно, что относительное радиальное движение стенок канала имеет два резонанса: на собственной частоте канала при ${{\Omega }^{2}} = 1$ и на частоте зарождения первой квазипродольной волны при ${{\Omega }^{2}} = 1 + 2\varepsilon \alpha {\text{/}}\left( {1 + 3\varepsilon } \right)$. На низких и высоких частотах радиальное движение стенок канала ослабевает.
Из формул (2.3), (2.4), (3.16), (3.21) для распространяющихся волн получим:
При $\left| {n{\kern 1pt} *} \right|\sim 1$, $\eta \sim 1$ это отношение всегда много меньше единицы, в том числе и на резонансе канала, что позволяет считать граничное условие (2.6) выполняющимся приближенно на всех частотах.
Волновое число неоднородных волн $\kappa {\kern 1pt} *$ при известных $k{\kern 1pt} *$ (3.20) и $A{\kern 1pt} *$ (3.21) следует из уравнения (2.21):
При $\varepsilon \ll 1$, $\eta \sim 1$ на всех частотах $\left| {\kappa {\kern 1pt} *} \right| \gg \left| {k{\kern 1pt} *} \right|$, откуда следует, что область неоднородных волн вблизи торцов трубки весьма мала в сравнении с длиной продольной волны.
Входная акустическая проводимость трубки с тонкой жесткой пластинкой на торце согласно (2.1) имеет вид:
где $P(0)$ – звуковое давление на торец. Используя граничные условия (2.15)–(2.19) для определения (2.22), найдем входные проводимости полубесконечных ($h \to \infty $) трубок:при пластинке без трения
(3.22)
$Y(0) = \frac{{k{\kern 1pt} *}}{{\omega \rho (1 - \varepsilon )}}\frac{{1 - \frac{{ik{\kern 1pt} *}}{{\kappa {\kern 1pt} *}}}}{{1 - \frac{{ik{\kern 1pt} *}}{{\kappa {\kern 1pt} *}} - \frac{{{{k}^{{ * 2}}}}}{{{{\kappa }^{{ * 2}}}}}}} \approx \frac{{k{\kern 1pt} *}}{{\omega \rho (1 - \varepsilon )}};$при пластинке, приклеенной к торцу,
(3.23)
$Y(0) = \frac{{k{\kern 1pt} *}}{{\omega \rho (1 - \varepsilon )}}\frac{1}{{1 - \frac{{ik{\kern 1pt} *}}{{\kappa {\kern 1pt} *}}}}$Здесь второй множитель в правой части отражает влияние радиального закрепления входной поверхности трубки. В первом же случае ролью свободного от касательных напряжений торца чаще всего можно пренебречь.
В работе [17] приведены результаты измерений на установке “Импульсная труба” акустических характеристик образцов разной длины из резины с цилиндрическими каналами. Предполагалось, что длина каждого образца обеспечивает выполнение условия $n{\kern 1pt} ''{\kern 1pt} {{k}_{l}}h > 2$, позволяющего считать образец полубесконечным. Каналы в образцах несквозные – “со стороны основания оставляется тонкая диафрагма (толщина ее около 0.5 мм)” [17]. Для каждого образца измеряли входную проводимость, приведенную к проводимости сплошной среды с волновым сопротивлением $\rho (1 - \varepsilon ){{c}_{l}}$, т.е.
где под $Y(0)$ следует понимать либо (3.22), либо (3.23) – в зависимости от предположения о характере колебаний торцевой поверхности образца, граничащей с водой. Тогда получим:для “скользкой” пластинки:
для пластинки, приклеенной к торцу трубки:
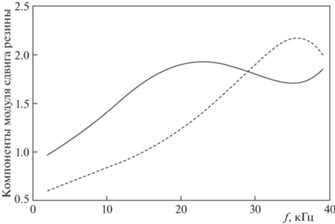
На рис. 3 приведены средние по измерениям на 1–3 образцах значения $P$ (черные точки) и $Q$ (белые точки), аппроксимированные частотными зависимостями $P(f)$ и $Q(f)$ в виде полиномов пятой степени (сплошная линия). Подставив эти зависимости в левые части выражений (3.24) или (3.25), получим уравнения для нахождения комплексного модуля сдвига (3.7) резины образцов. В первом случае это уравнение квадратное, и значения $\mu {\text{*}}(f)$ относительно $P(f)$ и $Q(f)$ находятся точно. При этом на высоких частотах величина коэффициента сдвиговых потерь возрастает до $\eta (f) > 6$, что нереально и говорит о непригодности представления о “скользкой” пластинке на входном торце образца. Во втором случае уравнение для $\mu {\text{*}}(f)$ переходит в квадратное, лишь если пренебречь в знаменателе правой части (3.25) малым слагаемым ${{\left( {k{\text{*/}}\kappa {\text{*}}} \right)}^{2}}$, так что решение не будет точным. Его можно улучшить, умножив на близкий к единице комплексный линейный полином и варьируя коэффициенты последнего. Компоненты уточненного модуля сдвига $\mu {\text{*}}(f)$ показаны на рис. 4. Подстановка их в правую часть уравнения (3.25) дает представленные на рис. 3 пунктирные кривые, близкие к исходным $P(f)$ и $Q(f)$. Результат рис. 4 вполне реалистичен до частот $f \approx 20$ кГц и несколько сомнителен на высоких частотах, где данных о $\mu (f)$ и $\eta (f)$ в [17] нет.
Рис. 3.
Частотные зависимости компонентов приведенной входной проводимости ${{Y}_{\varepsilon }} = P + iQ$ образцов работы [17]: $ \bullet $ – активная проводимость $P$; $\bigcirc $ – реактивная проводимость $Q$; $\rlap{--} $ – аппроксимирующие кривые $P(f)$ и $Q(f)$; – – – – кривые проверки решения для $\mu {\text{*}}(f)$.
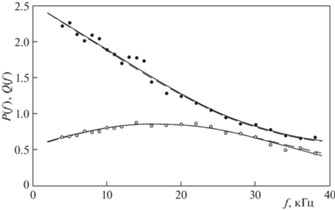
Рис. 4.
Частотные зависимости расчетных компонентов комплексного модуля сдвига μ*( f ) = = $\mu (f)\left[ {1 - i\eta (f)} \right]$ резины измеренных образцов: $\rlap{--} $ – модуль сдвига $\mu (f) \times {{10}^{{ - 7}}}$ Па, – – – – коэффициент сдвиговых потерь $\eta (f)$.
Заключение. Показано, что для распространяющейся в вязкоупругой среде с цилиндрическими каналами звуковой волны дисперсионное уравнение имеет такую же форму, как для других известных резонансных микронеоднородных сред. Это тем более справедливо, чем меньше коэффициент перфорации $\varepsilon $ (объемная концентрация каналов). Поскольку теория учитывает неоднородные волны вблизи торцевых поверхностей трубки, она применима к перфорированным резиновым слоям произвольно малой толщины с двумя типами граничных условий на поверхностях слоев [18].
Развитую здесь теорию можно привлечь к измерениям упругих параметров вязкоупругих материалов с помощью “Импульсной трубы” или вибростола. При определении модуля сдвига резины образцов работы [17] более подходящим (как и в [18]) оказалось допущение о сцеплении входного торца трубки с тонкой жесткой пластинкой.
Список литературы
Тютекин В.В. Распространение упругих волн в среде с цилиндрическими каналами // Акуст. ж. 1956. Т. 2. № 3. С. 291–301.
Вовк А.Е. Некоторые вопросы распространения упругих волн в твердых волноводах. Дисс. на соискание уч. ст. к.ф.-м.н. Москва, 1967. 128 с.
Шейба Л.С., Шляпочников С.А. Об одном классе собственных колебаний упругого цилиндра // Акуст. ж. 1974. Т. 20. № 2. С. 331–333.
Ляв А. Математическая теория упругости. М.; Л.: ОНТИ НКТП СССР, 1935. 473 с.
Рэлей. Теория звука. Том 1. М.: Гостехиздат, 1955. 503 с.
Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука, 1987. 247 с.
Казаков Л.И. Акустические свойства упругой среды с цилиндрическими каналами // Деп. в ВИНИТИ 12.09.84 № 6203–84. Деп. 26 с.
Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970. 712 с.
Фейнман Р., Лейтон Р., Сендс М. Фейнмановские лекции по физике. Физика сплошных сред. М.: Мир, 1977. 288 с.
Ландсберг Г.С. Оптика. М.: Наука, 1976. 926 с.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982. 620 с.
Гинзбург В.Л. Об общей связи между поглощением и дисперсией звуковых волн // Акуст. ж. 1955. Т. 1. № 1. С. 31–39.
Вовк А.Е., Тютекин В.В. О “сверхвязких” продольных волнах в упругой среде // Акуст. ж. 1961. Т. 7. № 2. С. 256–257.
Скучик Е. Основы акустики. Том II. М.: Иностр. лит., 1959. 565 с.
Викторова Р.Н., Тютекин В.В. Физические основы создания звукопоглощающих материалов с использованием среды с комплексной плотностью // Акуст. ж. 1998. Т. 44. № 3. С. 331–336.
Казаков Л.И. Ячеечные модели вязкоупругой среды с твердыми сферическими включениями // Акуст. ж. 2022. Т. 68. № 2. С. 173–181.
Вовк А.Е., Пастернак Р.Н., Тютекин В.В. Экспериментальное исследование волновых свойств среды с цилиндрическими каналами // Акуст. ж. 1958. Т. 4. № 1. С. 24–32.
Казаков Л.И. Акустические характеристики нагруженных перфорированных слоев // Деп. в ВИНИТИ 19.08.87. № 6092. В87. 17 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


