1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 5, 2022

Прикладная математика и механика, 2022, T. 86, № 5, стр. 638-653

К расчетам больших неизотермических деформаций упруговязкопластических материалов

А. С. Бегун 1, 2, *, А. А. Буренин 1, **, Л. В. Ковтанюк 1, 2, ***

1 Институт машиноведения и металлургии ДВО РАН
Комсомольск-на-Амуре, Россия

2 Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия

* E-mail: ustinova@iacp.dvo.ru
** E-mail: aab@imim.ru
*** E-mail: lk@iacp.dvo.ru

Поступила в редакцию 18.05.2022
После доработки 15.06.2022
Принята к публикации 15.06.2022

Полный текст (PDF)

Аннотация

Предлагается метод и обсуждаются результаты расчетов в связанной задаче теории больших деформаций о деформировании материала цилиндрического слоя, удерживаемого между жесткими цилиндрическими поверхностями. Материал слоя принимается упруговязкопластическим, контакт его с шероховатыми границами при повороте внешней из них происходит с трением, порождающим тепло, теплотворным считается и необратимое деформирование. Рассчитывается полный цикл процесса квазистатического деформирования от его начала до полной разгрузки и остывания слоя материала. Указываются моменты времени начала и окончания скольжения материала вдоль его жесткой граничной поверхности, начала и окончания его пристеночного вязкопластического течения.

Ключевые слова: упругость, пластичность, вязкопластическое течение, большие деформации, теплопроводность, связанное термодеформирование

1. Введение. В каждом термодинамическом процессе параметры состояния задаются [1] дифференциальными уравнениями своего изменения (переноса, кинетическими уравнениями). Термодинамический процесс деформирования тел в таком своем качестве не является исключением. В общем случае этот процесс является необратимым и неравновесным [2]. С целью составления математической модели процесса деформирования полные деформации, которые возможно измерить экспериментально, приходится разделить на обратимую и необратимую составляющие. Данное разделение необходимо является гипотетическим, поскольку эти составляющие опытно неизмеримы. Но именно такие составляющие предстают в качестве термодинамических параметров состояния [2, 3] и для них необходимо указать дифференциальные уравнения их изменения. К этим основным термодинамическим параметрам состояния процесса деформирования могут добавляться иные, позволяющие учитывать специфические особенности процесса, например, повреждаемость [4, 5], но в таком случае добавляются и соответствующие дифференциальные уравнения изменения для добавляемых параметров состояния [5, 6].

Кинематический характер вводимых термодинамических параметров состояния, коими являются обратимые и необратимые составляющие полных деформаций, неизбежно приводит и к трудностям при записи для них дифференциальных уравнений их изменения. Наряду с источниками (скоростями изменения) этих составляющих деформаций, дифференциальные уравнения изменения обязаны включать в себя потоковые слагаемые [2], определяющие взаимозависимость параметров состояния в процессе деформирования [2, 3]. Для источников в уравнениях изменения термодинамических параметров состояния в согласии с уравнением баланса энтропии формулируются определяющие законы (упругости, пластичности, ползучести и др.), а потоковые слагаемые обязаны обеспечить геометрическую корректность кинематики построенной теории больших деформаций. Основные трудности связаны как раз с последним обстоятельством и именно в этом допускались основные неточности в самых ранних построениях кинематики больших деформаций упругопластических материалов. Геометрически безупречная такая кинематика впервые, по-видимому, была построена в [7] на основе так называемого “мультипликативного” разделения полных деформаций на свои обратимую и необратимую составляющие. Основанием для данного разделения послужила гипотеза о взаимно однозначном соответствии каждому текущему состоянию тела наряду с недеформированным состоянием еще одного гипотетического состояния, когда в теле отсутствуют обратимые деформации (состояние разгрузки) и напряжения.

Последующее развитие данного подхода в построении кинематики больших упругопластических деформаций обсуждалось в [8]. Из-за широкого его распространения до настоящего времени уделим ему некоторое внимание. Имеются в “мультипликативном” подходе очевидные нестыковки. Состоят они в неединственности гипотетического состояния разгрузки получаемого предельным переходом при неограниченном разбиении тела на элементарные объемы с последующим снятием с них нагрузок. В качестве дифференциальных уравнений изменения термодинамических параметров состояния, а ими остаются обратимые и необратимые деформации, предлагается принять выбранные объективные производные составляющих полных деформаций. Задача “выбора” данных производных [9] оказывается задачей “выбора” взаимодействия между обратимыми и необратимыми деформациями в процессе деформирования. Для решения последней задачи имеется достаточное число уточняющих предложений [10–15], включая предложения по учету деформационной анизотропии [16, 17].

Несомненным достоинством “мультипликативного” разделения полных деформаций на их составляющие является геометрическая корректность построенной на такой основе кинематики конечных упругопластических деформаций. Однако, как ни странно, именно в этом заключается и основной недостаток этого подхода к построению теории. Необходимость постоянной отсылки в процессе решения задач теории к гипотетическому разгрузочному состоянию не позволяет получить такие решения даже в простейших одномерных случаях. Известны только многочисленные приближенные численные решения [12, 15, 18–24]. Попытки разрешить такие задачи, формулируя их в скоростях перемещений и деформаций, с необходимостью приводят к задаче “выбора” объективной производной по времени от тензора напряжений [20, 24]. В [25] исследовались решения, получаемые при разном “выборе” данных производных (Зарембо–Яумана, Грина–Нагди, Ли и др.). При таком выборе метода решений не исключено получение ошибочного решения [26]. Необходимо отметить публикации [27–31] отечественных авторов, предлагающие теории больших упругопластических деформаций с кинематикой, отличной от способа “мультипликативного” разделения деформаций на обратимые (упругие) и необратимые (пластические, вязкопластические) их составляющие.

Разделение полных деформаций на обратимую и необратимую составляющие с помощью формулирования для них дифференциальных уравнений их изменения на основе представлений [2, 28] было предложено в [32]. Предполагалось, что такое “простое” разделение получит свое обобщение в работах других авторов, но этого не последовало. Здесь кратко повторим этапы построения данной модели на примере ее связанного варианта с температурными эффектами. Представляется это важным для заинтересованного читателя. Укажем также особенности решения в рамках такой модели термоупругопластического деформирования конкретной краевой задачи теории. Заметим, что при определении обратимых и необратимых деформаций записью для таких термодинамических параметров состояния дифференциальных уравнений их изменения получили свое решение, включая точные, целый ряд одномерных краевых задач теории, часть их составили содержание [3]. В [33–36] решается задача об изменениях в механизме производства необратимых деформаций на упругопластических и упруговязкопластических границах, продвигающихся по деформируемым материалам. Связанные задачи теории больших упруговязкопластических деформаций, когда необратимое деформирование порождает тепло, рассматривались в [37–40]. Здесь рассмотрим еще одну такую задачу.

2. Принимаемая модель процесса деформирования. Движение точек деформируемого материала зададим в пространственных переменных Эйлера

(2.1)
${\mathbf{u}} = {\mathbf{x}} - {\mathbf{\xi }} = {\mathbf{u}}({\mathbf{x}},t)$

Здесь ${\mathbf{x}}$, ${\mathbf{\xi }}$ – векторы, указывающие место точек деформируемого тела в текущем и свободном его состоянии соответственно, ${\mathbf{u}}$ – вектор перемещений. Для тензора дисторсии ${\mathbf{a}} = \partial {\mathbf{\xi }}{\text{/}}\partial {\mathbf{x}}$ и метрического тензора ${\mathbf{g}} = {\mathbf{a}} \cdot {{{\mathbf{a}}}^{{\text{т}}}}$ имеем уравнение их изменения [3, 9]

(2.2)
$\frac{{d{\mathbf{a}}}}{{dt}} + {\mathbf{a}} \cdot \nabla {\mathbf{v}} = 0,\quad \frac{{d{\mathbf{g}}}}{{dt}} + {\mathbf{g}} \cdot \nabla {\mathbf{v}} + {\mathbf{g}} \cdot {{\nabla }^{{\text{т}}}}{\mathbf{v}} = 0;\quad {\mathbf{v}} = \frac{{d{\mathbf{u}}}}{{dt}} = \frac{{d{\mathbf{x}}}}{{dt}}$

Во введенных обозначениях “мультипликативное” разделение полных деформаций на обратимую (упругую) ${\mathbf{e}}$ и необратимую (пластическую) ${\mathbf{p}}$ составляющие связано [7, 9, 22] со следующим представлением для метрического тензора

${\mathbf{g}} = ({\mathbf{I}} - 2{\mathbf{e}}) \cdot ({\mathbf{I}} - 2{\mathbf{p}})$

Считая тепловое расширение–сжатие также обратимым процессом, обобщим последнее соотношение в форме

${\mathbf{g}} = ({\mathbf{I}} - 2{\mathbf{m}}) \cdot ({\mathbf{I}} - 2{\mathbf{p}});\quad {\mathbf{m}} = {\mathbf{e}} + \alpha {{T}_{0}}\theta {\mathbf{I}},\quad \theta = {{T}_{0}}^{{ - 1}}(T - {{T}_{0}})$

Здесь $T$, ${{T}_{0}}$ – текущая температура и температура свободного состояния тела (комнатная температура), $\alpha $ – коэффициент линейного расширения, ${\mathbf{I}}$ – единичный тензор. Тензоры ${\mathbf{m}}$ и ${\mathbf{p}}$ приобретают механический смысл в качестве обратимых и необратимых деформаций процесса деформирования за счет принятия гипотезы о существовании единственного состояния полной разгрузки.

Отказываясь от назначенного механического смысла ${\mathbf{m}}$ и ${\mathbf{p}}$, то есть от принятия гипотезы разгрузочного состояния, запишем [28]

(2.3)
${\mathbf{g}} = ({\mathbf{I}} - {\mathbf{m}}) \cdot ({\mathbf{I}} - 2{\mathbf{p}}) \cdot ({\mathbf{I}} - {\mathbf{m}})$

В (2.3) ${\mathbf{m}}$ и ${\mathbf{p}}$ уже нельзя называть обратимыми и необратимыми деформациями. Что это такое и почему для них оставлены обозначения с ясным механическим смыслом выясним далее, а пока (2.3) некоторое алгебраическое соотношение, способное вместе с (2.2) привести к дифференциальным уравнениям изменения

(2.4)
$\frac{{d{\mathbf{m}}}}{{dt}} = \nabla {\mathbf{v}} - {\mathbf{b}} - {\mathbf{m}} \cdot {{\nabla }^{{\text{т}}}}{\mathbf{v}} + {\mathbf{b}} \cdot {{{\mathbf{m}}}^{{\text{т}}}},\quad \frac{{d{\mathbf{p}}}}{{dt}} = \frac{1}{2}\left( {{\mathbf{b}} + {{{\mathbf{b}}}^{{\text{т}}}}} \right) - {\mathbf{p}} \cdot {{{\mathbf{b}}}^{{\text{т}}}} - {\mathbf{b}} \cdot {{{\mathbf{p}}}^{{\text{т}}}}$

В (2.4) введены обозначения

${\mathbf{b}} = {{{\mathbf{Y}}}^{{ - {\mathbf{1}}}}}\frac{{d{\mathbf{Y}}}}{{dt}},\quad {\mathbf{a}} = {\mathbf{Y}} \cdot {{({\mathbf{I}} - {\mathbf{m}})}^{{\text{т}}}},\quad {\mathbf{p}} = \frac{1}{2}\left( {{\mathbf{I}} - {\mathbf{Y}} \cdot {{{\mathbf{Y}}}^{{\text{т}}}}} \right)$

Следовательно ${\mathbf{p}}$ – симметричный тензор. Для того, чтобы тензор ${\mathbf{m}}$ был симметричным необходимо в согласии с первым равенством из (2.4) потребовать

(2.5)
${\mathbf{b}} \cdot ({\mathbf{I}} - {\mathbf{m}}) - ({\mathbf{I}} - {\mathbf{m}}) \cdot {{{\mathbf{b}}}^{{\text{т}}}} = ({\mathbf{I}} - {\mathbf{m}}) \cdot \nabla {\mathbf{v}} - ({\mathbf{I}} - {\mathbf{m}}) \cdot {{{\mathbf{b}}}^{{\text{т}}}}$

Равенство (2.5) можно рассматривать в качестве тензорного уравнения для поиска такого ${\mathbf{b}}$, чтобы ${\mathbf{m}}$ оказался симметричным тензором. Решение (2.5) было построено А.И. Лурье [41] и имеет вид

(2.6)
${\mathbf{b}} = {\mathbf{\Phi }} + ({\mathbf{I}} \cdot {\mathbf{m}}) \cdot {\mathbf{h}}$

Здесь ${\mathbf{h}}$ произвольный симметричный тензор. Кососимметричный ${\mathbf{\Phi }} = - {{{\mathbf{\Phi }}}^{{\text{т}}}}$ тензор вычисляется зависимостям

$\begin{gathered} {\mathbf{\Phi }} = {\mathbf{\omega }} + {\mathbf{z}},\quad \nabla {\mathbf{v}} = {\mathbf{\varepsilon }} + {\mathbf{\omega }};\quad {\mathbf{\varepsilon }} = \frac{1}{2}\left( {\nabla {\mathbf{v}} + {{\nabla }^{{\text{т}}}}{\mathbf{v}}} \right),\quad {\mathbf{\omega }} = \frac{1}{2}\left( {\nabla {\mathbf{v}} - {{\nabla }^{{\text{т}}}}{\mathbf{v}}} \right) \\ {\mathbf{z}} = {\mathbf{z}}({\mathbf{\varepsilon }},{\mathbf{m}}) = {{C}^{{ - 1}}}({{B}^{2}}\left( {({\mathbf{\varepsilon }} \cdot {\mathbf{m}} - {\mathbf{m}} \cdot {\mathbf{\varepsilon }}) + B\left( {{\mathbf{\varepsilon }} \cdot {{{\mathbf{m}}}^{2}} - {{{\mathbf{m}}}^{2}} \cdot {\mathbf{\varepsilon }}} \right)} \right. + {\mathbf{m}} \cdot {\mathbf{\varepsilon }} \cdot {{{\mathbf{m}}}^{2}} - \left. {{{{\mathbf{m}}}^{2}} \cdot {\mathbf{\varepsilon }} \cdot {\mathbf{m}}} \right) \\ B = 2 - {{M}_{1}},\quad C = 8 - 8{{M}_{1}} + 3M_{1}^{2} - {{M}_{2}} - \frac{1}{3}M_{1}^{3} + \frac{1}{3}{{M}_{3}} \\ {{M}_{2}} = \operatorname{tr} {\mathbf{m}},\quad {{M}_{2}} = {\mathbf{m}} \cdot \cdot {\kern 1pt} {\mathbf{m}}\quad {{M}_{3}} = {\mathbf{m}} \cdot \cdot {\kern 1pt} {{{\mathbf{m}}}^{2}} \\ \end{gathered} $

Исключая с помощью (2.6) из (2.4) неизвестный в них тензор ${\mathbf{b}}$, приходим к дифференциальным зависимостям

(2.7)
$\begin{gathered} \frac{{d{\mathbf{m}}}}{{dt}} = \varepsilon - {\mathbf{h}} - {\mathbf{\Phi }} + {\mathbf{\omega }} - {\mathbf{m}} \cdot (\nabla {\mathbf{v}} - {\mathbf{h}}) + ({\mathbf{\Phi }} + {\mathbf{h}}) \cdot {\mathbf{m}} - {\mathbf{m}} \cdot {\mathbf{h}} \cdot {\mathbf{m}} \\ \frac{{d{\mathbf{p}}}}{{dt}} = {\mathbf{h}} - \frac{1}{2}({\mathbf{m}} \cdot {\mathbf{h}} + {\mathbf{h}} \cdot {\mathbf{m}}) + ({\mathbf{\Phi }} - {\mathbf{h}}) \cdot {\mathbf{p}} + {\mathbf{p}} \cdot ({\mathbf{\Phi }} - {\mathbf{h}}) + {\mathbf{p}} \cdot {\mathbf{m}} \cdot {\mathbf{h}} + {\mathbf{h}} \cdot {\mathbf{m}} \cdot {\mathbf{p}} \\ \end{gathered} $

Во всех вышеприведенных кинематических соотношениях неизвестным остается произвольный симметричный тензор ${\mathbf{h}}$. Если положить его равным нулю, то получим

(2.8)
$\frac{{D{\mathbf{p}}}}{{Dt}} = \frac{{d{\mathbf{p}}}}{{dt}} - \Phi \cdot {\mathbf{p}} - {\mathbf{p}} \cdot \Phi = 0$

Замечаем, что дифференциальное соотношение (2.8) можно рассматривать в качестве объективной производной по времени от тензора ${\mathbf{p}}$. Она обратится в производную Зарембо–Яумана [42] если только положить равным нулю (${\mathbf{z}} = 0$) нелинейную составляющую тензора вращений ${\mathbf{\Phi }}$. Равенство (2.8) тогда означает, что тензор ${\mathbf{p}}$ неизменен в условиях ${\mathbf{h}} = 0$. Если считать, что ${\mathbf{p}}$ – необратимые деформации, то ${\mathbf{h}} = 0$ оказывается условием обратимого деформирования в условиях предваряющих пластическое течение и при разгрузке. Отметим, что такое деформирование кинематически определено. В условиях пластического течения для определенности кинематики следует указать тензор ${\mathbf{h}}$, что только из кинематических соображений невозможно. При разгрузке (${\mathbf{h}} = 0$) согласно (2.8) изменяются компоненты неизменного тензора ${\mathbf{p}}$ и их изменение нелинейно зависит от изменений обратимых деформаций (${\mathbf{z}}(\varepsilon ,{\mathbf{m}}) \ne 0$).

При пластическом течении ${\mathbf{h}} \ne 0$. С целью определения механического смысла до сих пор произвольного тензора ${\mathbf{h}}$ рассмотрим следствие закона сохранения энергии

(2.9)
$\rho \frac{{d\gamma }}{{dt}} + \operatorname{div} {\mathbf{q}} = {\mathbf{\sigma }} \cdot \cdot \,\varepsilon $

Здесь $\gamma $ – плотность распределения внутренней энергии, ${\mathbf{q}}$ – вектор потока тепла, $\sigma $ – тензор напряжений. Если ввести иной термодинамический потенциал $\Psi = \gamma - TS$ (плотность распределения свободной энергии) и предположить, что $\Psi = \Psi ({\mathbf{m}},T)$, то из (2.9) можно получить [3]

(2.10)
$\sigma = \rho \frac{{\partial \Psi }}{{\partial {\mathbf{m}}}}({\mathbf{I}} - {\mathbf{m}})$
(2.11)
$\frac{{\partial (\rho s)}}{{\partial t}} = - \operatorname{div} {\mathbf{J}} - {{T}^{{ - 2}}}{\mathbf{q}} \cdot \cdot \,\nabla T + {{T}^{{ - 1}}}\sigma \cdot \cdot \,{{{\mathbf{\varepsilon }}}^{p}}$

Упрощающее предположение о том, что термодинамический потенциал $\Psi = \Psi ({\mathbf{m}},T)$ не зависит от необратимых деформаций, является гипотетическим, позволяющем разделить консервативную и диссипативную составляющие процесса деформирования. Оно используется в абсолютном большинстве публикаций [9, 11, 18, 22] посвященных расчетам больших деформаций. В (2.11) $s$ – плотность распределения энтропии, $J = \rho s{\mathbf{v}} + {{T}^{{ - 1}}}{\mathbf{q}}$ – поток энтропии, ${{\varepsilon }^{p}} = ({\mathbf{I}} - {\mathbf{m}}) \cdot {\mathbf{h}}$ – тензор скоростей изменения необратимых (в нашем случае пластических) деформаций ${\mathbf{p}}$. Таким способом тензор ${\mathbf{h}}$ однозначно связывается с тензором ${{\varepsilon }^{p}}$ и дифференциальные уравнения (2.7) приобретают свою окончательную форму

(2.12)
$\begin{gathered} \frac{{D{\mathbf{m}}}}{{Dt}} = {\mathbf{\varepsilon }} - {{\varepsilon }^{{\mathbf{p}}}} - \frac{1}{2}\left( {({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} + {\mathbf{z}}) \cdot {\mathbf{m}} + {\mathbf{m}} \cdot ({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - {\mathbf{z}})} \right) \\ \frac{{D{\mathbf{p}}}}{{Dt}} = {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - {\mathbf{p}} \cdot {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} \cdot {\mathbf{p}} \\ \end{gathered} $

Производная по времени в (2.12) задается зависимостями (2.8). Для тензора полных деформаций Альманси ${\mathbf{d}}$ следует его представление через обратимую ${\mathbf{m}}$ и необратимую ${\mathbf{p}}$ составляющие

(2.13)
${\mathbf{d}} = {\mathbf{m}} + {\mathbf{p}} - \frac{1}{2}{\mathbf{m}} \cdot {\mathbf{m}} - {\mathbf{m}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{m}} + {\mathbf{m}} \cdot {\mathbf{p}} \cdot {\mathbf{m}}$

Отсюда тензором обратимых деформаций следовало бы называть тензор ${\mathbf{c}} = {\mathbf{m}} - \frac{1}{2}{\mathbf{m}} \cdot {\mathbf{m}}$. Однако использование в качестве обратимых деформаций только главной линейной части последнего привело к значительным удобствам в записи дифференциального уравнения изменения обратимых деформаций (2.12) и аналога формулы Мурнагана (2.10) в областях необратимого деформирования и разгрузки. Далее будет рассматриваться случай, в котором изменение объема деформируемого материала задается только его тепловым расширением, а механически он остается несжимаемым. В этом случае из (2.10) следует [3]

(2.14)
$\begin{gathered} {\mathbf{\sigma }} = - {{P}_{1}}{\mathbf{I}} + {{(1 + 3\alpha {{T}_{0}}\theta )}^{{ - 1}}}\frac{{\partial W}}{{\partial {\mathbf{d}}}} \cdot ({\mathbf{I}} - 2{\mathbf{d}}),\quad где\quad {\mathbf{p}} = 0 \\ {\mathbf{\sigma }} = - {{P}_{2}}{\mathbf{I}} + {{(1 + 3\alpha {{T}_{0}}\theta )}^{{ - 1}}}\frac{{\partial W}}{{\partial {\mathbf{m}}}} \cdot ({\mathbf{I}} - {\mathbf{m}}),\quad где\quad {\mathbf{p}} \ne 0 \\ \end{gathered} $

В (2.14) ${{P}_{1}}$, ${{P}_{2}}$ – добавочные неизвестные функции гидростатического давления, $W = W({\mathbf{m}},\theta )$ = ${{\rho }_{0}}\Psi ({\mathbf{m}},T)$ – термоупругий потенциал. Полагая деформируемый материал изотропным и механически несжимаемым, для последнего принимаем наиболее простое представление [3]

(2.15)
$\begin{gathered} W = W({{J}_{1}},{{J}_{2}},\theta ) = - 2\mu {{J}_{1}} - \mu {{J}_{2}} + b{\text{ }}J_{1}^{2} + (b - \mu ){{J}_{1}}{{J}_{2}} - \chi J_{1}^{3} + {{\nu }_{1}}{{J}_{1}}\theta + \\ + \;{{\nu }_{2}}{{\theta }^{2}} - {{\nu }_{3}}{{J}_{1}}{{\theta }^{2}} - {{\nu }_{4}}{{J}_{1}}^{2}\theta - {{\nu }_{5}}{{J}_{2}}\theta - {{\nu }_{6}}{{\theta }^{3}} + \; \ldots \\ {{J}_{1}} = \left\{ {\begin{array}{*{20}{c}} {{{L}_{k}}\quad при\quad {\mathbf{p}} = 0} \\ {{{I}_{k}}\quad при\quad {\mathbf{p}} \ne 0} \end{array}} \right. \\ {{L}_{1}} = \operatorname{tr} {\mathbf{d}},\quad {{L}_{2}} = {\mathbf{d}} \cdot \cdot {\mathbf{d}},\quad {{I}_{1}} = \operatorname{tr} {\mathbf{c}},\quad {{I}_{2}} = {\mathbf{c}} \cdot \cdot {\mathbf{c}},\quad {\mathbf{c}} = {\mathbf{m}} - \frac{1}{2}{\mathbf{m}} \cdot {\mathbf{m}} \\ \end{gathered} $

Здесь $\mu $ – модуль сдвига, $b$, $\chi $, ${{\nu }_{m}}$, ($m = 1,2, \ldots 6$), – термомеханические постоянные [43]. Если в уравнении баланса энтропии (2.11) закон теплопроводности принять в форме Фурье, то с учетом (2.15) получаем уравнение теплопроводности. В областях, деформирующихся по-разному, это уравнение имеет различия в своей записи:

в области обратимого деформирования, предваряющей пластическое течение

(2.16)
$(1 + {{\beta }_{1}}\theta + {{\beta }_{2}}\operatorname{tr} {\mathbf{d}})\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}{\mathbf{\varepsilon }} \cdot \cdot \,{\mathbf{d}} = g\Delta \theta $

в пластической области

(2.17)
$(1 + {{\beta }_{1}}\theta + {{\beta }_{2}}\operatorname{tr} {\mathbf{c}})\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}(\varepsilon - {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}}) \cdot \cdot \,{\mathbf{d}} = g\Delta \theta - \frac{1}{{2{{\nu }_{2}}}}\sigma \cdot \cdot \,{{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}}$

в области разгрузки

(2.18)
$\begin{gathered} (1 + {{\beta }_{1}}\theta + {{\beta }_{2}}\operatorname{tr} {\mathbf{c}})\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}\varepsilon \cdot \cdot \,{\mathbf{c}} = g\Delta \theta \\ {{\beta }_{1}} = \frac{{{{\nu }_{2}}(1 - 3\alpha {{T}_{0}}) - 3{{\nu }_{6}}}}{{{{\nu }_{2}}}},\quad {{\beta }_{2}} = - \frac{{{{\nu }_{3}}}}{{{{\nu }_{2}}}},\quad {{\beta }_{3}} = - \frac{{{{\nu }_{1}} + {{\nu }_{5}}}}{{{{\nu }_{2}}}} \\ \end{gathered} $

Здесь $g$ – коэффициент температуропроводности.

В качестве пластического потенциала (условия течения) далее используется следующее обобщение условия пластичности Треска–Сен-Венана [3, 43]

(2.19)
$\begin{gathered} max\left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| = 2k + 2\eta max\left| {\varepsilon _{k}^{p}} \right| \\ k = {{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}}}{{\theta _{m}^{2}}}} \right);\quad {{\theta }_{m}} = ({{T}_{m}} - {{T}_{0}})T_{0}^{{ - 1}} \\ \end{gathered} $

В (2.19) ${{\sigma }_{j}}$, $\varepsilon _{k}^{p}$ – главные значения тензоров напряжений и скоростей пластических деформаций; $k$, ${{k}_{0}}$ – текущий предел пластического течения и его значение при комнатной температуре; ${{T}_{m}}$ – температура плавления деформируемого материала; $\eta $ – коэффициент вязкого сопротивления пластическому течению. Замыкаем построенную математическую модель деформирования принятием принципа максимума Мизеса [44] с формулированием ассоциированного закона пластического течения

(2.20)
${{{\mathbf{\varepsilon }}}^{p}} = \xi \frac{{\partial f(\sigma ,{{{\mathbf{\varepsilon }}}^{p}})}}{{\partial {\mathbf{\sigma }}}},\quad f({\mathbf{\sigma }},{{{\mathbf{\varepsilon }}}^{p}}) = max\left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| - 2\eta \left| {\varepsilon _{k}^{p}} \right| - 2k = 0;\quad \xi > 0$

2. Начальное обратимое деформирование. Пусть материал, термомеханические свойства которого задаются зависимостями, представленными ранее, составляет цилиндрический слой, ограниченный поверхностями $r = {{r}_{0}}$ и $r = R$ (${{r}_{0}} < R$). Цилиндр $r \leqslant {{r}_{0}}$ полагаем жестко закрепленным, а граничная поверхность слоя $r = R$ поворачивается вокруг центральной оси. До момента начала процесса деформирования деформации в материале слоя отсутствуют, а напряженное состояние задается единственным параметром начального поджатия: ${{\sigma }_{{rr}}}({{r}_{0}},0) = {{\sigma }_{0}}$. Таким образом, основными искомыми зависимыми переменными задачи оказываются угол закручивания $\psi = \psi (r,t)$ и угловая скорость $\omega = \frac{{d\psi }}{{dt}} = \omega (r,t)$. Кинематические начальные условия, таким образом, являются однородными: $\psi (r,0) = 0$ и $\omega (r,0) = 0$. Граничные условия задачи зададим в форме

(3.1)
${{\psi }_{R}} = \psi (R,t) = \left\{ \begin{gathered} a{{t}^{2}}\quad при\quad 0 \leqslant t \leqslant {{t}_{1}} \hfill \\ a{{t}_{1}}t - \frac{1}{2}at_{1}^{2}\quad при\quad {{t}_{1}} \leqslant t \leqslant {{t}_{2}} \hfill \\ a{{t}_{1}}t - \frac{1}{2}{{a}_{1}}{{(t - {{t}_{2}})}^{2}} - \frac{1}{2}at_{1}^{2}\quad при\quad {{t}_{2}} \leqslant t \leqslant {{t}_{3}} \hfill \\ \end{gathered} \right.$

Здесь $a$, ${{a}_{1}}$, ${{t}_{1}}$, ${{t}_{2}}$, ${{t}_{3}}$ – задаваемые параметры задачи.

На первоначальном этапе процесса деформирования контакт материала с жесткими стенками осуществляется согласно закону сухого трения покоя

(3.2)
$\begin{gathered} \left| {{{\sigma }_{{r\varphi }}}} \right| \leqslant {{f}_{0}}\left| {{{\sigma }_{{rr}}}} \right|\quad при\quad r = {{r}_{0}}\quad и\quad r = R \\ \omega ({{r}_{0}},t) = 0,\quad \psi ({{r}_{0}},t) = 0,\quad \omega (R,t) = {{\omega }_{R}},\quad \psi (R,t) = {{\psi }_{R}} \\ \end{gathered} $

Здесь ${{f}_{0}}$ – коэффициент трения покоя. Кинематические зависимости в данном случае позволяют записать

(3.3)
$\begin{gathered} {{u}_{r}} = r(1 - cos\psi (r,t)),\quad {{u}_{\varphi }} = rsin\psi (r,t) \\ {{d}_{{rr}}} = - \frac{1}{2}{{r}^{2}}\psi _{{,r}}^{2} = - 2{{d}^{2}},\quad {{d}_{{r\varphi }}} = \frac{1}{2}r{{\psi }_{{,r}}} = d \\ \end{gathered} $

Для компонент тензора напряжений согласно (2.14) и (2.15) можно получить

(3.4)
${{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - {{P}_{1}} - 2(\mu + b){{d}^{2}} = - \tau ,\quad {{\sigma }_{{\varphi \varphi }}} = - \tau + 2\mu {{d}^{2}},\quad {{\sigma }_{{r\varphi }}} = 2\mu d$

Здесь записаны компоненты тензора напряжений с точностью до слагаемых второго порядка по упругим деформациям. Уравнения равновесия

(3.5)
${{\sigma }_{{rr,r}}} + {{r}^{{ - 1}}}({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}) = 0,\quad {{\sigma }_{{r\varphi ,r}}} + 2{{r}^{{ - 1}}}{{\sigma }_{{r\varphi }}} = 0$
с помощью (3.3) интегрируются, и решение такой изотермической задачи записывается в форме

(3.6)
$\begin{gathered} {{\sigma }_{{r\varphi }}} = \frac{c}{{{{r}^{2}}}},\quad {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = \frac{{{{c}^{2}}}}{{4\mu }}\left( {\frac{1}{{r_{0}^{4}}} - \frac{1}{{{{r}^{4}}}}} \right) + {{\sigma }_{0}} \\ {{\sigma }_{{\varphi \varphi }}} = \frac{{{{c}^{2}}}}{{4\mu }}\left( {\frac{1}{{r_{0}^{4}}} - \frac{3}{{{{r}^{4}}}}} \right) + {{\sigma }_{0}},\quad \psi = \frac{c}{{2\mu }}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{r}^{2}}}}} \right) \\ \omega = \frac{{\dot {c}}}{{2\mu }}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{r}^{2}}}}} \right),\quad \dot {c} = \frac{{dc}}{{dt}},\quad c = c(t) = \frac{{a\mu {{t}^{2}}}}{{r_{0}^{{ - 2}} - {{R}^{{ - 2}}}}} \\ \end{gathered} $

Решение (3.6) справедливо до момента времени $t = {{t}_{0}}$, когда на поверхности $r = {{r}_{0}}$ произойдет проскальзывание материала и начнется разогрев его за счет пристеночного трения. Принимаем, что проскальзывание произойдет раньше начала вязкопластического течения. Для этого считаем, что ${{f}_{0}}{{\sigma }_{0}} < k$. С этого момента $t = {{t}_{0}}$ граничное условие (3.2) следует заменить на

(3.7)
$\left| {{{\sigma }_{{r\varphi }}}} \right| = f\left| {{{\sigma }_{{rr}}}} \right| + \varsigma \left| \omega \right|\quad при\quad r = {{r}_{0}}\quad и\quad t > {{t}_{0}} = \sqrt {\frac{{{{f}_{0}}{{\sigma }_{0}}r_{0}^{2}}}{{a\mu }}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{R}^{2}}}}} \right){\kern 1pt} } ,$
где $\varsigma $ – постоянная вязкого трения; $f$ – коэффициент сухого трения скольжения. При выполнении условий проскальзывания (3.7) начинается разогрев материала за счет пристеночного трения на поверхности $r = {{r}_{0}}\,$:

(3.8)
$\theta (r,{{t}_{0}}) = 0,\quad \theta ({{r}_{0}},t) = {{\alpha }_{1}}\psi ({{r}_{0}},t),\quad {{\theta }_{{,r}}}(R,t) = 0$

В (3.8) ${{\alpha }_{1}}$ – постоянный коэффициент теплопроизводства за счет трения.

Для компонент тензора напряжений из (2.14) и (2.15) теперь следует

(3.9)
$\begin{gathered} {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - {{P}_{1}} - 2(b + \mu ){{d}^{2}} + ({{\nu }_{1}} + 6\mu \beta )\theta - \left( {{{\nu }_{3}} + 18\mu {{\beta }^{2}} + 3{{\nu }_{1}}\beta } \right){{\theta }^{2}} = - {{\tau }_{1}} \\ {{\sigma }_{{\varphi \varphi }}} = - {{\tau }_{1}} + 2\mu {{d}^{2}},\quad {{\sigma }_{{r\varphi }}} = 2(\mu - \theta ({{\nu }_{1}} + {{\nu }_{5}} + 3\mu \beta ))d,\quad \beta = \alpha {{T}_{0}} \\ \end{gathered} $

Разрешая второе из уравнений равновесия (3.5) с использованием (3.9), находим

(3.10)
$d = \frac{{c(t)}}{{2{{r}^{2}}(\mu - l\theta )}},\quad {{m}_{{r\varphi }}} = d,\quad {{m}_{{rr}}} = - \frac{3}{2}{{d}^{2}},\quad {{m}_{{\varphi \varphi }}} = \frac{1}{2}{{d}^{2}};\quad l = {{\nu }_{1}} + {{\nu }_{5}} + 3\mu \beta $

Вместе с уравнением теплопроводности (следствием (2.15)) для определения неизвестных $\psi (r,t)$, $\theta (r,t)$, $c(t)$ имеем систему уравнений с начальными и граничными условиями

(3.11)
$\begin{gathered} \begin{gathered} \left( {1 + {{\beta }_{1}}\theta + {{\beta }_{3}}\frac{{{{c}^{2}}l}}{{2{{r}^{4}}{{{\left( {\mu - l\theta } \right)}}^{3}}}}} \right)\frac{{\partial \theta }}{{\partial t}} + \frac{{{{\beta }_{3}}c\dot {c}}}{{2{{r}^{4}}{{{\left( {\mu - l\theta } \right)}}^{2}}}} = g\left( {\frac{{{{\partial }^{2}}\theta }}{{\partial {{r}^{2}}}} + {{r}^{{ - 1}}}\frac{{\partial \theta }}{{\partial r}}} \right) \\ \end{gathered} \\ \frac{{\partial \psi }}{{\partial r}} = \frac{c}{{{{r}^{3}}\left( {\mu - l\theta } \right)}},\quad \dot {\psi }\left( {{{r}_{0}},t} \right) = - f{{\varsigma }^{{ - 1}}}{{\sigma }_{0}} + r_{0}^{{ - 2}}{{\varsigma }^{{ - 1}}}c,\quad \psi (R,t) = \frac{{a{{t}^{2}}}}{2} \\ \theta (r,{{t}_{0}}) = 0,\quad \theta ({{r}_{0}},t) = {{\alpha }_{1}}\psi ({{r}_{0}},t),\quad {{\theta }_{{,r}}}(R,t) = 0 \\ \end{gathered} $

Задача (3.11), как и все последующие, разрешалась приближенно с помощью конечно-разностной схемы. Согласно найденным таким способом распределениям температуры и перемещений деформации и напряжения находятся согласно (3.9) и (3.10). Но такое решение справедливо лишь до момента времени $t = {{t}_{*}}$, когда на стенке $r = {{r}_{0}}$ выполнится условие пластического течения (2.18). В нашем случае оно сводится к требованию ${{\sigma }_{{r\varphi }}}({{r}_{0}},{{t}_{*}}) = k$. Для момента времени $t = {{t}_{*}}$ имеем уравнение

(3.12)
$\begin{gathered} c({{t}_{*}}) = {{k}_{0}}r_{0}^{2}\left( {1 - {{\theta }^{2}}({{r}_{0}},{{t}_{*}})\theta _{m}^{{ - 2}}} \right) \\ \end{gathered} $

4. Вязкопластическое течение. Область II вязкопластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ при $t > {{t}_{*}}$ развивается от граничной поверхности $r = {{r}_{0}}$ посредством продвижения ее границы $r = {{r}_{1}}(t)$. В области I при ${{r}_{1}}(t) \leqslant r \leqslant R$ материал продолжает деформироваться обратимо. Кинематические соотношения (2.12) и (2.13) в рассматриваемом случае позволяют записать:

(4.1)
$\begin{gathered} {{{v}}_{\varphi }} = r\omega ,\quad {{\varepsilon }_{{r\varphi }}} = \frac{{\partial {{d}_{{r\varphi }}}}}{{\partial t}} = \frac{1}{2}\left( {\frac{{\partial {{{v}}_{\varphi }}}}{{\partial r}} - \frac{{{{{v}}_{\varphi }}}}{r}} \right) = \frac{1}{2}r\frac{{{{\partial }^{2}}\psi }}{{\partial r\partial t}} \\ {{\varepsilon }_{{r\varphi }}} = \varepsilon _{{r\varphi }}^{e} + \varepsilon _{{r\varphi }}^{p} = \frac{{\partial {{m}_{{r\varphi }}}}}{{\partial t}} + \frac{{\partial {{p}_{{r\varphi }}}}}{{\partial t}} \\ \varepsilon _{{rr}}^{p} = \frac{{d{{p}_{{rr}}}}}{{dt}} + 2{{p}_{{r\varphi }}}\left( {{{\Phi }_{{\varphi r}}} + \varepsilon _{{r\varphi }}^{p}} \right),\quad \varepsilon _{{\varphi \varphi }}^{p} = \frac{{d{{p}_{{\varphi \varphi }}}}}{{dt}} + 2{{p}_{{r\varphi }}}\left( {{{\Phi }_{{r\varphi }}} + \varepsilon _{{r\varphi }}^{p}} \right) \\ \end{gathered} $

Обратимые деформации задают напряжения в области течения согласно зависимостям

(4.2)
$\begin{gathered} {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - {{P}_{2}} - 2(b + \mu )m_{{r\varphi }}^{2} + ({{\nu }_{1}} + 6\mu \beta )\theta - ({{\nu }_{3}} + 18\mu {{\beta }^{2}} + 3{{\nu }_{1}}\beta ){{\theta }^{2}} = - {{\tau }_{2}} \\ {{\sigma }_{{\varphi \varphi }}} = - {{\tau }_{1}} + 2\mu m_{{r\varphi }}^{2},\quad {{\sigma }_{{r\varphi }}} = 2(\mu - \theta l){{m}_{{r\varphi }}} \\ \end{gathered} $

Следствием выбранного условия вязкопластического течения и ассоциированного с ним закона имеем соотношения

(4.3)
${{\sigma }_{{r\varphi }}} = k + \eta \varepsilon _{{r\varphi }}^{p},\quad \xi = \varepsilon _{{r\varphi }}^{p}{{(k + \eta \varepsilon _{{r\varphi }}^{p})}^{{ - 1}}},\quad \varepsilon _{{r\varphi }}^{p} = \frac{1}{\eta }\left( {\frac{c}{{{{r}^{2}}}} - {{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}}}{{\theta _{m}^{2}}}} \right)} \right)$

Выполняя условие равенства напряжений на границе пластической области, получим уравнение для вычисления закона продвижения упругопластической границы

(4.4)
$r = {{r}_{1}}(t) = \sqrt {\frac{{c(t)}}{{{{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}({{r}_{1}}(t),t)}}{{\theta _{m}^{2}}}} \right)}}} $

Система дифференциальных уравнений для вычислений распределения температуры и угла поворота теперь состоит: из уравнений теплопроводности, записываемых отдельно для температуры ${{\theta }^{I}}(r,t)$ и области вязкопластического течения ${{\theta }^{{II}}}(r,t)$, из уравнений для углов поворота ${{\psi }^{I}}(r,t)$ и ${{\psi }^{{II}}}(r,t)$, функции времени $c(t)$ и уравнения (4.4) для закона продвижения границы области вязкопластического течения. Вместе с краевыми условиями такая задача теперь предстает в виде

$\begin{gathered} \left( {1 + {{\beta }_{1}}{{\theta }^{I}} + \frac{{{{\beta }_{3}}l{{c}^{2}}}}{{2{{r}^{4}}{{{\left( {\mu - l{{\theta }^{I}}} \right)}}^{3}}}}} \right){{{\dot {\theta }}}^{I}} + \frac{{{{\beta }_{3}}c\dot {c}}}{{2{{r}^{4}}{{{\left( {\mu - l{{\theta }^{I}}} \right)}}^{2}}}} = g\left( {\theta _{{,rr}}^{I} + {{r}^{{ - 1}}}\theta _{{,r}}^{I}} \right) \\ \end{gathered} $
$\begin{gathered} \left( {1 + {{\beta }_{1}}{{\theta }^{{II}}} + \frac{{{{\beta }_{3}}l{{c}^{2}}}}{{2{{r}^{4}}{{{\left( {\mu - l{{\theta }^{{II}}}} \right)}}^{3}}}}} \right){{{\dot {\theta }}}^{{II}}} + \frac{{{{\beta }_{3}}c\dot {c}}}{{2{{r}^{4}}{{{\left( {\mu - l{{\theta }^{{II}}}} \right)}}^{2}}}} = \\ = g\left( {\theta _{{,rr}}^{{II}} + {{r}^{{ - 1}}}\theta _{{,r}}^{{II}}} \right) - \frac{c}{{2{{\nu }_{1}}\eta {{r}^{2}}}}\left( {\frac{c}{{{{r}^{2}}}} - {{k}_{0}}\left( {1 - \frac{{{{\theta }^{{I{{I}^{2}}}}}}}{{\theta _{m}^{2}}}} \right)} \right) \\ \end{gathered} $
(4.5)
$\begin{gathered} \psi _{{,r}}^{I} = \frac{c}{{{{r}^{3}}\left( {\mu - l{{\theta }^{I}}} \right)}} \\ \dot {\psi }_{{,r}}^{{II}} = \frac{{\dot {c}}}{{{{r}^{3}}\left( {\mu - l{{\theta }^{{II}}}} \right)}} + \frac{{lc}}{{{{r}^{3}}\left( {\mu - l{{\theta }^{{II}}}} \right)}}{{{\dot {\theta }}}^{{II}}} + \frac{2}{\eta }\left( {\frac{c}{{{{r}^{3}}}} - \frac{{{{k}_{0}}}}{r}\left( {1 - \frac{{{{\theta }^{{II}}}^{2}}}{{\theta _{m}^{2}}}} \right)} \right) \\ \end{gathered} $
$c\left( t \right) = {{k}_{0}}r_{1}^{2}\left( {1 - \frac{{{{{({{\theta }^{I}}({{r}_{1}},t))}}^{2}}}}{{\theta _{m}^{2}}}} \right),\quad {{\theta }^{{II}}}({{r}_{0}},t) = {{\alpha }_{1}}{{\psi }^{{II}}}({{r}_{0}},t),\quad {{\theta }^{I}}({{r}_{1}},t) = {{\theta }^{{II}}}({{r}_{1}},t)$
$\theta _{{,r}}^{I}(R,t) = 0,\quad {{\psi }^{I}}(R,t) = \frac{1}{2}a{{t}^{2}},\quad {{\dot {\psi }}^{I}}({{r}_{0}},t) = - f{{\varsigma }^{{ - 1}}}{{\sigma }_{0}} + r_{0}^{{ - 2}}{{\varsigma }^{{ - 1}}}c(t)$

Приближенное численное разрешение задачи (4.5) встраивается таким способом в общий алгоритм расчетов. Для этого приходится использовать две изменяющихся на каждом временном шаге расчетов сетки дискретизации расчетной области. В области обратимого деформирования $r = {{r}_{1}}_{{i + 1}} + h_{{i + 1}}^{e}j$, $j = \overline {0,{{N}^{e}} - 1} $, $h_{{i + 1}}^{e} = (1 - {{r}_{1}}_{{i + 1}}){{({{N}^{e}})}^{{ - 1}}}$. В области вязкопластического течения $r = {{r}_{0}} + h_{{i + 1}}^{p}j$, $j = \overline {1,{{N}^{p}}} $, $h_{{i + 1}}^{p} = ({{r}_{1}}_{{i + 1}} - {{r}_{0}}){{({{N}^{p}})}^{{ - 1}}}$. На каждом временном шаге расчетов $t = {{t}_{*}} + \Delta t(i + 1)$, $i = \overline {0,N} $ сетка меняется с учетом изменения положения упруговязкопластической границы. Значения угла поворота и температуры в узлах новой сетки на предыдущем временном шаге находятся интерполяцией.

Согласно рассчитанным распределениям температуры $\theta (r,t)$, угла поворота $\psi (r,t)$ и значений функций $c(t)$ определяются распределения иных искомых величин $\omega (r,t)$, ${{p}_{{r\varphi }}}(r,t)$, ${{m}_{{r\varphi }}}(r,t)$, ${{\sigma }_{{r\varphi }}}(r,t)$. Для диагональных компонент деформаций следует система уравнений

(4.6)
$\begin{gathered} {{m}_{{rr}}} + {{m}_{{\varphi \varphi }}} = - m_{{r\varphi }}^{{\text{2}}},\quad {{p}_{{rr}}} + {{p}_{{\varphi \varphi }}} = - {\text{2}}p_{{r\varphi }}^{{\text{2}}},\quad {{m}_{{rr}}} = {{p}_{{\varphi \varphi }}} - \frac{{\text{3}}}{{\text{2}}}m_{{r\varphi }}^{{\text{2}}} - {\text{2}}{{m}_{{r\varphi }}}{{p}_{{r\varphi }}} \\ \frac{{\partial {{p}_{{\varphi \varphi }}}}}{{\partial t}} = \varepsilon _{{\varphi \varphi }}^{p} + 2\varepsilon _{{r\varphi }}^{2}{{p}_{{r\varphi }}} + 4{{\varepsilon }_{{r\varphi }}}{{p}_{{r\varphi }}}({{m}_{{\varphi \varphi }}} - 1){{({{m}_{{rr}}} + {{m}_{{\varphi \varphi }}} - 2)}^{{ - 1}}} \\ \end{gathered} $

Напряжение ${{\sigma }_{{rr}}}$ находится интегрированием первого уравнения из (3.5) с учетом (4.2). По найденному ${{\sigma }_{{rr}}}$ вычисляются ${{\sigma }_{{\varphi \varphi }}}$ и неизвестная функция $p(r,t)$ добавочного гидростатического давления.

5. Деформирование при постоянной и уменьшающейся угловой скорости. Согласно задаваемым уравнениям (3.1) после момента времени $t = {{t}_{1}}$ угловая скорость ${{\omega }_{R}}(t) = a{{t}_{1}}$ становится постоянной. Область вязкопластического течения при $t > {{t}_{1}}$ продолжает развиваться. Рост области продолжается даже после момента времени ${{t}_{2}}$, когда вращение тормозится. При $t > {{t}_{2}}$ находится момент времени $t = t{\text{*}}$ ($t* > {{t}_{2}}$), после которого граница области течения, остановившись, начинает продвижение в обратную сторону. Последующий закон движения обозначим через $r = {{r}_{2}}(t)$. Теперь деформируемый материал разделен на три области, где его деформирование протекает по-разному: в области ${{r}_{0}} \leqslant r \leqslant {{r}_{2}}(t)$ продолжается вязкопластическое течение; в области разгрузки ${{r}_{2}}(t) \leqslant r \leqslant {{r}_{1}}(t*)$ пластические деформации не меняются; в области ${{r}_{1}}(t*) \leqslant r \leqslant R$ деформирование обратимо.

Уравнения теплопроводности (2.16)–(2.18) следует записать применительно к рассматриваемому случаю. Таким способом получаем систему уравнений вместе с краевыми условиями вполне аналогичную (4.5). Из-за громоздкости здесь ее не приводим. Решение такой задачи осуществляется тем же конечно-разностным методом на изменяющихся на каждом временном шаге сетках.

С момента времени $t = {{t}_{3}}$ (находится из соотношения $c({{t}_{3}}) = f{{\sigma }_{0}}r_{0}^{2}$) на поверхности $r = {{r}_{0}}$ проскальзывание завершается и выполняется условие прилипания (3.2) так, что $\psi ({{r}_{0}},t) = \psi ({{r}_{0}},{{t}_{3}})$. При $t > {{t}_{3}}$ материал начинает остывать; свяжем такое остывание с условием

(5.1)
$\theta ({{r}_{0}},t) = \theta ({{r}_{0}},{{t}_{3}})(1 - {{\alpha }_{2}}(t - {{t}_{3}}))$

Продвигающаяся граница области вязкопластического течения $r = {{r}_{2}}(t)$ в некоторый момент времени $t = {{t}_{4}}$ достигает поверхности $r = {{r}_{0}}$ и область вязкопластического течения исчезает. Для дальнейших расчетов остаются две области: область с накопленными необратимыми деформациями ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t*)$ и область, в которой происходило только обратимое деформирование ${{r}_{1}}(t*) \leqslant r \leqslant R$. Момент времени $t = {{t}_{4}}$ вычисляется решением уравнения

(5.2)
$\begin{gathered} r_{0}^{2}{{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}({{r}_{0}},{{t}_{4}})}}{{\theta _{m}^{2}}}} \right) = c({{t}_{4}}) \\ \end{gathered} $

Поворот внешней жесткой поверхности $\begin{gathered} r = R \\ \end{gathered} $ останавливается в момент времени $\begin{gathered} t = {{t}_{5}} = a{{b}^{{ - 1}}}{{t}_{1}} + {{t}_{2}} \\ \end{gathered} $. После этого (при $\begin{gathered} t > {{t}_{5}} \\ \end{gathered} $) материал продолжает охлаждаться и в нем продолжается перераспределение напряжений вплоть до полного выравнивания температуры до комнатной по всему продеформированному материалу.

6. Результаты расчетов. При проведении расчетов независимые безразмерные переменные выбирались в форме: $\tilde {r} = r{{R}^{{ - 1}}}$, $\begin{gathered} \tilde {t} = at \\ \end{gathered} $, напряжения относились к модулю сдвига $\mu $. Постоянными задачи и материала предписывались следующие значения: ${{k}_{0}}{{\mu }^{{ - 1}}} = 0.00621$, ${{{r}_{0}}{{R}^{{ - 1}}} = 0.5}$, $a{{b}^{{ - 1}}} = 1$, $\varsigma a{{\mu }^{{ - 1}}} = 0.005$, $a\eta {{\mu }^{2}} = 0.004$, ${{\beta }_{1}} = 0.5$, ${{\beta }_{3}} = - 0.5$, $l{{\mu }^{{ - 1}}} = 0.001$, ${{\nu }_{1}}{{\mu }^{{ - 1}}} = 0.02$, $f{{\sigma }_{0}}{{\mu }^{{ - 1}}} = 0.005$, ${{\alpha }_{1}} = 100$, ${{\alpha }_{2}} = 50$, $g{{R}^{2}} = 10$. Приведенные далее графические зависимости были получены именно при таких значениях постоянных.

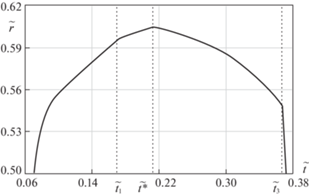
Графическая зависимость рис. 1 иллюстрирует развитие и схлопывание области вязкопластического течения со временем. Вертикальными прямыми пунктирными отрезками на рис. 1 отмечены характерные моменты времени $\begin{gathered} {{{\tilde {t}}}_{1}} \\ \end{gathered} $, $\tilde {t}{\kern 1pt} *$ и $\begin{gathered} {{{\tilde {t}}}_{3}} \\ \end{gathered} $, когда угловая скорость $\begin{gathered} {{\omega }_{R}} \\ \end{gathered} $ перестает расти, когда упруговязкопластическая граница начинает двигаться в обратную сторону и когда заканчивается проскальзывание соответственно.

Рис. 1.

Изменение области вязкопластического течения в процессе деформирования.

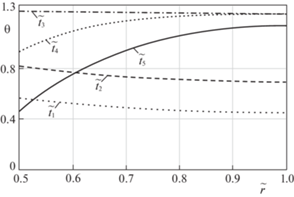
Распределение температуры по материалу в разные моменты времени показано графически на рис. 2. Тепло производится за счет пристеночного трения и необратимого деформирования.

Рис. 2.

Распределение температуры в различные моменты времени.

Ниспадающие кривые рис. 2 соответствуют моментам времени, при которых отток тепла через границу $r = R$ превалирует над его производством за счет вязкопластического течения.

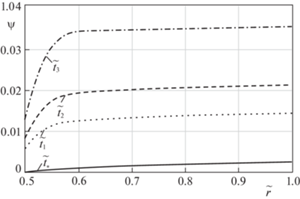
На рис. 3 показано распределение угла поворота в различные моменты времени.

Рис. 3.

Распределение угла поворота в различные моменты времени.

Заключение. Рассматриваемая здесь задача рассчитывает не отдельное состояние упругопластического тела в зависимости от действий конкретных нагрузок, а процесс упруговязкопластического деформирования от его начала до полной разгрузки и остывания. Возможное производство тепла в процессе связывается с трением материла о шероховатую его границу и его необратимым деформированием. При этом совершенно необходимо подчеркнуть определяющую роль дифференциальных уравнений изменения (переноса) обратимых и необратимых деформаций. Именно следуя такому подходу (соотношения (2.12) и следующие из них зависимости (4.1)) удается получить систему дифференциальных уравнений, последующее разрешение которой в рамках сеточного конечно-разностного метода уже не встречает дополнительных трудностей. Для расчетов процессов неизотермического деформирования в неодномерных задачах теории при таком подходе представляется возможным создание соответствующего вычислительного модуля расчетов. Для этого представленное решение может послужить в качестве средства тестирования создаваемых алгоритмов и вычислительных процедур. Преимущество расчетов на такой основе может оказаться значимым.

Работа выполнена в рамках проекта РНФ (грант 22-11-00163).

Список литературы

  1. де Гроот С., Мазур П. Неравновесная термодинамика. М.: Мир, 1964. 456 с.

  2. Мясников В.П. Уравнения движения упругопластических материалов при больших деформациях // Вестн. ДВО РАН. 1996. № 4. С. 8–13.

  3. Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации и упругое последействие. Владивосток: Дальнаука, 2013. 312 с.

  4. Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.

  5. Волков И.А., Коротких Ю.Г. Уравнения состояния вязкоупругопластических сред с повреждениями. М.: Физматлит, 2008. 424 с.

  6. Волков И.А., Игумнов Л.А. Введение в континуальную механику поврежденной среды. М.: Физматлит, 2017. 310 с.

  7. Lee E.H. Elastic-plastic deformation at finite strains // Trans. ASME. Ser. E. J. Appl. Mech. 1969. V. 36. № 1. P. 1–6.

  8. Левитас В.И. Большие упругопластические деформации материалов при высоком давлении. Киев.: Наук. думка, 1987. 231 с.

  9. Naghdi P.M. A critical review of the state of finite plasticity // ZAMP. 1990. V. 41. P. 315–394.

  10. Meyers A., Schievbe P., Bruhns O.T. Some comments on objective rates of symmetric Eulerian tensors with application to Eulerian strain rates // Acta Mech. 2000. V. 139. P. 91−103.

  11. Xiao H., Bruhns O.T., Meyers A. A consistent finite elastoplasticity theory combining additive and multiplicative decomposition of the stretching and deformation gradient // Int. J. Plasticity. 2000. V. 16. P. 143−177.

  12. Khoei A.R., Bakhshiani A., Mofid M. An implicit algorithm for hypoelasto-plastic and hypoelasto-viscoplastic endochronic theory in finite strain isotropic-kinematic-hardening model // Int. J. Solids&Struct. 2003. V. 40 (13–14). P. 3393–3423.

  13. Asghari M., Naghdabadi R. On the objective corotational rates of Eulerian strain measures. // J. Elasticity. 2008. V. 90. P. 175–207.

  14. Shen L.-J. Constitutive relations for isotropic or kinematic hardening at finite elastic-plastic deformations // Int. J. Solids&Struct. 2006. V. 43. P. 5613−5627.

  15. Султанов Л.У. Исследование конечных упругопластических деформаций: алгоритм решения, численные примеры // Уч. зап. Казан. ун-та. Сер. Физ.-матем. науки. 2017. Т. 159. кн. 4. С. 509–517.

  16. Shutov A.V., Ihlemann J. Analysis of some basic approaches to finite strain elasto-plasticity in view of reference change // Int. J. Plasticity. 2014. V. 63. P. 183–197.

  17. Shutov A.V., Larichkin A.Y., Shutov V.A. Modelling of cyclic creep in the finite strain range using a nested split of the deformation gradient // ZAMM. 2017. V. 97. № 9. P. 1083–1099.

  18. Simo J.C. Algorithms for static and dynamic multiplicative plasticity that preserve the classical return mapping schemes of the infinitesimal theory // Comp. Meth. Appl. Mech. Engng. 1992. V. 99. P. 61–112.

  19. Stein E., Sagar G. Theory and finite element computation of cyclic martensitic phase transformation at finite strain // Int. J. Numer. Meth. Engng. 2007. V. 74. P. 1–31.

  20. Helm D. Stress computation in finite thermoviscoplasticity // Int. J. Plasticity. 2006. V. 22 (9). P. 1699–1727.

  21. Har J. A unified stress update algorithm for explicit transient shell dynamics with combined isotropic-kinematic hardening in Eulerian rate-type phenomenological finite elasto-plasticity models // Comp. Meth. Appl. Mech. Eng. 2007. V. 196. P. 3248–3275.

  22. Голованов А.И., Султанов Л.У. Математические модели вычислительной нелинейной механики деформируемых сред деформаций. Казань: КФУ, 2009. 465 с.

  23. Wriggers P. Nonlinear Finite Element Methods. Springer. Sci.&Business Media, 2008. 560 p.

  24. Shutov A.V. Efficient implicit integration for finite-strain viscoplasticity with a nested multiplicative split // Comp. Meth. Appl. Mech. Engng. 2016. V. 306. P. 151–174.

  25. Xia Z., Ellyin F. A stress rate measure for finite elastic plastic deformations // Acta Mech. 1993. V. 98. P. 1–14.

  26. Ивлев Д.Д. Из истории дискуссий в механике. Три дискуссии // Теор. и прикл. мех. 2012. Вып. 27. С. 5–10.

  27. Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации: теория, алгоритмы, приложения. М.: Наука, 1986. 232 с.

  28. Быковцев Г.И., Шитиков А.В. Конечные деформации упругопластических сред // Докл. АН СССР. 1990. Т. 311. № 1. С. 59–62.

  29. Чернышов А.Д. Определяющие уравнения для упругопластического тела при конечных деформациях // Изв. РАН. МТТ. 2000. № 1. С. 120–128.

  30. Новокшанов Р.С., Роговой А.А. О построении эволюционных определяющих соотношений для конечных деформаций // Изв. РАН. МТТ. 2002. № 4. С. 77–95.

  31. Роговой А.А. Определяющие соотношения для конечных упруго-неупругих деформаций // ПМТФ. 2005. Т. 46. № 5. С. 138–149.

  32. Буренин А.А., Быковцев Г.И., Ковтанюк Л.В. Об одной простой модели для упругопластической среды при конечных деформациях // Докл. РАН. 1996. Т. 347. № 2. С. 199–201.

  33. Бегун А.С., Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации в условиях изменяющихся механизмов их производства и проблема задания пластических потенциалов // Докл. РАН. 2016. Т. 470. № 3. С. 275–278.

  34. Белых С.В., Буренин А.А., Ковтанюк Л.В., Прокудин А.Н. Об учете вязких свойств материалов в теории больших упругопластических деформаций // Чебышевский сб. 2017. Т. 18. № 3. С. 108–130.

  35. Begun A.S., Burenin A.A., Kovtanyuk L.V., Lemza A.O. On the mechanisms of production of large irreversible strains in materials with elastic, viscous and plastic properties // Arch. Appl. Mech. 2020. V. 90 (4). P. 829–845.

  36. Kovtanyuk L.V., Panchenko G.L. Mathematical modelling of the production process of irreversible strains under the heating and cooling of a flat heavy layer on an inclined surface // Lobachevskii J. Math. 2021. V. 42. № 8. P. 1998–2005.

  37. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Неизотермическое движение упруговязкопластической среды в трубе в условиях изменяющегося перепада давления // Докл. РАН. 2015. Т. 464. № 3. С. 284–287.

  38. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Развитие и торможение вязкопластического течения в слое в условиях его нагрева за счет трения о шероховатую плоскость // ПМТФ. 2015. Т. 56. № 4. С. 101–111.

  39. Prokudin A.N., Firsov S.V. Antiplane strain of hardening elastoviscoplastic medium // J. Sib. Fed. Univ. Math. Phus. 2018. V. 11. № 4. P. 399–400.

  40. Бегун А.С., Ковтанюк Л.В. Вискозиметрическое течение упруговязкопластического материала при его нагреве вследствие пристеночного трения // ПМТФ. 2021. № 5. С. 89–99.

  41. Лурье А.И. Дифференцирование по тензорному аргументу // в сб.: Вопросы математической физики. Л.: Наука, 1976. С. 48–57.

  42. Прагер В. Введение в механику сплошных сред. М.: Изд-во иностр. лит., 1963. 312 с.

  43. Ковтанюк Л.В., Шитиков А.В. О теории больших упругопластических деформаций материалов при учете температурных и реологических эффектов // Вестн. ДВО РАН. 2006. № 4. С. 87–93.

  44. Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал