Прикладная математика и механика, 2022, T. 86, № 6, стр. 998-1012

1. Введение. К настоящему времени вышло много работ, описывающих распределение давления в трещине ГРП при работе нефтяной скважины. В большинстве из них рассматривается стационарная фильтрация (см., напр., [1]). Модели, приведенные в [2–5], описывают нестационарную фильтрацию жидкости в трещине и показывают связь между постоянным давлением, поддерживаемым после ее начала работы, и расходом жидкости на скважине или изменение давления при поддержании постоянного расхода. В статье [5] приводятся решения для нахождения распределения давления в трещине ГРП конечной длины и, окружающем трещину пласте. В работе [6] рассмотрены режимы работы скважины с кусочно-постоянными изменениями давления на скважине или расхода жидкости.

В данной работе рассматриваются более общие режимы работы нефтяной скважины; случаи ступенчатого и непрерывного изменения давления или изменения дебита скважины. И в том и другом случае получены точные аналитические решения, описывающие распространение давления в трещине, по которым, в свою очередь, используя закон Дарси, можно определить фильтрационные потоки в пласте и трещине. Показана практическая значимость полученных результатов.

Полученные теоретические результаты апробируются на данных измерений суточного дебита и изменения давления на забое реальной нефтяной скважины. По начальному П-образному режиму изменения дебита скважины и, соответствующим данным изменения давления был найден коэффициент, определяемый характеристиками пласта и трещины ГРП (значениями проницаемостей и пористости трещины и пласта, шириной и высотой трещины, вязкостью флюида). Далее, по аналитическим решениям, полученным в работе, по кривой годового изменения дебита скважины получена кривая изменения давления на забое. Из представленных в работе графиков следует достаточно хорошее совпадение теоретических кривых с промысловыми данными.

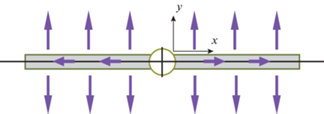
2. Основные уравнения. Рассмотрим нефтяную скважину с вертикальной, закрепленной пропантом трещиной, полученной путем гидроразрыва пласта (ГРП) (рис. 1). Пласт предполагается однородным, ширина трещины d_f  значительно меньше ее высоты h_f. Считаем, что жидкость в пласте течет перпендикулярно плоскости трещины и, далее, по трещине течет от скважины (билинейная схема). Предполагается, что давление жидкости в пласте и трещине мало зависит от изменения глубины, поэтому рассматриваем движение флюида в трещине, как квазиодномерное вдоль оси OX, направленной вдоль трещины. В силу симметрии можно рассматривать одно крыло трещины. Начало координат поместим на стенку забойного участка. Ось OY направим перпендикулярно трещине. Отсчет будет идти от границы “пласт–трещина”. Скелет пористой среды пласта и трещины считаем несжимаемым, длину трещины бесконечной.

Основываясь на законе сохранения масс, законе Дарси в работах [2–5] получена система уравнений, описывающая фильтрацию флюида в трещине ГРП и пласте:

где ${{{{\unicode{230} }}}_{i}} = \left( {{{\rho }_{0}}{{C}^{2}}{{k}_{i}}} \right){\text{/}}\left( {\mu {{m}_{i}}} \right)$ – коэффициент пьезопроводности. Здесь и в дальнейшем индексы i = f и p соответствуют значениям параметров в трещине и пласте, окружающем трещину. Через ρ₀ обозначим первоначальную невозмущенную плотность жидкости, ${{v}_{i}}$ – скорость жидкости, m_i – пористость, μ – динамическая вязкость, k_i – коэффициент проницаемости, d_f  – ширина трещины, С – скорость звука для флюида, P_f  = P_f (t, x), P_p = P_p(t, x, y) – давление в трещине и пласте, соответственно. Второе слагаемое в правой части уравнения (2.1) выражает интенсивность притока флюида через стенки в трещину. Жидкость считаем слабосжимаемой $~\left| {{{\rho }_{i}} - {{\rho }_{0}}} \right| \ll {{\rho }_{0}}$. Индекс (0) соответствует начальному состоянию.

Давление в трещине и в пласте на поверхности стенки трещины совпадает:

Вдали от трещины считаем, что давление постоянно и равно первоначальному значению P₀:

Система уравнений (2.1)–(2.2) сводится в работе [4] к одному интегро-дифференциальному уравнению, описывающему распределение давления в трещине ГРП:

Здесь мы считаем, что при $t \to - \infty $ система находится в покое, т.е.

Из сравнения слагаемых в уравнении (2.5) можно получить критические условия для характерного времени $\tilde {t}$, когда левая часть этого уравнения, отвечающая за упругоемкость флюида в трещине несущественна (см. [4]).

Для рассматриваемых задач справедлива оценка

Для нефтепромысловых задач обычно рассматриваются времена, удовлетворяющие условию (2.6) (минуты, часы, сутки). Поэтому будем вместо (2.5) пользоваться упрощенным уравнением

3. Случай последовательного скачкообразного закона изменения давления в скважине. В работе [4] получено решение задачи о распространении давления в трещине ГРП при резком изменении давления в момент времени τ на постоянную величину $\Delta {{P}_{{\left( w \right)}}} = {{P}_{{\left( w \right)}}} - {{P}_{0}}$. Предполагается, что далее давление поддерживается постоянным ($\Delta {{P}_{{\left( w \right)~}}} = \operatorname{const} $, $t \geqslant \tau $). Для определенности будем в дальнейшем считать, что $\Delta {{P}_{{\left( w \right)~}}} > 0$, т. е. рассматривается случай, когда жидкость нагнетается в пласт, случай откачивания жидкости из скважины приводит лишь к изменению знака величины $\Delta {{P}_{{\left( w \right)}}}$.

Эти условия запишем в виде

В работе [4] получено решение поставленной задачи через специальную функцию

Распределение давления в трещине находится, как

На основе этого решения можно определить формулу для объемного расхода флюида в одном крыле трещины на единицу высоты трещины:

Введем величину $\mathcal{F} = \frac{\mu }{{\sqrt {{{\mathcal{X}}_{f}}{\text{/}}2~~} {{d}_{f}}{{k}_{f}}}}$ (от англ. Feature – характеристика, свойство), характеризующую проводимость трещины. Используя выражение для ${{\mathcal{X}}_{f}}$ из (3.2) и выражения для коэффициентов пьезопроводности ${{{{\unicode{230} }}}_{p}}$, ${{{{\unicode{230} }}}_{f}}$, входящих в уравнения (2.1) и (2.2), для параметра $\mathcal{F}$ можем записать:

Отсюда

Здесь использовано

где Γ – Гамма-функция, и $\Gamma \left( {\frac{5}{4}} \right) = \frac{1}{4}\Gamma \left( {\frac{1}{4}} \right) \approx 0.906$.

Рассмотренное уравнение (2.7), линейное для ΔP_f, это позволяет (см. [6]), представленную формулу (3.2) для нахождения расхода, обобщить для случая, когда давление изменяется скачкообразно в моменты времени ${{\tau }_{1}},{{\tau }_{2}}, \ldots ,{{\tau }_{n}}$ и на участках $\left[ {{{\tau }_{i}},{{\tau }_{{i + 1}}}} \right)$, i = 1, 2, …, n принимает постоянные значения.

Пусть в исходном состоянии жидкость в скважине и трещине неподвижна

В момент времени $t = {{\tau }_{1}}$ скважина начинает функционировать при постоянном перепаде давления $\Delta {{P}_{{\left( w \right)1~}}}$ до момента времени ${{\tau }_{2}}$, с момента времени ${{\tau }_{2}}~$скважина функционирует при перепаде давления $\Delta {{P}_{{\left( w \right)2~}}}$ до момента времени ${{\tau }_{3}}$ и т.д. Для удобства записи формулы будем считать, что $\Delta {{P}_{{\left( w \right)0}}} = 0~$. Тогда решение, описывающее изменение давления в трещине, может быть записано в виде

здесь $H\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {1,\quad {\text{при}}\quad t \geqslant 0,} \\ {0,\quad {\text{при}}\quad t < 0.} \end{array}} \right.$ – функция Хевисайда.

Далее, по аналогии с (3.2), получим величину расхода на единицу высоты трещины:

Объем флюида, поступающий (расходуемый) за время, прошедшее с момента τ начала работы скважины до момента времени t через два крыла трещины высотой ${{h}_{f}}$, будет определяться формулой

4. Случай непрерывного изменения давления на скважине. Пусть первоначальное давление в пласте и на забое равно P₀, давление в скважине изменяется непрерывно:

Разобьем временной промежуток $[{{\tau }_{0}},t)$ точками ${{\tau }_{0}},{{\tau }_{1}},{{\tau }_{2}}$, …, τ_n. Введем следующую сумму:

Согласно (3.5), выражение (4.1) соответствует ступенчатому изменению давления на скважине. При ${\text{max}}\left( {~{{\tau }_{i}} - {{\tau }_{{i - 1}}}} \right) \to 0$ оно может рассматриваться, как интегральная сумма для интеграла

Отсюда можно найти расход жидкости на скважине:

где ${\text{Gil}}'\left( 0 \right) = {{\left. {\left( {\frac{d}{{dz}}{\text{Gil}}\left( z \right)~} \right)} \right|}_{{z = 0}}} = - \frac{1}{\pi }\int_0^\infty {{{\eta }^{{ - \frac{3}{4}}}}~{{e}^{{ - \eta }}}~d\eta } = - \frac{{\Gamma \left( {\frac{1}{4}} \right)}}{\pi }~$.

Поэтому

то есть

Формулы (4.2) и (4.3) позволяют, зная непрерывный закон изменения давления на скважине, определять закон изменения расхода жидкости в скважине с вертикальной трещиной ГРП и в самой трещине.

5. Решения, соответствующие кусочно-постоянным законам изменения расхода жидкости на скважине. Пусть до момента времени $\tau $ флюид в пласте и трещине находится в покое (${{{v}}_{p}} = {{{v}}_{f}} = 0$). В работах [3], [4] получен закон изменения давления при постоянном расходе. Пусть, первоначальный расход жидкости на скважине до момента времени $t = \tau $ нулевой, и, начиная с момента времени $t = \tau $ поддерживается постоянный расход q. Тогда распределение давления в трещине ГРП выражается формулой при ($\tau \leqslant t$)

где (см. [3, 4]) ${\text{Zil}}\left( z \right) = \mathop \smallint \limits_0^z \,{\text{Gil}}\left( \xi \right)d\xi - {\text{\;специальная функция}}{\text{.}}$

Так как $\Delta {{P}_{{\left( w \right)}}} = {{\left. {\Delta {{P}_{f}}} \right|}_{{x = 0}}}$, из (5.1) получим закон изменения перепада давления на скважине:

Величина ${\text{Zil}}\left( 0 \right) \approx 0.78$. Графики функций ${\text{Gil}}\left( z \right)$ и ${\text{Zil}}\left( z \right)$ приведены в работе [4].

В силу линейности уравнения (2.7), выше представленное решение (5.1), можно обобщить для случаев, когда расход представляет кусочно-постоянную функцию.

Пусть до момента τ₁ флюид в пласте находится в покое и расход жидкости на скважине ${{q}_{0}} = 0$, в момент времени τ₁ расход выходит на значение ${{q}_{1}}$ и поддерживается постоянным до момента времени τ₂, когда он резко изменяется до величины ${{q}_{2}}$ и держится постоянным до момента τ₃, и так далее.

Решение, описывающее эволюцию давления в трещине, принимает вид:

Для перепада давления $\Delta {{P}_{{\left( w \right)}}}$ между значениями на забое скважины и пластом $\left( {\Delta {{P}_{{\left( w \right)}}} = \Delta {{P}_{f}}\left( {t,0} \right)} \right)$ получим

6. Случай непрерывного изменения расхода жидкости на скважине. Рассмотрим теперь случай, когда расход жидкости на скважине изменяется непрерывно, начиная с нулевого значения q = q(t), q(0) = 0, t ≥ 0.

Разобьем временной промежуток $[{{\tau }_{0}},t)$ точками ${{\tau }_{0}},{{\tau }_{1}},{{\tau }_{2}}$, …, τ_n. Введем следующую сумму:

При ${\text{max}}\left( {{{\tau }_{i}} - {{\tau }_{{i - 1}}}} \right) \to 0$ $\left( {i = 1,2, \ldots ,n} \right)$ она может рассматриваться, как интегральная сумма для интеграла

позволяющего определить распространение давления в трещине ГРП. Отсюда, подставляя значение $x = 0$, получаем закон изменения давления на забое скважины при известном непрерывном изменении расхода:

7. Результаты расчетов. На основе полученных аналитических решений, рассмотрим численные примеры. Для параметров, определяющих физические свойства флюида, а также пласта, подверженного ГРП (если специально не оговорено иное) примем следующие величины: $~{{\rho }_{0}} = {{10}^{3}}$ кг/м³, $~{{m}_{f}} = 0.3$, $\mu = {{10}^{{ - 3}}}$ Па · с, $C = 1500$ м/с, ${{k}_{p}} = {{10}^{{ - 15}}}$ м², ${{m}_{p}} = 0.1$, ${{k}_{f}} = {{10}^{{ - 10}}}$ м², ${{d}_{f}} = 5 \times {{10}^{{ - 3}}}$ м.

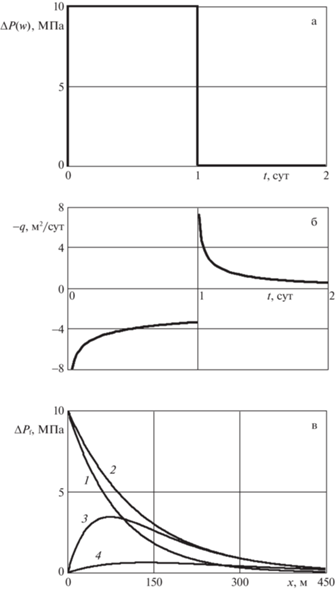
Рассмотрим эволюцию фильтрационных полей в трещине и дебит жидкости через нее при заданном законе изменения давления в забое скважины. Поскольку уравнения, описывающие поле давления движения в трещине и окружающем ее пласте, представляют собой линейно однородные интегро-дифференциальные уравнения, то решения, описывающие возмущения давления в пласте и трещине, пропорционально изменяются относительно исходного пластового давления, то есть задание начального пластового давления при получении решений роли не играет. Допустим в исходном состоянии пластовое давление однородно и вдали от скважины сохраняется постоянное значение. Это означает, что здесь рассматриваем “начальный” этап эксплуатации скважины, в течение которого дальняя граница трещины ГРП и пласта слабо влияют на эволюцию давления в трещине и пласте. Пусть (рис. 2а) в момент времени $t = 0$ давление в забое повышается на 10 МПа и поддерживается постоянным в течение суток. Далее, давление опускается до исходного значения и сохраняется постоянным. Видно (рис. 2б), что в течение суток происходит нагнетание $(q < 0)$, а далее (t > 1 сутки) происходит поступление жидкости в скважину. На рис. 2в представлена эволюция давления в трещине ГРП. Линии 1, 2, 3 и 4 соответствуют моментам времени t = 6 часов, 1 сутки, 1 сутки и 30 минут, 2 суток.

Заметим, что в моменты скачкообразного изменения давления расход жидкости на скважине приобретает бесконечное значение (всплеск), но количество извлекаемой или закачиваемой жидкости за любой промежуток времени конечно и изменяется непрерывно.

Рассмотрим случай, когда перепад давления $\Delta {{P}_{{\left( w \right)}}}$ растет по линейному закону от нулевого значения до значения $\Delta {{P}_{{\left( w \right)1}}}$ за время ${{\tau }_{1}}$. Тогда

В этом случаи из (4.2) для эволюции давления в трещине получим

На основе (4.3), используя решение (7.2), для расхода жидкости на единицу высоты трещины получим

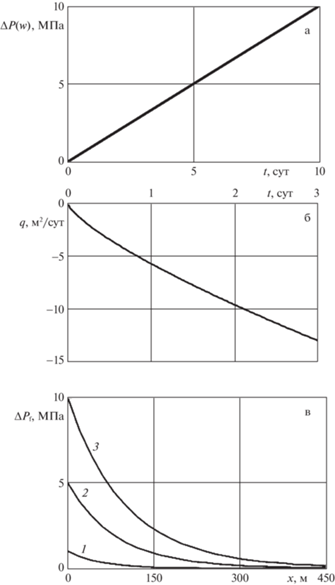
На рис. 3 представлено линейное изменение давления (а) в скважине и соответствующее изменение расхода жидкости на единицу высоты трещины (б), а также эволюция поля давления (в) в трещине ГРП для линейного изменения давления. Приняты следующие значения $\Delta {{P}_{{\left( w \right)1}}} = 10$ МПа, ${{\tau }_{1}} = 1$ сутки, линии 1, 2, 3 соответствуют моментам времени $t = 1$, 5 и 10 сут.

Пусть теперь давление $\Delta {{P}_{{\left( w \right)}}}$ в скважине в течение времени ${{\tau }_{1}}$ линейно растет до значения $\Delta {{P}_{{\left( w \right)1}}}$, затем снижается по линейному закону до нулевого значения до момента времени ${{\tau }_{2}}$ (Λ – образное изменение). Тогда для значений времени $t$ между ${{\tau }_{1}}$ и ${{\tau }_{2}}$ получим значения давления в трещине:

Если ${{\tau }_{2}} = 2{{\tau }_{1}}$ для несжимаемой жидкости при значениях времен $0 < t < {{\tau }_{1}}$ величина расхода будет изменяться по формуле (7.3), а при временах ${{\tau }_{1}} < t < {{\tau }_{2}}$ при принятых выше параметрах трещины и вязкости жидкости по формуле

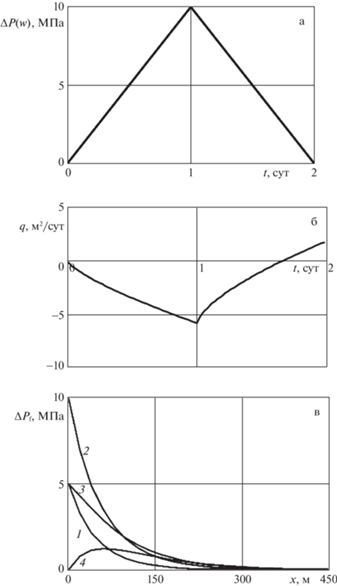
На рис. 4а представлено Λ-образное изменение давления, соответствующий закон изменения расхода на единицу высоты трещины (б), а также эволюция давления в трещине (в) при ΔP₁ = 10 МПа, τ₂ = 2τ₁ = 2 суток. Линии 1, 2, 3 и 4 соответствуют моментам времени t = 0.5 суток, 1 сутки, 1.5 суток и 2 суток.

Наиболее важной с целью приложения является задача определения графика изменения давления, когда известен закон изменения дебита скважины. Решение таких задач и их сопоставление с промысловыми данными для кривых “дебит – забойное давление” позволяет судить о коллекторских характеристиках в призабойной зоне пласта. Наиболее простой и интересной задачей в этом плане является задача определения характеристик пласта для П-образного по времени дебиту.

Пусть до момента времени ${{\tau }_{0}} = 0$ расход был нулевой и, затем мгновенно повышается до значения $q$ и это значение поддерживается постоянным до момента времени $\tau $. Начиная с это момента расход становится нулевым. Тогда на основе общего решения (5.3) будем иметь

Отсюда при $x = 0$ получим выражение для перепада давления между забойным и пластовым значениями

Величины всех параметров, входящих в формулы (3.2) и (3.3), обычно являются известными, кроме проводимости трещины ${{d}_{f}}{{k}_{f}}$. Значение этого параметра можно определить из П-образного закона изменения дебита и соответствующего изменения давления на забое скважины.

На рис. 5 представлено для П-образного изменения дебита (а) – изменение давления на забое скважины (б), и эволюция давления в трещине ГРП (в) при величине расхода на единицу высоты трещины q = 1 м²/сут. Цифры 1, 2, 3 и 4 на линиях соответствуют моментам времени t = 0.5, 1, 1.5, 2 суток.

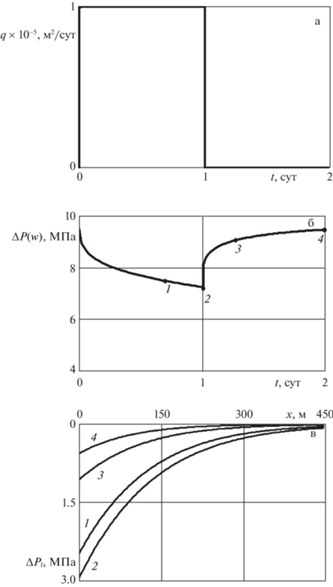
Видно, что для П-образного закона изменения давления соответствующая кривая для перепада давления $\Delta {{P}_{{\left( w \right)}}}$ имеет форму зубчика. Причем максимальная величина зубчика достигается при $t = \tau $.

Согласно формуле (7.7) для величины зубчика можем записать

Эта формула по величине “зубчика” $\Delta {{P}_{{\left( w \right)}}}\left( \tau \right)$ наблюдаемого при П-образном дебите определяет неизвестную величину проводимости трещин ${{d}_{f}}{{k}_{f}}$.

Действительно, из (7.8), учитывая выражение для $\mathcal{F}$ из (3.3), получаем

При положительном значении дебита ($q > 0$) значения “зубчика” отрицательны, поэтому в правой части выражения (7.9) стоит знак минус.

8. Сравнение результатов численных расчетов с промысловыми данными. На рис. 6а представлена кривая изменения дебита во времени для реальной промысловой скважины. Для параметров скважины и пласта использованы следующие данные: ${{m}_{p}} = 0.17$, ${{k}_{p}} = {{10}^{{ - 15}}}$ м², $\mu = 0.00115$ Па · с, высота трещины $h = 18.3$ м. Кривая для дебита аппроксимировалась кусочно-постоянными значениями c интервалом $\Delta \tau $ = 1 сут. Видно, что в начальный период (примерно до 28 суток) скважина два цикла работала в режиме П-образного дебита с общим расходом $Q_{1}^{{\left( 1 \right)}} = 17$ м³/сут, $Q_{2}^{{\left( 2 \right)}} = 2.4$ м³/сут.

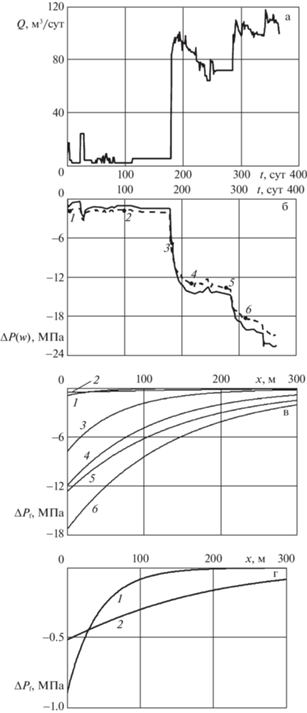
Причем величины зубчиков для изменения давления составляют $\Delta P_{{\left( w \right)}}^{{\left( 1 \right)}} = 1.26$ MПа (для ${{\tau }_{1}} = 4$ сут), $\Delta P_{{\left( w \right)}}^{{\left( 2 \right)}} = 2.14$ МПа (для 29 сут).

Для практического применения запишем формулу (5.4) изменения давления на забое скважины в виде

Здесь ${{Q}_{0}},{{Q}_{1}},{{Q}_{2}}$, …, ${{Q}_{n}}$ – значения дебита скважины в моменты времени ${{\tau }_{0}} = 0,{{\tau }_{1}},{{\tau }_{2}}$, …, ${{\tau }_{n}}$. При этом может быть выбрана любая единица измерения времени (часы, сутки) и дебита (м³/ч, т/сут, бар/сут). По величине первого “зубчика” определим величину ${{C}_{f}}$ = $\Delta P_{{\left( w \right)}}^{{\left( 1 \right)}}{\text{/}}\tau _{1}^{{1/4}}$, которую при подстановке в формулу (8.1) можем использовать для определения изменения давления на скважине.

Согласно формуле (7.9) определяется проводимость трещины. В рассматриваемом примере ${{d}_{f}}{{k}_{f}} = 2.2 \times {{10}^{{ - 12}}}$ м³.

Проводились расчеты, согласно решению (5.4), для продолжительного этапа, который длился 365 суток. На рис. 6б сплошная линия давления соответствует промысловым значениям, а пунктирная линия – рассчитанным по формулам (5.4). На рис. 6в представлена эволюция давления в трещине, согласно решению (5.3). Линии 1, 2, 3, 4, 5 и 6 показывают распределение давление в трещине ГРП в моменты времени t = = 2, 100, 185, 220, 280, 320 сут, соответствующим различным характерным изменениям дебита скважины.

Заключение. Получены аналитические решения, описывающие эволюцию давления в трещине по известным законам изменения давления на забое скважины или дебита скважины. Эти решения позволяют получить кривые “дебит–давление на забое”. Наиболее важным результатом, представляется решение для П-образного изменения дебита: сопоставление кривых “дебит–давление на забое” с промысловыми данными, что позволяет оценить по величине “зубчика” на кривой давления проводимость трещины ГРП.

Исследование выполнено за счет гранта Российского научного фонда № 21-11-00207, https://rscf.ru/project/21-11-00207/