Прикладная математика и механика, 2022, T. 86, № 6, стр. 977-997

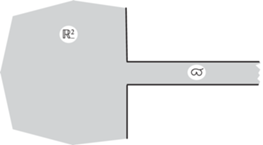
1. Упругий волновод. Пусть $\Pi _{ \pm }^{h} = \{ x = \left( {{{x}_{1}},{{x}_{2}}} \right):~ \pm {{x}_{1}} > {{\ell }^{h}},\left| {{{x}_{2}}} \right| < 1\} $ – две упругие полуполосы-рукава, соединенные тонкой (h > 0 – малый параметр) перемычкой ${{\Theta }}_{{}}^{h} = \{ x$ : : $\left| {{{x}_{1}}} \right| \leqslant {{\ell }^{h}}$, $\left| {{{x}_{2}}} \right| < h\} $. Масштабированием ширина полуполос сведена к двум, т.е. декартовы координаты $\left( {{{x}_{1}},{{x}_{2}}} \right)$ и все геометрические параметры сделаны безразмерными. Полудлина перемычки

будет подобрана так, чтобы обеспечить необычные свойства упругого – однородного и изотропного, с постоянными Ламе $\lambda > 0$ и $\mu > 0~$ – волновода (рис. 1)

При учете симметрии относительно оси абсцисс дополним плоскую задачу теории упругости

искусственными условиями на средней линии фигуры (1.2)

Здесь ${{\nabla }_{x}} = \operatorname{grad} $, ${{\nabla }_{x}}\, \cdot = \operatorname{div} $, ${{\Delta }_{x}} = {{\nabla }_{x}} \cdot {{\nabla }_{x}}$ – оператор Лапласа, $u = \left( {{{u}_{1}},{{u}_{2}}} \right)$ – вектор смещений, ρ > 0 – плотность материала и κ > 0 – частота колебаний, $n = \left( {{{n}_{1}},{{n}_{2}}} \right)$ – единичный вектор внешней нормали, определенный почти всюду на границе $\partial {{\Xi }^{h}}$, кроме восьми угловых точек, на которых краевые условия (1.4) не ставятся, $\sigma _{1}^{{\left( n \right)}}\left( u \right)$ и $\sigma _{2}^{{\left( n \right)}}\left( u \right)~$ – компоненты вектора нормальных напряжений

Наконец, ${{\delta }_{{j,k}}}$ – символ Кронекера.

Соотношения (1.5) исключают из рассмотрения изгибные колебания волновода, т.е. он подвержен только продольным колебаниям. Укажем волны, распространяющиеся в его рукавах $\Pi _{ \pm }^{h}$

Вектор-функции ${{W}^{ \pm }}$ и число $\theta $ суть решения спектральных задач для систем обыкновенных дифференциальных уравнений на отрезке (–1.1)

Анализируя соотношения (1.8), приходим к равенствам

где $W_{1}^{0}$ и $W_{2}^{0}$ – вещественные функции, четная и нечетная соответственно.

Амплитудные части (1.9) зафиксируем так, чтобы соблюсти условия отрогональности и нормировки ([3], гл.5, § 2)

Симплектическая (полуторалинейная и антиэрмитова) форма (1.11) происходит от формулы Грина для оператора Ламе и потому не зависит от параметра $R$ для волн (1.7). Величина $Q\left( {w,w} \right)$ пропорциональна проекции на ось абсцисс вектора Умова [1] переноса энергии волной $w$, т.е. принимается энергетический принцип излучения Умова–Мандельштама ([2], гл. 1), ([3], гл. 5), [4].

Вариационная формулировка задачи (1.3)–(1.5) сводится к интегральному тождеству [5, 6]

на подпространстве вектор-функций из класса Соболева

При этом ${{\left( { \cdot , \cdot } \right)}_{{{{{{\Xi }}}^{h}}}}}$ – натуральное скалярное произведение в пространстве Лебега ${{L}^{2}}\left( {{{{{\Xi }}}^{h}}} \right)$, а $\frac{1}{2}E\left( {{{u}^{h}},{{u}^{h}};{{{{\Xi }}}^{h}}} \right)~$ – функционал упругой энергии

Поскольку билинейная форма (1.13) симметрична, положительна и замкнута в пространстве H¹(Ξ^h), вариационной (1.12) и дифференциальной (1.3)–(1.5) задачам отвечает ([7], гл. 10) положительный самосопряженный оператор ${{A}^{h}}$ в гильбертовом пространстве ${{L}^{2}}(({{{{\Xi }}}^{h}})$, непрерывный спектр ${{\wp }_{c}}$ которого – замкнутая положительная полуось $\overline {{{\mathbb{R}}_{ + }}} = \left[ {0, + \infty } \right)$. При $\kappa = \kappa _{\dag }^{0} = 0$ (основная точка отсечки) у задачи (1.3), (1.4) в цельной полосе Π = (–1, 1) × $\mathbb{R}$ в силу дополнительного условия (1.5) есть только одно (с точностью до постоянного множителя) ограниченное решение – продольное жесткое смещение ${{e}_{{\left( 1 \right)}}}$ = (1, 0). Следовательно, вблизи начала координат кратность непрерывного спектра равна единице, и вторая точка отсечки $\kappa _{\dag }^{1}$ внутри непрерывного спектра ${{\wp }_{c}}$ положительна. Зафиксируем какую-то частоту

Основная цель работы – подобрать размер (1.1) тонкой балки так, чтобы волна (1.7), приходящая с бесконечности в рукаве ${{\Pi }}_{--}^{h}$, почти полностью проникала через перемычку Θ^h в рукав ${{\Pi }}_{ + }^{h}$ и уходила в нем на бесконечность. Ввиду симметрии волновода (1.2) можно ограничиться рассмотрением приходящей волны ${{w}^{ + }}$в полуполосе ${{\Pi }}_{--}^{h}$, а почти полное ее прохождение означает, что решение дифракционной задачи (1.3)–(1.5)

приобретает коэффициенты рассеяния $s_{ \pm }^{h}$, удовлетворяющие соотношениям

Здесь ${{\chi }_{ \pm }}$ – гладкие срезающие функции

Остаток $\widetilde {{{W}^{h}}}\left( x \right)$ затухает при ${{x}_{1}} \to \pm \infty $ экспоненциальной скоростью. Закон сохранения энергии обеспечивает равенство

Следовательно, одна из формул (1.16) влечет за собой другую.

По причине малой толщины перемычки в ситуации общего положения, наоборот, реализуется почти полное отражение волны ${{w}^{ + }}$ в рукаве ${{\Pi }}_{--}^{h}$, т.е. коэффициенты рассеяния в поле (1.15) удовлетворяют соотношениям

Ранее эффект аномального прохождения волн через узкие щели и каналы обнаружен [8–13] для скалярных задач (акустические среды, волны на поверхности весомой жидкости и пр.), причем вопрос ставился по-разному: показать [8–11], что эффект проявляется на какой-частоте при помощи аналитических или численных методов, или подогнать [12, 13] геометрические параметры для его реализации на заданной наперед частоте путем применения усовершенствованного асимптотического анализа. При анализе векторной задачи (1.3)–(1.5) применяется процедура [14–17] точной настройки параметров волновода для обеспечения необычных свойств волновых процессов, однако в отличие от скалярных задач [12, 13] какие-либо явные формулы для упругих полей и их характеристик недоступны, а результат достигается путем вывода определенных априорных связей между величинами, формирующими асимптотические формулы для коэффициентов рассеяния $s_{ \pm }^{h}$.

В разд. 2 перечислены специальные решения вспомогательных задач и установлены нужные связи между их числовыми характеристиками. В разд. 3 представлен собственно асимптотический анализ, включающий процедуру понижения размерности [18, 19] на тонкой перемычке ${{{{\Theta }}}^{h}}$ и метод сращиваемых асимптотических разложений [20, 21] в зонах ее присоединения к массивным рукавам, а разд. 4 посвящен процедуре точной настройки геометрических параметров, обеспечивающей искомый эффект почти полного прохождения волны. Отметим, что, поскольку согласно ограничениям (1.5), (1.14) в волноводе (1.2) имеется только одна пара распространяющихся волн (1.7), унитарность и симметричность матрицы рассеяния означает, что почти полное прохождение волны w⁺ в направлении “от $--\infty $ к $ + \infty $” гарантирует тот же эффект для волны w^–, распространяющейся в направлении “от $ + \infty $ к $--\infty $”.

В конце статьи обсуждаются сопутствующие вопросы. В разд. 5, 1°, описаны способы обоснования полученных асимптотических представлений, в частности, пояснено, что в формулах (1.16) и (1.18) бесконечно малые $o\left( 1 \right)$ равны $O\left( {h\left( {1 + \left| {\ln h} \right|} \right)} \right)$. Далее перечислены доступные обобщения формы и упругих свойств волновода, а также ограничения вводимые по необходимости. Кроме того, приведены упрощенный (акустический волновод; разд. 5, 4°) и усложненный (пространственный упругий волновод; разд. 5, 5°) варианты постановки задачи и приемы их исследования.

2. Вспомогательные задачи. 1°. Перемычка. Стандартная асимптотическая процедура понижения размерности ([18], гл. 15 и 16), ([19], гл. 1 § 3) в задаче (1.3)–(1.5), суженной на тонкую перемычку, приводит к одномерной модели продольных колебаний балки. Именно, введем растянутую поперечную координату η = h^–1x₂ и, заменив многоточием младшие – не существенные в предпринимаемом анализе – члены, подставим разложение вектора смещений

в уравнения (1.3) на прямоугольнике $(--{{\ell }^{0}},{{\ell }^{0}}) \times \left( {--h,h} \right)$ и краевые условия (1.5) на его сторонах $(--{{\ell }^{0}}{\text{\;}},{{\ell }^{0}}) \times \left\{ { \pm h} \right\}$. Соберем множители при одинаковых степенях малого параметра $h$ и последовательно решим задачи Неймана для обыкновенных дифференциальных уравнений на отрезке (–1, 1). Две задачи для компонент вектора ${{{v}}^{0}}$ дают выражение для первого поправочного члена представления (2.1)

Здесь $~{{e}_{{\left( 2 \right)}}}$ = (0, 1) – орт оси ординат. Компонента ${v}_{2}^{{''}}$ второй поправки ${v}{\kern 1pt} ''$ равна нулю, а условие разрешимости задачи для первой компоненты

превращается в обыкновенное дифференциальное уравнение относительно продольной координаты x₁

В уравнении (2.3) взято предельное (h = 0) значение размера (1.1) перемычки ${{{{\Theta }}}^{h}}$, а замена ${{\ell }^{0}} \mapsto {{\ell }^{h}}$ будет задействована в разд. 3 и 4.

Поскольку тонкая балка присоединена к массивным телам, уравнение (2.3) замыкается [24] условиями Дирихле

Зафиксируем главный член в представлении (1.1)

так, чтобы однородная задача (2.3), (2.4) приобрела нетривиальное решение – собственную функцию

2°. Пограничный слой. Вблизи концов перемычки ${{{{\Theta }}}^{h}}$, т.е. около точек $P_{ \pm }^{h}$ = $\left( { \pm {{\ell }^{0}},0} \right)$, возникает [18], [22–24] явление пограничного слоя, которое, как обычно, опишем в растянутых координатах

Для определенности рассмотрим левый (знак минус) конец перемычки и не будем писать верхний индекс ± у координат ${{\xi }_{j}}$. Соответствующая плоская статическая задача теории упругости

поставлена на объединении $\Upsilon $ полуплоскости $\mathbb{R}_{{--~}}^{2} = \{ \xi :{{\xi }_{1}} < 0\} $ и полуполосы $\varpi = \left[ {0, + \infty } \right)$ × $\left( {--1,1} \right)$ (рис. 2). Условия (2.8) и (2.9) унаследованы от условий (1.4) и (1.5), а инерционный член исчез из системы (2.7) потому, что мало последнее вычитаемое в преобразованном дифференциальном операторе

Применим метод сращиваемых асимптотических разложений [20, 21], в рамках которого при построении главных членов асимптотики требуется найти все решения задачи (2.7)–(2.9) с не более чем логарифмическим ростом в полуплоскости и не более чем линейным ростом в полуполосе. Одно из таких решений очевидно – постоянный вектор ${{Z}^{0}} = {{e}_{{\left( 1 \right)}}}$. Второе ${{Z}^{1}}$ задано своим поведением на бесконечности

Здесь ${\mathbf{b}} \in \mathbb{R}$ – несущественная для дальнейшего постоянная, $B$ – решение Буссинеска–Фламана [25, 26] о сосредоточенной силе, действующей на полуплоскость

Кроме того, $\left( {\rho ,\varphi } \right) \in {{\mathbb{R}}_{ + }} \times \left( {--\frac{\pi }{2},\frac{\pi }{2}} \right)$ – система полярных координат, а явный вид угловой части B¹ решения (2.12) не понадобится. Важны только известные формулы для полярных компонент тензора напряжений

Следовательно

и поэтому равна нулю сумма главных векторов сил, порожденных полем смещений Z¹ на бесконечности в полуплоскости и в полуполосе. Именно последнее обстоятельство обеспечивает существование решения ${{Z}^{1}}$ задачи (2.7)–(2.9) с заданным поведением при |ξ| → ∞ и ${{\xi }_{1}} \to + \infty $. Отсутствие в правой части формулы (2.11) постоянного слагаемого фиксирует это решение. Согласно общим результатам [27, пример 1.12 и теорема 5.8] всякое решение задачи (2.7)–(2.9) с указанными ограничениями на рост – линейная комбинация ${{c}_{0}}{{Z}^{0}} + {{c}_{1}}{{Z}^{1}}$. Соотношения (2.10) и (2.11) можно почленно дифференцировать при соглашениях ${{\nabla }_{\xi }}O\left( {{{{\left| \xi \right|}}^{{--p}}}} \right)$ = $O\left( {{{{\left| \xi \right|}}^{{--p--1}}}} \right)$ и ${{\nabla }_{\xi }}O\left( {{{e}^{{--\varepsilon {{\xi }_{1}}}}}} \right)$ = $O\left( {{{e}^{{--\varepsilon {{\xi }_{1}}}}}} \right)$.

3°. Рукава. Асимптотика поля (1.15) внутри рукавов $\Pi _{ \pm }^{h}$ описывается при помощи решений задачи теории упругости в не зависящей от параметра h полуполосе ${{{{\Pi }}}^{{ \sqsupset ~}}}$ = = $\left( {--\infty ,0} \right) \times \left( {--1,1} \right)$

Краевое условие (2.15) поставлено на проколотом торце полуполосы, и далее понадобится поле смещений G, порожденное сосредоточенной в начале координат $\mathcal{O}$ продольной силой

Коэффициенты G и g зависят лишь от постоянных Ламе λ и µ, а правила ${{\nabla }_{x}}O\left( {{{{\left| x \right|}}^{{--p}}}} \right)$ = = $O\left( {{{{\left| x \right|}}^{{--p--1}}}} \right)$ и ${{\nabla }_{x}}O\left( {{{e}^{{\varepsilon {{x}_{1}}}}}} \right)$ = $O\left( {{{e}^{{\varepsilon {{x}_{1}}}}}} \right)$ разрешают почленное дифференцирование соотношений (2.17) и (2.18).

Еще одно поле W, гладкое вблизи точки $\mathcal{O}$ и равное сумме приходящей w⁺ и отраженной волн, допускает представление

Модуль коэффициента отражения s равен единице согласно закону сохранения энергии и условиям нормировки и ортогональности (1.10). Применим формулу интегрирования по частям для вектор-функций W и G в длинном (R → +∞) прямоугольнике с вырезанным полукругом

и вычислим предел при учете соотношений (1.10), (1.11) и (2.13). В результате обнаружим связь коэффициентов в представлениях (2.17)–(2.19)

Аналогичная формула Грина для вектор-функции G на обеих позициях вместе с равенствами (1.10), (1.11) и (2.13) дают соотношение

При этом $\left( {r,\varphi } \right)$ – система полярных координат, а σ^(r)(u) – вектор с компонентами (1.6) и нормалью (–cos φ, sin φ).

Полуполоса ${{{{\Pi }}}^{{ \sqsupset ~}}}$ получается из полуполосы ${{\Pi }}_{--}^{h}$ заменой координат

при сохранении вектора смещений. По причине изотропности упругого материала подстановки обеспечивает переход от ${{{{\Pi }}}^{{ \sqsupset ~}}}$ к $\Pi _{ + }^{h}$ и от задачи (2.14)–(2.16) в ${{{{\Pi }}}^{{ \sqsupset ~}}}$ к задаче (1.3)–(1.4) в $\Pi _{ + }^{h}$. Замены (2.22) будут применены в асимптотических конструкциях на рукаве $\Pi _{ + }^{h}$, а преобразованные таким образом поля G и W обозначим ${{G}_{ \circlearrowleft }}$ и ${{W}_{ \circlearrowleft }}$. Аналогичные операции нужны и при формировании пограничного слоя в окрестности точки $P_{ + }^{h}$.

3. Построение асимптотики. Простые асимптотические представления поля (1.15) на рукавах

дополним усложненным согласно формулам (2.1) и (2.2) из разд. 2, 1°, представлением на перемычке

При этом остатки $\tilde {W}_{ \pm }^{0}$ в разложениях (3.1) и (3.2) затухают на бесконечности с экспоненциальной скоростью, а $s_{ \pm }^{0}$ – главные члены асимптотик коэффициентов рассеяния в поле (1.15)

Как и ранее, многоточие заменяет младшие асимптотические члены, оцененные далее в разд. 5, 1°. Неизвестные коэффициент c и функция ${{{v}}^{0}}$, удовлетворяющая уравнению (2.3) и продолженная по гладкости за пределы интервала $\left( {--{{\ell }^{0}},{{\ell }^{0}}} \right)$, подлежат определению, а v – собственная функция (2.6) задачи (2.3), (2.4), причем

В зонах присоединения перемычки к массивным частям волновода (1.2), т.е. около точек $P_{ \pm }^{h}$, введем внутренние разложения поля (1.10)

и согласуем их с внешними разложениями (3.1)–(3.3) при помощи процедуры сращивания [20, 21].

Сначала обследуем окрестность точки $P_{--}^{h}$ со стороны перемычки и, отбросив члены $O\left( h \right)$ при учете формул (2.6) и (3.5), преобразуем разложение (3.3) к форме

Сравним правую часть соотношения (3.7) с представлением (2.11) решения Z¹ задачи (2.7)–(2.9) и привлечем в конструкцию еще одно решение ${{Z}^{0}}$ = ${{e}_{{\left( 1 \right)}}}Z$. В итоге приходим к равенству

В силу формул (2.10) и (2.12) внутреннее разложение (3.6), (3.8) около точки $P_{--}^{h}$ в рукаве ${{\Pi }}_{--}^{h}$ принимает вид

Множитель $\ln h$ возник из-за связи ${{r}_{{h--}}}: = \left| {x--P_{--}^{h}} \right| = h\rho $ радиальных переменных и присутствия логарифма в решении Буссинеска–Фламана (2.12). Согласно процедуре сращивания [20, 21] сингулярность этого решения передается члену $W_{--}^{0}$ внешнего разложения (3.1), который и соответствующий коэффициент отражения заданы формулами

Закончим сращивание разложений (3.1) и (3.7), сравнив множители при жестком поступательном смещении ${{e}_{{\left( 1 \right)}}}$ в правых частях соотношений (3.9) и (3.10). В результате получим краевое условие для функции ${{{v}}^{0}}$ из представления (3.3)

Сращивание внешних (3.1), (3.3) и внутреннего (3.6) разложений около точки $P_{ + }^{h}$ проводится по той же схеме при учете подстановок (2.22) и отсутствия приходящей волны ${{w}^{--}}$ в рукаве $\Pi _{ + }^{h}$. Формула (3.5) для собственной функции ${v}$ задачи (2.3), (2.4) уточняет внешнее разложение (3.3) около концевой точки $P_{ + }^{h}$ перемычки ${{{{\Theta }}}^{h}}$

Представление (2.11) решения ${{Z}^{1}}$ задачи (2.7)–(2.9) и формулы (2.22), меняющие знак у первой компоненты преобразованного решения $Z_{ \circlearrowleft }^{1}$, дают главный член внутреннего разложения (3.6)

Полностью реализуя процедуру сращивания разложений (3.6), (3.14) и (3.2) в окрестности точки $P_{ + }^{h}$, находим выражения для поля $W_{ + }^{0}$ в $\Pi _{ + }^{h}~$и сопутствующего коэффициента прохождения $s_{ + }^{0}$ волны w⁺, а также краевое условие в точке ${{\ell }^{0}}$ для асимптотической поправки ${{{v}}^{0}}$ на перемычке

В силу предположения о собственном числе (2.5) задача (2.3), (3.12), (3.17) приобретает одно условие разрешимости

Согласно формулам для величин $f_{ \pm }^{0}$ соотношение (3.18) принимает вид

и связывает неизвестные $\ell '$ и ${\mathbf{c}}{\text{\;}}$ в представлениях (1.1) и (3.3).

4. Подбор размеров перемычки. В распоряжении имеется один свободный вещественный параметр $\ell '$ из формулы (1.1) для размера ${{\ell }^{h}}$. Употребим его для упрощения формулы (3.19) и положим

При этом $T \in \mathbb{R}$ – новый свободный параметр. Тот факт, что величина (4.1) зависит от большого параметра $\ln h$ не влияет на проведенные выкладки, так как поправочное слагаемое $h\ell _{T}^{'}\left( {\ln h} \right)$ в представлении (1.1) остается малым, однако он привносит множитель $1 + \left| {\ln h} \right|$ в мажоранту из оценки (5.5). Теперь равенство (3.19) принимает вид

и при учете соотношений (3.11), (3.16) и (2.20), (2.21) находим главные члены асимптотик коэффициентов рассеяния

Закон сохранения энергии (1.18) предоставляет простую проверку проведенных вычислений

Подведем итог, предположив, что ${\mathbf{g}} \ne 0$ для придания смысла формулам (4.2). В случае $T$ = 0 имеем $s_{--}^{0} = 0~$и $s_{ + }^{0} = {{\left( {--1} \right)}^{m}}$, т.е. выполнены соотношения (1.5), означающее почти полное прохождение волны ${{w}^{ + }}$ из рукава $\Pi _{--}^{h}$ через перемычку в рукав $\Pi _{ + }^{h}$. Этот эффект неустойчив и требует точной настройки размера

прямоугольника ${{{{\Theta }}}^{h}}$ согласно формулам (2.5) и (4.1) при $T = 0$.

Если нарушить базовое равенство (2.5), то при любом малом возмущении $h\ell '$ полудлины ${{\ell }^{0}}$ перемычки реализуется почти полное отражение волны w⁺, приходящей с бесконечности в рукаве $~\Pi _{--}^{h}$, а именно, соотношения (1.18). Вытекающие из равенств (4.2) формулы

для главных членов асимптотики (3.4) коэффициентов рассеяния показывают, как почти полное прохождение трансформируется в почти полное отражение волны при увеличении отклонения $2h\left| T \right|$ от критического размера (4.4).

Гипотетическая ситуация ${\mathbf{g}} = {\mathbf{0}}$ требует отдельного обсуждения. Во-первых, к связям (2.20) и (2.21) числовых параметров можно добавить еще одну связь

обеспеченное представлениями (2.18), (2.19) и вытекающим из них равенством $G\left( x \right)$ = = $\overline {G\left( x \right)} $ – ${\mathbf{\bar {g}}}W\left( x \right)$, однако все эти связи не позволяют найти коэффициент ${\mathbf{g}}$. Во-вторых, поскольку ограничение ${\mathbf{g}} = {\mathbf{0}}$ устраняет из представления (2.18) волну w⁺, решение$~G$ задачи (2.14)–(2.16) исчезает на бесконечности с экспоненциальной скоростью и становится вещественным, т.е. $\operatorname{Im} {\mathbf{G}} = {\mathbf{0}}$. Кроме того, ${{W}_{1}}\left( \mathcal{O} \right) = 0$ согласно связи (2.20), а значит, при критическом размере $\ell _{0}^{*}~\left( {\ln h} \right)$ соотношение (3.19) справедливо при всяком множителе c (он определяется при построении младших асимптотических членов), но все-таки $s_{--}^{0} = {\mathbf{s}}$ и $s_{ + }^{0} = 0$ в любом случае согласно соотношениям (3.11) и (3.16); иными словами, эффект почти полного прохождения пропадает.

Покажем, что неравенство ${{{\mathbf{g}}}^{\kappa }}: = {\mathbf{g}} \ne 0$ выполнено по крайней мере для малых частот κ > 0, при которых асимптотические формулы для волн (1.7) можно найти при помощи одномерной модели балки, подставив решение обыкновенного дифференциального уравнения (2.3)

в разложение (3.16) с $h = 1$. При учете формул (2.2) и ${{e}^{{ \pm i{{\theta }^{0}}\kappa {{x}_{1}}}}}$ = $1 \pm i{{\theta }^{0}}\kappa {{x}_{1}}$ + $O\left( {{{\kappa }^{2}}~x_{1}^{2}} \right)$ получим соотношение

Множитель ${{a}^{0}}$ нужен для соблюдения в главном условия нормировки (1.10). Процедура ([28], гл. 9) вывода асимптотической формулы (4.6) применялась [29, 30] к двумерным и трехмерным изотропным и анизотропным упругим волноводам.

В качестве внешнего, справедливого на удалении от торца полуполосы, разложения возьмем выражение

Коэффициент ${{{\mathbf{g}}}^{\kappa }}$ oпределим при сращивании с внутренним, пригодным в конечной части волновода ${{{{\Pi }}}^{{ \sqsupset ~}}}$, разложением

Здесь ${{c}^{\kappa }}$ – неизвестный множитель, а ${{G}^{0}}$ – решение задачи (2.14)–(2.16) при $\kappa = 0$, для которого верны представления

В поле ${{G}^{0}}$ сосредоточенная в точке $\mathcal{O}$ сила компенсирована продольной силой на бесконечности. Приравнивая в разложениях (4.7) и (4.8), (4.9) коэффициенты при ${{e}_{{\left( 1 \right)}}}$ и ${{x}_{j}}{{e}_{{\left( j \right)}}}$, находим, что ${{c}^{\kappa }} = {{a}^{0}}{{\kappa }^{{--1/2}}}{{{\mathbf{g}}}^{\kappa }}$ и

Соотношение (4.8) показывает, что в самом деле коэффициент ${{{\mathbf{g}}}^{\kappa }}$ в представлении (2.18) решения ${{G}^{\kappa }}$ задачи (2.14)–(2.16) о действии сосредоточенной продольной силы на торце полуполосы ${{\Pi }^{{ \sqsupset ~}}}$ = $\left( {--\infty ,0} \right) \times \left( {--1,1} \right)$ отличен от нуля при малой частоте $\kappa > 0$.

5. Несколько замечаний. 1°. Подтверждение асимптотических конструкций. Построению асимптотических разложений решений краевых задач на сочленениях областей с различными предельными размерностями посвящено большое количество публикаций, в которых рассмотрены спектральные [31–36], [8–10, 12, 13] и статические [37–40] скалярные уравнения и система уравнений теории упругости [23, 24, 41–45]. Симметрия волновода и постановка искусственных условий (1.5) значительно упрощают процедуру обоснования асимптотических представлений решения и его характеристик, так как введенные условия аннулируют повороты точек на оси абсцисс и тем самым по сути компенсируют векторную природу упругих полей. В частности, для вектор-функций, подчиненных первому ограничению (1.5), выполнено упрощенное неравенство Корна [46] на усеченном волноводе ${{\Xi }^{h}}\left( R \right)$ = $\{ x \in {{\Xi }^{h}}{\kern 1pt} :\left| {{{x}_{1}}} \right| < R\} $

Для сохранения независимости множителя ${{c}_{R}}$ от толщины $~2h$ балки $~{{{{\Theta }}}^{h}}$ в общей ситуации левая часть неравенства (5.1) должна быть заменена [46] суммой

Появление в сумме (5.2) степеней малого параметра $h$ с положительными показателями значительно усложняет как асимптотические представления полей смещений и напряжений на перемычке, так и процедуру их обоснования (см., например, ([19], гл. 4) и [24]).

Как обычно в методе сращиваемых разложений, внешние (3.1)–(3.3) и внутренние (3.7) разложения соединяются в единое глобальное асимптотическое приближение посредством срезающих функций. Простейший способ – применить разбиение единицы [21], однако воспользуемся более точной конструкцией [18, 47, 48], привлекающей срезающие функции с “перехлестывающимися” носителями

Здесь $\chi $ – гладкая функция с малым носителем, равная единице в окрестности начала координат и подобранная так, что ${{\chi }_{--}}{{\chi }_{ + }} = 0$. Положим

В обеих формулах (5.3) и (5.4) члены разложений, подвергшиеся сращиванию в разд. 3, учтены дважды – и в первых и во вторых слагаемых из правых частей, однако такое дублирование устранено вычитаемыми, содержащими суммы названных членов. Именно, $M_{0}^{h}$ – выражение, полученное в конце преобразования (3.7), т.е. незатухающие при $\xi _{1}^{ \pm } \to \mp \infty $ члены вектор-функций (3.8) и (3.13), а $M_{ + }^{h}$ и $M_{--}^{h}$ – главные члены представлений (3.10) и (3.15) или составляющие вектор-функций (3.8) и (3.13), которые не исчезают в пределе при $\left| {{{\xi }^{ \pm }}} \right| \to \infty $ в полуплоскости $\mathbb{R}_{--}^{2}$. Невязки, оставленные построенным приближенном асимптотическом решением $W_{{\left( {{\text{as}}} \right)}}^{h}$ в уравнениях (1.3) и краевых условиях (1.4) оказывается малыми из-за достаточно быстрого затухания остатков в упомянутых представлениях. Последнее действие для вывода оценок

остатков в представлениях (3.4) коэффициентов рассеяния – применение техники весовых пространств с отделенной асимптотикой ([3], гл. 5), [15, 17]. Нормы в таких пространствах включают модули коэффициентов рассеяния, и поэтому малость функционала из правой части интегрального тождества (1.12) для разности $~{{W}^{h}}--W_{{\left( {{\text{as}}} \right)}}^{h}$ обеспечивает неравенства (5.5). Изложены [12, 17] особенности определения норм, связанные с наличием тонких элементов конструкций.

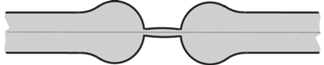
2°. Доступные обобщения. Если материал волновода ортотропный с осями ${{x}_{1}}$ и ${{x}_{{2~}}}$ упругой симметрии, то приведенные выкладки и рассуждения требуют лишь незначительных изменений – нужные формулы для одномерной модели тонкой балки можно найти, например, в ([19], гл. 4, § 2). Допустимы симметричные относительно оси абсцисс возмущения формы волновода (1.2) (ср. рис. 3) – уравнение продольных колебаний искривленной балки также известны. Некоторые осложнения возникают в том случае, если основания балки и границы рукавов искривлены в окрестности зон присоединения перемычки. Именно, в окрестности точек $P_{ \pm }^{h}$ приходится ввести локальные криволинейные координаты $\left( {{{n}_{ \pm }},{{s}_{ \pm }}} \right)$, в которых оператор Ламе из системы (1.3) принимает вид $\left( {2 \times 2} \right)$-матрицы $L\left( {{{n}_{ \pm }},{{s}_{ \pm }},{{\partial }_{{{{n}_{ \pm }}}}},{{\partial }_{{{{s}_{ \pm }}}}}} \right)$ дифференциальных операторов второго порядка с переменными коэффициентами, однако главные (после “заморозки” коэффициентов в точке $P_{ \pm }^{h}$ с координатами ${{n}_{ \pm }} = 0$ и ${{s}_{ \pm }} = 0$) части этих операторов принимают вид $L\left( {{{\partial }_{{{{n}_{ \pm }}}}},{{\partial }_{{{{s}_{ \pm }}}}}} \right)$, а значит, при построении пограничных слоев растяжение координат в h^–1 раз по-прежнему приводит к задаче (2.7)–(2.9) на сочленении $\Upsilon $ (рис. 2).

3°. Изгибные колебания перемычки. Для проведенного асимптотического анализа принципиальна зеркальная симметрия волновода (1.2) относительно оси абсцисс и постановка искусственных условий (1.5). Дело в том, что собственные частоты поперечных колебаний имеют вид $\kappa _{\sim }^{h} = h\kappa _{\sim }^{0}$, где $\kappa _{\sim }^{0}$ – собственные частоты одномерной балки Кирхгофа с защемленными концами

Итак, спектр тонкой балки характеризуется концентрацией собственных частот около точки $\kappa = 0$, а значит, на частоте (1.14) количество распространяющихся волн, которые следует учесть в асимптотической процедуре из разд. 3, неограниченно возрастает при $h \to + 0$. Это обстоятельство делает разработанную процедуру бесполезной, а переход к ультранизким частотам $\kappa = O\left( h \right)$ требует существенной модификации процедуры, так как строение непрерывного спектра задачи теории упругости в полуполосах $\Pi _{ \pm }^{h}$ без искусственных условий (1.5) существенно искажается и обеспечивает иные непривычные эффекты [29].

4°. Плоский акустический волновод. Проиллюстрируем проведенные в разд. 2–4 выкладки на примере скалярной задачи, в которой доступны явные формулы, и воспроизведем в упрощенном виде результаты [12]. Рассмотрим краевую задачу для оператора Лапласа

При этом u^h – давление в акустической среде, а частота κ берется из интервала (1.14) с точкой отсечки $\kappa _{\dag }^{1} = \pi {\text{/}}2$ непрерывного спектра ${{\wp }_{c}} = \left[ {0, + \infty } \right)$. Формулы (2.19) с поршневыми волнами (1.7) принимают вид

Функция Грина $G$ c особенностью в начале координат $\mathcal{O}$ удовлетворяет соотношениям (2.17) и (2.18), в которых

Ключевые связи (2.20), (2.21) и (4.5), разумеется, сохраняются, и, что важно, ${\mathbf{g}} \ne {\mathbf{0}}$. Процедура сращивания приводит к прежним соотношениям (3.11), (3.16) и (3.19), а выбор размера $\ell _{0}^{'}~\left( {\ln h} \right)$ в определениях (1.1), (4.1) обеспечивает эффект почти полного прохождения волны ${{w}^{ + }}$ из рукава $~{{\Pi }}_{--}^{h}$ через тонкий акустический канал ${{{{\Theta }}}^{h}}$ в рукав $~{{\Pi }}_{ + }^{h}$. Вместе с тем, явные аналитические формулы для величин b и ImG в представлениях (2.10) и (2.17) специальных решений задач Неймана для уравнения Пуассона в областях $\Upsilon $ и ${{{{\Pi }}}^{ \sqsupseteq }}$ недоступны, т.е. и в скалярном случае для определения критической длины перемычки ${{{{\Theta }}}^{h}}$ нужно применять численные методы.

5°. Пространственные задачи. Рассмотрим трехмерные цилиндры

и составленный из них упругий однородный изотропный волновод (1.2). При этом Ω и $\omega $ – области на плоскости ${{\mathbb{R}}^{2}}$, ограниченными кусочно-гладкими контурами и обладающие зеркальной симметрией относительно осей $~{{x}_{2}}$ и ${{x}_{3}}$. Одномерная модель Кирхгофа–Клебша тонкого стержня (5.6) представляет собой систему четырех обыкновенных дифференциальных уравнений – двух четвертого порядка, предоставляющих осредненные изгибы стержня, и двух второго порядка, описывающих продольную деформацию и закручивание. Для того чтобы применить предложенную в разд. 3 процедуру, необходимо дополнить пространственную задачу теории упругости искусственными условиями, которые нейтрализуют собственные частоты поперечных колебаний в ультра-низкочастотном диапазоне.

Первый набор таких условий на срединной плоскости ${{\Sigma }}_{3}^{h}$ = $\left\{ {x \in {{{{\Xi }}}^{h}}{\kern 1pt} :{{x}_{3}} = 0} \right\}$ тела ${{{{\Xi }}}^{h}}$

оставляет в шестимерном линеала жестких смещений (крестом обозначено векторное произведение) только продольное поступательное смещение ${{c}^{0}}{{e}_{{\left( 1 \right)}}}$ вдоль оси ${{x}_{1}}$. Таким образом, в одномерной модели стержня ${{{{\Theta }}}^{h}}$ остаются лишь одно уравнение второго порядка, а исходную задачу можно сузить на половину $~{{\Xi }}_{ \boxminus }^{h} = \{ ~x \in {{{{\Xi }}}^{h}}{\kern 1pt} :{{x}_{1}} = 0\} $ волновода ${{{{\Xi }}}^{h}} \subset {{\mathbb{R}}^{3}}$. Кроме того, продолжения компоненты $u_{1}^{h}$ по четности и компонент $u_{2}^{h}$, $u_{3}^{h}$ по нечетности через плоскость {x : x₃ = 0} сохраняют гладкость решения $~u_{ \boxminus }^{h}$, удовлетворяющего искусственным краевым условиям на поверхности $\Sigma _{3}^{h}$ ⊂ $\partial \Xi _{ \boxminus }^{h}$, а также систему уравнений (1.3) в теле ${{{{\Xi }}}^{h}}$ и краевые условия (1.4) на поверхности $\partial {{{{\Xi }}}^{h}}$. Иными словами, восстановленное поле удовлетворяет всей задаче в трехмерном волноводе (1.2).

Приведем еще две группы приемлемых искусственных условий

Здесь фигурируют декартовы компоненты ${{\sigma }_{{pq}}}\left( {{{u}^{h}};x} \right)$, $p,q = 1,2,3$, тензора напряжений и поверхности ${{\Sigma }}_{3}^{h}$ = $\left\{ {x \in {{{{\Xi }}}^{h}}{\kern 1pt} :{{x}_{j}} = 0,{{x}_{{5--j}}} > 0} \right\}$ при $j = 2~$ и $j = 3$. Теперь в линеале (5.7) остаются поступательные смещения $c_{1}^{0}{{e}_{{\left( 1 \right)}}}$ и повороты $\left( {0,--c_{1}^{1}{{x}_{3}},c_{1}^{1}{{x}_{2}}} \right)$ вокруг оси ${{x}_{{1,}}}$, а подходящие продолжения через плоскости $\left\{ {x{\kern 1pt} :{{x}_{2}} = 0} \right\}$ и $\left\{ {x{\kern 1pt} :{{x}_{3}} = 0} \right\}$ вектора смещений $u_{ \boxplus }^{h}$ в четвертушке ${{\Xi }}_{ \boxplus }^{h}$ на весь волновод $~{{{{\Xi }}}^{h}}$ сохраняют гладкость поля и соотношения (1.3), (1.4).

Указаны [49] и другие способы постановки искусственных условий на срединных плоскостях тела ${{{{\Xi }}}^{h}}$, устраняющие из одномерной модели тонкого стержня оба уравнения четвертого порядка. Аналогичные проведенным в разд. 3 и 4 выкладки и рассуждения позволят обнаружить аномальное прохождение упругих волн через тонкий соединительный стержень в пространственном упругом волноводе, однако результаты в этом направлении не публиковались.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 22-11-00046).