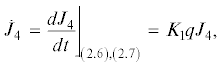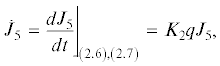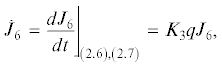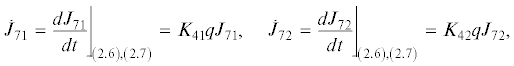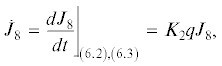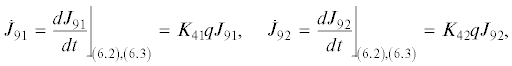Прикладная математика и механика, 2022, T. 86, № 6, стр. 839-856

1. Введение. В динамике твердого тела с неподвижной точкой важное значение имеют как классические случаи полной интегрируемости (Эйлера, Лагранжа и Ковалевской), так и случаи частичной интегрируемости, когда удается получить дополнительный частный интеграл. По-видимому, первый такой случай с линейным частным интегралом, зависящим от двух фазовых переменных, был найден в 1890 г. В. Гессом [1]. Этот “случай Гесса” был сразу же замечен и получил существенное продвижение в работах отечественных ученых [2, 3]. Дальнейшее развитие результатов исследований подробно представлено в монографиях по динамике твердого тела [4–6], где случаю Гесса посвящены целые разделы.

Исследования случая Гесса, его аналогов и обобщений успешно продолжаются и в настоящее время по нескольким направлениям. Изучались [7] периодические и квазипериодические движения тяжелого твердого тела при условиях Гесса, строились [8] частные точные аналитические решения, представимые тригонометрическими функциями времени. С использованием аналога интеграла Гесса для усредненной системы рассматривалось [9] движение твердого тела в условиях, когда точка подвеса совершает высокочастотные периодические колебания малой амплитуды.

Указаны [10] аналоги случаев Гесса для гироскопа в кардановом подвесе и уравнений Чаплыгина, описывающих падение твердого тела в жидкости. Установлена аналогия с задачей Суслова и дан критический обзор классических и современных исследований случая Гесса [11]. Применением алгоритма Ковачича найдены [12] две ситуации для случая Гесса, в которых существуют лиувиллевы решения.

Методом Рауса выявлено [13], что уравнения вращательного движения твердого тела в случае Гесса имеют довольно богатый набор стационарных решений. Доказана неинтегрируемость на множестве уровня интеграла Гесса [14, 15] и отмечена актуальность исследования задачи Гесса для уравнений тяжелого твердого тела и в настоящее время. Следовательно, не менее актуальны эти же вопросы касательно аналогов случая Гесса и для более сложных механических систем, таких, как гиростат.

Подход Гесса был впервые распространен на уравнения движения гиростата в [16], где был найден зависящий от двух фазовых переменных аналог интеграла Гесса для уравнений тяжелого гиростата. Был получен [17] аналог случая Гесса–Сретенского для уравнений движения гиростата в псевдоевклидовом пространстве.

Объектом исследования в данной статье являются уравнения движения гиростата с неподвижной точкой при действии момента сил (потенциальных, гироскопических, циркулярно-гироскопических). Основные цели состоят в получении аналогов случая Гесса для гиростата при действии такого рода момента сил. С использованием аналогов частного интеграла Гесса устанавливаются эргодические свойства компоненты вектора угловой скорости, не входящей в интеграл Гесса. Рассматриваются также вопросы построения стационарных решений и получения условий их устойчивости с помощью метода интегральных связок Четаева [18].

2. Дифференциальные уравнения движения, первые интегралы и постановка задачи. Рассмотрим векторную форму уравнений движения гиростата с неподвижной точкой под действием момента сил

Здесь $\omega = \operatorname{col} \left( {p,q,r} \right)$ – вектор угловой скорости, $\gamma = \operatorname{col} \left( {{{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}} \right)$ – единичный вектор оси симметрии силового поля, заданные проекциями на оси связанной системы координат, $I = {{I}^{T}} > 0$ – симметричная положительно определенная матрица тензора инерции относительно неподвижной точки, $\lambda = \operatorname{col} \left( {{{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}}} \right)$ – вектор гиростатического момента. Суммарный вектор $M = M\left( {t,\gamma ,\omega } \right)$ момента сил, действующих на гиростат, складывается из момента потенциальных сил $\gamma \times \frac{{\partial U}}{{\partial \gamma }}$, момента гироскопических сил $S\gamma \times \omega $ и момента циркулярно-гироскопических сил $L\left( {t,\gamma ,\omega } \right)\omega \times \gamma $. Здесь $U\left( \gamma \right)$ – некоторая непрерывно дифференцируемая функция (потенциал), $S = {{S}^{T}}$ – некоторая симметричная матрица, $L\left( {t,\gamma ,\omega } \right)$ – произвольная непрерывная функция. Отметим, что момент вида $S\gamma \times \omega $ возникает вследствие действия сил Лоренца при вращении заряженного твердого тела, помещенного в однородное магнитное поле с неизменным вектором напряженности [19]. Момент вида $L\omega \times \gamma $, $L = \operatorname{const} $ возникает при вращении ферромагнитного тела в постоянном и однородном магнитном поле [20, 21].

Система (2.1), (2.2) имеет три первых интеграла:

Первые интегралы энергии (2.3) и момента (2.4) определяют момент $M$ в правой части (2.1) единственным образом с точностью до циркулярно-гироскопической составляющей $L\left( {t,\gamma ,\omega } \right)\omega \times \gamma $ [22].

Далее всюду будем считать матрицу инерции диагональной $I = \operatorname{diag} \left( {A,B,C} \right)$. Запишем систему (2.1), (2.2) и первые интегралы в координатной форме

Здесь ${{\left( {S\gamma } \right)}_{i}}$ означает i-ю компоненту вектора $S\gamma $.

Задачи исследования в данной статье состоят в том, чтобы:

1) установить аналоги случая Гесса [1] для системы (2.6), (2.7) при различных предположениях на правые части уравнений движения;

2) показать, что частные интегралы Гесса существуют и при отсутствии момента потенциальных сил и порождают новый общий интеграл;

3) установить эргодические свойства компоненты $q\left( t \right)$ решения системы (2.6), (2.7);

4) выявить стационарные решения, которые задаются постоянными, обращающими правые части уравнений движения (2.6), (2.7) в нуль;

5) используя первые интегралы получить методом интегральных связок Четаева [18] достаточные условия устойчивости выявленных стационарных решений;

6) установить аналоги случая Гесса [1] для более общей по сравнению с (2.6), (2.7) системы при действии дополнительного момента циркулярных сил.

3. Аналоги интеграла Гесса. Справедливо следующее

Утверждение 1. Пусть для системы (2.6), (2.7) выполняются условия:

1. Функция $U\left( \gamma \right)$ имеет вид $U\left( \gamma \right)$ = $F\left( {~{{\mu }_{1}}{{\gamma }_{1}} + {{\mu }_{3}}{{\gamma }_{3}}} \right)$, где $F\left( \theta \right)$ – произвольная непрерывно дифференцируемая функция одного аргумента $\theta = {{\mu }_{1}}{{\gamma }_{1}} + {{\mu }_{3}}{{\gamma }_{3}}$.

2. Компонента ${{\lambda }_{2}}$ вектора гиростатического момента $\lambda = \operatorname{col} \left( {{{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}}} \right)$ удовлетворяет равенству ${{\lambda }_{2}} = 0$.

3. $\mu _{3}^{2}C\left( {A - B} \right) = \mu _{1}^{2}A\left( {B - C} \right)$.

4. Матрица $S$ имеет вид $S = \left( {\begin{array}{*{20}{c}} {{{s}_{{11}}}}&0&{{{s}_{{13}}}} \\ 0&0&0 \\ {{{s}_{{13}}}}&0&{{{s}_{{33}}}} \end{array}} \right)$, причем выполнены равенства ${{s}_{{11}}}{{\mu }_{3}} - {{s}_{{13}}}{{\mu }_{1}} = 0$, ${{s}_{{13}}}{{\mu }_{3}} - {{s}_{{33}}}{{\mu }_{1}} = 0$.

5. $L = L\left( {t,\gamma ,\omega } \right) \equiv 0$.

Тогда функция

удовлетворяет равенству где ${{K}_{1}} = \frac{{{{\mu }_{3}}\left( {A - B} \right)}}{{{{\mu }_{1}}A}} = \frac{{{{\mu }_{1}}\left( {B - C} \right)}}{{{{\mu }_{3}}C}}$, и система (2.6), (2.7) имеет помимо интегралов (2.8)–(2.10) дополнительный частный интеграл

Доказательство. Вычисляя производную от задаваемой формулой (3.1) функции ${{J}_{4}}$ в силу системы (2.6), (2.7) при условиях 1–5, получаем

Тем самым установлено также, что (3.3) является при условиях утверждения 1 частным интегралом системы (2.6), (2.7).

Замечание 1. Если при выполнении условий 1–4 утверждения 1 условие 5 не выполнено, но функция $L = L\left( {t,\gamma ,\omega } \right)$ представима в виде произведения $L = {{L}_{0}}\left( {~{{J}_{4}}} \right){{L}_{1}}\left( {t,\gamma ,\omega } \right)$, где ${{L}_{0}}\left( 0 \right) = 0$, а функция ${{L}_{1}}\left( {t,\gamma ,\omega } \right)$ произвольна, то (3.3) останется частным интегралом системы, хотя дифференциальное соотношение (3.2) уже не будет выполнено.

Необходимо также отметить, что (3.3) это фактически не аналог, а c точностью до константы и есть интеграл Гесса, найденный в [1] для классического случая тяжелого твердого тела, которому соответствуют нулевые значения параметров $\lambda = 0$, $L \equiv 0$, $S = 0$ и тождественная функция $F\left( \theta \right) = \theta $.

Далее будем рассматривать те случаи, когда линейный частный интеграл зависит от четырех переменных.

Справедливо следующее

Утверждение 2. Пусть для системы (2.6), (2.7) выполняются условия 1–3 утверждения 1 и, кроме того, условия:

4. Матрица $S$ имеет вид $S = \left( {\begin{array}{*{20}{c}} {{{s}_{{11}}}}&0&{{{s}_{{13}}}} \\ 0&0&0 \\ {{{s}_{{13}}}}&0&{{{s}_{{33}}}} \end{array}} \right)$, причем выполнено равенство ${{s}_{{11}}}\mu _{3}^{2}$ – $2{{s}_{{13}}}{{\mu }_{1}}{{\mu }_{3}}$ + + ${{s}_{{33}}}\mu _{1}^{2}$ = 0.

5. $L = L\left( {t,\gamma ,\omega } \right) \equiv {{L}_{2}} = \frac{{A\left( {{{s}_{{11}}}{{\mu }_{3}} - {{s}_{{13}}}{{\mu }_{1}}} \right)}}{{{{\mu }_{3}}\left( {A - B} \right)}}$.

Тогда функция

удовлетворяет равенству где ${{K}_{2}}$ = $\frac{{{{\mu }_{3}}\left( {A - B} \right)}}{{{{\mu }_{1}}A}}$ = $\frac{{{{\mu }_{1}}\left( {B - C} \right)}}{{{{\mu }_{3}}C}}$ = $\frac{{{{s}_{{11}}}{{\mu }_{3}} - {{s}_{{13}}}{{\mu }_{1}}}}{{{{\mu }_{1}}{{L}_{2}}}}$ = $\frac{{{{s}_{{13}}}{{\mu }_{3}} - {{s}_{{33}}}{{\mu }_{1}}}}{{{{\mu }_{3}}{{L}_{2}}}}$, и система (2.6), (2.7) имеет помимо интегралов (2.8)–(2.10) дополнительный частный интеграл

Доказательство. Вычисляя производную от задаваемой формулой (3.4) функции ${{J}_{5}}$ в силу системы (2.6), (2.7) при условиях 1–5, получаем

Тем самым установлено также, что (3.6) является при условиях утверждения 2 частным интегралом системы (2.6), (2.7).

Замечание 2. Если при выполнении условий 1–4 утверждения 2 условие 5 не выполнено, но функция $L = L\left( {t,\gamma ,\omega } \right)$ представима в виде суммы $L = {{L}_{2}}$ + ${{L}_{0}}\left( {{{J}_{5}}} \right){{L}_{1}}\left( {t,\gamma ,\omega } \right)$, где ${{L}_{0}}\left( 0 \right) = 0$, а функция ${{L}_{1}}\left( {t,\gamma ,\omega } \right)$ произвольна, то (3.6) останется частным интегралом системы, хотя дифференциальное соотношение (3.5) уже не будет выполнено.

Теперь будем рассматривать те случаи, когда задающая момент гироскопических сил матрица $S$ является диагональной.

Утверждение 3. Пусть для системы (2.6), (2.7) выполняются условия 1–3 утверждения 1 и, кроме того, условия:

4. Матрица $S$ имеет вид $S = \operatorname{diag} \left( {{{s}_{{11}}},{{s}_{{22}}},{{s}_{{33}}}} \right)$, причем выполнено равенство $\mu _{3}^{2}({{s}_{{11}}} - {{s}_{{22}}})$ = = $\mu _{1}^{2}\left( {{{s}_{{22}}} - {{s}_{{33}}}} \right)$.

5. $L = L\left( {t,\gamma ,\omega } \right) \equiv {{L}_{3}} = \frac{{B{{s}_{{22}}} - C{{s}_{{33}}}}}{{B - C}}$.

Тогда функция

удовлетворяет равенству где ${{K}_{3}} = \frac{{{{\mu }_{3}}\left( {A - B} \right)}}{{{{\mu }_{1}}A}}$ = $\frac{{{{\mu }_{1}}\left( {B - C} \right)}}{{{{\mu }_{3}}C}}$ = $\frac{{~{{\mu }_{3}}\left( {{{s}_{{11}}} - {{s}_{{22}}}} \right)}}{{{{\mu }_{1}}({{L}_{0}} - {{s}_{{22}}})}}$ = $\frac{{~{{\mu }_{1}}\left( {{{s}_{{22}}} - {{s}_{{33}}}} \right)}}{{{{\mu }_{3}}({{L}_{0}} - {{s}_{{22}}})}}$, и система (2.6), (2.7) имеет помимо интегралов (2.8)–(2.10) дополнительный частный интеграл

Доказательство. Вычисляя производную от задаваемой формулой (3.7) функции ${{J}_{6}}$ в силу системы (2.6), (2.7) при условиях 1–5, получаем

Тем самым установлено также, что (3.9) является при условиях утверждения 3 частным интегралом системы (2.6), (2.7).

Замечание 3. Если при выполнении условий 1–4 утверждения 3 условие 5 не выполнено, но функция $L = L\left( {t,\gamma ,\omega } \right)$ представима в виде суммы $L = {{L}_{3}}$ + ${{L}_{0}}\left( {{{J}_{6}}} \right){{L}_{1}}\left( {t,\gamma ,\omega } \right)$, где ${{L}_{0}}(0) = 0$, а функция ${{L}_{1}}\left( {t,\gamma ,\omega } \right)$ произвольна, то (3.9) останется частным интегралом системы, хотя дифференциальное соотношение (3.8) уже не будет выполнено.

Необходимо отметить, что близкий аналог случая Гесса для системы (2.6), (2.7) с $\lambda = 0$, $L \equiv 0$, диагональной матрицей $S$ и линейным потенциалом $U\left( \gamma \right)$ был указан ранее в работе [19].

Теперь рассмотрим тот случай, когда на гиростат не действует момент потенциальных сил. Введем обозначения:

Утверждение 4. Пусть для системы (2.6), (2.7) выполняются условия:

1. Момент потенциальных сил отсутствует, т.е. $U\left( \gamma \right) \equiv 0$.

2. Компонента ${{\lambda }_{2}}$ вектора гиростатического момента $\lambda = \operatorname{col} \left( {{{\lambda }_{1}},{{\lambda }_{2}},{{\lambda }_{3}}} \right)$ удовлетворяет равенству ${{\lambda }_{2}} = 0$.

3. Моменты инерции удовлетворяют неравенствам $A > B > C$.

4. Матрица $S$ имеет вид $S = \operatorname{diag} \left( {{{s}_{{11}}},{{s}_{{22}}},{{s}_{{33}}}} \right)$, причем выполнено равенство $A\left( {B - C} \right)\left( {{{s}_{{11}}} - {{s}_{{22}}}} \right)$ = $C\left( {A - B} \right)\left( {{{s}_{{22}}} - {{s}_{{33}}}} \right)$.

5. $L = L\left( {t,\gamma ,\omega } \right) \equiv {{L}_{4}} = \operatorname{const} $.

Тогда задаваемые формулами (3.10) две функции ${{J}_{{71}}}$ и ${{J}_{{72}}}$ удовлетворяют равенствам

где ${{K}_{{41}}} = \frac{{{{b}_{2}}\left( {A - B} \right)}}{{{{b}_{1}}A}}$, ${{K}_{{42}}} = - \frac{{{{b}_{2}}\left( {A - B} \right)}}{{{{b}_{1}}A}}$, и система (2.6), (2.7) имеет помимо интегралов (2.8)–(2.10) два дополнительных частных интеграла и общий интеграл независимый от интегралов ${{J}_{1}},~{{J}_{2}},~{{J}_{3}}$, следовательно, система (2.6), (2.7) интегрируема.

Доказательство. Вычисляя производную от задаваемой формулой (3.10) функции ${{J}_{{71}}}$ в силу системы (2.6), (2.7) при условиях 1–5, получаем

Аналогичным образом получим ${{\dot {J}}_{{72}}} = {{K}_{{42}}}q{{J}_{{72}}}$. Дифференциальные соотношения (3.11) доказаны. Тем самым установлено также, что (3.12) являются при условиях утверждения 4 частными интегралами системы (2.6), (2.7).

Рассмотрим теперь функции (3.10) и (3.13) вдоль произвольного решения системы (2.6), (2.7), обозначая их зависимость от времени ${{J}_{{71}}}\left[ t \right]$, ${{J}_{{72}}}\left[ t \right]$, ${{J}_{7}}\left[ t \right]$. Тогда интегрируя (3.11), приходим к равенствам ${{J}_{{71}}}\left[ t \right]$ = ${{J}_{{71}}}\left[ 0 \right]\exp \left( {\mathop \smallint \nolimits_0^t {{K}_{{41}}}q\left( \tau \right)d\tau } \right)$, ${{J}_{{72}}}\left[ t \right]$ = = ${{J}_{{72}}}\left[ 0 \right]\exp \left( {\mathop \smallint \nolimits_0^t {{K}_{{42}}}q\left( \tau \right)d\tau } \right)$, Отсюда с учетом равенства ${{K}_{{41}}} + {{K}_{{42}}} = 0$ находим

Тем самым установлено, что ${{J}_{7}}\left[ t \right]$ сохраняется вдоль каждого решения, т.е. система (2.6), (2.7) имеет общий интеграл (3.13). Независимость интегралов вытекает из того, что ранг матрицы Якоби равен 4. Утверждение доказано.

Замечание 4. Если при выполнении условий 1–4 утверждения 4 условие 5 не выполнено, но функция $L = L\left( {t,\gamma ,\omega } \right)$ представима в виде суммы $L = {{L}_{4}}$ + ${{L}_{0}}\left( {{{J}_{7}}} \right){{L}_{1}}\left( {t,\gamma ,\omega } \right)$, где ${{L}_{0}}\left( 0 \right) = 0$, а функция ${{L}_{1}}\left( {t,\gamma ,\omega } \right)$ произвольна, то (3.12) останутся частными интегралами системы, хотя дифференциальные соотношения (3.11) уже не будут выполнены.

4. О поведении $q\left( t \right)$ вне множества Гесса. Множеством Гесса будем называть ${{H}_{i}} = \left\{ {\left( {\omega ,\gamma } \right):~{{J}_{i}}\left( {\omega ,\gamma } \right) = 0} \right\}$, где ${{J}_{i}}\left( {\omega ,\gamma } \right)$ есть какой-либо из приведенных выше пяти частных интегралов ${{J}_{4}}$, ${{J}_{5}}$, ${{J}_{6}}$, ${{J}_{{71}}}$, ${{J}_{{72}}}$ для системы уравнений движения гиростата (2.6), (2.7), являющихся аналогами интеграла Гесса.

Произвольное решение $~\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ будем называть отделенным от множества Гесса, если $\inf \{ \rho \left( {\left( {\omega \left( t \right),\gamma \left( t \right)} \right),H} \right)$, $ - \infty < t < + \infty \} $ = ${{\rho }_{0}} > 0$. Здесь $\rho \left( {\left( {\omega ,\gamma } \right),{{H}_{i}}} \right)$ – расстояние от точки $\left( {\omega ,\gamma } \right)$ до множества ${{H}_{i}}$.

Утверждение 5. Пусть для системы уравнений движения гиростата (2.6), (2.7) выполняются условия какого-либо из утверждений 1–4, и, значит, система имеет частный интеграл аналог интеграла Гесса.

Тогда для всякого решения $\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$, отделенного от множества Гесса, его компонента $q\left( t \right)$ совершает колебания с нулевым средним значением $\mathop {\lim }\limits_{t \to \pm \infty } \frac{1}{t}\mathop \smallint \nolimits_0^t q\left( \tau \right)d\tau = 0$.

Доказательство. Пусть выполнены условия какого-либо из утверждений 1–4, для определенности утверждения 1 (для других случаев рассуждения совершенно идентичны). Рассмотрим произвольное решение $\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$, не лежащее на множестве Гесса ${{H}_{4}}$. Из существования интегралов ${{J}_{1}}$ и ${{J}_{3}}$ вытекает ограниченность решения $\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ при всех $ - \infty < t < + \infty $. Значит на этом решении будет ограничена сверху и снизу при всех $ - \infty < t < + \infty $ и задаваемая формулой (3.1) функция ${{J}_{4}}$. Интегрируя дифференциальное равенство (3.2), получаем ${{J}_{4}}\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ = ${{J}_{4}}\left( {\omega \left( 0 \right),\gamma \left( 0 \right)} \right)\exp \left( {\mathop \smallint \nolimits_0^t {{K}_{1}}q\left( \tau \right)d\tau } \right)$, поэтому из ограниченности функции ${{J}_{4}}$ вдоль решения $\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ следует, что $\mathop \smallint \nolimits_0^t {{K}_{1}}q\left( \tau \right)d\tau $ < $ + \infty $ при всех $ - \infty < t < + \infty $. Если предположить теперь, что существует последовательность $\left| {{{t}_{k}}} \right| \to + \infty $ при $k \to + \infty $ такая, что $\mathop \smallint \nolimits_0^{{{t}_{k}}} {{K}_{1}}q\left( \tau \right)d\tau \to - \infty $, то это повлечет ${{J}_{4}}\left( {\omega \left( {{{t}_{k}}} \right),\gamma \left( {{{t}_{k}}} \right)} \right) \to 0$ при $k \to + \infty $, что противоречит тому условию, что решение $\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ отделено от множества Гесса ${{H}_{4}}$. Таким образом, при всех $ - \infty < t < + \infty $ ограничен интеграл $ - \infty $ < $\mathop \smallint \nolimits_0^t {{K}_{1}}q\left( \tau \right)d\tau $ < ∞, а так как ${{K}_{1}}$ отличная от нуля постоянная, то значит ограничен и интеграл $ - \infty < \mathop \smallint \nolimits_0^t q\left( \tau \right)d\tau < + \infty $. Следовательно, среднее значение равно нулю $\mathop {\lim }\limits_{t \to \pm \infty } \frac{1}{t}\mathop \smallint \nolimits_0^t q\left( \tau \right)d\tau = 0$. Утверждение доказано.

Следствие 1. Для любого стационарного решения $~\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ = $\left( {\bar {p},\bar {q},\bar {r},\overline {{{\gamma }_{1}}} ,\overline {{{\gamma }_{2}}} ,\overline {{{\gamma }_{3}}} } \right)$ = = const, не лежащего в множестве Гесса, всегда будет $\bar {q} = 0$.

Это следствие может быть очень полезным при отыскании всех стационарных решений системы (2.6), (2.7). Необходимо отметить также, что на самом множестве Гесса возможны стационарные решения с $\bar {q} \ne 0$ (см., например, [13], стационарное решение (V)).

5. Стационарные решения и их устойчивость. В этом разделе приведем три различных типа стационарных решений $\left( {\bar {p},\bar {q},\bar {r},{{{\bar {\gamma }}}_{1}},{{{\bar {\gamma }}}_{2}},{{{\bar {\gamma }}}_{3}}} \right)$ = const системы (2.6), (2.7) и проведем анализ их устойчивости вторым методом Ляпунова, используя в качестве функций Ляпунова связки интегралов, конструируемые по методу Четаева [18].

Утверждение 6. При $U\left( \gamma \right) = F\left( {~{{\mu }_{1}}{{\gamma }_{1}} + {{\mu }_{3}}{{\gamma }_{3}}} \right)$, где $F\left( \theta \right)$ – некоторая дважды непрерывно дифференцируемая функция, система (2.6), (2.7) имеет два стационарных решения (состояния покоя)

где $\sigma = + 1$ или $\sigma = - 1$. Те стационарные решения (5.1), для которых выполняется условие $\sigma \frac{{dF\left( {\sigma \sqrt {\mu _{1}^{2} + \mu _{3}^{2}} } \right)}}{{d\theta }} < 0$, являются устойчивыми по Ляпунову.

Доказательство. Подстановкой в систему (2.6), (2.7) легко проверить, что (5.1) является стационарным решением при условиях утверждения 6. Введем обозначения для отклонений от невозмущенного стационарного движения

В этих переменных интегралы уравнений возмущенного движения выпишутся следующим образом:

Здесь и далее через ${{\bar {J}}_{i}}$ обозначено значение интеграла ${{J}_{i}}$ на стационарном решении. Функцию Ляпунова строим в виде линейно-квадратичной связки (комбинации) интегралов уравнений возмущенного движения

Коэффициенты ${{\alpha }_{3}}$ и ${{\beta }_{3}}$ с целью уничтожения линейных слагаемых в связке и подавления возможно отрицательного квадратичного слагаемого выберем следующим образом:

Тогда для квадратичной части связки будет справедлива оценка снизу

При выполнении условия $\sigma \frac{{dF\left( {\sigma \sqrt {\mu _{1}^{2} + \mu _{3}^{2}} } \right)}}{{d\theta }} < 0$ квадратичная часть связки ${{V}_{2}}$, а значит и вся связка $V$ будет положительно определенной функцией. Справедливость утверждения 6 следует теперь из теоремы Ляпунова об устойчивости.

Замечание 5. Так как при доказательстве утверждения 6 не использовался интеграл ${{J}_{2}}$, то это утверждение справедливо и в том случае, когда в системе (2.6), (2.7) матрица $S$ является произвольной симметричной переменной $S = S\left( {t,\omega ,\gamma } \right)$.

Необходимо отметить, что устойчивость состояний покоя (5.1) в классическом случае Гесса для тяжелого твердого тела, которому соответствует $F\left( \theta \right) = \theta $, изучалась в работе [23], где была установлена лишь условная устойчивость относительно множества Гесса (поскольку использовался частный интеграл Гесса) состояния покоя (5.1), отвечающего значению $\sigma = - 1$. Для другого состояния покоя (5.1), отвечающего значению $\sigma = 1$, в [23] была доказана неустойчивость по линейному приближению. Как следует из утверждения 6, если $F\left( \theta \right) = \theta $, то условие устойчивости выполняется только при $\sigma = - 1$. Если же функция $F\left( \theta \right)$ не сводится к тождественной, то устойчивыми могут быть оба состояния покоя (5.1). Например, это будет иметь место в случае $F\left( \theta \right) = a{{\theta }^{2}}$, $a < 0$.

Рассмотрим теперь устойчивость одноосного перманентного вращения. Введем для краткости обозначения ${{f}_{1}} = \frac{{dF\left( {~{{\mu }_{1}}\sigma } \right)}}{{d\theta }}$, ${{f}_{2}} = \frac{{{{d}^{2}}F\left( {~{{\mu }_{1}}\sigma } \right)}}{{d{{\theta }^{2}}}}$.

Утверждение 7. Если матрица $S$ диагональная $S = \operatorname{diag} \left( {{{s}_{{11}}},{{s}_{{22}}},{{s}_{{33}}}} \right)$, а потенциал имеет вид $U\left( \gamma \right) = F\left( {~{{\mu }_{1}}{{\gamma }_{1}} + {{\mu }_{3}}{{\gamma }_{3}}} \right)$, где $F\left( \theta \right)$ – некоторая дважды непрерывно дифференцируемая функция, то система (2.6), (2.7) имеет два стационарных решения (перманентных вращения)

где $\sigma = + 1$ или $\sigma = - 1$. Те из решений (5.2), для которых выполняются условия являются устойчивыми по Ляпунову.

Доказательство. Подстановкой в систему (2.6), (2.7) легко проверить, что (5.2) является стационарным решением при условиях утверждения 7. Интегралы уравнений возмущенного движения выпишутся следующим образом:

Функцию Ляпунова по методу Четаева [18] строим в виде связки интегралов уравнений возмущенного движения

Коэффициенты ${{\alpha }_{i}}$, $i = 2,3$ с целью уничтожения линейных слагаемых в связке выберем следующим образом

Тогда квадратичная часть ${{V}_{2}}\left( x \right)$ интеграла $V\left( x \right)$ уравнений возмущенного движения запишется так

Так как коэффициенты ${{\beta }_{2}}$ и ${{\beta }_{3}}$ можно взять сколь угодно большими положительными, то для положительной определенности ${{V}_{2}}\left( x \right)$ необходимо и достаточно [24] установить положительную определенность ${{V}_{2}}\left( x \right)$ на множестве $\Theta = \{ {{x}_{4}} = 0$, $A\sigma {{x}_{1}} + {{\lambda }_{3}}{{x}_{6}} = 0\} $. На этом множестве ${{V}_{2}}\left( x \right)$ распадается на сумму двух квадратичных форм от двух переменных. Применяя к каждой из них критерий Сильвестра, придем к неравенствам (5.3), (5.4). Утверждение доказано.

Отметим, что неравенства (5.3), (5.4) всегда можно выполнить за счет выбора элементов матрицы $S = \operatorname{diag} \left( {{{s}_{{11}}},{{s}_{{22}}},{{s}_{{33}}}} \right)$, т.е. всегда возможна гироскопическая стабилизация перманентного вращения (5.2).

Рассмотрим теперь устойчивость перманентных вращений, образующих целое семейство.

Утверждение 8. Если матрица $S$ диагональная $S = \operatorname{diag} \left( {{{s}_{{11}}},{{s}_{{22}}},{{s}_{{33}}}} \right)$, а потенциал имеет вид $U\left( \gamma \right)$ = ${{\mu }_{1}}{{\gamma }_{1}} + {{\mu }_{3}}{{\gamma }_{3}}$, то система (2.6), (2.7) имеет при всех $0 < \varphi < 2\pi $, $\varphi \ne \frac{\pi }{2}k$, k – целое число, при которых выполняется неравенство

два стационарных решения (перманентных вращения) где ${{{{\Omega }}}_{i}}$ – один из корней квадратного уравнения

Те из решений (5.6), для которых выполняются условия

являются устойчивыми по Ляпунову.

Входящие в неравенство (5.9) числа $b,c,{{\alpha }_{3}}$ определяются в процессе доказательства.

Доказательство. Неравенство (5.5) обеспечивает вещественность корней уравнения (5.7). Подстановкой в систему (2.6), (2.7) легко проверить, что (5.6) является стационарным решением при условиях утверждения 8. Интегралы уравнений возмущенного движения выпишутся следующим образом:

Функцию Ляпунова по методу Четаева [18] строим в виде связки интегралов уравнений возмущенного движения

Коэффициенты ${{\alpha }_{i}}$, $i = 2,3$ с целью уничтожения линейных слагаемых в связке выберем следующим образом

Тогда интеграл $V\left( x \right)$ уравнений возмущенного движения запишется так

Так как коэффициенты ${{\beta }_{2}}$ и ${{\beta }_{3}}$ можно взять сколь угодно большими положительными, то для положительной определенности $V\left( x \right)$ необходимо и достаточно [24] установить положительную определенность $V\left( x \right)$ на множестве $\Theta = \{ 2{{\bar {\gamma }}_{1}}{{x}_{4}}$ + $2{{\bar {\gamma }}_{3}}{{x}_{6}}$ = 0, $A{{\bar {\gamma }}_{1}}{{x}_{1}}$ + $C{{\bar {\gamma }}_{3}}{{x}_{3}}$ + $\left( {A\bar {p} + {{\lambda }_{1}} + {{s}_{{11}}}{{{\bar {\gamma }}}_{1}}} \right){{x}_{4}}$ + $\left( {C\bar {r} + {{\lambda }_{3}} + {{s}_{{33}}}{{{\bar {\gamma }}}_{3}}} \right){{x}_{6}}$ = 0}.

На этом множестве справедливы равенства

где $a = - \frac{{{{{\bar {\gamma }}}_{1}}}}{{{{{\bar {\gamma }}}_{3}}}}$, $b = - \frac{{A{{{\bar {\gamma }}}_{1}}}}{{C{{{\bar {\gamma }}}_{3}}}}$, $c = - \frac{1}{{C{{{\bar {\gamma }}}_{3}}}}\left[ {A\bar {p} + {{\lambda }_{1}} + {{s}_{{11}}}{{{\bar {\gamma }}}_{1}} - \frac{{{{{\bar {\gamma }}}_{1}}}}{{{{{\bar {\gamma }}}_{3}}}}\left( {C\bar {r} + {{\lambda }_{3}} + {{s}_{{33}}}{{{\bar {\gamma }}}_{3}}} \right)} \right]$ и $V\left( x \right)$ представляет собой сумму двух квадратичных форм от двух переменных

Применяя к каждой из них критерий Сильвестра, придем к неравенствам (5.8), (5.9). Утверждение доказано.

6. Аналоги случая Гесса при действии момента циркулярных сил. Будем теперь рассматривать систему (2.1) при действии момента

где $W$ – некоторая симметричная матрица, а все другие слагаемые момента $M$ уже были описаны выше в разделе 2. Отметим, что момент вида $W\omega \times \gamma $ возникает, например, при вращении сверхпроводящего или ферромагнитного тела в магнитном поле под действием эффекта Барнетта–Лондона [25]. В этом разделе будем строить аналоги частного интеграла Гесса для гиростата при действии момента (6.1), считая матрицы $S = \operatorname{diag} \left( {{{s}_{{11}}},{{s}_{{22}}},{{s}_{{33}}}} \right)$ и $W = \operatorname{diag} \left( {{{w}_{{11}}},{{w}_{{22}}},{{w}_{{33}}}} \right)$ диагональными. Уравнения движения (2.1) тогда запишутся следующим образом

Отметим, что система (6.2), (6.3) имеет интеграл момента (2.4) и геометрический интеграл (2.5), а полная энергия (2.3) уже не будет первым интегралом для этой системы.

Справедливо следующее

Утверждение 9. Пусть для системы (6.2), (6.3) выполняются условия 1–3 утверждения 1 и, кроме того, условия:

4. Матрицы $S$ и $W$ диагональные, причем выполнено равенство

5. $L = L\left( {t,\gamma ,\omega } \right) \equiv {{L}_{8}}$ = ${{s}_{{22}}} - {{w}_{{33}}} + \frac{A}{{A - B}}\left( {{{s}_{{11}}} - {{s}_{{22}}} + {{w}_{{11}}} - {{w}_{{22}}}} \right)$.

Тогда функция

удовлетворяет равенству где ${{K}_{2}} = \frac{{{{\mu }_{3}}\left( {A - B} \right)}}{{{{\mu }_{1}}A}} = \frac{{{{\mu }_{1}}\left( {B - C} \right)}}{{{{\mu }_{3}}C}}$, и система (3.2), (3.3) имеет помимо интегралов (2.4) и (2.5) дополнительный частный интеграл

Доказательство. Вычисляя производную от задаваемой формулой (6.4) функции ${{J}_{8}}$ в силу системы (6.2), (6.3) при условиях 1–5, получаем

Тем самым установлено также, что (6.6) является при условиях утверждения 8 частным интегралом системы (6.2), (6.3).

Замечание 6. Если при выполнении условий 1–4 утверждения 9 условие 5 не выполнено, но функция $L = L\left( {t,\gamma ,\omega } \right)$ представима в виде суммы $L = {{L}_{8}}$ + ${{L}_{0}}\left( {{{J}_{8}}} \right){{L}_{1}}\left( {t,\gamma ,\omega } \right)$, где ${{L}_{0}}\left( 0 \right) = 0$, а функция ${{L}_{1}}\left( {t,\gamma ,\omega } \right)$ произвольна, то (6.6) останется частным интегралом системы, хотя дифференциальное соотношение (6.5) уже не будет выполнено.

Теперь рассмотрим тот случай, когда на гиростат не действует момент потенциальных сил. Введем обозначения:

Утверждение 10. Пусть для системы (6.2), (6.3) выполняются условия 1–3 утверждения 4 и, кроме того, условия:

4. Матрицы $S$ и $W$ диагональные, причем выполнено равенство

5. $L = L\left( {t,\gamma ,\omega } \right) \equiv {{L}_{9}}$ = const.

Тогда задаваемые формулами (6.7) две функции ${{J}_{{91}}}$ и ${{J}_{{92}}}$ удовлетворяют равенствам

где ${{K}_{{41}}} = \frac{{{{b}_{2}}\left( {A - B} \right)}}{{{{b}_{1}}A}}$, ${{K}_{{42}}} = - \frac{{{{b}_{2}}\left( {A - B} \right)}}{{{{b}_{1}}A}}$, и система (6.2), (6.3) имеет помимо интегралов (2.9), (2.10) два дополнительных частных интеграла и общий интеграл независимый от интегралов $~{{J}_{2}}$, ${{J}_{3}}$.

Доказательство аналогично доказательству утверждения 4.

Так как система (6.2), (6.3) не имеет интеграла энергии, то, в отличие от утверждения 4, теперь для интегрируемости необходимо отыскать еще один независимый интеграл. По той же причине здесь нет аналога утверждения 5 о нулевом среднем для $q\left( t \right)$ вне множества Гесса. Однако можно доказать аналог следствия из утверждения 5.

Утверждение 11. Если выполнены условия утверждения 9 или 10, то для любого стационарного решения $~\left( {\omega \left( t \right),\gamma \left( t \right)} \right)$ = $(\bar {p},\bar {q},\bar {r},\overline {{{\gamma }_{1}}} ,\overline {{{\gamma }_{2}}} ,\overline {{{\gamma }_{3}}} )$ = const, не лежащего в множестве Гесса, всегда будет $\bar {q} = 0$.

Доказательство. Пусть выполнены условия утверждения 9. Рассмотрим произвольное стационарное решение $(\bar {p},\bar {q},\bar {r},\overline {{{\gamma }_{1}}} ,\overline {{{\gamma }_{2}}} ,\overline {{{\gamma }_{3}}} )$ = const, не лежащее в множестве Гесса ${{J}_{8}} = 0$. На нем функция ${{J}_{8}} = {{J}_{8}}\left( {\bar {p},\bar {r},\overline {{{\gamma }_{1}}} ,\overline {{{\gamma }_{3}}} } \right)$ принимает постоянное значение. С другой стороны, ${{J}_{8}}\left[ t \right]$ = ${{J}_{8}}\left[ 0 \right]\exp \mathop \smallint \nolimits_0^t {{K}_{2}}\bar {q}d\tau $ = ${{J}_{8}}\left[ 0 \right]\exp \left( {{{K}_{2}}\bar {q}t} \right)$ может быть постоянной только при $\bar {q} = 0$. В случае выполнения условий утверждения 10 рассуждения аналогичны.

Заключение. В заключение отметим кратко некоторые возможные направления развития полученных в статье результатов. В статье получено 6 аналогов случая Гесса для уравнений движения гиростата при действии момента гироскопических и циркулярных сил. Такого рода аналоги, в которых система имеет линейный частный интеграл, могут существовать и при других условиях. В этой связи представляет интерес выяснить, каким условиям должен удовлетворять момент $M\left( {t,\gamma ,\omega } \right)$ в системе (2.1), чтобы она имела линейный частный интеграл типа Гесса.

Для классического случая Гесса для твердого тела еще П.А. Некрасовым было получено [3] линейное уравнение второго порядка с переменными коэффициентами. В самое последнее время А.С. Кулешовым такое уравнение было преобразовано [12] к виду, допускающему применение алгоритма Ковачича. Это позволило установить, какие типы лиувиллевых решений могут реализоваться в случае Гесса для уравнений движения твердого тела с неподвижной точкой. Возможно, что такой подход будет результативным и для аналогов случая Гесса, полученных в данной статье.

Выявлены три группы стационарных движений и проведен анализ их устойчивости методом Четаева. Целесообразно расширить перечень стационарных движений, используя метод Рауса, как это было сделано в [13] для уравнений твердого тела в случае Гесса, а также провести более полный анализ устойчивости, аналогично тому, как это сделано в работах [26–28] для гиростата с одними потенциальными силами. При этом использование аналога линейного частного интеграла Гесса, как показано в [22], может расширять условия устойчивости относительно множества Гесса.