Прикладная математика и механика, 2022, T. 86, № 6, стр. 958-976

1. Введение. Интенсивная деятельность человека по освоению природных ресурсов Мирового океана включает разведку и добычу полезных ископаемых, транспортировку товаров, использование энергетических и биологических ресурсов, а также многие другие аспекты. Одним из последствий включения океана в сферу экономических интересов является возникновение и распространение загрязнений различного характера. Аварии с утечками нефти происходят при добыче, сборе и хранении нефти, из резервуаров, во время операций по сливу, отпуску нефтепродуктов потребителям, при транспортировке по трубопроводам и т.д. Количество утечек достигает больших значений и, по разным данным, колеблется от 5 до 17% от объема производства. При этом теряется не только ценное сырье, но и наносится значительный ущерб окружающей среде. Попадая в природные экосистемы, нефтяные углеводороды надолго вызывают нарушение биологического баланса.

В последние годы во всем мире прилагаются значительные усилия по совершенствованию системы предотвращения и ликвидации последствий аварийных разливов нефти и нефтепродуктов, но проблема по-прежнему остается актуальной. При планировании и проведении работ по борьбе с аварийными разливами углеводородов возникает необходимость прогнозирования распространения нефти в море. Такие прогнозы позволяют, в частности, предупреждать о возможности нефтяного загрязнения прибрежной зоны, о пересечении зон интенсивной хозяйственной деятельности нефтяным пятном, курсами судов и т.д. Распространение нефти в море при аварийных разливах представляет собой сложный процесс, для описания которого необходимо учитывать большое количество различных факторов.

Экспериментальному и теоретическому изучению растекания нефти и нефтепродуктов посвящена довольно обширная научная литература, как физико-техническая [1–9], посвященная проблеме описания динамики самого процесса, так и экологическая [10–12], направленная на решение возникающих проблем очистки морских районов, направлений. В условиях Арктики возникает дополнительная проблема, связанная с распространением нефтепродуктов над и под ледяным покровом Северного Ледовитого океана, а также на заснеженной поверхности [13, 14].

Подавляющее большинство упомянутых работ содержит, ставшее почти обязательным, сравнение экспериментальных результатов с теоретическими предсказаниями, что связано с неполнотой различных математических моделей распространения, полуэмпирических по своей природе и, отчасти, даже эвристических. Такое положение дел делает необходимым проведение более глубокого изучения модели распространения, самая продвинутая версия которой, достигнутая в [8], все еще недостаточно точна для требуемого в настоящее время уровня понимания процессов, происходящих при распространении нефтепродуктов в различных природных условиях.

В большинстве естественных ситуаций разливы нефтепродуктов происходят на двумерной поверхности (открытые водные пространства заливов, озер, морей и т.д.), но возможны особые условия (каналы, реки, узкие аквариумы и т.д.), когда поверхность разлива можно считать одномерной [15]. Этот факт приводит к необходимости создания отдельных моделей для одномерного и двумерного распространения.

Испарение нефтепродуктов или их отдельных компонентов, приводящее к значительному изменению физико-химических свойств разливающегося вещества [16, 17], требует усложнения математической модели в направлении учета уменьшения массы разливающегося вещества и пространственно-временной зависимости его термодинамических параметров.

Математическая модель при наличии потоков воды требует дополнительного усложнения, поскольку необходимо учитывать вязко-адвективный перенос пятна нефтепродуктов приповерхностным потоком воды [8, 13].

В данной работе представлена упрощенная математическая модель, позволяющая исследовать основные динамические параметры процесса растекания. В этой модели химический состав и все термодинамические параметры среды считаются постоянными величинами, масса растекающегося пятна предполагается неизменной, все среды однородны и изотропны.

Поскольку характерные скорости переноса вещества, сопровождающие процесс разлива нефти, значительно ниже, чем скорости звука в любой среде, все среды считаются несжимаемыми.

2. Осесимметричное растекание нефти. Растекание нефти сопровождается рядом механических и термодинамических процессов. Поэтому при создании модели распространения необходимо учитывать следующие основные факторы, влияющие на динамику разлива:

– Переход потенциальной энергии системы нефть–вода в кинетическую энергию в гравитационном поле из-за изменения геометрических характеристик разлива с течением времени.

– Вязкое вовлечение воды в движение из-за касательных напряжений на границе нефть-вода, вызванных горизонтальной составляющей поля скоростей в нефти. В то же время горизонтальное движение нефти замедляется.

– Создание течения в воде, вызванного вертикальным смещением нижней границы разлива нефти.

– Создание движения воды во время разлива нефти из-за явления сопротивления формы разлива нефти, сопровождающегося ее движением в воде.

– Изменение количества поверхностной энергии системы “масло в воде” по причине изменения площадей контактных границ “масло–вода”, “масло–воздух”, “воздух–вода”.

– Вязкие тепловые потери в масле и воде.

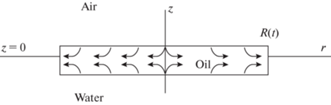
Ниже приведен приблизительный расчет параметров разлива, модель которого основана на форме нефтяного пятна в виде диска, его радиус $R(t)$ и толщина $h(t)$ являются функциями времени. Структура потока масла внутри диска такова, что в верхней части частицы жидкого масла движутся вниз и от центра диска, а в нижней части – вверх и от центра диска, как показано на рис. 1. Этот тип потока соответствует движению поверхностей пятна во время разлива: верхняя граница (граница раздела масло–воздух) перемещается вниз, а нижняя (граница раздела масло–вода) перемещается вверх.

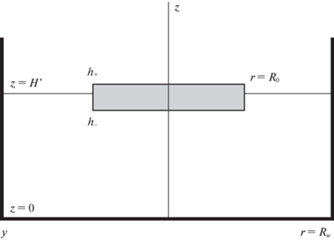
Для описания энергетических соотношений системы нефть–вода используется модель нефтяного пятна, размещенного на поверхности воды, содержащейся в цилиндрической области радиуса ${{R}_{w}}$. Первоначально, в отсутствие нефти, глубина воды была равна $H$. Пусть в какой-то момент времени радиус нефтяного пятна равен ${{R}_{o}}$, а толщина равна $h$.

Координаты верхней и нижней границ нефтяного пятна во времени задаются значениями $z = {{h}_{ \pm }}(t)$, так что толщина пятна равна

и его радиус равен ${{R}_{o}}$. Уровень свободной поверхности воды в это время обозначается символом $H{\kern 1pt} '$. Одним из параметров проблемы является объем нефтяного пятна который остается неизменным в течение всего времени разлива.

На основе закона сохранения объема воды

и законе Архимеда получаются необходимые соотношения где $\rho = {{{{\rho }_{o}}} \mathord{\left/ {\vphantom {{{{\rho }_{o}}} {{{\rho }_{w}}}}} \right. \kern-0em} {{{\rho }_{w}}}}$, ${{R}_{*}} = {{{{R}_{o}}} \mathord{\left/ {\vphantom {{{{R}_{o}}} {{{R}_{w}}}}} \right. \kern-0em} {{{R}_{w}}}}$.

В постоянном гравитационном поле потенциальная энергия системы, показанной на рис. 2, с учетом (2.5) определяется соотношением

Поверхностная энергия определяется выражением

где ${{\sigma }_{{ij}}}$ – коэффициент поверхностного натяжения на границе раздела $i$-й и $j$-й сред.

Кинетическая энергия системы состоит из кинетической энергии нефти и воды и имеет вид

где ${\mathbf{v}}$ и ${\mathbf{w}}$ – поля скоростей в нефти и воде соответственно.

Скорость диссипации вязкой энергии в системе определяется выражением

где ${{\Sigma }_{i}} = \sigma _{{rr}}^{2} + 2\sigma _{{rz}}^{2} + \sigma _{{zz}}^{2}$, причем элементы тензора вязких напряжений вычисляются для $i$-й среды.

Таким образом, имеют место соотношения

В выражениях (2.6) и (2.7) значения $\frac{\pi }{2}R_{w}^{2}{{H}^{2}}{{\rho }_{w}}g$ и $\pi R_{w}^{2}{{\sigma }_{{aw}}}$ описывают потенциальную и поверхностную энергию воды перед нанесением на нее нефтяного пятна. Отказ от этих членов и перенос начала координат оси $z$ на исходную поверхность воды, с учетом того факта, что размер акватории значительно больше размера разлива, устремление внешнего радиуса ${{R}_{w}}$ системы к бесконечности (${{R}_{w}} \to \infty $ ~ ${{R}_{*}} \to 0$), и введение обозначения ${{R}_{0}} = R(t)$ для сокращения записи, приводит к окончательным выражениям для энергетических характеристик разлива нефти

где ${{M}_{o}}$ – масса нефти, которая является постоянной величиной, где ${{\lambda }_{S}} = \sqrt {{{\left| {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}} \right|} {{{\rho }_{o}}g}}} \right. \kern-0em} {{{\rho }_{o}}g}}} $ – капиллярная постоянная контактной линии “нефть–вода–воздух”,

Уравнение динамики энергии системы имеет вид

Для того чтобы система уравнений (2.1), (2.2), (2.11)–(2.16) приводила к конструктивным результатам, необходимо задаться моделью поля скоростей в нефти и воде.

где точка над символом обозначает производную по времени, а поле скорости в воде удовлетворяет условиям

Поле скоростей, как в нефти, так и в воде состоит из двух частей – потенциальной и вихревой. Потенциальная часть обусловлена перемещением границ нефтяного пятна. Вихревая часть обусловлена вязким трением в рассматриваемых средах и возникает в результате развития потенциального потока.

Поскольку обе среды считаются несжимаемыми, то есть удовлетворяющими уравнению

то компоненты потенциальной части поля скоростей в нефти с учетом условий (2.17) принимают вид

В воде потенциальная часть поля скорости определяется движением нижней части масляного диска со скоростью ${{\dot {h}}_{ - }}$ и определяется соотношениями

и граничными условиями (2.18).

В (2.21) $M(r - r{\kern 1pt} '{\kern 1pt} ,z - {{h}_{ - }},\psi ,t)$ есть некоторая функция координат и времени, явная форма которой в будущем не понадобится.

Вязкое вовлечение воды нефтью влечет за собой развитие вихревой составляющей полей скорости, как в воде, так и в нефти. Учет этого явления приводит к изменению записи полей скорости в нефти (см. Приложение)

и в воде при $r \leqslant R(t)$где введены обозначения

Здесь ${{\nu }_{o}}$, ${{\nu }_{w}}$ кинематические, и ${{\eta }_{o}}$, ${{\eta }_{w}}$ динамические вязкости нефти и воды, соответственно.

Расчет вязких потерь. Вязкие потери в нефти рассчитываются на основе выражений (2.22), из которых следует

и тогда, согласно (2.10), имеет место

В результате мощность вязких потерь в нефти определяется выражением

где $\zeta _{h}^{o} = \frac{h}{{2\sqrt {{{\nu }_{o}}t} }}$.

Точное значение выражения (2.27) вычислено, но оно слишком громоздко, поэтому ниже приведены два предельных значения этого выражения при $\zeta _{h}^{o} \ll 1$ (что соответствует случаю, когда толщина разлива намного меньше толщины вязкого пограничного слоя в нефти на границы вода–нефть, что эквивалентно большим значениям времени $t$ после начала разлива)

и при $\zeta _{h}^{o} \gg 1$ (когда выполняется обратное соотношение для упомянутых выше толщин, что характерно для динамики разлива в начальные моменты времени)

Поскольку в реальных условиях $h \ll R$ и $\sqrt {{{\nu }_{o}}t} \ll R$, то даже для самых вязких сортов нефти во все моменты времени наблюдения за процессом, выражения (2.28), (2.29) характеризуются небольшой погрешностью вычислений.

Вязкие потери в воде рассчитываются на основе выражений (2.23), из которых следует

Тогда, согласно (2.10), имеет место

Основная часть вязких потерь в воде – это величина

в которой можно устремить глубину моря $H$ в бесконечность (это связано с быстрым уменьшением значений элементов тензора вязких напряжений (2.30) при удалении от нижней границы нефтяного пятна), в результате чего для всех моментов времени справедлив результат погрешность которого невелика из-за справедливости соотношения ${{\nu }_{w}}t \ll {{R}^{2}}$ на протяжении всего процесса разлива.

Расчет кинетической энергии. Этот расчет выполняется в соответствии с соотношением (2.14) при $H \to \infty $, и с учетом малости значения

Как показывают расчеты, проведенные на основе выражений (2.22) для поля скорости в нефти, кинетическая энергия радиального движения пропорциональна величине ${{\dot {R}}^{2}}$, а вертикального движения – ${{\dot {h}}^{2}}$. Тогда, согласно (2.33), энергией вертикального движения можно пренебречь, в результате чего кинетическая энергия нефти задается приближенным выражением

Движение воды во время разлива нефти вызвано тремя основными механизмами – вязким захватом воды потоком нефти (вязкий член в поле скоростей (2.23)), генерацией потенциального потока воды из-за смещения вверх нижней границы нефтяного пятна (члены с ${{\partial \,{{\Phi }_{w}}} \mathord{\left/ {\vphantom {{\partial \,{{\Phi }_{w}}} {\partial \,r}}} \right. \kern-0em} {\partial \,r}}$ и ${{\partial \,{{\Phi }_{w}}} \mathord{\left/ {\vphantom {{\partial \,{{\Phi }_{w}}} {\partial \,z}}} \right. \kern-0em} {\partial \,z}}$ в (2.23)) и генерированием потока воды из-за явления сопротивления формы, растекающегося олеина.

Поскольку максимальное значение потенциальной части поля скорости в воде ограничено значением $\left| {{{{\dot {h}}}_{ - }}} \right| < \left| {\dot {h}} \right|$, этой частью кинетической энергии воды можно пренебречь по сравнению с энергией воды, увлекаемой за счет вязких эффектов, основная часть которых описывается значением

Явная форма величины кинетической энергии воды, обусловленной явлением сопротивления формы, задается выражением

где ${{C}_{{sh}}}$ – коэффициент сопротивления формы, точное значение которого неизвестно.

Уравнение динамики энергии. На основе уравнения (2.16) и выражений, полученных выше, уравнение энергетической динамики системы может быть записано в виде

где $\Pi $ определяется выражением (2.12), ${{E}_{S}}$ – (2.13), ${{\dot {E}}_{\nu }}$ – (2.28), (2.29), (2.32), ${{{\text{T}}}_{o}}$ – (2.34) и ${{{\text{T}}}_{w}}$ – (2.35).

Анализ выражений (2.34) и (2.35) показывает, что поскольку $\frac{{2 - \sqrt 2 }}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} \ll 1$ и $\frac{1}{{\zeta _{h}^{w}}} < 1$ (при начальной толщине разлива $h = 1$ м это значение сопоставимо с единицей, только начиная со времени $t\sim {{10}^{3}}$ с, когда процесс разлива почти завершен), значением ${{{\text{T}}}_{w}}$ следует пренебречь по сравнению с ${{{\text{T}}}_{o}}$. Затем, при подстановке необходимых значений в (2.37), формируется несколько громоздкое нелинейное уравнение, учитывающее множество факторов, влияющих на процесс растекания нефти по поверхности воды

где $\alpha = 1 - {{\kappa }_{{ow}}}\operatorname{erfc} ({{\zeta }_{h}})$, $\sigma = {{\sigma }_{{ow}}} + {{\sigma }_{{oa}}} - {{\sigma }_{{aw}}}$.

Введение переменной $F = {{\pi }^{2}}{{R}^{4}}$ – квадрата площади разлива нефти – преобразует уравнение (2.38) к виду

где введены обозначения

Анализ экспериментальных данных с минеральным маслом Volga M8B-SAE 20 API показывает, что значение $\frac{3}{4}\frac{{{{{\dot {F}}}^{2}}}}{F}$ значительно меньше значения $\ddot {F}$, и им можно пренебречь. В то же время выражение для коэффициента ${{d}^{2}}$ в (2.40) указывает на значительный вклад вязких потерь только в начальные моменты времени разлива, когда вязкие напряжения в среде имеют существенные значения. Это позволяет не учитывать последний член уравнения (2.39). В результате таких приближений уравнение динамики энергии принимает вид

более того, коэффициенты этого уравнения рассматриваются как постоянные значения, несмотря на наличие в них зависящего от времени значения $\alpha $. Такой подход обусловлен тем, что скорость изменения $\alpha $ значительно меньше скорости изменения радиуса растекания $R$

Решение уравнения (2.41). Решение этого уравнения делится на два варианта.

I. Разлив нефти, ограниченный по площади, когда на поверхности воды может образоваться масляная линза, как конечное равновесное состояние системы. Этому случаю соответствует значение $\operatorname{sign} (\sigma ) = 1$. Тогда из (2.41) следует, что существует предельная величина ${{F}_{*}}$, определяемая выражением

чему соответствуют предельная площадь пятна ${{S}_{*}}$ и предельный радиус ${{R}_{*}}$, описываемые соотношениями

Точно такое же предельное значение ${{F}_{*}}$ существует для уравнения (2.39) и при учете отброшенных нелинейных членов. В целях дальнейшего исследования вводится обозначение

Тогда, если ${{a}^{4}} < \,\,{{b}^{2}}$, то решение (2.41) записывается в виде

где ${{F}_{0}} = {{\left. F \right|}_{{t\, = \,0}}}$, ${{F}_{1}} = {{\left. {\dot {F}} \right|}_{{t\, = \,0}}}$ – величины, определяемые начальными условиями.

Как видно из (2.45), площадь разлива $S = {{F}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ проявляет колебательное и затухающее поведение во времени. Частота колебаний вблизи положения равновесия определяется величиной $2\pi \,b$, а коэффициент затухания колебаний во времени определяется величиной ${{a}^{2}}$.

В случае существенного значения коэффициента затухания, когда ${{a}^{4}} > \,\,{{b}^{2}}$, решение (2.41) имеет вид

Графики соотношений (2.45) и (2.46) будут представлены в разд. 3.

II. Разлив нефти с неограниченной площадью происходит, когда нет предельного состояния равновесия системы, что соответствует значению ${\text{sign}}(\sigma ) = - 1$. В этом случае вводятся значения

и решение уравнения (2.41) имеет вид (2.46), в который подставляются значения (2.47). Зависимость площади неограниченного разлива от времени показана на рис. 3.

Решение (2.47) включает в себя два экспоненциальных члена, один из которых пропорционален $\exp ( - ({{a}^{2}} + \sqrt {{{a}^{4}} + {{b}^{2}}} )t)$, а другой – значению $\exp ((\sqrt {{{a}^{4}} + {{b}^{2}}} - {{a}^{2}})t)$. Первый член быстро затухает во времени, а второй неограниченно увеличивается, что обусловлено некомпенсированной силой поверхностного натяжения, действующей на границе контакта трех сред и направленной радиально от края нефтяного пятна во внешнюю область.

3. Экспериментальные результаты и сравнение с аналитической моделью. Эксперименты проводились с различными типами органических и минеральных масел и непосредственно с сырой нефтью. Исследование динамики распространения несмешивающейся примеси по поверхности воды проводилось в прямоугольной кювете длиной 50 см, шириной 40 см и глубиной 5 см. Чтобы избежать бликов от поверхности воды и пятен углеводородов, поверхность жидкости освещалась сверху тремя разнесенными источниками света, расположенными рядом с кюветой по бокам.

Экспериментальный метод включал нанесение различных количеств моторного масла Volga M8B-SAE 20 API (${{\rho }_{{\text{o}}}} = 883.7$ кг/м³, ${{\nu }_{o}} = 3.34 \times {{10}^{{ - 4}}}$ м²/с, при температуре $T$ = 20°C) и сырой нефти Мамонтовского месторождения (${{\rho }_{{\text{o}}}} = 878.0$ кг/м³, ν_o = = $2.15 \times {{10}^{{ - 5}}}$ м²/с, при температуре $T$ = 20°C) на поверхность известного объема воды и дальнейший мониторинг ее распространения по поверхности жидкости. Ход экспериментов записывался с помощью цифровой камеры в автоматическом режиме в течение 4 часов, съемка велась с частотой 360 кадров в минуту, а полученные последовательности кадров обрабатывались и анализировались. Положение масляного пятна регистрировали с использованием метода фотометрии обработанных изображений, полученных из исходных кадров методами пакетной обработки.

Переменными параметрами экспериментов были объем моторного масла, температура и соленость воды. В каждой серии экспериментов регистрировались два из вышеуказанных параметров, и для разных значений оставшегося параметра измерялась временная зависимость области распространения.

Для устранения случайных ошибок экспериментальные данные были подвергнуты дополнительной обработке с использованием модифицированного алгоритма сдвига (MSA) [18], который показал стабильную работоспособность при выделении полезного сигнала на фоне шума вплоть до отношения сигнал/шум –15 дБ.

Ниже приведены только самые характерные экспериментальные зависимости из множества измерительных результатов.

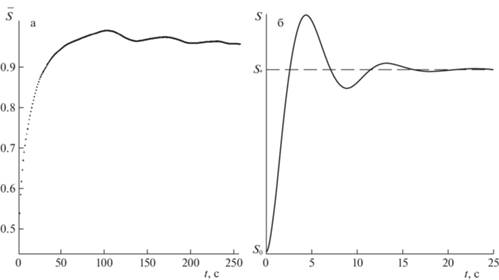
Растекание машинного масла. На рис. 4, а красными точками показана экспериментальная зависимость площади разлива моторного масла Volga M8B-SAE 20 API от времени. Данные нормируются по своему максимальному значению, черные точки являются результатом обработки набора красных точек алгоритмом MSA. Все последующие экспериментальные данные, представленные здесь, также подвергались обработке алгоритмом MSA.

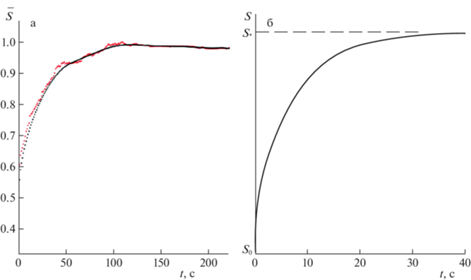
Как можно видеть, поведение кривой $\bar {S}(t)$ на рис. 4, а хорошо соответствует зависимости (2.46), проиллюстрированной на рис. 4, б. Здесь и на рис. 5, б отсчеты времени безразмерны и являются условными, причины чего будут объяснены далее.

Согласно (2.46) отклонение от положения равновесия $F = {{F}_{*}}$ описывается двумя убывающими показателями $\exp ( - {{a}^{2}}t + \mu t)$ и $\exp ( - {{a}^{2}}t - \mu t)$. В начальные моменты времени вклад от члена содержащего $\exp ( - {{a}^{2}}t - \mu t)$ уменьшается наиболее быстро. В последующие моменты времени, когда основной вклад в отклонение вносит член, содержащий $\exp ( - {{a}^{2}}t + \mu t)$, скорость снижения отклонения уменьшается по сравнению с начальными моментами времени. Этот факт отражен в поведении кривой на рис. 5, б.

Колебательный режим, описываемый соотношением (2.45), также наблюдался экспериментально, и его обработанные данные представлены на рис. 5, а.

Видно, что площадь разлива растет со временем, начиная с определенного значения ${{S}_{0}}$, достигает значения ${{S}_{*}}$, проскакивает его по инерции, после чего возникает возвратная сила, ускорение $\ddot {F}$ меняет знак (становится отрицательным), площадь разлива начинает уменьшаться, достигает значения ${{S}_{*}}$, проскакивает его по инерции, после чего возникает возвратная сила, ускорение $\ddot {F}$ меняет знак (становится положительным), площадь разлива начинает увеличиваться, достигает значения ${{S}_{*}}$, проскакивает его по инерции, ускорение $\ddot {F}$ меняет знак (становится отрицательным) и т.д. Амплитуда колебаний постепенно уменьшается из-за передачи энергии от нефтяного пятна к воде (член ${{a}^{2}}\dot {F}$ в уравнении (2.41)). В конце концов, нефтяное пятно приобретает свой стационарный размер.

Разница в поведении ограниченной области разлива на рис. 4 и 5 объясняется тем фактом, что в случае решения (2.46) скорость перехода кинетической энергии нефтяного топлива в кинетическую энергию воды (из-за явления сопротивления формы) значительно больше, чем скорость перехода к поверхностной энергии на границе раздела контактирующих сред, в отличие от случая решения (2.45), когда наблюдается обратная корреляция этих скоростей.

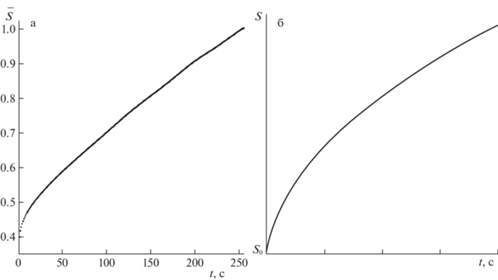
Растекание сырой нефти. Сырая нефть демонстрирует иное поведение, связанное с неограниченным разливом углеводородов, экспериментальные данные для которой показаны на рис. 4,а. Поскольку размеры лабораторной установки не позволяют отследить разлив на большой площади, как на рис. 3, сравнение с теоретическими результатами (2.46), (2.47) проводится только за небольшие промежутки времени от начала процесса. Расчеты, представленные на рис. 6,б, выполненные в соответствии с соотношениями (2.46), (2.47), показывают хорошее качественное совпадение эксперимента и теории. Здесь следует подчеркнуть, что график на рис. 6,б представляет точную начальную часть графика, показанного на рис. 3.

Сравнения экспериментальных и теоретических результатов, представленные в этом разделе, носят исключительно качественный характер из-за недостатка вычислительных данных. Невозможно провести количественное сравнение для всех экспериментальных ситуаций из-за отсутствия некоторых количественных характеристик тестируемых сред. Чтобы доказать этот факт, достаточно привести уравнение (2.41) к безразмерной форме путем введения новых переменных

подстановка, которая в (2.41) приводит это уравнение к виду

Свойства решений этого однопараметрического уравнения определяются величиной $\varepsilon $, значение которой задается массой олеина ${{M}_{o}}$, плотностью и вязкими свойствами воды и олеина – коэффициентом $\alpha $, суммарным поверхностным натяжением $\sigma $ на линии контакта трех сред и коэффициентом сопротивления формы ${{C}_{{sh}}}$. И если первые три значения известны с достаточной степенью точности, то оценки коэффициента сопротивления формы пятна машинного масла или сырой нефти, разливающейся по воде, в настоящее время неизвестны. Получение таких оценок требует сложных и трудоемких измерений, что является отдельной научной задачей.

Следует также отметить, что значение коэффициента сопротивления формы включено как в шкалу размеров разлива ${{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{a}^{4}}}}} \right. \kern-0em} {{{a}^{4}}}}$, так и в несколько временных шкал: ${{a}^{{ - 2}}}$, ${{\mu }^{{ - 1}}}$, и т.д. (см. выражения (2.45)–(2.47)).

Проверка справедливости уравнения (2.41) с помощью экспериментальных измерений. Уравнение (2.41) было получено в приближении малости отношения $\left| {{{3{{{\dot {F}}}^{2}}} \mathord{\left/ {\vphantom {{3{{{\dot {F}}}^{2}}} {4F\ddot {F}}}} \right. \kern-0em} {4F\ddot {F}}}} \right|\,$, то есть предполагалось выполненным условие

На рис. 7, a и б представлены расчетные значения (3.3), выполненные на основе данных обработки для рис. 4, a и 5, a.

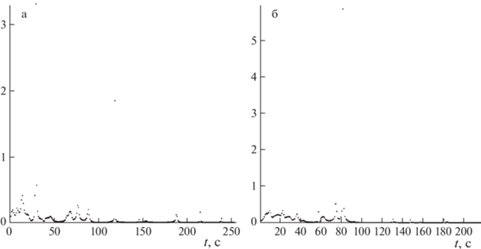
Как видно из представленных графиков, в подавляющем большинстве точек (от 95% и более) соотношение (3.3) безусловно выполняется, что подтверждает правомерность использования приближенного уравнения (2.41) для рассматриваемой задачи.

Заключение. Построенная теоретическая модель растекания в виде приближенного уравнения (2.41), общего как для ограниченной, так и для неограниченной площади разлива олеина, позволила получить явные аналитические решения для любого момента времени процесса, не разделяя его на отдельные временные отрезки, как это было сделано в [5, 6, 8].

Теоретический анализ процесса разлива нефтепродуктов на поверхности воды показал, что его динамика, набор временных масштабов и предельные размеры хорошо описываются приближенным уравнением (2.41), управляющими параметрами которого являются три значения – ${{a}^{2}}$, ${{b}^{2}}\operatorname{sign} (\sigma )$ и ${{c}^{2}}$, введенные соотношениями (2.40). Первое значение, ${{a}^{2}}$, определяется коэффициентом сопротивления формы нефтяного пятна, растекающегося по поверхности воды, массой разлитого олеина и значением ${{\alpha }^{2}}$, которое описывает динамику процесса взаимного вовлечения воды и олеина. Это значение описывает вклад тормозящей силы, возникающей в результате пространственного перераспределения водных и масляных масс в процессе растекания. Второе значение, ${{b}^{2}}\operatorname{sign} (\sigma )$, определяется значением результирующего коэффициента поверхностного натяжения на линии контакта воздух–вода–олеин, массой пролитого олеина и значением ${{\alpha }^{2}}$. Это значение отвечает за учет роли поверхностных сил (как растягивающих пятно, так и сжимающих его, в зависимости от конкретной ситуации) в процессе растекания. Третье значение, ${{c}^{2}}$, описывает влияние сил выталкивания и эффекты взаимного вовлечения воды и нефти на динамику процесса.

Эффекты вязкого трения одной среды о другую с учетом динамики разлива учитываются в зависимости от коэффициентов вовлечения воды и олеина, значения которых приведены в соответствующих выражениях (П.10)–(П.12). Также показано, что преобразованием общих энергетических запасов системы в тепловую энергию из-за внутреннего трения можно пренебречь, на что указывает хорошее совпадение экспериментальных и теоретических результатов.

В случае, когда характерные свойства среды таковы, что существует предельное состояние в виде пятна олеина конечной площади (соотношения (2.45, 2.46)), которое формируется в виде углеводородной линзы [20], и характеризует растекание на его конечной стадии либо затухающими колебаниями (2.45), либо монотонным достижением предельного значения (2.46). В первом случае колебательное поведение обусловлено превышающим влиянием сил поверхностного натяжения по сравнению с силой сопротивления формы пятна, а во втором случае имеет место обратное соотношение сил.

Если свойства контактирующих сред таковы, что нет предельного размера олеинового пятна, что является следствием превышения коэффициента поверхностного натяжения на границе воздух–вода над суммой коэффициентов на границах вода–олеин и воздух–олеин, то наблюдается неограниченное растекание, площадь которого растет экспоненциально с течением времени (2.47).

Работоспособность полученного унифицированного уравнения динамики разлива олеина подтверждается сравнением с экспериментальными результатами, которые выявили те же режимы для разных типов олеинов, что и в теоретическом описании.

Работа выполнена при финансовой поддержке проекта Российской Федерации в лице Министерства образования и науки России № 075-15-2020-802.