Прикладная математика и механика, 2022, T. 86, № 6, стр. 938-957

Известно [1–3], что осциллирующий конечный объем жидкости будет излучать акустические волны. Сказанное относится и к жидко-капельным аэрозолям естественного происхождения: туманам, облакам, дождям. В связи с изучением таких геофизических объектов [4–6] представляется актуальным провести исследование зависимости интенсивности акустического излучения от такого аэрозоля и его частоты от номера осциллирующей моды, и физико-химических характеристик среды.

При расчетах в первом порядке приближений по безразмерной амплитуде осцилляций центрально симметричная (нулевая) и трансляционная (первая) моды выпадают из рассмотрения в силу необходимости сохранения объема капли и неподвижности ее центра масс [2]. Нулевая и первая моды появляются в спектре возбужденных мод только в асимптотических расчетах более высоких порядков малости, чем первый, причем, трансляционная мода возбуждается лишь тогда, когда в спектре изначально возбужденных мод имеются две или больше с последовательными номерами [7]. Представляется интересным сравнить между собой интенсивности и частоты монопольного и дипольного излучений, а также сравнить их с общей интенсивностью акустического излучения, получаемого в линейных расчетах.

1. Физическая постановка задачи. Все исследование проведем на простейшем примере неподвижной слабо заряженной сферической капли идеальной несжимаемой идеально проводящей жидкости радиуса $R$, осциллирующей во внешнем однородном электростатическом поле напряженностью ${{{\mathbf{E}}}_{0}}$. Обозначим плотность жидкости ${{\rho }_{1}}$, а коэффициент поверхностного натяжения границы раздела сред – $\sigma $. Внешнюю среду примем идеальной сжимаемой с диэлектрической проницаемостью ${{\varepsilon }_{{ex}}}$ и плотностью ${{\rho }_{2}}$, в которой звук распространяется со скоростью ${v}$. В дальнейших рассуждениях малым зарядом капли будем пренебрегать (он нужен только для того чтобы обеспечить неподвижность капли).

Согласно экспериментальным данным [8] капля, помещенная в электрическое поле, вытягивается в сфероид, ориентированный осью симметрии z в направлении напряженности электрического поля ${{{\mathbf{E}}}_{0}}$. Полагая центр масс капли неподвижным, найдем, что в вакууме [9] ${{e}^{2}} = {{9E_{0}^{2}R} \mathord{\left/ {\vphantom {{9E_{0}^{2}R} {16\pi }}} \right. \kern-0em} {16\pi }}\sigma \equiv 9w$, где $e$ – эксцентриситет капли, а $w$ – безразмерный параметр Тейлора, характеризующий устойчивость капли по отношению к индуцированному заряду [8]. Так как сфероидальность равновесной формы капли определяется наличием внешнего электростатического поля, будем считать ${{E}_{0}}\sim e$.

В настоящей задаче, чтобы избежать рассмотрения нескольких крайних ситуаций, напряженность поля примем равной ${{E}_{0}} = 0.17$ СГСЭ, которая может реализоваться и в приземном слое и внутри облака. Размеры капель в туманах, облаках и в дожде изменяются от единиц микрон до долей миллиметра. В итоге, беря максимальное значение радиуса дождевой капли $R = 3.5$ мм, найдем, что ${{e}^{2}}$ во всех ситуациях будет меньше $ \approx {\kern 1pt} 2 \times {{10}^{{ - 5}}}$, т.е. будет малым параметром.

Все расчеты задачи проведем в сферической системе координат $\left( {r,\theta ,\varphi } \right)$, начало которой поместим в центре масс капли. Полярный угол $\theta $ будем отсчитывать от направления вектора ${{{\mathbf{E}}}_{0}}$. Для упрощения расчетов задачи ограничимся осесимметричной постановкой.

Из-за теплового движения молекул жидкости поверхность капли возмущается осцилляциями весьма малой амплитуды $\left| \xi \right|\sim \sqrt {\kappa \,T{\text{/}}\sigma } $, где $\kappa $ – постоянная Больцмана, $T$ – абсолютная температура [10]. В результате капиллярного волнового движения создается искажение $\xi (\theta ,t)$ равновесной сфероидальной формы поверхности капли. При комнатных температурах для любых жидкостей величина тепловой амплитуды $\left| \xi \right|$ составляет не более $1 \times {{10}^{{ - 8}}}$ см. Тогда для капель реальных жидкостей естественного происхождения (дождь, облака, туманы) с характерными размерами $R > 1$ μм амплитуда осцилляций много меньше радиуса: $\left| \xi \right| \ll R$. Однако при наличии внешних неконтролируемых силовых воздействий (коагуляция, дробление, лобовое сопротивление, трение о воздух и т.п.) амплитуда осцилляций может быть увеличена [11, 12]. В этой связи введем второй малый параметр $\varepsilon \sim e$.

2. Математическая формулировка задачи. Форму капли как в начальный, так и во все последующие моменты времени будем считать осесимметричной. Уравнение возмущенной поверхности капли в любой момент можно записать в виде:

где $r(\theta )$ – функция, описывающая равновесную сфероидальную форму капли. В качестве второго малого параметра примем величину отношения амплитуды осцилляций к радиусу капли $\varepsilon \equiv \max \left| {\xi (\theta ,t)} \right|{\text{/}}R \ll 1$, т.е. безразмерную амплитуду осцилляций. Величину $\varepsilon $ определим ниже, исходя из требования асимптотичности необходимых разложений.

Волновые движения в капле и в сжимаемой окружающей среде будут потенциальными с потенциалами скоростей ${{\psi }_{m}}(r,\theta ,t)$: ${{{\mathbf{V}}}_{m}}(r,\theta ,t)$ = $\nabla {{\psi }_{m}}(r,\theta ,t)$, где ${{{\mathbf{V}}}_{m}}(r,\theta ,t)$ – поле скоростей внутри ($m = 1$) и вне капли ($m = 2$) [2].

Математическая формулировка задачи о расчете спектра капиллярных осцилляций незаряженной капли, нелинейно осциллирующей во внешнем электростатическом поле имеет вид:

Поведение гидродинамического потенциала внешней среды ${{\psi }_{2}}(r,\theta ,t)$ на бесконечности описывается условием излучения Зоммерфельда [3]:

Кроме того, потребуем выполнения дополнительных интегральных условий: неизменности полного объема, отсутствия движения центра масс осциллирующей капли и равенства нулю ее суммарного заряда:

где ${\mathbf{n}}$ – вектор единичной нормали к возмущенной поверхности капли: $F\left( {r,\theta ,t} \right)$ = = $r - r\left( {\theta ,t} \right)$, рассчитывается на поверхности капли по формуле ${\mathbf{n}} = \nabla F{\text{/}}\left| {\nabla F} \right|$.

Рассматривая случай многомодовой начальной деформации равновесной сфероидальной формы (см., напр., [7]), начальные условия сформулируем в виде начального возмущения, определяемого суперпозицией произвольного числа колебательных мод, и равенства нулю скорости всех точек на поверхности капли:

где $\Xi $ – множество значений номеров изначально возбужденных колебательных мод осциллирующей капли; ${{P}_{j}}\left( \mu \right)$ – полином Лежандра $j$-го порядка; $j$ – целое число, $\mu \equiv \cos \theta $; ${{h}_{j}}$ – константа, учитывающая парциальный вклад $j$-й колебательной моды в начальное искажение капли; ${{\tilde {\xi }}_{0}}$ и ${{\tilde {\xi }}_{1}}$ – константы, определяемые из интегральных условий (2.9) в начальный момент времени, имеющие смысл амплитуд нулевой и первой мод: где o и O – символы порядка [13].

В приведенной постановке задачи (2.2)–(2.10): ${{\Phi }_{s}}(t)$ – постоянное значение электрического потенциала вдоль поверхности капли; $k = \frac{{{{\omega }_{n}}}}{{v}}$ – волновое число; ${{P}_{{0m}}}$ – давления внутренней ($m = 1$) и внешней ($m = 2$) сред в равновесном состоянии; P_E = = $\frac{{{{\varepsilon }_{{ex}}}{{{\left( {\nabla \Phi } \right)}}^{2}}}}{{8\pi }}$ – давление электрического поля; ${{P}_{\sigma }} = \sigma H$ – давление капиллярных сил, $H$ – средняя кривизна возмущенной поверхности капли в данной точке; ${{P}_{1}} = {{P}_{{01}}}$ – ‒ ${{\rho }_{1}}\frac{{\partial {{\psi }_{1}}}}{{\partial t}}$ – $\frac{1}{2}{{\rho }_{1}}{{\left( {\nabla {{\psi }_{1}}} \right)}^{2}}$ – давление внутри капли; ${{P}_{2}} = {{P}_{{02}}}$ – ${{\rho }_{2}}\frac{{\partial {{\psi }_{2}}}}{{\partial t}}$ – $\frac{1}{2}{{\rho }_{2}}{{\left( {\nabla {{\psi }_{2}}} \right)}^{2}}$ + + $\frac{{{{\rho }_{2}}}}{{2{{{v}}^{2}}}}{{\left( {\frac{{\partial {{\psi }_{2}}}}{{\partial t}}} \right)}^{2}}$ – давление во внешней среде.

В уравнениях (2.2), (2.4), (2.7), (2.10) принято, что электрическое поле в окружающем каплю пространстве определяется электростатическим потенциалом $\Phi (r,\theta ,t)$, связанным с напряженностью поля ${\mathbf{E}}$ соотношением: ${\mathbf{E}} = - \nabla \Phi (r,\theta ,t)$.

Моделируя каплю проводником, получим, что характерное время перераспределения индуцированных внешним электрическим полем зарядов много меньше характерного гидродинамического времени осцилляций поверхности капли:

где ${{\varepsilon }_{{in}}}$ – диэлектрическая проницаемость жидкой капли, $\chi $ – удельная электропроводность жидкости. Принимая для оценки характеристики дождевой капли $R = 0.25$ см, ${{\rho }_{1}} = 1$ г/см³, $\sigma = 73$ дин/см, ${{\varepsilon }_{{in}}} = 80$, $\chi = 9 \times {{10}^{6}}$ СГСЭ, получим, что время релаксации индуцированного заряда в жидкости меньше гидродинамического времени на четыре порядка величины.

Принимая во внимание, что составляющие гидродинамических потенциалов поля скоростей внутри и вне капли $\psi _{1}^{{\left( k \right)}}(r,\theta ,t)$, $\psi _{2}^{{\left( k \right)}}(r,\theta ,t)$ ($k = 1,2$) являются периодическими функциями по времени $\psi _{m}^{{\left( k \right)}}(r,\theta ,t)$ ~ $\exp \left( {i{{\omega }_{n}}t} \right)$ ($m = 1,2$), получим, что волновое уравнение (2.3) для $\psi _{2}^{{\left( k \right)}}(r,\theta ,t)$ примет вид однородного уравнения Гельмгольца:

3. Асимптотические разложения функций. Для отыскания решения сформулированной задачи с точностью до слагаемых второго порядка малости по $\varepsilon $ включительно воспользуемся классическими методами теории возмущений [13]. В рамках метода многих масштабов перейдем от единственного времени $t$ к его различным масштабам, выраженным через малый параметр $\varepsilon $ в виде: ${{T}_{m}} = {{\varepsilon }^{m}}t$ $\left( {m = 0,1,2, \ldots } \right)$. Искомые величины $\xi (\theta ,t)$, ${{\psi }_{m}}(r,\theta ,t)$, $\Phi (r,\theta ,t)$, а также давления ${{P}_{m}}\left( {r,\theta ,t} \right)$, ${{P}_{E}}\left( {r,\theta ,t} \right)$, ${{P}_{\sigma }}$ в динамическом граничном условии (2.6), представим в виде зависимостей от двух временных масштабов ${{T}_{0}}$, ${{T}_{1}}$ и запишем их в виде асимптотических разложений по $\varepsilon $:

где индекс “eq” относится к величинам, определяющим равновесное состояние капли. Здесь электрический потенциал $\Phi (r,\theta ,t)$ имеет асимптотическое разложение по целым степеням малого параметра $\varepsilon $, так как ${{E}_{0}}\sim e\sim \varepsilon $. В данных разложениях $\varepsilon {{\Phi }^{{\left( 0 \right)}}}(r,\theta )$ ≡ ${{\Phi }^{{\left( {{\text{eq}}} \right)}}}(r,\theta )$ описывает потенциал электростатического поля в окрестности равновесной капли, а компонента ${{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t)$ является поправкой к электрическому потенциалу, связанному с возмущением поверхности капли.

Для удобства дальнейших разложений целесообразно ввести формальный параметр ${{\beta }_{E}}\sim {\text{1}}$, определяемый соотношением: ${{E}_{0}} = {{\beta }_{E}}\varepsilon $. В окончательных выражениях можно легко перейти к ${{E}_{0}}$, если положить ${{\beta }_{E}}\varepsilon = {{E}_{0}}$.

При переходе к переменным ${{T}_{0}}$, ${{T}_{1}}$ в уравнениях (2.5), (2,6), (2.11) производные по времени вычисляются следующим образом [13]:

Поправки волнового возмущения ${{\xi }^{{\left( k \right)}}}(r,\theta ,t)$ ($k = 1,2$) к форме поверхности капли запишем в виде ряда по осесимметричным полиномам Лежандра:

Решения уравнений Лапласа (2.2) для поправок к гидродинамическому и электростатическому потенциалам $\psi _{1}^{{\left( k \right)}}(r,\theta ,t)$ ($k = 1,2$), ${{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t)$ при выполнении условий ограниченности (2.4) имеют вид:

Решение уравнения Гельмгольца (2.12) при выполнении условия излучения Зоммерфельда (2.8) представляется в виде разложения по полиномам Лежандра:

где $h_{n}^{{\left( 2 \right)}}\left( z \right)$ – сферическая функция Бесселя третьего рода [14].

4. Разложение равновесного состояния. Учтем, что наша задача содержит два малых параметра: ${{e}^{2}}$ и $\varepsilon $, величины которых находятся в соотношении $\varepsilon \sim e$. Будем учитывать это обстоятельство в нижеследующих разложениях.

Подставляя разложения (3.1) в уравнения (2.2)–(2.10), проведем анализ равновесного состояния системы.

Чтобы найти потенциал ${{\Phi }^{{\left( {{\text{eq}}} \right)}}}(r,\theta )$ в явном виде, сформулируем краевую задачу:

где ${{{\mathbf{n}}}_{0}}$ – вектор единичной нормали к невозмущенной равновесной поверхности капли. Решение сформулированной задачи имеет вид:

Уравнение равновесной формы капли с осью симметрии $z$, направленной коллиниарно электростатическому полю, можем записать в виде:

Функцию $h(\theta )$, учитывающую отклонение от сферической формы капли, представим в виде ряда по полиномам Лежандра:

где ${{P}_{n}}\left( \mu \right)$ – осесимметричный полином Лежандра $n$-го порядка [14]. Ограничение нижнего индекса суммирования $n$ определяется удовлетворением условий постоянства объема капли и отсутствия ее трансляционного движения.

В уравнении (4.3) амплитуды отдельных мод ${{\alpha }_{n}}$ ($n \geqslant 2$) будем искать в явном виде из условия (2.6) для равновесного состояния системы:

где ${{H}_{0}}$ – средняя кривизна равновесной, невозмущенной капиллярным волновым движением поверхности капли в данной точке.

Подставляя (4.1), (4.3) в (4.4), из баланса давлений в произвольной точке равновесной поверхности капли:

приравниванием амплитудных коэффициентов ${{\alpha }_{n}}$ при полиномах Лежандра одинакового порядка, учитывая (4.2) и переходя от формального параметра ${{\beta }_{E}}$ к физическим обозначениям, легко найдем равновесную форму капли:

Выражение (4.6) соответствует уравнению сфероида, вытянутого вдоль направления электрического поля, в сферической системе координат [15, 16].

5. Задача первого порядка по $\varepsilon $. Подставляя в систему уравнений (2.5)–(2.7), (2.9)–(2.10) асимптотические разложения (3.1) с учетом (3.2) и собирая слагаемые первого порядка малости по $\varepsilon $, получим задачу для отыскания амплитудных коэффициентов $M_{n}^{{\left( 1 \right)}}$, $A_{n}^{{\left( 1 \right)}}$, $B_{n}^{{\left( 1 \right)}}$ в функциях ${{\xi }^{{\left( 1 \right)}}}(\theta ,t)$, $\psi _{m}^{{\left( 1 \right)}}(r,\theta ,t)$ ($m = 1,2$), связанных с линейными осцилляциями капли:

Подстановка разложений (3.3), (3.4) при $k = 1$ в уравнения (5.1)–(5.2) позволяет найти соотношения между коэффициентами $M_{0}^{{\left( 1 \right)}}$, $M_{1}^{{\left( 1 \right)}}$, $A_{n}^{{\left( 1 \right)}}$, $B_{n}^{{\left( 1 \right)}}$ в виде:

Из динамического граничного условия (5.2) после несложных преобразований перейдем к однородному дифференциальному уравнению второго порядка, относительно амплитудных коэффициентов $M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},\;{{T}_{1}}} \right)$ при $n \geqslant 2$:

Общее решение дифференциального уравнения (5.5) представим в виде:

где $C_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)$, $\bar {C}_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)$ – комплексно сопряженные величины. Зависимость функций $c_{n}^{{\left( 1 \right)}}$, $b_{n}^{{\left( 1 \right)}}$ от более медленного масштаба времени ${{T}_{1}}$ найдем при рассмотрении задачи второго порядка малости по $\varepsilon $.

В уравнении (5.5) квадрат частоты $\omega _{n}^{2}$ осцилляций незаряженной сферической капли определяется соотношением:

Для отыскания амплитудных множителей $F_{n}^{{\left( 1 \right)}}$, входящих в разложение для поправки к электрическому потенциалу ${{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t)$, из уравнений (2.7), (2.10) выделим слагаемые, пропорциональные:

Выпишем решение, найденное подстановкой разложений (3.3), (3.5) в систему уравнений (5.8), (5.9), в виде:

В (5.8) $\Phi _{s}^{{\left( 1 \right)}} = 0$.

6. Задача второго порядка по $\varepsilon $. Для нахождения коэффициентов второго порядка $M_{n}^{{\left( 2 \right)}}$, $A_{n}^{{\left( 2 \right)}}$, $B_{n}^{{\left( 2 \right)}}$ в функциях ${{\xi }^{{\left( 2 \right)}}}(\theta ,t)$, $\psi _{m}^{{\left( 2 \right)}}(r,\theta ,t)$ ($m = 1,2$) приведем систему уравнений, получающуюся подстановкой в (2.5)–(2.7), (2.9)–(2.10) разложений (3.1) при выполнении дифференцирования (3.2) и группировкой слагаемых, пропорциональных ${{\varepsilon }^{2}}$:

Используя разложения (3.3), (3.4) при $k = 1,2$ и решения первого порядка малости (5.3), (5.4), из условий (6.1), (6.4), (6.5) найдем выражения для искомых амплитуд $M_{0}^{{\left( 2 \right)}}$, $M_{1}^{{\left( 2 \right)}}$, $A_{n}^{{\left( 2 \right)}}$, $B_{n}^{{\left( 2 \right)}}$ в виде:

где $C_{{mk,lp}}^{{nq}}$ – коэффициенты Клебша–Гордана [14], имеющие отличные от нуля значения при $\left| {m - l} \right| \leqslant n \leqslant m + l$, $m + l + n$ – четное и $k + p = q$.

Подставим в баланс давлений второго порядка малости (6.2) исходные разложения (3.3)–(3.6) и решение (5.6), откуда получим неоднородное дифференциальное уравнение относительно амплитудных коэффициентов $M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$ ($n \geqslant 2$):

где $T_{0}^{ + }\left( n \right) \approx - \frac{{n + 1}}{{{{n}^{2}}}}$, ${{S}_{0}}\left( m \right) \approx \left( {m + 1} \right)\left( {\left( {m + 1} \right)\left( {\frac{2}{{{{m}^{2}}}} + \frac{1}{{m - 1}}} \right){{K}_{{m,k,n}}} - \frac{1}{{{{m}^{2}}}}{{\alpha }_{{m,k,n}}}} \right).$

В (6.6) аббревиатура “к.с.” означает слагаемые, комплексно-сопряженные к выписанным, $\bar {C}_{k}^{{\left( 1 \right)}}$ – комплексно-сопряженная к $C_{k}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)$ величина.

Для того, чтобы в решении дифференциального уравнения (6.6) отсутствовали неравномерности (т.е. неограниченно нарастающие со временем члены), в правой части уравнения (6.6), имеющей смысл внешнего воздействия с частотой ${{\omega }_{n}}$, равной частоте осцилляций капли, необходимо исключить секулярные слагаемые, пропорциональные $\exp \left( {i{{\omega }_{n}}{{T}_{0}}} \right)$.

Таким образом, приравнивая нулю выражение:

и, применяя соотношение (5.7) для $C_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)$, выраженной через функции $c_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)$, $b_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)$, несложно определить зависимость этих функций от временного масштаба ${{T}_{1}}$: где постоянные интегрирования $c_{n}^{{\left( 0 \right)}}$, $b_{n}^{{\left( 0 \right)}}$ находятся из начальных условий (2.11).

В итоге, при использовании условия (6.7) для амплитуд $M_{n}^{{\left( 1 \right)}}\left( t \right)$ будет справедливо соотношение:

Общее решение уравнения (6.6) при $n \geqslant 2$ с учетом исключенных секулярных членов будем искать в виде:

Подстановка разложения (3.1) в (2.11) при использовании (3.2) позволяет привести начальные условия первого порядка малости по $\varepsilon $:

Из решения системы (6.10) с учетом (3.3) при $k = 1$ и (6.7) действительные коэффициенты $c_{n}^{{\left( 0 \right)}}$, $b_{n}^{{\left( 0 \right)}}$ примут вид:

Для отыскания явного вида коэффициентов $c_{n}^{{\left( 2 \right)}}$, $b_{n}^{{\left( 2 \right)}}$ в решении (6.9) зададим начальные условия второго порядка малости по $\varepsilon $:

(напомним, что константы ${{\xi }_{1}}$ и ${{\xi }_{1}}$ пропорциональны ${{\varepsilon }^{2}}$). Из выписанных начальных условий найдем:

Наконец, подставляя (6.11), (6.12) в решения первого и второго порядков (6.8), (6.9), уравнение осциллирующей поверхности капли (2.1) приобретет следующий вид:

Заметим, что амплитудные коэффициенты $M_{0}^{{\left( 2 \right)}}\left( t \right)$, $M_{1}^{{\left( 2 \right)}}\left( t \right)$ в (6.13), (6.14) рассчитываются из условий сохранения объема капли (6.4) и отсутствия движения ее центра масс (6.5).

7. Монопольное акустическое излучение. Наличие в спектре капиллярных осцилляций второго порядка амплитуды нулевой моды ${{\alpha }_{0}}\left( t \right)$ = $R{{\varepsilon }^{2}}M_{0}^{{\left( 2 \right)}}\left( t \right)$, соответствующей радиальным пульсациям капли, превращает ее в источник звуковых волн монопольного типа.

Согласно (6.13) частота осцилляций центрально-симметричной моды ($n = 0$) в два раза выше частоты колебательной моды начальной деформации капли: ${{\omega }_{0}} = 2{{\omega }_{j}}$.

Выражение для интенсивности монопольного излучения, связанного с центрально-симметричной (нулевой) модой во втором порядке малости по $\varepsilon $, при условии $\lambda \gg R$ ($\lambda $ – длина излучаемой акустической волны), определяется ([6], с. 402) или ([3], с. 206), формулой:

В (7.1) амплитуда радиальной скорости ${{U}_{0}}$ движения точек поверхности капли находится в виде:

Подставляя (7.2) в (7.1) и придавая синусу его максимальное значение, с учетом того, что $\omega R{\text{/}}{v} \ll 1$, запишем окончательное выражение интенсивности монопольного излучения:

Используя полученное аналитическое выражение (7.3), оценим по порядку величины мощность монопольного звукового излучения от различных жидко-капельных объектов искусственного и естественного происхождения.

Источниками акустического излучения в конвективных облаках являются мелкие осциллирующие капли с типичными размерами от 3 до 30 мкм и максимальной концентрацией в облаке. Число таких капелек в 1 см³ облака ~10³ [18, 19]. Известно, что в процессе развития кучево-дождевых облаков в результате слияния внутриоблачных капель образуются мелкие дождевые капли размером $0.01 \leqslant R \leqslant 0.025$ см, относящиеся к мороси, и укрупненные дождевые капли при $0.025 \leqslant R \leqslant 0.35$ см. Более крупные капли, радиус которых превышает 0.35 см, при падении в воздухе разбиваются из-за аэродинамического сопротивления [20, 21]. Заметим, что осцилляции рассматриваемых облачных и дождевых капель могут быть вызваны коагуляцией неодинаковых по размеру капель из-за разностей их скоростей падения, дроблением на более мелкие в результате электростатической неустойчивости, а также электрического взаимодействия крупных заряженных капель с малыми электрически нейтральными [18]. Для нижеследующих оценок величину отношения амплитуды начальной деформации равновесной формы капли к ее радиусу примем, равную $\left| \xi \right|{\text{/}}R\sim e$. В анализируемом случае для характерных значений напряженности внешнего электрического поля величина параметра Тейлора много меньше критического значения ${{w}_{{{\text{кр}}}}} \approx 0.05$ [9]. Из этого следует, что большая часть капель находится далеко от предела электрогидродинамической неустойчивости по отношению к индуцированным зарядам.

Для получения численных оценок примем характеристики единичной капли и внешней среды: $\varepsilon = 0.001$, ${{\varepsilon }_{{ex}}} = 1$, ${{h}_{j}} = 1$, $\sigma = 73$ дин/см, ${{\rho }_{1}} = 1$ г/м³, ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м³, ${v} = 3.3 \times {{10}^{4}}$ см/с, ${{E}_{0}} = 0.17$ СГСЭ ($\sim {\kern 1pt} 2 \times {{10}^{{ - 4}}}{{E}_{{0{\text{кр}}}}}$ (${{E}_{{0{\text{кр}}}}}$ – критическое значение напряженности поля) при $R = 3$ мкм и $\sim {\kern 1pt} 7 \times {{10}^{{ - 3}}}{{E}_{{0{\text{кр}}}}}$ при $R = 0.35$ см). При принятых выше значениях физических величин и радиусе дождевой капли $R = 0.35\;см$ квадрат эксцентриситета капли ${{e}^{2}} = {{9E_{0}^{2}R} \mathord{\left/ {\vphantom {{9E_{0}^{2}R} {16\pi }}} \right. \kern-0em} {16\pi }}\sigma $ ≈ $2.5 \times {{10}^{{ - 5}}}$.

В соответствие с (7.3) положим, что возбуждение центрально-симметричной моды во втором порядке малости по $\varepsilon $ связано с наличием изначально возбужденной колебательной моды $j = 2$. Из (7.3) несложно видеть, что изменение интенсивности монопольного излучения от одной капли при изменении ее радиуса и напряженности внешнего электрического поля пренебрежимо мало. Интенсивность монопольного излучения капли при принятом выше соотношении между малыми параметрами и значениях входящих в (7.3) физических величин ${{I}_{0}}\sim 3 \times {{10}^{{ - 15}}}$ эрг/с.

8. Дипольное акустическое излучение.

Появление во втором порядке малости по $\varepsilon $ амплитуды первой моды ${{\alpha }_{1}}\left( t \right)$ = = $R{{\varepsilon }^{2}}M_{1}^{{\left( 2 \right)}}\left( t \right)$, соответствующей поступательному движению, приводит к генерации звуковых волн дипольного типа.

Из (6.14) следует, что возбуждение первой (трансляционной) моды ($n = 1$) имеет место, когда в спектре изначально возбужденных мод присутствуют две колебательные моды с последовательно возрастающими номерами $j - 1$, $j$.

В случае, когда равновеликий радиус $R$ капли сравним по величине с ${{\left( {{v}{\text{/}}{{\omega }_{n}}} \right)}^{{1{\text{/}}2}}}$, и при выполнении условий $\lambda \gg R$, $R{{\left( {{{\omega }_{n}}{\text{/}}2\nu } \right)}^{{1{\text{/}}2}}} \ll 1$, интенсивность дипольного акустического излучения, порождаемого осцилляциями трансляционной моды во втором порядке, находится в соответствии с известным выражением [6], стр. 401:

где $\nu $ – кинематическая вязкость окружающей каплю сжимаемой среды.

В (8.1) амплитудное значение скорости движения ${{U}_{1}}$ поверхности капли представляется в виде:

Для проведения качественной оценки по порядку величины в (8.2) заменим синусы на их максимальные значения, и из (8.1) получим:

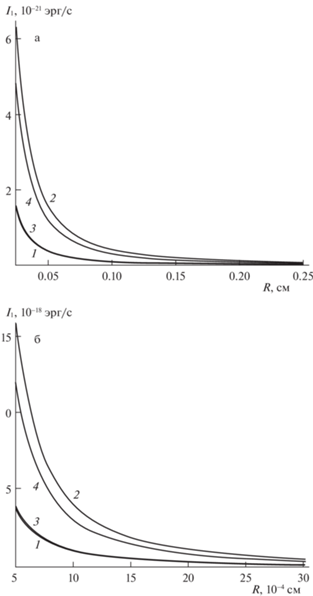
В отличие от монопольного излучения дипольное зависит от радиуса. На рис. 1 приведены и графики зависимости интенсивности дипольного акустического излучения ${{I}_{1}}$ дождевых и облачных капель от радиуса. Видно, что интенсивность дипольного излучения от облачных капель примерно на три порядка больше, чем от дождевых.

На рис. 2 приведены зависимости частот осцилляций центрально-симметричной моды, связанной с монопольным излучением (кривая 1), и трансляционной моды, определяющей дипольное излучение (кривые 2, 3), от размера дождевой капли. Видно, что увеличение радиуса приводит к быстрому снижению частоты.

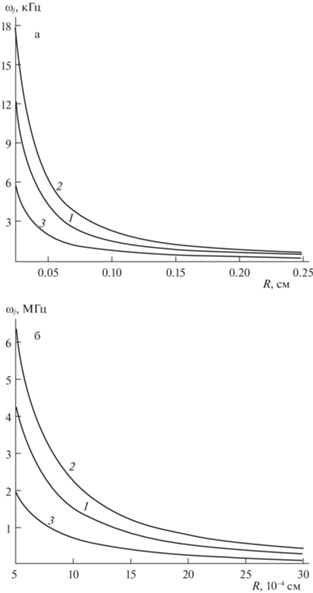
Из рис. 2 следует, что облачные капли излучают на ультразвуковых частотах в диапазоне от десятых долей МГц до 6 МГц. Но дождевые капли генерируют акустические волны в диапазоне слышимых человеческим ухом звуковых частот от десятых долей кГц до 18 кГц.

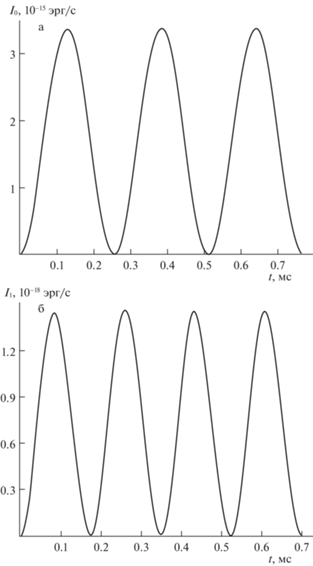
Если задаться вопросом о временной зависимости интенсивности монопольного и дипольного излучений, то оказывается, что она зависит качественно и количественно от количества мод, возбужденных в начальный момент времени. На рис. 3 приведены зависимости интенсивности излучения монопольной компоненты излучения от времени при простейшей начальной деформации типа $\varepsilon {{P}_{2}}\left( \mu \right)$ и дипольной компоненты также при простейшей начальной деформации вида $\varepsilon \left( {{{P}_{2}}\left( \mu \right) + {{P}_{3}}\left( \mu \right)} \right){\text{/}}2$. Из сравнения рис. 3, а и 3, б следует, что интенсивность монопольного излучения на шесть порядков превышает интенсивность дипольного и происходит на больших частотах, но в качественном отношении графики тривиальны.

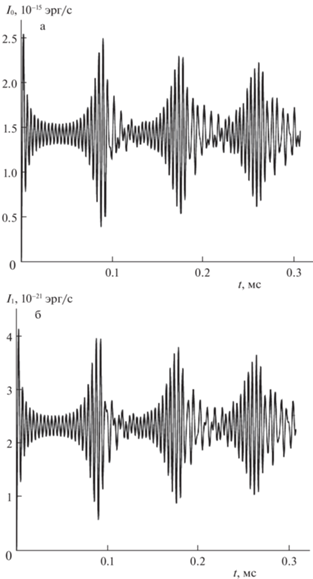
Если взять более сложные начальные деформации (см. рис. 4), то временной ход зависимости интенсивности монопольного и дипольного излучений становится более сложным, приобретая качественный вид биений. Амплитуда звукового сигнала начинает заметно зависеть от времени, хотя монопольное излучение по-прежнему на шесть порядков более интенсивно.

Проведенные оценки справедливы и для туманов с характерными размерами капель 2–10 мкм [22], излучающих акустические волны в ультразвуковом диапазоне частот.

Естественно задаться вопросом о причине возбуждения центрально симметричной и трансляционной мод в асимптотических расчетах более высоких порядков по малому параметру $\varepsilon $, чем первый. Представляется, что такой причиной может быть сам применяемый асимптотический метод, оставляющий в расчетах порядка $n$ (где $n$ – целое число) погрешность ~${{\varepsilon }^{n}}$, которая частично (на величину $ \sim {\kern 1pt} \varepsilon $) исправляется в расчетах следующего порядка малости. В этом случае появление в расчетах второго порядка малости в спектре возбуждаемых мод центрально симметричной и трансляционной носит компенсационный характер.

Заключение. В асимптотических расчетах второго порядка малости по отношению амплитуды начальной деформации к радиусу незаряженной капли идеальной несжимаемой жидкости, осциллирующей во внешнем электростатическом поле, показано, что возбуждение нулевой моды приводит к генерации в среде акустических волн монопольного типа. Присутствие в спектре изначально возбужденных мод двух и более с последовательными номерами приводит к появлению трансляционной (первой) моды в спектре возбуждающихся во втором порядке мод – генерирующей излучение акустических волн дипольного типа. Для дождевых капель, излучающих в диапазоне слышимых звуковых волн, монопольная компонента излучения на 6 порядков величины интенсивнее, чем дипольная составляющая. В случае излучения монопольного характера граница между ультразвуковыми и слышимыми звуковыми волнами смещается в область больших размеров капель (более чем в 1.5 раза) в сравнении с дипольным акустическим излучением. Кроме того, в отличие от электромагнитного излучения [23] влияние индуцированного заряда на интенсивность акустического излучения весьма мало.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 19-19-00598 “Гидродинамика и энергетика капли и капельных струй: формирование, движение, распад, взаимодействие с контактной поверхностью”, https://rscf.ru/project/19-19-00598/).