1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 6, 2022

Прикладная математика и механика, 2022, T. 86, № 6, стр. 784-800

О нелинейных колебаниях трехосного эллипсоида на гладкой горизонтальной плоскости

А. П. Маркеев 1, 2, *

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

2 Московский авиационный институт (НИУ)
Москва, Россия

* E-mail: anat-markeev@mail.ru

Поступила в редакцию 30.05.2022
После доработки 20.07.2022
Принята к публикации 20.07.2022

Полный текст (PDF)

Аннотация

Рассматривается движение однородного эллипсоида по неподвижной горизонтальной плоскости в однородном поле тяжести. Плоскость считается абсолютно гладкой, а полуоси эллипсоида различными. Существует положение устойчивого равновесия, когда эллипсоид опирается на плоскость наинизшей точкой своей поверхности. Исследуются нелинейные колебания эллипсоида в окрестности этого равновесия. Анализ осуществляется при помощи методов классической теории возмущений, КАМ – теории и алгоритмов компьютерной алгебры. Получена нормальная форма функции Гамильтона возмущенного движения до членов шестой степени включительно относительно отклонений от положения равновесия. Дано приближенное аналитическое представление колмогоровского множества условно-периодических колебаний, указана оценка меры этого множества. Исследована задача о существовании и орбитальной устойчивости периодических движений, рождающихся из устойчивого равновесия в резонансном и нерезонансном случаях.

Ключевые слова: твердое тело, условно-периодические и периодические колебания, устойчивость

Задача о движении твердого тела, соприкасающегося с твердой поверхностью, имеет почти трехсотлетнюю историю [1]. Эта задача интересна не только с общетеоретической точки зрения, она важна своими приложениями в машиностроении, приборостроении, транспорте. Интерес исследователей к этой задаче не ослабевает. Наоборот, в связи с бурным развитием работ по созданию робототехники этот интерес, по-видимому, возрастает все более и более.

Много исследований посвящено механико-математическим моделям, в которых предполагается, что твердое тело движется по плоскости, являющейся гладкой. В данной статье рассматривается динамика однородного трехосного эллипсоида на абсолютно гладкой плоскости в однородном поле тяжести. Этой задаче посвящено довольно много исследований. Отметим только основные из них.

В статье [2] получены условия, необходимые для устойчивости перманентного вращения эллипсоида вокруг его оси, направленной вдоль вертикали. Строгая нелинейная задача об устойчивости этого вращения исследована недавно в статье [3]; в этой же статье исследована устойчивость такого движения эллипсоида, в котором он касается плоскости одним из своих главных сечений, которое считалось близким к кругу. Общая задача о существовании и устойчивости перманентных вращений и регулярных прецессий тяжелого твердого тела на гладкой горизонтальной плоскости подробно изучена в [4–6].

В статьях [7, 8] при помощи КАМ-теории дан качественный анализ движения на неподвижной гладкой плоскости трехосного эллипсоида, мало отличающегося от шара.

Вопросы интегрируемости уравнений движения тяжелого твердого тела на гладкой плоскости изучались в [9–12]. В частности, показано [10], что в задаче о движении близкого к шару однородного трехосного эллипсоида не существует необходимый для интегрируемости интеграл, дополнительный к интегралу энергии.

Ниже исследуются нелинейные колебания однородного трехосного эллипсоида в окрестности его устойчивого положения равновесия. Используются кассические и современные методы исследования динамических систем, описываемых уравненями Гамильтона [13–15]. Необходимые вычисления существенно опираются на преобразование Биркгофа [16] и его модификации [17], удобные для их компьютерной реализации.

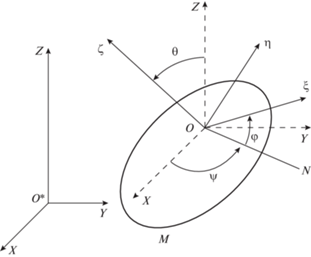
1. Введение. Уравнения движения. Рассмотрим движение однородного эллипсоида по неподвижной абсолютно гладкой плоскости в однородном поле тяжести. Полуоси $a,b$ и $c$ эллипсоида считаем различными и полагаем, что $a < b < c$. В системе координат $O\xi \eta \varsigma $ с началом в центре тяжести $O$ эллипсоида его поверхность задается уравнением

(1.1)
$\frac{{{{\xi }^{2}}}}{{{{a}^{2}}}} + \frac{{{{\eta }^{2}}}}{{{{b}^{2}}}} + \frac{{{{\varsigma }^{2}}}}{{{{c}^{2}}}} = 1$

Ориентация эллипсоида относительно неподвижной системы координат ${{O}_{*}}XYZ$ задается (см. рис. 1) углами Эйлера $\psi ,\theta ,\varphi $ или матрицей направляющих косинусов ${{a}_{{ij}}}$:

${{a}_{{11}}} = \cos \psi \cos \varphi - \sin \psi \sin \varphi \cos \theta ,\quad {{a}_{{12}}} = - \cos \psi \sin \varphi - \sin \psi \cos \varphi \cos \theta $
${{a}_{{13}}} = \sin \psi \sin \theta $
(1.2)
${{a}_{{21}}} = \sin \psi \cos \varphi + \cos \psi \sin \varphi \cos \theta ,\quad {{a}_{{22}}} = - \sin \psi \sin \varphi + \cos \psi \cos \varphi \cos \theta $
${{a}_{{23}}} = - \cos \psi \sin \theta $
${{a}_{{31}}} = \sin \varphi \sin \theta ,\quad {{a}_{{32}}} = \cos \varphi \sin \theta ,\quad {{a}_{{33}}} = \cos \theta $
Рис. 1.

На рис. 1 показана также система координат $OXYZ$, оси которой параллельны соответствующим осям системы ${{O}_{*}}XYZ$, через $ON$, как принято, обозначена линия узлов.

Координаты точки $M$, которой эллипсоид касается неподвижной опорной плоскости ${{O}_{*}}XY$, определяются [1] равенствами

(1.3)
$\xi = - \frac{{{{a}^{2}}}}{f}{{a}_{{31}}},\quad \eta = - \frac{{{{b}^{2}}}}{f}{{a}_{{32}}},\quad \varsigma = - \frac{{{{c}^{2}}}}{f}{{a}_{{33}}},$
где $f$ – расстояние от центра тяжести эллипсоида до плоскости ${{O}_{*}}XY$,

(1.4)
$f = \sqrt {{{a}^{2}}a_{{31}}^{2} + {{b}^{2}}a_{{32}}^{2} + {{c}^{2}}a_{{33}}^{2}} $

Так как плоскость абсолютно гладкая, то проекция центра тяжести эллипсоида на плоскость ${{O}_{*}}XY$ движется равномерно и прямолинейно. Не ограничивая общность, будем считать, что она неподвижна и, следовательно, точка $O$ движется вдоль фиксированной прямой, параллельной вертикальной оси ${{O}_{*}}Z$. При этом координаты точки $M$ на плоскости ${{O}_{*}}XY$ вычисляются [1] по формулам

(1.5)
${{X}_{M}} = {{a}_{{11}}}\xi + {{a}_{{12}}}\eta + {{a}_{{13}}}\varsigma ,\quad {{Y}_{M}} = {{a}_{{21}}}\xi + {{a}_{{22}}}\eta + {{a}_{{23}}}\varsigma $

Пусть $mg$ – вес эллипсоида, а $A,B,C$ – его главные центральные моменты инерции,

(1.6)
$A = \frac{1}{5}m\left( {{{b}^{2}} + {{c}^{2}}} \right),\quad B = \frac{1}{5}m\left( {{{c}^{2}} + {{a}^{2}}} \right),\quad C = \frac{1}{5}m\left( {{{a}^{2}} + {{b}^{2}}} \right)$

Обобщенные импульсы ${{p}_{\psi }},{{p}_{\theta }},{{p}_{\varphi }}$, соответствующие углам Эйлера $\psi ,\theta ,\varphi $, определяются [1] равенствами

(1.7)
$\begin{gathered} {{p}_{\psi }} = {{e}_{2}}\dot {\psi } + {{e}_{4}}\dot {\theta } + C\cos \theta \dot {\varphi },\quad {{p}_{\theta }} = {{e}_{4}}\dot {\psi } + {{e}_{3}}\dot {\theta } + m{{f}_{\theta }}{{f}_{\varphi }}\dot {\varphi } \\ {{p}_{\varphi }} = C\cos \theta \dot {\psi } + m{{f}_{\theta }}{{f}_{\varphi }}\dot {\theta } + {{e}_{1}}\dot {\varphi }, \\ \end{gathered} $
где точкой обозначено дифференцирование по времени $t$, ${{f}_{\theta }}$ и ${{f}_{\varphi }}$ – частные производные функции (1.4) по $\theta $ и $\varphi $ соответственно, а

(1.8)
$\begin{gathered} {{e}_{1}} = C + mf_{\varphi }^{2},\quad {{e}_{2}} = \left( {A{{{\sin }}^{2}}\varphi + B{{{\cos }}^{2}}\varphi } \right){{\sin }^{2}}\theta + C{{\cos }^{2}}\theta \\ {{e}_{3}} = A{{\cos }^{2}}\varphi + B{{\sin }^{2}}\varphi + mf_{\theta }^{2},\quad {{e}_{4}} = (A - B)\sin \theta \sin \varphi \cos \varphi \\ \end{gathered} $

Угол прецессии $\psi $ является циклической координатой, поэтому импульс ${{p}_{\psi }}$ постоянен во все время движения. Будем считать, что ${{p}_{\psi }} = 0$. Из (1.6)–(1.8) тогда следует, что при известных функциях $\theta (t)$, $\varphi (t)$ величина $\dot {\psi }$ может быть найдена из равенства

(1.9)
$\dot {\psi } = - \frac{{\left( {{{b}^{2}} - {{a}^{2}}} \right)\sin \theta \sin \varphi \cos \varphi \dot {\theta } + \left( {{{a}^{2}} + {{b}^{2}}} \right)\cos \theta \dot {\varphi }}}{{\left[ {\left( {{{b}^{2}} + {{c}^{2}}} \right){{{\sin }}^{2}}\varphi + \left( {{{c}^{2}} + {{a}^{2}}} \right){{{\cos }}^{2}}\varphi } \right]{{{\sin }}^{2}}\theta + \left( {{{a}^{2}} + {{b}^{2}}} \right){{{\cos }}^{2}}\theta }}$

Изменение переменных $\theta ,\varphi $ со временем определяется дифференциальными уравнениями

(1.10)
$\frac{{d\theta }}{{dt}} = \frac{{\partial H}}{{\partial {{p}_{\theta }}}},\quad \frac{{d\varphi }}{{dt}} = \frac{{\partial H}}{{\partial {{p}_{\varphi }}}},\quad \frac{{d{{p}_{\theta }}}}{{dt}} = - \frac{{\partial H}}{{\partial \theta }},\quad \frac{{d{{p}_{\varphi }}}}{{dt}} = - \frac{{\partial H}}{{\partial \varphi }}$
(1.11)
$\begin{gathered} H = \frac{{{{e}_{1}}{{e}_{2}} - {{C}^{2}}{{{\cos }}^{2}}\theta }}{{2\Delta }}p_{\theta }^{2} + \frac{{{{e}_{2}}{{e}_{3}} - e_{4}^{2}}}{{2\Delta }}p_{\varphi }^{2} + \frac{{C{{e}_{4}}\cos \theta - {{e}_{2}}m{{f}_{\theta }}{{f}_{\varphi }}}}{\Delta }{{p}_{\theta }}{{p}_{\varphi }} + mgf \\ \Delta = {{e}_{1}}{{e}_{2}}{{e}_{3}} - {{e}_{1}}e_{4}^{2} - {{C}^{2}}{{e}_{3}}{{\cos }^{2}}\theta + 2m{{f}_{\theta }}{{f}_{\varphi }}C{{e}_{4}}\cos \theta - {{m}^{2}}f_{\theta }^{2}f_{\varphi }^{2}{{e}_{2}} \\ \end{gathered} $

Уравнения движения (1.10) допускают частное решение, в котором $\theta \equiv \pi {\text{/}}2$, $\varphi \equiv \pi {\text{/}}2$. Это решение отвечает устойчивому положению равновесия эллипсоида, в котором он опирается на плоскость точкой $M$ своей поверхности, лежащей на наименьшей оси эллипсоида. Цель статьи состоит в исследовании нелинейных колебаний эллипсоида в окрестности этого положения равновесия.

2. Функция Гамильтона возмущенного движения и ее предварительное преобразование. Введем возмущения ${{q}_{1}},{{q}_{2}}$ углов Эйлера $\theta ,\varphi $ и безразмерные импульсы ${{p}_{1}},{{p}_{2}}$ возмущенного движения по формулам

(2.1)
$\theta = \frac{\pi }{2} + {{q}_{1}},\quad \varphi = \frac{\pi }{2} + {{q}_{2}},\quad {{p}_{\theta }} = m{{a}^{{3{\text{/}}2}}}{{g}^{{1{\text{/}}2}}}{{p}_{1}},\quad {{p}_{\varphi }} = m{{a}^{{3{\text{/}}2}}}{{g}^{{1{\text{/}}2}}}{{p}_{2}},$
и перейдем еще к безразмерному времени $\tau = {{(g{\text{/}}a)}^{{1{\text{/}}2}}}t$. Функция Гамильтона возмущенного движения может быть представлена в виде сходящегося ряда по формам четных степеней относительно ${{q}_{1}},{{q}_{2}},{{p}_{1}},{{p}_{2}}$. Отвечающая линеаризованным уравнениям возмущенного движения квадратичная форма имеет вид

(2.2)
${{H}_{2}} = \frac{1}{2}\left( {\frac{{{{c}^{2}} - {{a}^{2}}}}{{{{a}^{2}}}}q_{1}^{2} + \frac{{5{{a}^{2}}}}{{{{c}^{2}} + {{a}^{2}}}}p_{1}^{2}} \right) + \frac{1}{2}\left( {\frac{{{{b}^{2}} - {{a}^{2}}}}{{{{a}^{2}}}}q_{2}^{2} + \frac{{5{{a}^{2}}}}{{{{a}^{2}} + {{b}^{2}}}}p_{2}^{2}} \right)$

Соответствующие функции (2.2) канонические уравнения описывают малые линейные колебания эллипсоида с частотами ${{\omega }_{i}}$ $(i = 1,2)$,

(2.3)
${{\omega }_{1}}{\text{ }} = \sqrt {\frac{{5\left( {{{c}^{2}} - {{a}^{2}}} \right)}}{{{{c}^{2}} + {{a}^{2}}}}} ,\quad {{\omega }_{2}}{\text{ }} = \sqrt {\frac{{5\left( {{{b}^{2}} - {{a}^{2}}} \right)}}{{{{a}^{2}} + {{b}^{2}}}}} $

При принятом ранее предположении $a < b < c$ справедливо неравенство $0 < {{\omega }_{2}} < {{\omega }_{1}}$ < $\sqrt 5 $.

Для исследования нелинейной задачи целесообразно предварительно перейти к переменным ${{u}_{1}},{{u}_{2}}$, ${{{v}}_{1}},{{{v}}_{2}}$, отвечающим нормальным координатам линейной задачи. Для этого сделаем каноническое унивалентное преобразование ${{q}_{i}},{{p}_{i}} \to {{u}_{i}},{{{v}}_{i}}$по формулам:

(2.4)
${{q}_{1}} = a\sqrt {\frac{{{{\omega }_{1}}}}{{{{c}^{2}} - {{a}^{2}}}}} {{u}_{1}},\quad {{q}_{2}} = a\sqrt {\frac{{{{\omega }_{2}}}}{{{{b}^{2}} - {{a}^{2}}}}} {{u}_{2}},\quad {{p}_{1}} = \frac{1}{a}\sqrt {\frac{{{{c}^{2}} - {{a}^{2}}}}{{{{\omega }_{1}}}}} {{{v}}_{1}},\quad {{p}_{2}} = \frac{1}{a}\sqrt {\frac{{{{b}^{2}} - {{a}^{2}}}}{{{{\omega }_{2}}}}} {{{v}}_{2}}$

В новых переменных возмущенное движение описывается уравнениями с функцией Гамильтона, задающейся рядом

(2.5)
$H = \frac{1}{2}{{\omega }_{1}}\left( {u_{1}^{2} + {v}_{1}^{2}} \right) + \frac{1}{2}{{\omega }_{2}}\left( {u_{2}^{2} + {v}_{2}^{2}} \right) + \sum\limits_{s = 2}^\infty {{{H}_{{2s}}}} ,\quad {{H}_{{2s}}} = \sum\limits_{{{{v}}_{1}} + {{{v}}_{2}} + {{\mu }_{1}} + {{\mu }_{2}} = 2s} {{{h}_{{{{{v}}_{1}}{{{v}}_{2}}{{\mu }_{1}}{{\mu }_{2}}}}}u_{1}^{{{{\nu }_{1}}}}u_{2}^{{{{\nu }_{2}}}}} {v}_{1}^{{{{\mu }_{1}}}}{v}_{2}^{{{{\mu }_{2}}}}$

Отметим принципиально важное для дальнейшего анализа свойство разложения (2.5): в каждом его члене сумма показателей ${{\nu }_{i}} + {{\mu }_{i}}$ $(i = 1,2)$ является четным числом.

Коэффициенты форм четвертой и шестой степеней, после проведения довольно громоздких вычислений с привлечением алгоритмов компьютерной алгебры, можно выразить через частоты ${{\omega }_{1}}$ и ${{\omega }_{2}}$. Оказалось, что 27 из 35-ти коэффициентов формы ${{H}_{4}}$ тождественно равны нулю. Остальные 8 коэффициентов имеют вид

${{h}_{{4000}}} = - \frac{5}{{12}} - \frac{1}{{24}}\omega _{1}^{2},\quad {{h}_{{2200}}} = - \frac{{5{{\omega }_{2}}}}{{4{{\omega }_{1}}}},\quad {{h}_{{2020}}} = - \frac{1}{2}\omega _{1}^{4},\quad {{h}_{{2002}}} = - \frac{{5\delta \delta _{1}^{2}{{\omega }_{2}}}}{{4{{\omega }_{1}}}}$
(2.6)
${{h}_{{1111}}} = - \frac{1}{2}\delta \omega _{2}^{2}\left[ {25 - 60\omega _{1}^{2} + \left( {1 + 2\omega _{2}^{2}} \right)\omega _{1}^{4}} \right],\quad {{h}_{{0400}}} = - \frac{5}{{12}} - \frac{1}{{24}}\omega _{2}^{2}$
${{h}_{{0220}}} = \frac{1}{4}\delta {{\delta }_{1}}{{\delta }_{2}}{{\omega }_{1}}{{\omega }_{2}},\quad {{h}_{{0202}}} = - \frac{1}{2}\omega _{2}^{4}$

Здесь приняты обозначения

(2.7)
${{\delta }_{i}} = \omega _{i}^{2} - 5\quad (i = 1,2),\quad \delta = \frac{1}{{\omega _{1}^{2}\omega _{2}^{2} - 25}}$

Из 84-х коэффициентов формы ${{H}_{6}}$ тождественно равны нулю 72. Для остальных 12-ти коэффициентов можно получить следующие выражения:

${{h}_{{6000}}} = \frac{1}{{720{{\omega }_{1}}}}\left( {100 + 110\omega _{1}^{2} + 19\omega _{1}^{4}} \right),\quad {{h}_{{4200}}} = \frac{{{{\omega }_{2}}}}{{48\omega _{1}^{2}}}\left( {50 + 20\omega _{1}^{2} + 3\omega _{1}^{4}} \right)$
${{h}_{{4020}}} = \frac{{\omega _{1}^{3}}}{6}\left( {10 + \omega _{1}^{2} + 3\omega _{1}^{4}} \right),\quad {{h}_{{4002}}} = \frac{{5\delta \delta _{1}^{3}{{\omega }_{2}}}}{{12\omega _{1}^{2}}}$
${{h}_{{3111}}} = \frac{{\delta \omega _{2}^{2}}}{{12{{\omega }_{1}}}}\left[ { - 25\left( {5 + 17\omega _{1}^{2}} \right) - 5\left( {43 - 10\omega _{2}^{2}} \right)\omega _{1}^{4} - \left( {329 - 2\omega _{2}^{2}} \right)\omega _{1}^{6} + 6\left( {1 + 2\omega _{2}^{2}} \right)\omega _{1}^{8}} \right]$
${{h}_{{2400}}} = \frac{1}{{48{{\omega }_{1}}}}\left( {50 + 20\omega _{2}^{2} + 3\omega _{2}^{2}\omega _{1}^{2}} \right)$
${{h}_{{2220}}} = \frac{{\delta \omega _{1}^{2}{{\omega }_{2}}}}{2}\left[ {25{{\delta }_{2}} - 25\left( {1 + \omega _{2}^{2}} \right)\omega _{1}^{2} + \left( {5 + \omega _{2}^{4}} \right)\omega _{1}^{4}} \right]$
${{h}_{{2202}}} = \frac{{\delta \omega _{2}^{2}}}{{8{{\omega }_{1}}}}\left[ { - 125 + 5\left( {15 - 20\omega _{2}^{2} + 4\omega _{2}^{4}} \right)\omega _{1}^{2} - 15\left( {1 + 8\omega _{2}^{2}} \right)\omega _{1}^{4} + {{{\left( {1 + 2\omega _{2}^{2}} \right)}}^{2}}\omega _{1}^{6}} \right]$
${{h}_{{1311}}} = \frac{1}{6}\delta {{\omega }_{2}}\left[ {5\left( {25 - 60\omega _{1}^{2} + \omega _{1}^{4}} \right) + 2\left( { - 200 - 45\omega _{1}^{2} + 12\omega _{1}^{4}} \right)\omega _{2}^{2} + } \right.$
$ + \;\left( {75 - 150\omega _{1}^{2} + \omega _{1}^{4}} \right)\left. {\omega _{2}^{4} + 6\omega _{1}^{4}\omega _{2}^{6}} \right]$
${{h}_{{0600}}} = \frac{1}{{720{{\omega }_{2}}}}\left( {100 + 110\omega _{2}^{2} + 19\omega _{2}^{4}} \right)$
${{h}_{{0420}}} = \frac{1}{{24}}\delta {{\delta }_{1}}\delta _{2}^{2}{{\omega }_{1}},\quad {{h}_{{0402}}} = \frac{1}{6}\omega _{2}^{3}\left( {10 + \omega _{2}^{2} + 3\omega _{2}^{4}} \right)$

3. О возможных резонансах. Если для натуральных чисел ${{l}_{1}}$ и ${{l}_{2}}$ выполняется соотношение

(3.1)
${{l}_{1}}{{\omega }_{1}} = {{l}_{2}}{{\omega }_{2}},$
то имеет место резонанс порядка $l = {{l}_{1}} + {{l}_{2}}$ (так как ${{\omega }_{1}} > {{\omega }_{2}}$, то ${{l}_{2}} > {{l}_{1}} \geqslant 1$).

Введем безразмерные параметры $x,y$, положив ${{a}^{2}} = x{{c}^{2}}$, ${{b}^{2}} = y{{c}^{2}}$. Область допустимых значений параметров $x,y$ (в силу того, что $a < b < c$) задается неравенством

(3.2)
$0 < x < y < 1$

Частоты (2.3) выражаются через $x,y$ по формулам

(3.3)
${{\omega }_{1}} = \sqrt {\frac{{5(1 - x)}}{{1 + x}}} ,\quad {{\omega }_{2}} = \sqrt {\frac{{5(y - x)}}{{y + x}}} $

И из соотношения (3.1) следует уравнение соответствующей резонансной кривой

(3.4)
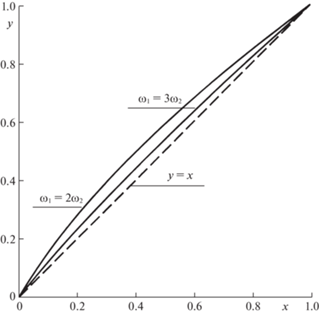
$y = x\frac{{\left( {l_{2}^{2} - l_{1}^{2}} \right)x + l_{2}^{2} + l_{1}^{2}}}{{\left( {l_{2}^{2} + l_{1}^{2}} \right)x + l_{2}^{2} - l_{1}^{2}}}$

На рис. 2 показаны кривые, отвечающие резонансам ${{\omega }_{1}} = 2{{\omega }_{2}}$ и ${{\omega }_{1}} = 3{{\omega }_{2}}$.

Рис. 2.

Несложно проверить, что все резонансные кривые (3.4) лежат в области

(3.5)
$\frac{{x(3x + 5)}}{{5x + 3}} \geqslant y > x$

Левой границей этой области является кривая ${{\omega }_{1}} = 2{{\omega }_{2}}$. В области

(3.6)
$\frac{{x(3x + 5)}}{{5x + 3}} < y < 1,$
лежащей на рис. 2 левее и выше кривой ${{\omega }_{1}} = 2{{\omega }_{2}}$ не реализуется ни один из резонансов (3.1).

4. О нормализации функции Гамильтона (2.5). Следуя [16, 17], введем вместо переменных ${{u}_{i}}$, ${{{v}}_{i}}$ новые канонически сопряженные переменные ${{Q}_{i}}$, ${{P}_{i}}$ при помощи производящей функции $S$ вида

(4.1)
$S = {{u}_{1}}{{P}_{1}} + {{u}_{2}}{{P}_{2}} + {{S}_{4}} + {{S}_{6}},\quad {{S}_{{2k}}} = \sum\limits_{{{{v}}_{1}} + {{{v}}_{2}} + {{\mu }_{1}} + {{\mu }_{2}} = 2k} {{{s}_{{{{{v}}_{1}}{{{v}}_{2}}{{\mu }_{1}}{{\mu }_{2}}}}}u_{1}^{{{{\nu }_{1}}}}u_{2}^{{{{\nu }_{2}}}}} P_{1}^{{{{\mu }_{1}}}}P_{2}^{{{{\mu }_{2}}}},\quad (k = 2,3)$

Неявно замена ${{u}_{i}},{{{v}}_{i}} \to {{Q}_{i}},{{P}_{i}}$ задается формулами

(4.2)
${{Q}_{i}} = \frac{{\partial S}}{{\partial {{P}_{i}}}},\quad {{{v}}_{i}} = \frac{{\partial S}}{{\partial {{u}_{i}}}}\quad (i = 1,\;2)$

Из (4.1), (4.2) следует, что старые переменные выражаются через новые при помощи сходящихся рядов по степеням ${{Q}_{1}},{{Q}_{2}},{{P}_{1}},{{P}_{2}}$:

(4.3)
${{u}_{i}} = {{Q}_{i}} - \frac{{\partial {{S}_{4}}}}{{\partial {{P}_{i}}}} + \sum\limits_{j = 1}^2 {\frac{{{{\partial }^{2}}{{S}_{4}}}}{{\partial {{P}_{i}}\partial {{Q}_{j}}}}} \frac{{\partial {{S}_{4}}}}{{\partial {{P}_{j}}}} - \frac{{\partial {{S}_{6}}}}{{\partial {{P}_{i}}}} + {{O}_{7}},\quad {{{v}}_{i}} = {{P}_{i}} + \frac{{\partial {{S}_{4}}}}{{\partial {{Q}_{i}}}} - \sum\limits_{j = 1}^2 {\frac{{{{\partial }^{2}}{{S}_{4}}}}{{\partial {{Q}_{i}}\partial {{Q}_{j}}}}} \frac{{\partial {{S}_{4}}}}{{\partial {{P}_{j}}}} + \frac{{\partial {{S}_{6}}}}{{\partial {{Q}_{i}}}} + {{O}_{7}}$

Здесь ${{S}_{4}}$ и ${{S}_{6}}$ – функции из (4.1), в которых аргументы ${{u}_{1}},{{u}_{2}}$ заменены на ${{Q}_{1}},{{Q}_{2}}$. Символом ${{O}_{n}}$ здесь и далее обозначается совокупность членов не ниже $n$-й степени относительно ${{Q}_{1}},{{Q}_{2}},{{P}_{1}},{{P}_{2}}$.

Подставив выражения (4.3) в функцию Гамильтона (2.5) и подобрав подходящим образом коэффициенты ${{s}_{{{{\nu }_{1}}{{\nu }_{2}}{{\mu }_{1}}{{\mu }_{2}}}}}$ форм ${{S}_{4}}$ и ${{S}_{6}}$, можно упростить (нормализовать) формы четвертой и шестой степеней в новой функции Гамильтона (ее, как и старую функцию (2.5), будем обозначать через $H$).

Так как в разложении (2.5) нет форм 3-й и 5-й степеней, а в форме 4-й степени суммы показателей ${{\nu }_{1}} + {{\mu }_{1}}$ и ${{\nu }_{2}} + {{\mu }_{2}}$ четны (см. п. 2), то все резонансы до пятого порядка включительно (${{\omega }_{1}} = 2{{\omega }_{2}}$, ${{\omega }_{1}} = 3{{\omega }_{2}}$, ${{\omega }_{1}} = 4{{\omega }_{2}}$, $2{{\omega }_{1}} = 3{{\omega }_{2}}$) не препятствуют приведению функции Гамильтона (2.5) к нормальной форме вида

(4.4)
$\begin{gathered} H = {{H}^{{(0)}}}({{r}_{1}},{{r}_{2}}) + {{O}_{6}},\quad {{H}^{{(0)}}} = {{\omega }_{1}}{{r}_{1}} + {{\omega }_{2}}{{r}_{2}} + {{c}_{{20}}}r_{1}^{2} + {{c}_{{11}}}{{r}_{1}}{{r}_{2}} + {{c}_{{02}}}r_{2}^{2} \\ \left( {{{Q}_{i}} = \sqrt {2{{r}_{i}}} \sin {{\varphi }_{i}},\quad {{P}_{i}} = \sqrt {2{{r}_{i}}} \cos {{\varphi }_{i}}} \right) \\ \end{gathered} $

При этом

(4.5)
$\begin{gathered} {{c}_{{20}}} = - \frac{1}{{16}}\left( {4\omega _{1}^{4} + \omega _{1}^{2} + 10} \right),\quad {{c}_{{02}}} = - \frac{1}{{16}}\left( {4\omega _{2}^{4} + \omega _{2}^{2} + 10} \right) \\ {{c}_{{11}}} = \frac{{{{\omega }_{1}}{{\omega }_{2}}\left[ {75 - 10\left( {\omega _{1}^{2} + \omega _{2}^{2}} \right) + \omega _{1}^{2}\omega _{2}^{2}} \right]}}{{4\left( {\omega _{1}^{2}\omega _{2}^{2} - 25} \right)}}, \\ \end{gathered} $
а отличные от тождественного нуля коэффициенты формы ${{S}_{4}}$ в производящей функции (4.1) вычисляются по следующим формулам:

${{s}_{{3010}}} = \frac{{12\omega _{1}^{4} - 5\omega _{1}^{2} - 50}}{{192{{\omega }_{1}}}},\quad {{s}_{{0301}}} = \frac{{12\omega _{2}^{4} - 5\omega _{2}^{2} - 50}}{{192{{\omega }_{2}}}}$
${{s}_{{1030}}} = - \frac{{4\omega _{1}^{4} + \omega _{1}^{2} + 10}}{{64{{\omega }_{1}}}},\quad {{s}_{{0103}}} = - \frac{{4\omega _{2}^{4} + \omega _{2}^{2} + 10}}{{64{{\omega }_{2}}}}$
(4.6)
$\begin{gathered} {{s}_{{1012}}} = \frac{{{{\omega }_{2}}\left[ {25\left( {\omega _{2}^{2} - 10} \right) + \left( {100 - 120\omega _{2}^{2} + \omega _{2}^{4}} \right)\omega _{1}^{2} + 2\left( { - 5 + \omega _{2}^{2} + 2\omega _{2}^{4}} \right)\omega _{1}^{4}} \right]}}{{16\left( {\omega _{1}^{2} - \omega _{2}^{2}} \right)\left( {\omega _{1}^{2}\omega _{2}^{2} - 25} \right)}} \\ {{s}_{{0121}}} = - \frac{{{{\omega }_{1}}\left[ {25\left( {\omega _{1}^{2} - 10} \right) + \left( {100 - 120\omega _{1}^{2} + \omega _{1}^{4}} \right)\omega _{2}^{2} + 2\left( { - 5 + \omega _{1}^{2} + 2\omega _{1}^{4}} \right)\omega _{2}^{4}} \right]}}{{16\left( {\omega _{1}^{2} - \omega _{2}^{2}} \right)\left( {\omega _{1}^{2}\omega _{2}^{2} - 25} \right)}} \\ \end{gathered} $
${{s}_{{1210}}} = \frac{{{{\omega }_{2}}\left[ {25\left( {10 - 3\omega _{2}^{2}} \right) + \left( { - 50 + 120\omega _{2}^{2} + \omega _{2}^{4}} \right)\omega _{1}^{2} + 2\left( {5 - 2\omega _{2}^{2} - 2\omega _{2}^{4}} \right)\omega _{1}^{4}} \right]}}{{16\left( {\omega _{1}^{2} - \omega _{2}^{2}} \right)\left( {\omega _{1}^{2}\omega _{2}^{2} - 25} \right)}}$
${{s}_{{2101}}} = \frac{{ - 500\omega _{2}^{2} + 10\left( {25 + 15\omega _{2}^{2} + \omega _{2}^{4}} \right)\omega _{1}^{2} - 5\left( {5 + 28\omega _{2}^{2}} \right)\omega _{1}^{4} + \omega _{2}^{2}\left( {3 + 4\omega _{2}^{2}} \right)\omega _{1}^{6}}}{{16{{\omega }_{1}}\left( {\omega _{1}^{2} - \omega _{2}^{2}} \right)\left( {\omega _{1}^{2}\omega _{2}^{2} - 25} \right)}}$

После вычисления функции ${{S}_{4}}$ и величин (4.5) можно, выбрав нужным образом форму ${{S}_{6}}$, максимально упростить (нормализовать) совокупность членов шестой степени в новой функции Гамильтона. Из двух возможных резонансов шестого порядка ${{\omega }_{1}} = 5{{\omega }_{2}}$ и $2{{\omega }_{1}} = 4{{\omega }_{2}}$ первый не скажется на виде нормальной формы членов шестой степени (из-за четности величин ${{\nu }_{1}} + {{\mu }_{1}}$ и ${{\nu }_{2}} + {{\mu }_{2}}$ в разложении (2.5)). Второй же резонанс (который на самом деле является резонансом третьего порядка, не повлиявшим на структуру нормальной формы (4.4)) существенен при нормализации членов шестой степени. Этот резонансный случай изучается в разд. 8 статьи.

5. Невырожденность и изоэнергетическая невырожденность системы с функцией Гамильтона ${{H}^{{(0)}}}$. Рассмотрим определитель ${{D}_{2}}$ второго порядка

(5.1)
${{D}_{2}} = \det \left\| {\begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial r_{1}^{2}}}}&{\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial {{r}_{1}}\partial {{r}_{2}}}}} \\ {\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial {{r}_{2}}\partial {{r}_{1}}}}}&{\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial r_{2}^{2}}}} \end{array}} \right\| = 4{{c}_{{20}}}{{c}_{{02}}} - c_{{11}}^{2}$

Покажем, что система с функцией Гамильтона ${{H}^{{(0)}}}$ из (4.4) является невырожденной. Это означает [14, 15], что ${{D}_{2}} \ne 0$. Действительно, принимая во внимание (4.5) и (3.3), определитель (5.1) можно записать в виде функции от $x,y$:

(5.2)
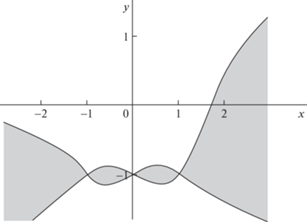
$\begin{gathered} {{D}_{2}} = \frac{{25}}{{64{{{(1 + x)}}^{2}}{{{(1 + y)}}^{2}}{{{(x + y)}}^{2}}}}[(487{{x}^{2}} - 828x + 525){{y}^{4}} - \\ - \;(724{{x}^{3}} - 2270{{x}^{2}} + 2516x - 1050){{y}^{3}} + (501{{x}^{4}} - 2236{{x}^{3}} + 3502{{x}^{2}} - \\ - \;2516x + 525){{y}^{2}} - 2x(16{{x}^{4}} - 437{{x}^{3}} + 1118{{x}^{2}} - 1135x + 414)y - \\ - \;{{x}^{2}}(64{{x}^{4}} + 32{{x}^{3}} - 501{{x}^{2}} + 724x - 487)] \\ \end{gathered} $

На рис. 3 в плоскости $x,y$ сплошными линиями показаны ветви кривой ${{D}_{2}} = 0$, а серым цветом выделены области ${{D}_{2}} < 0$. В остальной части рисунка величина ${{D}_{2}}$ положительна. Область (3.2) допустимых значений параметров $x,y$ попадает в область ${{D}_{2}} > 0$ рисунка. И, следовательно, система с функцией Гамильтона ${{H}^{{(0)}}}$ является невырожденной.

Рис. 3.

Покажем еще, что выполнено также условие изоэнергетической невырожденности, означающее [14, 15] отличие от нуля определителя ${{D}_{3}}$ третьего порядка,

(5.3)
${{D}_{3}} = \det \left\| {\begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial r_{1}^{2}}}}&{\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial {{r}_{1}}\partial {{r}_{2}}}}}&{{{\omega }_{1}}} \\ {\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial {{r}_{2}}\partial {{r}_{1}}}}}&{\frac{{{{\partial }^{2}}{{H}^{{(0)}}}}}{{\partial r_{2}^{2}}}}&{{{\omega }_{2}}} \\ {{{\omega }_{1}}}&{{{\omega }_{2}}}&0 \end{array}} \right\| = - 2\left( {{{c}_{{20}}}\omega _{2}^{2} - {{c}_{{11}}}{{\omega }_{1}}{{\omega }_{2}} + {{c}_{{02}}}\omega _{1}^{2}} \right)$

В переменных $x,y$ имеем

(5.4)
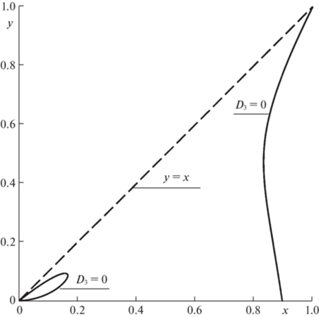
$\begin{gathered} {{D}_{3}} = \frac{{25}}{{4{{{(1 + x)}}^{2}}(1 + y){{{(x + y)}}^{2}}}}\left[ {\left( {{{x}^{2}} - 18x + 21} \right){{y}^{3}} + \left( {26{{x}^{3}} + {{x}^{2}} - 44x + 21} \right){{y}^{2}} - } \right. \\ \left. { - \;x\left( {23{{x}^{3}} - 36{{x}^{2}} - x + 18} \right)y - {{x}^{2}}\left( {8{{x}^{3}} + 23{{x}^{2}} - 26x - 1} \right)} \right] \\ \end{gathered} $

На рис. 4 сплошными линиями показаны ветви кривой ${{D}_{3}} = 0$. Они лежат правее и ниже прямой $y = x$. В области же (3.2) допустимых значений $x,y$ величина ${{D}_{3}}$ отлична от нуля (там ${{D}_{3}} > 0$).

Рис. 4.

6. Условно-периодические колебания. 1. Общее решение дифференциальных уравнений приближенной системы с функцией Гамильтона ${{H}^{{(0)}}}({{r}_{1}},{{r}_{2}})$ из (4.4) описывается равенствами

(6.1)
${{Q}_{i}} = \sqrt {2{{r}_{{i0}}}} \sin {{\varphi }_{i}},\quad {{P}_{i}} = \sqrt {2{{r}_{{i0}}}} \cos {{\varphi }_{i}},\quad {{\varphi }_{i}} = {{\Omega }_{i}}\tau + {{\varphi }_{{i0}}}\quad (i = 1,2)$
(6.2)
${{\Omega }_{1}} = {{\omega }_{1}} + 2{{c}_{{20}}}{{r}_{{10}}} + {{c}_{{11}}}{{r}_{{20}}},\quad {{\Omega }_{2}} = {{\omega }_{2}} + {{c}_{{11}}}{{r}_{{10}}} + 2{{c}_{{02}}}{{r}_{{20}}},$
где ${{r}_{{i0}}},{{\varphi }_{{i0}}}$ – постоянные, являющееся начальными значениями переменных ${{r}_{i}},{{\varphi }_{i}}$. Если полуоси эллипсоида таковы, что нет резонанса (3.1), то для малых значений ${{r}_{{i0}}}$ движения в приближенной системе будут условно-периодическими колебаниями с рационально независимыми частотами (6.2).

Но в предыдущем разд. показано, что приближенная система невырождена. Поэтому, согласно КАМ-теории, движения в полной системе, описываемой функцией Гамильтона (4.4), для большинства начальных условий также будут условно-периодическими с частотами (6.2). Множество начальных условий, не принадлежащих упомянутому большинству (колмогоровскому множеству), имеет малую меру: в окрестности ${{r}_{1}} + {{r}_{2}} < \mu $ его относительная мера имеет порядок ${{\mu }^{{\frac{{l - 3}}{4}}}}$, где $l$ – порядок, до которого отсутствуют резонансы вида (3.1) [14]. Согласно разд. 3, в области безразмерных параметров $x,y$, задаваемой неравенством (3.5), можно считать, что $l = 5$. Если же параметры $x,y$ принадлежат области (3.6) (где отсутствуют резонансы (3.1)), то величина $l$ может быть сколь угодно большой. Для области (3.6) относительная мера множества, дополнительного к колмогоровскому множеству, имеет порядок $\exp \left( { - \frac{{{{c}_{1}}}}{{{{\mu }^{{{{c}_{2}}}}}}}} \right)$, ${{c}_{1}},{{c}_{2}}$ – const > 0.

2. Остановимся подробнее на приближенном описании движения эллипсоида при помощи уравнений с функцией ${{H}^{{(0)}}}$ из (4.4). Из соотношений (4.3) имеем

(6.3)
${{u}_{i}} = {{Q}_{i}} - \frac{{\partial {{S}_{4}}}}{{\partial {{P}_{i}}}} + {{O}_{5}},\quad {{{v}}_{i}} = {{P}_{i}} + \frac{{\partial {{S}_{4}}}}{{\partial {{Q}_{i}}}} + {{O}_{5}}$

Коэффициенты формы ${{S}_{4}}$ вычисляются по формулам (4.6).

Из (6.3) и (2.4) получаем выражения для углов Эйлера $\theta ,\varphi $

(6.4)
$\theta = \frac{\pi }{2} + {{q}_{1}} = \frac{\pi }{2} + a\sqrt {\frac{{{{\omega }_{1}}}}{{{{c}^{2}} - {{a}^{2}}}}} {{Q}_{1}} + {{O}_{3}},\quad \varphi = \frac{\pi }{2} + {{q}_{2}} = \frac{\pi }{2} + a\sqrt {\frac{{{{\omega }_{2}}}}{{{{b}^{2}} - {{a}^{2}}}}} {{Q}_{2}} + {{O}_{3}}$

Угол $\psi $ может быть найден при помощи равенства (1.9), из которого (при учете (6.4)) следует, что производная $\dot {\psi }$ имеет порядок ${{O}_{2}}$. Поэтому $\psi $ совершает “мелкие дрожания” в окрестности его начального значения ${{\psi }_{0}}$. Пренебрегая этими дрожаниями, можно считать, что $\psi = {{\psi }_{0}} = 0$. Из (1.2) тогда следует, что с погрешностью ${{O}_{2}}$ направляющие косинусы ${{a}_{{ij}}}$ определяются следующими равенствами:

(6.5)
${{a}_{{11}}} = {{a}_{{32}}} = - {{q}_{2}},\quad {{a}_{{21}}} = {{a}_{{33}}} = - {{q}_{1}},\quad {{a}_{{31}}} = - {{a}_{{12}}} = - {{a}_{{23}}} = 1,\quad {{a}_{{13}}} = {{a}_{{22}}} = 0$

3. Получим оценку реакции $R$ опорной плоскости ${{O}_{*}}XY$. Из (6.5) и (1.4) следует, что для расстояния $f$ центра тяжести эллипсоида до плоскости ${{O}_{*}}XY$ имеет место равенство $f = a + {{O}_{2}}$. Поэтому из уравнения

$m\frac{{{{d}^{2}}f}}{{d{{t}^{2}}}} = - mg + R,$
описывающего движение центра тяжести вдоль вертикали, следует, что $R = mg + {{O}_{2}}$. При малых отклонениях эллипсоида от положения равновесия реакция не обращается в нуль и эллипсоид не может оторваться от плоскости ${{O}_{*}}XY$.

4. Выпишем еще приближенные выражения (1.3) и (1.5) для траекторий точки касания $M$ на поверхности эллипсоида и на опорной плоскости. Из (1.3), (1.4), (6.5) и (6.1) следуют приближенные (с погрешностью ${{O}_{2}}$) формулы для координат точки $M$ в системе $O\xi \eta \varsigma $, жестко связанной с эллипсоидом:

(6.6)
$\xi = - a,\quad \eta = {{A}_{\eta }}\sin {{\varphi }_{2}},\quad \varsigma = {{A}_{\varsigma }}\sin {{\varphi }_{1}}\quad \left( {{{A}_{\eta }} = {{b}^{2}}\sqrt {\frac{{2{{\omega }_{2}}{{r}_{{20}}}}}{{{{b}^{2}} - {{a}^{2}}}}} ,\quad {{A}_{\varsigma }} = {{c}^{2}}\sqrt {\frac{{2{{\omega }_{1}}{{r}_{{10}}}}}{{{{c}^{2}} - {{a}^{2}}}}} } \right)$

Из (1.5), (6.5) и (6.6) с погрешностью ${{O}_{2}}$ находим выражения для координат точки $M$ на плоскости ${{O}_{*}}XY$:

$\begin{gathered} {{X}_{M}} = - {{A}_{X}}\sin {{\varphi }_{2}},\quad {{Y}_{M}} = - {{A}_{Y}}\sin {{\varphi }_{1}} \\ \left( {{{A}_{X}} = \sqrt {2{{\omega }_{2}}\left( {{{b}^{2}} - {{a}^{2}}} \right){{r}_{{20}}}} ,\quad {{A}_{Y}} = \sqrt {2{{\omega }_{1}}\left( {{{c}^{2}} - {{a}^{2}}} \right){{r}_{{10}}}} } \right) \\ \end{gathered} $

При условно-периодических колебаниях проекция траектории точки $M$ на плоскость $O\eta \varsigma $ всюду плотно заполняет прямоугольник со сторонами $2{{A}_{\eta }}$ и $2{{A}_{\varsigma }}$, а на опорной плоскости ${{O}_{*}}XY$ траектория всюду плотно заполняет прямоугольник со сторонами $2{{A}_{X}}$ и $2{{A}_{Y}}$.

В качестве примера возьмем эллипсоид, у которого ${{b}^{2}} = 11{\text{/}}9{{a}^{2}}$, ${{c}^{2}} = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{{a}^{2}}$. Для него ${{\omega }_{1}} = 1$, ${{\omega }_{2}} = {{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } 2}} \right. \kern-0em} 2}$, а

${{A}_{\eta }} = \frac{{11a}}{{3\sqrt[4]{2}}}\sqrt {{{r}_{{20}}}} ,\quad {{A}_{\varsigma }} = 3a\sqrt {{{r}_{{10}}}} ,\quad {{A}_{X}} = \frac{{2a}}{{3\sqrt[4]{2}}}\sqrt {{{r}_{{20}}}} ,\quad {{A}_{Y}} = a\sqrt {{{r}_{{10}}}} $

7. О периодических колебаниях малой амплитуды. Уравнения (1.10) допускают два типа частных решений, для которых эллипсоид касается плоскости одним из своих главных сечений. Для решений первого типа эллипсоид касается оси ${{O}_{*}}Y$ главным сечением $\eta = 0$, которое во все время движения остается в вертикальной плоскости ${{O}_{*}}YZ$. В движениях второго типа эллипсоид касается оси ${{O}_{*}}X$ главным сечением $\varsigma = 0$, которое все время остается в плоскости ${{O}_{*}}XZ$.

Будем рассматривать эти движения, предполагая, что они представляют собой малые периодические колебания эллипсоида. Через $\varepsilon $ обозначим малый параметр, характеризующий отклонение углов $\theta $ и φ от их значений, отвечающих равновесию $\theta = \pi {\text{/}}2$, $\varphi = \pi {\text{/}}2$. Зависимость углов $\theta $ и φ от времени для этих колебаний может быть найдена из (6.1)–(6.4).

В колебаниях первого типа $\varphi \equiv \pi {\text{/}}2$, а

(7.1)
$\theta = \frac{\pi }{2} + \varepsilon a\sqrt {\frac{{{{\omega }_{1}}}}{{{{c}^{2}} - {{a}^{2}}}}} {{U}_{1}} + O\left( {{{\varepsilon }^{4}}} \right)$

В колебаниях второго типа $\theta \equiv \pi {\text{/}}2$,

(7.2)
$\varphi = \frac{\pi }{2} + \varepsilon a\sqrt {\frac{{{{\omega }_{2}}}}{{{{b}^{2}} - {{a}^{2}}}}} {{U}_{2}} + O\left( {{{\varepsilon }^{4}}} \right)$

В (7.1) и (7.2) приняты обозначения

${{U}_{i}} = \sin {{\varphi }_{i}} + {{\varepsilon }^{2}}\frac{{\sin {{\varphi }_{i}}}}{{192{{\omega }_{i}}}}\left[ {9\left( {4\omega _{i}^{4} + \omega _{i}^{2} + 10} \right) - 4\left( {12\omega _{i}^{4} + \omega _{i}^{2} + 10} \right){{{\sin }}^{2}}{{\varphi }_{i}}} \right]$
${{\varphi }_{i}} = {{\Omega }_{i}}\tau + {{\varphi }_{{i0}}},\quad \left( {i = 1,2} \right),\quad {{\Omega }_{1}} = {{\omega }_{1}} + {{c}_{{20}}}{{\varepsilon }^{2}} + O\left( {{{\varepsilon }^{4}}} \right),\quad {{\Omega }_{2}} = {{\omega }_{2}} + {{c}_{{02}}}{{\varepsilon }^{2}} + O\left( {{{\varepsilon }^{4}}} \right)$

Для исследования орбитальной устойчивости периодических колебаний (7.1) и (7.2) воспользуемся теоремой Мозера об инвариантных кривых. При малых $\varepsilon $ достаточным условием устойчивости будет условие изоэнергетической невырожденности ${{D}_{3}} \ne 0$ функции ${{H}^{{(o)}}}$ из (4.4) [14, 15]. В разд. 4 показано, что это условие выполняется. И, следовательно, при малых амплитудах периодические колебания обоих типов орбитально устойчивы.

8. О колебаниях при резонансе ${{\omega }_{1}} = 2{{\omega }_{2}}$. Сделав нормализуюшую замену переменных ${{u}_{i}},{{{v}}_{i}} \to {{Q}_{i}},{{P}_{i}}$ по формулам (4.3) и введя симплектические полярные координаты ${{r}_{i}},{{\varphi }_{i}}$ (см. (4.4)), получим функцию Гамильтона возмущенного движения (2.5) в виде ряда

(8.1)
$H = {{\omega }_{1}}{{r}_{1}} + \frac{1}{2}{{\omega }_{1}}{{r}_{2}} + \sum\limits_{m + n = 2}^3 {{{c}_{{mn}}}} r_{1}^{m}r_{2}^{n} + {{\alpha }_{{12}}}{{r}_{1}}r_{2}^{2}\cos (2{{\varphi }_{1}} - 4{{\varphi }_{2}}) + {{O}_{{10}}}$

Коэффициенты нормальной формы (8.1) можно записать в виде следующих функций от ${{\omega }_{1}}$:

${{c}_{{20}}} = - \frac{1}{{16}}\left( {10 + \omega _{1}^{2} + 4\omega _{1}^{4}} \right),\quad {{c}_{{02}}} = - \frac{1}{{64}}\left( {40 + \omega _{1}^{2} + \omega _{1}^{4}} \right)$
${{c}_{{11}}} = \frac{{\omega _{1}^{2}\left( {300 - 50\omega _{1}^{2} + \omega _{1}^{4}} \right)}}{{8\left( {\omega _{1}^{4} - 100} \right)}},\quad {{c}_{{30}}} = \frac{{48\omega _{1}^{8} + 24\omega _{1}^{6} + 255\omega _{1}^{4} + 60\omega _{1}^{2} - 100}}{{256{{\omega }_{1}}}}$
${{c}_{{03}}} = \frac{{3\omega _{1}^{8} + 6\omega _{1}^{6} + 255\omega _{1}^{4} + 240\omega _{1}^{2} - 1600}}{{2048{{\omega }_{1}}}}$
(8.2)
${{c}_{{21}}} = \frac{1}{{384{{\omega }_{1}}{{{\left( {\omega _{1}^{4} - 100} \right)}}^{2}}}}\left( {16\omega _{1}^{{16}} + 24\omega _{1}^{{14}} - 2681\omega _{1}^{{12}} - 3740\omega _{1}^{{10}} + } \right.$
$\left. { + \;87\,500\omega _{1}^{8} - 82\,000\omega _{1}^{6} + 4\,440\,000\omega _{1}^{4} - 2\,800\,000\omega _{1}^{2} + 4\,000\,000} \right)$
${{c}_{{12}}} = - \frac{1}{{384{{\omega }_{1}}{{{\left( {\omega _{1}^{4} - 100} \right)}}^{2}}}}\left( {2\omega _{1}^{{16}} + 12\omega _{1}^{{14}} - 787\omega _{1}^{{12}} + 680\omega _{1}^{{10}} + } \right.$
$\left. { + \;70\,000\omega _{1}^{8} - 386\,000\omega _{1}^{6} + 1\,230\,000\omega _{1}^{4} - 4\,400\,000\omega _{1}^{2} + 8\,000\,000} \right)$
(8.3)
${{\alpha }_{{12}}} = \frac{{3\omega _{1}^{3}\left( {\omega _{1}^{4} - 89\omega _{1}^{2} - 450} \right)}}{{512\left( {\omega _{1}^{2} + 10} \right)}}$

Для исследования периодических движений, обусловленных наличием резонанса ${{\omega }_{1}} = 2{{\omega }_{2}}$, сделаем в (8.1) унивалентное каноническое преобразование ${{\varphi }_{i}},{{r}_{i}} \to {{\chi }_{i}},{{R}_{i}}$ по формулам

(8.4)
${{r}_{1}} = {{R}_{1}},\quad {{r}_{2}} = {{R}_{2}} - 2{{R}_{1}},\quad {{\varphi }_{1}} = {{\chi }_{1}} + 2{{\chi }_{2}},\quad {{\varphi }_{2}} = {{\chi }_{2}}$

Если в преобразованной функции (8.1) отбросить последнее слагаемое ${{O}_{{10}}}$, то придем к приближенной системе с циклической координатой ${{\chi }_{2}}$. Помимо интеграла энергии, эта система имеет еще интеграл ${{R}_{2}} = \tilde {c}$ = const > 0. Если вместо ${{\chi }_{1}},{{R}_{1}}$ ввести новые канонически сопряженные переменные $\chi ,\rho $ по формулам

(8.5)
${{\chi }_{1}} = \chi ,\quad {{R}_{1}} = \tilde {c}\rho \quad (0 < \rho < 1{\text{/}}2),$
а в качестве независимой переменной принять величину $s = \tilde {c}\tau $, то получим систему с одной степенью свободы, являющуюся приближенной моделью для описания рассматриваемого резонанса. Ее функция Гамильтона $\Gamma (\chi ,\rho ;\tilde {c})$ будет такой:

(8.6)
$\begin{gathered} \Gamma = \left[ {{{c}_{{11}}} - 4{{c}_{{02}}} + \tilde {c}({{c}_{{12}}} - 6{{c}_{{03}}})} \right]\rho + \left[ {{{c}_{{20}}} - 2{{c}_{{11}}} + 4{{c}_{{02}}} - \tilde {c}\left( {4{{c}_{{12}}} - {{c}_{{21}}} - 12{{c}_{{03}}}} \right)} \right]{{\rho }^{2}} + \\ + \;\tilde {c}\left( {{{c}_{{30}}} - 2{{c}_{{21}}} + 4{{c}_{{12}}} - 8{{c}_{{03}}}} \right){{\rho }^{3}} + \tilde {c}{{\alpha }_{{12}}}\rho {{\left( {1 - 2\rho } \right)}^{2}}\cos 2\chi \\ \end{gathered} $

Соответствующие канонические уравнения имеют вид

(8.7)
$\frac{{d\rho }}{{ds}} = - \frac{{\partial \Gamma }}{{\partial \chi }} = \tilde {c}2{{\alpha }_{{12}}}\rho \left( {1 - 2\rho } \right)\sin 2\chi ,\quad \frac{{d\chi }}{{ds}} = \frac{{\partial \Gamma }}{{\partial \rho }}$

Эти уравнения допускают четыре отличающихся одно от другого равновесных решения ${{\chi }_{*}},{{\rho }_{*}}$, в которых

(8.8)
${{\chi }_{*}} = \frac{{k\pi }}{2}\quad (k = 0,1,2,3),$
а ${{\rho }_{*}}$ – корень квадратного относительно $\rho $ уравнения
(8.9)
$\frac{{\partial \Gamma }}{{\partial \rho }} = 0,$
в левой части которого $\cos 2\chi $ заменен на ${{( - 1)}^{k}}$. При малых значениях параметра $\tilde {c}$ этот корень можно представить в виде ряда по степеням $\tilde {c}$: ${{\rho }_{*}} = {{\rho }_{0}} + \tilde {c}{{\rho }_{1}} + \ldots $. Из (8.6) и (8.9) следует, что для ${{\rho }_{0}}$ можно получить такое выражение:
(8.10)
${{\rho }_{0}} = \frac{{{{c}_{{11}}} - 4{{c}_{{02}}}}}{{4{{D}_{3}}}}\omega _{1}^{2},$
где ${{D}_{3}}$ задается равенством (5.3).

Из выражений (8.2) для ${{c}_{{mn}}}$ (с учетом того, что $0 < {{\omega }_{1}} < \sqrt 5 $) видно, что величина ${{c}_{{11}}} - 4{{c}_{{02}}}$ положительна. Кроме того, согласно разд. 5, величина ${{D}_{3}} > 0$. Вычисления показывают, что $0 < {{\rho }_{0}} < 0.406834$, а своего максимального значения величина ${{\rho }_{0}}$ достигает, когда $b = 1.021617a$, $c = 1.089528a$.

Характеристическое уравнение линеаризованной в окрестности равновесия ${{\chi }_{*}},{{\rho }_{*}}$ системы (8.7) имеет вид

(8.11)
${{\lambda }^{2}} + {{( - 1)}^{k}}4\tilde {c}{{\rho }_{0}}{{\alpha }_{{12}}}\omega _{1}^{2}\frac{{{{{({{c}_{{11}}} - {{c}_{{20}}})}}^{2}}}}{{{{D}_{3}}}} + O\left( {{{{\tilde {c}}}^{2}}} \right) = 0$

Из (8.2) и (8.3) несложно усмотреть, что ${{c}_{{11}}} \ne {{c}_{{20}}}$, а ${{\alpha }_{{12}}} < 0$. И так как ${{D}_{3}} > 0$, то при малых $\tilde {c}$ найденным равновесиям в случае четных $k$ в фазовой плоскости отвечают особые точки типа седло, а в случае нечетных $k$ – точки типа центр.

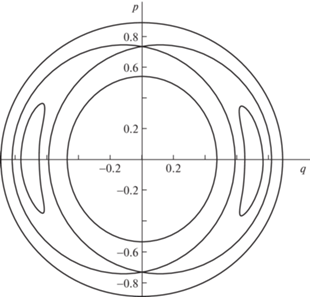
Для иллюстрации сказанного на рис. 5 показан фазовый портрет системы (8.7) в плоскости $q = \sqrt {2\rho } \sin \chi $, $p = \sqrt {2\rho } \cos \chi $.

Рис. 5.

Принято, что параметр $\tilde {c} = 1{\text{/}}10$, а форма эллипсоида такова, что ${{b}^{2}} = 3{\text{/}}2{{a}^{2}}$, ${{c}^{2}} = 9{{a}^{2}}$.

Для такого эллипсоида ${{\omega }_{1}} = 2$, ${{\omega }_{2}} = 1$, а равновесное значение ${{\rho }_{*}} = 0.268311$ для седел и ${{\rho }_{*}} = 0.252613$ для центров.

При помощи метода Пуанкаре [13] можно показать, что в полной системе с функцией Гамильтона (8.1) существуют периодические движения, аналитические относительно $\varepsilon $ ($\varepsilon $ – порядок величин ${{q}_{i}},{{p}_{i}}$ в (2.1)), которые в переменных ${{Q}_{1}},{{Q}_{2}}$ записываются (с погрешностью ${{O}_{2}}$) в виде

${{Q}_{1}} = \sqrt {2\tilde {c}{{\rho }_{*}}} \sin \left( {k\pi {\text{/}}2 + 2{{\varphi }_{2}}} \right),\quad {{Q}_{2}} = \sqrt {2\tilde {c}\left( {1 - 2{{\rho }_{*}}} \right)} \sin {{\varphi }_{2}},\quad {{\varphi }_{2}} = {{\Omega }_{2}}\tau + {{\varphi }_{0}}$
(8.12)
${{\Omega }_{2}} = {{\omega }_{2}} + \left[ {{{c}_{{11}}}{{\rho }_{*}} + 2{{c}_{{02}}}\left( {1 - 2{{\rho }_{*}}} \right)} \right]\tilde {c} + $
$ + \;\left\{ {{{c}_{{21}}}\rho _{*}^{2} + 2\left[ {{{c}_{{12}}} + {{{( - 1)}}^{k}}{{\alpha }_{{12}}}} \right]{{\rho }_{*}}\left( {1 - 2{{\rho }_{*}}} \right) + 3{{c}_{{03}}}{{{\left( {1 - 2{{\rho }_{*}}} \right)}}^{2}}} \right\}{{\tilde {c}}^{2}} + O\left( {{{{\tilde {c}}}^{3}}} \right)$

При четных $k$ эти периодические движения орбитально неустойчивы, а при нечетных – устойчивы.

Для координат $\xi ,\eta ,\varsigma $ точки касания $M$ на поверхности эллипсоида аналогично разд. 6 можно получить такие приближенные выражения:

(8.13)
$\xi = - a,\quad \eta = {{b}^{2}}\sqrt[4]{{\frac{5}{{{{b}^{4}} - {{a}^{4}}}}}}{{Q}_{2}},\quad \varsigma = {{c}^{2}}\sqrt[4]{{\frac{5}{{{{c}^{4}} - {{a}^{4}}}}}}{{Q}_{1}},$
а для координат ${{X}_{M}},{{Y}_{M}}$ точки $M$ на плоскости ${{O}_{*}}XY$ – выражения

(8.14)
${{X}_{M}} = \left( {{{a}^{2}} - {{b}^{2}}} \right)\sqrt[4]{{\frac{5}{{{{b}^{4}} - {{a}^{4}}}}}}{{Q}_{2}},\quad {{Y}_{M}} = \left( {{{a}^{2}} - {{c}^{2}}} \right)\sqrt[4]{{\frac{5}{{{{c}^{4}} - {{a}^{4}}}}}}{{Q}_{1}}$

В (8.13), (8.14) ${{Q}_{1}}$ и ${{Q}_{2}}$ вычисляются по формулам (8.12).

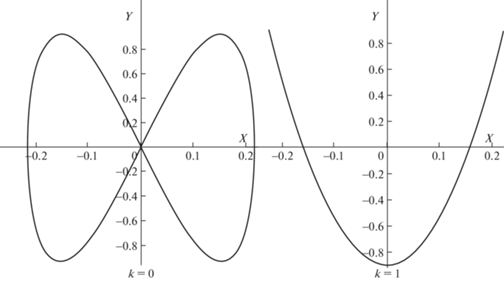
Траектории проекции точки $M$ на главную плоскость $O\eta \varsigma $ эллипсоида, как и траектории точки $M$ на опорной плоскости ${{O}_{*}}XY$, существенно различны в случаях четных и нечетных значений $k$. При четных $k$ (когда периодическое движение неустойчиво) они являются “лежащими восьмерками”, а при нечетных $k$ (когда периодическое движение орбитально устойчиво) – дважды проходимыми за период параболами.

На рис. 6 показаны траектории точки касания $M$на плоскости ${{O}_{*}}XY$ для случаев $k = 0$ и $k = 1$. Как и на рис. 5, принято, что ${{b}^{2}} = 3{\text{/}}2{{a}^{2}}$, ${{c}^{2}} = 9{{a}^{2}}$, а $\tilde {c} = 1{\text{/}}10$. В качестве единицы длины принята длина полуоси $a$ эллипсоида. При таком выборе параметров для $k = 0$

${{X}_{M}} = - 0.215262\sin {{\varphi }_{2}},\quad {{Y}_{M}} = - 0.926605\sin 2{{\varphi }_{2}},$
а для $k = 1$

${{X}_{M}} = - 0.222435\sin {{\varphi }_{2}},\quad {{Y}_{M}} = - 0.899089\cos 2{{\varphi }_{2}}$
Рис. 6.

Работа выполнена за счет гранта Российского научного фонда (проект № 19-11-00116) в Московском авиационном институте (Национальном исследовательском университете) и в Институте проблем механики им. А.Ю. Ишлинского РАН.

Список литературы

  1. Маркеев А.П. Динамика тела, соприкасающегося с твердой поверхностью. М.; Ижевск: Ин-т компьют. исслед., 2014. 496 с.

  2. Puiseux V. Solution de quelques question relatives au mouvement d’un corps solide pesant pos’e sur un plan horizontale // J. des math’ematiques pures et appliqu’ees. 1852. T. 17. P. 1–30.

  3. Маркеев А.П., Мощук Н.К. Об устойчивости движения эллипсоида на абсолютно гладкой горизонтальной плоскости // Механика твердого тела. Киев, 1984. Вып. 16. С. 56–64.

  4. Карапетян А.В. Об устойчивости стационарных движений тяжелого твердого тела на абсолютно гладкой горизонтальной плоскости // ПММ. 1981. Т. 45. Вып. 3. С. 504–511.

  5. Карапетян А.В., Рубановский В.Н. О бифуркации и устойчивости перманентных вращений тяжелого трехосного эллипсоида на гладкой плоскости // ПММ. 1987. Т. 51. Вып. 2. С. 260–267.

  6. Карапетян А.В., Румянцев В.В. Устойчивость консервативных и диссипативных систем. Итоги науки и техники. Общая механика. Т. 6. М.: ВИНИТИ, 1983. 132 с.

  7. Маркеев А.П. О движении тяжелого однородного эллипсоида на неподвижной горизонтальной плоскости // ПММ. 1982. Т. 46. Вып. 4. С. 553–567.

  8. Маркеев А.П., Мощук Н.К. Качественный анализ движения тяжелого твердого телана гладкой горизонтальной плоскости // ПММ. 1983. Т. 47. Вып. 1. С. 37–42.

  9. Буров А.А. О частных интегралах уравнений движения твердого тела по гладкой горизонтальной плоскости // В сб.: Задачи исследования устойчивости и стабилизации движения. М.: ВЦ АН СССР, 1985. С.118–121.

  10. Буров А.А., Карапетян А.В. О несуществовании дополнительного интеграла в задаче о движении тяжелого твердого эллипсоида по гладкой плоскости // ПММ. 1985. Т. 49. Вып. 3. С. 501–503.

  11. Сальникова Т.В. О существовании дополнительных аналитических интегралов в динамике твердого тела. Дис. … канд. физ.-мат. наук. М., 1985. 101 с.

  12. Сумбатов А.С. Некоторые инвариантные соотношения в задаче о движении тела по горизонтальной гладкой плоскости // ПММ. 1988. Т. 52. Вып. 4. С. 34–41.

  13. Малкин И.Г. Некоторые задачи теории нелинейных колебаний. М.: Гостехиздат, 1956. 492 с.

  14. Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики. М.: Эдиториал УРСС, 2002. 416 с.

  15. Мозер Ю. Лекции о гамильтоновых системах. М.: Мир, 1973. 167 с.

  16. Биркгоф Дж.Д. Динамические системы. М.; Л.: Гостехиздат, 1941. 320 с.

  17. Джакалья Г.Е. О. Методы теории возмущений для нелинейных систем. М.: Наука, 1979. 320 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал