1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 86, № 6, 2022

Прикладная математика и механика, 2022, T. 86, № 6, стр. 926-937

Устойчивость адвективного течения в горизонтальном теплоизолированном снизу слое жидкости с твердыми границами

К. Г. Шварц 1, *, Ю. А. Шварц 1, **

1 Пермский государственный национальный исследовательский университет
Пермь, Россия

* E-mail: kosch@psu.ru
** E-mail: jul-schwarz@psu.ru

Поступила в редакцию 15.05.2022
После доработки 05.08.2022
Принята к публикации 15.08.2022

Полный текст (PDF)

Аннотация

Исследуется устойчивость адвективного течения в плоском горизонтальном слое несжимаемой жидкости с твердыми границами. На верхней границе слоя задано линейное распределение температуры, нижняя граница теплоизолированная. Плоскопараллельное течение, возникшее под действием горизонтальной конвекции, описывается аналитически в виде точного решения уравнений Навье–Стокса в приближении Буссинеска. В рамках линейной теории исследуется устойчивость адвективного течения на нормальные возмущения при различных значениях числа Прандтля. Определяются наиболее опасные моды, строятся нейтральные кривые. В рамках нелинейной постановки задачи изучается структура конечно-амплитудных возмущений в надкритической области вблизи минимумов нейтральных кривых.

Ключевые слова: горизонтальная конвекция, адвективные течения, точное решение, нормальные возмущения, устойчивость, конечно-амплитудные возмущения

Адвективное течение возникает в плоском горизонтальном слое несжимаемой жидкости при наличии продольного градиента температуры [1]. В ситуации, когда температура на одной или обеих его горизонтальных границах является линейной функцией ($T = Ax$, где $x$ – продольная координата, $A$ – постоянный горизонтальный температурный градиент на границах слоя), течение описывается аналитическим выражением, которое является точным решением уравнений Навье–Стокса [2, 3]. Если обе границы твердые, на которых задано условие прилипания, то возникает течение Остроумова–Бириха [4]. Устойчивость такого течения исследована в [5]. В обзоре [3] описан класс подобных аналитических решений, обзор устойчивости различных адвективных, описанных таким образом течений, представлен в [6].

В последние годы появилось аналитическое описание адвективных термокапиллярных течений в условиях невесомости [7, 8], представлены точные решения уравнений Навье–Стокса, описывающие плоскопараллельное адвективное течение в горизонтальном слое несжимающейся жидкости с твердыми границами, на которых задано линейное распределение температуры разных знаков, либо линейный горизонтальный температурный градиент [9], с внутренним линейным источником тепла [10], при наличии условия проскальзывания Навье [11], при наличии акустической волны [12–14], исследована устойчивость адвективного течения феррожидкости [15]. Сформулирован новый класс точных решений уравнений Навье–Стокса, описывающих адвективные течения, когда температура на границах слоя распределяется по квадратичному закону. Задача сводится к решению нелинейной системы нестационарных одномерных уравнений [16–18]. В работе [19] был учтен слабый наклон слоя и в качестве жидкости была рассмотрена бинарная молекулярная смесь с положительной термодиффузией. В этой задаче тоже имеется точное аналитическое решение, в предельном случае вырождающееся в классическое плоскопараллельное движение Остроумова–Бириха. В этой работе было показано, что реализующееся течение переносит примесь в один угол и в результате данная система может использоваться как сепаратор для жидких молекулярных смесей.

Адвективное течение в горизонтальном слое жидкости с обеими теплоизолированными границами описано аналитически в [19]. В этом случае кубический профиль скорости остается неизменным, а в профиле температуры отсутствуют зоны потенциально неустойчивой стратификации, тем самым исключаются моды неустойчивости рэлеевской природы. Линейный анализ устойчивости, проведенный в [20], показал, что опасные гидродинамические моды возникают при малых числах Прандтля (Pr) от 0.015 до 0.27. Имеется немало работ по исследованию подобных течений при наличии однородного продольного градиента температуры численно и аналитически как в двумерной постановке [21–24], так и в трехмерной [25, 26], а также опубликованы экспериментальные работы [27, 28].

Влияние вращения на адвективное течение в плоском слое жидкости при числе Прандтля (Pr) равного 0.1 с твердыми границами с одной нижней теплоизолированной границей исследовалось в [29], где было выявлено несколько наиболее опасных мод неустойчивости. Это побудило к изучению влияния Pr на устойчивость адвективного течения в горизонтальном слое жидкости при теплоизолированной нижней границе при отсутствии вращения.

1. Математическая модель. Рассмотрим бесконечный горизонтальный слой несжимаемой жидкости шириной $2h$ с твердыми границами, помещенный в однородное поле тяжести. Движение жидкости описывается уравнениями конвекции в приближении Буссинеска [1] в декартовой системе координат $Oxyz$ ($z$ – вертикальная, $x$, $y$ – горизонтальные координаты). Выбрав в качестве единиц измерения длины, времени, скорости, температуры и давления $h$, ${{h}^{2}}{\text{/}}\nu $, $g\beta A{{h}^{3}}{\text{/}}\nu $, $Ah$, ${{\rho }_{0}}g\beta A{{h}^{3}}$ (где $\nu $ – кинематическая вязкость, $\beta $ – коэффициент теплового расширения, $g$ – ускорение свободного падения, ${{\rho }_{0}}$ – средняя плотность) получим исходные уравнения в безразмерном виде

$\frac{{\partial u}}{{\partial t}} + {\text{Gr}}\left[ {u\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial x}} + \Delta u$
$\frac{{\partial {v}}}{{\partial t}} + {\text{Gr}}\left[ {u\frac{{\partial {v}}}{{\partial x}} + {v}\frac{{\partial {v}}}{{\partial y}} + w\frac{{\partial {v}}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial y}} + \Delta {v}$
(1.1)
$\frac{{\partial w}}{{\partial t}} + {\text{Gr}}\left[ {u\frac{{\partial w}}{{\partial x}} + {v}\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial z}} + \Delta w + T$
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$
$\frac{{\partial T}}{{\partial t}} + {\text{Gr}}\left[ {u\frac{{\partial T}}{{\partial x}} + {v}\frac{{\partial T}}{{\partial y}} + w\frac{{\partial T}}{{\partial z}}} \right] = \frac{1}{{{\text{Pr}}}}\Delta T$
${\text{Gr}} = \frac{{g\beta A{{h}^{4}}}}{{{{\nu }^{2}}}},\quad {\text{Pr}} = \frac{\nu }{\chi }$

Здесь $u$, ${v}$, $w$ – компоненты вектора скорости v, $T$ – температура и $p$ – давление, зависящие от времени $t$ и пространственных координат $x$, $y$, $z$; Gr – число Грасгофа, $\chi $ – коэффициент температуропроводности, оператор Лапласа $\Delta = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}}$ + ${{\partial }^{2}}{\text{/}}\partial {{y}^{2}}$ + ${{\partial }^{2}}{\text{/}}\partial {{z}^{2}}$. Граничные условия в безразмерном виде имеют вид:

(1.2)
$z = - 1{\kern 1pt} :\;\frac{{\partial T}}{{\partial z}} = 0,\quad {\mathbf{v}} = 0;\quad z = 1{\kern 1pt} :\;T = x,\quad {\mathbf{v}} = 0$

Течение замкнутое:

(1.3)
$\int\limits_{ - 1}^1 {udz} = 0,\quad \int\limits_{ - 1}^1 {{v}dz} = 0$

Краевая задача (1.1)–(1.3) имеет аналитическое решение [24]:

(1.4)
$\begin{gathered} {{u}_{0}}\left( z \right) = \frac{1}{6}\left( {{{z}^{3}} - z} \right),\quad {{{v}}_{0}}\left( z \right) \equiv {{w}_{0}}\left( z \right) \equiv 0,\quad {{T}_{0}} = x + \operatorname{Gr} \Pr {{\tau }_{0}}\left( z \right) \\ {{\tau }_{0}}\left( z \right) = \frac{1}{{360}}\left[ {3{{z}^{5}} - 10{{z}^{3}} + 15z - 8} \right] \\ \end{gathered} $

Скорость имеет антисимметричный кубический профиль и совпадает с [4] для твердых границ, профиль температуры не обладают симметрией.

2. Линейная теория. Для исследования устойчивости адвективного течения (1.4) применяется метод малых возмущений [5]

(2.1)
${\mathbf{v}} = {{{\mathbf{v}}}_{0}} + {\mathbf{V}},\quad {{{\mathbf{v}}}_{0}} = \left( {{{u}_{0}}0,0} \right),\quad {\mathbf{V}} = \left( {U,V,W} \right),\quad T = {{T}_{0}} + \theta ,\quad P = {{p}_{0}} + P{\kern 1pt} '$
$\frac{{\partial {\mathbf{V}}}}{{\partial t}} + \operatorname{Gr} \left[ {\left( {{\mathbf{V}}\nabla } \right){\mathbf{V}} + \left( {{\mathbf{V}}\nabla } \right){{{\mathbf{v}}}_{0}} + \left( {{{{\mathbf{v}}}_{0}}\nabla } \right){\mathbf{V}}} \right] = - \nabla P{\kern 1pt} '\; + \Delta {\mathbf{V}} + \theta {{i}_{z}};\quad {{i}_{z}} = \left( {0,0,1} \right)$
(2.2)
$\operatorname{div} {\mathbf{V}} = 0$
$\frac{{\partial \theta }}{{\partial t}} + \operatorname{Gr} \left[ {{\mathbf{V}}\nabla \theta + {\mathbf{V}}\nabla {{T}_{0}} + {{{\mathbf{v}}}_{0}}\nabla \theta } \right] = \frac{1}{{{\text{Pr}}}}\Delta \theta $
(2.3)
$z = - 1{\kern 1pt} :\;\;U = V = W = 0,\quad \frac{{\partial \theta }}{{\partial z}} = 0$
(2.4)
$z = 1{\kern 1pt} :\;\;U = V = W = 0,\quad \theta = 0$

Здесь V, $\theta $, P ′ – малые возмущения вектора скорости, температуры и давления. В рамках линейной теории устойчивости в уравнениях (2.2)–(2.4) пренебрегаем малыми квадратичными по возмущениям V и $\theta $ слагаемыми. Полученная система линейных уравнений имеет решения в виде нормальных возмущений, пропорциональных $\exp \left( {\lambda t + {{k}_{x}}x + {{k}_{y}}y} \right)$, где $\lambda = {{\lambda }_{1}} + i{{\lambda }_{2}}$, – декремент, определяющий временной ход возмущений. Вещественные коэффициенты ${{k}_{x}}$ и ${{k}_{y}}$ – это компоненты волнового вектора вдоль осей $Ox$ и $Oy$. Следуя [1, 5], изучаются два хорошо известных [12] предельных случая. Это плоские периодические возмущения в виде валов с осью, параллельной оси $Ox$ и пространственные спиральные периодические по y возмущения в виде валов с осью, перпендикулярной к оси $Ox$.

Случай плоских возмущений. Уравнения возмущений выводятся из линеаризованной системы (2.2)–(2.4) в предположении, что производная по $y$ от всех функций равна нулю (${{k}_{y}} = 0$). Возмущения скорости и температуры являются функциями времени $t$ и двух пространственных координат $x$ и $z$. Численным методом, описанном в [29–31], решается начально-краевая задача для системы линейных уравнений в частных производных по времени $t$ и переменной $z$.

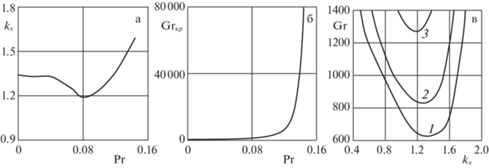
Расчеты показали, что аналогично [20, 22] только при малых значениях числа Прандтля ($0 \leqslant \Pr < 0.16$) возникает опасная колебательная гидродинамическая мода. Волновое число ${{k}_{x}}$ убывает при $0 \leqslant \Pr < 0.08$ (рис. 1а) и принимает минимальное значение ${{k}_{x}} = 1.19$ при $\Pr = 0.08$, а затем оно монотонно возрастает с ростом числа Прандтля. Критическое число Грасгофа (${\text{G}}{{{\text{r}}}_{{{\text{кр}}}}}$) возрастает при всех значениях Pr (рис. 1б). На рис. 1в представлены характерные нейтральные кривые при 1 – $\Pr = 0.04$, 2 – $\Pr = 0.06$ и 3 – $\Pr = 0.08$.

Рис. 1.

Случай спиральных возмущений. Уравнения спиральных возмущений выводятся из системы (2.2)–(2.4) в предположении, что производные в ней по $x$ от всех функций равны нулю (${{k}_{x}} = 0$). Имеются три компоненты вектора возмущения скорости, а также возмущения температуры, которые являются функциями времени $t$ и двух пространственных переменных $y$, $z$. Полученная начально-краевая задача решается по вычислительной схеме аналогично случаю плоских возмущений.

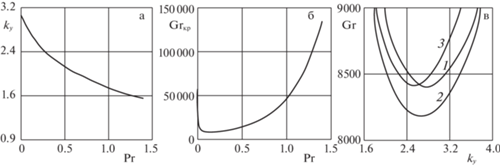
Расчеты показали, что в отличие от плоских возмущений при малых значениях числа Прандтля возникает опасная монотонная гидродинамическая мода. С ростом Pr волновое число ${{k}_{y}}$ уменьшается (рис. 2а), критическое число Грасгофа уменьшается от 57243.4 до 8182.7 при $0 \leqslant \Pr < 0.14$ (рис.2б), то есть происходит дестабилизация адвективного течения на данном интервале. При $\Pr = 0.14$ ${\text{G}}{{{\text{r}}}_{{{\text{кр}}}}}$ достигает минимального значения, затем оно монотонно возрастает с ростом числа Прандтля, течение становится более устойчивым. В качестве примера на рис. 2в представлены нейтральные кривые при 1 – $\Pr = 0.1$, 2 – $\Pr = 0.14$ и 3 – $\Pr = 0.2$.

Рис. 2.

3. Конечно-амплитудные возмущения. Возмущения конечной амплитуды в надкритической области исследуются на основе нелинейной системы уравнений (2.2)–(2.4).

Случай плоских возмущений. Для плоских периодических по $x$ возмущений система имеет вид

$\frac{{\partial \varphi }}{{\partial t}} + {\text{Gr}}\left[ { - \frac{{\partial \psi }}{{\partial z}}\frac{{\partial \varphi }}{{\partial x}} + \frac{{\partial \psi }}{{\partial x}}\frac{{\partial \varphi }}{{\partial z}} + {{u}_{0}}\left( z \right)\frac{{\partial \varphi }}{{\partial x}} + u_{0}^{{''}}\left( z \right)\frac{{\partial \psi }}{{\partial x}}} \right] = \Delta \varphi - \frac{{\partial \theta }}{{\partial x}}$
(3.1)
$\Delta \psi + \varphi = 0$
$\frac{{\partial \theta }}{{\partial t}} + {\text{Gr}}\left[ { - \frac{{\partial \psi }}{{\partial z}}\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \psi }}{{\partial x}}\frac{{\partial \theta }}{{\partial z}} + {{u}_{0}}\left( z \right)\frac{{\partial \theta }}{{\partial x}} - \frac{{\partial \psi }}{{\partial z}} + \operatorname{Ra} \theta _{0}^{'}\left( z \right)\frac{{\partial \psi }}{{\partial x}}} \right] = \frac{1}{{\Pr }}\Delta \theta $
(3.2)
$z = - 1{\kern 1pt} :\;\;\psi = 0,\quad \frac{{\partial \psi }}{{\partial z}} = 0,\quad \frac{{\partial \theta }}{{\partial z}} = 0$
(3.3)
$z = 1{\kern 1pt} :\;\;\psi = 0,\quad \frac{{\partial \psi }}{{\partial z}} = 0,\quad \theta = 0$
(3.4)
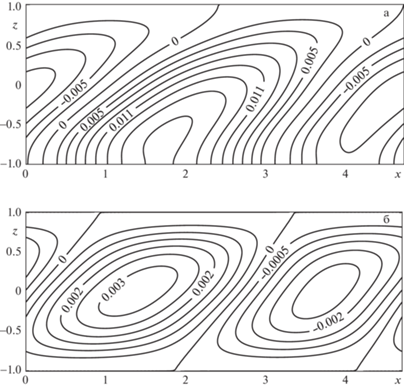
$\psi \left( {t,0,z} \right) = \psi \left( {t,L,z} \right),\quad \varphi \left( {t,0,z} \right) = \varphi \left( {t,L,z} \right),~\quad \theta \left( {t,0,z} \right) = \theta \left( {t,L,z} \right),$
где $L$ – длина волны возмущений, оператор Лапласа $\Delta = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}}$ + ${{\partial }^{2}}{\text{/}}\partial {{z}^{2}}$, $\psi \left( {t,x,z} \right)$, $\varphi \left( {t,x,z} \right)$, $\theta \left( {t,x,z} \right)$ – конечно-амплитудные возмущения функции тока (U = –∂ψ/∂z, W = ∂ψ/∂x), вихря скорости (φ = ∂U/∂z – ∂W/∂x = –Δψ) и температуры.

Нелинейная задача (3.1)–(3.4) решалась численно методом сеток [31]. В рамках двухполевого метода [33] использовалась явная конечно-разностная схема. Уравнение Пуассона для функции тока решалась методом последовательной верхней релаксации. Основные расчеты проводились на сетке 101 × 200, они подтвердили критические значения числа Грасгофа, найденные в линейной теории. Было выявлено два типа конечно-амплитудных возмущений. При малых значениях числа Прандтля в диапазоне $0 \leqslant \Pr < 0.033$ вдоль слоя образуется пара чередующихся теплых и холодных пятен. На рис. 3а представлены изотермы возмущения температуры при $\Pr = 0.02$, для ${\text{Gr}} = 600$ выше критического, ${{k}_{x}} = 1.33$. В силу теплоизоляции нижней границы слоя жидкости тепловые пятна имеют форму близкую к полуокружности. Соответственно возникает цепочка вихрей, попарно вращающихся по часовой и против часовой стрелки (рис. 3б). Центры вихрей расположены в середине слоя вблизи центров теплого и холодного пятна. Несмотря на наличие линейного распределения температуры на верхней границе, при $\Pr = 0.02$ структура конечно-амплитудных возмущений скорости для плоских возмущений практически совпала с результатами работы [22], где обе горизонтальные границы слоя жидкости теплоизолированные. Это свидетельствует о превалирующем влиянии температурной стратификации в центре слоя жидкости на конечно-амплитудные возмущения скорости и слабом влиянии изменения граничных условий (3.3).

Рис. 3.

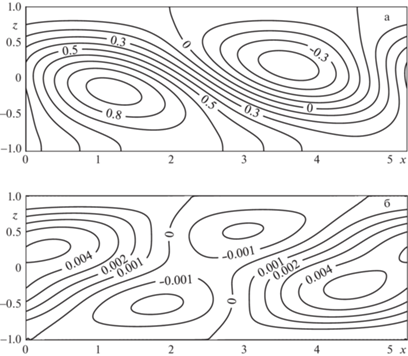
При значениях $\Pr \geqslant 0.033$ имеется пара теплых и холодных пятен эллиптической формы, движущихся вдоль слоя, например, как на рис. 4а при $\Pr = 0.08$, для ${\text{Gr}} = 2000$ выше критического и ${{k}_{x}} = 1.19$. Формируется четверка вихрей, попарно локализованных вблизи верхней и нижней границы, движущихся в том же направлении вдоль слоя, что и конечно-амплитудные возмущения температуры (рис. 4б).

Рис. 4.

Случай спиральных возмущений. Для пространственных периодических по $y$ возмущений система принимает вид

$\frac{{\partial \Phi }}{{\partial t}} + {\text{Gr}}\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial \Phi }}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \Phi }}{{\partial z}}} \right] = \Delta \Phi - \frac{{\partial \theta }}{{\partial y}}$
(3.5)
$\begin{gathered} \Delta \Psi + \Phi = 0 \\ \frac{{\partial U}}{{\partial t}} + {\text{Gr}}\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial U}}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial U}}{{\partial z}} + u_{0}^{'}\left( z \right)\frac{{\partial \Psi }}{{\partial y}}} \right] = \Delta U \\ \end{gathered} $
$\frac{{\partial \theta }}{{\partial t}} + {\text{Gr}}\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial \theta }}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \theta }}{{\partial z}} + U + \operatorname{Ra} \theta _{0}^{'}\left( z \right)\frac{{\partial \Psi }}{{\partial y}}} \right] = \frac{1}{{\Pr }}\Delta \theta $
(3.6)
$z = - 1{\kern 1pt} :\;\;\Psi = 0,\quad U = 0,\quad \frac{{\partial \theta }}{{\partial z}} = 0$
(3.7)
$z = 1{\kern 1pt} :\;\;\Psi = 0,\quad U = 0,\quad \theta = 0$
(3.8)
$\begin{gathered} \Psi \left( {t,0,z} \right) = \Psi \left( {t,L,z} \right),\quad \Phi \left( {t,0,z} \right) = \Phi \left( {t,L,z} \right) \\ U\left( {t,0,z} \right) = U\left( {t,L,z} \right),\quad \theta \left( {t,0,z} \right) = \theta \left( {t,L,z} \right), \\ \end{gathered} $
где оператор Лапласа $\Delta = {{\partial }^{2}}{\text{/}}\partial {{y}^{2}}$ + ${{\partial }^{2}}{\text{/}}\partial {{z}^{2}}$. Имеются все три компоненты возмущений скорости, которые зависят от времени $t$ и двух пространственных координат $y$ и $z$. $\Psi \left( {t,y,z} \right)$ – конечно-амплитудные возмущения функции тока $(V = - \partial \Psi {\text{/}}\partial z$, $W = \partial \Psi {\text{/}}\partial y)$, описывающие проекцию возмущений скорости на плоскость $yOz$, $U\left( {t,y,z} \right)$ – конечно-амплитудные возмущения первой компоненты скорости, описывающие проекцию возмущений скорости на плоскость $xOz$ или $xOy$, $\Phi \left( {t,y,z} \right)$, $\theta \left( {t,y,z} \right)$ – конечно-амплитудные возмущения вихря скорости ($\Phi $ = ∂V/∂z – ∂W/∂y = –ΔΨ) и температуры. Этот подход использовался ранее во многих работах, например [12, 30].

Нелинейная задача (3.5)–(3.8) решалась численно методом сеток [31]. Основные расчеты проводились на сетке 101 × 200. Расчеты показали, что при всех рассматриваемых значениях числа Прандтля в областях с неустойчивой температурной стратификацией возникает система бегущих винтообразных вихрей.

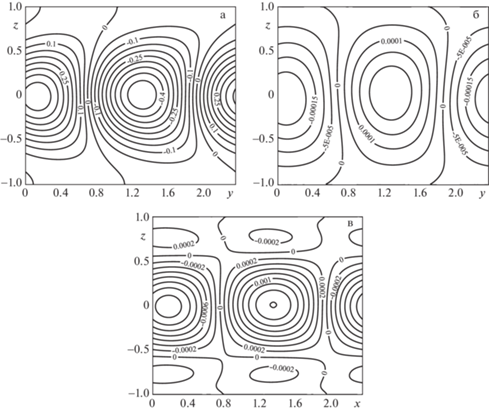
На рис. 5 представлены изотермы конечно-амплитудных возмущений температуры $\theta \left( {t,y,z} \right)$, изолинии возмущений функции тока $\Psi \left( {t,y,z} \right)$ и компоненты скорости $U\left( {t,y,z} \right)$ при $\Pr = 0.14$ для числа Грасгофа ${\text{Gr}} = 9000$ выше критического, ${{k}_{y}} = 2.66$. В середине вдоль слоя движется пара теплых и холодных пятен (рис. 5а). Проекция движения, описанная функцией возмущения функции тока вблизи порога устойчивости, представляет собой движущуюся вдоль оси $Oy$ цепочку вращающихся в противоположных направлениях вихрей, занимающих весь слой (рис. 5б). Одновременно x-ая компонента возмущения скорости, описывает в центре слоя вращающиеся то против, то по часовой стрелке движущихся вдоль оси $Oy$ вихрей в плоскости $xOy$. Центры вихрей расположены вблизи центров теплого и холодного пятна. Таким образом, в центре слоя формируется трехмерное вихревое движение, вблизи же верхней и нижней границы слоя имеются цепочки движущихся вдоль оси $Oy$ слабых вихрей, вращающихся в плоскости $xOy$ (рис. 5в).

Рис. 5.

Заключение. Представлено точное решение уравнений Навье–Стокса, записанное в приближении Обербека–Буссинеска и описывающее адвективное течение несжимаемой жидкости в горизонтальном слое с твердыми границами, условием теплоизоляции на нижней границе и линейным распределением температуры на верхней границе.

В рамках линейной теории устойчивости показано, что на всем рассматриваемом диапазоне числа Прандтля при числах Грасгофа выше критических для плоских возмущений развивается колебательная неустойчивость, а для спиральных возмущений монотонная. С ростом числа Прандтля адвективное течение становится более устойчивым на плоские возмущения. Минимальное критическое число Грасгофа для спиральных возмущений равное 8182.7 достигается при $\Pr = 0.14$. Плоские возмущения являются опаснее спиральных возмущений.

Поведение конечно-амплитудных возмущений, возникающих в слое жидкости при значениях числа Грасгофа выше критического, исследовано конечно-разностным методом сеток на основе нелинейной задачи. За порогом устойчивости возникают нестационарные периодические конечно-амплитудные возмущения скорости и температуры в виде системы вихрей и температурных пятен различной конфигурации.

Список литературы

  1. Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений. М.: Наука, 1989. 320 с.

  2. Остроумов Г.А. Свободная конвекция в условиях внутренней задачи. М.: Гостехтеориздат, 1952. 286 с.

  3. Андреев В.К. Решения Бириха уравнений конвекции и некоторые его обобщения // Препринт № 1–10. Красноярск: СО РАН. ИВМ, 2010.

  4. Бирих Р.В. О термокапиллярной конвекции в горизонтальном слое жидкости // ПМТФ. 1966. № 3. С. 69–72.

  5. Gershuni G.Z., Laure P., Myznikov V.M., Roux B., Zhukhovitsky E.M. On the stability of plane-parallel advective flows in long horizontal layers // Microgravity Q. 1992. V. 2. № 3. P. 141–151.

  6. Андреев В.К., Бекежанова В.Б. Устойчивость неизотермических жидкостей (обзор) // ПМТФ. 2013. № 2. С. 3–20.

  7. Шварц К.Г. Устойчивость термокапиллярного адвективного течения в медленно вращающемся слое жидкости в условиях невесомости // Изв. РАН. МЖГ. 2012. № 1. С. 44–58.

  8. Аристов С.Н., Шварц К.Г. Адвективное течение во вращающейся жидкой пленке // ПМТФ. 2016. Т. 57. № 1 (335). С. 216–223. https://doi.org/10.15372/PMTF20160121

  9. Шварц К.Г. Плоскопараллельное адвективное течение в горизонтальном слое несжимаемой жидкости с твердыми границами // Изв. РАН. МЖГ. 2014. № 4. С. 26–30.

  10. Шварц К.Г. Плоскопараллельное адвективное течение в горизонтальном слое несжимаемой жидкости с внутренним линейным источником тепла // ПММ. 2018. Т. 82. Вып. 1. С. 25–30.

  11. Шварц К.Г., Шварц Ю.А. Устойчивость адвективного течения в горизонтальном слое несжимаемой жидкости при наличии условия проскальзывания Навье // Изв. РАН. МЖГ. 2020. № 1. С. 33–44.

  12. Любимов Д.В., Шкляев С.В. Об устойчивости адвективного термоакустического течения // Изв. РАН. МЖГ. 2000. № 3. С. 10–21.

  13. Любимова Т.П., Никитин Д.А., Скуридин Р.В. О влиянии акустической волны на устойчивость адвективного течения в плоском слое // Вестн. Пермского ун-та. Сер.: Мат. Мех. Информ. 2011. Вып. 5 (9). С. 143–147.

  14. Иванцов А.О. Слабонелинейный анализ устойчивости термоакустического адвективного течения // Вестн. Пермского ун-та. Физика. 2019. № 3. С. 28–44.

  15. Slavtchev S., Hennenberg M., Valhev G. et al. Stability of ferrofluid flows in a horizontal channel subjected to a longitudinal temperature gradient and an oblique magnetic field // Microgr. Sci. Technol. 2008. V. 20. Iss. 1. P. 199–203.https://doi.org/10.1007/s12217-008-9027-2

  16. Аристов С.Н., Шварц К.Г. Конвективный теплообмен при локализованном нагреве плоского слоя несжимаемой жидкости // Изв. РАН. МЖГ. 2013. № 3. С. 53–58.

  17. Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теорет. основы хим. технол. 2016. Т. 50. № 3. С. 294–301.

  18. Бурмашева Н.В., Ларина Е.А., Просвиряков Е.Ю. Течение типа Куэтта с учетом идеального скольжения на контакте с твердой поверхностью // Вестн. Томского гос. ун-та. Мат. и мех. 2021. № 74. С. 79–94.

  19. Демин В.А. Конвективные сепараторы // Прикл. физ. 2013. № 4. С. 60–67.

  20. Hart J. A note on the stability of low-Prandtle-number Hadley circulations // J. Fluid Mech. 1983. V. 132. P. 271–281.

  21. Laure P. Etude des mouvements de convection dans une cavite rectangulaire soumise a un gradient de temperature horizontal // J. Mec. Theor. 1987. V. 6. P. 351–382.

  22. Kuo H.P., Korpela S.A. Stability and finite amplitude natural convection in a shallow cavity with insulated top and bottom and heated from a side // Phys. Fluids. 1988. V. 31 (1). P. 33–42.

  23. Wang P., Daniels P.G. Numerical solutions for the flow near the end of a shallow laterally heated cavity // J. Engng. Math. 1994. V. 28. P. 211–226.

  24. Любимов Д.В., Любимова Т.П., Никитин Д.А. и др. Устойчивость адвективного течения бинарной смеси в плоском горизонтальном слое с идеально теплопроводными границами // Изв. РАН. МЖГ. 2010. № 3. С. 129–139.

  25. Lybimova T.P., Lybymov D.V., Morozov V.A. et al. Stability of convection in a horizontal channel subjected to a longitudinal temperature gradient. Pt. 1. Effect of aspect ratio and Prandtl number // J. Fluid Mech. 2009. V. 635. P. 275–295.

  26. Любимова Т.П., Никитин Д.А. Устойчивость адвективного течения в горизонтальном канале прямоугольного сечения с адиабатическими границами // Изв. РАН. МЖГ. 2011. № 2. С. 82–91.

  27. Mizev A., Mosheva E., Kostarev K. et al. Stability of solutal advective flow in a horizontal shallow layer // Phys. Rev. Fluids. 2017. V. 2. № 10. 103903.

  28. Demin V.A., Kostarev K.G., Mizev A.I. et al. On convective instability of the counter propagating fluxes of inter-soluble liquids // Rus. J. Nonlin. Dyn. 2014. V. 10. № 2. P. 195–208.

  29. Шварц К.Г. Устойчивость адвективного течения во вращающемся горизонтальном теплоизолированном снизу слое несжимаемой жидкости с твердыми границами при малом числе Прандтля // Изв. РАН. МЖГ. 2022. № 2. С. 38–50.

  30. Аристов С.Н., Шварц К.Г. Вихревые течения адвективной природы во вращающемся слое жидкости. Пермь: Перм. ун-т, 2006. 155 с.

  31. Тарунин Е.Л., Шварц К.Г. Исследование линейной устойчивости адвективного течения методом сеток // Выч. технол. 2001. Т. 6. № 6. С. 108–117.

  32. Шварц К.Г. Конечно-амплитудные пространственные возмущения адвективеого течения во вращающемся горизонтальном слое жидкости // Выч. технол. 2001. Т. 6. Спец. вып. Ч. 2. Тр. Межд. конф. RDAMM-2001. С. 702–707.

  33. Тарунин Е.Л. Вычислительный эксперимент в задачах свободной конвекции. Иркутск: Изд-во Иркут. ун-та, 1990. 225 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал