Программирование, 2019, № 2, стр. 6-16

ВЫЧИСЛЕНИЕ РЕЗОНАНСНОГО МНОЖЕСТВА МНОГОЧЛЕНА ПРИ ОГРАНИЧЕНИЯХ НА КОЭФФИЦИЕНТЫ

А. Б. Батхин^a, b, *

^a Институт прикладной математики им. М.В. Келдыша РАН
125047 Москва, Миусская пл., дом 4, Россия

^b Московский физико-технический институт
141701 Долгопрудный, Институтский переулок, 9, Россия

^* E-mail: batkhin@gmail.com

Поступила в редакцию 24.07.2018
После доработки 01.09.2018
Принята к публикации 11.09.2018

DOI: 10.1134/S0132347419020043

Полный текст (PDF)

Аннотация

В работе рассматриваются методы вычисления так называемого обобщенного дискриминантного множества некоторого многочлена, корни которого связаны линейным соотношением. С помощью q-аналога классической теории исключений и алгоритмов компьютерной алгебры описаны методы вычисления параметрического представления этого множества, которые реализованы в виде библиотеки системы компьютерной алгебры Maple. Их работа демонстрируется на одном содержательном примере.

I. ВВЕДЕНИЕ

Некоторое время тому назад в связи с исследованием формальной устойчивости положений равновесия многопараметрических систем Гамильтона [1] автор столкнулся с проблемой адекватного описания такого алгебраического многообразия в пространстве $\Pi $ коэффициентов приведенного многочлена

(1)

${{f}_{n}}(x) = {{x}^{n}} + {{a}_{1}}{{x}^{{n - 1}}} + \ldots + {{a}_{{n - 1}}}x + {{a}_{n}},$

на котором последний имеет либо кратные корни (в этом случае многообразие называется дискриминантным множеством $\mathcal{D}({{f}_{n}})$), либо соизмеримые корни (в этом случае многообразие называется резонансным множеством ${{\mathcal{R}}_{q}}({{f}_{n}})$).

Вначале, в работах [2–4] с использованием классической теории исключений была рассмотрена структура дискриминантного множества $\mathcal{D}({{f}_{n}})$ многочлена (1) в терминах полиномиальных идеалов, составленных из k-х субдискриминантов ${{\mathcal{D}}^{{(k)}}}({{f}_{n}})$ многочлена (1). Было показано, что оно состоит из подмногообразий ${{\mathcal{V}}_{k}}$ различных размерностей $k = 1,\; \ldots ,\;n - 1$. На каждом подмногообразии ${{\mathcal{V}}_{k}}$ многочлен ${{f}_{n}}(x)$ имеет k различных корней, кратность которых задается разбиением числа n. С геометрической точки зрения каждое из многообразий ${{\mathcal{V}}_{k}}$, $k = 2,\; \ldots ,\;n - 1$, размерности k представляет собой линейчатую развертывающуюся поверхность, роль направляющей для которой выполняет многообразие размерности на единицу меньшей. Это свойство позволило описать некоторую процедуру построения полиномиальной параметризации подмногообразия ${{\mathcal{V}}_{k}}$ с использованием параметрического представления направляющего подмногообразия ${{\mathcal{V}}_{{k - 1}}}$.

Затем, в работах [5–7] описанная выше конструкция была перенесена на случай соизмеримых корней с коэффициентом соизмеримости q. В этом случае свойство корней ${{t}_{i}}$, $i = 1,\; \ldots ,\;k$ многочлена ${{f}_{n}}(x)$ быть кратными заменено свойством образовывать геометрическую прогрессию длины k со знаменателем q. При этом исследование резонансного множества ${{\mathcal{R}}_{q}}({{f}_{n}})$ проводилось с использованием k-х субрезультатов матрицы Сильвестра пары многочленов ${{f}_{n}}(x)$ и ${{f}_{n}}(qx)$, что в случае нулевого корня приводило к некорректным результатам. Этот недостаток был устранен в работе [8] с помощью замены операции дифференцирования так называемым оператором Хана (Hahn operator [9]):

(2)

$({{\mathcal{A}}_{g}}f)(x)\;\mathop = \limits^{{\text{def}}} \;\left\{ \begin{gathered} \frac{{f(qx + \omega ) - f(x)}}{{(q - 1)x + \omega }},\quad x \ne {{\omega }_{0}}, \hfill \\ f'\left( {{{\omega }_{0}}} \right),\quad x = {{\omega }_{0}}, \hfill \\ \end{gathered} \right.$

индуцированным линейным отображением

(3)

$g(x) \equiv qx + \omega ,\quad q,\omega \in \mathbb{R},\quad q \ne \{ - 1,0\} $

с неподвижной точкой ${{\omega }_{0}} = \omega {\text{/}}(1 - q)$. Это позволило безо всяких изменений применить технику классической теории исключений к исследованию g-дискриминантного множества ${{\mathcal{D}}_{g}}({{f}_{n}})$, на котором многочлен ${{f}_{n}}(x)$ имеет по крайней мере пару корней ${{t}_{i}},\;{{t}_{j}}$, связанных соотношением t_j = $g({{t}_{i}})$.

Оператор Хана ${{\mathcal{A}}_{g}}$ является естественным обобщением следующих операторов, действующих на пространстве $\mathbb{P}$ многочленов над $\mathbb{R}$:

• $q$-дифференциального оператора Джексона

(4)

$({{\mathcal{A}}_{q}}f)(x) = \frac{{f(qx) - f(x)}}{{(q - 1)x}},$

при $\omega = 0$ и $q \ne 1$;

• разностного оператора

$({{\Delta }_{\omega }}f)(x) = \frac{{f(x + \omega ) - f(x)}}{\omega }$

при q = 1;

• классического дифференциального оператора $d{\text{/}}dx$ в пределе при $q \to 1$ и $\omega = 0$.

Далее в тексте, оператор Хана (2) и оператор Джексона (4), примененные к многочлену ${{f}_{n}}(x)$, названы его $g$-производной и q-производной соответственно. Для удобства читателя ниже приведем некоторые определения и обозначения, ставшие стандартными для q-исчисления.

Определение 1. Определим q-скобку ${{[a]}_{q}}$ числа a, сдвинутый q-факториал (q-символ Похгаммера) ${{(a;q)}_{n}}$, q-факториал ${{[n]}_{q}}!$, q-биномиальные (гауссовы) коэффициенты ${{\left[ \begin{gathered} n \\ k \\ \end{gathered} \right]}_{q}}$, q-бином ${{\{ x;t\} }_{{n;q}}}$ следующим образом

$\begin{gathered} {{[a]}_{q}} = \frac{{{{q}^{a}} - 1}}{{q - 1}},\quad a \in \mathbb{R}{\backslash }\{ 0\} , \\ {{(a;q)}_{n}} = \prod\limits_{k = 0}^{n - 1} {(1 - a{{q}^{k}}),\quad {{{(a;q)}}_{0}} = 1,} \\ {{[n]}_{q}}! = \prod\limits_{k = 1}^n {{{{[k]}}_{q}}} = \frac{{{{{(q;q)}}_{n}}}}{{{{{(1 - q)}}^{n}}}}, \\ \end{gathered} $

(5)

$\mathop {\left[ {\begin{array}{*{20}{c}} n \\ k \end{array}} \right]}\nolimits_q = \frac{{{{{[n]}}_{q}}!}}{{{{{[n - k]}}_{q}}!{{{[k]}}_{q}}!}} = \prod\limits_{i = 1}^k \,\frac{{{{q}^{{n - i + 1}}} - 1}}{{{{q}^{i}} - 1}},$

(6)

${{\{ x;t\} }_{{n;q}}} = \prod\limits_{i = 0}^{n - 1} \,\left( {x - {{q}^{i}}t} \right),\quad {{\{ x;t\} }_{{0;q}}} = 1.$

При $q \to 1$ все определенные выше объекты становятся классическими.

Основной результат работы [8] состоит в построении полиномиальной параметризации всех подмногообразий ${{\mathcal{V}}_{k}}$ размерности $k,1 \leqslant k \leqslant n - 1$ так называемого g-дискриминантного множества ${{\mathcal{D}}_{g}}({{f}_{n}})$.

Определение 2. Пару корней ${{t}_{i}}$, ${{t}_{j}}$, $i,j = 1,\; \ldots ,\;n$, $i \ne j$, многочлена ${{f}_{n}}(x)$ назовем g-связанной, если $g({{t}_{i}}) = {{t}_{j}}$ для $g(x)$ вида (3).

Множество в $\Pi $, на котором многочлен ${{f}_{n}}(x)$ имеет по крайней мере пару g-связанных корней назовем g-дискриминантным множеством многочлена ${{f}_{n}}(x)$ и обозначим ${{\mathcal{D}}_{g}}({{f}_{n}})$.

g-дискриминантное множество ${{\mathcal{D}}_{g}}({{f}_{n}})$ является таким обобщением дискриминантного множества, для которого роль кратных корней играют g‑связанные корни:

Определение 3. Последовательностью $Seq_{g}^{{(k)}}({{t}_{1}})$ g-связанных корней длины k назовем конечную последовательность $\{ {{t}_{i}}\} $, $i = 1,\; \ldots ,\;k$, каждый член которой начиная со второго, является g-связанным корнем предыдущего члена последовательности: $g({{t}_{i}}) = {{t}_{{i + 1}}}$. Начальный корень ${{t}_{1}}$ назовем порождающим корнем соответствующей последовательности.

Процедура вычисления параметризации g-дискриминантного множества основана на теореме, последовательное применение которой позволяет получить параметрическое представление многообразия ${{\mathcal{V}}_{{k + 1}}}$ размерности $k + 1$, если уже вычислена параметризация многообразия ${{\mathcal{V}}_{k}}$ размерности $k$.

Теорема 1 ([8, Теорема 3]). Пусть в пространстве $\Pi $ имеется многообразие ${{\mathcal{V}}_{l}}$, $dim{{\mathcal{V}}_{l}} = l$, на котором многочлен ${{f}_{n}}(x)$ имеет $l$ различных последовательностей g-связанных корней, причем последовательность корней $Seq_{g}^{{(m)}}({{t}_{1}})$ имеет длину $m > 1$. При этом другие корни $(l - 1)$-й последовательности не являются $g$-связанными со всеми корнями последовательности $Seq_{g}^{{(m)}}({{t}_{1}})$. Если ${{{\mathbf{r}}}_{l}}({{t}_{1}},\; \ldots ,\;{{t}_{l}})$ – параметризация многообразия ${{\mathcal{V}}_{l}}$, то для $0 < k < m$ формула

(7)

$\begin{gathered} {{{\mathbf{r}}}_{l}}({{t}_{1}},\; \ldots ,\;{{t}_{l}},{{t}_{{l + 1}}}) = {{{\mathbf{r}}}_{l}}({{t}_{1}},\; \ldots ,\;{{t}_{l}}) + \\ + \;\sum\limits_{i = 1}^k \,\mathop {\left[ {\begin{array}{*{20}{c}} k \\ i \end{array}} \right]}\nolimits_q \frac{{{{{[m - i]}}_{q}}!}}{{{{{[m]}}_{q}}!}}\left( {\mathcal{A}_{g}^{i}{{{\mathbf{r}}}_{l}}} \right)({{t}_{1}}){{\{ {{t}_{{l + 1}}};{{t}_{1}}\} }_{{i;g}}} \\ \end{gathered} $

задает параметризацию части многообразия ${{\mathcal{V}}_{{l + 1}}}$, на котором имеется две последовательности корней $Seq_{g}^{{(m - k)}}({{g}^{k}}({{t}_{1}}))$ и $Seq_{g}^{{(k)}}(g({{t}_{{l + 1}}}))$, а остальные последовательности корней такие же, как на исходном многообразии ${{\mathcal{V}}_{l}}$.

Поскольку теорема 1 работает для случая вещественных корней, то в общем случае необходимо дополнительное преобразование из следующего утверждения

Утверждение 1. Для того, чтобы получить параметрическое представление многообразия ${{\mathcal{V}}_{l}} \subset {{\mathcal{D}}_{g}}({{f}_{n}})$ размерности $l$, $l \leqslant 2$, на котором многочлен ${{f}_{n}}(x)$ имеет две последовательности g-связанных корней равной длины с порождающими корнями ${{t}_{k}}$ и ${{t}_{m}}$, необходимо к ним применить преобразование

(8)

${{t}_{k}} = {{t}_{k}} + \sqrt {{{t}_{m}}} {\kern 1pt} ,\quad {{t}_{m}} = {{t}_{k}} - \sqrt {{{t}_{m}}} {\kern 1pt} .$

Явно выписывая параметризацию многообразия ${{\mathcal{V}}_{1}}$, на котором многочлен ${{f}_{n}}(x)$ имеет последовательность $Seq_{g}^{{(n)}}({{t}_{1}})$ g-связанных корней наибольшей длины n (т. е. является g-биномом) и последовательно применяя формулы (7) и (8), удается получить параметрическое представление всех многообразий ${{\mathcal{V}}_{k}}$, $k = 2,\; \ldots ,\;n - 1$, составляющих g-дискриминантное множество ${{\mathcal{D}}_{g}}({{f}_{n}})$.

Замечание 1. В частном случае теоремы 1 при k = 1 формула (7) принимает вид

(9)

${{{\mathbf{r}}}_{l}}({{t}_{1}},\; \ldots ,\;{{t}_{l}},{{t}_{{l + 1}}}) = {{{\mathbf{r}}}_{l}}({{t}_{1}},\; \ldots ,\;{{t}_{l}}) + \frac{{{{t}_{{l + 1}}} - {{t}_{1}}}}{{{{{[m]}}_{q}}}}({{\mathcal{A}}_{g}}{{{\mathbf{r}}}_{l}})({{t}_{1}}).$

Формуле (9) можно дать следующую геометрическую интерпретацию. Зафиксируем для параметризации ${{{\mathbf{r}}}_{l}}({{t}_{1}},{{t}_{2}},\; \ldots ,\;{{t}_{l}})$ все параметры кроме параметра ${{t}_{1}}$. Выберем на многообразии ${{\mathcal{V}}_{l}}$ две точки с координатами ${\mathbf{r}}_{l}^{{(1)}} \equiv {{{\mathbf{r}}}_{l}}({{t}_{1}},{{t}_{2}},\; \ldots ,\;{{t}_{l}})$ и ${\mathbf{r}}_{l}^{{(2)}} \equiv {{{\mathbf{r}}}_{l}}(g({{t}_{1}})$, t₂, ..., t_l), и проведем через них секущую (одномерное линейное многообразие), выбрав величину ${{t}_{{l + 1}}}$ в качестве параметра на ней. Тогда, как показано в теореме 2 в [8], на этой секущей многочлен ${{f}_{n}}(x)$ имеет последовательность корней $Seq_{g}^{{(m - 1)}}({{g}^{k}}({{t}_{1}}))$, а остальные $n - m + 1$ корней простые. Таким образом, многообразие ${{\mathcal{V}}_{{l + 1}}}$ является линейчатой поверхностью с многообразием ${{\mathcal{V}}_{l}}$ в качестве направляющей.

Для проведения вычислений с g-дискриминантным множеством ${{\mathcal{D}}_{g}}({{f}_{n}})$ была создана программная библиотека процедур gDiscrSet для системы компьютерной алгебры Maple (см. [8. п. 4.4]). В ее новую версию были добавлены некоторые процедуры, в частности, процедура вычисления обобщенных субдискриминантов $D_{g}^{{(i)}}({{f}_{n}})$ и наибольшего общего делителя пары многочленов ${{f}_{n}}(x)$ и $({{\mathcal{A}}_{g}}{{f}_{n}})(x)$, использующая алгоритм псевдоделения Якоби [10, Section 4]. Все вычисления пп. II и IV выполнены с применением новой версии библиотеки gDiscrSet. В настоящее время данная библиотека переносится в систему SymPy [11], имеющую богатый набор полиномиальных алгоритмов, в частности, процедур для вычисления субрезультанов многочленов.

В данной работе рассматриваются важные с прикладной точки зрения аспекты. В разделе III предлагается методика вычисления корней характеристического многочлена матрицы квадратичной формы функции Гамильтона при наличии двухчастотного резонанса между собственными частотами. Эта методика легко переносится на случай многочастотного резонанса. Для числа степеней свободы 3 и 4 при условии двухчастотного резонанса приведены явные формулы корней многочлена. В разделе 3 рассматривается ситуация, когда сами коэффициенты ${{a}_{i}}$ многочлена (1) суть полиномы от вектора параметров s. Предлагается два способа получения параметризации g‑дискриминантного множества ${{\mathcal{D}}_{g}}({{f}_{n}})$ через параметры s, а именно, с помощью элиминационного идеала и с помощью g-производных многочлена (1). Наконец, в разделе IV подробно разобрана задача вычисления резонансного множества некоторого характеристического многочлена, возникающего при исследовании положений равновесия плоского двойного маятника с вязкоупругими шарнирами под действием следящей силы.

II. ВЫЧИСЛЕНИЕ СОИЗМЕРИМЫХ КОРНЕЙ

Во многих прикладных задачах возникает проблема определения корней многочлена ${{f}_{n}}(x)$ при каких-то дополнительных условиях на последние. В качестве примера рассмотрим проблему исследования формальной устойчивости положения равновесия многопараметрической системы Гамильтона при наличии резонанса между собственными частотами [7]. Наиболее распространенная схема исследования (подробнее, см. [12]) состоит из последовательных шагов.

1. Вначале функция Гамильтона H в окрестности положения равновесия раскладывается в ряд по однородным формам ${{H}_{k}}$ степени k:

$H({\mathbf{q}},{\mathbf{p}}) = \sum\limits_{k = 2}^\infty \,{{H}_{k}}({\mathbf{q}},{\mathbf{p}}).$

2. Затем квадратичная форма ${{H}_{2}}$ приводится к нормальной форме с помощью одного из алгоритмов [12, гл. 2] или [13, гл. 7].

3. Потом последовательно применяются методы нелинейной нормализации (симметризации). Наиболее распространенными методами нормализации являются метод Депри–Хори [12, гл. 11] или метод инвариантной нормализации Журавлёва (симметризации) [13, гл. 7, 8]. Объем статьи не позволяет дать подробный обзор программных средств вычисления нормальной формы системы дифференциальных уравнений с использованием системы символьных вычислений. Укажем здесь лишь некоторые из них. Программы нормализации гамильтоновых уравнений вблизи точек либрации в системе символьных вычислений REDUCE [14] были разработаны в Институте теоретической астрономии в 80-х–90-х годах прошлого века (подробнее см. в [15, Гл. 1]). Многие из этих алгоритмов были затем перенесены в современные системы компьютерной алгебры, как в проприетарные: Wolfram Mathematica [16], MapleSoft Maple [17], так и свободно распространяемые: SymPy [11]. Например, метод Депри–Хори нормализации системы Гамильтона в окрестности точек либрации реализованы в системе Maple в виде пакета “НФ” [15], в системе Wolfram Mathematica [18]. Метод инвариантной нормализации Журавлёва [19] реализован в системе Wolfram Mathematica. Этот метод был перенесен автором в систему MapleSoft Maple и применен к изучению центральных многообразий, связанных с точками либрации обобщенной задачи Хилла. Отметим программный комплекс [20], реализованный в языках программирования C++ и Python, ориентированный на применение к задачам молекулярной динамики.

Отметим, что для применения метода Депри–Хори необходимо вначале привести квадратичную часть ${{H}_{2}}$ гамильтониана H к нормальной форме. В методе симметризации это не является необходимым условием, но в обоих случаях требуется вычислить корни характеристического многочлена матрицы квадратичной формы гамильтониана ${{H}_{2}}$.

В случае резонанса между собственными частотами на корни характеристического многочлена накладывается условие их соизмеримости с коэффициентом q. Рассмотрим двухчастотный резонанс, то есть когда имеется лишь одна пара соизмеримых корней: ${{t}_{2}} = q{{t}_{1}}$, где q – некоторое рациональное число, а остальные $n - 2$ корня ${{t}_{i}}$, $i = 3,\; \ldots ,\;n$, попарно несоизмеримы. Тогда согласно теореме 1 в [8] в последовательности обобщенных субдискриминантов $D_{q}^{{(i)}}({{f}_{n}})$, $i = 0,\; \ldots ,\;n - 1$, первым отличным от нуля является субдискриминант $D_{q}^{{(1)}}({{f}_{n}})$. Следовательно, наибольший общий делитель пары многочленов ${{f}_{n}}(x)$ и $({{\mathcal{A}}_{q}}{{f}_{n}})(x)$ вычисляется по формуле утверждения 1 в [8]. Корень ${{t}_{1}}$ в таком случае есть

(10)

${{t}_{1}} = - \frac{{M_{1}^{{(1)}}({{f}_{n}})}}{{D_{q}^{{(1)}}({{f}_{n}})}},$

где $M_{1}^{{(1)}}({{f}_{n}})$ – некоторый минор $(n - 1)$-го порядка матрицы Сильвестра указанных выше многочленов (подробнее см. в [8, 21, 22]). Теперь исходный многочлен ${{f}_{n}}(x)$ может быть разложен на три множителя:

${{f}_{n}}(x) = (x - {{t}_{1}})(x - q{{t}_{1}}){{u}_{{n - 2}}}(x),$

а коэффициенты многочлена ${{u}_{{n - 2}}}(x)$ выражаются через корень ${{t}_{1}}$ и коэффициенты ${{a}_{i}}$, $i = 1,\; \ldots ,\;n$, многочлена (1) с помощью приведенной ниже процедуры. Напомним, что коэффициенты a_i исходного многочлена ${{f}_{n}}(x)$ выражаются через элементарные симметрические многочлены ${{\sigma }_{i}}$ степени $i$ от его корней [23]: a_i = (–1)ⁱσ_i(t₁, $q{{t}_{1}},{{t}_{3}}, \ldots ,{{t}_{n}})$, $i = 1,\; \ldots ,\;n$.

1. На первом шаге из соотношения

${{a}_{1}} = - {{\sigma }_{1}}({{t}_{1}},q{{t}_{1}},{{t}_{3}},\; \ldots ,\;{{t}_{n}}) = - ({{t}_{1}} + q{{t}_{1}} + {{\sigma }_{1}}({{t}_{3}},\; \ldots ,\;{{t}_{n}}))$

выражаем ${{\sigma }_{1}}({{t}_{3}},\; \ldots ,\;{{t}_{n}})$ через ${{a}_{1}},\;{{t}_{1}}$:

(11)

${{\sigma }_{1}}({{t}_{3}},\; \ldots ,\;{{t}_{n}}) = - {{[2]}_{q}}{{t}_{1}} - {{a}_{1}}.$

2. Поскольку

$\begin{gathered} {{\sigma }_{2}}({{t}_{1}},q{{t}_{1}},{{t}_{3}},\; \ldots ,\;{{t}_{n}}) = \\ = \;({{t}_{1}} + q{{t}_{1}}){{\sigma }_{1}}({{t}_{3}},\; \ldots ,\;{{t}_{n}}) + {{\sigma }_{2}}({{t}_{3}},\; \ldots ,\;{{t}_{n}}), \\ \end{gathered} $

то, подставляя полученное выше выражение (11) для ${{\sigma }_{1}}({{t}_{3}},\; \ldots ,\;{{t}_{n}})$ в равенство ${{a}_{2}} = {{\sigma }_{2}}({{t}_{1}},q{{t}_{1}},{{t}_{3}},\; \ldots ,\;{{t}_{n}})$, записываем ${{\sigma }_{2}}({{t}_{3}},\; \ldots ,\;{{t}_{n}})$ как выражение от ${{a}_{1}},\;{{a}_{2}},\;{{t}_{1}}$:

${{\sigma }_{2}}({{t}_{3}},\; \ldots ,\;{{t}_{n}}) = {{a}_{2}} + {{[2]}_{q}}{{t}_{1}}({{a}_{1}} + {{[2]}_{q}}{{t}_{1}}).$

3. Аналогично, на каждом последующем шаге $i = 3,\; \ldots ,\;n$, значение симметрического многочлена ${{\sigma }_{i}}({{t}_{3}},\; \ldots ,\;{{t}_{n}})$, вычисленного на корнях ${{t}_{j}}$, j = = $3, \ldots ,n$, рекуррентно выражается через значения симметрических многочленов ${{\sigma }_{k}}$ степеней $1 \leqslant k$ < i, коэффициентов ${{a}_{k}}$, $k = 1,\; \ldots ,\;i$, многочлена (1) и корня ${{t}_{1}}$, найденного в (10).

4. Найденные таким образом значения симметрических многочленов ${{\sigma }_{i}}({{t}_{3}},\; \ldots ,\;{{t}_{n}})$, i = 1, ..., n – 2, определяют коэффициенты многочлена ${{u}_{{n - 2}}}(x)$.

Для числа степеней свободы 3 или 4 в случае соизмеримых или $g$-связанных корней формулы для них могут быть получены явно.

Так для кубики ${{f}_{3}}(x)$ выражения для корней ${{t}_{1}},\;{{t}_{2}},\;{{t}_{3}}$ определяются из выражений для субдискриминанта $D_{q}^{{(1)}}({{f}_{3}})$ (формула (3.4) из [22]), минора $M_{1}^{{(1)}}({{f}_{3}})$ (формула (3.7) из [22]) и параметризации многообразия ${{\mathcal{V}}_{2}}({{f}_{3}})$ (формула (19) из [8] или формула (4.11) из [22]) для значения $\omega = 0$ и имеют вид

$\begin{gathered} {{t}_{1}} = \frac{{[3]_{q}^{2}{{a}_{3}} - {{q}^{2}}{{a}_{1}}{{a}_{2}}}}{{q{{{[2]}}_{q}}({{{[3]}}_{q}}{{a}_{2}} - qa_{2}^{2})}},\quad {{t}_{2}} = q{{t}_{1}}, \\ {{t}_{3}} = \frac{{qa_{1}^{3} - (2[3]_{q}^{2} - {{{[2]}}_{q}}){{a}_{1}}{{a}_{2}} + [3]_{q}^{2}{{a}_{3}}}}{{{{{[3]}}_{q}}{{a}_{2}} - qa_{2}^{2}}}. \\ \end{gathered} $

Для ${{f}_{4}}(x)$ выражения для корней ${{t}_{i}}$, $i = 1,2,3,4$, более громоздкие. Вначале вычисляем параметризацию многообразия ${{\mathcal{V}}_{1}}({{f}_{4}})$, на котором многочлен ${{f}_{4}}(x)$ является q-биномом (6), а его коэффициенты ${{a}_{i}}$, $i = 1,\; \ldots ,\;4$, выражаются через Гауссовы коэффициенты (5):

(12)

${{a}_{i}} = {{( - 1)}^{i}}\mathop {\left[ {\begin{array}{*{20}{c}} 4 \\ i \end{array}} \right]}\nolimits_q {{q}^{{\left( {\begin{array}{*{20}{c}} i \\ 2 \end{array}} \right)}}}{{t}_{1}},\quad i = 1,\; \ldots ,\;4.$

Применяя к (12) формулу (9), получим параметризацию многообразия ${{\mathcal{V}}_{2}}({{f}_{4}})$, на котором имеется последовательность длины 3 q-соизмеримых корней с начальным корнем ${{t}_{1}}$ и простой корень ${{t}_{2}}$:

(13)

$\begin{gathered} {{\mathcal{V}}_{2}}({{f}_{4}}):\{ {{a}_{1}} = - {{[3]}_{1}}{{t}_{1}} - {{t}_{2}},\;{{a}_{2}} = {{[3]}_{q}}(q{{t}_{1}} + {{t}_{2}}){{t}_{1}}, \\ {{a}_{3}} = - q({{q}^{2}}{{t}_{1}} + {{[3]}_{q}}{{t}_{2}})t_{1}^{2},\;{{a}_{4}} = {{q}^{3}}t_{1}^{3}{{t}_{2}}\} . \\ \end{gathered} $

Наконец, применяя последовательно для параметризации (13) формулы (9) и (8), получим параметрическое представление многообразия ${{\mathcal{V}}_{3}}({{f}_{4}})$

(14)

$\begin{gathered} {{\mathcal{V}}_{3}}({{f}_{4}}):\{ {{a}_{1}} = - {{[2]}_{q}}{{t}_{1}} - 2{{u}_{2}}, \\ {{a}_{2}} = qt_{1}^{2} + 2(q + 1){{t}_{1}}{{u}_{2}} + u_{2}^{2} - {{u}_{3}}, \\ {{a}_{3}} = - {{[2]}_{q}}{{t}_{1}}u_{2}^{2} - 2qt_{1}^{2}{{u}_{2}} + {{[2]}_{q}}{{t}_{1}}{{u}_{3}}, \\ {{a}_{4}} = qt_{1}^{2}(u_{2}^{2} - {{u}_{3}})\} , \\ \end{gathered} $

на котором ${{f}_{4}}(x)$ факторизуется следующим образом:

$\mathop {\left. {{{f}_{4}}(x)} \right|}\nolimits_{{{V}_{3}}} = (x - {{t}_{1}})(x - q{{t}_{1}})({{(x - {{u}_{2}})}^{2}} - {{u}_{3}}).$

Параметры ${{u}_{2}},{{u}_{3}}$ выражаются из (14):

$\begin{gathered} {{u}_{2}} = - \frac{1}{2}({{a}_{1}} + {{[2]}_{q}}{{t}_{1}}), \\ {{u}_{3}} = - \frac{1}{4}((3{{[3]}_{q}} - q)t_{1}^{2} + {{[2]}_{q}}{{a}_{1}}{{t}_{1}} + 4{{a}_{2}} - a_{1}^{2}), \\ \end{gathered} $

корни ${{t}_{{3,4}}} = {{u}_{2}} \pm \sqrt {{{u}_{3}}} $, ${{t}_{2}} = q{{t}_{1}}$, а $q$-соизмеримый корень ${{t}_{1}}$ находится по формуле (10), где субдискриминант $D_{q}^{{(1)}}({{f}_{4}})$ и минор $M_{1}^{{(1)}}({{f}_{4}})$ вычисляются с помощью матрицы Сильвестра пары многочленов ${{f}_{4}}(x)$ и $({{\mathcal{A}}_{q}}{{f}_{4}})(x)$ по формулам

$\begin{gathered} D_{1}^{{(1)}}({{f}_{4}}) = - {{q}^{3}}{{[2]}_{q}}{{[3]}_{q}}a_{1}^{3}{{a}_{3}} + {{q}^{4}}{{[2]}_{q}}a_{1}^{2}a_{2}^{2} - \\ - \;{{q}^{2}}{{[3]}_{q}}{{[4]}_{q}}a_{1}^{2}{{a}_{4}} + q{{[2]}_{q}}[4]_{q}^{2}{{a}_{2}}{{a}_{4}} - q[3]_{q}^{2}{{[4]}_{q}}a_{3}^{2} + \\ + \;{{q}^{2}}{{[2]}_{q}}({{[4]}_{q}}({{[2]}_{q}} + 1) - 2){{a}_{1}}{{a}_{2}}{{a}_{3}} - {{q}^{3}}[2]_{q}^{3}a_{2}^{3}, \\ \end{gathered} $

$\begin{gathered} M_{1}^{{(1)}}({{f}_{4}}) = - {{q}^{2}}[3]_{q}^{2}a_{1}^{3}{{a}_{4}} + {{q}^{4}}a_{1}^{2}{{a}_{2}}{{a}_{3}} + \\ + \;q[2]_{q}^{3}{{[4]}_{q}}{{a}_{1}}{{a}_{2}}{{a}_{4}} + {{q}^{3}}{{[3]}_{3}}{{a}_{1}}a_{3}^{2} - \\ - \;{{q}^{3}}[2]_{q}^{2}a_{2}^{2}{{a}_{3}} - {{[3]}_{q}}[4]_{q}^{2}{{a}_{3}}{{a}_{4}}. \\ \end{gathered} $

Замечание 2. Если имеет место многочастотный резонанс, то поступая аналогично, можно из наибольшего общего делителя многочленов ${{f}_{n}}(x)$ и $({{\mathcal{A}}_{q}}{{f}_{n}})(x)$ найти соизмеримые корни. Представляя многочлен ${{f}_{n}}(x)$ в виде ${{f}_{n}}(x) = \text{v}(x)u(x)$, где $\text{v}(x)$ имеет только соизмеримые корни, вычисляем коэффициенты многочлена $u(x)$ по указанной выше процедуре. Его корни суть остальные (несоизмеримые) корни исходного многочлена ${{f}_{n}}(x)$.

III. ПАРАМЕТРИЗАЦИЯ ПРИ ОГРАНИЧЕНИЯХ НА КОЭФФИЦИЕНТЫ

В прикладных задачах, в которых возникает необходимость исследовать обобщенный дискриминант ${{D}_{g}}({{f}_{n}})$, часто пространство параметров многочлена ${{f}_{n}}(x)$ не совпадает с пространством его коэффициентов. Далее рассмотрим два способа получения описания множества ${{\mathcal{D}}_{g}}({{f}_{n}})$ в этом случае. Для определенности будем считать, что все коэффициенты ${{a}_{i}}$, $i = 1,\; \ldots ,\;n$, приведенного многочлена ${{f}_{n}}(x)$ являются полиномами от некоторого набора параметров ${\mathbf{s}} = ({{s}_{1}},\; \ldots ,\;{{s}_{k}}) \in {{\mathbb{R}}^{k}}$, $0 < k < n$, которые назовем параметрами задачи. Переход от параметров задачи ${\mathbf{s}}$ к пространству коэффициентов $\Pi $ многочлена ${{f}_{n}}(x)$ задается отображением

$S:{{\mathbb{R}}^{k}} \to \Pi :{\mathbf{s}} \mapsto {\mathbf{a}}({\mathbf{s}}),$

матрица Якоби которого ${{J}_{S}} = \left[ {\tfrac{{\partial {{a}_{i}}}}{{\partial {{s}_{j}}}}} \right]$, $i = 1,\; \ldots ,\;n$, $j = 1,\; \ldots ,\;k$, может иметь ранг m, $0 \leqslant m \leqslant k$. Далее считаем, что ранг $m$ матрицы ${{J}_{S}}$ принимает наибольшее значение, что соответствует условию невырожденности отображения $S$.

A. Вычисление с помощью элиминационного идеала

Выберем некоторую компоненту ${{\mathcal{V}}_{l}}$ размерности l g-дискриминантного множества ${{\mathcal{D}}_{g}}({{f}_{n}})$. Тогда с помощью алгоритма, описанного в подпункте 4.4 в [8], можно вычислить параметрическое представление этого многообразия в виде

${{a}_{i}} = {{r}_{i}}({{t}_{1}},\; \ldots ,\;{{t}_{l}}),\quad i = 1,\; \ldots ,\;n.$

Составляем полиномиальный идеал

${{\mathcal{J}}_{l}} = \{ {{a}_{i}}({{s}_{1}},\; \ldots ,\;{{s}_{k}}) - {{r}_{i}}({{t}_{1}},\; \ldots ,\;{{t}_{l}}),\;\;i = 1,\; \ldots ,\;n\} ,$

состоящий из n многочленов от $k + l$ переменных. Этот идеал в пространстве ${\mathbf{s}}$ параметров задает некоторое алгебраическое многообразие, компоненты которого могут иметь размерности от 0 до $l - (n - k)$, если последняя величина неотрицательна. Для того чтобы получить его параметрическое представление, нужно вычислить элиминационный идеал [24, Ch. 3, § 1]. Эта задача решается с помощью вычисления базиса Грёбнера, если указать при этом такой лексикографический порядок, чтобы в первую очередь были исключены переменные ${{s}_{1}},\; \ldots ,\;{{s}_{k}}$. В большинстве систем компьютерной алгебры это может быть достаточно легко выполнено. Например, в системе Maple при использовании команды Basis из пакета Groebner следует указать лексикографический порядок lexdeg([${{s}_{1}},\; \ldots ,\;{{s}_{k}}$], [${{t}_{1}},\; \ldots ,\;{{t}_{l}}$]). В системе Mathematica при использовании процедуры GroebnerBasis – указать опцию MonomialOrder → EliminationOrder. Если элиминационный идеал вычислен, то его первые многочлены зависят только от параметров ${{t}_{i}}$, $i = 1,\; \ldots ,\;l$, а параметры ${{s}_{i}}$, $i = 1,\; \ldots ,\;k$, входят в остальные многочлены таким образом, что позволяет выразить их в виде рациональных функций от ${{t}_{i}}$. Число независимых параметров ${{t}_{i}}$ равно гильбертовой размерности идеала, и поэтому нужно среди l параметров ${{t}_{i}}$ выбрать $l - (n - k)$ независимых, а остальные выразить через них. Обозначим эти независимые параметры через ${{\tilde {t}}_{i}}$, $i = 1,\; \ldots ,\;l - (n - k)$. В итоге получим выражение исходных параметров ${{s}_{i}}$, $i = 1,\; \ldots ,\;k$ от $l - (n - k)$ независимых параметров ${{\tilde {t}}_{i}}$, а следовательно, и выражение для коэффициентов ${{a}_{i}}$, $i = 1,\; \ldots ,\;n$, через них.

B. Вычисление с помощью $g$-производных

Данный способ основан на теореме 1 и утверждении 1. Пусть многочлен ${{f}_{n}}(x)$ имеет последовательность g-связанных корней длины $m > 1$. Тогда, согласно указанным выше теореме 1 и утверждению 1, его $g$-производная по переменной $x$ имеет последовательность g-связанных корней длины $m - 1$. Следовательно, для того чтобы найти параметризацию многообразия ${{\mathcal{V}}_{l}}$, которое соответствует разбиению $[{{m}^{1}}{{1}^{{(n - m)}}}]$, необходимо решить относительно коэффициентов ${{a}_{i}}$, $i = 1,\; \ldots ,\;n$, систему уравнений

(15)

$\{ (\mathcal{A}_{{q,\omega }}^{i}{{f}_{n}})(x) = 0,i = 0,\; \ldots ,\;m - 1\} .$

Для этого можно опять использовать технику вычисления элиминационного базиса, описанную в предыдущем подпункте IIIA.

Наиболее эффективно этот способ работает в том случае, если некоторые из коэффициентов ${{a}_{i}}$ многочлена ${{f}_{n}}(x)$ принимают постоянные значения. В этом случае система (15) представляет собой систему линейных алгебраических уравнений относительно тех коэффициентов ${{a}_{i}}$, значения которых не фиксированы. Ее решение можно записать в виде рациональных выражений от параметра t. Этот параметр является порождающим для последовательности g-связанных корней соответствующей длины, а полученное решение позволяет задавать параметризацию многообразия, на котором многочлен ${{f}_{n}}(x)$ имеет такую последовательность связанных корней. Кроме того, с помощью этой параметризации и преобразования (7) теоремы 1 можно получить параметризацию многообразия, следующего в иерархии компонент g-дискриминантного множества.

IV. ПРИМЕР: ДВОЙНОЙ МАЯТНИК СО СЛЕДЯЩЕЙ СИЛОЙ

В работах [25, 26] рассматривалась задача об устойчивости в линейном приближении двойного маятника с вязкоупругими шарнирами под действием следящей силы. Механическая система на рис. 1 состоит из двух жестких невесомых стержней длины l, соединенных вязкоупругими шарнирами $O$ и $A$. Масса последнего равна $2m$. Шарниры имеют одинаковые коэффициенты упругости, но различные коэффициенты вязкости. Следящая сила $P$ приложена к свободному концу $B$ массы $m$ и направлена вдоль плеча AB.

Линеаризованные уравнения движения в переменных ${{\varphi }_{{1,2}}},\;{{\dot {\varphi }}_{{1,2}}}$ имеют характеристический многочлен $\chi (\lambda )$ вида [26]

(16)

$\begin{gathered} \chi (\lambda )\;\mathop = \limits^{{\text{def}}} \;{{\lambda }^{4}} + \frac{1}{2}({{\gamma }_{1}} + 6{{\gamma }_{2}}){{\lambda }^{3}} + \\ + \;\frac{1}{2}({{\gamma }_{1}}{{\gamma }_{2}} - 2p + 7){{\lambda }^{2}} + \frac{1}{2}({{\gamma }_{1}} + {{\gamma }_{2}})\lambda + \frac{1}{2}, \\ \end{gathered} $

где ${{\gamma }_{{1,2}}}$ и p – некоторые неотрицательные параметры, выражающиеся через физические характеристики системы (см. [25]).

В [26, пп. 3.5.3, 8.3.1] исследовались особенности границы множества устойчивости положения равновесия системы при малых значениях параметров ${{\gamma }_{{1,2}}}$. Здесь рассмотрим более общую задачу.

Задача. Описать q-дискриминантное (резонансное) множество ${{\mathcal{D}}_{q}}(\chi )$ характеристического многочлена (16), т.е. множество в пространстве параметров $\tilde {\Pi } = ({{\gamma }_{1}},{{\gamma }_{2}},p)$, на котором многочлен (16) имеет по крайней мере пару соизмеримых корней ${{\lambda }_{j}} = q{{\lambda }_{i}}$, $i \ne j$, $q\not { \in }\{ - 1,0\} $.

Для решения задачи вместо оператора Хана ${{\mathcal{A}}_{{q,\omega }}}$ используем его частный случай – q-производную Джексона (4), получающуюся при $\omega = 0$ и обозначаемую далее ${{\mathcal{A}}_{q}}$.

Решение задачи разобьем на две части. Вначале, используя метод подпункта 3В, получим параметризацию резонансного множества приведенной квартики – многочлена 4-й степени – при фиксированном значении его свободного члена, равном 1/2, и произвольных значениях остальных коэффициентов:

(17)

${{f}_{4}}(x)\;\mathop = \limits^{{\text{def}}} \;{{x}^{4}} + {{a}_{1}}{{x}^{3}} + {{a}_{2}}{{x}^{2}} + {{a}_{3}}x + \frac{1}{2}.$

Затем с помощью полученной параметризации и метода, описанного в подпункте IIIA, получим параметризацию $q$-дискриминантного множества ${{\mathcal{D}}_{q}}(\chi )$ в пространстве исходных параметров $\tilde {\Pi }$ задачи.

Число 4 – степень многочлена ${{f}_{4}}$ – имеет пять разбиений: $[{{4}^{1}}]$, $[{{1}^{1}}{{3}^{1}}]$, $[{{2}^{2}}]$, $[{{1}^{2}}{{2}^{1}}]$ и $[{{1}^{4}}]$. Первым четырем из них соответствуют компоненты q-дискриминантного множества ${{\mathcal{D}}_{q}}(\chi )$ – множества в пространстве $\Pi $ коэффициентов многочлена ${{f}_{4}}(x)$. Повторяя рассуждения подпункта IIIA, легко видеть, что их размерности равны соответственно 0, 1, 1, 2. Обозначим эти компоненты ${{\mathcal{V}}_{0}}({{f}_{4}})$, $\mathcal{V}_{1}^{1}({{f}_{4}})$, $\mathcal{V}_{1}^{2}({{f}_{4}}),{{\mathcal{V}}_{2}}({{f}_{4}})$ соответственно.

На компоненте ${{\mathcal{V}}_{0}}({{f}_{4}})$ многочлен (17) становится $q$-биномом ${{\{ x;{{t}_{1}}\} }_{{4;q}}}$ (6), свободный член которого ${{q}^{6}}t_{1}^{4} = 1{\text{/}}2$. Следовательно, компонента ${{\mathcal{V}}_{0}}({{f}_{4}})$ состоит из двух точек $\mathcal{T}_{1}^{ \pm }$, задаваемых значениями параметра ${{t}_{1}} = \pm {{2}^{{ - 1/4}}}{{q}^{{ - 3/2}}}$ при условии q > 0. Координаты этих точек суть

(18)

$\begin{gathered} \mathcal{T}_{1}^{ \pm }:\left\{ {{{a}_{1}} = \pm \frac{{{{{[2]}}_{q}}({{q}^{2}} + 1)}}{{{{2}^{{1/4}}}{{q}^{{3/2}}}}}} \right., \\ \left. {{{a}_{2}} = \frac{{{{{[3]}}_{q}}({{q}^{2}} + 1)}}{{{{q}^{2}}\sqrt 2 }},\;{{a}_{3}} = \frac{{{{a}_{1}}}}{{\sqrt 2 }}} \right\}. \\ \end{gathered} $

Эти точки являются особыми точками 2-го порядка многообразия ${{\mathcal{V}}_{2}}({{f}_{4}})$.

Для вычисления параметризации многообразия $\mathcal{V}_{1}^{1}({{f}_{4}})$ составим систему линейных алгебраических уравнений относительно параметров ${{a}_{1}},{{a}_{2}}$, a₃:

(19)

$\{ {{f}_{4}}(x) = 0,({{\mathcal{A}}_{q}}{{f}_{4}})(x) = 0,(\mathcal{A}_{q}^{2}{{f}_{4}})(x) = 0\} .$

Решение системы (19) легко может быть получено с помощью вычисления параметрического базиса Грёбнера [24, Ch. 2], задав лексикографический порядок для переменных ${{a}_{1}},\;{{a}_{2}},\;{{a}_{3}}$. Заменив параметр $x$ параметром ${{t}_{1}}$, оно примет вид

(20)

$\begin{gathered} \mathcal{V}_{1}^{1}({{f}_{4}}):\left\{ {{{a}_{1}} = - {{{[3]}}_{q}}{{t}_{1}} - \frac{1}{{2{{{(q{{t}_{1}})}}^{3}}}},} \right. \\ {{a}_{2}} = {{[3]}_{q}}\left( {qt_{1}^{2} + \frac{1}{{2{{q}^{3}}t_{1}^{2}}}} \right),\;\left. {{{a}_{3}} = - {{{(q{{t}_{1}})}}^{3}} - \frac{{{{{[3]}}_{q}}}}{{2{{q}^{2}}{{t}_{1}}}}} \right\}. \\ \end{gathered} $

На этом многообразии многочлен (17) имеет вид

$\mathop {\left. {{{f}_{4}}(x)} \right|}\nolimits_{\mathcal{V}_{1}^{1}({{f}_{4}})} = {{\{ x;{{t}_{1}}\} }_{{3;q}}}\left( {x - \frac{1}{{2{{{(q{{t}_{1}})}}^{3}}}}} \right).$

Многообразие $\mathcal{V}_{1}^{1}({{f}_{4}})$ является однопараметрическим семейством особых точек 1-го порядка многообразия ${{\mathcal{V}}_{2}}({{f}_{4}})$. Из параметризации (20) видно, что многообразие $\mathcal{V}_{1}^{1}({{f}_{4}})$ состоит из двух гладких кривых $\mathcal{L}_{1}^{ \pm }$, взаимно симметричных относительно оси $O{{a}_{2}}$. Каждая из этих кривых определяется соответственно положительными или отрицательными значениями параметра ${{t}_{1}}$ и проходит через соответствующую особую точку $\mathcal{T}_{1}^{ \pm }$. При $q \ne 1$ кривые $\mathcal{L}_{1}^{ \pm }$ не имеют особых точек.

Теперь к параметризации (20) применим преобразование (9) и получим такую параметризацию многообразия ${{\mathcal{V}}_{2}}({{f}_{4}})$, что многочлен (17) на нем будет раскладываться на два множителя

(21)

$\begin{gathered} \mathop {\left. {{{f}_{4}}(x)} \right|}\nolimits_{{{\mathcal{V}}_{2}}({{f}_{4}})} = {{\{ x;{{t}_{1}}\} }_{{2,q}}} \times \\ \times \;\left( {{{x}^{2}} - \frac{{(2{{q}^{2}}t_{1}^{4} - 1)t_{2}^{'} + ({{q}^{3}} + 1){{t}_{1}}}}{{2{{q}^{3}}t_{1}^{4}}}x + \frac{1}{{2qt_{1}^{2}}}} \right). \\ \end{gathered} $

Выполним следующую упрощающую замену параметра $t_{2}^{'}$

$t_{2}^{'} = \frac{{4{{q}^{3}}t_{1}^{4}{{t}_{2}} - ({{q}^{3}} + 1){{t}_{1}}}}{{2{{q}^{2}}t_{1}^{4} - 1}},$

которая приводит квадратный трехчлен в разложении (21) к наиболее простому виду. В этом случае параметризация многообразия ${{\mathcal{V}}_{2}}({{f}_{4}})$ примет вид

(22)

$\begin{gathered} {{\mathcal{V}}_{2}}({{f}_{4}}):\left\{ {{{a}_{1}}\;\mathop = \limits_{}^{} \; - {{{[2]}}_{q}}{{t}_{1}} - 2{{t}_{2}},} \right. \\ {{a}_{2}} = qt_{1}^{2} + 2{{[2]}_{q}}{{t}_{1}}{{t}_{2}} + \frac{1}{{2qt_{1}^{2}}}, \\ \left. {{{a}_{3}} = - 2qt_{1}^{2}{{t}_{2}} - \frac{{{{{[2]}}_{q}}}}{{2q{{t}_{1}}}}} \right\}, \\ \end{gathered} $

а многочлен ${{f}_{4}}(x)$ перепишется следующим образом:

(23)

$\mathop {\left. {{{f}_{4}}(x)} \right|}\nolimits_{{{\mathcal{V}}_{2}}({{f}_{4}})} = {{\{ x;{{t}_{1}}\} }_{{2;q}}}\left( {{{x}^{2}} - 2{{t}_{2}}x + \frac{1}{{2qt_{1}^{2}}}} \right).$

Как следует из теоремы 1, многообразие ${{\mathcal{V}}_{2}}({{f}_{4}})$ представляет собой объединение двух линейчатых поверхностей ${{\mathcal{S}}^{ \pm }}$, образованных секущими, пересекающими соответствующие кривые $\mathcal{L}_{1}^{ \pm }$ при значениях параметра ${{t}_{2}}$, равных,

$t_{2}^{'} = \frac{{2t_{1}^{4} + q}}{{4qt_{1}^{3}}},\quad t_{2}^{{''}} = \frac{{2{{q}^{5}}t_{1}^{4} + 1}}{{4{{q}^{3}}t_{1}^{3}}}.$

Рис. 1.

Двойной маятник состоит из жестких невесомых стержней длины l, соединенных вязкоупругими шарнирами $O$ и $A$. Следящая сила P приложена к свободному концу вдоль стержня AB.

Следовательно, кривые $\mathcal{L}_{1}^{ \pm }$ являются кривыми самопересечения поверхностей ${{\mathcal{S}}^{ \pm }}$. Поверхности ${{\mathcal{S}}^{ \pm }}$ взаимно симметричны относительно оси $O{{a}_{2}}$. Очевидно, что при $q \to 1$ имеем $t_{2}^{'} \to t_{2}^{{''}}$, секущие становятся касательными, а кривые $\mathcal{L}_{1}^{ \pm }$ – кривыми возврата.

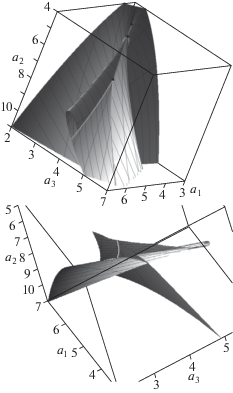
На рисунках 2 с разных ракурсов показаны участки поверхности ${{S}^{ + }}$ вместе с кривыми $\mathcal{L}_{1}^{ + }$ (голубым цветом), $\mathcal{L}_{2}^{ + }$ (пурпурным цветом) и особыми точками $\mathcal{T}_{i}^{ + }$, $i = 1,2,3$. Описание кривой $\mathcal{L}_{2}^{ + }$ и точек $\mathcal{T}_{{2,3}}^{ \pm }$ дано ниже.

Рис. 2.

Два разных ракурса поверхности ${{\mathcal{S}}^{ + }}$. Участок поверхности ${{\mathcal{S}}^{ + }}$. Голубым цветом (в цветном варианте рисунка) показана кривая $\mathcal{L}_{1}^{ + }$, пурпурным цветом показана кривая $\mathcal{L}_{2}^{ + }$, черным цветом показаны особые точки $\mathcal{T}_{1}^{ + }$, $\mathcal{T}_{2}^{ + }$, $\mathcal{T}_{3}^{ + }$.

Наконец, чтобы получить параметризацию многообразия $\mathcal{V}_{1}^{2}({{f}_{4}})$, на котором ${{f}_{4}}(x)$ имеет две последовательности q-связанных корней, нужно подобрать такое значение параметра ${{t}_{2}}$, чтобы квадратный трехчлен в разложении (23) стал $q$‑биномом. Для этого необходимо, чтобы q-дискриминант трехчлена ${{x}^{2}} - 2{{t}_{2}}x + 1{\text{/}}(2qt_{1}^{2})$, равный $(8{{(q{{t}_{1}}{{t}_{2}})}^{2}} - {{(q + 1)}^{2}}){\text{/}}(2qt_{1}^{2})$, обнулялся. Это достигается при $t_{2}^{ \pm } = \pm {{[2]}_{q}}{\text{/}}(2\sqrt 2 q{{t}_{1}})$. Покажем, что $\mathcal{V}_{1}^{2}({{f}_{4}})$ состоит из трех кривых $\mathcal{L}_{2}^{ \pm }$ и ${{\mathcal{L}}_{3}}$.

Подставим значение $t_{2}^{ + }$ в (22) и получим, что коэффициенты ${{a}_{i}}$, $i = 1,2,3$, выражаются через рациональное выражение от параметра ${{t}_{1}}$: t₁ + $1{\text{/}}(\sqrt 2 q{{t}_{1}})$. Это выражение принимает значения на двух интервалах $( - \infty ; - {{2}^{{3/4}}}{\text{/}}\sqrt q ]$ и $[{{2}^{{3/4}}}{\text{/}}\sqrt q ; + \infty )$.

Параметризация кривых $\mathcal{L}_{2}^{ \pm }$ имеет вид:

(24)

$\begin{gathered} \mathcal{L}_{2}^{ \pm }:\left\{ {{{a}_{1}} = - {{{[2]}}_{q}}\left( {{{t}_{1}} + \frac{1}{{\sqrt 2 q{{t}_{1}}}}} \right),} \right. \\ {{a}_{2}} = qt_{1}^{2} + \frac{{[2]_{q}^{2}}}{{\sqrt 2 q}} + \frac{1}{{2qt_{1}^{2}}}, \\ \left. {{{a}_{3}} = - \frac{{{{{[2]}}_{q}}}}{{\sqrt 2 }}\left( {{{t}_{1}} + \frac{1}{{\sqrt 2 q{{t}_{1}}}}} \right)} \right\}, \\ \end{gathered} $

где знаку “–” соответствует интервал (–∞; $ - {{2}^{{3/4}}}{\text{/}}\sqrt q ]$ изменения параметра ${{t}_{1}}$, а знаку “+” – интервал $[{{2}^{{3/4}}}{\text{/}}\sqrt q ; + \infty )$. Заметим, что кривые $\mathcal{L}_{2}^{ \pm }$ взаимно симметричны относительно оси $O{{a}_{2}}$. Структура параметризации (24) этих кривых такова, что каждая из них имеет точку остановки $\mathcal{T}_{2}^{ \pm }$, соответствующую значению параметра t₁ = $ \pm {{2}^{{ - 1/4}}}{{q}^{{ - 1/2}}}$ с координатами

(25)

$\begin{gathered} \mathcal{T}_{2}^{ \pm }:\;\;\left\{ {{{a}_{1}} = \pm \frac{{q + 1}}{{\sqrt q }}{{2}^{{3/4}}},} \right. \\ \left. {{{a}_{2}} = \frac{{{{q}^{2}} + 4q + 1}}{{q\sqrt 2 }},\;{{a}_{3}} = \frac{{{{a}_{1}}}}{{\sqrt 2 }}} \right\}. \\ \end{gathered} $

При этом каждая из поверхностей ${{\mathcal{S}}^{ \pm }}$ самопересекается по кривой $\mathcal{L}_{2}^{ \pm }$.

При подстановке значения $t_{2}^{ - }$ в (22) получим, что коэффициенты ${{a}_{i}}$, $i = 1,2,3$, выражаются через рациональное выражение от параметра ${{t}_{1}}$: ${{t}_{1}} - 1{\text{/}}(\sqrt 2 q{{t}_{1}})$. Параметризация кривой ${{\mathcal{L}}_{3}}$ имеет вид:

(26)

$\begin{gathered} {{\mathcal{L}}_{3}}:\left\{ {{{a}_{1}} = - {{{[2]}}_{q}}\left( {{{t}_{1}} - \frac{1}{{\sqrt 2 q{{t}_{1}}}}} \right),} \right. \\ {{a}_{2}} = qt_{1}^{2} - \frac{{[2]_{q}^{2}}}{{\sqrt 2 q}} + \frac{1}{{2qt_{1}^{2}}}, \\ \left. {{{a}_{3}} = - \frac{{{{{[2]}}_{q}}}}{{\sqrt 2 }}\left( {{{t}_{1}} - \frac{1}{{\sqrt 2 q{{t}_{1}}}}} \right)} \right\}. \\ \end{gathered} $

Поверхности ${{\mathcal{S}}^{ \pm }}$ пересекаются по кривой ${{\mathcal{L}}_{3}}$.

Многочлен ${{f}_{4}}(x)$ на многообразии $\mathcal{V}_{1}^{2}({{f}_{4}})$ раскладывается на произведение двух q-биномов

$\mathop {\left. {{{f}_{4}}(x)} \right|}\nolimits_{\mathcal{V}_{1}^{2}({{f}_{4}})} = {{\{ x;{{t}_{1}}\} }_{{2;q}}}\mathop {\left\{ {x;\frac{1}{{\sqrt 2 q{{t}_{1}}}}} \right\}}\nolimits_{2;q} .$

Кривые $\mathcal{L}_{1}^{ \pm }$ и $\mathcal{L}_{2}^{ \pm }$ пересекаются в следующих точках: в особых точках $\mathcal{T}_{1}^{ \pm }$ и в точках $\mathcal{T}_{3}^{ \pm }$ с координатами

(27)

$\mathcal{T}_{3}^{ \pm } = \left\{ {{{a}_{1}} = \pm \frac{{[2]_{q}^{2}}}{{{{2}^{{1/4}}}q}},\;{{a}_{2}} = \frac{{\sqrt 2 {{{[3]}}_{q}}}}{q},\;{{a}_{3}} = \frac{{{{a}_{1}}}}{{\sqrt 2 }}} \right\}.$

Точки $\mathcal{T}_{3}^{ \pm }$ интересны тем, что на них многочлен (17) имеет последовательность q-связанных корней длины 3 с порождающим корнем t₁ = $ \pm {{2}^{{ - 1/4}}}{\text{/}}q$ и простым корнем ${{t}_{2}} = \pm {{2}^{{ - 1/4}}}$, который совпадает со вторым корнем последовательности. Таким образом, этот набор корней соответствует двум разным разбиениям: $[{{1}^{1}}{{1}^{3}}]$ и $[{{2}^{2}}]$.

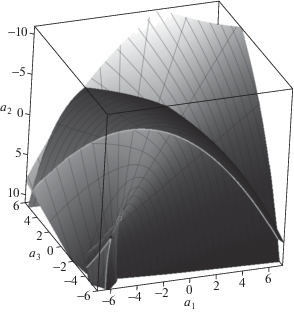
На рисунке 3 показаны поверхности ${{\mathcal{S}}^{ + }}$ и ${{\mathcal{S}}^{ - }}$, пересекающиеся по кривой ${{\mathcal{L}}_{3}}$ (показана желтым цветом). Видны участки кривых $\mathcal{L}_{1}^{ + }$ и $\mathcal{L}_{2}^{ + }$, а также некоторые из особых точек.

Рис. 3.

Поверхности ${{\mathcal{S}}^{ \pm }}$, пересекающиеся по кривой ${{\mathcal{L}}_{3}}$. Поверхности ${{\mathcal{S}}^{ \pm }}$, пересекающиеся по кривой ${{\mathcal{L}}_{3}}$ (желтый цвет в цветном варианте рисунка). Голубым цветом (в цветном варианте рисунка) показана кривая $\mathcal{L}_{1}^{ + }$, пурпурным цветом показана кривая $\mathcal{L}_{2}^{ + }$.

Отметим, что при $q \to 1$ все точки $\mathcal{T}_{1}^{ \pm }$, $\mathcal{T}_{2}^{ \pm }$ и $\mathcal{T}_{3}^{ \pm }$ сливаются в пару особых точек – точек возврата на кривых $\mathcal{L}_{1}^{ \pm }$ и $\mathcal{L}_{2}^{ \pm }$. Кривые $\mathcal{L}_{1}^{ \pm }$ превращаются в пределе в ребра возврата на поверхностях ${{\mathcal{S}}^{ \pm }}$.

Итак, параметризация компоненты размерности 2 $q$-дискриминантного множества ${{\mathcal{D}}_{q}}({{f}_{4}})$, состоящей из поверхностей ${{\mathcal{S}}^{ \pm }}$, задается формулой (22). Особые точки порядка 1 представляют собой гладкие кривые $\mathcal{L}_{1}^{ \pm }$, $\mathcal{L}_{2}^{ \pm }$, ${{\mathcal{L}}_{3}}$ и задаются соответственно формулами (20), (24) и (26). Особые точки порядка 2 определяются формулами (18), (25) и (27).

Преобразование $\mathcal{S}$, задающее переход от коэффициентов ${{a}_{1}},\;{{a}_{2}},\;{{a}_{3}}$ многочлена (17) к коэффициентам ${{\gamma }_{1}},\;{{\gamma }_{2}},\;p$ характеристического многочлена (16), невырождено и, следовательно, обратимо. Его несложно вычислить с помощью элиминационного идеала, как это описано в разделе IIIА:

(28)

$\begin{gathered} {{\gamma }_{1}} = \frac{2}{5}(6{{a}_{3}} - {{a}_{1}}),\quad {{\gamma }_{2}} = \frac{2}{5}({{a}_{1}} - {{a}_{3}}), \hfill \\ p = - \frac{2}{{25}}(a_{1}^{2} - 7{{a}_{1}}{{a}_{3}} + 6a_{3}^{2}) - {{a}_{2}} + \frac{7}{2}. \hfill \\ \end{gathered} $

Подставляя в (28) координаты точек $\mathcal{T}_{{1,2,3}}^{ \pm }$, параметризации кривых $\mathcal{L}_{{1,2}}^{ \pm }$ и параметризации поверхностей ${{\mathcal{S}}^{ \pm }}$, получим параметрическое представление этих объектов в пространстве $\tilde {\Pi }$ параметров задачи.

V. ЗАКЛЮЧЕНИЕ

В работе рассматривается ситуация, часто возникающая в различных прикладных задачах, когда для некоторого многочлена ${{f}_{n}}(x)$, коэффициенты которого суть полиномы от некоторого набора параметров s, его корни ${{t}_{i}}$ связаны определенным соотношением: ${{t}_{j}} = g({{t}_{i}})$, где g(x) = $qx + \omega $. Предлагается два основных приема, основанных на некотором обобщении классической теории исключений и алгоритмах компьютерной алгебры, позволяющих получить параметризацию в пространстве параметров g-дискриминантного множества многочлена ${{f}_{n}}(x)$. Их работа продемонстрирована на некотором примере.

БЛАГОДАРНОСТИ

Работа поддержана РФФИ, грант № 18-01-00422а.

Автор выражает благодарность рецензенту, чьи содержательные замечания способствовали улучшению работы.

Список литературы

Батхин А.Б., Брюно А.Д., Варин В.П. Множества устойчивости многопараметрических гамильтоновых систем. Прикладная математика и механика. 2012. Т. 76. № 1. С. 80–133.
Батхин А.Б. Структура дискриминантного множества вещественного многочлена. Чебышевский сборник. 2015. Т. 16. № 2. С. 23–34.
Батхин А.Б. Параметризация дискриминантного множества вещественного многочлена. Препринты ИПМ им. М.В. Келдыша № 76. М.: ИПМ им. М.В. Келдыша РАН. 2015. 36 с.
Батхин А.Б. Параметризация дискриминантного множества вещественного многочлена. Программирование. 2016. Т. 42. № 2. С. 8–21.
Батхин А.Б. О структуре резонансного множества вещественного многочлена. Чебышевский сборник. 2016. Т. 17. № 3. С. 5–17.
Батхин А.Б. Структура резонансного множества вещественного многочлена. Препринты ИПМ им. М.В. Келдыша. 2016. № 29. 23 с.
Батхин А.Б. Резонансное множество многочлена и проблема формальной устойчивости. Вестник ВолГУ. Серия 1. Математика. Физика. 2016. Т. 35. № 4. С. 5–23.
Батхин А.Б. Параметризация множества, определяемого обобщенным дискриминантом многочлена. Программирование. 2018. № 2. С. 5–17.
Hahn W. Über Orthogonalpolynome, die $q$–Differenzengleichungen genügen, Mathematische Nachrichten. 1949. № 2. P. 4–34.
Gathen J. von zur, Lücking T. Subresultants revisited, Theoretical Computer Science. 2003. V. 297. P. 199–239.
SymPy: symbolic computing in Python / Aaron Meurer, Christopher P. Smith, Mateusz Paprocki et al., Peer J Computer Science. 2017. V. 3. P. e103. https:// doi.org/10.7717/peerjcs.103
Маркеев А.П. Точки либрации в небесной механике и космодинамике. М. Гл. ред. физ.-мат. литер. изд-ва “Наука”. 1978. 352 с.
Журавлев В.Ф., Петров А.Г., Шундерюк М.М. Избранные задачи гамильтоновой механики. М.: ЛЕНАНД. 2015. 304 с.
Еднерал В.Ф., Крюков А.П., Родионов А.Я. Язык аналитических вычислений REDUCE. М.: МГУ. 1989. 176 с.
Шевченко И.И. Исследование некоторых проблем устойчивости и хаотического поведения в небесной механике: дис. . д-ра наук: 01.03.01 / Иван Иванович Шевченко; ГАО РАН. С.-Петербург. 2000. 257 с.
Wolfram S. The Mathematica Book. Wolfram Media, Inc. 2003. 1488 p.
Thompson I. Understanding Maple. Cambridge University Press. 2016. 228 p.
Прокопеня А.Н. Нормализация гамильтониана в ограниченной задаче многих тел методами компьютерной алгебры. Программирование. 2012. Т. 38. № 3. С. 65–78.
Шундерюк М.М. Применение метода инвариантной нормализации к построению асимптотических решений некоторых задач гамильтоновой механики: Диссертация на соискание ученой степени кандидата физико-математических наук: 01.02.01 / М.М. Шундерюк; Институт проблем механики РАН им. А.Ю. Ишлинского. М. 2014. 113 с.
Background and documentation of software for computing hamiltonian normal forms / Andrew D. Burbanks, Stephen Wiggins, Holger Waalkens, Roman Schubert. School of mathematics, University of Bristol, Bristol, University Walk, Bristol BS8 1TW. 2008.
Калинина Е.А., Утешев А.Ю. Теория исключения: Учеб. пособие. СПб.: Изд-во НИИ химии СПбГУ. 2002. 72 с.
Батхин А.Б. Вычисление обобщенного дискриминанта вещественного многочлена. Препринты ИПМ им. М.В. Келдыша. 2017. № 88. 40 с.
Прасолов В.В. Многочлены. М.: МЦНМО. 2014. 336 с.
Cox D., Little J., O’Shea D. Ideals, Varieties, and Algorithms. An Introduction to Computational Algebraic Geometry and Commutative Algebra. Undergraduate Texts in Mathematics. 3rd ed. edition. New York: Springer-Verlag. 2007. 551+xv p.
Herrmann G., Jong I.-C. On the destabilizing effect of damping in nonconservative elastic systems, Trans. AMSE, Journal of Applied Mechanics . 1965. V. 32. P. 592–597.
Майлыбаев А.А., Сейранян А.П. Многопараметрические задачи устойчивости. Теория и приложения в механике. М.: Физматлит. 2009. 400 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Программирование

Архивы выпусков Информация о журнале Отправить рукопись в журнал