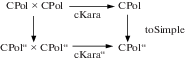Программирование, 2022, № 1, стр. 3-22
ДОКАЗАТЕЛЬНАЯ ПРОГРАММА ДЛЯ СПОСОБА КАРАЦУБЫ УМНОЖЕНИЯ МНОГОЧЛЕНОВ
a Институт программных систем им. А.К. Айламазяна РАН
152021 Ярославская обл., Переславский р-н, с. Веськово, ул. Петра Первого, “а”, Россия
* E-mail: mechvel@scico.botik.ru
Поступила в редакцию 28.05.2021
После доработки 17.06.2021
Принята к публикации 01.09.2021
- EDN: YPJZPJ
- DOI: 10.31857/S0132347422010071
Аннотация
Представлена разработка доказательной программы для способа Карацубы умножения многочленов одной переменной. Построено машинно-проверяемое доказательство равносильности функции способа Карацубы простейшему умножению многочленов “раскрытием скобок”. Это малая часть библиотеки DoCon-A машинно-проверяемых программ для вычислительной алгебры, созданной автором. Утверждение доказано для произвольного коммутативного кольца коэффициентов, а в системе DoCon-A задано доказательное построение структуры коммутативного кольца для области R[x] многочленов над коммутативным кольцом R. В системе DoCon-A программы включают определения соответствующих математических понятий и доказательства главных свойств применяемых алгоритмов. Эти доказательства проверяются компилятором. Применяется чисто функциональный язык программирования Agda, который также предоставляет конструкцию зависимых типов. Также рассматриваются некоторые общие вопросы построения доказательных программ в алгебре на языке Agda. Делается сравнение с подходом другого автора к построению в системе Coq некоторой разновидности алгоритма Карацубы.
1. ВВЕДЕНИЕ
Словоупотребление. Мы используем следующее словоупотребление.
Мп-доказательство – машинно-проверяемое полное формальное доказательство, воплощение – реализация или модель теории, свидетельство – доказательство. Слово “библиотека” обозначает библиотеку DoCon-A [1] доказательных программ компьютерной алгебры. Имя Agda иногда пишем кириллицей и склоняем по падежам.
Простейшим способом умножения целых чисел, представленных списком разрядов, является общеизвестный способ “в столбик”. В худшем случае для умножения чисел из n двоичных разрядов он требует порядка n2 действий над разрядами. В 1960 году А.А. Карацуба нашел более быстрый способ умножения [2, 3]. Его стоимость вычисления имеет порядок $O({{n}^{{{\text{lo}}{{{\text{g}}}_{2}}3}}})$. Позже был открыт еще более быстрый (асимптотически) способ [4], основанный на быстром преобразовании Фурье. Способ Карацубы также переносится на многочлены: [5], раздел 8.1.
Здесь мы занимаемся способом Карацубы, так как он проще выражается, имеет низкий порог выгодного применения, и до него дошла очередь.
Более подробно: cтатья относится главным образом к предмету “способы программирования вычислительной алгебры”. В программных библиотеках (системах) вычислительной алгебры есть такая разновидность библиотек: доказательные (сертифицированные) – в них методы снабжены мп-доказательствами. Автором разработана такая библиотека DoСon-A. Естественно, в каждой такой библиотеке все (как можно больше) включенные методы должны иметь доказательные программы. Для каждого значимого метода построение доказательной программы – это отдельная задача. В данном случае это задача построения доказательной программы для способа Карацубы умножения многочленов. Описание принципов построения библиотеки в целом могло бы быть предметом другой статьи. Если главные свойства умножения многочленов не снабжены мп-доказательствами, то тогда и почти все более сложные методы для многочленов тоже окажутся не полностью мп-доказанными (вычисление НОД, разложение на неприводимые, и так далее), так как доказательства их свойств опираются на доказательства для свойств арифметических действий для многочленов.
Кроме того, эта задача используется как площадка для проверки подходов к доказательному программированию алгебры вообще: эти же приемы могут быть использованы в других задачах. При этом проверяются способы использования средств языка Agda, подходы и практика применения отличаются от тех, что наработаны, например, в системе Coq (см. разделы 4, 6–8). Насколько знает автор, DoCon-A это пока что единственная не игрушечная общая библиотека компьютерной алгебры на языке Agda.
О единице стоимости вычисления: предполагается, что стоимость вычисления измеряется количеством простейших действий над мономами: умножение мономов, сложение коэффициентов, сравнение коэффициента с нулем, сравнение показателей мономов.
Эта оценка $O({{n}^{{{\text{lo}}{{{\text{g}}}_{2}}3}}})$ предполагает такое измерение стоимости. Здесь мы делаем такое же допущение.
В каких случаях это предположение является наиболее естественным с точки зрения оценки времени исполнения программы? Например, для случая коэффициентов из области $\mathbb{Z}{\text{/}}(b)$ остатков целых чисел по модулю некоторого $b$. Для этой области проводились испытания программы (раздел 6).
Программа испытывалась на возведении многочлена $x + 1$ в степень ${{2}^{n}}$ и на умножении случайных многочленов.
За определение умножения многочленов принимается умножение простейшим способом “раскрытия скобок”, когда умножение $f * g$ многочленов сводится к сложению произведений $m * g$, для всех мономов из f, а умножение $m * g$ выстраивается как список произведений монома $m$ на мономы многочлена $g$. При представлении многочлена списком мономов с условием упорядоченности показателей по убыванию и некотором естественном способе сложения многочленов получается, что простейшее умножение многочленов степени $n$ выполняет $O({{n}^{2}})$ умножений и сравнений мономов, и это оценка точная.
В библиотеке DoCon-A ([1], выпуск 3.2rс) построена структура коммутативного кольца для многочленов над произвольным коммутативным кольцом коэффициентов, вместе с соответствующими машинно-проверяемыми доказательствами. При этом доказательства построены для определения произведения многочленов через простейший способ умножения.
Целью представленного здесь исследования было построение такой функциональной программы для способа Карацубы умножения многочленов, которая
• включает в себя мп-доказательство его правильности,
• обладает необходимым быстродействием на практике, соответствующим оценке $O({{n}^{{{\text{lo}}{{{\text{g}}}_{2}}3}}})$,
• выражена исходным кодом приемлемого объема,
• компилируется за приемлемое время.
Правильность означает, что эта функция выдает результат, заданный определением умножения. Из доказательства такой равносильности легко строятся формальные доказательства главных свойств арифметики многочленов для способа Карацубы: законы переместительный, сочетательный, распределительный и другие. Ибо эти законы раньше формально доказаны для простейшего умножения.
Последнее условие о затратах компиляции включено по следующей причине. Компиляцией мы здесь называем такие действия системы Agda: а) проверку типов и б) порождение исполняемого кода. Проверка типов включает в себя проверку мп-доказательств путем проведения некоторых символьных вычислений с выражениями типов. Например, если программа содержит мп-доказательства утверждений из учебника алгебры объемом сто страниц, то для компилятора будет неприемлемо затратить неделю времени на проверку этих мп-доказательств.
Последовательность изложения такова.
В разделе 2 кратко даются общие сведения о представлении арифметики многочленов в программе.
В разделе 3 описывается алгоритм Карацубы для плотного и разреженного представления многочлена.
В разделе 4 даются предварительные общие сведения о программировании на языке с зависимыми типами, о возможном влиянии мп-доказательств в программе на производительность исполняемого кода.
В разделе 5 описывается подход к построению доказательной программы на языке Agda для способа Карацубы для разреженного представления многочлена, обсуждаются некоторые ее черты.
В разделе 6 описывается испытание на производительность функции karatsuba на примере возведения многочлена в степень ${{2}^{n}}$ двоичным способом и на других примерах, сравнение с программой на языке Haskell.
В разделе 7 обсуждаются издержки доказательного программирования на примере данной программы.
В разделе 8 наш подход к доказательному программированию способа Карацубы для многочленов сравнивается с подходом, описанным в диссертации [6] (с программированием в системе Coq). Также говорится о других работах в области автоматизированных систем поддержки формальных доказательств.
В Приложении 11.2 дается доказательство оценки $O({{n}^{{log3}}})$ стоимости вычисления способом Карацубы произведения многочленов для разреженного представления и нашей разновидности алгоритма. Также обсуждается оценка средней стоимости вычисления для этого алгоритма в зависимости от заданной степени разреженности 11.3.
1.1. Программа
Библиотека DoCon-A доказательных программ доступна в Интернете по адресу http://www.botik.ru/pub/local/Mechveliani/docon-A/3.2rc/
Программы написаны на языке Agda [9, 10]. Доказательная функция метода Карацубы содержится в модуле Pol/Karatsuba.agda, программа испытания содержится в модуле Pol/KTest.agda, установка библиотеки и запуск испытания описаны в файле install.txt архива библиотеки.
2. ОБ АРИФМЕТИКЕ МНОГОЧЛЕНОВ
Представляем моном (тип Mon в программе) в виде записи, содержащей коэффициент – элемент носителя (тип С) кольца R коэффициентов и показатель (тип $\mathbb{N}$ – натуральное число). Многочлен представлен в виде списка мономов, чьи коэффициенты ненулевые, а показатели упорядочены по убыванию. Например, многочлен $ - 2{{x}^{4}} + 1$ над целыми числами представлен в программе выражением
mkPol ((mkMon -2 4) :: (mkMon 1 0) :: []) nzCoefs ordExps
nzCoefs – это свидетельство неравенства нулю коэффициентов,
ordExps – свидетельство упорядоченности списка показателей 4 :: 0 :: [].
Равенство _=p_ многочленов определено как почленное равенство списков мономов, когда равенство коэффициентов выражено абстрактным равенством _≈_ в кольце R. Сложение многочленов выполнено как сложение их списков мономов: сочетание слияния двух упорядоченных списков мономов с приведением подобных членов и удалением получающихся нулевых мономов. Этот известный способ сложения f + g многочленов затрачивает количество действий не больше ${\text{max}}({\text{deg}}f)({\text{deg}}g)$.
Умножение f * g многочленов определяется как “раскрытие скобок”: сложение произведений m * g для всех мономов m из f. А умножение m * g на моном выстраивается как список произведений монома m на мономы многочлена g. При этом учитывается, что кольцо R может иметь делители нуля, и появляющиеся нулевые мономы удаляются.
Для таким образом определенной арифметики многочленов в библиотеке DoCon-A доказаны законы коммутативного кольца для области многочленов R[x]. Соответствующий модуль имеет заголовок
module Pol.Over-decComRing
(R : DecCommutativeRing)
(open DecCommutativeRing R using (Carrier))
(C-Show : Show Carrier) (C-Read : Read Carrier)
(var : Variable)
where
Этот модуль имеет четыре параметра:
R – коммутативное кольцо коэффициентов (приставка Dec означает разрешимое равенство, то есть задана функция распознавания равенства на носителе R),
C-Show – структура, задающая способ распечатки в строку элемента R,
C-Read – структура, задающая способ чтения из строки элемента R,
var – строка, изображающая переменную в распечатке многочлена.
В этом модуле запрограммированы функции арифметики многочленов и доказательства для них. Например, функция
polDecCommutativeRing : DecCommutativeRing
строит запись (record), представляющую структуру коммутативного кольца с разрешимым равенством для многочленов. То есть это функтор, строящий кольцо многочленов из данного коммутативного кольца R коэффициентов.
Чтобы воспользоваться функциями построенной области многочленов, программа должна открыть модуль, дав ему значения параметров. Например, арифметика целочисленных многочленов откроется по объявлению
open Pol.Over-decComRing Int.decCommutativeRing
Int.Show Int.Read “x”
Компилятор Агды проверит, содержит ли структура Int.decCommutativeRing доказательства структуры коммутативного кольца, и так далее. В области действия такого объявления компилятор воспримет функции +p, *p из этого модуля как действия над многочленами с целыми коэффициентами. Если же, например, подставлено значение параметра R = IntResidue, то эти функции будут восприниматься в смысле арифметики многочленов с коэффициентами по модулю заданного m (коэффициенты из $\mathbb{Z}$/(m)).
3. УМНОЖЕНИЕ МНОГОЧЛЕНОВ СПОСОБОМ КАРАЦУБЫ
В дальнейшем применяем следующие определения и словоупотребление.
$log$ обозначает логарифм по основанию 2.
Определение 1. Для метода M вычисления некоторой функции для пар многочленов выражение $C(M,n)$ обозначает наибольшую из стоимостей применения этого метода для многочленов степени не больше $n$, когда стоимость выражена числом простейших действий над мономами (см. начало Введения).
Оценка стоимости $M \in O({{n}^{\alpha }})$ для такого метода M означает, что существует натуральное число $c$ такое, что для любого $n > 0$ выполнено неравенство
3.1. Случай плотного представления многочлена
Пусть deg f = deg g = 2k, где k степень двойки. Представим
где $\deg {{f}_{1}} = \deg {{f}_{2}} = \deg {{g}_{1}} = \deg {{g}_{2}} = k$. ТогдаВ этой формуле умножение на моном вида ${{x}^{i}}$ и сложения имеют линейную стоимость по k. Но появляются четыре умножения многочленов степени k, и при простейшем способе эти умножения имеют стоимость квадратичную по k.
Учитывая равенство
Конечно, способ предполагает, что каждое из этих произведений вычисляется однажды, а потом в готовом виде подставляется в выражение (II) в разных местах. Сложений (вычитаний) стало больше, но они имеют линейную стоимость по $k$. Все это приводит к тому, что способ Карацубы удовлетворяет оценке $O({{k}^{{log3}}})$, (где $log3 < 1.59$). Это доказано в ([5], Theorem 8.3). Видно, что порядок роста стоимости существенно меньше, чем в простейшем способе умножения.
Случай произвольных степеней легко сводится к рассмотренному выше случаю таким образом:
Здесь $n = {\text{max}}({\text{deg}}{\kern 1pt} {\kern 1pt} f,{\text{deg}}{\kern 1pt} {\kern 1pt} g)$, $m = {{2}^{{1 + [logn]}}}$, а квадратные скобки обозначают целую часть вещественного числа. Нетрудно доказать, что оценка стоимости $O({{n}^{{log3}}})$ сохраняется (доказательство пропускаем, так как нам нужно доказательство для другой разновидности алгоритма).
3.2. Алгоритм для разреженного представления многочленов
О случаях разреженного и плотного представления многочлена. Обоснование.
В нашей библиотеке удобнее применять разреженное представление многочленов списками. Например: а) многочлен ${{x}^{{1000}}} + 1$ занимает в разреженном представлении много раз меньше памяти, чем в плотном, б) умножение ${{x}^{{100}}} * {{x}^{{90}}}$ многочленов занимает одно действие. Также имеется то удобство, что выбранное нами представление многочлена одной переменной оказывается частным случаем представления многочлена многих переменных. Ведь для многочленов многих переменных плотное представление не применимо в практике вычислений.
Арифметику многочленов в плотной записи мы не программировали, не относим это к первоочередным задачам.
Для плотного представления количество мономов в многочлене f равно $1 + ({\text{deg}}{\kern 1pt} {\kern 1pt} f)$. Для разреженного представления выполнено неравенство
число мономов в $f \leqslant 1 + ({\text{deg}}{\kern 1pt} {\kern 1pt} f).$
Это учитывается в доказательстве оценок стоимости вычисления.
Какой смысл имеет асимптотическая оценка $O({{n}^{\alpha }})$ стоимости вычисления для какого-либо метода M, действующего на разреженно представленных многочленах, если $n$ это степень многочлена?
Смысл такой же, как в Определении 1 из начала раздела. В обоих случаях стоимость вычисления измеряется количеством действий над мономами, а “размер” многочлена измеряется его степенью $n$ – несмотря на количество мономов.
В частности, многочлен большой степени может содержать мало мономов, например, один.
Ниже описывается способ Kara умножения многочленов в разреженной записи, который мы считаем разновидностью способа Карацубы. Способ для плотной записи будем называть Kara-dense. Главное отличие способа Kara состоит в следующем. Для четного $n$, многочлен делится на старшую часть ${{x}^{{n/2}}}{{f}_{1}}$ и младшую часть ${{f}_{2}}$, ${\text{deg}}{{f}_{1}} = n{\text{/}}2$, ${\text{deg}}{{f}_{2}} < n{\text{/}}2$ – почти как в способе Kara-dense, только ${{f}_{1}}$ и ${{f}_{2}}$ могут сильно отличаться по степени и количеству мономов. В дальнейшем умножение применяется рекурсивно к парам многочленов, которые могут иметь разные степени и разное количество мономов. Для выравнивания степеней применяется прибавление монома ${{x}^{m}}$ нужной степени, а потом делается поправка итога умножения. Для сведения метода к четной степени применяется (в дополнение к возможному предыдущему приему) расщепление многочлена на старший моном и хвост и поcледующая поправка итога.
Почему для исследования выбран метод умножения многочленов именно для разреженного представления многочлена?
С таким же успехом можно исследовать такую программу для плотного представления. Доказательство оценки стоимости для него уже известно, останется построить мп-доказательства. Но главное – это качество самой программы, с учетом системы, в которой она участвует, из этих соображений подбирается представление данных и изобретается алгоритм. Далее, для подтверждения надежности выводится теоретическая оценка стоимости вычисления и программируются мп-доказательства. Соображение “для этого представления данных легко получить такую-то оценку сложности, поэтому запрограммируем такой-то алгоритм” сомнительно с точки зрения разработки хорошей программы. В нашем же случае рассматриваются алгоритмы арифметики многочленов для разреженного представления.
Метод Kara умножения разреженно представленных многочленов.
Функция kara принимает сомножители f и $g$ расставленные так, что $m = {\text{deg}}{\kern 1pt} {\kern 1pt} f \leqslant n = {\text{deg}}{\kern 1pt} {\kern 1pt} g$. Она выдает произведение $fg$ путем следующего вычисления. Разбираются случаи
• (EE) m = n четное,
• (GE) m < n, n четное,
• (GO) m < n, n нечетное,
• (EO) m = n нечетное.
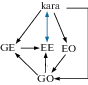
Этим случаям соответствуют функции EE, GE, GO, EO, (в программе caseEqualEvenDeg, caseGreaterEvenDeg, caseGreaterOddDeg, caseEqualOddDeg), которые вместе с функцией kara вызывают друг друга согласно диаграмме (рис. 1).
Всюду ниже применяем обозначение EE(n,f,g) = = EE f g, где f и g многочлены, n = max (deg f) (deg g). Также пишем EE(n), когда считаем, что остальные два аргумента суть любые f и g такие, что n = = max (deg f) (deg g).
В случае EE
сначала применяется функция splitPolAtDegree. Она расщепляет f на старшую часть higher, чьи мономы имеют степени не меньше $k = n{\text{/}}2$, и младшую часть f2, чьи мономы имеют степени меньше k. Многочлен higher представляется в виде ${{x}^{k}} * {{f}_{1}}$, соответственно, $f = {{x}^{k}} * {{f}_{1}} + {{f}_{2}}$. Такое же расщепление применяется к g : g = ${{x}^{k}} * {{g}_{1}} + {{g}_{2}}$. Функция splitPolAtDegree затрачивает не больше $2n$ действий. Затем применяется формула (II) раздела 3.1, где произведения ${{f}_{1}}{{g}_{1}}$, ${{f}_{2}}{{g}_{2}}$, $ss{\text{'}}$ вычисляются рекурсивным применением функции kara с предварительной расстановкой сомножителей согласно их степеням.
Здесь выполнены равенства deg f1 = deg g1 = = ${\text{deg}}{\kern 1pt} {\kern 1pt} s = {\text{deg}}{\kern 1pt} {\kern 1pt} s{\text{'}}$ = k. Но ${\text{deg}}{\kern 1pt} {\kern 1pt} {{f}_{2}}$ и ${\text{deg}}{\kern 1pt} {\kern 1pt} {{g}_{2}}$ могут оказаться любыми натуральными числами меньшими k – из-за разреженного представления.
В случае GE положим $F = {{x}^{n}} + f$ и вычислим $f * g = (F - {{x}^{n}}) * g = {\text{EE}}(F,g) - {{x}^{n}}g$, где вычисление ${{x}^{n}}g$ занимает не более $n$ действий над мономами.
В случае GO
число $p = n - 1$ четное. Представим $g = {\text{mon}} + g{\text{'}}$, где ${\text{mon}}$ старший моном в $g$. Тогда f * g = mon * f + $f * g{\text{'}}$, а $f * g{\text{'}}$ вычисляется через разбор следующих случаев для ${\text{deg}}{\kern 1pt} {\kern 1pt} g{\text{'}}$, ${\text{deg}}{\kern 1pt} {\kern 1pt} f$:
case $({\text{deg}}{\kern 1pt} {\kern 1pt} g{\text{'}} = ?p,\quad {\text{deg}}{\kern 1pt} {\kern 1pt} f = ?p)$ of
(True, True) -> ${\text{EE}}(f,g{\text{'}})$
(True, False) -> ${\text{GE}}(f,g{\text{'}})$
(False, True) -> ${\text{GE}}(g{\text{'}},f)$
(False, False) -> ${\text{GE}}(f,{{x}^{p}} + g{\text{'}}) - {{x}^{p}}f$
Во втором случае оказывается ${\text{deg}}{\kern 1pt} {\kern 1pt} g{\text{'}} = p$, ${\text{deg}}{\kern 1pt} {\kern 1pt} f$ < deg g, ${\text{deg}}{\kern 1pt} {\kern 1pt} f \leqslant p$, ${\text{deg}}{\kern 1pt} {\kern 1pt} f \ne p$.
Поэтому ${\text{deg}}{\kern 1pt} {\kern 1pt} f < {\text{deg}}{\kern 1pt} {\kern 1pt} g{\text{'}}$, и применяется ${\text{GE}}(f,g{\text{'}})$.
Подобным образом разбираются остальные случаи. В последнем случае выводятся неравенства ${\text{deg}}{\kern 1pt} {\kern 1pt} f,{\text{deg}}{\kern 1pt} {\kern 1pt} g{\text{'}} < p$, и потому применим вызов ${\text{GE}}(f,{{x}^{p}} + g{\text{'}})$.
В случае EO представим $f = {\text{mon}} + f{\text{'}}$ где ${\text{mon}}$ старший моном в f, и вычислим
О пороге применения: для каждой разновидности алгоритма и каждой системы программирования есть порог выгодности применения способа Карацубы для многочленов. Назовем это число kThreshold. Если какой-то из сомножителей имеет число мономов меньше порога, то в среднем выгоднее применять простейшее умножение. Например, для систем Glasgow Haskell 8.8.3, Agda 2.6.1 и нашей программы порог равен 18. (Этот порог не влияет на порядок роста сложности вычисления)
3.3. Об оценках стоимости вычисления
Оценка стоимости $O({{n}^{{log3}}})$ доказана в [5] (Theorem 8.3) для способа Карацубы для плотно представленных многочленов. Наша программа включает мп-доказательства правильности для несколько другого алгоритма (kara) – для разреженного представления.
В Приложении 11 дано доказательство оценки $O({{n}^{{log3}}})$ для алгоритма kara (для разреженной записи) – опять, в смысле Определения 1. Оно несколько более сложное. Это влечет за собой, например, такие последствия. Умножение ${{x}^{n}} * {{x}^{n}}$ многочленов займет одно действие какой бы большой ни была степень $n$. А способ Kara-dense будет в этом примере обрабатывать списки длины $n + 1$, и так далее, и затратит примерно $5 \cdot {{n}^{{log3}}}$ действий – очень много. Далее, добавим к ${{x}^{n}}$ еще много любых мономов степеней меньше $n$ и обозначим полученный многочлен f. Тогда при вычислении $f * f$ способ Kara во многих случаях затратит много действий – но не больше, чем $c \cdot {{n}^{{log3}}}$, где постоянная $c$ приблизительно не больше 50.
Назовем длиной многочлена f (в разреженной записи) количество ${\text{S}}(f)$ мономов в нем.
Об оценке в среднем для способа Kara в при неизменной степени разреженности:
автор проделал следующий опыт. При неизменной степени $n$ перемножаемых многочленов (в примерах было положено $n$ = 6000) программе kara подавались многочлены различных длин $s$. При изменении $s$ от $n + 1$ к меньшим значениям среднее время вычисления стремительно уменьшалось. В Приложении (раздел 11.3) дан набросок доказательства, который объясняет это явление. Именно, пусть $P(n,s)$ множество многочленов степени $n$, имеющих длину $s$, $C(n,s)$ – средняя стоимость вычисления по алгоритму Kara, когда сомножители берутся из множества $P(n,s)$. Если $n$ является степенью двойки, а степени мономов в сомножителях распределены равномерно на отрезке $[0,n]$ (в среднем они и будут распределены равномерно), то выполнена оценка
Вторая степень в этой оценке нам не мешает, так как важны значения $s$ достаточно малые в сравнении с $n$. Например:
• при $s < \sqrt n $ порядок стоимости окажется не больше $n$, тогда как
• при наибольшей длине $n + 1$ стоимость в наихудшем случае достигнет порядка не меньше ${{n}^{{3/2}}}$
(второе утверждение не доказано строго, оно взято из итогов испытаний программы). Уточнение этой оценки (по худшему случаю или в среднем) для общего случая а также построение строго доказательства может быть предметом отдельного исследования.
Перечислим итоги, которые показывают, что способ вычисления Kara (для разреженного представления) имеет смысл.
• Способ Kara имеет верхнюю оценку $O({{n}^{{log3}}})$ стоимости вычисления – такого же порядка, как способ Kara-dense (когда последний применяется к плотным записям тех же многочленов). И это много меньше (точной) оценки $O({{n}^{2}})$ стоимости для простейшего способа умножения.
• Эта оценка равномерна по длине многочленов степени не больше $n$: верна как для многочленов малой длины, так и для многочленов большой длины (максимум длины равен $n + 1$).
• Средняя (на опыте) стоимость вычисления способом Kara при неизменном $n$ быстро убывает с уменьшением длины сомножителей. Это дает преимущество в среднем быстродействии на сильно разреженных многочленах перед способом Kara-dense.
• Испытания программы (раздел 6) показывают соответствие верхней оценке по степени, и вообще, быструю работу программы.
• Программа способа Kara снабжена мп-доказательством равносильности простейшему умножению.
4. ПРЕДВАРИТЕЛЬНЫЕ ОБЪЯСНЕНИЯ О ПРОГРАММИРОВАНИИ С ЗАВИСИМЫМИ ТИПАМИ
Обсудим черты доказательной программы на языке Agda для метода kara (раздел 3.2).
Язык Agda [9, 10] основан на чистой функциональности, “ленивом” способе вычисления по умолчанию, поддержке обобщенного программирования (generic programming), аппарате зависимых типов. Приблизительно можно считать, что это язык Haskell, расширенный аппаратом зависимых типов. Зависимые типы позволяют адекватно описать алгебраическую область, зависящую от обычного значения ([11], Введение). Кроме того, этот аппарат позволяет вставлять в программу доказательства утверждений, и эти доказательства будут проверяться компилятором. Становится возможным описывать метод вычисления в программе так, как это делается в учебниках и научных статьях, вместе с доказательством правильности. Доказательства понимаются по умолчанию в смысле конструктивной математики [12, 13].
От известной системы Coq [14] (и ее языка Gallina) главные отличия состоят в “ленивом” вычислении по умолчанию, отсутствием разделения на язык задания вычислений и язык построения доказательств, одинаковой поддержкой как программирования быстрых вычислений, так и доказательств.
От известной системы Lean [15] главные отличия состоят в “ленивом” вычислении по умолчанию, чисто-функциональном программировании, одинаковой поддержкой как программирования быстрых вычислений, так и доказательств, требованием конструктивного доказательства по умолчанию.
Техника проверки доказательств компилятором (точнее – проверяльщиком типов – type checker) основана на том, что всякое утверждение S представляется подходящим типом T (зависящим от значений). Доказательство для S есть любая функция (завершающийся алгоритм), которая выдает любое значение v типа T. Проверяльщик типов проверяет отношение v : T посредством символьных вычислений с выражениями типов. Таким образом доказательство утверждения проверяется до начала компиляции в исполняемый код.
Недоказуемое высказывание соответствует пустому типу ⊥ c пустым множеством значений. Отрицание высказывания соответствует функции, отображающей соответствующий высказыванию тип в пустой тип. Импликация выражена типом S → T всех функций из S в Т, где S и T представляют соответствующие утверждения. Конъюнкция выражена произведением S × T типов, дизъюнкция выражена суммой S ${{ \cup }_{ + }}$ T типов. Доказательство индукцией по построению данного выражается в виде рекурсивно заданной функции. Применение леммы выражается в виде вызова функции, представляющей доказательство леммы.
Пока ограничиваемся только конструктивными доказательствами [12, 13] (без использования принципа Маркова для доказательства завершаемости алгоритмов). В частности, всякий объект существует лишь как итог некоторого данного алгоритма, и должно быть дано доказательство завершаемости этого алгоритма.
Мы часто пользуемся законом исключенного третьего – в конструктивной математике это возможно в тех (часто встречающихся) случаях, когда приведен алгоритм разрешения соответствующего отношения.
Наш подход в отношении конструктивизма таков. а) Конструктивное доказательство лучше, чем неконструктивное, так как дает больше знания. Например, завершающийся алгоритм построения объекта – это больше, чем неконструктивное доказательство его существования. b) Если нужно доказательcтво, а конструктивное доказательство не удается найти, то можно обойтись неконструктивным, использовав аксиому исключенного третьего – она просто записывается на языке Agda. Конечно, лучше явно выделить места, где она применяется.
Добавим, что есть широкая область в математике и научных вычислениях, где достаточно лишь конструктивного подхода, и пока что наша библиотека находится целиком в этой области. Но есть и еще большая область, где конструктивных доказательств не хватает.
Более подробные объяснения по данной системе программирования и примеры содержатся в [9, 11] и в руководстве по библиотеке [1].
4.1. О синтаксисе языка Agda
Имена операторов и отношений отделяются пробелами. Например, в строке
a+b≈0 : a + b ≈ 0#
программы a+b ≈ 0 есть имя значения, двоеточие отделяет имя значения от выражения типа, символы ‘+’ и ‘≈’ в выражении типа суть соответственно имя оператора сложения и имя двуместного отношения, 0# есть имя нулевой постоянной. Вся эта строка означает объявление: значение a+b≈0 имеет тип a + b ≈ 0# (и этот тип зависит от значений a, b, 0#).
Знак подчерка в имени отношения или операции означает, что в синтаксисе программы во входном выражении на этой позиции ставится выражение аргумента этой операции.
Знак равенства ‘=’ – это определение идентификатора (присваивание) – часть синтаксиса программы.
Равенство _≈_ – это знак отношения равенства на некоторой области, это отношение задается для каждой области программы пользователя или стандартной библиотекой.
4.2. Внешние и внутренние доказательства
В каком смысле функция на языке Agda может быть доказательством?
Если функция строит доказательство, то само тело этой функции является доказательством некоего общего утверждения. И это доказательство проверяется проверяльщиком типов в общем, символьном виде, так же, как читатель проверяет доказательство, изложенное в книге. Если и когда эта функция вычисляется во время исполнения, то она выдает доказательство для какого-то частного случая, и строение этого доказательства в обычных случаях бывает не нужно разбирать. Например, можно запрограммировать функцию m≤m+n (это ее имя), выражающую доказательство утверждения $\forall $ m n (m ≤ m + n) для натуральных чисел. Ее тело выражает общее доказательство, скажем, по индукции. А вычисление вызова (m≤m+n 2 9) во время исполнения выдаст только доказательство неравенства 2 ≤ 2 + 9.
Обычный подход к доказательному программированию таков. Алгоритм A программируется как некоторая функция F на Агде в духе языка Haskell, без построения доказательств. Затем пишутся функции мп-доказательств для выбранных свойств F: если аргументы F удовлетворяют таким-то условиям, то итог функции обладает таким-то свойством. При этом обычно доказательство по индукции следует рекурсивному построению функции F. Например, таким способом в библиотеке запрограммированы доказательства переместительного и сочетательного законов для сложения и простейшего умножения многочленов (если не учитывать свидетельства, содержащиеся в данных типа Pol). Назовем такие доказательства внешними. Они проверяются компилятором (в первой его части – проверке типов). При этом вычисление функции F при исполнении программы заведомо не вызывает функции доказательств.
Но на практике для многих функций оказывается чрезвычайно затруднительным построение внеших мп-доказательств. Возможно это следствие каких-то технических трудностей в воплощении языка Agda. Поэтому мы снабжаем многие функции внутренними доказательствами, то есть такими, которые являются частью итога функции. Их легче задать, чем внешние доказательства, они строятся в теле функции заодно с основной частью итога. Этот подход выгоден еще и тем, что уменьшает повторы кода, так как внутреннее доказательство использует уже развернутую внутреннюю среду. С другой стороны, в среднем часть доказательства занимает довольно много кода, и этот код мешает читателю разглядеть строение самого способа вычисления. В таком случае может быть полезно предварять программу комментарием с короткой записью основной функции, не снабженной доказательством.
Но раз построение доказательства включено в тело функции, то не получится ли так, что при исполнении программы на доказательство потратится время сравнимое с тем, что тратится на главный итог?
Не получится – при естественном способе программирования. Ибо Agda это язык “ленивого” исполнения по умолчанию. Поэтому, если функция F выдает пару
(<главный итог> , <доказательство>),
а функция – клиент G не использует существенно вторую часть пары, то при вычислении G эта часть вычисляться не будет. Существенным использованием данного мы называем разбор строения этого данного. Доказательства в языке Agda являются данными. Их можно разбирать на части, делать с ними содержательные вычисления, распечатывать.
Но в обычных научных вычислениях не требуется разбирать строение доказательств во время вычисления, функции – клиенту всегда достаточно лишь само наличие какого-то доказательства соответствующего типа. А это наличие выясняется проверяльщиком типов в символьном виде до начала исполнения программы. То есть в обычных научных вычислениях доказательства никогда не используются по существу при исполнении и потому не занимают ресурсов при исполнении. Например, функция lm выдает старший моном многочлена f, но нужен дополнительный аргумент hm-f : HasMon f – доказательство того, что многочлен не нулевой. Видя вызов (lm f hm-f) взятия старшего монома, проверяльщик проверит, имеет ли значение hm-f подходящий тип. А во время исполнения, при вычислении этого вызова данное hm-f разбираться/вычисляться не будет.
Так обстоит дело и с функцией karatsuba.
Мертвый код: проверяльщик типов выдает код для компилятора, в этом коде часто бывают участки доказательств, часто большие. Внешние доказательства легко узнать, и после проверки они удаляются компилятором. Но некоторые внутренние и ненужные (после проверки) доказательства проверяльщик не может распознать как ненужные, если функция сложно устроена. И эти “мертвые” доказательства задают работу компилятору и проникают в объектный код – хотя и не работают во время исполнения. В главе “run-time irrelevance annotation” в документации на систему Agda описаны обозначения Erased, @0, простановка которых в программу в правильных местах принуждает Агду удалить мертвый код до компиляции. Но в данном выпуске библиотеки эти дополнительные затраты компиляции малы в сравнении с остальными издержками, поэтому даже небольшое усложнение программы erased – обозначениями не имеет смысла.
4.3. Завершаемость
По умолчанию Agda должна убедиться в завершаемости каждой заданной функции (алгоритма). Указание TERMINATING избавляет проверяльщик типов от проверки завершаемости, но применение такого указания это отступление от доказательного программирования. Поэтому мы не применяем такое указание, так же, как не применяем указаний постулирования postulate, anything. Часто Agda сама убеждается в завершаемости путем обнаружения синтаксического уменьшения рекурсивных вызовов. Но также часто выдается сообщение “Termination checking failed”. В этом случае надо помочь Агде распознать завершаемость. Обычно проще всего ввести в функцию дополнительный аргумент в виде счетчика – натурального числа. Воспринимая неравенства, доказанные в теле функции для этого счетчика, Agda убеждается в завершаемости.
Доказательство завершаемости всегда неявное. Сравним на примере: на языке Agda можно выразить высказывание “функция f коммутативна”, но нет способа прямо выразить высказывание “функция f завершается” так, чтобы потом использовать в программе какое-то доказательство p для этого высказывания.
5. ПРОГРАММА СПОСОБА КАРАЦУБЫ НА ЯЗЫКЕ Agda
Функция способа Карацубы задана в модуле, объявленном как module Pol.Karatsuba (R : DecCommutativeRing).
Здесь коммутативное кольцо R с разрешимым равенством является параметром – это область коэффициентов. Подставляя различные воплощения для R, программист автоматически настраивает все функции из этого модуля на выбранную область коэффициентов.
Но в отличие от типа (Pol a) в Haskell-программе тип Pol в нашей Agda-программе в библиотеке DoCon-A скрывает в себе машинно-проверяемое условие определения представления многочлена: свидетельство неравенства нулю коэффициентов и свидетельство упорядоченности показателей (раздел 2). Функции арифметики многочленов строят эти свидетельства для итога действия, исходя из таких свидетельств для операндов. Есть и другие отличия.
Главным доказательством для функции karatsuba является доказательство ее равносильности простейшему умножению:
(f g : Pol) → (karatsuba f g) =p (f *p g) (IV)
Здесь _=p_ равенство многочленов, _*p_ простейшее умножение. Последние две сущности взяты из модулей, посвященных многочленам. Но мы сначала задаем функцию Карацубы в формате, включающем основное доказательство.
karatsuba-withProof : (f g : Pol) →
∃ (\h → h =p f *p g)
Выдается пара (h , eq), где h – произведение, eq – доказательство равенства h =p (f *p g). Это доказательство внутреннее, оно задается в теле функции в циклах, выражающих вычисления произведения.
Для вычисления произведения надо вызывать не эту функцию, а функцию
karatsuba : Op2 Pol
karatsuba f = proj1∘ karatsuba-withProof f
(_°_ – функция композиции). Она выдает первую часть итога вызова karatsuba-withProof. Доказательства различных свойств умножения способом karatsuba теперь просто получить переносом соответствующих доказательств для функции _*p_. Например, переместительный закон:
karatsuba-comm : Commutative _=p_ karatsuba
karatsuba-comm f g =
let open EqReasoning
(h , h=fg ) = karatsuba-withProof f g
(h’ , h’=gf) = karatsuba-withProof g f
in
begin 〈 polSetoid 〉 h ≈〈 h=fg 〉
f *p g ≈〈 *p-comm f g 〉
g *p f ≈〈 =p-sym h’=gf 〉
h’
end
Дадим пояснения. Здесь h = karatsuba f g, h’ = karatsuba g f, и требуется доказать h =p h’.
h = fg это доказательство равенства h =p (f *p g), взятое из итога вызова karatsuba-withProof f g. h’=gf это доказательство равенства h’ =p (g *p f), взятое из итога вызова karatsuba-withProof g f. В силу доказательств h=fg и закона *p-comm перестановочности простейшего умножения, доказанного в библиотеке, выводится равенство h =p (g *p f). Правая его часть равна h’ в силу равенства h’= gf, которое применяется справа налево и завершает доказательство.
В вызове (begin … end) в левой колонке записана последовательность значений, в которой каждое значение равно предыдущему. В каждой строке правой колонки записан вызов функции, которая выдает доказательство равенства значения в левой колонке следующему значению. Замечательно, что (begin … end) это не конструкция языка, а вызовы функций begin_ и _end из стандартной библиотеки, написанной на Агде (а применение функции может записываться префиксно, инфиксно или постфикстно). Такова же функция ≈〈_〉_, применяемая в правой колонке. Эти вызовы позволяют наглядно записать композицию применений закона транзитивности равенства.
5.1. Функция splitPolAtDegree
Функция
splitPolAtDegree :
{n : ℕ} {f : Pol} (hmF : HasMon f)
(n≤degF : n ≤ deg f hmF) →
SplitPolAtDegree n f
это главный шаг метода. Она воплощает расщепление из шага EE алгоритма Kara из раздела 3.2. Она принимает натуральное n (в программе – целая часть $({\text{deg}}{\kern 1pt} {\kern 1pt} f){\text{/}}2$), ненулевой многочлен f степени не меньше n и выдает структуру, описывающую разбиение f на старшую часть higher и младшую часть lower – как описано в разделе 3.2. Только некоторые аргументы и некоторые части итога суть доказательства свойств этого разбиения. В отдельном модуле дополнительно доказаны свойства этого разбиения. Например:
• hmH : HasMon higher – свидетельство того, что старшая часть ненулевая,
• splitEq : mons ≡ monsH ++ monsL – список мономов f синтаксически равен (propositional equality) соединению списка старших мономов и списка младших мономов,
• f≡p-higher+lower : f ≡p higher +p lower – f синтаксически равен сумме многочленов higher+lower (в смысле синтаксического равенства списков мономов),
• xn|h : xn| h – свидетельство “xn делит higher”, и выдается частное h0,
• f=xnh0+low : f = p (xn *p h0 +p lower)
Эти доказательства используются в мп-доказательстве теоремы (IV).
5.2. Функция karatsuba-withProof
Функция karatsuba-withProof разбирает случаи нулевых аргументов, упорядочивает два аргумента по степени и вызывает функцию
kara :
(f g : Pol) (hmF : HasMon f) (hmG : HasMon g) →
deg f hmF ≤ deg g hmG → (cnt : $\mathbb{N}$) →
deg g hmG ≤ cnt → ∃ (\h → h =p f *p g)
kara f g _ _ _ 0 _ = f *p g , =p-refl {f *p g}
kara f g hmF hmG e≤e’ (suc cnt) e’≤1+cnt =
considerCases (length mons <? kThreshold)
(length mons’ <? kThreshold)
(e =? e’) (2 |? e’)
Функция kara это главный цикл метода. Она принимает два многочлена, hmF и hmG суть свидетельства того, что они ненулевые, следующий аргумент это свидетельство неравенства deg f ≤ $ \leqslant {\text{deg}}{\kern 1pt} g$. Последние два аргумента суть счетчик cnt и свидетельство неравенства ${\text{deg}}g \leqslant cnt$. Они нужны для доказательства завершаемости функции.
При рекурсивном вызове функции kara счетчик уменьшается синтаксически от выражения (suc cnt) к выражению cnt, а степень второго многочлена уменьшается по меньшей мере на единицу. В начальном вызове cnt = deg g, а когда значение deg g достигает нуля, функция выдает итог. Поэтому Agda решает, что алгоритм завершается.
Первое предложение разбирает случай нулевого счетчика. В нем выдается произведение, вычисленное простейшим способом (а нам известно, что в этом случае оба многочлена суть постоянные). Поэтому вторая часть итога это доказательство тождественного равенства (вида X =p X).
Второе предложение это выход на разбор случаев и шаг рекурсии. Вызывается функция
considerCases : Dec (length mons < kThreshold) →
Dec (length mons’ < kThreshold) →
Dec (e ≡ e’) → Dec (2 | e’) →
∃ (\h → h =p f *p g),
которая сначала проверяет, достаточно ли мономов в f и g (проверка занимает не более kThreshold шагов). Если не достаточно много, то выполняется простейшее умножение f * p g. Если достаточно, то проверяются условия e ≡ e’, 2 | e (второе условие это делимость на 2). По их итогам вызывается одна из функций, воплощающих случаи (EE), (EO), (GE), (GO) из раздела 3.2. Например, случай (EE) вызывается в третьем предложении:
considerCases
(no |mons|≮kTh) (no _) (yes e≡e’) (yes 2|e’) =
let 2|e = subst (2 |_) (sym e≡e’) 2|e’
2≤e = |f|≮kThreshold⇒2≤deg-f {f} hmF
|mons|≮kTh
e≤1+cnt = subst (_≤ 1+cnt) (sym e≡e’)
e’≤1+cnt
in
caseEqualEvenDeg f g hmF hmG e≡e’ 2≤e 2|e
e≤1+cnt
– в обоих многочленах много мономов, e ≡ e’, e’ – четное. Здесь сначала доказывается, что e тоже делится на 2. Потом неравенство 2 ≤ e выводится из того, что число мономов не меньше порога (|mons| ≮ kTh). Потом неравенство e ≤ 1+cnt выводится из неравенства e’ ≤ 1 + cnt, данного выше в вызове kara. Наконец, функции caseEqualEvenDeg кроме многочленов f и g даются еще эти построенные доказательства 2 ≤ e, 2|e, e ≤ 1 + cnt.
Условие 2 ≤ e здесь нужно для возможности дальнейшего разбиения многочлена f. Если оно не выполнено, то из четности e следует e = 0 = e/2, и разбиение не уменьшит степени многочлена, и проверяльщик типов сообщит о неудаче доказательства завершаемости.
Функции для случаев (EO), (GE), (GO) разбирать не будем, а дадим лишь пояснения к функции caseEqualEvenDeg:
caseEqualEvenDeg :
(u v : Pol) (hmU : HasMon u)
(hmV : HasMon v) →
let dU = deg u hmU; dV = deg v hmV
in
dU ≡ dV → 2 ≤ dU → 2 | dU → dU ≤ 1+cnt →
∃ (\h → h =p u *p v)
caseEqualEvenDeg u v hmU hmV E≡E’ 2≤E 2|E
E≤1+cnt =
let
E = deg u hmU; E’ = deg v hmV
(k , E≡k*2) = 2|E
monE = mkMon 1# E – моном x^E
monK = mkMon 1# k
…
…
in
eeDeg monE monK ss’ f1g1 f2g2 , eq
Выражение (k, E≡k*2) = 2|E это определение отношения делимости, примененное к паре 2, E. Оно включает в себя частное k и доказательство равенства E ≡ k * 2.
Обозначения f1, g1, f2, g2, s, s’ – те же, что в формуле (II) из раздела 3 – с заменой f -> u, g -> v : $u = {{x}^{E}} * {{f}_{1}} + {{f}_{2}}$, и так далее. В первой части пары итога выдается значение
Это формула (II) из раздела 3. Здесь + это сложение многочленов, ‘-’ вычитание многочленов, ‘${{x}^{E}} * $’ и ‘${{x}^{K}} * $’ суть умножения на моном, a произведения f1g1, f2g2, ss’ вычисляются рекурсивным применением функции kara.
Во второй части пары выдается доказательство eq равенства H = u *p v, где _*p_ простейшее умножение многочленов. Для получения доказательства eq используется то, что kara тоже возвращает произведение в паре с доказательством, например:
(ss’ , ss’Eq) = kara s s’ hmS hmS’
(≤-reflexive degS≡degS’)
cnt degS’≤cnt,
где ss’Eq это доказательство равенства ss’ = p (s *p s’).
Равенство eq для H выводится из ss’Eq и из подобных же равенств для произведений путем замены в (IIA) f1g1 на f1 *p g1, f2g2 на f2 *p g2, ss’ на s *p s’ в силу соответствующих равенств и последующего применения законов коммутативного кольца (раскрытие скобок, приведение подобных членов и тому подобное). Все это формально расписывается в функции caseEqualEvenDeg.
А для этих формальных построений необходимы доказательства, которые надо подставлять в аргументы рекурсивных вызовов функции kara. Например, в вызов вычисления ss’ входит доказательство degS’ ≤ cnt неравенства deg s’ ≤ cnt. А в вызове caseEqualEvenDeg есть доказательство E ≤ 1+cnt : deg u ≤ suc cnt (suc это конструктор “следующий” для натуральных чисел). Оно нужно для доказательства завершаемости. Это доказательство получается следующим образом. 2 ≤ E = deg u ≤ suc cnt = 1 + cnt, поэтому E/2 ≤ cnt.
Имеем s’ = g1 +p g2, deg g1 = E/2, deg g2 < E/2.
В модулях для аддитивной части арифметики многочленов доказана лемма о том, что степень суммы не больше максимума степеней слагаемых. Поэтому deg s’ ≤ E/2 ≤ cnt. И даже это рассуждение содержит пробелы, так что в программе добавлены необходимые подробности.
В доказательстве встречаются такие определения значений, как f1*g1 = f1 *p g1. Эти символьные выражения участвуют в доказательстве, но в силу “ленивого” вычисления и устройства функции они не вычисляются во время исполнения.
6. ИСПЫТАНИЕ НА ПРИМЕРАХ
Модуль Pol/KTest.agda библиотеки содержит программу испытания на производительность функции karatsuba.
При целых коэффициентах и больших степенях многочленов влияние распухания коэффициентов в ходе вычисления может оказаться существенным. Поэтому во всех испытаниях областью коэффициентов полагается кольцо R = $\mathbb{Z}$/(b) остатков по модулю b. Значение b = 99991 выбрано из того соображения, что, нулевых мономов получается мало, и это дает более затратный случай для нашего алгоритма, опирающегося на разреженное представление многочлена.
Первое испытание – по худшему случаю, когда степень разреженности нулевая. Другие два испытания – на случайных многочленах средней степени разреженности.
Первое испытание таково.
Задается значение n : $\mathbb{N}$. Затем функция pk возводит многочлен f = x + 1 в степень ${{2}^{n}}$ двоичным способом – путем применения умножения способом Карацубы n раз. Например, для n = 12 умножение применяется 12 раз, и получается многочлен степени 4096.
Затем печатаются (1) степень pk, (2) многочлен pk – pk, (3) количество мономов в pk, (4) сумма коэффициентов pk в кольце R и измеряется время исполнения.
Эти данные выбраны так, чтобы распечатка не была большой и при этом все части многочлена pk были вычислены. Такие ухищрения нужны оттого, что вычисления выполняются “ленивым” способом.
Части (1), (2), (3) служат еще для проверки правильности (сама-то система Agda тоже может содержать ошибки).
Тот же многочлен вычисляется в этом модуле через простейшее умножение _*p_, он обозначен p. Замена pk -> p в функции main даст испытание для простейшего умножения.
Если в строке ‘check =’ заменить pk -p pk на p -p pk, то будет проверено равенство двух способов умножения на этом примере (хоть оно и доказано в программе для общего случая, но ошибки могут быть в самих системе Agda, компиляторах и, наконец, в компьютере).
Арифметика коэффициентов воплощена в самом общем виде. Библиотека содержит определение евклидова кольца (EuclideanDomain) и модуль Residue.Euclidean, в котором задана арифметика кольца E/(b) остатков для произвольных евклидова кольца E и элемента b в нем. В модуле Int.II задано воплощение euclideanDomain структуры евклидова кольца для целых чисел. Объявление
open import Int.II using ()
renaming (euclideanDomain to E)
вносит евклидову структуру для $\mathbb{Z}$, обозначая ее E. Далее, объявления
open Residue.Euclidean E b $\mathbb{Z}$-Read $\mathbb{Z}$-Show
using (Show0-r; Read-r; semiring-r;
decCommutativeRing-r)
renaming (EucResidue to R)
decCRing-r = decCommutativeRing-r b∤1
вносят структуры DecCommutativeRing и некоторые другие для области E/(b) остатков и дают имя R для носителя этой области. Например, действие умножения в области E/(b) можно теперь получить, объявив
open DecCommutativeRing decCRing-r using ()
renaming (_*_ to _*r_),
при этом оно получит имя *r.
Наконец, объявления
open import Pol.Karatsuba decCRing-r
open import Pol.Over-decComRing
decCRing-r Show-r Read-r “x”
вносят в поле действия функцию karatsubа и арифметику многочленов – обе для коэффициентов из области R остатков.
Приведем таблицу испытания для системы Agda-2.6.1, MAlonzo, ghc-8.8.3, Ubuntu-Linux 18.04 и персонального компьютера частоты 3 гигагерц (табл. 1).
Таблица 1.
| kThreshold = 18 | ||||
|---|---|---|---|---|
| время[sec] | ||||
| n | p-p, | pk-pk, | deg p | l(mons) |
| deg p, | deg pk, | |||
| length p | length pk | |||
| 9 | 0.3 | 0.2 | 512 | 513 |
| 10 | 1.3 | 0.8 | 1024 | 1025 |
| 11 | 5.1 | 2.5 | 2048 | 2049 |
| 12 | 21.1 | 7.7 | 4096 | 4097 |
| 13 | 84.2 | 25.0 | 8192 | 8193 |
| 14 | 349.6 | 78.0 | 16 384 | 16 385 |
Во второй колонке (“p-p”) – время для простейшего умножения, в третьей колонке (“pk-pk”) – для функции karatsuba.
Обозначим
• $f = x + 1$,
• $T(p,n)$ время вычисления p(n) из второй колонки этой таблицы,
• $T({{p}_{k}},n)$ время вычисления pk(n) из третьей колонки,
• $T(n),{{T}_{k}}(n)$ время вычисления произведения ${{f}^{m}} * {{f}^{m}}$ для $m = {{2}^{n}}$ (после того, как значение ${{f}^{m}}$ готово) простейшим способом и функцией karatsuba соответственно.
Тогда $T(n) = T(p,n + 1) - T(p,n)$,
${{T}_{k}}(n) = T({{p}_{k}},n + 1) - T({{p}_{k}},n)$.
Получаем таблицу стоимости возведения в квадрат многочлена степени ${{2}^{n}}$ (табл. 2):
Таблица 2.
| n | T(n) | Tk(n) | Tk(n+1)/Tk(k) |
|---|---|---|---|
| 9 | 1.0 | 0.6 | |
| 10 | 3.8 | 1.7 | 2.8 |
| 11 | 16.0 | 5.2 | 3.1 |
| 12 | 63.1 | 17.3 | 3.3 |
| 13 | 265.4 | 53.0 | 3.1 |
Отношения $T(n + 1){\text{/}}T(n),\,\,{{T}_{k}}(n + 1){\text{/}}{{T}_{k}}(n)$ показывают, как увеличивается время возведения в квадрат при удвоении степени многочлена – соответственно при простейшем умножении и при применении функции karatsuba. В первом случае это отношение равно приблизительно 4, для функции karatsuba оно равно приблизительно 3.1.
Первое как раз соответствует стоимости $c \cdot {{k}^{2}}$ вычисления произведения многочленов степени $k$, второе соответствует стоимости вычисления $c \cdot {{k}^{{log3.1}}}$.
Также программа испытывалась на случайных многочленах одинаковой степени n над коэффициентами из той же области R остатков. В табл. 3 p = f*g обозначает простейшее умножение, pk = karatsuba f g:
Таблица 3.
| n | время[sec] | ||
|---|---|---|---|
| p | pk | отношение T(pk) к предыдущему | |
| 1000 | 1.9 | 0.8 | |
| 2000 | 8.1 | 2.5 | 3.1 |
| 4000 | 33.0 | 7.5 | 3.0 |
| 8000 | 136.5 | 22.8 | 3.0 |
| 16 000 | 68.7 | 3.0 | |
| 32 000 | 219.4 | 3.2 | |
Таблица 4
| m | время[sec] | |
|---|---|---|
| p | pk | |
| 100 | 1.5 | 2.3 |
| 201 | 2.9 | 3.2 |
| … | ||
| 1000 | 16.0 | 7.7 |
| 1009 | 32.7 | 11.5 |
| 4002 | 65.6 | 17.1 |
| 8003 | 133.2 | 25.5 |
Здесь колонка “pk” соответствует стоимости вычисления приблизительно $c \cdot {{n}^{{log3.1}}}$.
Таблица 4 показывает испытание для разных степеней m = deg f, n = deg g, в том числе для нечетных m, при n = 9000.
Видно, что время вычисления в правой колонке растет гораздо медленнее, чем в случае одинаковых степеней.
6.1. Сравнение с программой без доказательств на языке Haskell
Также были запрограммированы на языке Haskell арифметика многочленов и способ Карацубы для нее, со всеми теми же алгоритмами, разумеется – без доказательств в программах. Коэффициенты считаются принадлежащими абстрактной области класса Num, что соответствует сигнатуре коммутативного кольца (но соблюдение законов кольца в данном случае лежит на программисте). В примере испытания в качестве коэффициентов берется та же область остатков по модулю b = 99 991, но она построена не подстановкой в общую конструкцию с евклидовым кольцом, а прямо запрограммирована для частного случая целых чисел по модулю b.
В системе Glasgow Haskell 8.8.3 примеры из вышеприведенной таблицы вычисляются примерно в 4 раза быстрее. Множитель 2 происходит из того, что область $\mathbb{Z}$/(b) задана более прямо. Другой множитель 2 – из того, что, вообще, Agda является языком несколько более высокого уровня абстракции, к тому же логическим языком, и это влечет за собой некоторую плату в части производительности.
7. ОБ ИЗДЕРЖКАХ ДОКАЗАТЕЛЬНОГО ПРОГРАММИРОВАНИЯ
Сравним программы для способа Карацубы в случае программирования на языке Haskell – без доказательств и на языке Agda – с доказательствами в программе.
Нижеприводимые показатели даются только для модуля Karatsuba при условии, что остальные модули библиотеки уже скомпилированы (замечание об особом способе компиляции приведено в середине Введения), и – для систем Glasgow Haskell 8.8.3 и Agda-2.6.1 - MAlonzo соответственно.
Производительность программы на Агде в 2 раза ниже, а порядок роста стоимости вычисления такой же.
Объем исходной программы на Агде больше в 6 раз.
Программа на Агде собирается в исполняемую в 100 раз дольше (на машине в 3 гигагерц – 300 sec.).
Объектный код программы на Агде в 130 раз больше.
Его можно сократить в два раза за счет вставки в исходную программу в критических местах обозначения @0 по удалению ненужного кода. Но мы посчитали, что для данного примера выигрыш не стоит даже небольшого усложнения программы, ибо время сборки и производительность заметно не меняются.
Такова на сегодня цена полностью адекватного способа программирования символьных математических вычислений в системе Agda. И на наш взгляд эта цена приемлема, ибо доказательств много, они – полные, а библиотека DoCon-A в настоящее время содержит много разных определений понятий, лемм и алгоритмов.
Но: трудоемкость составления доказательств велика.
Она может быть сильно сокращена за счет добавления в библиотеку специальных доказывателей для различных разделов алгебры и логики, например, для доказательства равенств в коммутативных алгебрах, в конечных группах, и так далее, отдельно для каждой особенной предметной области.
На конференции в городе Bath в 2013 году некий слушатель жаловался на то, что он, как ни старается, не может писать доказательства на Агде.
В последствии автор составил (пользуясь подсказками разработчиков системы Агда) перечень главных практических советов, следуя которым он сумел построить доказательства в системе Agda для многих утверждений, вошедших в библиотеку DoCon-A ([1], выпуск 3.2rc, руководство manual.pdf из архива библиотеки, раздел 1.2), и которых, похоже, достаточно для продолжения проекта библиотеки.
8. О ДРУГИХ РАБОТАХ ПО ДАННОМУ ПРЕДМЕТУ
Метод Карацубы для многочленов применяется в различных известных библиотеках научных вычислений, например, в MAPLE. Но в этих библиотеках речь не идет о доказательной программе.
В диссертации [6] 2014 года среди некоторых других замечательных методов и программ описана разработка как раз доказательной программы для способа Карацубы в системе Coq при поддержке математической библиотеки MathComp. Главные отличия от нашей разработки таковы.
• Выбрано плотное представление многочлена в виде списка коэффициентов (среди которых возможны нули).
• При расщеплении многочлена степени $n$ выделяется многочлен степени $[n{\text{/}}2]$ (целая часть). Но для этого способа не приведено доказательства оценки сложности вычисления. Вывести эту оценку предложено в упражнении 8.5 книги [5], где это упражнение названо непростым.
• Применен подход data refinement, который годится, вообще, для многих методов вычисления.
Подход data refinement (в случае метода Карацубы для многочленов) состоит в том, что сначала, так же, как у нас, многочлен определяется в виде зависимого типа. В нашем подходе данное “многочлен” включает два доказательства (начало раздела 2), в подходе [6] это только доказательство неравенства нулю старшего коэффициента – назовем этот тип CPol (обозначения CPol, CPol’, toSimple, cKara, cKara’ введены здесь нами).
Потом программируются простейший алгоритм умножения многочленов и способ Карацубы – с учетом зависимого типа для многочлена, то есть с построением доказательств для старшего коэффициента. Назовем последнюю программу cKara. Потом программируется доказательство равносильности этих двух функций. После этого места наши подходы расходятся. Наша программа уже готова. А в подходе [6] делаются дополнительные построения, описанные ниже.
Доказательная программа в системе Coq, действующая над данными зависимых типов, может иметь сильно меньшую производительность, чем программа без доказательств на простых типах. Поэтому вводится простой тип для многочлена – не включающий доказательcтв, назовем его CPol’. И программируются арифметические действия и способ Карацубы для простого типа. Эта программа (назовем ее cKara') свободна от доказательств и приспособлена для быстрого исполнения.
Далее, программируется отображение toSimple: CPol → CPol’, которое просто удаляет доказательство из данного типа CPol. Программируется доказательство того, что отображение toSimple является инъективным гомоморфизмом относительно сложения. Это доказательство весьма простое. Так же просто программируется доказательство того, что отображение cKara равносильно отображению cKara’ – в смысле коммутативности диаграммы (рис. 2).
Отсюда следует, что а) правильность программы cKara’ выведена из правильности программы cKara, б) для быстрого вычисления можно применять функцию cKara’.Это разумный подход. И он легко может быть применен в нашей библиотеке. Но для нашей библиотеки он пока что представляется излишним, так как в языке Agda программы по умолчанию выполняются “лениво”, и как описано в разделе 4.2, даже наличие внутренних доказательств не сказывается существенно на производительности исполняемого кода. Это подтверждается таблицей затрат времени из раздела 6, сравнением по порядку роста стоимости вычисления и по производительности с программой, написанной на языке Haskell (раздел 6.1), и примерами некоторых других алгоритмов из библиотеки. К тому же отпадает необходимость повторного программирования метода.
Вообще же, что касается нашего подхода к программированию алгебры: он состоит в стремлении построить достаточно богатую библиотеку доказательных программ научных вычислений на основе минималистичного подхода, избегая введения различных излишних языков и парадигм. Не знаем, что потребуется дальше, но пока оказываются достаточными лишь язык Agda и библиотека, на нем же написанная. Главное же содержание проекта – выражение математических построений, методов, алгоритмов и доказательств в математически адекватном виде, в большой общности, на подходящем функциональном языке программирования, и с учетом производительности программ.
8.1. О важности мп-доказательств вообще
Система построения формальных машинно- проверяемых доказательств помогает найти ошибки в математических доказательствах. Например, в начале работы [7] названы несколько важных проблем, получивших сначала неверные решения, и это подвигло автора статьи [7] к разработке средств автоматической проверки доказательств и автоматизированной поддержки поиска доказательств (proof assistant) [8].
Введение диссертации [6] также содержит внушительный перечень важных примеров попыток решения проблем, которые подвигают исследователей к применению системы автоматизированной поддержки проверки и построения доказательств.
Далее, имеется особый новый (но не совсем полноценный) вид доказательств в математике: с привлечением вычисления, делаемого какой-то программой вычислительной алгебры. Естественно, мп-доказательство необходимых свойств такой программы делает целевое доказательство более полноценным.
9. ЗАКЛЮЧЕНИЕ
Написанная выше программа на языке Agda умножения многочленов способом Карацубы для разреженного представления и соответствующего особого алгоритма (раздел 3.2) обладает необходимой производительностью при исполнении, сопровождается машинно-проверяемым доказательством правильности, и для ее алгоритма доказана (в Приложении 11 ) требуемая оценка стоимости вычисления.
Испытание программы на производительность на разных примерах описано в разделе 6.
В разделе 4.2 объяснено, почему наличие “внутренних” доказательств в этой программе не влияет существенно на производительность исполняемого кода.
Исходный код программы имеет приемлемый объем и компилируется за приемлемое время (раздел 7).
Как и во всех системах доказательного программирования, существенной является проблема трудоемкости построения полных формальных доказательств.
Доказательная программа метода Карацубы для многочленов воплощена на основе библиотеки DoCon-A [1] доказательных программ вычислительной алгебры.
Список литературы
Мешвелиани С.Д. DoCon-A. Библиотека доказательных программ компьютерной алгебры. Переславль-Залесский, 2021. http://www.botik.ru/pub/local/Mechveliani/docon-A/
Карацуба А.А., Офман Ю.П. Умножение многозначных чисел на автоматах // Доклады АН СССР. Т. 145. № 2. С. 293–294. http://www.mathnet.ru/links/d3321404ffd85ead867863cb5e410f00/dan26729.pdf
Карацуба А.А. Сложность вычисления. Тр. МИАН. 1995. Т. 211. С. 186–202. http://www.mathnet.ru/links/f3297054555b746ec1241c8805a22c62/tm1120.pdf
Шёнхаге A., Штрассен B. (Schönhage A., Strassen V.). Scnelle Multiplikation grosser Zahlen. Computing. Т. 7. № 3–4. С. 281–292. Русский перевод: Кибернетический сборник, нов. сер. вып. 10. М.: Мир, 1973. С. 87–98.
Gathen J., Gerhard J. Modern Computer Algebra. 3rd ed. Cambridge University Press, 2013.
Mörtberg A. Formalizing Refinements and Constructive Algebra in Type Theory. Тезисы диссертации. Department of Computer Science and Engineering Chalmers University of Technology and University of Gothenburg SE-412 96 Gothenburg, Sweden Gothenburg, 2014. 142 с. https://www-sop.inria.fr/members /Anders.Mortberg/thesis/doc/v0.1/karatsuba.html
Voevodsky V. Univalent Foundations. Princeton, Nj, March 26, 2014. https://www.math.ias.edu/~vladimir/Site3/Univalent_Foundations_files/2014_IAS.pdf
Voevodsky V. UniMath. Библиотека программ в системе Coq, формализующая существенную часть математики с точки зрения юнивалентной теории. https://github.com/UniMath/UniMath
Norell U. Dependently Typed Programming in Agda. AFP 2008: Advanced Functional Programming, Lecture Notes in Computer Science, V. 5832. Springer, Berlin Heidelberg, 2008. P. 230–266.
Agda. A proof assistant. A dependently typed functional programming language and its system. http://wiki.portal.chalmers.se/agda/pmwiki.php.
Мешвелиани С.Д. O зависимых типах и интуиционизме в программировании математики. В электронном журнале Программные системы: теория и приложения. 2014. Т. 5. Вып. 3. С. 27–50. http://psta.psiras.ru/read/psta2014_3_27-50.pdf
Martin-Loef, Per. Intuitionistic type theory. Bibliopolis, ISBN 88-7088-105-9. 1984. 91 c.
Марков А.А. О конструктивной математике. Проблемы конструктивного направления в математике. 2. Конструктивный математический анализ, Сборник работ // Тр. МИАН СССР. Т. 67. М., Л.: Изд-во АН СССР, 1962. С. 8–14.
Chlipala A. Certified Programming with Dependent Types: A Pragmatic Introduction to the Coq Proof Assistant. MIT Press, 2013. http://adam.chlipala.net/cpdt/
de Moura L., Kong S., Avigad J., van Doorn F., von Raumer J. The Lean Theorem Prover. 25th International Conference on Automated Deduction (CADE-25), Berlin, Germany, 2015. https://leanprover.github.io/papers/system.pdf.
The Coq Effective Algebra Library. https://github.com/CoqEAL/CoqEAL/
Дополнительные материалы отсутствуют.
Инструменты
Программирование