1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 64, № 3, 2019

Радиотехника и электроника, 2019, T. 64, № 3, стр. 259-264

Поверхностная волна на границе гиперболического магнитооптического одноосного метаматериала и изотропного диэлектрика

Е. В. Кузнецов 1, 2, *, А. М. Мерзликин 1, 2

1 Всероссийский научно-исследовательский институт автоматики им. Н.Л. Духова
127055 Москва, ул. Сущевская, 22, Российская Федерация

2 Институт теоретической и прикладной электродинамики РАН
125412 Москва, ул. Ижорская, 13, Российская Федерация

* E-mail: evgenykuznet@gmail.com

Поступила в редакцию 15.09.2017
После доработки 21.02.2018
Принята к публикации 28.02.2018

Полный текст (PDF)

Аннотация

Рассмотрено распространение поверхностной волны вдоль границы гиперболического магнитооптического одноосного метаматериала и изотропного диэлектрика. Найдено дисперсионное уравнение поверхностной волны и распределение электрического поля в системе. Показано, что поверхностная волна данной системы отличается от других типов поверхностных волн тем, что волновой вектор поверхностной волны обладает не только мнимой, но и действительной частью в направлении, перпендикулярном границе раздела; кроме того, поверхностная волна в гиперболическом магнитооптическом одноосном метаматериале обладает гибридной поляризацией, поэтому существует только одна поверхностная волна для заданного направления волнового вектора.

ВВЕДЕНИЕ

Современный интерес к изучению поверхностных волн вызван субволновой локализацией поля и его усилением вблизи поверхности [1]. Субволновая локализация поля открывает возможности применения поверхностных волн в качестве волноведущей среды [2, 3], поскольку удается уменьшить размеры волноведущей структуры, а также в фотолитографии [4], поскольку поверхностные волны позволяют преодолеть дифракционные ограничения плоских волн, тем самым повышая разрешение фотолитографии. Усиление поля вблизи поверхности дает возможность использовать поверхностные волны в чувствительных элементах биосенсоров [5–7], поскольку осаждение частиц происходит вблизи поверхности и за счет усиления поля увеличивается чувствительность сенсора.

Наиболее известными поверхностными волнами являются: поверхностный плазмон-поляритон [8], распространяющийся вдоль границы сред с различными диэлектрическими проницаемостями, и поверхностная волна, распространяющаяся вдоль границы фотонного кристалла [9, 10]. Недостаток поверхностных плазмонов заключается в омических потерях в металле. Поверхностные моды в фотонном кристалле также имеют ограничения: для создания высокодобротной моды в фотонном кристалле требуется низкий уровень шероховатости поверхности слоев [11].

Альтернативой поверхностного плазмона является дьяконовская волна [12] – поверхностная волна, распространяющаяся на границе изотропной среды и одноосного кристалла. В данной волне отсутствуют омические потери, и, кроме того, в отличие от фотонного кристалла она имеет одну границу, что уменьшает потери за счет шероховатости поверхности. Однако дьяконовская волна имеет очень узкий угловой диапазон распространения, что сильно затрудняет ее использование [13]. Поэтому продолжаются поиски новых типов поверхностных волн.

В частности, были обнаружены дьяконовские поверхностные волны в гиперболическом слоистом метаматериале [14] (среде, имеющей отрицательную компоненту диэлектрической проницаемости), гиперболическом двухосном кристалле [15], в гиперболической гиромагнитной среде [16] и гиперболическом хиральном материале [17, 18]. Использование метаматериалов позволяет расширить угловой диапазон распространения поверхностных волн.

Цель данной работы – исследовать поверхностную волну на границе гиперболического магнитооптического одноосного метаматериала (ГМОМ) и диэлектрика.

ПОВЕРХНОСТНАЯ ВОЛНА В ГМОМ

В отсутствие магнитного поля изочастота ГМОМ (поверхность постоянной частоты в пространстве волновых векторов) представляет собой комбинацию двуполостного гиперболоида и сферы, которые пересекаются в двух точках [17]. В точках пересечения оба собственных решения обладают одинаковым волновым вектором, но ортогональными поляризациями, иными словами, распространение волны в данном направлении вырождено по поляризации. Как показано в работах [17, 19–22] приложение внешнего магнитного поля приводит к снятию вырождения: изочастота в точках пересечения расщепляется и перезамыкается. Между двумя частями изочастоты образуется запрещенная зона. В запрещенной зоне волновой вектор становится комплексным, и поэтому возможно образование поверхностной волны на границе ГМОМ и диэлектрика.

При наличии внешнего магнитного поля в гиротропном материале связь между электрической индукцией и полем описывается уравнением

(1)
$\vec {D} = \hat {\varepsilon }\vec {E} + i\left[ {\vec {E} \times \vec {g}} \right],$
где $\vec {g}$ – вектор гирации, пропорциональный внешнему магнитному полю, а $\hat {\varepsilon }$ – тензор диэлектрической проницаемости материала в отсутствие магнитного поля. Допустим, что магнитное поле приложено вдоль оси x, тогда связь между электрической индукцией и электрическим полем можно описать при помощи нового тензора диэлектрической проницаемости:

(2)
$\hat {\varepsilon } = \left( {\begin{array}{*{20}{c}} {{{\varepsilon }_{1}}}&0&0 \\ 0&{{{\varepsilon }_{2}}}&{ - ig} \\ 0&{ig}&{{{\varepsilon }_{2}}} \end{array}} \right).$

Используя уравнения Максвелла совместно с тензором диэлектрической проницаемости (2), можно записать уравнение, определяющее собственные волны системы:

(3)
$\begin{gathered} \left\{ \begin{gathered} \operatorname{rot} \vec {E} = - \frac{1}{c}\frac{{\partial{ \vec {H}}}}{{\partial t}} \hfill \\ \operatorname{rot} \vec {H} = \frac{1}{c}\frac{{\partial{ \vec {D}}}}{{\partial t}} \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} \vec {H} = \left[ {\vec {n} \times \vec {E}} \right] \hfill \\ \vec {D} = - \left[ {\vec {n} \times \vec {H}} \right] \hfill \\ \end{gathered} \right. \Rightarrow \\ \Rightarrow \vec {D} = {{n}^{2}}\vec {E} - \vec {n}\left( {\vec {n}\vec {E}} \right) \Rightarrow \left( {{{n}^{2}}{{\delta }_{{ik}}} - {{n}_{i}}{{n}_{k}} - {{\varepsilon }_{{ik}}}} \right){{E}_{k}} = 0. \\ \end{gathered} $
Здесь ${{\delta }_{{ik}}}$ – символ Кронекера, а $\vec {n} = {{\vec {k}} \mathord{\left/ {\vphantom {{\vec {k}} {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}},$ где $\vec {k}$ – волновой вектор в среде, а ${{k}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }.$ Система уравнений (3) совместна тогда и только тогда, когда ее детерминант равен 0. Из этого требования получаем уравнение, аналогичное уравнению Френеля [23]

(4)
$\begin{gathered} {{n}^{2}}\left( {{{\varepsilon }_{1}}n_{x}^{2} + {{\varepsilon }_{2}}\left( {n_{y}^{2} + n_{z}^{2}} \right)} \right) - 2{{\varepsilon }_{1}}{{\varepsilon }_{2}}n_{x}^{2} - \\ - \,\,{{\varepsilon }_{2}}\left( {{{\varepsilon }_{1}} + {{\varepsilon }_{2}}} \right)\left( {n_{y}^{2} + n_{z}^{2}} \right) + {{\varepsilon }_{1}}\varepsilon _{2}^{2} - \\ - {{g}^{2}}\left( {{{\varepsilon }_{1}} - n_{y}^{2} - n_{z}^{2}} \right) = 0. \\ \end{gathered} $

Уравнение (4) определяет изочастоту ГМОМ. Будем полагать, что компонента ${{\varepsilon }_{1}}$ отрицательна. В отсутствие магнитного поля ($\vec {g} = 0$) изочастота представляет собой сферу и два гиперболоида. Эти фигуры пересекаются в двух точках (рис. 1).

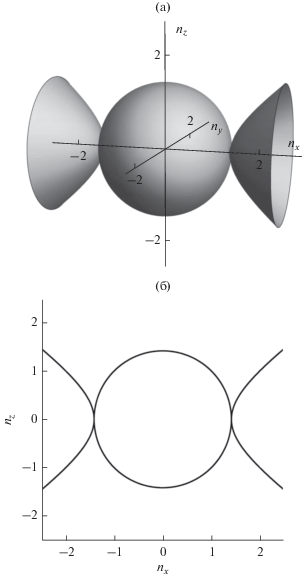
Рис. 1.

Изочастота ГМОМ в отсутствие магнитного поля (a), сечение изочастоты плоскостью nzOnx (б). Компоненты тензора диэлектрической проницаемости ${{\varepsilon }_{1}} = - 1,$ ${{\varepsilon }_{2}} = 2.$

При намагничивании изочастота в точке самопересечения расщепляется (рис. 2). Этот эффект известен в обыкновенных двухосных гиротропных кристаллах [19], в двухосных гиперболических метаматериалах [15] и хиральных гиперболических метаматериалах [16, 17].

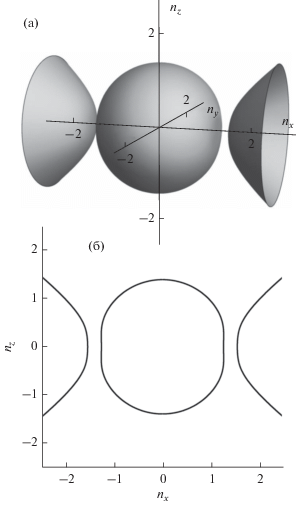
Рис. 2.

Изочастота ГМОМ (a), сечение изочастоты плоскостью nzOnx (б). Компоненты тензора диэлектрической проницаемости ${{\varepsilon }_{1}} = - 1,$ ${{\varepsilon }_{2}} = 2,$ величина недиагональных элементов тензора диэлектрической проницаемости $g = 0.4.$

В запрещенной зоне волновые вектора собственных мод комплексные. Данный факт наводит на мысль о том, что на границе ГМОМ и изотропной среды может распространяться поверхностная волна, убывающая в обе стороны от границы (рис. 3).

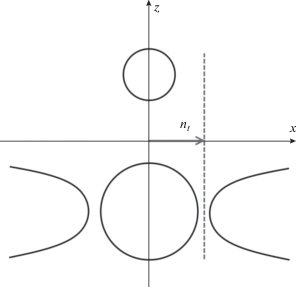
Рис. 3.

Изочастоты ГМОМ и изотропного диэлектрика, показывающие ориентацию ГМОМ относительно границы раздела двух сред, ${{n}_{t}}$ – компонента волнового вектора поверхностной волны, параллельная границе раздела.

Рассмотрим этот вопрос детальнее. Сначала найдем собственные волновые векторы в ГМОМ. Допустим, что волновой вектор имеет компоненты ${{n}_{x}}$ и ${{n}_{y}}.$ Эти компоненты параллельны границе раздела и сохраняются при переходе от ГМОМ к диэлектрику. Тогда из уравнения (4) находим ${{n}_{z}}\,:$

(5)
${{n}_{z}} = \pm \sqrt { - \frac{{\tilde {\varepsilon }n_{x}^{2} + 2{{\varepsilon }_{2}}n_{y}^{2} + {{g}^{2}} - {{\varepsilon }_{2}}\tilde {\varepsilon } \pm \sqrt {{{{\left( {{{\varepsilon }_{\Delta }}{{\varepsilon }_{2}} + {{g}^{2}}} \right)}}^{2}} + 2\left( {\tilde {\varepsilon }{{g}^{2}} - \varepsilon _{\Delta }^{2}{{\varepsilon }_{2}}} \right)n_{x}^{2} + \varepsilon _{\Delta }^{2}n_{x}^{4}} }}{{2{{\varepsilon }_{2}}}}} ,$
где ${{\varepsilon }_{\Delta }} = {{\varepsilon }_{1}} - {{\varepsilon }_{2}},$ $\tilde {\varepsilon } = {{\varepsilon }_{1}} + {{\varepsilon }_{2}}.$ Среди четырех корней уравнения (5) физический смысл имеют только два корня, обладающие отрицательной мнимой частью, поскольку тогда решение будет убывать при $z \to - \infty .$

Поляризации собственных мод можно найти из уравнения (3). Получаем

(6)
${{\vec {E}}_{k}} = \left( \begin{gathered} {{n}_{x}}\left( {{\text{i}}g{{n}_{{z,k}}} - {{n}_{y}}\left( { - {{\varepsilon }_{2}} + n_{{z,k}}^{2} + n_{x}^{2} + n_{y}^{2}} \right)} \right) \hfill \\ n_{{z,k}}^{2}n_{x}^{2} - \left( { - {{\varepsilon }_{1}} + n_{{z,k}}^{2} + n_{y}^{2}} \right)\left( { - {{\varepsilon }_{2}} + n_{x}^{2} + n_{y}^{2}} \right) \hfill \\ {{\varepsilon }_{1}}\left( { - {\text{i}}g + {{n}_{{z,k}}}{{n}_{y}}} \right) + {\text{i}}g\left( {n_{{z,k}}^{2} + n_{y}^{2}} \right) - {{n}_{{z,k}}}{{n}_{y}}\left( {n_{{z,k}}^{2} + n_{x}^{2} + n_{y}^{2}} \right) \hfill \\ \end{gathered} \right),\,\,\,\,k = 1,2,3,4,$
где ${{n}_{{z,k}}}$ – корни уравнения (5). Магнитное поле собственных мод можно найти из уравнения

(7)
$\operatorname{rot} \vec {E} = i{{k}_{0}}\vec {H}.$

В изотропном диэлектрике над кристаллом волновой вектор удовлетворяет уравнению

(8)
${{n}_{z}} = \pm \sqrt {{{\varepsilon }_{a}} - n_{x}^{2} - n_{y}^{2}} .$

А собственные моды распадаются на поперечную электрическую и поперечную магнитную волны:

(9)
$\begin{gathered} {{{\vec {E}}}_{{1,2}}} = \left( \begin{gathered} {{n}_{x}}{{n}_{z}} \hfill \\ {{n}_{x}}{{n}_{z}} \hfill \\ - n_{x}^{2} - n_{y}^{2} \hfill \\ \end{gathered} \right),\,\,\,\,{{{\vec {H}}}_{{1,2}}} = \left( \begin{gathered} {{\varepsilon }_{a}}{{n}_{y}} \hfill \\ {{\varepsilon }_{a}}{{n}_{x}} \hfill \\ 0 \hfill \\ \end{gathered} \right), \\ {{{\vec {E}}}_{{3,4}}} = \left( \begin{gathered} - {{n}_{x}} \hfill \\ {{n}_{y}} \hfill \\ 0 \hfill \\ \end{gathered} \right),\,\,\,\,{{{\vec {H}}}_{{3,4}}} = \left( \begin{gathered} - {{n}_{x}}{{n}_{z}} \hfill \\ - {{n}_{x}}{{n}_{z}} \hfill \\ n_{x}^{2} + n_{y}^{2} \hfill \\ \end{gathered} \right). \\ \end{gathered} $

Будет искать решение для поверхностной волны в виде суммы собственных мод с неопределенными коэффициентами в обеих средах. Для существования поверхностной волны должны выполнять условия непрерывности тангенциальных компонент электрического и магнитного полей на границе раздела сред. Получаем систему из четырех уравнений с четырьмя неизвестными:

(10)
$\left\{ \begin{gathered} {{C}_{1}}{{E}_{{1x,{\text{Г М О М }}}}} + {{C}_{2}}{{E}_{{2x,{\text{Г М О М }}}}} = {{C}_{3}}{{E}_{{1x,a}}} + {{C}_{4}}{{E}_{{2x,a}}} \hfill \\ {{C}_{1}}{{H}_{{1y,{\text{Г М О М }}}}} + {{C}_{2}}{{H}_{{2y,{\text{Г М О М }}}}} = {{C}_{3}}{{H}_{{1y,a}}} + {{C}_{4}}{{H}_{{2y,a}}} \hfill \\ {{C}_{1}}{{E}_{{1y,{\text{Г М О М }}}}} + {{C}_{2}}{{E}_{{2y,{\text{Г М О М }}}}} = {{C}_{3}}{{E}_{{1y,a}}} + {{C}_{4}}{{E}_{{2y,a}}} \hfill \\ {{C}_{1}}{{H}_{{1x,{\text{Г М О М }}}}} + {{C}_{2}}{{H}_{{2x,{\text{Г М О М }}}}} = {{C}_{3}}{{H}_{{1x,a}}} + {{C}_{4}}{{H}_{{2x,a}}} \hfill \\ \end{gathered} \right.,$

где ЕГМОМ и НГМОМ соответствуют поляризациям собственных мод в ГМОМ, заданных уравнениями (6) и (7), а ${{E}_{a}}$ и ${{H}_{a}}$ – поляризациям собственных мод в диэлектрике, заданных уравнением (9). Система (10) совместна тогда и только тогда, когда ее детерминант равен 0. Из этого условия получаем дисперсионное уравнение поверхностной волны. Конечное дисперсионное уравнение имеет весьма громоздкий вид, поэтому мы не приводим его здесь. Решение дисперсионного уравнения в плоскости $\left\{ {{{n}_{x}},{{n}_{y}}} \right\}$ показано на рис. 4.

Рис. 4.

Дисперсионная картина. Серые кривые – изочастоты объемных мод в ГМОМ, черные кривые – поверхностные моды.

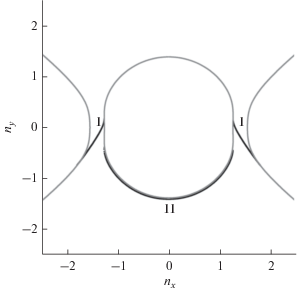
Можно выделить две области, I и II, дисперсионной кривой поверхностных мод. Область I находится в запрещенной зоне гиперболического кристалла. Эта кривая граничит с дисперсионной кривой объемных мод гиперболического метаматериала. В граничных точках поверхностная мода переходит в объемную моду в гиперболическом метаматериале. Область II находится вне изочастоты объемных мод гиперболического кристалла. Дисперсионная кривая поверхностных мод прилегает к кривой объемных мод, а в граничных точках кривая сливается с дисперсионной кривой объемных мод. Таким образом, поверхностная волна возникает не только в образовавшейся запрещенной зоне ГМОМа, но и вблизи части изочастоты, похожей на сферу.

Граничные условия (10) можно записать в виде равенства адмиттансов ${{\gamma }_{1}} = {{{{H}_{y}}} \mathord{\left/ {\vphantom {{{{H}_{y}}} {{{E}_{x}}}}} \right. \kern-0em} {{{E}_{x}}}}$ и ${{\gamma }_{2}} = {{{{H}_{x}}} \mathord{\left/ {\vphantom {{{{H}_{x}}} {{{E}_{y}}}}} \right. \kern-0em} {{{E}_{y}}}}.$ В отсутствие намагниченности связь магнитного и электрического поля каждой собственной моды ГМОМ можно описать при помощи скалярного адмиттанса [24]. В тензорном виде эта связь запишется в виде ${{H}_{\alpha }} = {{\gamma }_{{\alpha \beta }}}{{E}_{\beta }},$ где ${{\gamma }_{{\alpha \beta }}}$ – диагональный тензор. В изотропной среде связь магнитного и электрического поля также описывается скалярным адмиттансом. Поэтому система уравнений (10) распалась бы на совокупность двух независимых уравнений, и в системе могли бы быть две поверхностные волны. При намагничивании собственное решение в ГМОМ гибридизуется, а связь электрического и магнитного полей описывается тензорным адмиттансом ${{H}_{\alpha }} = {{\gamma }_{{\alpha \beta }}}{{E}_{\beta }},$ где ${{\gamma }_{{\alpha \beta }}}$ – недиагональный тензор. Поскольку граничные условия можно записать как равенство диагональных адмиттансов, необходимо получить в ГМОМ решение, обладающее диагональным тензором адмиттансов. Это возможно только при сложении двух собственных мод, и уравнения не разделяются на совокупность независимых уравнений. Поэтому в системе существует только одна поверхностная волна.

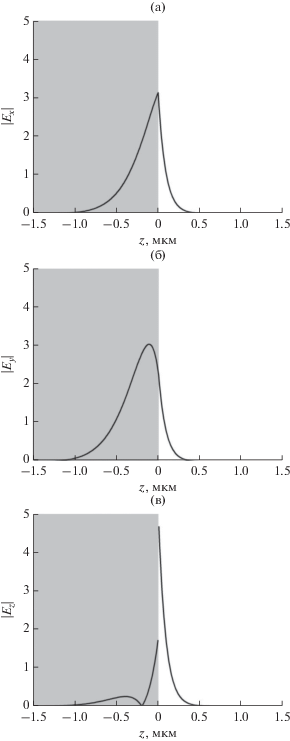
Найдем распределение электрического поля собственных мод системы. Для этого подставим собственный волновой вектор в уравнение (10) и найдем константы. На рис. 5 показано распределение электрического поля собственной моды системы, соответствующей области I дисперсионной кривой.

Рис. 5.

Распределение модуля компонент электрического поля поверхностной моды системы, соответствующей области I на рис. 4. Волновой вектор ${{n}_{x}} = 1.5,$ ${{n}_{y}} = - 0.325.$ Серый регион соответствует ГМОМ, белый – диэлектрику.

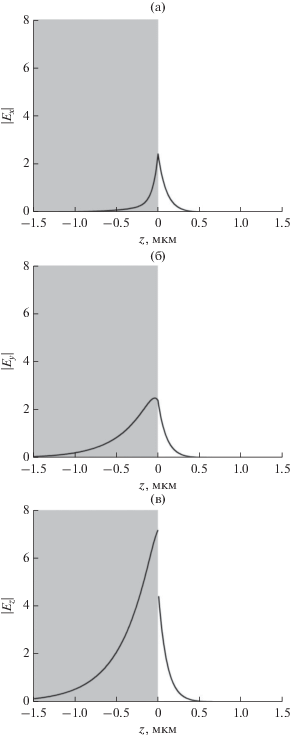
На рис. 6 показано распределение электрического поля собственной моды системы, соответствующей области II дисперсионной кривой. Поле собственной моды, принадлежащей области II локализовано преимущественно в гиперболическом кристалле.

Рис. 6.

Распределение модуля компонент электрического поля поверхностной моды системы, соответствующей области II на рис. 4. Волновой вектор ${{n}_{x}} = 0.5,$ ${{n}_{y}} = - 1.32.$ Серый регион соответствует ГМОМ, белый – диэлектрику.

При $g \to 0$ поверхностные моды переходят в объемные моды гиперболического одноосного метаматериала. Отметим, что помимо затухания в обе стороны от границы раздела, собственная мода осциллирует в ГМОМ (рис. 5в), что связано с наличием действительной части у волнового вектора в ГМОМ (5).

ЗАКЛЮЧЕНИЕ

Таким образом, в работе показано, что изочастота ГМОМ в точке самопересечения расщепляется при приложении внешнего магнитного поля. Получено дисперсионное уравнение поверхностных волн на границе ГМОМ и диэлектрика. Существуют две области дисперсионных кривых: одна внутри запрещенной зоны ГМОМ, а другая вблизи части изочастоты ГМОМ, похожей на сферу. Найдено распределение электрического поля собственных мод. Второй тип поверхностных волн имеет распределение поля, близкое к объемным модам в ГМОМ. Собственные волны в ГМОМ обладают гибридной поляризацией, поэтому для заданного направления волнового вектора существует только одна поверхностная волна.

Список литературы

  1. Polo J., Mackay T., Lakhtakia A. Electromagnetic Surface Waves: A Modern Perspective. Newnes: Elsevier, 2013.

  2. Lal S., Link S., Halas N.J. // Nature Photonics. 2007. V. 1. № 11. P. 641.

  3. Bozhevolnyi S.I., Volkov V. S., Devaux E. et al. // Nature. 2006. V. 440. № 7083. P. 508.

  4. Srituravanich W., Fang N., Sun C. et al. // Nano Lett. 2004. V. 4. № 6. P. 1085.

  5. Farmer A., Friedli A., Wright S., Robertson W. // Sensors Actuators B: Chemical. 2012. V. 173. P. 79.

  6. Sinibaldi A., Danz N., Descrovi E. et al. // Sensors Actuators B: Chemical. 2012. V. 174. P. 292.

  7. Liedberg B., Nylander C., Lunström I. // Sensors and Actuators. 1983. V. 4. P. 299.

  8. Zayats A.V., Smolyaninov I.I., Maradudin A.A. // Phys. Rep. 2005. V. 408. № 3–4. P. 131.

  9. Yeh P., Yariv A., Cho A.Y. // Appl. Phys. Lett. 1978. V. 32. № 2. P. 104.

  10. Dong H.Y., Wang J., Cui T.J. // Phys. Rev. B. 2013. V. 87. № 4. P. 045406.

  11. Photonic Crystals: Physics and Technology / Eds. by Sibilia C., Benson T.M., Marciniak M., Szoplik T. Milan: Springer, 2005.

  12. Дьяконов М.И. // ЖЭТФ. 1988. Т. 94. № 4. С. 119.

  13. Takayama O., Crasovan L., Johansen S. et al. // Electromagnetics. 2008. V. 28. № 3. P. 126.

  14. Zapata-Rodriguez C.J., Sorní J.A., Vukovic S. et al. // Proc. 16th Int. Conf. on Transparent Optical Networks. Graz. 6–10 Jul. 2014. N.Y.: IEEE, 2014. P.We.P.18

  15. Gao W.-L., Fang F.-Z., Liu Y.-M., Zhang S. // Light Sci. Appl. 2015. V. 4. № 9. P. 328.

  16. Chern R.-L., Yu Y.-Z. // Opt. Express. 2017. V. 25. № 10. P. 11801.

  17. Gao W., Lawrence M., Yang B. // Phys. Rev. Lett. 2015. V. 114. № 3. P. 037402.

  18. Gao J., Lakhtakia A., Lei M. // Phys. Rev. A. 2010. V. 81. № 1. P. 1615.

  19. Kuznetsov E.V., Merzlikin A.M. // J. Opt. 2017. V. 19. № 5. P. 055610.

  20. Merzlikin A.M., Levy M., Jalali A. A., Vinogradov A.P. // Phys. Rev. B. 2009. V. 79. № 19. P. 195103.

  21. Ignatov A.I., Merzlikin A.M., Levy M., Vinogradov A.P. // Materials. 2012. V. 5. № 6. P. 1055.

  22. Wang F., Lakhtakia A. // Phys. Rev. B. 2009. V. 79. № 19. P. 193102.

  23. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982.

  24. Merzlikin A.M., Vinogradov A.P., Lagarkov A.N. // Phys. B. Cond. Matt. 2010. V. 405. № 14. P. 2986.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал