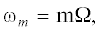Радиотехника и электроника, 2020, T. 65, № 2, стр. 135-140

ВВЕДЕНИЕ

Электрические параметры атмосферы Земли зависят от вращающихся с Землей электронов и ионов, распределенных по высоте над Землей по сложным законам [1–3]. Изучению напряженностей электромагнитного поля (ЭМП), возбуждаемых вращающимися электрическими зарядами, посвящен ряд работ [3–5]. При этом решения задач определения векторов напряженностей ЭМП получены с применением нековариантных уравнений электродинамики в неинерциальных (вращающихся) системах отсчета, и поэтому их нельзя считать корректными. Ниже строгое решение задачи об излучении ЭМП вращающимся с постоянной угловой частотой электрическим зарядом получено на основе ковариантных уравнений электродинамики [6].

1. ПОСТАНОВКА ЗАДАЧИ

Введем в неограниченное пространство, заполненное средой с однородными диэлектрической $\varepsilon $ и магнитной $\mu $ проницаемостями, инерциальную (декартову) систему отсчета $K\left( {x,y,z,i{{v}_{\phi }}t} \right) = $ $ = K\left( {R,\theta ,{\text{\;}}\varphi ,{\text{\;}}i{{v}_{\phi }}t} \right) = K({{x}^{j}}),$ где $i$ – мнимая единица, ${{v}_{\phi }} = {{\left( {\varepsilon \mu } \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$ $t$ – время, ${{x}^{j}} = {{x}^{1}},{{x}^{2}},{{x}^{3}},{{x}^{0}},$ j = 1, 2, 3, 0, ${{x}^{\alpha }} = R,\theta ,\varphi $ – сферические координаты, $\alpha = 1,2,3$ и покоящуюся в ней точку наблюдения $P\left( {p,t} \right),$ где p = ${{x}^{1}},{{x}^{2}},{{x}^{3}} = R,\theta ,\varphi .~$ Введем вращающуюся с постоянной угловой частотой ${\Omega }$ жесткую систему отсчета $K{\kern 1pt} {\text{'}}\left( {R{\kern 1pt} ',\theta {\kern 1pt} ',\varphi {\kern 1pt} ',i{{{v}}_{\phi }}t} \right)$ = $K{\kern 1pt} {\text{'}}\left( {{{x}^{{\alpha '}}},i{{v}_{\phi }}t} \right),$ $\alpha {\kern 1pt} ' = 1{\kern 1pt} ',2{\kern 1pt} ',3{\kern 1pt} '$ и совместим начала сферических систем координат. Полярную ось $\theta = \theta {\kern 1pt} ' = 0$ направим вдоль оси вращения. Обозначим через $P{\kern 1pt} {\text{'}}\left( {p{\kern 1pt} {\text{'}},t} \right),$ где $p{\kern 1pt} ' = R{\kern 1pt} ',\theta {\kern 1pt} ',\varphi {\kern 1pt} ',$ покоящуюся в $K{\kern 1pt} '$ точку наблюдения. Координаты точек наблюдения $P\left( {p,t} \right)$ в “неподвижной” системе отсчета K и $~P{\kern 1pt} {\text{'}}\left( {p{\kern 1pt} {\text{'}},t} \right)$ – во введенной вращающейся K ' связаны соотношениями

Во вращающейся системе отсчета $K{\kern 1pt} '$ в области сторонних источников $V_{{\hat {j}}}^{{\text{'}}}$ задан в точке $p_{0}^{{\text{'}}} = (a,\theta _{0}^{{\text{'}}},\varphi _{0}^{{\text{'}}})$ покоящийся электрический статический заряд $Q{\kern 1pt} {\text{'}}$ со скалярной плотностью $\hat {\rho }{\kern 1pt} {{{\text{'}}}^{E}}.$ Радиус вращения a задан в $K{\kern 1pt} '.$ Плотности сторонних электрического ${{\vec {\hat {j}}}^{{'E}}}$ и магнитного ${{\vec {\hat {j}}}^{{'H}}}$ токов отсутствуют.

Необходимо найти составляющие векторов напряженностей электрических и магнитных полей $\vec {E}{\kern 1pt} {\text{',}}$ $\vec {H}{\kern 1pt} {\text{'}}$ и $\vec {E}$, $\vec {H}$ соответственно в системах отсчета $K{\kern 1pt} {\text{'}}$ и $K$.

В трехмерном пространстве, соответствующем $K{\kern 1pt} {\text{'}}$, тензор кривизны пространства отличен от нуля. Поэтому пространство является римановым пространством. Следовательно, уравнения электродинамики для ЭМП в $K{\kern 1pt} {\text{'}}$ могут быть записаны [6] в трехмерной форме для трехмерных объектов: напряженности электрического поля – ковариантного вектора $\vec {E}{\kern 1pt} ' = {{E}_{{\alpha {\kern 1pt} {\text{'}}}}} = \left( {{{E}_{{1{\kern 1pt} '}}},{{E}_{{2{\kern 1pt} '}}},{{E}_{{3{\kern 1pt} '}}}} \right)$ = $ = \left( {{{E}_{{R{\kern 1pt} '}}},R{\kern 1pt} '{{E}_{{\theta {\kern 1pt} '}}},R{\kern 1pt} '{\text{sin}}\theta {\kern 1pt} {\text{'}}{{E}_{{\varphi {\kern 1pt} '}}}} \right),$ напряженности магнитного поля – контравариантной бивекторной плотности веса $ + 1$ $\hat {\vec {H}}{\kern 1pt} ' = {{\hat {H}}^{{\alpha {\kern 1pt} {\text{'}}\beta {\kern 1pt} {\text{'}}}}}$ = $\left( {{{{\hat {H}}}^{{2{\kern 1pt} {\text{'}}3{\text{'}}}}}, - {{{\hat {H}}}^{{1{\kern 1pt} {\text{'}}3{\kern 1pt} {\text{'}}}}},{{{\hat {H}}}^{{1{\kern 1pt} {\text{'}}2{\kern 1pt} {\text{'}}}}}} \right) = $ = $\left( {{{H}_{{R{\kern 1pt} '}}},R{\kern 1pt} {\text{'}}{{H}_{{\theta {\kern 1pt} '}}},R{\kern 1pt} {\text{'sin}}\theta {\kern 1pt} {\text{'}}{{H}_{{\varphi {\kern 1pt} {\text{'}}}}}} \right),$ электрической индукции – контравариантной векторной плотности веса $ + 1$, $\hat {\vec {D}}{\kern 1pt} ' = {{\hat {D}}^{{\alpha {\kern 1pt} '}}} = \left( {{{{\hat {D}}}^{{1{\kern 1pt} {\text{'}}}}},{{{\hat {D}}}^{{2{\kern 1pt} {\text{'}}}}},{{{\hat {D}}}^{{3{\kern 1pt} {\text{'}}}}}} \right)$ = $\left( {R{\kern 1pt} {{'}^{2}}{\text{sin}}\theta {\kern 1pt} {\text{'}}{{{\hat {D}}}^{{R{\kern 1pt} '}}}{\text{\;}},} \right.$ $\left. {R{\kern 1pt} {\text{'sin}}\theta {\kern 1pt} {\text{'}}{{{\hat {D}}}^{{\theta {\kern 1pt} '}}},{\text{\;}}R{\kern 1pt} {\text{'}}{{{\hat {D}}}^{{\varphi {\kern 1pt} {\text{'}}}}}} \right),$ магнитной индукции – ковариантного вектора $\vec {B}{\kern 1pt} ' = {{B}_{{\alpha {\kern 1pt} '\beta {\kern 1pt} '}}} = \left( {{{B}_{{2{\kern 1pt} '3{\kern 1pt} '}}}, - {{B}_{{1{\kern 1pt} '3{\kern 1pt} '}}},{{B}_{{1{\kern 1pt} '2{\kern 1pt} '}}}} \right)$ = $ = \left( {{{R}^{{'{\kern 1pt} 2}}}{\text{sin}}\theta {\kern 1pt} {\text{'}}{{B}_{{\theta {\kern 1pt} '{\varphi }{\kern 1pt} {\text{'}}}}}{\text{\;}}, - R{\kern 1pt} {\text{'sin}}\theta {\kern 1pt} {\text{'}}{{B}_{{R{\kern 1pt} '\varphi \,'}}},R{\kern 1pt} {\text{'}}{{B}_{{R{\kern 1pt} {\text{'}}\theta {\kern 1pt} {\text{'}}}}}} \right){\text{\;}}$ в виде

где

2. РЕШЕНИЕ ЗАДАЧИ

Общее решение задачи получено путем разложения составляющих электрического векторного потенциала по системе векторных собственных функций риманова пространства и разделения ЭМП на сумму полей электрического и магнитного типов с помощью электрического ${{V}^{{'E}}}\left( {p{\kern 1pt} ',t} \right)$ и магнитного ${{V}^{{'H}}}\left( {p{\kern 1pt} ',t} \right)$ потенциалов Дебая. Последние представлены в виде разложения по функциям Маркова $U_{{nm}}^{{'E}}$ и $U_{{nm}}^{{'H}}{\text{\;}}$ [6]:

где $\varepsilon ,$ $\mu $ – диэлектрическая и магнитная проницаемости, измеренные в $K{\kern 1pt} {\text{'}}{\text{.}}$

Тогда радиальные составляющие индукций

Если подставить значение стороннего заряда (3) в выражения для функций $U_{{nm}}^{{'E,H}}$ [6] и выполнить интегрирование, то получим

где $x = {{k}_{m}}a,$ $y = {{k}_{m}}R{\kern 1pt} {\text{',}}$ штрих над круглой скобкой означает производную по $x$, $W = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \varepsilon }} \right. \kern-0em} \varepsilon }} ,$ $P_{n}^{m}\left( {{\text{cos}}\theta {\kern 1pt} {\text{'}}} \right)$ – присоединенные полиномы Лежандра, ${{j}_{n}}\left( x \right),$ $h_{n}^{{\left( 2 \right)}}\left( x \right)$ – сферические функции Бесселя, ${{k}_{m}} = {{m{\Omega }} \mathord{\left/ {\vphantom {{m{\Omega }} {{{v}_{\phi }}}}} \right. \kern-0em} {{{v}_{\phi }}}},$

Поскольку в системе отсчета $K{\kern 1pt} {\text{'}}$ составляющие векторов напряженностей электрического поля (ЭП) [6] можно представить в виде

а составляющие векторов напряженностей магнитного поля (МП) –

то из выражений (6)–(9) следует: во вращающейся системе отсчета статический электрический заряд возбуждает, кроме статического ЭП, статическое МП; эти ЭП и МП не образуют ЭМП; векторы напряженностей ЭП и МП имеют все составляющие; появление всех составляющих вектора $\vec {H}{\kern 1pt} {\text{'}}$ в (9) обязано воздействию эквивалентного гравитационного поля и на заряд, и на ЭП. Первые слагаемые составляющих пространственного спектра в (8) и (9) обусловлены электрическим зарядом, а вторые – обязаны своим появлением вращению заряда.

Для анализа зависимостей составляющих пространственного спектра ЭП (8) и МП (9) от расстояния $R{\kern 1pt} {\text{'}}$ учтем, что, применяя к функциям $U_{{nm}}^{{{\text{'}}E,H}}$ асимптотические разложения сферических функций [7], имеем в дальней зоне при $R{\kern 1pt} {\text{'}} \gg a$ (но ${{k}_{m}}a \ll 1,$ ${{k}_{m}}R{\kern 1pt} ' > n$):

а в ближней зоне при $R{\kern 1pt} {\text{'}} < a,$ (но ${{k}_{m}}R{\kern 1pt} ' < 1,$ ${{k}_{m}}a \gg 1,$ ${{k}_{m}}a > n$) –

где ${{\phi }_{n}} = \pi {{\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} 2}} \right. \kern-0em} 2} - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4},$ ${\text{Г}}\left( {n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)$ – гамма-функция.

Эти выражения показывают, что в (8) и (9) имеются компоненты пространственного спектра, которые при увеличении расстояния $R{\kern 1pt} '$ в дальней зоне уменьшаются не быстрее, чем ${{\left( {{{k}_{m}}R{\kern 1pt} '} \right)}^{{ - 1}}},$ а в ближней зоне – увеличиваются как ${{\left( {{{k}_{m}}R{\kern 1pt} '} \right)}^{{n - 1}}}.$

Наибольший практический интерес представляет ЭМП в “неподвижной” системе отсчета $K$. Для преобразования ЭП и МП из $K{\kern 1pt} '$ в $K$ используем преобразование продольных составляющих электрической ${{\hat {D}}^{{{\text{'}}R{\kern 1pt} {\text{'}}}}}$ и магнитной $B_{{\theta {\kern 1pt} '\varphi {\kern 1pt} '}}^{{\text{'}}}$ индукций в составляющие ${{\hat {D}}^{R}}\left( {p,t} \right)$ и ${{B}_{{\theta \varphi }}}\left( {p,t} \right)$ [6]:

Так как согласно (1) $~R{\kern 1pt} {\text{'}} = R,$ $~\theta {\kern 1pt} {\text{'}} = \theta ,$ $~\varphi {\kern 1pt} ' = \varphi - {\Omega }t,$ то получим

где составляющие частотного спектра имеют вид

а функции ${{U}^{{E,H}}}\left( p \right)$ определяются по (6) и (7) путем замены $R{\kern 1pt} {\text{'}} = R,$ $\theta {\kern 1pt} {\text{'}} = \theta ,$ $\varphi {\kern 1pt} ' = \varphi .$ При этом векторы напряженностей ЭМП в системе отсчета $K$

где комплексные амплитуды составляющих векторов представимы в виде

Выражения (5) и (10), (11) показывают, что имеются составляющие частотного спектра, изменяющиеся в дальней зоне как ${{R}^{{ - 1}}},$ в системе имеется волновой процесс, значит, возбуждается ЭМП.

Определим поле излучения вращающегося заряда в вакууме, где ${{v}_{\phi }}$ равна скорости света с. В дальней зоне, используя асимптотику сферических функций Ганкеля и ее производной при ${{k}_{m}}R \to \infty $ [8], получим спектральные составляющие отличных от нуля составляющих векторов электрического поля в виде, удобном для проведения дальнейших расчетов:

где

Спектральные составляющие отличных от нуля составляющих векторов магнитного поля в дальней зоне связаны с составляющими векторов электрического поля характеристическим сопротивлением пространства $W.~~$Поля излучения на спектральных составляющих, как видно из полученных формул, определяются только суммой по индексу n.

Таким образом, поле излучения вращающегося статического заряда в неподвижной системе отсчета так же, как и поле вращающегося диполя [9], представляет собой дискретный спектр частот частоты вращения ${\Omega }.$

4. РЕЗУЛЬТАТЫ РАСЧЕТА

Рассчитаем спектр электромагнитного излучения вращающегося заряда (сгустка электронов) в адронном коллайдере. Длина кольца коллайдера $\ell $ = 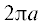= 27 × 10³ м, скорость движения сгустка электронов по окружности $v = \Omega a\,\,(v < c).$ Тогда $~{{k}_{m}}a = m\frac{{\Omega }}{c}a = m\kappa ,$ где $\kappa $ – отношение линейной скорости $v$ движения заряда по окружности к скорости света $c$.

В расчете при скорости движения заряда с параметром κ = 0.5 достаточно [8] удерживать 10 членов ряда по n, т.е. N = 10. Считаем, что заряд вращается в экваториальной плоскости $\theta _{0}^{{\text{'}}}{\text{\;}}$ = = π/2, а угол $\varphi _{0}^{{\text{'}}}$ примем равным нулю.

Расчет спектра излучения показал, что в плоскости вращения присутствуют только азимутальные составляющие ${{e}_{{m,\varphi }}}$. При κ = 0.1 частота первой гармоники равна 1.11 кГц. Амплитуда первой гармоники, нормированная по амплитуде первой гармоники при осевом наблюдении, составляет 0 дБ, второй –14 дБ, а третьей –29.5 дБ.

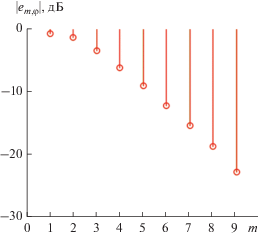
Снижение скорости движения заряда по окружности приводит к существенному подавлению второй гармоники и значительному затуханию третьей, т.е. к обужению спектра. Напротив, повышение скорости движения заряда (κ > 0.1) ведет к расширению спектра. На рис. 1 показан в логарифмическом масштабе нормированный по амплитуде первой гармоники азимутальной составляющей ${{e}_{{1,\varphi }}}$ при осевом наблюдении ($\theta $ = 0°) амплитудный спектр азимутальной составляющей ${{e}_{{m,\varphi }}}$ поля излучения в экваториальной плоскости ($\theta $ = π/2) и $\varphi $ = 0 вращающегося заряда при κ = 0.5. В отличие от общепринятого изображения спектра здесь показаны величины затухания гармоник по отношению к нормирующему значению. Частота первой гармоники в этом случае равна 5.55 кГц.

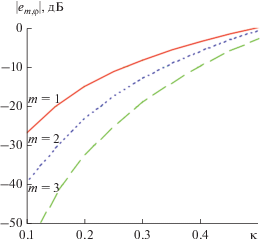
Зависимости трех первых гармоник спектра в экваториальной плоскости от параметра κ, изменяющегося в пределах 0.1…0.5 показаны на рис. 2. Эти зависимости наглядно иллюстрируют расширение спектра при увеличении κ. Поле излучения сложным образом зависит от отношения линейной скорости движения заряда по окружности к скорости света, поскольку аргументы функций Бесселя и их производных зависят от κ.

Выясним зависимость поля излучения от радиуса окружности, по которой вращается заряд. Коэффициент, стоящий перед суммой в (12), может быть преобразован к виду $\frac{{Q{\kern 1pt} '}}{{4{\pi }\varepsilon R}}m\frac{{{{\kappa }^{2}}}}{a}.$ Откуда следует, что поле излучения на гармониках спектра обратно пропорционально радиусу окружности. Таким образом, радиус окружности влияет только на величину спектральных составляющих и никак не сказывается на огибающей спектра.

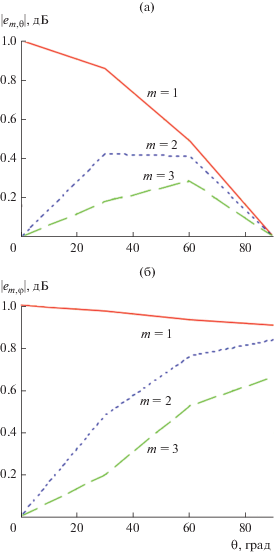
На рис. 3а и 3б представлены зависимости амплитуд гармоник соответственно ${{e}_{{m,\theta }}}$ и ${{e}_{{m,\varphi }}}$ при κ = 0.5 от угла наблюдения $\theta $. Из приведенных графиков следует, что в плоскости вращения ($\theta $ = 90°) поляризация излучения на спектральных составляющих линейная ($~{{e}_{{m,\theta }}}$ = 0). С уменьшением угла наблюдения ${\theta }$ поляризация на гармониках спектра является эллиптической, а при ${\theta }$ = 0° спектр вырождается в монохроматический, причем $\left| {{{e}_{{1,\theta }}}~} \right|~$ = $\left| {{{e}_{{1,\varphi }}}~} \right|~$ при сдвиге фаз между ними π/2. Поляризация становится круговой.

ЗАКЛЮЧЕНИЕ

Таким образом, задача об излучении вращающегося статического заряда решена строго с помощью уравнений электродинамики в ковариантной форме, соответствующих неинерциальной системе отсчета. Во вращающейся системе, жестко связанной с зарядом, статический электрический заряд возбуждает кроме статического электрического статическое магнитное поле. Эти поля имеют все составляющие, но они не образуют ЭМП. Появление всех составляющих магнитного поля обязано воздействию эквивалентного гравитационного поля и на заряд и на электрическое поле.

В “неподвижной” системе отсчета поля́, преобразованные из вращающейся системы, представляют собой частотный спектр частоты вращения. Поперечные составляющие гармоник частотного спектра изменяются в дальней зоне как 1/R, в системе имеется волновой процесс, т.е. возбуждается ЭМП.

Результаты расчета, представленные в виде графиков, соответствуют физическим представлениям о поведении излучаемых полей в эависимости от угла наблюдения. Ширина спектра зависит в основном от относительной линейной скорости движения заряда по окружности, а уровень спектральных составляющих обратно пропорционален радиусу окружности. При уменьшении радиуса кривизна пространства возрастает и отмеченные выше эффекты проявляются в большей степени.