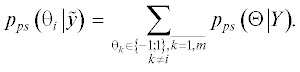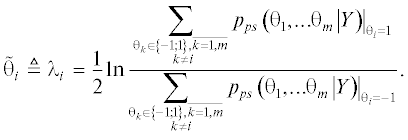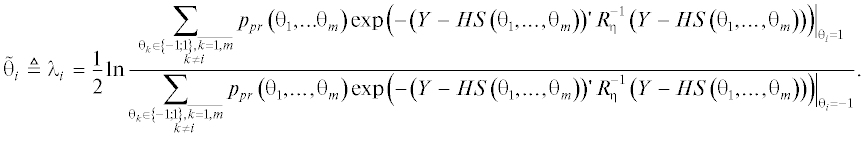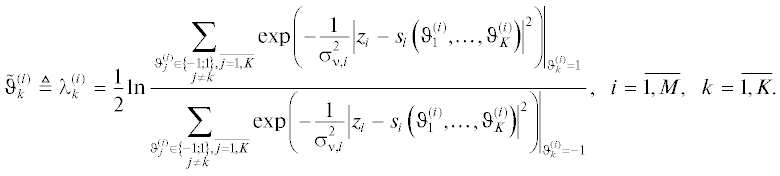Радиотехника и электроника, 2020, T. 65, № 3, стр. 257-266
Байесовское оценивание с последовательным отказом и учетом априорных знаний
М. Г. Бакулин a, *, В. Б. Крейнделин a, В. А. Григорьев b, В. О. Аксенов b, **, А. С. Щесняк b
a Московский технический университет связи и информатики
111024 Москва, ул. Авиамоторная, 8а, Российская Федерация
b Университет ИТМО
197101 Санкт-Петербург, Кронверкский просп., 49, Российская Федерация
* E-mail: m.g.bakulin@gmail.com
** E-mail: voaksenov@ifmo.ru
Поступила в редакцию 09.08.2018
После доработки 18.03.2019
Принята к публикации 27.03.2019
Аннотация
Рассмотрен метод синтеза алгоритмов оценивания, использующий байесовский подход при последовательном учете априорных знаний. Показано, что отсутствие знаний о виде априорного распределения или отказ от этих знаний из-за невозможности вывода байесовского алгоритма оценивания может быть имитирован заменой истинного априорного распределения другим распределением с большей энтропией, при этом известные алгоритмы небайесовского оценивания могут быть получены путем классического байесовского правила. Предложен подход последовательного отказа от части априорных знаний и его последующего учета для синтеза алгоритма оценивания. Приведены примеры практического использования предложенного подхода для синтеза алгоритма демодуляции сигналов в системах связи с MIMO-каналом.
1. ПОСТАНОВКА ЗАДАЧИ
Основным разделом статистического синтеза и анализа является теория статистических решений и оценок. В связи с широким развитием техники передачи цифровой информации сфера использования теории оценивания существенно расширилась, и она стала широко применяться в области демодуляции цифровых сигналов, т.е. сигналов с конечным дискретным множеством значений.
От объема учитываемых априорных знаний зависит не только эффективность полученных оценок, но и сложность реализации алгоритма оценивания. Например, отказываясь от каких-либо априорных сведений, можно, вместо оценивания дискретного параметра использовать более простой алгоритм оценивания непрерывного параметра, а на этапе принятия окончательного решения преобразовать эти оценки, задействуя априорную информацию о дискретности параметра.
Важно не дублировать одну и ту же априорную информацию.
В статье показано, как использовать байесовский подход с последовательным отказом и последующим учетом априорных знаний об оцениваемых параметрах.
Справедливо уравнение наблюдения:
где $\eta \sim \mathbb{C}\mathbb{N}\left( {0,{{R}_{\eta }}} \right)$ – $N$-мерный комплексный вектор отсчетов гауссовского шума наблюдения, $H$ – $\left( {N \times M} \right)$-мерная известная матрица; $Y$ – $N$-мерный комплексный вектор наблюдения; $X\left( \Theta \right)$ = = ${{\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}\left( {{{\theta }_{1}}} \right)}&{{{x}_{2}}\left( {{{\theta }_{2}}} \right)}& \cdots &{{{x}_{M}}\left( {{{\theta }_{M}}} \right)} \end{array}} \right]}^{T}}$ – М-мерный вектор комплексных символов, каждый из которых является нелинейной комплекснозначной функцией ${{x}_{i}}\left( {{{\theta }_{i}}} \right)$ параметра ${{\theta }_{i}}$, $i = \overline {1,M} ;$ $\Theta = {{\left[ {\begin{array}{*{20}{c}} {{{\theta }_{1}}}& \cdots &{{{\theta }_{M}}} \end{array}} \right]}^{T}}$ – М‑мерный вектор случайных величин. Функциональные зависимости ${{x}_{i}}\left( \centerdot \right)$ могут быть как одинаковыми для всех $i$, так и разными.
Задача состоит в том, чтобы по полученным наблюдениям $Y$оценить вектор символов $\Theta $, причем здесь рассматривается случай, когда число оцениваемых параметров (размерность вектора $\Theta $) равно числу комплексных символов (размерности вектора $X$). Это условие необязательное, и в общем случае переменная ${{\theta }_{i}}$ может быть вектором.
В данной постановке задача хорошо известна и имеет множество приложений: оценивание случайных процессов [1, 2], многопользовательское детектирование [3, 4], детектирование в условиях межсимвольных или межканальных помех [5], детектирование сигналов в MIMO системах [6–8] и т.п.
Полная информация об оцениваемом векторе $\Theta $ содержится в апостериорном распределении, которое вычисляется по формуле Байеса [1, 2]
где ${{p}_{{pr}}}\left( \Theta \right)$ – априорное распределение вектора $\Theta $; $\Lambda \left( {Y\left| \Theta \right.} \right)$ – функция правдоподобия, определяемая уравнением наблюдения, –
Зная апостериорное распределение, можно вычислить точечные или интервальные оценки вектора $\Theta $.
Процедура вычисления апостериорного распределения может быть трудоемкой из-за нелинейности уравнения наблюдения относительно оцениваемого параметра, многомерности и зависимости компонентов оцениваемого вектора.
Для решения такой задачи часто используют приближенные методы, например, “линейные” методы оценивания (детектирования), суть которых состоит в следующем.
Введем обозначение для вектора комплексных случайных величин $X = {{\left[ {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{2}}}& \cdots &{{{x}_{M}}} \end{array}} \right]}^{T}},$ где ${{x}_{i}} \triangleq {{x}_{i}}({{\theta }_{i}})$. Тогда уравнение наблюдения относительно данного вектора будет линейным
и, следовательно, для оценивания вектора $X$ можно применять известные методы, использующие частичную априорную информацию. К последним, например, относятся метод минимума среднеквадратического отклонения (МСКО)11 [1], предусматривающий использование информации об априорном математическом ожидании ${{\bar {X}}_{{pr}}}$ и корреляционной матрице ${{V}_{{pr}}}$ и описываемый следующими выражениями:
(3)
$\begin{gathered} {{{\hat {X}}}_{{{\text{МСКО}}}}} = {{{\bar {X}}}_{{pr}}} + {{K}_{{{\text{МСКО}}}}}(Y - H{{{\bar {X}}}_{{pr}}}), \\ {{V}_{{{\text{МСКО}}}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H + V_{{pr}}^{{ - 1}}} \right)}^{{ - 1}}} = \\ = {{V}_{{pr}}} - {{K}_{{{\text{МСКО}}}}}\left( {H{{V}_{{pr}}}} \right), \\ {{K}_{{{\text{МСКО}}}}} = {{V}_{{pr}}}H{\kern 1pt} '{{\left( {H{{V}_{{pr}}}H{\kern 1pt} '\,\, + {{R}_{\eta }}} \right)}^{{ - 1}}}, \\ \end{gathered} $или метод наименьших квадратов (МНК) [1], также известный в теории демодуляции как декоррелятор (в англоязычных публикациях этот метод известен под названием “Zero-Forcing”)
(4)
$\begin{gathered} {{{\hat {X}}}_{{{\text{МНК}}}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H} \right)}^{{ - 1}}}H{\kern 1pt} 'R_{\eta }^{{ - 1}}Y, \\ {{V}_{{{\text{МНК}}}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H} \right)}^{{ - 1}}}. \\ \end{gathered} $Далее, как правило, используется следующий подход. Распределение ошибок оценивания предполагается гауссовским $p\left( {X - \hat {X}} \right)\sim \mathbb{C}\mathbb{N}\left( {{{{\hat {X}}}_{{ps}}},{{V}_{{ps}}}} \right)$ с параметрами, определяемыми методом оценивания. После этого каждая оценка ${{\hat {x}}_{{i,ps}}}$ рассматривается независимо от оценок других символов как новое уравнение наблюдения [9]
с гауссовским шумом ${{\mu }_{i}}\sim \mathbb{C}\mathbb{N}\left( {0,{v}_{{ps}}^{{(ii)}}} \right)$, где $v_{{ps}}^{{(ii)}}$ – i‑й диагональный элемент корреляционной матрицы ${{V}_{{ps}}}.$
Затем по формуле Байеса вычисляется апостериорное распределение случайного параметра ${{\theta }_{i}}$
(5)
${{p}_{{ps}}}\left( {{{\theta }_{i}}\left| {{{{\hat {x}}}_{{i,ps}}}} \right.} \right) = \frac{{\Lambda \left( {{{{\hat {x}}}_{{i,ps}}}\left| {{{\theta }_{i}}} \right.} \right){{p}_{{pr}}}\left( {{{\theta }_{i}}} \right)}}{{\int\limits_{{{\theta }_{i}}} {\Lambda \left( {{{{\hat {x}}}_{{i,ps}}}\left| {{{\theta }_{i}}} \right.} \right){{p}_{{pr}}}\left( {{{\theta }_{i}}} \right)d{{\theta }_{i}}} }},$и его оценка
(6)
${{\hat {\theta }}_{i}} = \mathbb{F}\left( {{{p}_{{ps}}}\left( {{{\theta }_{i}}\left| {{{{\hat {x}}}_{{i,ps}}}} \right.} \right)} \right),$где $\mathbb{F}\left( {{{p}_{{ps}}}\left( {{{\theta }_{i}}\left| {{{{\hat {x}}}_{{i,ps}}}} \right.} \right)} \right)$ – некоторый нелинейный функционал от апостериорного распределения, определяемый видом выбранного критерия оптимизации (максимума апостериорной плотности или вероятности, минимума СКО и т.п.).
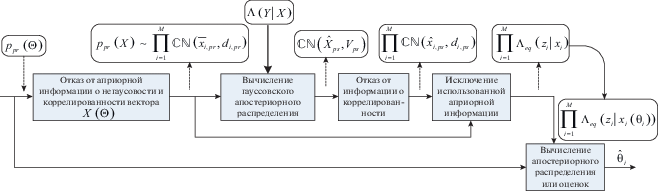
Традиционное определение “линейные” к алгоритмам детектирования (3), (4), (5), (6) применяется не совсем корректно, так как в итоге окончательные оценки символов ${{\hat {\theta }}_{i}}$ вычисляются путем нелинейного преобразования исходного наблюдения $Y$. Оно относится лишь к первой, промежуточной части алгоритма – оценивания символов ${{x}_{i}}$. Сама возможность использования линейных алгоритмов основана на том факте, что символы ${{x}_{i}}$ являются функциями разных случайных параметров ${{x}_{i}}\left( {{{\theta }_{i}}} \right)$, т.е. они функционально независимы. Это позволяет после получения оценок перейти от многомерной задачи оценивания к M одномерным задачам и использовать раздельную обработку и оценивание искомых параметров ${{\theta }_{i}}$. Вся процедура использования линейных алгоритмов основана на нескольких полуэмпирических подходах, не связанных общей идеей. Поэтому в некоторых случаях, как будет показано далее, это приводит к потерям в качестве оценивания.
Далее предлагается подход, соединяющий воедино все этапы оценивания и позволяющий более точно вычислить искомое апостериорное распределение и получить оценки с более высоким качеством. Предложенный метод проверен на примере демодуляции и декодировании в системах MIMO.
2. БАЙЕСОВСКИЙ ПОДХОД ВЫЧИСЛЕНИЯ АПОСТЕРИОРНОГО РАСПРЕДЕЛЕНИЯ С НЕПОЛНЫМ УЧЕТОМ АПРИОРНОЙ ИНФОРМАЦИИ
Рассмотрим задачу оценивания комплексного вектора $X$ при наблюдении (4). Вся информация об оцениваемом векторе содержится в апостериорном распределении
при вычислении которого используется априорное распределение ${{p}_{{pr}}}\left( X \right)$ и функция правдоподобия
При негауссовом многомерном априорном распределении задача вычисления апостериорного распределения является достаточно трудоемкой и не всегда может быть решена. Поэтому существуют определенные небайесовские критерии, позволяющие вычислять оценки вектора $X$ более просто.
Среди этих критериев можно выделить такие, которые используют не полную априорную информацию, а лишь ее часть, или вообще ее не используют. Среди них можно выделить, например, критерий минимума среднеквадратического отклонения [1], в котором в качестве априорной информации используется только априорное математическое ожидание и корреляционная матрица, или критерий наименьших квадратов, который вообще не использует никакой априорной информации.
Рассмотрим подход вычисления оптимальных оценок, основанный на вычислении и использовании апостериорного распределения при неполном учете априорной информации.
Пусть в исходном случае имеется полная априорная информация, которая заключена в априорном распределении ${{p}_{{pr}}}\left( X \right).$ Объем этой априорной информации характеризуется энтропией источника сообщений
Отказ от какой-либо части априорной информации приводит к увеличению энтропии источника сообщения. Следовательно, процедура отказа может быть имитирована заменой исходного априорного распределения ${{p}_{{ps}}}\left( X \right)$ другим распределением ${{\tilde {p}}_{{ps}}}\left( X \right),$ характеризующим источник сообщения с большей энтропией. Существуют различные варианты перехода от распределений с меньшей энтропией к распределению с более высокой энтропией.
Известно [10, 11], что среди распределений с фиксированной средней мощностью наибольшей энтропией обладает гауссовское распределение, причем наилучшей аппроксимацией негауссовской плотности гауссовской по критерию минимума расстояния Кульбака является распределение, у которого математическое ожидание и дисперсия равны истинным значениям [12]. То же самое имеет место и для распределения векторной случайной величины, т.е. максимум энтропии
при ограничениях на функцию плотности вероятности
будет иметь место при следующем априорном распределении:
Следующий путь увеличения энтропии состоит в отказе от зависимости априорного распределения [12], т.е. в данном случае имеется в виду использование вместо истинной корреляционной матрицы ${{V}_{{pr}}}$ диагональной априорной корреляционной матрицы
где $d_{{pr}}^{{(i)}} = v_{{pr}}^{{(ii)}},$ $v_{{pr}}^{{(ii)}}$ – диагональные элементы корреляционной матрицы ${{V}_{{pr}}}.$
И, наконец, последним шагом в увеличении энтропии априорной информации является увеличение априорных дисперсий вплоть до бесконечности, т.е. использование следующего априорного распределения22
Таким образом, предлагаемый подход постепенного отказа от априорной информации, сопровождающегося использованием априорных распределений с большим значением энтропии, позволяет создавать алгоритмы оценивания разной степени приближения и разной сложности, оставаясь при этом в рамках единого байесовского подхода. В табл. 1 приведены последовательные шаги исключения априорной информации и получаемые при этом алгоритмы вычисления апостериорного распределения (его параметров), а также связь между этими параметрами и известными оценками.
Таблица 1.
Сопоставление априорной информации с априорным и апостериорным распределениями, с оценками
| Априорная информация | Априорное распределение | Апостериорное распределение | Оценки |
|---|---|---|---|
| Полная априорная информация | ${{p}_{{pr}}}\left( X \right)$ | ${{p}_{{ps}}}\left( {X\left| Y \right.} \right) = C\Lambda \left( {Y\left| X \right.} \right){{p}_{{pr}}}\left( X \right)$ | $\begin{gathered} {{{\hat {X}}}_{{{\text{МАП}}}}} = \mathop {\arg \max }\limits_X \left( {{{p}_{{ps}}}\left( {X\left| Y \right.} \right)} \right) \hfill \\ {{{\hat {X}}}_{{{\text{МСКО}}}}} = \int\limits_X {X{{p}_{{ps}}}\left( {X\left| Y \right.} \right)dX} \hfill \\ \end{gathered} $ |
| Отказ от информации о негауссовости априорного распределения | ${{\tilde {p}}_{{pr}}}\left( X \right) \sim \mathbb{C}\mathbb{N}\left( {{{{\bar {X}}}_{{pr}}},{{V}_{{pr}}}} \right)$ | $\begin{gathered} {{{\tilde {p}}}_{{ps}}}\left( {X\left| Y \right.} \right) \sim \mathbb{C}\mathbb{N}\left( {{{{\bar {X}}}_{{ps}}},{{V}_{{ps}}}} \right) \\ {{{\bar {X}}}_{{ps}}} = {{{\bar {X}}}_{{pr}}} + K(Y - H{{{\bar {X}}}_{{pr}}}) \\ {{V}_{{ps}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H + V_{{pr}}^{{ - 1}}} \right)}^{{ - 1}}} = {{V}_{{pr}}} - KH{{V}_{{pr}}} \\ \end{gathered} $ где $\begin{gathered} K = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H + V_{{pr}}^{{ - 1}}} \right)}^{{ - 1}}}H{\kern 1pt} 'R_{\eta }^{{ - 1}} = \\ = {{V}_{{pr}}}H{\kern 1pt} '{{\left( {H{{V}_{{pr}}}H{\kern 1pt} ' + {{R}_{\eta }}} \right)}^{{ - 1}}} \\ \end{gathered} $ |
${{\tilde {X}}_{{{\text{МАП,2}}}}} = {{\tilde {X}}_{{{\text{МСКО,2}}}}} = {{\bar {X}}_{{ps}}}$ |
| Отказ от информации о зависимости (коррелированности) априорного распределения | $\begin{gathered} {{{\tilde {p}}}_{{pr}}}\left( X \right) = \prod\limits_{i = 1}^M {{{{\tilde {p}}}_{{pr}}}({{x}^{{(i)}}})} \hfill \\ {{{\tilde {p}}}_{{pr}}}\left( {{{x}_{i}}} \right) \sim \mathbb{C}\mathbb{N}\left( {\bar {x}_{{pr}}^{{(i)}},d_{{pr}}^{{(i)}}} \right) \hfill \\ \end{gathered} $ | $\begin{gathered} {{{\tilde {p}}}_{{ps}}}\left( {X\left| Y \right.} \right) \sim \mathbb{C}\mathbb{N}\left( {{{{\bar {X}}}_{{ps}}},{{V}_{{ps}}}} \right) \\ {{{\bar {X}}}_{{ps}}} = {{{\bar {X}}}_{{pr}}} + K(Y - H{{{\bar {X}}}_{{pr}}}) \\ {{V}_{{ps}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H + D_{{pr}}^{{ - 1}}} \right)}^{{ - 1}}} = {{D}_{{pr}}} - KH{{D}_{{pr}}} \\ \end{gathered} $ где $\begin{gathered} K = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H + D_{{pr}}^{{ - 1}}} \right)}^{{ - 1}}}H{\kern 1pt} 'R_{\eta }^{{ - 1}} = \\ = {{D}_{{pr}}}H{\kern 1pt} '{{\left( {H{{D}_{{pr}}}H{\kern 1pt} ' + {{R}_{\eta }}} \right)}^{{ - 1}}} \\ {{D}_{{pr}}} = diag\left( {d_{{pr}}^{{(i)}},i = \overline {1,M} } \right) \\ \end{gathered} $ |
${{\tilde {X}}_{{{\text{МАП,3}}}}} = {{\tilde {X}}_{{{\text{МСКО,3}}}}} = {{\bar {X}}_{{ps}}}$ |
| Полный отказ от априорной информации | $\begin{gathered} {{{\tilde {p}}}_{{pr}}}\left( X \right) \sim \mathbb{C}\mathbb{N}\left( {{{O}_{M}},d{{I}_{M}}} \right), \\ d \to \infty \\ \end{gathered} $ | $\begin{gathered} {{{\tilde {p}}}_{{ps}}}\left( {X\left| Y \right.} \right) \sim \mathbb{C}\mathbb{N}\left( {{{{\bar {X}}}_{{ps}}},{{V}_{{ps}}}} \right) \\ {{{\bar {X}}}_{{ps}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H} \right)}^{{ - 1}}}H{\kern 1pt} 'R_{\eta }^{{ - 1}}Y \\ {{V}_{{ps}}} = {{\left( {H{\kern 1pt} 'R_{\eta }^{{ - 1}}H} \right)}^{{ - 1}}} \\ \end{gathered} $ | ${{\tilde {X}}_{{{\text{МАП,4}}}}} = {{\tilde {X}}_{{{\text{МСКО,4}}}}} = {{\bar {X}}_{{ps}}}$ |
Сравнивая выражения для линейных оценок МСКО (3) и МНК (4), с выражениями для параметров апостериорных распределений из второй и четвертой строк этой таблицы, соответственно, можно заметить, что алгоритм вычисления линейной оценки МСКО является результатом синтеза с использованием байесовского подхода без учета знаний о негауссовости априорного распределения, а линейный алгоритм МНК также может быть получен с использованием байесовского подхода, при полном отсутствии априорной информации, что имитируется гауссовским априорным распределением с бесконечной дисперсией (бесконечной энтропией).
3. ПОСЛЕДОВАТЕЛЬНЫЙ УЧЕТ АПРИОРНОЙ ИНФОРМАЦИИ ПРИ БАЙЕСОВСКОМ ОЦЕНИВАНИИ
Отказ от информации о негауссовости априорного распределения для модели (2), позволяет получить простые алгоритмы оценивания, однако приводит к потерям. Но поскольку эта информация известна, то возникает вопрос, нельзя ли на следующем этапе использовать, хотя бы частично, информацию о негауссовости априорного распределения без существенного усложнения алгоритма.
Рассмотрим следующий подход. Отказ от негауссовости привел к тому, что вычисленное апостериорное распределение для модели (2) является гауссовским ${{\tilde {p}}_{{ps}}}\left( {\left. X \right|Y} \right)\sim \mathbb{C}\mathbb{N}\left( {{{{\bar {X}}}_{{ps}}},{{V}_{{ps}}}} \right)$ для всех вариантов отказа от априорных сведений (строки 2–4 табл. 1). После вычисления параметров апостериорного распределения откажемся от апостериорной зависимости между элементами вектора $X$, тогда можно записать
(7)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} }_{{ps}}}\left( {X\left| Y \right.} \right) = \prod\limits_{i = 1}^M {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} }}_{{ps}}}\left( {{{x}_{i}}\left| Y \right.} \right)} ,$где ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} }_{{ps}}}\left( {\left. {{{x}_{i}}} \right|Y} \right)\sim \mathbb{C}\mathbb{N}\left( {{{{\bar {x}}}_{{i,ps}}},d_{{ps}}^{{(i)}}} \right),$ $d_{{ps}}^{{(i)}} \triangleq {v}_{{ps}}^{{(ii)}}$ – i-й диагональный элемент корреляционной матрицы ${{V}_{{ps}}}.$
В апостериорном распределении ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} }_{{ps}}}\left( {{{x}_{i}}\left| Y \right.} \right)$ содержится часть априорной информации, используемой в виде гауссовского распределения ${{\tilde {p}}_{{pr}}}\left( {{{x}_{i}}} \right).$ Представим ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} }_{{ps}}}\left( {{{x}_{i}}} \right)$ как результат, полученный вычислением по формуле Байеса
где ${{\Lambda }_{{eq}}}\left( {{{z}_{i}}\left| {{{x}_{i}}} \right.} \right)$ – некоторая эквивалентная функция правдоподобия с эквивалентным наблюдением ${{z}_{i}},$ которая может быть найдена следующим образом:
Так как плотности ${{\tilde {p}}_{{pr}}}\left( {{{x}_{i}}} \right)$ и ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} }_{{ps}}}\left( {{{x}_{i}}} \right)$ являются нормальными, то и эквивалентная функция правдоподобия также будет описываться гауссовской плотностью. Опуская промежуточные преобразования, получим
(8)
${{\Lambda }_{{eq}}}\left( {{{z}_{i}}\left| {{{x}_{i}}} \right.} \right) = C\exp \left( { - \frac{1}{{\sigma _{\nu }^{2}}}{{{\left| {{{z}_{i}} - {{x}_{i}}} \right|}}^{2}}} \right),$где
Функция правдоподобия ${{\Lambda }_{{eq}}}\left( {{{z}_{i}}\left| {{{x}_{i}}} \right.} \right)$ может рассматриваться как результат использования в качестве модели следующего эквивалентного уравнения наблюдения:
где ${{\nu }_{i}}\sim \mathbb{C}\mathbb{N}\left( {0,\sigma _{{\nu ,i}}^{2}} \right)$ – отсчет эквивалентного комплексного гауссовского шума.
Применяя эквивалентную функцию правдоподобия, можно найти уточненное апостериорное распределение, использующее истинное априорное распределение для каждого элемента вектора $X$
и из него найти необходимые оценки, например, оценку, оптимальную по критерию МСКО
Полученные выражения можно использовать для синтеза нелинейного алгоритма оценивания вектора Θ в модели (1). Пусть априорное распределение вектора $\Theta $ является независимым, т.е. представимо в виде
Это может быть следствием отказа от априорной информации о зависимости случайных величин и следствием отсутствия этой информации.
Следующим шагом будет переход от априорного распределения ${{p}_{{pr}}}\left( \Theta \right)$ к априорному распределению вектора $X \triangleq X(\Theta )$
где параметры этого распределения определяются исходным априорным распределением
Очевидно, что истинное априорное распределение ${{p}_{{pr}}}\left( X \right)$ не является гауссовским, так как, во-первых, функция ${{x}_{i}}\left( {{{\theta }_{i}}} \right)$ нелинейная с ограниченной областью значений, а, во-вторых, сам параметр ${{\theta }_{i}}$, как правило, имеет негауссовское априорное распределение, однако на данном шаге мы не будем использовать информацию о негауссовости априорного распределения случайной величины ${{x}_{i}} \triangleq {{x}_{i}}\left( {{{\theta }_{i}}} \right).$
В соответствии со строкой 3 табл. 1 апостериорное распределение при данном объеме учитываемой априорной информации будет гауссовским ${{p}_{{ps}}}\left( X \right)\sim \mathbb{C}\mathbb{N}\left( {{{{\hat {X}}}_{{ps}}},{{V}_{{ps}}}} \right)$ с параметрами
где $K = {{D}_{{pr}}}H{\kern 1pt} '{{\left( {H{{D}_{{pr}}}H{\kern 1pt} '\,\, + {{R}_{\eta }}} \right)}^{{ - 1}}}.$
Следующим шагом является переход от апостериорного распределения коррелированных случайных величин к независимому распределению (7) и вычисление параметров эквивалентной функции правдоподобия ${{\Lambda }_{{eq}}}\left( {{{z}_{i}}\left| {{{x}_{i}}} \right.} \right)$ в соответствии с (9).
Учитывая, что ${{x}_{i}} \triangleq {{x}_{i}}\left( {{{\theta }_{i}}} \right)$, можем записать апостериорное распределение для оцениваемой случайной величины ${{\theta }_{i}}$
Далее апостериорное распределение может использоваться по назначению в зависимости от выбранного критерия.
На рис. 1 приведена блок-схема описанного подхода вычисления апостериорного распределения (или оценок) вектора параметров для модели (1). Отметим, что традиционное использование линейных алгоритмов оценивания для этой модели, например, алгоритма МСКО, отличается отсутствием блока исключения использованной априорной информации, что в итоге может приводить к ухудшению качества вычисленных оценок. Использованная дополнительная процедура вычисления параметров эквивалентной функции правдоподобия незначительно увеличивает сложность. В общем случае добавляется M операций действительного деления, 3M операции действительного умножения и 5M операций сложения.
4. ДЕМОДУЛЯЦИЯ В СИСТЕМАХ MIMO С ПОСЛЕДОВАТЕЛЬНЫМ ОТКАЗОМ И УЧЕТОМ АПРИОРНОЙ ИНФОРМАЦИИ
Пусть дана модель уравнения наблюдения для системы связи с MIMO-каналом
где $\eta \sim N\left( {0,{{R}_{\eta }}} \right)$ – комплексный гауссовский шум, $\Theta = {{\left[ {\begin{array}{*{20}{c}} {{{\theta }_{1}}}& \cdots &{{{\theta }_{m}}} \end{array}} \right]}^{T}}$ – $m$-мерный вектор двоичных символов (битов) ${{\theta }_{i}} \in \left\{ { - 1;1} \right\},$ $i = \overline {1,m} ,$ которые нужно оценить; $Y$ – $N$-мерный комплексный вектор наблюдения; $S\left( \Theta \right)$ – М-мерный вектор комплексных квадратурно-амплитудно модулированных (КАМ) символов. Для классической системы с пространственным мультиплексированием имеем
где $\vartheta _{k}^{{(l)}}$ – k-й из совокупности K двоичных символов, входящих в состав l-го КАМ-символа, число точек созвездия которого равно ${{2}^{K}}$. Между элементами вектора $\Theta $ и битами КАМ-символов существует следующее соответствие:
при этом $m = KM.$ Общее число комбинаций вектора КАМ-символов $S\left( \Theta \right)$ равно ${{2}^{{KM}}}$.
Случайные величины ${{\theta }_{i}}$ являются дискретными и в данном случае могут принимать всего два значения, 1 и –1. Поэтому для них оценки могут быть двух видов – “жесткие” и “мягкие”. Оценки, принимающие значения согласно области значений оцениваемой случайной величины, называются “жесткими” оценками. Они, как правило, соответствуют критериям максимума апостериорной вероятности или максимального правдоподобия
“Мягкие” оценки или “мягкие” решения могут принимать значения, отличающие от области значений оцениваемой случайной величины. Для одномерной двоичной случайной величины $\theta = \pm 1$ распределение характеризуется вероятностями $P\left\{ {\theta = 1} \right\} = {{p}_{0}}$ и $P\left\{ {\theta = - 1} \right\} = {{p}_{1}} = 1 - {{p}_{0}}.$ Аналитически это распределение можно представить двумя способами [6, 13]:
где $\mu = E\left\{ \theta \right\} = \left( {{{p}_{0}} - {{p}_{1}}} \right)$ – математическое ожидание; $\lambda = \frac{1}{2}\ln \frac{{{{p}_{0}}}}{{{{p}_{1}}}}.$
Между параметрами $\mu $ и $\lambda $ существует однозначная связь
Таким образом, в параметре $\mu $ или в связанном с ним параметре $\lambda = {\text{arcth}}\left( \mu \right)$ содержится полная информация о распределении двоичной случайной величины. Нетрудно показать, что параметр $\mu $ является оптимальной оценкой бита по критерию минимума среднеквадратического отклонения, т.е.
Оба параметра $\mu $ и $\lambda $ могут использоваться в качестве “мягкой” оценки бита. Однако, как показывает практика, с точки зрения точности вычислений предпочтительней оказываются логарифмические параметры, т.е. параметр $\lambda $. Поэтому в дальнейшем в качестве “мягкой” оценки бита будем использовать именно его, т.е.
(11)
$\tilde {\theta } \triangleq \lambda = \frac{1}{2}\ln \frac{{{{p}_{{ps}}}\left( {\theta = \left. 1 \right|Y} \right)}}{{{{p}_{{ps}}}\left( {\theta = \left. { - 1} \right|Y} \right)}}.$Следует отметить, что из “мягких” оценок можно легко вычислить “жесткую” оценку
Рассмотрим вычисление “мягких” оценок для демодулятора сигналов в MIMO-канале. Для модели наблюдения (10) с учетом равной вероятности комбинаций и представления сигналов в виде функции битов $S\left( \Theta \right)$ апостериорное распределение будет определяться выражением
Для вычисления апостериорного распределения i-го бита необходимо усреднить многомерное апостериорное распределение ${{p}_{{ps}}}\left( {\Theta \left| Y \right.} \right)$ по всем битам кроме i-го. Для дискретного распределения операция усреднения выполняется путем суммирования
С учетом этого и формулы (10) “мягкая” оценка i‑го бита будет определяться выражением
Таким образом, оптимальный алгоритм вычисления “мягких” оценок битов для MIMO-канала в общем случае описывается следующим выражением:
Алгоритм вычисления мягких оценок (12) имеет очень высокую сложность $ \sim KM{{2}^{{KM}}}$ даже при независимых и равновероятных комбинациях битов. Данное выражение допускает некоторое упрощение, но порядок сложности все равно остается $ \sim {{2}^{{KM}}}$. Поэтому на практике используют различные приближенные методы, которые позволяют уменьшить число перебираемых комбинаций. Среди наиболее простых методов можно выделить так называемые “линейные” алгоритмы оценивания.
Суть этих методов состоит в том, что сначала путем линейной обработки находятся оценки КАМ-символов, а затем эти оценки используются в качестве новых независимых наблюдений для мягкой демодуляции битов. При этом сложность демодуляции одного символа будет пропорциональна ${{2}^{K}}$.
Используем байесовский подход, основанный на последовательном учете априорной информации, описанный в предыдущих разделах.
Сначала вычислим параметры априорного распределения вектора $S = \left[ {{{s}_{1}},...,{{s}_{M}}} \right] \triangleq S\left( {{{\theta }_{1}},...,{{\theta }_{m}}} \right)$. Для независимых и равновероятных битов имеем
Очевидно, что априорные распределения случайных величин ${{s}_{i}}$ будут негауссовскими, но согласно описанному ранее подходу на данном шаге мы отказываемся от этой информации и используем распределение, наихудшее с точки зрения максимума энтропии сообщения, т.е. гауссовское априорное распределение ${{p}_{{pr}}}\left( S \right) = \mathbb{C}\mathbb{N}\left( {0,{{I}_{M}}} \right)$, где ${{I}_{M}}$ – единичная матрица размером $\left( {M \times M} \right).$
С учетом этого (согласно третьей строке табл. 1) параметры апостериорного гауссовского распределения ${{p}_{{ps}}}\left( S \right) = \mathbb{C}\mathbb{N}\left( {{{{\hat {S}}}_{{ps}}},{{V}_{{ps}}}} \right)$ будут
Как уже отмечалось, эти оценки полностью совпадают с линейными оценками МСКО.
Для дальнейшего синтеза алгоритма демодуляции отказываемся от апостериорной зависимости компонентов вектора $S$ и используем апостериорное распределение
Для исключения априорной информации, которую мы использовали при вычислении априорных математических ожиданий и дисперсий перейдем к эквивалентным функциям правдоподобия ${{\Lambda }_{{eq}}}\left( {{{z}_{i}}\left| {{{x}_{i}}} \right.} \right)$ (8) с параметрами
(13)
${{z}_{i}} = \frac{{{{{\hat {s}}}_{{i,ps}}}}}{{1 - d_{{ps}}^{{(i)}}}},\,\,\,\,\sigma _{{\nu ,i}}^{2} = \frac{{d_{{ps}}^{{(i)}}}}{{1 - d_{{ps}}^{{(i)}}}},$где при выводе этих выражений учитывалось, что ${{\bar {s}}_{{i,pr}}} = 0,\,\,d_{{pr}}^{{(i)}} = 1.$
Следует отметить, что отличие полученного алгоритма от известного алгоритма демодуляции с использованием линейных оценок МСКО в данном случае заключается только в операциях вычисления параметров эквивалентной функции правдоподобия (13), что усложняет алгоритм всего на M операций действительного деления, M операций действительного сложения и на 3М операций действительного умножения.
Учитывая независимость и равновероятность комбинаций битов, получим
Нетрудно видеть, что сложность вычисления “мягких” оценок битов пропорциональна MK2K плюс сложность МСКО-алгоритма (~M3) и плюс сложность вычисления параметров эквивалентных функций правдоподобия (~M). Если учесть, что в большинстве систем связи используются квадратные КАМ-созвездия с кодированием Грея, которое допускает раздельную обработку квадратурных составляющих, то сложность вычисления по формуле (14) будет составлять 2MK2K/2.
Недостатком (14) является большой динамический диапазон суммируемых чисел в числителе и знаменателе дроби, что ухудшает точность вычисления при ограниченной разрядности вычислений. Чтобы избежать этого, можно использовать следующий прием. Введем обозначение для метрик аргументов экспоненциальной функции
где $l_{k}^{{( + )}} = \overline {1,{{2}^{{{K \mathord{\left/ {\vphantom {K 2}} \right. \kern-0em} 2}}}}} $ – номера комбинаций двоичных битов $\vartheta _{1}^{{(i)}}, \ldots ,\vartheta _{K}^{{(i)}}$ для всех возможных значений $\vartheta _{j}^{{(i)}} \in \left\{ { - 1;1} \right\}$, и фиксированном значении k-го бита $\vartheta _{k}^{{(i)}} = 1,$ аналогично $l_{k}^{{( - )}} = \overline {1,{{2}^{{{K \mathord{\left/ {\vphantom {K 2}} \right. \kern-0em} 2}}}}} $ – номера комбинаций при $\vartheta _{k}^{{(i)}} = - 1$. С учетом этого выражение (14) можно преобразовать к виду
Преимущества этой формулы состоят в том, что динамический диапазон аргументов экспоненциальной функции, самих сумм и их отношений существенно меньше, чем в исходном выражении. Из этой формулы вытекает приближенный алгоритм вычисления “мягкой” оценки, если ограничиться первым слагаемым
5. МОДЕЛИРОВАНИЕ
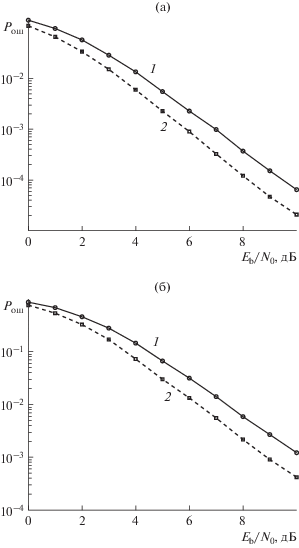
Для проверки предложенного подхода последовательного учета априорной информации и сравнения его с аналогичными алгоритмами было проведено моделирование системы с MIMO-каналом со следующими условиями моделирования: число передающих антенн $M = 8$, число приемных антенн $N = 8$, модуляция 16 КАМ, MIMO-канал с независимыми релеевскими замираниями.
Были исследованы зависимости вероятности ошибки на бит для системы без кодирования и вероятности ошибки на бит и на кадр для систем с кодированием от отношения сигнал/шум на бит. В качестве канального кода использовался турбо-код со скоростью кодирования 1/2 и длиной кадра 573 бита.
Детектор, синтезированный с использованием предложенного подхода (рис. 2), имеет характеристики помехоустойчивости на 0.3 дБ лучше, чем аналогичный по сложности МСКО-детектор. Это улучшение незначительное, так как в системе без кодирования используются жесткие оценки битов, которые соответствуют критерию максимума апостериорной вероятности и используют не всю информацию.
Рис. 2.
Зависимости вероятности ошибки на бит от отношения сигнал/шум на бит в системе с MIMO-каналом без кодирования для МСКО-детектора (1) и детектора, использующего предложенный подход с последовательным отказом и учетом априорной информации (2).
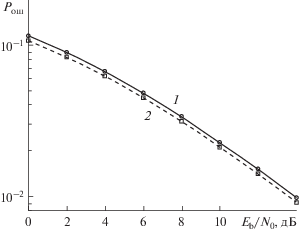
Для системы с кодированием явно видно преимущество предложенного подхода (рис. 3а и 3б). Помехоустойчивость полученного алгоритма лучше на 1…1.5 дБ. Это объясняется более корректным использованием априорной информации и, как следствие, более точным вычислением “мягких” оценок битов.
ЗАКЛЮЧЕНИЕ
Таким образом, предложен подход к решению задачи нелинейного оценивания, основанный на последовательном учете априорной информации. Показано, что путем отказа от части априорной информации можно упрощать алгоритмы оценивания. Причем отказ от априорной информации может быть имитирован заменой исходного априорного распределения другим с большей энтропией, например, вместо негуассовского – гауссовское, вместо многомерного зависимого – многомерное независимое, вместо распределения с фиксированной дисперсией – распределение с бесконечной дисперсией, и т.п.
При этом синтез алгоритмов оценивания остается в рамках единого байесовского подхода и оперирует понятиями априорного распределения, функции правдоподобия и апостериорного распределения. Это позволяет учесть априорную информацию, используемую на промежуточных шагах синтеза, и более точно использовать неучтенную информацию на последующих шагах.
Приведенный пример использования данного подхода для синтеза алгоритма оценивания двоичных битов при передаче информации в системах связи с MIMO показывает преимущество при разработке демодуляторов с линейными алгоритмами оценивания символов за счет более точного учета априорной информации, вследствие чего формируются оценки битов с лучшим качеством оценивания, чем известные линейные алгоритмы.
Список литературы
Седж Э., Мелс Дж. Теория оценивания и ее применение в связи и управлении. М.: Связь, 1976.
Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991.
Verd’u S. Multiuser Detection. Cambridge: Univ. Press, 1998.
Advances in Multiuser Detection / Ed. M.L. Honig. Hoboken: John Wiley & Sons, Inc., 2009.
Li Y., Vucetic B., Sato Y. // IEEE Trans. 1995. V. IT-41. № 3. P. 704.
Шлома А.М., Бакулин М.Г., Крейнделин В.Б., Шумов А.П. Новые алгоритмы формирования и обработки сигналов в системах подвижной связи / Под ред. А.М. Шломы. М.: Горячая линия-Телеком, 2008.
Бакулин М.Г., Варукина Л.А., Крейнделин В.Б. Технология MIMO: принципы и алгоритмы. М.: Горячая линия–Телеком, 2014.
Bai L., Choi J. Low Complexity MIMO Detection. N.Y.: Springer, 2012.
Tüchler M., Singer A.C., Koetter R. // IEEE Trans. 2002. V. SP-50. № 3. P. 673.
Ту Дж., Гонсалес Р. Принципы распознавания образов. М.: Мир, 1978.
Куликовский Л.Ф., Мотов В.В. Теоретические основы информационных процессов. М.: Высш. школа, 1987.
Шеннон К. Работы по теории информации и кибернетике. М.: Изд-во иностр. лит., 1963.
Бакулин М.Г. // Электросвязь. 2000. № 1. С. 11.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника