Радиотехника и электроника, 2020, T. 65, № 3, стр. 267-276

ВВЕДЕНИЕ

Как известно, касательно намагниченная ферритовая пленка – одна из немногих реальных сред, в которой могут возбуждаться и распространяться с малыми потерями обратные волны. В работе [1] обратные спиновые волны (ОСВ) были описаны с использованием магнитостатического приближения, из-за чего их часто называют обратными объемными магнитостатическими волнами (МСВ). В дальнейшем многие свойства этих волн и различные устройства на их основе были исследованы и описаны в ряде монографий [2–9] и статей [10–23]. В частности, в работах [13, 16] теоретически и экспериментально установлено, что при возбуждении ОСВ линейным преобразователем возникают две волны, характеризующиеся противоположно направленными волновыми векторами и различным¹¹ распределением магнитного потенциала в сечении ферритовой пластины. Кроме того, в [16, 18] было найдено, что в зависимости от ориентации волнового вектора (или возбуждающего преобразователя) наибольшее значение магнитного потенциала может находиться как на поверхности, так и внутри ферритовой пластины.

Очевидно, что для разработки спин-волновых устройств необходимо знать, при какой ориентации волнового вектора распределение магнитного потенциала ОСВ имеет точку экстремума непосредственно на поверхности ферритовой пластины и при какой ориентации волнового вектора на поверхности пластины реализуется наибольшее отношение амплитуд магнитных потенциалов, описывающих две волны с противоположно направленными волновыми векторами. Ответы на эти вопросы дают представленные ниже исследования, являющиеся логическим продолжением работ [16, 21].

1. ОСНОВНЫЕ СООТНОШЕНИЯ. ФИЗИЧЕСКИЙ СМЫСЛ НОРМИРОВАННОЙ АМПЛИТУДЫ МАГНИТНОГО ПОТЕНЦИАЛА $\Psi _{0}^{{\text{н}}}$(х)

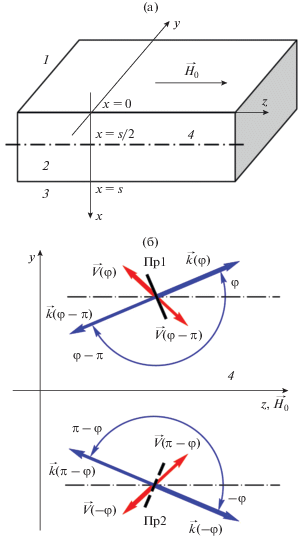
Рассмотрим бесконечную пластину 2 толщиной s из изотропного феррита (рис. 1а). Пластина 2, окруженная полупространствами вакуума 1 и 3, намагничена до насыщения касательным однородным магнитным полем $\overrightarrow {{{H}_{0}}} $ и характеризуется тензором магнитной проницаемости $\overleftrightarrow {{{\mu }_{2}}}$. Используя уравнения Максвелла в магнитостатическом и безобменном приближениях и вводя магнитный потенциал Ψ по аналогии с работой [1], можно получить уравнения для потенциала Ψ₂ и потенциалов Ψ₁ и Ψ₃ внутри и вне ферритовой пластины. Подставляя решение для магнитного потенциала

Рис. 1.

Геометрия задачи в пространстве (а) и в плоскости ферритовой пластины (б) (вид со стороны поверхности x = 0): 1 и 3 – полупространства вакуума, 2 – ферритовая пластина (пленка); 4 – ось симметрии бесконечной касательно намагниченной ферритовой пластины; Пр1 и Пр2 – симметричные друг другу при повороте относительно оси 4 преобразователи, лежащие соответственно на поверхностях x = 0 и x = s. Изображены волновые векторы $\overrightarrow k (\varphi )$ и $\overrightarrow k (\varphi - \pi )$, $\overrightarrow k ( - \varphi )$ и $\overrightarrow k (\pi - \varphi )$, их ориентации φ и φ – π, –φ и π–φ и соответствующие векторы групповой скорости $\overrightarrow V (\varphi )$ и $\overrightarrow V (\varphi - \pi )$, $\overrightarrow V ( - \varphi )$ и $\overrightarrow V (\pi - \varphi )$ для волн, возбуждаемых преобразователями Пр1 и Пр2 соответственно ($\overrightarrow k $ и $\overrightarrow V $ для полезных волн показаны жирными векторами).

в граничные условия (определяемые непрерывностью нормальной компоненты СВЧ магнитной индукции и потенциала на границах сред), получим систему уравнений

где μ = 1 + ω_Mω_H/($\omega _{H}^{2}$ – ω²) и ν = ω_Mω/($\omega _{H}^{2}$ – ω²) – компоненты тензора магнитной проницаемости феррита, ω_H = γH₀, ω_M = 4πγM₀, ω = 2πf, γ – гиромагнитная постоянная, 4πM₀ – намагниченность насыщения феррита, f – частота волны, A, B, C, D – произвольные коэффициенты, а k_1x, k_2x, k_3x, k_y и k_z – компоненты волнового вектора (причем k_1x, k_2x и k_3x – положительные числа), связанные соотношениями k_1x = k_3x = ($k_{y}^{2}$ + $k_{z}^{2}$)^1/2, k_2x = ($ - k_{y}^{2} - {{k_{z}^{2}} \mathord{\left/ {\vphantom {{k_{z}^{2}} \mu }} \right. \kern-0em} \mu }$)^1/2.

Для описания ОСВ в полярной системе координат воспользуемся соотношениями y = –r sin φ, z = r cos φ и введем волновой вектор $\overrightarrow k $, модуль которого k связан с волновыми числами k_y, k_z, k_1x и k_2x соотношениями k_y = –k sinφ, k_z = k cosφ, k_2x = = αk и k_1x = k, где

а φ – угол, задающий ориентацию вектора $\overrightarrow k $ относительно оси z (углы при исследовании ОСВ удобно отсчитывать от оси z, являющейся для этой волны осью коллинеарного распространения). В полярной системе координат связь между коэффициентами A, B, C и D, следующая из системы (2), и дисперсионное уравнение ОСВ, полученное в результате решения (2), имеют вид

где введено обозначение μ_⊥ = (μ² – ν²)/μ. Из уравнения (5) величину k можно явно выразить через угол φ и параметры ферритовой пластины

где номер моды m принимает значения натуральных чисел (m = 1, 2, 3, …).

Подставляя (4) в (1), запишем магнитный потенциал Ψ_j внутри и вне пленки (j = 1, 2 или 3) в виде Ψ_j = Ψ_j0exp(–ikr), где амплитуды потенциала Ψ_j0 в каждой среде определяются выражениями

Для краткости амплитуду потенциала, состоящую из трех функций Ψ₁₀, Ψ₂₀ и Ψ₃₀ обозначим Ψ₀. Точно также, через $\Psi _{0}^{{\text{н}}}$ обозначена нормированная амплитуда потенциала

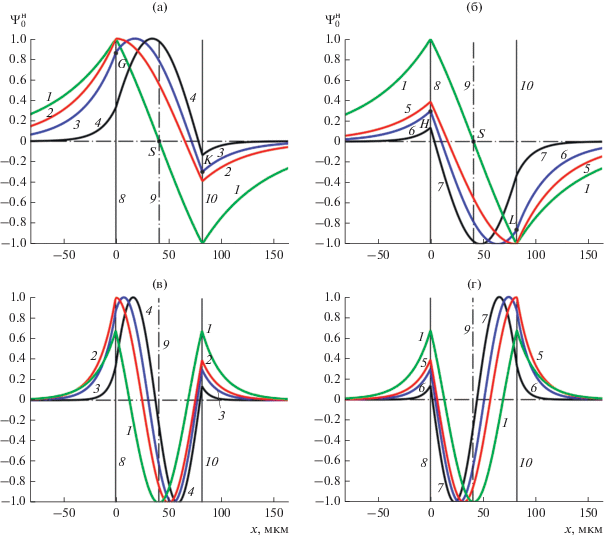
где нормировочная величина Ψ_0макс(φ) представляет собой максимальное значение модуля функции Ψ₂₀/B на отрезке 0 ≤ x ≤ s. (Выражение для величины Ψ_0макс(φ) получено далее, см. формулу (11).) Распределение амплитуды $\Psi _{0}^{{\text{н}}}(x)$, рассчитанное в соответствии с (8) при различных значениях φ для первой и второй мод ОСВ, показано на рис. 2. Расчеты выполнены для частоты ОСВ f = 2000 МГц и параметров поля и пленки, использованных в [16, 21, 22]: H₀ = 367 Э, 4πM₀ = 1870 Гс, s = 82 мкм.

Рис. 2.

Нормированное распределение амплитуды магнитного потенциала $\Psi _{0}^{{\text{н}}}(x)$ для первой (а и б) и второй (в и г) мод ОСВ при f = 2000 МГц и следующих положительных (а и в) и отрицательных (б и г) значениях угла φ: 0° и 180° (1), φ_экст1 = 16.3° и φ_экст2 = 163.7° (2), φ_R1 = 23.9° и φ_R2 = 156.1° (3), 40° и 160° (4), φ_экст4 = –16.3° и φ_экст3 = –163.7° (5), φ_R4 = –23.9° и φ_R3 = –156.1° (6), – 40° и –160° (7). Координаты x = 0, x = s/2 = 41 мкм и x = s = 82 мкм обозначены прямыми 8–10, причем прямая 9 является осью зеркальной симметрии, при которой кривые $\Psi _{0}^{{\text{н}}}(x)$ на рис. 2в симметричны кривым $\Psi _{0}^{{\text{н}}}(x)$ на рис. 2г. Для первой моды ОСВ точками G, H, K и L отмечены значения $\Psi _{0}^{{\text{н}}}(x = 0)$ и $\Psi _{0}^{{\text{н}}}(x = s)$ на кривых 3 и 6, а точкой S – центр симметрии, при которой кривые $\Psi _{0}^{{\text{н}}}(x)$ на рис. 2а симметричны кривым $\Psi _{0}^{{\text{н}}}(x)$ на рис. 2б.

Поясним, чем отличаются нормированные и ненормированные зависимости $\Psi _{0}^{{\text{н}}}(x,\varphi )$ и ${{\Psi }_{0}}(x,\varphi )$. Поскольку касательно намагниченная ферритовая пластина симметрична самой себе при повороте на 180° вокруг единственной оси симметрии (см. рис. 1, ось 4), параллельной вектору $\overrightarrow {{{H}_{0}}} $ и проходящей через середину пластины, а одинаковые линейные преобразователи Пр1 и Пр2 (см. рис. 1б), расположенные на поверхностях пластины x = 0 и x = s, отображаются при данном повороте друг на друга²², то и зависимости волн $\Psi _{0}^{{\text{н}}}(x,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x, - \varphi )$, возбуждаемых этими преобразователями, должны быть симметричны. Действительно, из рис. 2 видно, что эти зависимости либо центрально симметричны (для нечетных мод), либо зеркально симметричны (для четных мод). Для ненормированных зависимостей ${{\Psi }_{0}}(x,\varphi )$ и ${{\Psi }_{0}}(x, - \varphi )$ такая симметрия не имеет места³³, поэтому они неадекватно описывают соотношение амплитуд при тождественных геометриях возбуждения волн, хотя и могут использоваться для вычислений.

2. УГЛЫ φ_экст, ПРИ КОТОРЫХ ЗАВИСИМОСТЬ $\Psi _{0}^{{\text{н}}}(x)$ ИМЕЕТ ТОЧКУ ЭКСТРЕМУМА НА ПОВЕРХНОСТИ ФЕРРИТОВОЙ ПЛАСТИНЫ ДЛЯ ВСЕХ МОД ОСВ

Как видно из рис. 2, при φ = 0 и φ = 180° распределение потенциала $\Psi _{0}^{{\text{н}}}(x)$ имеет одинаковую (по абсолютной величине) амплитуду на обеих поверхностях пластины (кривые 1), причем это распределение имеет m – 1 точек экстремума, в которых ${{\partial \Psi _{0}^{{\text{н}}}} \mathord{\left/ {\vphantom {{\partial \Psi _{0}^{{\text{н}}}} {\partial x}}} \right. \kern-0em} {\partial x}} = 0.$ То есть для первой моды зависимость $\Psi _{0}^{{\text{н}}}(x)$ не имеет точек экстремума, для второй моды имеет одну точку экстремума и т.д. С изменением угла φ (в любую сторону от направлений φ = 0 и φ = 180°) при некоторых значениях φ = ±φ_экст и φ = π ± φ_экст на зависимости $\Psi _{{20}}^{{\text{н}}}(x)$ возникает еще одна m-я точка экстремума, локализованная на одной из поверхностей пластины. При дальнейшем изменении угла φ эта m-я точка экстремума смещается от поверхности к середине пластины (см. рис. 2, кривые 2–7).

Для вычисления угла φ_экст найдем вначале координату x = x_экст, которая соответствует точке экстремума на зависимости $\Psi _{{20}}^{{\text{н}}}(x)$. Чтобы определить эту координату найдем производную ${{\partial \Psi _{0}^{{\text{н}}}} \mathord{\left/ {\vphantom {{\partial \Psi _{0}^{{\text{н}}}} {\partial x}}} \right. \kern-0em} {\partial x}},$ продифференцировав выражение (8) и приравняем ее нулю:

Из уравнения (9) легко найти координату x_экст:

Получим также выражение для нормировочной величины Ψ_0макс(φ), стоящей в формуле (8). Подставляя $\sin (\alpha k{{x}_{{{\text{экст}}}}})$ из соотношения (9) в (7), используя соотношение $\cos (\alpha k{{x}_{{{\text{экст}}}}})$ = ${1 \mathord{\left/ {\vphantom {1 {(1}}} \right. \kern-0em} {(1}} + {{\operatorname{tg} }^{2}}(\alpha k{{x}_{{{\text{экст}}}}}){{)}^{{1/2}}}$ и учитывая (10), можно найти значение зависимости Ψ₂₀(x) в точке экстремума при x = x_экст и записать следующее выражение для нормировочной величины Ψ_0макс(φ):

Отметим, что зависимость ${{\Psi }_{{20}}}(x)$ для первой моды ОСВ не имеет точек экстремума для углов φ из интервалов значений –φ_экст1 < φ < φ_экст1 и π – φ_экст1 < < φ < π + φ_экст1. Поэтому, чтобы получить нормированное распределение $\Psi _{{20}}^{{\text{н}}}(x)$ для таких углов φ, необходимо нормировать зависимость ${{\Psi }_{{20}}}(x)$ на максимальное значение, реализующееся на одной из поверхностей пленки.

Найдем теперь из выражения (9) параметры волны, при которых зависимость $\Psi _{{20}}^{{\text{н}}}(x)$ имеет точку экстремума (максимум) прямо на поверхности ферритовой пленки при x = 0 (рис. 2а, кривая 2). Полагая в (9) x_экст = 0, получим простое уравнение для вычисления угла φ_экст

В интервале значений – π < φ_экст ≤ π уравнение (12) имеет два решения, φ_экст1 и φ_экст2 = π – φ_экст1, причем величина φ_экст1 определяется выражением

Поскольку ν < 0 во всем диапазоне существования ОСВ, то угол φ_экст1 – величина положительная.

Из справедливости уравнения (12) следует, что при φ = φ_экст коэффициент A в (4) равен нулю, нормировочная величина в (11) ${{\Psi }_{{{\text{0макс}}}}}({{\varphi }_{{{\text{экст}}}}})$ равна единице, а зависимость $\Psi _{{20}}^{{\text{н}}}(x,{{\varphi }_{{{\text{экст}}}}})$, определяемая выражением (8), представляет собой обычную косинусоиду

где следует использовать значения α и k при φ = = φ_экст.

Для нахождения угла φ_экст, при котором зависимость $\Psi _{{20}}^{{\text{н}}}(x)$ имеет точку экстремума⁴⁴ на поверхности x = s, положим в (9) x_экст = s. В итоге получим

Находя величину tg(αks) из соотношения (5) и подставляя ее в (15), получим уравнение

Раскрывая скобки, учитывая (3) и приводя подобные, можно разложить уравнение (16) на множители, одним из которых является множитель $1 - \nu \sin {{\varphi }_{{{\text{экст}}}}}.$ То есть для вычисления угла φ_экст получаем простое уравнение

В интервале значений – π < φ_экст ≤ π уравнение (17) имеет два решения, φ_экст3 = φ_экст1 – π и φ_экст4 = = – φ_экст1, где величина φ_экст1 определяется выражением (13).

Таким образом, зависимость $\Psi _{0}^{{\text{н}}}(x)$ имеет точку экстремума непосредственно на одной из поверхностей ферритовой пластины при четырех углах ${{\varphi }_{{{\text{экст1}}}}} = - \arcsin ({1 \mathord{\left/ {\vphantom {1 \nu }} \right. \kern-0em} \nu }),$ φ_экст2 = π – φ_экст1, φ_экст3 = = φ_экст1 – π и φ_экст4 = – φ_экст1.

Следует отметить, что все формулы, приведенные в этом разделе, справедливы для всех мод ОСВ.

Зависимости углов φ_экст1… φ_экст4 от частоты волны f удобно изображать в полярной системе координат вместе с зависимостями углов отсечки ОСВ $\varphi _{{{\text{отс}}}}^{{{\text{ОСВ}}}}(f)$ и углов отсечки поверхностной спиновой волны (ПСВ) $\varphi _{{{\text{отс}}}}^{{{\text{ПСВ}}}}(f)$ (рис. 3, кривые 1–4, 5–8 и 9–12 соответственно). Напомним, что углами отсечки спиновой волны называют углы, при которых k → ∞, т.е. углы наклона асимптот изочастотной зависимости⁵⁵. Таким образом, каждый угол отсечки определяет предельную ориентацию волнового вектора при данной частоте.

Рис. 3.

Зависимости углов φ_экст1–φ_экст4 (кривые 1–4), углов отсечки волнового вектора ОСВ $\varphi _{{{\text{отс1}}}}^{{{\text{ОСВ}}}}$–$\varphi _{{{\text{отс4}}}}^{{{\text{ОСВ}}}}$ (кривые 5–8) и углов отсечки волнового вектора ПСВ $\varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}$–$\varphi _{{{\text{отс4}}}}^{{{\text{ПСВ}}}}$ (кривые 9–12) от частоты волны f. Отрезки 13–16 соответствуют значениям углов максимальной невзаимности ОСВ φ_R1–φ_R4, а окружности 17, 18 и 19 соответствуют значениям частот f_H = ω_H/2π = 1029 МГц, ${{f}_{ \bot }} = {{{{\omega }_{ \bot }}} \mathord{\left/ {\vphantom {{{{\omega }_{ \bot }}} {2\pi }}} \right. \kern-0em} {2\pi }}$ = 2539 МГц и f = (ω_H + ω_M/2)/2π = 3649 МГц. На диаграмме показаны области φ_ОСВ и φ_ПСВ, соответствующие множеству всех возможных ориентаций волнового вектора обратной и поверхностной волн в ферритовой пластине.

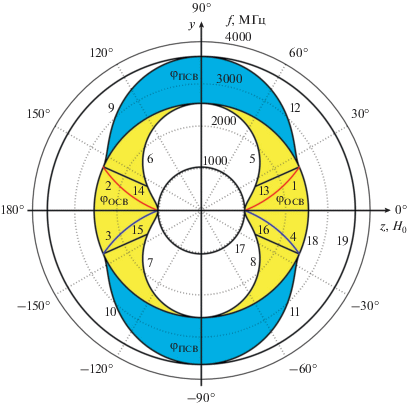
На рис. 3 также отмечены области φ_ОСВ и φ_ПСВ, соответствующие всем возможным ориентациям волнового вектора для ОСВ и ПСВ в ферритовой пластине (подробнее см. [21]). Анализируя рис. 2 и 3, можно отметить следующие свойства и особенности представленных зависимостей.

Зависимости φ_экст1(f) – φ_экст4(f) (см. рис. 3 кривые 1–4) и зависимости углов отсечки ПСВ $\varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}(f)$ – $\varphi _{{{\text{отс4}}}}^{{{\text{ПСВ}}}}(f)$ (кривые 9–12) имеют с окружностью ${{f}_{ \bot }} = {{{{\omega }_{ \bot }}} \mathord{\left/ {\vphantom {{{{\omega }_{ \bot }}} {2\pi }}} \right. \kern-0em} {2\pi }}$ = ${{\sqrt {\omega _{\operatorname{H} }^{2} + {{\omega }_{{\rm H}}}{{\omega }_{\operatorname{M} }}} } \mathord{\left/ {\vphantom {{\sqrt {\omega _{\operatorname{H} }^{2} + {{\omega }_{{\rm H}}}{{\omega }_{\operatorname{M} }}} } {2\pi }}} \right. \kern-0em} {2\pi }}$ = 2539 МГц (см. рис. 3, 18) общие точки при значениях углов $\varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}),$ $\varphi _{{{\text{отс2}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}) = \pi - \varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}),$ $\varphi _{{{\text{отс3}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}) = $ $ = \varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}) - \pi $ и $\varphi _{{{\text{отс4}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}) = - \varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }}),$ где $\varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }})$ называют максимальным углом отсечки ПСВ при $f \to {{f}_{ \bot }}$и находят по формуле⁶⁶, полученной в [1]

Поскольку при заменах φ на π – φ и –φ на φ – π выражения (3), (6), (8) и (11) не меняются, то любой точке N(f, φ) из областей φ_ОСВ или φ_ПСВ и точке N_y(f, π – φ), симметричной точке N относительно оси y, соответствуют волны с одинаковыми зависимостями амплитуды магнитного потенциала, т.е.

В то же время точке N(f, φ) и точке N_z(f, – φ), симметричной точке N относительно оси z, соответствуют волны с разными, хотя и симметричными (как показано в разделе 1) зависимостями амплитуд $\Psi _{0}^{{\text{н}}}(x,f,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x,f, - \varphi ).$

Из симметрии зависимостей $\Psi _{0}^{{\text{н}}}(x,f,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x,f, - \varphi )$ и равенств (19) следует, что соотношения между четырьмя зависимостями $\Psi _{0}^{{\text{н}}}(x,\varphi ),$ $\Psi _{0}^{{\text{н}}}(x,\pi - \varphi ),$ $\Psi _{0}^{{\text{н}}}(x, - \varphi )$ и $\Psi _{0}^{{\text{н}}}(x,\varphi - \pi )$ фиксированы, и этот факт позволяет найти отношение между амплитудами двух волн с противоположно направленными волновыми векторами (см. разд. 3).

3. УГЛЫ МАКСИМАЛЬНОЙ НЕВЗАИМНОСТИ ОСВ φ_R

При возбуждении волн линейным преобразователем, может потребоваться осуществить эксперимент, в котором невзаимное свойство ОСВ проявляется в максимальной степени, т.е. когда на одной из поверхностей ферритовой пластины реализуется наибольшее отношение R амплитуд потенциалов $\Psi _{0}^{{\text{н}}}$ двух волн с противоположно направленными волновыми векторами. Для расчета таких геометрий возбуждения обозначим амплитуды потенциала $\Psi _{{20}}^{{\text{н}}}$ при некоторых произвольных ориентациях волнового вектора φ и φ – π точками G и H на поверхности пластины x = 0 и точками K и L на поверхности x = s (см. рис. 2 кривые 3 и 6). Так как зависимости $\Psi _{0}^{{\text{н}}}(x,f,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x,f,\varphi - \pi )$ центрально симметричны (для нечетных мод) либо зеркально симметричны (для четных мод), то искомое отношение R для поверхностей x = 0 и x = s можно записать соответственно в виде⁷⁷

Отношение амплитуд $\Psi _{{20}}^{{\text{н}}}$ при ориентации вектора $\overrightarrow k $под углом φ на поверхностях пластины x = 0 и x = s в соответствии с выражением (8) имеет вид

Для противоположной ориентации волнового вектора φ – π отношение амплитуд потенциала $\Psi _{{20}}^{{\text{н}}}$ на поверхностях пластины x = s и x = 0 будет равно

Так как зависимости $\Psi _{0}^{{\text{н}}}(x,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x,\varphi - \pi )$ симметричны, то левые части выражений (22) и (23) равны, а их разность равна нулю⁸⁸, т.е.

Поделив выражения (20) и (21), с учетом соотношений (22)–(24), получим

Найдя величину ctg(αks) из уравнения (5) и подставив ее в (25), имеем

Вычислим угол φ_R, при котором ∂R/∂φ = 0. Дифференцируя выражение (26) по φ, приравнивая нулю числитель полученного выражения и приводя подобные, получим уравнение

из которого, используя выражения для μ и ν, можно вывести соотношения

Решениями уравнения (28) являются четыре угла φ_R1, φ_R2 = π – φ_R1, φ_R3 = φ_R1 – π и φ_R4 = – φ_R1, где величина φ_R1 определяется выражениями

Очевидно, что в силу справедливости соотношения (см. § 2.5.2.1.7 в [25])

углы, определяемые выражениями (29) и (18), тождественны:

причем при выбранных параметрах φ_R1 = 23.9°.

Таким образом, показано, что на обеих поверхностях ферритовой пластины x = s и x = 0 отношение нормированных амплитуд потенциалов двух волн, характеризующихся противоположно направленными волновыми векторами, имеет точки экстремума при максимальных углах отсечки ПСВ $\varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }})$ … $\varphi _{{{\text{отс4}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }})$, которые применительно к ОСВ можно кратко называть углами максимальной невзаимности φ_R1 … φ_R4.

Отметим, что ранее [18] отмечалось следующее: “Вблизи критического угла⁹⁹ α_c значение пространственной фазы объемных МСВ на верхней поверхности близко к значению π/2, при котором магнитостатический потенциал Ψ достигает своего максимума. Это соответствует наибольшей невзаимности (т.е. наибольшей асимметрии распределения функции Ψ по толщине пленки)”. Эти утверждения не совсем корректны: на поверхности пленки магнитостатический потенциал $\Psi _{0}^{{\text{н}}}$ достигает своего максимума для первой моды ОСВ в интервале углов 0 ≤ φ ≤ φ_экст1 (см. рис. 2а), а для второй моды – при угле φ = φ_экст1 (см. рис. 2в), но не при φ = φ_R1 (как утверждают авторы [18]); наибольшая асимметрия распределения функции $\Psi _{0}^{{\text{н}}}$ имеет место не “вблизи”, а точно при φ = φ_R1. В аннотации же работы [18] написано, что “направление волнового вектора …, которое совпадает с углом отсечки для поверхностных МСВ, … соответствует наибольшей асимметрии распределения магнитостатического потенциала по толщине пленки”. Поскольку в работе [18] это утверждение не доказано, то следует считать его предположением, которое, тем не менее, оказалось справедливым и доказано в данной работе.

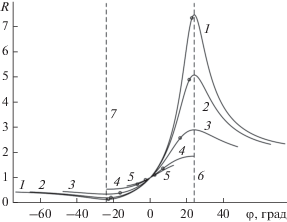
Вернемся к обсуждению полученных результатов. Как видно из рис. 3, отрезки 13–16, соответствующие углам φ_R1…φ_R4, пересекают кривые 5–8, описывающие углы отсечки ОСВ $\varphi _{{{\text{отс1}}}}^{{{\text{ОСВ}}}}$…$\varphi _{{{\text{отс4}}}}^{{{\text{ОСВ}}}}$, на некоторой граничной частоте f_R. Очевидно, возникают следующие вопросы: чему равна величина f_R и имеет ли зависимость R(φ) точки экстремума на частотах, меньших значения f_R. Ответить можно, анализируя зависимости R(φ), рассчитанные по формулам (20) и (26) при различных значениях частоты f (рис. 4): для частот f > f_R зависимости R(φ) (кривые 1 – 3) имеют максимум при φ = φ_R1 = 23.9° и минимум при φ = φ_R4 = –23.9°. Однако с уменьшением f интервал углов, в котором существуют ОСВ, тоже уменьшается и при f = f_R зависимость R(φ) имеет экстремумы при значениях φ, равных одновременно углам φ_R1, φ_R4 и углам отсечки ОСВ $\varphi _{{{\text{отс1}}}}^{{{\text{ОСВ}}}}$, $\varphi _{{{\text{отс4}}}}^{{{\text{ОСВ}}}}$ (см. рис. 4 кривая 4), описываемым выражениями [21]

Рис. 4.

Отношение нормированных амплитуд потенциала R двух ОСВ, характеризующихся противоположно направленными волновыми векторами, на поверхности x = 0 в зависимости от ориентации φ волнового вектора для следующих значений частоты: f = = 2450 (1), 2350 (2), 2000 (3), f_R = 1393.6 (4), 1150 МГц (5). Углы максимальной невзаимности: φ_R1 = 23.9° (6) и φ_R4 = –23.9° (7). Значения, соответствующие углам φ_экст1 и φ_экст4 для соответствующих частот, отмечены на кривых кружочками.

Таким образом, из условия ${{\varphi }_{R}}_{1} = \varphi _{{{\text{отс1}}}}^{{{\text{ОСВ}}}}$ легко вычислить значение граничной частоты f_R. Приравнивая выражения (29) и (32) найдем

При используемых параметрах пластины и поля получим f_R = 1393.6 МГц.

Для частот f < f_R зависимость R(φ) не имеет точек экстремума (кривая 5 на рис. 4) и величина R принимает наибольшее и наименьшее значения при углах близких к углам отсечки ОСВ φ → $\varphi _{{{\text{отс}}}}^{{{\text{ОСВ}}}}.$

Таким образом, как видно из рис. 4, отношение R нормированных амплитуд потенциалов двух волн с противоположными ориентациями волновых векторов φ_R1 и φ_R1 – π максимально, а при ориентациях φ_R4 и φ_R4 – π – минимально. Для сравнения на зависимостях R(φ) отмечены значения R(φ_экст1) и R(φ_экст4), при которых величина $\Psi _{0}^{{\text{н}}}$ на одной из поверхностей ферритовой пластины максимальна (см. рис. 4, кружочки). Как видно, для частот, лежащих вблизи начальной частоты спектра ОСВ ${{f}_{ \bot }} = {{{{\omega }_{ \bot }}} \mathord{\left/ {\vphantom {{{{\omega }_{ \bot }}} {2\pi }}} \right. \kern-0em} {2\pi }},$ значения углов φ_экст1, φ_экст4 и φ_R1, φ_R4 близки (что видно из сравнения кривых 1–4 и 13–16).

4. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ И ВОЗМОЖНОСТИ ИХ ПРАКТИЧЕСКОГО ИСПОЛЬЗОВАНИЯ

Полученные выше результаты могут быть использованы на практике для возбуждения в ферритовой пластине ОСВ с определенными свойствами. Поэтому рассмотрим кратко особенности возбуждения спиновых волн линейным преобразователем. Пусть на поверхности пластины x = 0 расположен линейный преобразователь, у которого одна (любая) из нормалей параллельна¹⁰¹⁰ волновому вектору $\overrightarrow k $ и наклонена к вектору $\overrightarrow {{{H}_{0}}} $ под углом φ. Как известно, лишь часть СВЧ-энергии, подводимая к преобразователю, расходуется на возбуждение “полезной” волны с ориентацией вектора $\overrightarrow k $ под углом φ, другая же часть энергии тратится на возбуждение “побочной” волны с противоположной ориентацией вектора $\overrightarrow k $ под углом φ – π.

На практике важно уметь определять направления распространения полезной и побочной волн. Из рис. 2 видно, что волнам, у которых абсолютное значение амплитуды потенциала на поверхности x = 0 больше, чем на поверхности x = s (т.е. $\left| {\Psi _{0}^{{\text{н}}}(x~\, = \,~0,~f,~\varphi )} \right|$ > $\left| {\Psi _{0}^{{\text{н}}}(x\,~ = \,~s,~f,~\varphi )} \right|$), соответствуют точки области φ_ОСВ, лежащие выше оси z на рис. 3. Очевидно, что если на поверхности x = 0 расположить линейный преобразователь, то возбуждаемой им полезной волне на рис. 3 будут соответствовать именно эти точки области φ_ОСВ, а побочной волне – точки, лежащие ниже оси z. При этом ориентации φ, описывающие полезную волну, лежат в интервалах значений 0 < φ < $\varphi _{{{\text{отс1}}}}^{{{\text{ОСВ}}}}$ и $\varphi _{{{\text{отс2}}}}^{{{\text{ОСВ}}}}$ < φ < π, а ориентации φ, описывающие побочную волну – в интервалах значений –π < φ < < $\varphi _{{{\text{отс3}}}}^{{{\text{ОСВ}}}}$ и $\varphi _{{{\text{отс4}}}}^{{{\text{ОСВ}}}}$ < φ < 0. Точно также волнам, у которых амплитуда на поверхности x = s больше, чем на поверхности x = 0 (т.е. $\left| {\Psi _{0}^{{\text{н}}}(x\,~ = \,~s,~f,~\varphi )} \right|$ > > $\left| {\Psi _{0}^{{\text{н}}}(x\,~ = ~\,0,~f,~\varphi )} \right|$), соответствуют точки области φ_ОСВ, лежащие ниже оси z на рис. 3. Очевидно, что если возбуждать ОСВ со стороны поверхности x = s, то все будет наоборот: полезной волне будут соответствовать точки области φ_ОСВ, лежащие ниже оси z, а побочной – точки, лежащие выше оси z на рис. 3 (и соответствующие интервалы значений φ, лежащие ниже или выше оси z).

Отмеченные выше свойства ОСВ наглядно отображает также рис. 1б, где волновые векторы $\overrightarrow k $ и соответствующие им векторы групповой скорости $\overrightarrow V $, изображенные жирными стрелками, описывают полезные волны, возбуждаемые преобразователями Пр1 и Пр2. Напомним, что для приема волн в анизотропных средах именно в направлении вектора $\overrightarrow V $следует располагать приемный преобразователь, но ориентировать его необходимо так же, как возбуждающий преобразователь.

Следует также отметить, что в соответствии с работой [16], отношение амплитуд полезной и побочной волн R_эксп в эксперименте примерно равно¹¹¹¹ отношению амплитуд магнитного потенциала этих волн R на поверхности ферритовой пластины, где расположен преобразователь.

Таким образом, из сказанного следует, что, например, для первой моды ОСВ с частотой f = = 2000 МГц при ориентации преобразователя под углом φ = φ_R1 = 23.9° кроме полезной волны (соответствующей ориентации волнового вектора φ_R1) возбудится еще и побочная волна с ориентацией волнового вектора φ – π = φ_R3 = –156.1°, причем отношение амплитуд полезной и побочной волн должно быть примерно равно отношению нормированных амплитуд их потенциалов R(φ_R1 = 23.9^о) = ${{\Psi _{0}^{{\text{н}}}(G)} \mathord{\left/ {\vphantom {{\Psi _{0}^{{\text{н}}}(G)} {\Psi _{0}^{{\text{н}}}(H)}}} \right. \kern-0em} {\Psi _{0}^{{\text{н}}}(H)}}$ = 0.865/0.298 = 2.9 (см. рис. 2 и кривую 3 на рис. 4). Для частоты ОСВ f = 2450 МГц и той же ориентации преобразователя получим R (φ_R1 = 23.9°) = 7.5 (см. рис. 4 кривая 1). То есть можно осуществлять возбуждение ОСВ с различным отношением амплитуд полезной и побочной волн или же с разной степенью невзаимности.

Кроме того, на практике может возникнуть необходимость передать энергию ОСВ с возбуждающего преобразователя на приемный при минимальных потерях. Пусть, для определенности, ОСВ возбуждается со стороны поверхности x = 0. В этом случае для первой моды ОСВ при изменении угла φ от 0 до угла отсечки $\varphi _{{{\text{отс1}}}}^{{{\text{ОСВ}}}}$ амплитуда побочной волны $\Psi _{0}^{{\text{н}}}(x = 0,\varphi - \pi )$ уменьшается (см. рис. 2б кривые 1, 5–7), тогда как аналогичная амплитуда полезной волны $\Psi _{0}^{{\text{н}}}(x = 0,\varphi )$ максимальна в интервале углов 0 ≤ φ ≤ φ_экст1 (см. рис. 2а кривые 1–4). То есть если сориентировать преобразователь под углом φ = φ_экст1, то амплитуда возбуждающейся полезной волны на поверхности x = 0 будет максимальна, а амплитуда побочной волны – достаточно мала. Например, для первой моды ОСВ при частоте f = 2450 МГц получим R(φ_экст1) = 7.3 (см. рис. 4 кружочек на кривой 1), вдобавок к этому получим минимальные потери при передаче энергии полезной волны.

Таким образом, в ферритовой пластине, как и в случае с ПСВ (см., например, [6, рис. 6.14 ]), можно реализовать невзаимное возбуждение ОСВ с противоположно направленными волновыми векторами, причем степень невзаимности, определяемая величиной R, существенно зависит от ориентации преобразователя φ.

ЗАКЛЮЧЕНИЕ

Исследованы невзаимные свойства мод обратной спиновой волны, распространяющейся в касательно намагниченной ферритовой пластине. В частности, предложена нормировка амплитуд магнитного потенциала, при которой зависимости $\Psi _{0}^{{\text{н}}}(x,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x, - \varphi )$, рассчитанные при ориентациях волнового вектора под углами φ и – φ, симметричны для всех мод волны. Рассмотрено, как на поверхности ферритовой пластины изменяются амплитуды потенциала $\Psi _{0}^{{\text{н}}}(x,\varphi )$ и $\Psi _{0}^{{\text{н}}}(x,\varphi - \pi )$ двух волн с противоположно направленными волновыми векторами, ориентированными под углами φ и φ – π. Установлено, что отношение R амплитуд потенциалов этих двух волн существенно зависит от величины φ, причем экстремальные значения величины R для всех мод волны имеют место при значениях φ_R1 … φ_R4, равных максимальным углам отсечки поверхностной спиновой волны $\varphi _{{{\text{отс1}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }})$ … $\varphi _{{{\text{отс4}}}}^{{{\text{ПСВ}}}}({{f}_{ \bot }})$. Найдено, что если на одной поверхности пластины отношение R максимально, то на другой поверхности пластины это отношение минимально и равно 1/R. Обнаружено, что существует значение частоты f_R, которое делит диапазон существования обратных спиновых волн на два частотных интервала: в интервале f_H < f < f_R зависимость R(φ) является монотонной (т.е. величина R принимает максимальное и минимальное значения при углах, близких к углам отсечки волнового вектора), а в интервале f_R < < f < ${{f}_{ \bot }}$ зависимость R(φ) имеет точки экстремума (максимум и минимум). Получено аналитическое выражение для ориентации φ_экст1 волнового вектора, при которой на распределении амплитуды магнитного потенциала m-й моды волны $\Psi _{0}^{{\text{н}}}(x)$ в сечении ферритовой пластины возникает m-я точка экстремума, лежащая на одной из поверхностей пластины. Найдено, что для первой моды волны амплитуда потенциала максимальна на поверхности пластины при ориентациях волнового вектора, лежащих в интервале значений 0 ≤ φ ≤ φ_экст1. Сформулированы рекомендации по практическому использованию полученных результатов при возбуждении обратных спиновых волн с невзаимными свойствами.