Радиотехника и электроника, 2020, T. 65, № 4, стр. 380-387

ВВЕДЕНИЕ

В настоящее время в связи с все более интенсивным развитием систем подвижной радиосвязи и, соответственно, ужесточением требований, предъявляемых к ним, происходит перенасыщение объектов связи (например, башен, мачт, опор и т.п.) радиосредствами различных диапазонов частот, типов и назначения. Следствием этого является ухудшение и без того сложной электромагнитной обстановки, напрямую влияющей на обеспечение работоспособности систем радиосвязи. Поэтому вопросы обеспечения электромагнитной совмести (ЭМС) радиоэлектронных средств (РЭС) на данный момент особенно актуальны и нуждаются в дальнейшей проработке.

Вследствие того, что обычно РЭС, а точнее, их составные части – антенны, располагаются на компактных площадках, традиционные подходы к обеспечению ЭМС (пространственное разнесение антенн в случае направленных антенн, их разворот относительно друг друга и т.д.) не всегда применимы. В связи с этим в настоящее время существует потребность в разработке новых мер к обеспечению ЭМС РЭС, компактно располагаемых на объектах. Перспективный подход к совершенствованию ЭМС связан с использованием искусственных композитных структур с проводящими включениями зеркально-асимметричной формы – киральных метаматериалов [1, 2] в качестве подстилающих поверхностей, а также средств дополнительного экранирования.

Как показывает анализ отечественной и зарубежной литературы, а также результаты исследований [3], использование в составе антенных систем дополнительных экранов и подстилающих поверхностей на основе киральных метаматериалов позволяет существенно уменьшить взаимное влияние между излучателями и тем самым повысить развязку между ними.

В виду того, что киральные метаматериалы представляют собой сложную электродинамическую структуру, возникает ряд сложностей, связанных с их электродинамическим анализом. На сегодняшний день наиболее распространенным подходом к анализу подобных структур является использование зарубежных программных комплексов EMCoS, CST Microwave Studio, HFSS, Feko и т.п. В основу данных комплексов положены численные методы, предполагающие разбиение исследуемой структуры на элементарные ячейки. При этом очень важным является выбор шага дискретизации структуры. В случае если этот шаг будет относительно большим, то разбиение будет достаточно грубым и исходные свойства структуры могут существенным образом исказиться. Особенно это касается резонансных структур, в том числе и киральных метаматериалов, где небольшие отклонения в геометрии структуры могут привести к большим погрешностям результатов расчета. Безусловно, при уменьшении шага дискретизации точность результатов расчета будет повышаться, однако будут существенно расти и требования к вычислительным ресурсам. Кроме того, ввиду “закрытости” используемых в данных комплексах алгоритмов, вопрос доверия к полученным результатам по-прежнему остается открытым.

Перспективными методами анализа подобных антенных систем, содержащих структуры из киральных метаматериалов, являются проекционные методы [4]. В данной работе был использован метод сингулярных интегральных представлений электрического поля, приводящий к неоднородному сингулярному интегральному уравнению или системе таких уравнений. В отличие от самосогласованного подхода к решению краевых задач электродинамики [5–7] данный подход предполагает наличие заданных сторонних источников электромагнитного поля, но не накладывает ограничения на их вид (т.е. может использоваться источник ЭДС, электромагнитная волна и т.п.). В работах [8, 9] была разработана математическая модель микрополосковой структуры с одиночным излучателем, расположенным на подложке из кирального метаматериала. Поверхность подложки считалась однородной. Метод интегральных уравнений в задачах отражения электромагнитных волн от неоднородных границ раздела сред подробно описан в [10–12]. Было получено сингулярное интегральное уравнение с особенностью Коши относительно неизвестной функции распределения поверхностной плотности тока по излучателю. Как показали результаты исследований, подобный подход обладает рядом достоинств, основными из которых являются высокая точность и сходимость получаемых результатов расчета, а также относительно невысокие требования к вычислительным ресурсам. Следует также отметить, что численное решение сингулярных интегральных уравнений является корректной математической задачей по Адамару.

Цель данной работы – проанализировать двухэлементную микрополосковую структуру (МПС) с подложкой из кирального метаматериала.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВУХЭЛЕМЕНТНОЙ МИКРОПОЛОСКОВОЙ СТРУКТУРЫ С КИРАЛЬНОЙ ПОДЛОЖКОЙ

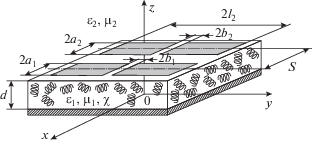
Рассмотрим МПС, представляющую собой подложку из кирального метаматериала конечной толщины $d$, металлизированную с нижней стороны, на которой параллельно друг к другу на расстоянии $S$ расположены два плоских прямоугольных излучателя (рис. 1). Длина излучателей $2{{l}_{1}}$ и $2{{l}_{2}},$ а ширина $2{{a}_{1}}$ и $2{{a}_{2}}$ соответственно. Относительные диэлектрические и магнитные проницаемости киральной подложки равны ${{\varepsilon }_{1}}$ и ${{\mu }_{1}}$. Кроме того, при описании кирального метаматериала вне зависимости от типа проводящих включений зеркально-асимметричной формы также используется некий коэффициент, а именно параметр киральности $\chi $ [1, 2], связывающий векторы напряженностей поля с векторами индукции в материальных уравнениях [1, 2, 13, 14]:

где ${{\varepsilon }_{0}}$, ${{\mu }_{0}}$ – электрическая и магнитная постоянные.

В выражениях (1), верхние знаки соответствуют киральной среде на основе правосторонних элементов (например, правовинтовых спиралей), а нижние – на основе левосторонних.

Над киральной подложкой и, соответственно, над излучателями расположено диэлектрическое полупространство с параметрами ${{\varepsilon }_{2}}$, ${{\mu }_{2}}$.

Будем считать, что напряженность сторонних электрических полей, возбуждающих излучатели, имеет лишь одну продольную составляющую $\vec {E}_{1}^{{{\text{ст}}}} = \left( {0,E_{{1y}}^{{{\text{ст}}}},0} \right)$ и $\vec {E}_{2}^{{{\text{ст}}}} = \left( {0,E_{{2y}}^{{{\text{ст}}}},0} \right).$ Ширина излучателей много меньше как их длины, так и длины волны $\lambda $ $\left( {2{{a}_{1}},2{{a}_{2}} \ll 2{{l}_{1}},2{{l}_{2}},\lambda } \right),$ поэтому значение продольной компоненты плотности поверхностного тока ${{\eta }_{y}}$ будет гораздо больше значения поперечной компоненты ${{\eta }_{x}}$. Исходя из данных соображений поперечной компонентной плотности поверхностного тока ${{\eta }_{x}}$ можно пренебречь. Предполагается также, что излучатели являются идеально проводящими и бесконечно тонкими. Считается, что источники электродвижущей силы (ЭДС), приложенные к зазорам излучателей, являются гармоническими и формируемые ими токи являются непрерывными как в областях зазоров, так и на плечах. Ширина зазоров излучателей при этом равна $2{{b}_{1}}$ и $2{{b}_{2}}$ соответственно. На поверхности излучателей должны выполняться следующие граничные условия для тангенциальных составляющих напряженности электрического поля (${{E}_{{1\tau }}},$ ${{E}_{{2\tau }}}$) и продольных составляющих плотности поверхностного тока (${{\eta }_{{1y}}},$ ${{\eta }_{{2y}}}$):

где ${{l}_{{01}}}$ и ${{l}_{{02}}}$ – координаты центров зазоров излучателей 1 и 2 соответственно (точки питания).

Как и в случае одноэлементной МПС [8, 9], на поверхностях излучателей фурье-образы ${{\vec {T}}_{\tau }} = \left\{ {{{T}_{x}},{{T}_{y}}} \right\}$ тангенциальных составляющих напряженностей электрических полей ${{\vec {E}}_{\tau }}$ связаны с фурье-образами $\vec {F} = \left\{ {{{F}_{x}},{{F}_{y}}} \right\}$ поверхностных плотностей токов $\vec {\eta }$ через матрицу поверхностных импедансов $\left[ Z \right]$ границы раздела диэлектрик–киральная среда с односторонней металлизацией:

где ${{Z}_{{ij}}}$ $\left( {i,j = 1,2} \right)$ – элементы матрицы поверхностных импедансов $\left[ Z \right]$, которые являются функциями переменных $\beta $, h фурье-пространства: ${{Z}_{{ij}}} = {{Z}_{{ij}}}\left( {\beta ,h} \right).$

Поскольку матрица поверхностных импедансов связывает именно фурье-образы, то возникает необходимость разложения напряженностей электрического и магнитного полей, а также поверхностных плотностей токов в интегралы Фурье.

Следует отметить, что на поверхности подложки предполагается выполнение следующих граничных условий:

где $E_{x}^{{\left( 1 \right)}}$ и $E_{x}^{{\left( 2 \right)}},$ $E_{y}^{{\left( 1 \right)}}$ и $E_{y}^{{\left( 2 \right)}}$ – x- и y-составляющие вектора напряженности электрического поля на границе раздела в киральном слое 1 и в диэлектрическом полупространстве 2 соответственно, $H_{x}^{{\left( 1 \right)}}$ и $H_{x}^{{\left( 2 \right)}},$ $H_{y}^{{\left( 1 \right)}}$ и $H_{y}^{{\left( 2 \right)}}$ – x- и y-составляющие вектора напряженности магнитного поля на границе раздела в киральном слое 1 и в диэлектрическом полупространстве 2 соответственно, ${{\eta }_{x}}$, ${{\eta }_{y}}$ – x- и y-составляющие вектора плотности тока на поверхностях излучателей.

Аналогичные граничные условия справедливы и для соответствующих фурье-образов напряженностей электрического и магнитного полей и поверхностных плотностей токов.

Метод определения матрицы поверхностных импедансов границы раздела диэлектрик–киральная среда с односторонней металлизацией, подробно описан в [15, 16], там же приведены аналитические выражения для определения ее элементов.

Определим ${{T}_{y}}$ из (3) и выполним обратное преобразование Фурье, предварительно найдя ${{Z}_{{11}}}$ [15] и не забывая при этом, что согласно выбранной физической модели ${{\eta }_{{1x}}} = {{\eta }_{{2x}}} = 0.$ В результате получаем следующее выражение для $E_{y}^{{}}$ на поверхности подложки $z = d$:

где

Поскольку ширина излучателей много меньше длины волны, то поперечные вариации продольных составляющих поверхностных плотностей токов можно считать квазистатическими [17, 18]. В связи с этим функции распределения плотностей токов ${{\eta }_{{1y}}}\left( {x{\kern 1pt} ',y{\kern 1pt} '} \right)$ и $\eta _{{2y}}^{{}}\left( {x,y} \right)$ можно представить в виде

где ${{f}_{1}}\left( y \right)$ и ${{f}_{2}}\left( y \right)$ – функции, описывающие продольные распределения поверхностных плотностей токов на излучателях.

Несобственный интеграл в выражении (5) является расходящимся, поскольку асимптотическое представление элемента матрицы поверхностных импедансов ${{Z}_{{11}}}\left( {\beta ,h} \right)$ при $\left| h \right| \to \infty $ имеет вид

Используя аналитические условия излучения для слоистых сред [19], выделим аналитически особенность в представлении (5). Для этого прибавим и вычтем в подынтегральном выражении в (5) слагаемые с асимптотическим сомножителем $Z_{{11}}^{\infty }\left( h \right).$ Затем, подставив (6) в (4), учитывая граничные условия для плотности поверхностного тока на концах излучателей (2а), производя интегрирование по $y{\kern 1pt} '$ по частям и выполняя ряд математических преобразований, получим сингулярное интегральное представление (СИП) y‑составляющей напряженности электрического поля на поверхности подложки ($z = d$):

где

После подстановки СИП (7) в граничные условия (2б) получим систему сингулярных интегральных уравнений (СИУ) относительно неизвестных функций $f_{1}^{'}\left( {y{\kern 1pt} '} \right)$ и $f_{2}^{'}\left( {y{\kern 1pt} '} \right)$:

Здесь учтено, что СИП (7) справедливо на всей поверхности подложки, включая оси симметрии излучателей 1 ($x = 0$) и 2 ($x = S$).

Для решения полученной системы СИУ (8) предлагается использовать метод моментов. В качестве базисных функций были использованы полиномы Чебышева 1-го рода:

Кроме того, в целях упрощения процедуры интегрирования, в ядрах данной системы СИУ экспоненты были разложены в ряды по функциям Бесселя и полиномам Чебышева 1-го и 2-го рода [19]:

где ${{\delta }_{{0,p}}}$ – символ Кронекера,

Также было использовано известное соотношение для полиномов Чебышева [20]

Результаты исследований показали, что при определенном количестве членов аппроксимирующего ряда данный метод позволяет достичь необходимой точности вычисления.

Функции продольных распределений поверхностных плотностей токов на излучателях определяются в соответствии со следующим выражением:

В свою очередь, функция распределения тока определяется как:

2. АПРОБАЦИЯ РАЗРАБОТАННОЙ МОДЕЛИ ДВУХЭЛЕМЕНТНОЙ МИКРОПОЛОСКОВОЙ СТРУКТУРЫ С КИРАЛЬНОЙ ПОДЛОЖКОЙ

При разработке новых моделей любых электродинамических структур непременно возникает ряд вопросов, связанных с достоверностью и точностью получаемых с ее помощью результатов расчета. В целях апробации разработанной модели двухэлементной МПС с киральной подложкой было проведено сравнение токовых функций, вычисленных на основе данной математической модели, а также с помощью программного комплекса Feko 7.0, на примере решения тестовой задачи. В обоих случаях модель представляла собой диэлектрическую подложку (параметр киральности равен нулю) толщиной $d = 0.1\lambda ,$ металлизированную с нижней стороны, на которой параллельно расположены два прямоугольных плоских излучателя длиной $2{{l}_{1}} = 2{{l}_{2}} = 0.5\lambda $ и шириной $2{{a}_{1}} = 2{{a}_{2}} = 0.05\lambda {\kern 1pt} .$ При этом излучатели расположены на расстоянии, равном $S = \lambda .$ Диэлектрическая и магнитная проницаемости подложки и диэлектрического полупространства равны ε₁ = μ₁ = $ = {{\varepsilon }_{2}} = {{\mu }_{2}} = 1.$

На рис. 2 представлены функции распределения тока по излучателю 1 и излучателю 2, полученные для разных вариантов возбуждения. В частности, на рис. 2а приведены токовые функции для случая синфазного возбуждения излучателей, а на рис. 2б – для случая квадратурного возбуждения (фаза напряжения, приложенного к зазору излучателя 2, сдвинута относительно фазы напряжения, приложенного к зазору излучателя 1, на ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$).

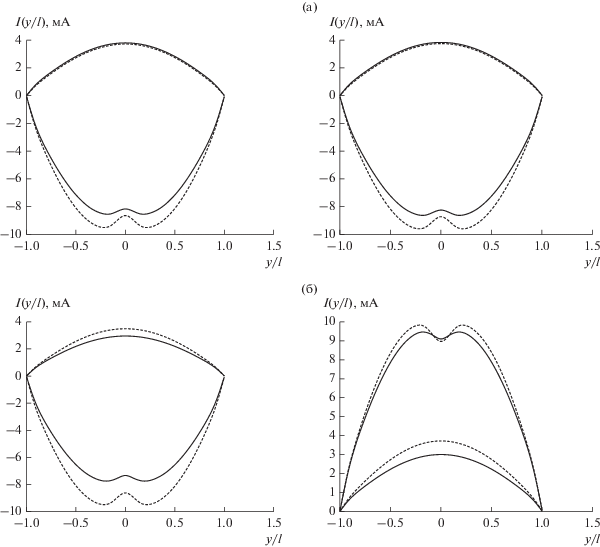
Из данных графиков видно, что вычисленные с помощью различных методов функции распределения тока практически совпадают, что в свою очередь свидетельствует об адекватности разработанной модели.

3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

На основе разработанной математической модели двухэлементной микрополосковой излучающей структуры с киральной подложкой были рассчитаны функции распределения тока по излучателям для синфазного (рис. 3а) и квадратурного (рис. 3б) способов возбуждения, а также для различных типов киральных подложек, а именно подложек на основе левосторонних элементов и правосторонних элементов, при следующих общих параметрах: ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 1{\kern 1pt} ,$ ${{\mu }_{1}} = {{\mu }_{2}} = 1{\kern 1pt} ,$ 2a₁ = 2a₂ = $ = 0.05\lambda {\kern 1pt} ,$ $2b = 0.02\lambda {\kern 1pt} ,$ $d = 0.1\lambda {\kern 1pt} ,$ $2{{l}_{1}} = 2{{l}_{2}} = 0.5\lambda {\kern 1pt} ,$ $S = 0.25\lambda {\kern 1pt} ,$ $\chi = 0.2.$

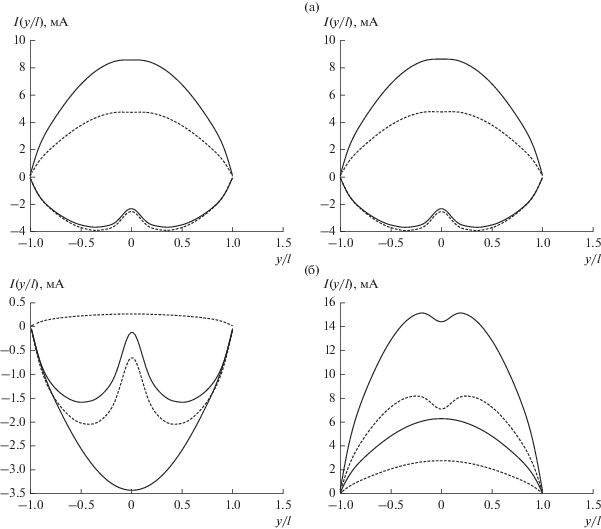
Как видно из графиков, приведенных на рис. 3, распределение тока по излучателям сильно зависит от типа киральной подложки.

При проведении расчетов значение амплитуды напряжения в зазоре излучателя было принято равным 1 В ($V = 2b{{E}_{0}} = 1\,\,{\text{В,}}$ где ${{E}_{0}}$ – амплитуда напряженности стороннего электрического поля, приложенного к зазору излучателя).

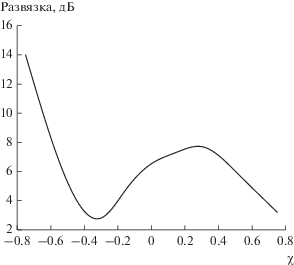
Для определения возможности уменьшения взаимного влияния между излучателями (в контексте обеспечения ЭМС – повышения развязки) было проведено исследование двухэлементной МПС с киральной подложкой с целью определения зависимости развязки от параметров структуры, в частности, от параметра киральности. На рис. 4 приведена зависимость развязки между излучателем 1 и излучателем 2 МПС от параметра киральности при следующих параметрах: ${{\varepsilon }_{1}} = {{\varepsilon }_{2}} = 1{\kern 1pt} ,$ ${{\mu }_{1}} = {{\mu }_{2}} = 1{\kern 1pt} ,$ $2{{a}_{1}} = 2{{a}_{2}} = 0.05\lambda {\kern 1pt} ,$ $2b = 0.02\lambda {\kern 1pt} ,$ $d = 0.1\lambda {\kern 1pt} ,$ $2{{l}_{1}} = 2{{l}_{2}} = 0.5\lambda {\kern 1pt} ,$ $S = 0.5\lambda {\kern 1pt} .$ Как уже было упомянуто, нулевое значение параметра киральности соответствует подложке, выполненной из диэлектрика. Положительные значения параметра киральности соответствуют киральной подложке на основе правосторонних элементов, отрицательные – на основе левосторонних. Из рис. 4 видно, что при некоторых параметрах использование подстилающих поверхностей из кирального метаматериала позволяет повысить уровень развязки между излучателями.

* * *

Таким образом, в работе предложена математическая модель двухэлементной микрополосковой излучающей структуры с подложками из кирального метаматериала различных типов, позволяющая определять функции распределения плотности тока на поверхностях излучателей, которые, в свою очередь, позволяют рассчитывать поле в любой точке пространства, включая ближнюю зону, а кроме того, определять другие характеристики структуры. Проведена апробация разработанной модели. На основании представленной зависимости уровней развязки между излучателями от параметра киральности, был сделан вывод о перспективности применения подстилающих поверхностей на основе киральных метаматериалов в антенных системах с целью совершенствования обеспечения электромагнитной совместимости радиоэлектронных средств.