Радиотехника и электроника, 2020, T. 65, № 4, стр. 372-379
Алгоритмы гибридного проекционного метода для анализа возбуждения неоднородного диэлектрического тела вращения радиальным магнитным диполем
Е. И. Семерня a, С. П. Скобелев a, b, *
a Московский физико-технический институт (государственный университет)
141700 Московской обл., Долгопрудный, Институтский пер., 9, Российская Федерация
b ПАО “Радиофизика”
125363 Москва, ул. Героев Панфиловцев, 10, Российская Федерация
* E-mail: s.p.skobelev@mail.ru
Поступила в редакцию 16.04.2019
После доработки 16.04.2019
Принята к публикации 23.04.2019
Аннотация
Рассмотрена задача возбуждения тела вращения, состоящего из однородной диэлектрической сферы и внешнего неоднородного диэлектрического слоя, магнитным диполем, расположенным на оси вращения. Разработаны алгоритмы решения, основанные на гибридном проекционном методе, включающем проектирование электромагнитных полей на поперечные сферические функции и применение одномерного метода конечных элементов для решения полученной системы обыкновенных дифференциальных уравнений. Алгоритмы также обобщены на случай идеально проводящей внутренней сферы. Приведены результаты сравнения, характеризующие эффективность метода, а также результаты расчета диаграммы направленности диполя в присутствии проводящей сферы, окруженной неоднородной диэлектрической оболочкой в форме вытянутого сфероида в одном случае и плазменной оболочкой такой же формы в другом.
ВВЕДЕНИЕ
Задача рассеяния электромагнитных волн на неоднородных диэлектрических телах вращения представляет большой интерес для моделирования линзовых антенн, биологических образований в медицине, осадков в метеорологии и радиолокационных целей, включая возвращаемые космические аппараты, метеоритные следы и струи от ракетных двигателей.
В общем случае эта задача в строгой постановке может быть решена только численными методами. К таким методам относятся проекционные методы [1–3], метод конечных элементов [4, 5], метод, основанный на слоистой модели неоднородного тела с однородными слоями, с последующим применением метода интегральных уравнений для эквивалентных токов на поверхностях слоев [6], и метод интегральных уравнений для токов поляризации [7, 8].
Цель данной работы – разработка алгоритма решения задачи на основе гибридного проекционного метода (ГПМ), примененного ранее к электродинамическому анализу неоднородных сфер и цилиндров [9, 10]. Такой подход представляет интерес, так как он обладает некоторыми потенциальными преимуществами, отмеченными в [9, 10], по сравнению с методами, перечисленными выше. Далее рассмотрен случай возбуждения тела вращения радиальным магнитным диполем, расположенным на оси вращения вблизи поверхности тела.
1. ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ
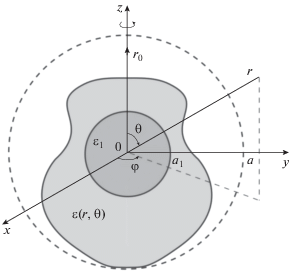
Продольное сечение диэлектрического тела вращения, расположенного в свободном пространстве в декартовых координатах x, y, z и сферических координатах r, θ, φ, показано на рис. 1. Тело состоит из однородной сферы радиусом a1 и относительной диэлектрической проницаемостью ε1 с центром, расположенным в начале координат. Указанная сфера окружена неоднородным внешним слоем с относительной диэлектрической проницаемостью ε(r,θ). Неоднородность слоя может проявляться также и отличием его внешней поверхности от сферической поверхности. Относительная магнитная проницаемость сферы и неоднородного слоя считается равной единице.
Здесь мы предполагаем, что рассматриваемое тело возбуждается радиальным магнитным диполем, расположенным на оси вращения z на расстоянии r0 от начала координат. Цель задачи – определить поле, излученное диполем в присутствии тела, включая диаграмму направленности (ДН) диполя, и определить поле внутри тела.
Так как поле диполя является осесимметричным, а диполь – магнитным, то ненулевыми составляющими векторного поля остаются только азимутальная составляющая напряженности электрического поля Eφ, радиальная составляющая напряженности магнитного поля Hr и меридиональная составляющая напряженности магнитного поля Hθ. Указанные составляющие должны удовлетворять уравнениям Максвелла:
(1)
$\frac{1}{r}\frac{{\partial (r{{H}_{\theta }})}}{{\partial r}} - \frac{1}{r}\frac{{\partial {{H}_{r}}}}{{\partial \theta }} = - i\omega {{\varepsilon }_{0}}\hat {\varepsilon }{\kern 1pt} {{E}_{\varphi }},$(2)
$\frac{1}{{r\sin {\kern 1pt} \theta }}\frac{{\partial (\sin {\kern 1pt} \theta {\kern 1pt} {{E}_{\varphi }})}}{{\partial \theta }} = i\omega {{\mu }_{0}}{{H}_{r}} - j_{r}^{m},$(3)
$ - \frac{1}{r}\frac{{\partial (r{{E}_{\varphi }})}}{{\partial r}} = i\omega {{\mu }_{0}}{{H}_{\theta }},$где ε0 и μ0 – электрическая и магнитная постоянные свободного пространства соответственно, $\hat {\varepsilon }$ – относительная диэлектрическая проницаемость соответствующей области,
(4)
$j_{r}^{m}(r,\theta ,\varphi ) = {{I}^{m}}l\frac{{\delta (r - {{r}_{0}})\delta (\theta - 0)\delta (\varphi - 0)}}{{{{r}^{2}}\sin {\kern 1pt} \theta }}$– плотность магнитного тока диполя с дипольным моментом, определяемым магнитным током ${{I}^{m}}$ и длиной l, и ω – круговая частота в гармонической зависимости полей от времени, взятой в виде exp(–iωt).
Определяя Hr и Hθ из (2) и (3) и подставляя их в (1), получим уравнение
(5)
$\begin{gathered} \frac{{{{\partial }^{2}}(r{{E}_{\varphi }})}}{{\partial {{r}^{2}}}} + \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial \theta }}\left[ {\frac{1}{{\sin {\kern 1pt} \theta }}\frac{{\partial (r{{E}_{\varphi }}\sin {\kern 1pt} \theta )}}{{\partial \theta }}} \right] + \\ + \,\,{{k}^{2}}\hat {\varepsilon }{\kern 1pt} r{{E}_{\varphi }} = - \frac{{\partial j_{r}^{m}}}{{\partial \theta }}, \\ \end{gathered} $где $k = \omega \sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} = 2\pi {\kern 1pt} /{\kern 1pt} \lambda $ – волновое число (λ – длина волны в свободном пространстве).
Введем в рассмотрение сферу радиусом a с центром, расположенным в начале координат, которая охватывает рассматриваемое тело и диполь, как показано на рис. 1, и рассмотрим уравнение (5) в областях $r \geqslant a$, ${{a}_{1}} \leqslant r \leqslant a$ и $0 \leqslant r \leqslant {{a}_{1}}$. В первой области $\hat {\varepsilon } = 1$, а правая часть в (5) равна нулю. Уравнение (5) в этом случае решается хорошо известным методом разделения переменных [11, с. 81–82], применяя который можно записать решение в виде суперпозиции сферических волн, расходящихся от рассеивателя:
(6)
${{E}_{\varphi }}(r,\theta ) = \frac{{{{E}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {{{R}_{q}}{{\zeta }_{q}}(kr){{T}_{q}}(\theta )} ,$где Rq – неизвестные коэффициенты, ζq(kr) – функции Риккати–Ханкеля первого рода,
– ортонормированные поперечные функции, определяемые присоединенными функциями Лежандра $P_{q}^{1}(\cos \theta )$ [11], и
– множитель, через который поле диполя в дальней зоне можно определить по формуле
(9)
${{E}_{{\varphi \infty }}}(r,\theta ) = {{E}_{0}}\frac{{\exp (ikr)}}{{kr}}\exp ( - ik{{r}_{0}}\cos \theta )\sin {\kern 1pt} \theta .$Решение уравнения (5) для поля в центральной области, не содержащей источников и где $\hat {\varepsilon } = {{\varepsilon }_{1}}$, может быть записано в виде разложения
(10)
${{E}_{\varphi }}(r,\theta ) = \frac{{{{E}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {{{B}_{q}}{{\psi }_{q}}({{k}_{1}}r){{T}_{q}}(\theta )} ,$где Bq – неизвестные коэффициенты, ψq(k1r) – функции Риккати–Бесселя и ${{k}_{1}} = k\sqrt {{{\varepsilon }_{1}}} $.
Решение уравнения (5) для поля в области ${{a}_{1}} \leqslant r \leqslant a$, где $\hat {\varepsilon } = \varepsilon (r,\theta )$ внутри слоя и $\hat {\varepsilon } = 1$ вне слоя, будем искать в виде разложения
(11)
${{E}_{\varphi }}(r,\theta ) = {{E}_{0}}\sum\limits_{q = 1}^\infty {{{E}_{q}}(r){{T}_{q}}(\theta )} $по поперечным функциям (7) с неизвестными переменными коэффициентами Eq(r).
Электрические поля (6), (10) и (11), а также соответствующие поперечные магнитные поля, определяемые из уравнения (3), должны быть непрерывными на сферических поверхностях при $r = {{a}_{1}}$ и $r = a$. Проектирование указанных граничных условий на поперечные функции (7) с весом sinθ дает следующие соотношения для коэффициентов разложения:
(13)
${{\left. {\frac{{d[r{{E}_{p}}(r)]}}{{dr}}} \right|}_{{r = {{a}_{1}}}}} = \sqrt {{{\varepsilon }_{1}}} {{B}_{p}}\psi _{p}^{'}({{k}_{1}}{{a}_{1}}),$где $p = 1,\,2,\,...$ .
Электрическое поле (11) должно удовлетворять уравнению (5). Подставляя (11) в (5) и проектируя (5) на поперечные функции (7), получим систему обыкновенных дифференциальных уравнений:
(16)
$\begin{gathered} \frac{{{{d}^{2}}{{U}_{p}}}}{{d{{r}^{2}}}} - \frac{{p(p + 1)}}{{{{r}^{2}}}}{{U}_{p}} + \\ + \,\,{{k}^{2}}\sum\limits_{q = 1}^\infty {{{W}_{{pq}}}{{U}_{q}}} = - ik{{A}_{p}}\delta (r - {{r}_{0}}), \\ \end{gathered} $где ${{U}_{q}}(r) = kr{{E}_{q}}(r)$,
(17)
${{W}_{{pq}}}(r) = \int\limits_0^\pi {\hat {\varepsilon }(r,\theta ){{T}_{p}}(\theta ){{T}_{q}}(\theta )\sin {\kern 1pt} \theta {\kern 1pt} d\theta } ,$и $p = 1,\,2,\,...$
Решение уравнений (16) осуществляется аналогично работам [9, 10] с использованием одномерного метода конечных элементов. Согласно последнему решение ищем в виде разложения
где ${{U}_{{nq}}}$ – постоянные коэффициенты разложения, подлежащие определению, N – число узлов с координатами ${{r}_{n}} = {{a}_{1}} + (n - 1)\Delta ,$ $\Delta = {{(a - {{a}_{1}})} \mathord{\left/ {\vphantom {{(a - {{a}_{1}})} {(N - 1)}}} \right. \kern-0em} {(N - 1)}},$ и fn(r) – треугольные функции [12] с вершинами в указанных узлах. Следующая операция состоит в проектировании (16) на треугольные функции ${{f}_{{n'}}}(r)$. Интегрирование первого слагаемого в (16) по частям и учет (13) и (15) сводит (16) к следующим алгебраическим уравнениям:
(20)
$\begin{gathered} - \sqrt {{{\varepsilon }_{1}}} \psi _{p}^{'}({{k}_{1}}{{a}_{1}}){{B}_{p}}{{\delta }_{{n'1}}} + \sum\limits_{n = 1}^N {\sum\limits_{q = 1}^\infty {Z_{{n'n}}^{{pq}}{{U}_{{nq}}}} } + \\ + \,\,\zeta _{p}^{'}(ka){{R}_{p}}{{\delta }_{{n{\kern 1pt} 'N}}} = - i{{A}_{p}}{{f}_{{n{\kern 1pt} '}}}({{r}_{0}}), \\ \end{gathered} $где ${{\delta }_{{n{\kern 1pt} 'n}}}$ – символ Кронекера и
(21)
$Z_{{n{\kern 1pt} 'n}}^{{pq}} = I_{{n{\kern 1pt} 'n}}^{{(1)}} - [q(q + 1)I_{{n{\kern 1pt} 'n}}^{{(2)}} + I_{{n{\kern 1pt} 'n}}^{{(3)}}]{{\delta }_{{pq}}}$– матричные элементы, определяемые интегралами
(22)
$I_{{n{\kern 1pt} 'n}}^{{(1)}} = k\int\limits_{{{a}_{1}}}^a {{{f}_{{n{\kern 1pt} '}}}{{f}_{n}}{{W}_{{pq}}}dr} ,$(23)
$I_{{n{\kern 1pt} 'n}}^{{(2)}} = \frac{1}{k}\int\limits_{{{a}_{1}}}^a {\frac{{{{f}_{{n{\kern 1pt} '}}}{{f}_{n}}}}{{{{r}^{2}}}}dr} ,$(24)
$I_{{n{\kern 1pt} 'n}}^{{(3)}} = \frac{1}{k}\int\limits_{{{a}_{1}}}^a {\frac{{d{{f}_{{n{\kern 1pt} '}}}}}{{dr}}\frac{{d{{f}_{n}}}}{{dr}}dr} $для $n{\kern 1pt} ' = 1,2,...,N.$
Уравнение (12), где $k{{a}_{1}}{{E}_{p}}({{a}_{1}}) = {{U}_{{1p}}},$ уравнения (20) и уравнение (14), где $ka{{E}_{p}}(a) = {{U}_{{Np}}}$, образуют полную систему линейных алгебраических уравнений, размер которой после усечения равен (N + 2)L, где L – число учитываемых меридиональных гармоник в (6), (10) и (11). Как и в работах [10, 12], матрица системы имеет блочную трехдиагональную структуру. После решения системы мы можем рассчитать поля в центральной области и неоднородном слое, а также поле, излученное в свободное пространство. В частности, используя асимптотическое выражение ${{\zeta }_{q}}(kr) \approx {{( - i)}^{{q + 1}}}\exp (ikr)$ для функций Риккати–Ханкеля при больших kr и представляя поле (6) в форме (9), мы можем рассчитать ДН диполя в присутствии тела вращения
как множитель, стоящий после произведения E0exp(ikr)/(kr).
2. МОДИФИКАЦИИ МЕТОДА
Если магнитный диполь оказывается вне сферы, введенной для решения задачи, т.е. если ${{r}_{0}} > a$, то алгоритм, описанный выше, может быть модифицирован следующим образом. Полное поле в свободном пространстве вне указанной сферы вместо (6) представляется в виде
(26)
${{E}_{\varphi }}(r,\theta ) = \frac{{{{E}_{0}}}}{{kr}}\sum\limits_{q = 1}^\infty {[A_{q}^{ - }{{\psi }_{q}}(kr) + {{R}_{q}}{{\zeta }_{q}}(kr)]{{T}_{q}}(\theta )} ,$где
– соответствует полю диполя, падающему на сферу.
Соотношения (14) и (15), следующие из граничных условий, должны быть заменены формулами
(29)
${{\left. {\frac{{d[r{{E}_{p}}(r)]}}{{dr}}} \right|}_{{r = a}}} = A_{p}^{ - }\psi _{p}^{'}(ka) + {{R}_{p}}\zeta _{p}^{'}(ka),$правая часть в уравнении (16) должна быть равна нулю, а правые части в уравнениях (20), которые должны решаться совместно с (8) и (28), должны иметь вид $ - {\kern 1pt} A_{p}^{ - }\psi _{p}^{'}(ka){{\delta }_{{n{\kern 1pt} '{\kern 1pt} N}}}.$
Наконец, ДН (25) должна быть модифицирована как
(30)
$F(\theta ) = \exp ( - ik{{r}_{0}}\cos \theta )\sin \theta + \sum\limits_{q = 1}^\infty {{{{( - i)}}^{{q + 1}}}{{R}_{q}}{{T}_{q}}(\theta )} ,$где первое слагаемое в правой части – ДН диполя в отсутствие тела.
Вторая модификация связана со случаем, когда вместо диэлектрической сферы внутри тела находится идеально проводящая сфера. Электрическое поле в слое (11) в этом случае должно быть равно нулю на поверхности сферы, т.е. ${{E}_{p}}({{a}_{1}}) = 0.$ Это условие исключает уравнение (12) из дальнейшего рассмотрения, а первая треугольная функция в разложении (19) должна быть также исключена. Это обстоятельство приводит к исключению первого слагаемого из уравнений (20). Координаты узлов, в которых расположены вершины треугольных функций, теперь будут определяться как ${{r}_{n}} = {{a}_{1}} + n\Delta ,$ где $\Delta = {{(a - {{a}_{1}})} \mathord{\left/ {\vphantom {{(a - {{a}_{1}})} N}} \right. \kern-0em} N}$ и $n = 1,\,2,\,...,\,N$. В результате порядок усеченной системы алгебраических уравнений (20) и (14) становится равным (N + 1)L вместо (N + 2)L в предыдущем случае. После решения системы характеристики излучения диполя могут быть рассчитаны так же, как и в случае диэлектрической сферы.
3. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ И РЕЗУЛЬТАТЫ
Алгоритм и его модификации, описанные выше, были реализованы в нескольких программах в среде МАТЛАБ. Вычисление интегралов (23) и (24), не зависящих от $\hat {\varepsilon }$, проводилось с использованием явных выражений, не приведенных здесь для краткости. Вычисление интеграла (22) проводилось с использованием разложения функции Wpq(r) по треугольным функциям, как в (19), с последующим аналитическим интегрированием произведений указанных функций [13, Приложение 5.1 ]. Работа программ контролировалась несколькими способами, включая сравнение результатов с данными, полученными другими методами, применимыми к случаю слоя из однородного диэлектрика. Некоторые характерные результаты приведены ниже.
В качестве первого примера рассмотрим однородную диэлектрическую сферу (радиус a0 и диэлектрической проницаемостью ε), возбуждаемую диполем, расположенным на расстоянии h от ее поверхности. Задача в этом случае имеет строгое аналитическое решение. В частности, ДН диполя может быть рассчитана согласно (30), где ${{r}_{0}} = {{a}_{0}} + h$,
(31)
${{R}_{q}} = - A_{q}^{ - }\frac{{m\psi _{q}^{'}(m\alpha ){{\psi }_{q}}(\alpha ) - {{\psi }_{q}}(m\alpha )\psi _{q}^{'}(\alpha )}}{{m\psi _{q}^{'}(m\alpha ){{\zeta }_{q}}(\alpha ) - {{\psi }_{q}}(m\alpha )\zeta _{q}^{'}(\alpha )}},$$m = \sqrt \varepsilon $ и $\alpha = k{{a}_{0}}$. Сместим теперь эту сферу вниз из начала координат на расстояние ${{z}_{0}}$, как показано во вставке на рис. 2, и применим ГПМ для решения задачи. Входные параметры задачи в этом случае определим следующим образом: ${{a}_{1}} = {{a}_{0}} - {{z}_{0}},$ $a = {{a}_{0}} + {{z}_{0}},$ ${{r}_{0}} = {{a}_{1}} + h$ и $\varepsilon (r,\theta ) = {{\varepsilon }_{1}} = \varepsilon .$ Интеграл (17) в этом случае определяется формулой
(32)
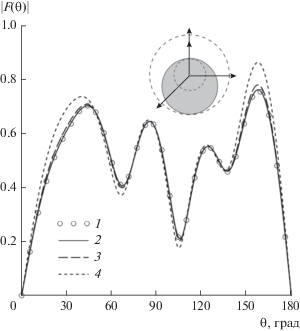
${{W}_{{pq}}} = {{\delta }_{{pq}}} + (\varepsilon - 1){{N}_{p}}{{N}_{q}}\int\limits_{ - 1}^{{{x}_{r}}} {P_{p}^{1}P_{q}^{1}dx} ,$Рис. 2.
Амплитудная ДН диполя в присутствии однородной диэлектрической сферы с параметрами a0= = 0.5λ, ε = 5 + 0.2i: 1 – расчет по строгой формуле (33) при учете L = 17 членов ряда (32), 2–4 – расчет ГПМ при N = 41 (2), 21 (3) и 11 (4). На вставке – геометрия задачи для смещения сферы.
где Nq – нормировочный коэффициент, указанный перед $P_{q}^{1}$ в (7), и
(33)
${{x}_{r}}(r) = \cos {\kern 1pt} {{\theta }_{r}} = \frac{{a{{a}_{1}} - {{r}^{2}}}}{{(a - {{a}_{1}})r}}$– косинус угловой координаты точки на поверхности смещенной сферы, а интеграл от произведения присоединенных функций Лежандра вычисляется с использованием соотношений, которые мы вывели для неопределенных интегралов:
(34)
$\begin{gathered} F_{{p,q}}^{1} = \int {P_{p}^{1}P_{q}^{1}dx} = \frac{1}{{p + q + 1}} \times \\ \times \,\,\left[ {xP_{p}^{1}P_{q}^{1} + \frac{{(q + 1)P_{{q - 1}}^{1}P_{p}^{1} - (p + 1)P_{{p - 1}}^{1}P_{q}^{1}}}{{p - q}}} \right] \\ \end{gathered} $для $q \ne p$,
(35)
$\begin{gathered} F_{{p,p}}^{1} = \frac{{(2p - 1)(p + 1)}}{{(2p + 1)(p - 1)}}F_{{p - 1,p - 1}}^{1} + \\ + \,\,\frac{p}{{p - 1}}\left[ {\frac{{2p - 1}}{{2p + 1}}F_{{p + 1,p - 1}}^{1} - F_{{p,p - 2}}^{1}} \right] \\ \end{gathered} $для $p > 1$ и $F_{{1,1}}^{1} = x(1 - {{{{x}^{2}}} \mathord{\left/ {\vphantom {{{{x}^{2}}} 3}} \right. \kern-0em} 3}{\kern 1pt} ).$
Амплитудная ДН диполя при a0= 0.5λ, ε = 5 + 0.2i и h = 0.1λ была рассчитана с использованием строгой формулы (31) при учете L = 17 членов ряда (30), а также с применением ГПМ для сферы, смещенной вниз на расстояние z0= 0.2λ (рис. 2). Входные параметры были заданы следующим образом: a = a0 + z0= 0.7λ, a1= a0 – z0= 0.3λ, r0 = 0.4λ и ε = ε1 = 5 + 0.2i. Расчеты проведены c учетом L = = 17 членов ряда (25) при числе треугольных функций N в (19), использованных на интервале a – a1= = 0.4λ, равном 11, 21 и 41. Как видим, результаты, соответствующие ГПМ, сходятся к точному решению при увеличении N. Мы также наблюдаем, что ДН диполя имеет несколько лепестков, что объясняется проникновением поля диполя внутрь сферы с последующими переотражениями там.
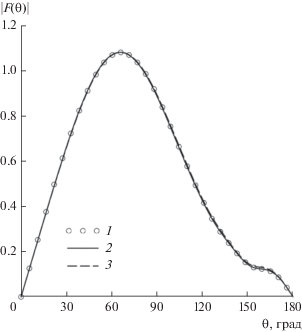
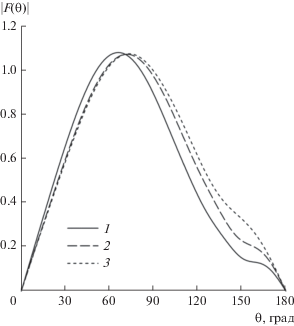
Амплитудные ДН диполя в задаче с геометрическими параметрами, указанными выше, но для сферы с проницаемостью ε = ε1 = –5 + 0.2i, что соответствует плазме на частоте ниже плазменной частоты [14], и с проницаемостью ε = ε1 = 0.4 + 0.2i, соответствующей частоте, превышающей плазменную частоту, приведены на рис. 3 и 4 соответственно. Здесь также наблюдаем сходимость результатов, полученных предлагаемым методом при L = 17 и увеличении числа используемых треугольных функций N, к результатам точного решения. Однолепестковая форма ДН в этих случаях существенно отличается от предыдущего случая, что объясняется резким снижением уровня поля внутри сферы при удалении точки наблюдения от ее поверхности. Аналогичную форму имеет ДН магнитного диполя в присутствии идеально проводящей сферы.
Рис. 3.
Амплитудная ДН диполя в присутствии однородной плазменной сферы с параметрами a0= 0.5λ, ε = –5 + 0.2i: 1 – расчет по строгой формуле (33) при учете L = 17 членов ряда (32), 2–4 – расчет ГПМ при N = 41 (2), 11 (3) и 7 (4).
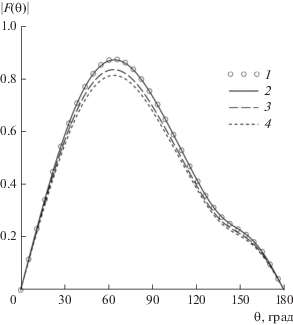
Рис. 4.
Амплитудная ДН диполя в присутствии однородной плазменной сферы с параметрами a0= 0.5λ, ε = 0.4 + 0.2i: 1 – расчет по строгой формуле (33) при учете L = 17 членов ряда (32), 2 и 3 – расчет ГПМ при N = 11 и 5 соответственно.
Второй пример соответствует магнитному диполю, расположенному над идеально проводящей сферой радиусом a1, расположенной внутри диэлектрического сфероида, один из фокусов которого совпадает с центром сферы, как показано во вставке на рис. 5. Размеры сфероида задаются его апофокусным расстоянием, совпадающим с радиусом внешней сферы a, и перифокусным расстоянием b. Указанные параметры определяют размер большой полуоси ae = (a + b)/2 и фокусное расстояние fe = (a – b)/2, через которые можно определить размер малой полуоси ${{b}_{e}} = \sqrt {a_{e}^{2} - f_{e}^{2}} = \sqrt {ab} $. Будем считать, что проницаемость сфероида зависит только от радиальной координаты и зададим эту зависимость линейной функцией
(36)
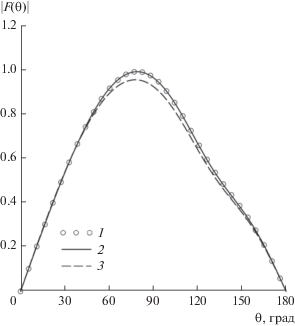
$\varepsilon (r) = \frac{{({{\varepsilon }_{a}} - {{\varepsilon }_{{{{a}_{1}}}}})r + {{\varepsilon }_{{{{a}_{1}}}}}a - {{\varepsilon }_{a}}{{a}_{1}}}}{{a - {{a}_{1}}}},$Рис. 5.
Амплитудная ДН диполя в присутствии идеально проводящей сферы, расположенной внутри диэлектрического сфероида: 1 – ${{\varepsilon }_{{{{a}_{1}}}}}$ = εa = 5, МВИ; 2 – ${{\varepsilon }_{{{{a}_{1}}}}}$ = εa = 5, ГПМ, L = 29, N = 51; 3 – ${{\varepsilon }_{{{{a}_{1}}}}}$ = 5, εa = 1; 4 ‒ ${{\varepsilon }_{{{{a}_{1}}}}}$ = 5 + 0.4i, εa = 1, ГПМ, L = 29, N = 51. На вставке – геометрия задачи для сферы внутри сфероида.
где ${{\varepsilon }_{{{{a}_{1}}}}} = \varepsilon ({{a}_{1}})$ и ${{\varepsilon }_{a}} = \varepsilon (a)$. Функция (17) в этом случае определяется формулой Wpq(r) = δpqε(r) для ${{a}_{1}} \leqslant r \leqslant b$ и формулой (32) для $b \leqslant r \leqslant a$, где ε следует заменить на ε(r), а косинус угловой координаты точки на поверхности тела теперь определяется формулой
(37)
${{x}_{r}} = {{({{p}_{e}} - r)} \mathord{\left/ {\vphantom {{({{p}_{e}} - r)} {({{x}_{e}}r)}}} \right. \kern-0em} {({{x}_{e}}r)}},$полученной с использованием уравнения эллипса $r(\theta ) = {{{{p}_{e}}} \mathord{\left/ {\vphantom {{{{p}_{e}}} {(1}}} \right. \kern-0em} {(1}} + {{x}_{e}}\cos \theta )$, записанного в полярных координатах с полюсом в фокусе, где ${{p}_{e}} = {{b_{e}^{2}} \mathord{\left/ {\vphantom {{b_{e}^{2}} {{{a}_{e}}}}} \right. \kern-0em} {{{a}_{e}}}}$ = = ${{2ab} \mathord{\left/ {\vphantom {{2ab} {(a + b)}}} \right. \kern-0em} {(a + b)}}$ – фокальный параметр и ${{x}_{e}} = {{{{f}_{e}}} \mathord{\left/ {\vphantom {{{{f}_{e}}} {{{a}_{e}}}}} \right. \kern-0em} {{{a}_{e}}}} = $ = ${{(a - b){\kern 1pt} } \mathord{\left/ {\vphantom {{(a - b){\kern 1pt} } {(a + b)}}} \right. \kern-0em} {(a + b)}}$ – эксцентриситет.
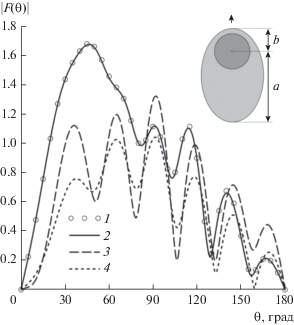
Амплитудные ДН диполя, соответствующие геометрическим параметрам a1= 0.4λ, a = 1.5λ, b = 0.5λ и r0= 0.7λ, приведены на рис. 5. Задача для однородного сфероида может быть также решена, например, хорошо известным методом вспомогательных источников (МВИ) [14], представленных в виде осесимметричных кольцевых азимутальных электрических токов. Кольцевые источники в количестве 160 × 2 были расположены на софокусных сфероидальных вспомогательных поверхностях с размерами больших полуосей, равных ${{a}_{e}} \pm 0.05\lambda $. Кроме того, 40 кольцевых источников были расположены на сферической вспомогательной поверхности радиусом ${{a}_{1}} - 0.05\lambda $ внутри центральной сферы. Угловые координаты источников на сфероидах задавались параметрически [15], что обеспечивало наиболее быстрое уменьшение невязки выполнения граничных условий, а на сфере – равномерно. Указанные параметры обеспечивали выполнение граничных условий на поверхности диэлектрического сфероида и на поверхности внутренней сферы с погрешностью, не превышающей 10–6. ДН диполя, соответствующая МВИ, использовалась в качестве эталона. Кривая 2, совпадающая с 1, соответствует ГПМ с использованием L = 21 меридиональных гармоник и N = 100 треугольных функций. ДН 3, полученная ГПМ с использованием указанного количества гармоник и треугольных функций, соответствует неоднородному сфероиду без потерь с ${{\varepsilon }_{{{{a}_{1}}}}}$ = 5 и εa = 1, а ДН 4 – сфероиду с потерями при ${{\varepsilon }_{{{{a}_{1}}}}}$ = 5 + 0.4i и εa = 1. Как видим, и неоднородный диэлектрик, и наличие потерь в этом случае может заметно влиять на форму ДН диполя.
Амплитудные ДН диполя, соответствующие геометрическим параметрам, указанным выше, но со сферой, находящейся внутри плазменного сфероида, приведены на рис. 6. Кривые, соответствующие однородному сфероиду с ${{\varepsilon }_{{{{a}_{1}}}}}$ = εa = –5 + 0.2i, получены с использованием МВИ и ГПМ с входными параметрами, такими же, как и в предыдущем случае. Кривая 3, полученная с использованием ГПМ, соответствует неоднородному плазменному сфероиду с ${{\varepsilon }_{{{{a}_{1}}}}}$ = –5 + 0.2i и εa = 1. Результаты, полученные при исследовании влияния проницаемости плазмы на ДН диполя, приведены на рис. 7. Кривая 1 и 2 соответствуют проницаемостям сфероида у поверхности сферы εa1= –5 + 0.4i и ${{\varepsilon }_{{{{a}_{1}}}}}$ = = 0.4 + 0.4i, а εa = 1 в обоих случаях. Кривая 3 соответствует отсутствию плазмы, т.е. ${{\varepsilon }_{{{{a}_{1}}}}}$ = εa = 1. Результаты, приведенные на рис. 7, показывают, что ДН диполя имеет однолепестковую форму, которая практически не зависит ни от неоднородности плазменного шлейфа, ни от потерь в нем, что объясняется резким снижением уровня поля при увеличении расстояния от поверхности сфероида до точки наблюдения. Поле диполя отражается в основном от освещенной поверхности сфероида. Согласно рис. 7 форма ДН диполя также слабо зависит от действительной части проницаемости плазмы и близка к форме ДН диполя в присутствии идеально проводящей сферы без оболочки.
ЗАКЛЮЧЕНИЕ
Таким образом, рассмотрена задача возбуждения неоднородного диэлектрического тела вращения в виде однородной диэлектрической или идеально проводящей сферы, окруженной неоднородной диэлектрической оболочкой, радиальным магнитным диполем, расположенным на оси вращения. Для решения задачи было разработано несколько алгоритмов, основанных на ГПМ, включающем проектирование электромагнитных полей на поперечные сферические функции и применение одномерного метода конечных элементов для решения полученной системы обыкновенных дифференциальных уравнений.
Разработанные алгоритмы были реализованы в соответствующих программах на языке МАТЛАБ, работа которых была проверена несколькими способами. Проверки включали рассмотрение однородной диэлектрической сферы, задача возбуждения которой допускает строгое аналитическое решение. ГПМ в этом случае был применен для сферы с центром, смещенным из начала координат, и продемонстрирована сходимость результатов к точному решению при увеличении числа функций, учитываемых в разложении искомых полей. Вторым объектом, использованным для проверки, была идеально проводящая сфера, расположенная внутри однородного вытянутого диэлектрического сфероида. Результаты решения задачи с использованием ГПМ в этом случае сравнивались с результатами, полученными методом вспомогательных источников с контролируемой точностью выполнения граничных условий на поверхностях сферы и сфероида.
В работе также получены новые результаты для ДН диполя в присутствии проводящей сферы, окруженной неоднородной диэлектрической оболочкой в форме вытянутого сфероида с зависимостью проницаемости сфероида от радиальной координаты по линейному закону. Показано, что ДН диполя в случае оболочки из обычного диэлектрика заметно отличается от ДН диполя для случая однородной оболочки. Результаты также показывают заметное влияние потерь в оболочке на форму ДН, что объясняется проникновением поля диполя внутрь сфероида и переотражениями между поверхностью последнего и поверхностью внутренней сферы.
Результаты, полученные для случая плазменной оболочки, показывают, что ДН диполя имеет однолепестковую форму, которая слабо зависит как от неоднородности шлейфа, так и от потерь в нем. Этот факт объясняется слабым проникновением поля внутрь плазменного сфероида, что приводит к формированию ДН в основном только освещенной частью поверхности сфероидальной оболочки.
Список литературы
Ильинский А.С., Свешников А.Г. // ЖВМ и МФ. 1971. Т. 11. № 4. С. 960.
Малушков Г.Д. // Изв. вузов. Радиофизика. 1975. Т. 18. № 2. С. 269.
Stout B., Neviere M., Popov E. // J. Opt. Soc. Am. A. 2005. V. 22. № 11. P. 2385.
Morgan M.A., Mei K.K. // IEEE Trans. 1979. V. AP-27. № 2. P. 202.
Greenwood A.D., Jin J.-M. // IEEE Trans. 1999. V. AP-47. № 8. P. 1260.
Govind S., Wilton D.R., Glisson A.W. // IEEE Trans. 1984. V. AP-32. № 11. P. 1163.
Kucharski A.A. // IEEE Trans. 2000. V. AP-48. № 8. P. 1202.
Maнeнкoв C.A. // PЭ. 2018. T. 63. № 1. C. 3.
Gabdullina A.R., Smolnikova O.N., Skobelev S.P. // Proc. 11th Eur. Conf. on Antennas and Propagation (EuCAP'2017). Paris, France, 19–24 March 2017. P. 1096.
Nekrasova E.S., Skobelev S.P. // Proc. 2017 Fourth Intern. Conf. on Engineering and Telecommunication (En&T 2017), Moscow, Russia, 29–30 November 2017. P. 82.
Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.
Скобелев С.П., Япарова А.А. // РЭ. 2007. Т. 52. № 3. С. 311.
Скобелев С.П. Фазированные антенные решетки с секторными парциальными диаграммами направленности. М.: Физматлит, 2010.
Кюркчан А.Г., Маненков С.А., Негорожина Е.С. // РЭ. 2006. Т. 51. № 11. С. 1285.
Коробкина А.В., Скобелев С.П. // Радиотехника. 2017. № 4. С. 60.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника