1. На главную
  2. Электронные версии
  3. Радиотехника и электроника
  4. T. 65, № 4, 2020

Радиотехника и электроника, 2020, T. 65, № 4, стр. 388-389

Изменение структуры поля метачастиц при распространении импульсного волнового поля, направленно излученного апертурным источником

В. В. Шевченко *

Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация

* E-mail: sto@cplire.ru

Поступила в редакцию 31.10.2019
После доработки 31.10.2019
Принята к публикации 05.11.2019

Полный текст (PDF)

Аннотация

Приведены результаты анализа изменения поперечного размера эффективной формы и радиуса кривизны фазового волнового фронта поля метачастиц при их направленном распространении от апертурного источника импульсного волнового поля.

1. В работах [1–3] были введены понятия и рассмотрены некоторые свойства метачастиц импульсных волновых полей (электромагнитного, акустического), направленно излученных апертурными источниками (антеннами, лазерами, акустическими мембранами) и распространяющихся в свободном пространстве и в однородных изотропных средах. В данной работе приводятся преобразованные выражения для параметров структурных функций поля метачастиц: поперечного размера эффективной формы и радиуса кривизны фазового волнового фронта поля метачастиц, которые изменяются в процессе распространения метачастиц от апертуры источника. При этом изменяющаяся часть эффективной формы поля метачастиц является цилиндрической в ближней области от апертуры источника, квазицилиндрической в области дифракции Френеля, квазиконусной в области дифракции Фраунгофера и конусной в дальней области от апертуры источника импульсного волнового поля.

2. Функциональная зависимость

(1)
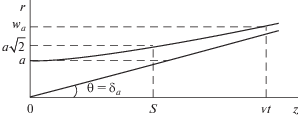
$\begin{gathered} {{w}_{a}}\left( z \right) = a{{\left[ {1 + {{{\left( {\frac{z}{S}} \right)}}^{2}}} \right]}^{{1/2}}}, \\ ~S = k{{a}^{2}} = {{2\pi {{a}^{2}}} \mathord{\left/ {\vphantom {{2\pi {{a}^{2}}} \lambda }} \right. \kern-0em} \lambda } = {a \mathord{\left/ {\vphantom {a {{{\delta }_{a}}}}} \right. \kern-0em} {{{\delta }_{a}}}}, \\ \end{gathered} $

показывает (рис. 1) изменение полуширины (радиуса) эффективной формы поля метачастиц при прохождении расстояния $z = vt$ в процессе распространения метачастиц от излучающей апертуры источника импульсного волнового поля [1–3]. Здесь приняты следующие обозначения: a – радиус круглой излучающей апертуры источника импульсного волнового поля,

(2)
$k = \frac{\omega }{v} = \frac{{2\pi }}{\lambda },\,\,\,\,{{\delta }_{a}} = \frac{1}{{ka}},$
Рис. 1.

$\omega $ – круговая частота волнового поля, $v$ – скорость распространения, $\lambda ~$ – длина волны поля метачастиц, при этом

(3)
${{\delta }_{a}} = \frac{1}{\pi }\frac{\lambda }{{2a}},\,\,\,\,\delta _{a}^{2} \ll 1\,\,\,\,{\text{при}}\,\,\,\,\frac{\lambda }{{2a}} \leqslant 1.$

Значение $z = S~$ можно интерпретировать как расстояние от апертуры источника поля до условной границы перехода импульсного волнового поля из области дифракции Френеля в область дифракции Фраунгофера (см. также ниже).

3. Функциональная зависимость

(4)
$R\left( z \right) = z\left[ {1 + {{{\left( {\frac{S}{z}} \right)}}^{2}}} \right]$

показывает (рис. 2) изменение радиуса кривизны фазового волнового фронта поля метачастиц при их распространении от апертуры источника импульсного волнового поля [1]. Из графика рис. 2 видно, что радиус кривизны фазового волнового фронта поля метачастиц имеет минимальное значение ${{R}_{{{\text{min}}}}} = 2S~$ при $z = S$. При этом ${{w}_{a}}\left( S \right) = a\sqrt 2 $ (см. рис. 1).

Рис. 2.

Приведенный результат указывает на то, что расстояние $z = S$ от апертуры источника поля соответствует не условной, а вполне определенной границе перехода от набранной фокусировки (уменьшения радиуса кривизны фронта) поля метачастиц к началу расфокусировки (увеличения радиуса кривизны фронта) поля метачастиц в процессе их распространения от источника поля. Сказанное относится и к импульсному волновому полю в целом, направленно излученному с $R\left( 0 \right) = \infty ,$ т.е. c плоским фазовым фронтом поля на апертуре источника.

Список литературы

  1. Шeвчeнкo B.B. // PЭ. 2018. T. 63. № 9. C. 899.

  2. Шeвчeнкo B.B. // PЭ. 2019. T. 64. № 3. C. 265.

  3. Шeвчeнкo B.B. // PЭ. 2019. T. 64. № 11. C. 1122.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Радиотехника и электроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал