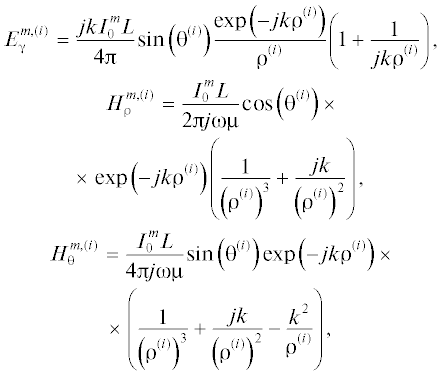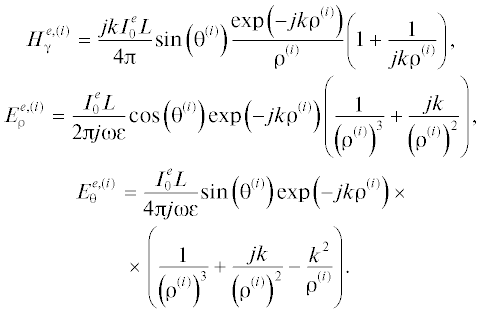Радиотехника и электроника, 2020, T. 65, № 4, стр. 330-341

ВВЕДЕНИЕ

Данная работа посвящена описанию численно-аналитического метода расчета характеристик передачи скрученного волновода прямоугольного поперечного сечения. Указанный метод является одним из вариантов метода интегральных уравнений, сформулированного в работах [1, 2] на основе интегральной формы записи леммы Лоренца. Впервые идеология метода была изложена в работе [3].

Волноводная скрутка представляет собой нерегулярный участок экранированной волноведущей структуры прямоугольного поперечного сечения, в которой в зависимости от продольной координаты меняются не форма или размеры контура поперечного сечения, а только его положение. Положение контура определяется зависящим от продольной координаты z углом его поворота Φ(z) относительно аналогичного контура начала скрутки. Нерегулярные участки СВЧ-тракта типа скрутки наиболее часто применяются в антенных устройствах [4] для поворота плоскости поляризации.

При решении дифракционной задачи для волноводной скрутки можно использовать такие распространенные и электродинамически обоснованные методы, как метод поперечных сечений [5, 6] и метод частичных областей (МЧО) [7, 8]. Первый метод используется для расчета характеристик передачи нерегулярных направляющих структур с медленно меняющимися по продольной координате параметрами [5]. В связи с этим его применение для расчета коротких по продольной координате волноводных скруток с относительно большим значением угла поворота плоскости поляризации (компактных скруток) приводит к получению результатов, содержащих значительную погрешность. Второй метод (МЧО) применим к расчету скруток с любыми значениями длин и углов поворота плоскости поляризации, однако требует больших затрат машинного времени и громоздкой процедуры алгебраизации расчетного алгоритма.

Предлагаемый в данной работе численно-аналитический метод расчета характеристик передачи продольно-азимутально нерегулярных волноводных направляющих структур имеет преимущества по отношению к указанным выше методам как в скорости счета, так и в достаточно простой процедуре алгебраизации задачи.

1. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ В ДИФРАКЦИОННОЙ ЗАДАЧЕ О РАСЧЕТЕ ХАРАКТЕРИСТИК ПЕРЕДАЧИ ВОЛНОВОДНОЙ СКРУТКИ ПРЯМОУГОЛЬНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

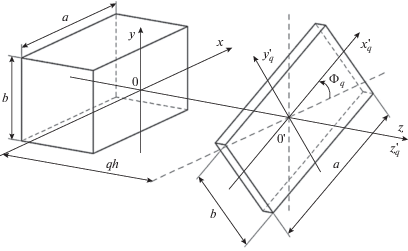
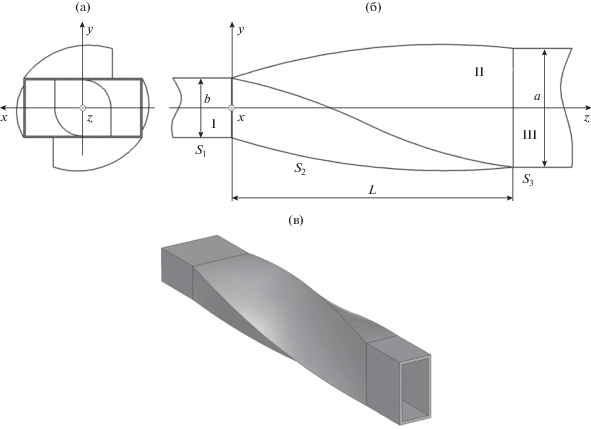
Рассматриваемая направляющая структура схематически изображена на рис. 1. Она представляет собой объем V, ограниченный поверхностями S = S₁ + S₂ + S₃ и ${{S}_{{ \bot 1,2}}},$ в котором существуют электромагнитные поля $\left( {{{{\vec {Е}}}_{1}};{{{\vec {Н}}}_{1}}} \right)$ и $\left( {{{{\vec {Е}}}_{2}};{{{\vec {Н}}}_{2}}} \right),$ созданные соответственно источниками $\vec {j}_{1}^{{e,m}}$ и $\vec {j}_{2}^{{e,m}}.$ Здесь S₁ и S₃ – боковые поверхности первого (область I) и второго (область III) регулярных волноводов соответственно, S₂ – боковая поверхность нерегулярной области волноводной скрутки (область II), которая имеет длину L по продольной координате z; ${{S}_{{ \bot 1,2}}}$ – плоскости поперечных сечений, ограничивающие область рассматриваемой направляющей структуры по продольной координате z.

Указанные поля и источники согласно лемме Лоренца связаны соотношением

В качестве полей ${{\vec {Е}}_{1}}$ и ${{\vec {Н}}_{1}}$ возьмем решения уравнений Максвелла, которые соответствуют волне, распространяющейся в направляющей структуре, и удовлетворяют на поверхности S граничным условиям непрерывности касательной компоненты электрического поля и нормальной компоненты магнитного поля:

Источники $\vec {j}_{2}^{{e,m}}$ являются вспомогательными и располагаются в конечной области внутри направляющей структуры вблизи плоскости z = 0. Они создают поле сферической волны, удовлетворяющее нулевому граничному условию в точках, бесконечно удаленных от источников. Своеобразие формулировки леммы Лоренца в данном случае заключается в том, что она записывается для полей, соответствующих различным краевым задачам в одном и том же объеме. Одна краевая задача для нерегулярного волновода, другая для неограниченного пространства. Такую формулировку леммы Лоренца можно назвать обобщенной.

В соответствии с методикой, предложенной в работе [1], бесконечно удаляя сечения ${{S}_{{ \bot 1,2}}}$ от начала координат (z_1,2 → ±∞) и учитывая, что источники $\vec {j}_{1}^{{e,m}},$ отнесенные в z_1,2, в открытом пространстве создают поле сферической волны $\left( {{{{\vec {E}}}_{0}};{{{\vec {H}}}_{0}}} \right),$ удовлетворяющие условиям

в месте расположения вспомогательных источников, исключаем из уравнения (1) токи $\vec {j}_{1}^{{e,m}}$ и, выбрав в качестве вспомогательных источников элементарные электрические и магнитные диполи, получаем интегральные уравнения Фредгольма второго рода:

Решая интегральные уравнения (3), (4) при граничных условиях (2), определяем искомые поля ${{\vec {Е}}_{1}}$ и ${{\vec {Н}}_{1}}$ в нерегулярной направляющей структуре. При этом отсутствуют ограничения на длину волноводной скрутки по продольной координате и на значение угла поворота контура поперечного сечения второго регулярного волновода относительно того же контура первого волновода.

Рассмотрим направляющую структуру, схематически изображенную на рис. 1. Поперечные размеры первого (область I), второго (область III) волноводов, а также области волноводной скрутки (область II) одинаковы: a – размер широкой стенки, b – размер узкой стенки поперечного сечения. Пусть со стороны первого волновода падает одна из его собственных волн. В результате дифракции этой волны, происходящей в нерегулярной области волноводной скрутки, в первом волноводе возбуждается бесконечный набор отраженных волн с коэффициентами отражения $R_{{mn}}^{E},$ (для E-волн) и $R_{{mn}}^{H}$ (для H-волн). Во втором волноводе образуется бесконечный набор прошедших волн с коэффициентами прохождения $B_{{mn}}^{E}$ (для E-волн) и $B_{{mn}}^{H}$ (для H-волн).

Продольные составляющие электрического и магнитного полей в области I (–∞ < z ≤ 0) записываются следующим образом:

где ${\chi }_{{mn}}^{{({\text{I}})}}$ – поперечное волновое число прямоугольного волновода I, ${\beta }_{{mn}}^{{({\text{I}})}}$ – продольное волновое число прямоугольного волновода I.

Остальные компоненты электрического и магнитного полей электромагнитных волн выражаются (см., например, [9]) через составляющие (5) и (6) из уравнений Максвелла:

где ε и μ – диэлектрическая и магнитная проницаемости среды соответственно.

Из уравнений (7) получаем выражения для поперечных компонент напряженностей полей волн электрического типа:

Поперечные компоненты полей волн магнитного типа выражаем через продольные:

Используя соотношения (5), (6), (8) и (9), можно записать все компоненты электромагнитных полей волн H- и Е-типов в волноводе I.

Связь волновых чисел в области I (–∞ < z ≤ 0) выглядит следующим образом:

Поперечные волновые числа в области I определяются как:

Так как поперечные размеры областей I, II и III остаются неизменными, соотношения (10) и (11) справедливы для всей рассматриваемой направляющей структуры:

Для решения рассматриваемой дифракционной задачи требуется иметь выражения для компонент полей волн E- и H-типов на поверхности нерегулярной области, а также на поверхности второго регулярного экранированного прямоугольного волновода. Для записи компонент полей на поверхности и нахождения значений поверхностных интегралов нерегулярной области рассматриваемой направляющей структуры каждому ее поперечному сечению сопоставляется вспомогательный регулярный волновод сравнения (ВС) [5] с теми же сечением и распределением параметров заполняющей среды. Искомое поле ищется в виде суперпозиции полей собственных волн ВС. Сшивание полей на торцевых границах ВС проводится не в явном виде через граничные условия, а косвенно – через интегральные уравнения (3) и (4) [2]. Амплитудные коэффициенты электромагнитных волн определяются как решения неоднородной системы линейных алгебраических уравнений (СЛАУ).

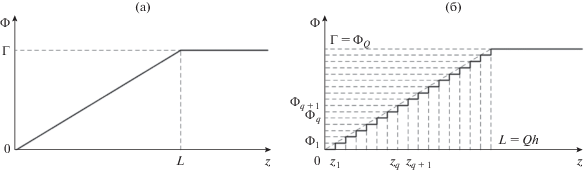
Таким образом, нерегулярную область скрутки фактически удается представить как каскадное соединение конечного числа Q отрезков направляющих структур в виде регулярных ВС с размером h по продольной координате z. Размер широкой стенки в поперечном сечении каждого такого волновода равен a, размер узкой стенки – b. Декартову систему (x, y, z) будем называть базовой системой координат (БСК). Каждый ВС, имеющий размеры a × b × h, повернут вокруг оси z БСК на угол Φ = Φ(z), зависящий от значения продольной координаты z. На рис. 2а изображена зависимость Φ(z) в нерегулярной области II (0 < z < L) и в области второго регулярного волновода (L ≤ z < ∞). На рис. 2б изображена ступенчатая аппроксимация линейной зависимости Φ(z), соответствующая представлению нерегулярной области в виде каскада ВС. Индекс q на рисунке соответствует порядковому номеру регулярного ВС, Q – количество указанных регулярных ВС в скрутке, h – размер шага дискретизации скрутки (длина ВС по продольной координате z). Угол Γ является углом поворота контура поперечного сечения второго регулярного волновода относительно такого же контура первого волновода. Этот угол (при z ≥ L) не зависит от продольной координаты z, поэтому на рис. 2а и 2б при z ≥ L зависимость Φ(z) представляет прямую, параллельную оси z.

На рис. 3 изображена взаимная ориентация первого регулярного волновода и q-го ВС. Показанную на рисунке декартову систему координат $\left( {x_{q}^{'},y_{q}^{'},z_{q}^{'}} \right)$ будем называть локальной системой координат (ЛСК) q-го ВС (далее – ЛCК_q). Она жестко привязана к поверхности q-го ВС. А именно, две оси ЛCК_q (оси $x_{q}^{'}$ и $y_{q}^{'}$) лежат в поперечном сечении ВС, как изображено на рисунке, направление оси $z_{q}^{'}$ совпадает с вектором фазовой скорости распространяющейся в волноводной скрутке электромагнитной волны (совпадает с осью z). Из рисунка видно, что ЛСК_q $\left( {x_{q}^{'},y_{q}^{'},z_{q}^{'}} \right)$ в нерегулярной области поворачивается относительно БСК (x, y, z) вокруг оси z на тот же угол, что и контур рассматриваемого поперечного сечения в области волноводной скрутки.

Для определения связи между БСК и ЛСК_q необходимо использовать формулы преобразования координат, которые имеют вид [10]:

Используя соотношения (5), (6), (8), (9) и (12), можно записать все компоненты полей волн H- и Е-типов в нерегулярной области волноводной скрутки. Заменив в формуле (12) Ф_q на Г и использовав указанные соотношения, получаем запись компонент полей электромагнитных волн в области второго регулярного волновода.

В исходных интегральных уравнениях (3) и (4) присутствуют поля вспомогательных источников, в качестве которых выбраны продольно ориентированные элементарные электрические и магнитные диполи. В сферической системе координат компоненты электромагнитного поля, создаваемого магнитным диполем, представимы в виде

а компоненты поля, создаваемого электрическим диполем, – в виде

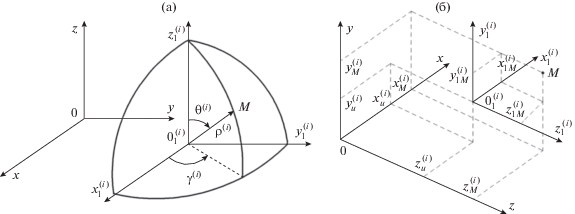
Здесь $k = {\omega }\sqrt {{\mu \varepsilon }} $, i – номер вспомогательного источника [9]. Формулы, связывающие сферическую систему координат $\left( {{{{\rho }}^{{(i)}}}{\text{,}}{{{\theta }}^{{(i)}}}{\text{,}}{{{\gamma }}^{{(i)}}}} \right),$ в которой описываются компоненты полей вспомогательных источников, и БСК (x, y, z), в которой записываются компоненты полей рассматриваемой направляющей структуры (рис. 4а и рис. 4б), имеют вид:

При продольном расположении вспомогательных источников компоненты создаваемых ими полей в декартовой системе координат (x, y, z) имеют вид [11]:

Левая часть уравнения (4), в котором присутствует вспомогательное поле, создаваемое магнитным диполем, записывается в виде:

где S₁ – боковая поверхность регулярной области I (–∞ < z ≤ 0), S₂ – боковая поверхность нерегулярной области II (0 < z < L), S₃ – боковая поверхность регулярной области III (L ≤ z < ∞).

Правая часть этого уравнения имеет вид:

Левая часть уравнения (3), в котором присутствует вспомогательное поле, создаваемое электрическим диполем, записывается в виде

Правая часть уравнения (3) имеет вид

Далее, записываем интегральные уравнения (3) и (4) в 4N точках (N – номер приближения), в которых располагаем продольно ориентированные элементарные электрические и магнитные диполи. Подставляя компоненты полей в указанные интегральные уравнения, находим численные значения поверхностных интегралов. В результате получаем неоднородную систему 4N линейных алгебраических уравнений, решая которую, находим неизвестные амплитудные коэффициенты волн E- и H-типов.

2. РЕЗУЛЬТАТЫ РАСЧЕТА ХАРАКТЕРИСТИК ПЕРЕДАЧИ ВОЛНОВОДНОЙ СКРУТКИ

На рис. 5 представлены результаты расчета зависимостей модулей коэффициентов отражения и прохождения основной волны H₁₀ прямоугольного волновода от нормированной частоты ka при различных значениях длины волноводной скрутки L. Угол поворота волноводной скрутки Г = 90°. Результаты получены в диапазоне нормированных частот 3.14 ≤ ka ≤ 6.28, соответствующем одномодовому режиму работы направляющей структуры в первом приближении при учете одной волны H₁₀ в областях регулярных волноводов и волноводной скрутки.

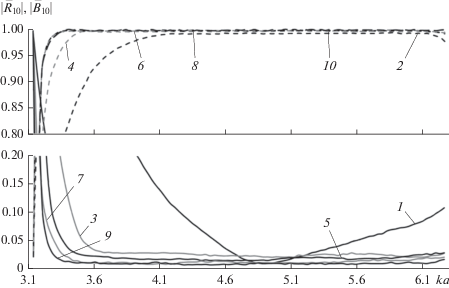
На рисунке кривые 1 и 2 – соответственно модули коэффициентов отражения и прохождения волны H₁₀ при длине скрутки L = a, кривые 3 и 4 – при L = 2a, кривые 5 и 6 – при L = 3a, кривые 7 и 8 – при L = 4a, кривые 9 и 10 – при L = 5a. Из рисунка видно, что при L ≥ 2a величина коэффициента стоячей волны по напряжению (КСВН) в полосе нормированных частот 3.6 ≤ ka ≤ 6.28 не превышает значения 1.06. Данный факт свидетельствует о хорошем согласовании волноводов во всем исследуемом диапазоне частот.

Для оценки точности полученных результатов при численной реализации разработанного алгоритма были найдены зависимости относительных погрешностей выполнения закона сохранения энергии (ЗСЭ) от нормированной частоты при различных значениях длины волноводной скрутки L. Относительная погрешность выполнения ЗСЭ определяется как

где β₁₀ – продольное волновое число волны H₁₀, β_mn – продольные волновые числа волн H_mn и E_mn, m и n – индексы волн по широкой и узкой стенкам направляющей структуры соответственно. Результаты расчета частотной зависимости относительной погрешности выполнения ЗСЭ представлены на рис. 6.

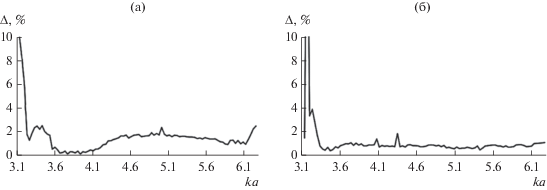
Из рисунка видно, что значения относительной погрешности выполнения ЗСЭ не превышают 2.5% во всем исследуемом диапазоне нормированных частот, за исключением области вблизи критической частоты основной волны H₁₀. При решении поставленной дифракционной задачи были использованы четыре вспомогательных источника магнитного типа (элементарные магнитные диполи). В рамках использованного приближения можно утверждать, что выбранное месторасположение вспомогательных источников обеспечивает выполнение условия непревышения указанной относительной погрешности предельно допустимого значения, составляющего 5%.

В рамках данной работы были рассчитаны характеристики передачи волноводной скрутки в более широком диапазоне нормированных частот 3.14 ≤ ka ≤ 12.56, соответствующем многомодовому режиму ее работы. На рис. 7 представлены результаты расчета зависимостей модулей коэффициентов отражения и прохождения основной волны прямоугольного волновода H₁₀ от нормированной частоты при различных значениях длины волноводной скрутки. Угол поворота волноводной скрутки Г = 90°. Результаты расчета получены в шестом приближении.

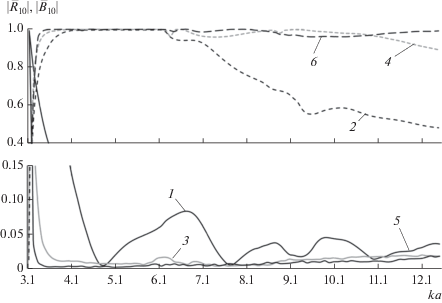
На рис. 7 кривые 1 и 2 – соответственно модули коэффициентов отражения и прохождения волны H₁₀ при длине скрутки L = a, кривые 3 и 4 – при L = 3a, кривые 5 и 6 – при L = 5a.

В частотном диапазоне, соответствующем многомодовому режиму работы, кривые модулей коэффициентов отражения и прохождения волны H₁₀ имеют сложную частотную зависимость, связанную с особенностями энергетического обмена волны H₁₀ с другими волнами, распространяющимися в исследуемой направляющей структуре. Наблюдаются локальные максимумы и минимумы частотных зависимостей характеристик передачи вблизи критических частот волн высших типов, что может быть объяснено возникновением ее взаимодействия с одной из указанных волн.

На рис. 8 представлены частотные зависимости модулей коэффициентов отражения и прохождения волн H₁₀, H₂₀, H₀₁, H_21,E₂₁ и H₃₀ при длине волноводной скрутки L = 5a. Угол поворота волноводной скрутки Г = 90°.

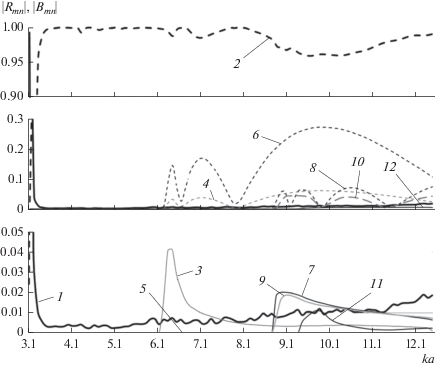
Из рисунка видно, что в частотном диапазоне, соответствующем многомодовому режиму работы волноводной скрутки, в результате дифракции волны H₁₀ возбуждаются и распространяются в регулярных волноводах также волны H₂₀, H₀₁, H_21,E₂₁ и H₃₀. Кривые 1 и 2 на рис. 8 – соответственно модули коэффициентов отражения и прохождения волны H₁₀, кривые 3 и 4 – волны H₂₀, кривые 5 и 6 – волны H₀₁, 7 и 8 – волны H₂₁, кривые 9 и 10 – волны E₂₁, кривые 11 и 12 – волны H₃₀.

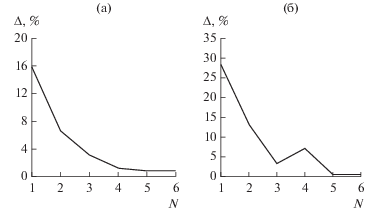
На рис. 9 представлены зависимости относительной погрешности выполнения ЗСЭ от нормированной частоты в многомодовом частотном диапазоне при различных значениях длины волноводной скрутки. Указанные зависимости найдены с целью оценки точности результатов расчета при численной реализации разработанного алгоритма. Из рисунка видно, что относительная погрешность выполнения ЗСЭ во всем рассматриваемом диапазоне нормированных частот, за исключением области вблизи критической частоты волны H_10, не превышает 4%. Вблизи критических частот волн высших типов наблюдаются “всплески” погрешности выполнения ЗСЭ.

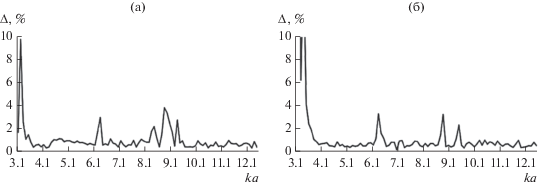
Исходя из представленных выше частотных зависимостей относительной погрешности выполнения ЗСЭ можно сделать вывод о выполнении условия непревышения указанной погрешности порогового значения (5%). Задача решена в приближении N = 6 при учете пяти волн H-типа и одной волны Е-типа. В соответствии с этим вблизи нерегулярной области направляющей структуры располагались двадцать продольно ориентированных магнитных диполей и четыре электрических диполя. При определении их координат использовались рекомендации, приведенные в работах [12, 13].

Для того чтобы подтвердить достоверность полученных результатов расчета характеристик передачи волноводной скрутки с помощью разработанного алгоритма, было проведено их сравнение с результатами расчета, полученными с использованием средства автоматизированного проектирования (САПР) CST Microwave Studio. На рис. 10 представлены результаты расчета характеристик передачи рассматриваемой направляющей структуры при длине волноводной скрутки L = 4a, полученные посредством предлагаемого алгоритма и САПР. Угол поворота волноводной скрутки Г = 90°.

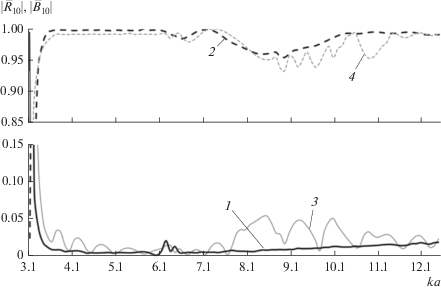
На рисунке кривые 1 и 2 – соответственно модули коэффициентов отражения и прохождения, полученные с помощью разработанного алгоритма, кривые 3 и 4 – полученные при помощи САПР. Сравнение характеристик передачи позволяет сделать вывод о качественном и количественном совпадении результатов. Отклонение результатов расчета, полученных с помощью САПР, от результатов, полученных с использованием разработанного алгоритма, не превышает 3.5%, что подтверждает корректность алгоритма в диапазоне нормированных частот, соответствующем многомодовому режиму работы волноводной скрутки, при учете конечного набора волн высших типов.

Для оценки обоснованности предлагаемого в данной работе метода расчета и созданного на его основе алгоритма, а также достоверности полученных результатов проведено исследование сходимости решений поставленной дифракционной задачи. Результаты исследования представлены на рис. 11. Из рисунка видно, что при увеличении номера приближения относительная погрешность выполнения ЗСЭ Δ уменьшается и стремится к нулю. При этом различие между численными значениями характеристик передачи в пятом и шестом приближениях не превышает 0.2%. Дальнейшее увеличение номера приближения приводит к незначительному изменению численных значений модулей коэффициентов отражения и прохождения и одновременно к значительному увеличению порядка СЛАУ. Проведенное исследование позволяет выбрать “рабочее” приближение N = 6 для расчета характеристик передачи волноводной скрутки прямоугольного поперечного сечения.

ЗАКЛЮЧЕНИЕ

Предложен численно-аналитический метод расчета характеристик передачи продольно-азимутально нерегулярной направляющей структуры в виде волноводной скрутки прямоугольного поперечного сечения. Представленный алгоритм построен на основе метода интегральных уравнений [1–3, 8]. Для записи компонент полей на поверхности нерегулярного волновода и нахождения значений поверхностных интегралов, входящих в исходные интегральные уравнения, каждому участку нерегулярной области рассматриваемой направляющей структуры сопоставляется регулярный волновод сравнения. Искомое поле ищется в виде суперпозиции полей собственных волн соответствующих волноводов сравнения. Сшивание полей на границах указанных участков разбиения нерегулярной области осуществляется косвенно через интегральные уравнения (3) и (4).

С использованием разработанного алгоритма найдены частотные зависимости модулей коэффициентов отражения и прохождения основной волны H₁₀ волноводных скруток различных длин как в одномодовом, так и в многомодовом режимах. Рассчитаны характеристики передачи волн высших типов и исследовано их влияние на коэффициенты отражения и прохождения основной волны H₁₀. Точность и корректность результатов расчетов подтверждена приведенными в работе зависимостями относительной погрешности выполнения закона сохранения энергии от нормированной частоты и сравнением с результатами, полученными с помощью САПР. Обоснованность применения метода интегральных уравнений и построенного на его основе численно-аналитического алгоритма подтверждена исследованием сходимости результатов расчета в зависимости от номера приближения, в котором решалась дифракционная задача. Одним из главных достоинств предлагаемого метода является хорошо контролируемая достоверность полученных результатов. Метод обладает нестандартной процедурой вывода интегральных уравнений и достаточной общностью в применении к решению внутренних краевых дифракционных задач.