Радиотехника и электроника, 2020, T. 65, № 4, стр. 342-352
Электродинамический анализ одномерной решетки со случайными параметрами
С. Е. Банков *
Институт радиотехники и электроники им. В.А. Котельникова РАН
125009 Москва, ул. Моховая, 11, стр. 7, Российская Федерация
* E-mail: sbankov@yandex.ru
Поступила в редакцию 26.09.2019
После доработки 26.09.2019
Принята к публикации 25.10.2019
Аннотация
Предложен метод электродинамического анализа бесконечных одномерных антенных решеток со случайными параметрами. Представленный подход основан на использовании метода компенсирующих источников и метода обобщенной матрицы рассеяния, которые позволяют анализировать бесконечные неоднородные антенные решетки, содержащие дефекты периодической структуры в виде элементов с параметрами, отличающимися от параметров регулярной структуры. Решетка анализируется в предположении малых отклонений ее параметров от средних значений. В указанном приближении получены оценки для дисперсии амплитуд отраженных от входов решетки волн и дисперсии некогерентного поля излучения. Рассмотрен режим квазипериодического возбуждения решетки. Предложенный метод использован для анализа решетки ленточных вибраторов со случайной длиной. Получена зависимость дисперсии коэффициента отражения решетки от ее параметров. Показано, что теоретическая оценка дисперсии совпадает с ее значением, полученным методом статистических испытаний, при помощи которого анализируется вибраторная решетка конечной длины.
1. ПОСТАНОВКА ЗАДАЧИ
Статистический анализ радиоэлектронного устройства является типовым этапом его разработки [1], позволяющим оценить устойчивость технического решения к погрешностям, которые неизбежно возникают в ходе изготовления. В полной мере данное утверждение относится к фазированным антенным решеткам (ФАР), которые в настоящее время представляют собой сложные радиоэлектронные комплексы, выполняющие широкий набор функций [2].
Актуальность задачи статистического анализа ФАР не вызывает сомнений. В настоящее время теоретической основой ее решения является статистическая теория антенн (СТА), созданная Я.С. Шифриным [3]. В наиболее полном виде современное ее состояние отражено в монографии [4]. Отмеченная выше теория позволяет получать оценки для статистических параметров полей излучения, которые создаются случайными источниками.
Такой подход оказывается весьма эффективным, когда источник статистических отклонений параметров решетки находится вне излучающего полотна. Как правило, источниками таких отклонений считают электронные компоненты, формирующие амплитудно-фазовое распределение поля в раскрыве решетки: фазовращатели, усилители и другие элементы приемо-передающих модулей. Статистическая теория антенн позволяет эффективно оценивать их влияние на диаграмму направленности ФАР. Следует отметить, что при этом предполагается, что излучающая часть решетки, которую часто называют излучающим полотном, является объектом с детерминированными параметрами.
В то же время необходимо сказать, что, как всякий физический объект, излучающее полотно также имеет случайные параметры, которые обусловлены погрешностями изготовления и установки элементарных излучателей (ЭИ). Поэтому оценка их влияния на функционирование ФАР является актуальной задачей. При определенных допущениях мы можем использовать СТА для ее решения. В частности, к ним относится предположение о пренебрежимо малом влиянии взаимодействия ЭИ в решетке. Однако неоднократно было показано (см., например, [5]), что такое предположение является весьма грубым приближением, использование которого может привести к качественно неверным выводам.
Учет взаимодействия ЭИ ставит под сомнение возможность непосредственного использования СТА, поскольку само распределение случайных источников становится результатом решения сложной электродинамической задачи. Ее сложность связана с тем, что решетка со случайными параметрами, строго говоря, является непериодической структурой, так как все ее элементы отличаются друг от друга. При этом наибольшую проблему представляет анализ ФАР больших электрических размеров с большим коэффициентом усиления (КУ).
В связи с тем, что задача электродинамического анализа ФАР с большими размерами даже для одинаковых ЭИ представляет весьма значительную сложность, в этом случае можно эффективно использовать приближение бесконечной решетки [6]. Если решетка бесконечна и однородна, то граничная задача для нее сводится к анализу одного периода, который часто называют каналом Флоке [7]. Его электрические размеры относительно невелики, и поэтому эффективное решение граничной задачи может быть получено с использованием современных систем электродинамического моделирования, таких как HFSS и CST MWS [8].
Для решетки со случайными параметрами строго использовать приближение канала Флоке невозможно, так как даже бесконечная структура оказывается непериодической. Поэтому единственным подходом для оценки характеристик такой ФАР оказывается прямое численное решение граничной задачи для решетки больших, но конечных электрических размеров. Очевидно, что реализация такого решения потребует очень больших затрат временных и компьютерных ресурсов.
Целью данной работы является получение теоретических статистических оценок для показателей качества решетки со случайными параметрами. При этом под решеткой понимаем исключительно излучающую часть ФАР. Мы будем рассматривать бесконечные одномерные или линейные решетки. Известно, что понятие диаграммы направленности для бесконечной структуры неприменимо [5], так как она, вне зависимости от типа ЭИ, имеет вид дельта-функции. Поэтому наибольший интерес для нас представляет такой показатель качества как коэффициент отражения ЭИ. Мы получим теоретическую оценку дисперсии модуля амплитуды волны, отраженной от входа ЭИ.
Для решения поставленной выше задачи нам необходимо определенным образом описать антенную решетку. Теоретический задел такого описания представлен в [9]. В ней развит метод компенсирующих источников (МКИ) для случая бесконечных линейных ФАР. Впервые МКИ был предложен в работе [10]. Он был использован для электродинамического анализа двумерных неоднородных фотонных и электромагнитных кристаллов. Развитие МКИ для анализа излучающих структур потребовало его существенной модификации, которая связана с использованием метода обобщенной матрицы рассеяния (ОМР). Метод ОМР (МОМР) был разработан и использован для анализа ФАР с большими электрическими размерами [11, 12].
Известно несколько модификаций МОМР. Все они основаны на разделении поля в окрестности ЭИ на возбуждающее и рассеянное поля, связанные друг с другом с помощью оператора рассеяния. Оба вида полей должны быть записаны в стандартной форме в виде разложений по некоторой системе функций. В качестве таких функций будем использовать векторные сферические гармоники (ВСГ), которые являются решениями уравнений Максвелла в сферических координатах. Пример применения метода МОМР с разложением по ВСГ (РВСГ) для анализа больших линейных решеток представлен в [13].
Достоинством МОМР и построенного на его основе МКИ является то, что они простым образом учитывают индивидуальные особенности ЭИ, которые полностью описываются при помощи операторов рассеяния. При использовании РВСГ оператор рассеяния имеет вид матрицы, связывающей амплитуды рассеянных и возбуждающих ВСГ.
Операторы рассеяния однократно определяются для уединенных излучателей, а затем многократно используются в рамках МОМР и МКИ для описания взаимодействия ЭИ. Такое разделение этапов позволяет существенно повысить эффективность алгоритмов численного решения сложной граничной задачи.
2. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОМР-МКИ
Основные положения МОМР. В данном разделе мы изложим основные положения и уравнения МОМР и МКИ, полученные в работе [9] для линейной бесконечной решетки. Они необходимы нам для решения поставленных выше задач. Будем описывать положение ЭИ в линейной решетке, ориентированной вдоль оси 0х, с помощью индекса $\nu $, который изменяется от минус до плюс бесконечности.
Для определения типа ВСГ используем один векторный индекс $N$:
где $n$ – угломестный индекс ВСГ, а $m$ – азимутальный индекс.
Введем по аналогии с работой [13] векторы ${{{\mathbf{\vec {E}}}}_{{i,s\nu }}},$ ${{{\mathbf{\vec {H}}}}_{{i,s\nu }}},$ ${{{\mathbf{A}}}_{{i,s\nu }}}.$ Векторы ${{{\mathbf{\vec {E}}}}_{{i,s\nu }}},$${{{\mathbf{\vec {H}}}}_{{i,s\nu }}},$ формируются из векторов электрического и магнитного полей возбуждающих и рассеянных ВСГ (нижние индексы $i,s$), а векторы ${{{\mathbf{A}}}_{{i,s\nu }}}$ состоят из амплитуд указанных ВСГ. Важно отметить, что поля ВСГ задаются в локальных системах координат, связанных с ЭИ с номером $\nu $. Явные выражения для полей ВСГ можно найти в [14].
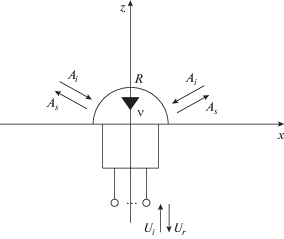
Каждый ЭИ окружен полусферой с электрическим радиусом $R$ (рис. 1). Важно, что полусферы соседних ЭИ не имеют точек пересечения. Источником возбуждающих волн для μ-го ЭИ являются волны рассеянные всеми элементами решетки, за исключением μ-го. Источником рассеянных волн этого излучателя является дифракция возбуждающих волн на нем, а также падающие волны на его входы. Предполагаем, что таких входов может быть не один, а несколько. Объединяя амплитуды падающих волн ${{U}_{{i\mu ,j}}}$ ($j$ – номер входа), получаем вектор падающих волн μ-го ЭИ-${{{\mathbf{U}}}_{{i\mu }}}$. Аналогично можно получить вектор отраженных волн ${\mathbf{U}}_{{r\mu }}^{{}}$.
Отметим, что при отсутствии пересечений сфер, окружающих ЭИ, они оказываются расположенными вне областей, занятых источниками, что позволяет нам представить поля на них в виде разложений по ВСГ:
(2)
$\begin{gathered} {{{\vec {E}}}_{\nu }} = {{{\vec {E}}}_{{i\nu }}} + {{{\vec {E}}}_{{s\nu }}},\,\,\,\,{{{\vec {H}}}_{\nu }} = {{{\vec {H}}}_{{i\nu }}} + {{{\vec {H}}}_{{s\nu }}}, \\ \left( \begin{gathered} {{{\vec {E}}}_{{i,s\nu }}} \hfill \\ {{{\vec {H}}}_{{i,s\nu }}} \hfill \\ \end{gathered} \right) = {{{\mathbf{A}}}_{{i,s\nu }}}\left( \begin{gathered} {\mathbf{\vec {E}}}_{{i,s\nu }}^{{}} \\ {\mathbf{\vec {H}}}_{{i,s\nu }}^{{}} \\ \end{gathered} \right), \\ \end{gathered} $Нам необходимо различать векторы в пространстве ВСГ, а также векторы отраженных/падающих волн от векторов, заданных в физическом пространстве. Для обозначения векторов первых типов используем символы вида ${\mathbf{A}}$, а для обозначения векторов физического пространства используем стрелки $ \to $. В этом случае символ ${\mathbf{\vec {E}}}$ обозначает вектор в пространстве ВСГ, элементами которого являются векторы из физического пространства, символ ${\mathbf{A}}$ описывает вектор из пространства ВСГ, элементами которого являются скалярные величины. Произведение вида ${\mathbf{A\vec {E}}}$ – это скалярное произведение в пространстве ВСГ, результатом которого является вектор из физического пространства.
Следующий этап МОМР – определение связи между амплитудами волн, рассеянных $\nu $-м ЭИ и амплитудами волн, падающих на $\mu $-й ЭИ. Для определения указанной связи нам необходимо осуществить разложение поля рассеянной волны $\nu $-го ЭИ в системе координат $\mu $-го ЭИ. Вне зависимости от способа решения этой задачи мы приходим к следующему соотношению:
Матрицы ${\mathbf{K}}$ описывают искомую связь между амплитудами рассеянных на $\nu $-м и возбуждающих на μ-м элементах волн. Назовем их матрицами связи.
Далее необходимо ввести оператор рассеяния ЭИ, который связывает амплитуды возбуждающих и рассеянных волн ЭИ. Отметим, что наряду с ВСГ он может возбуждаться волноводными волнами со стороны своих портов. Оператор рассеяния находим в результате решения электродинамической граничной задачи. Будем полагать, что оно известно и может быть записано в следующей форме:
(4)
$\begin{gathered} {{{\mathbf{A}}}_{{s\mu }}} = {{{\mathbf{L}}}_{{ss\mu }}}{{{\mathbf{A}}}_{{i\mu }}} + {{{\mathbf{L}}}_{{sw\mu }}}{{{\mathbf{U}}}_{{i\mu }}}, \\ {{{\mathbf{U}}}_{{r\mu }}} = {{{\mathbf{L}}}_{{ws\mu }}}{{{\mathbf{A}}}_{{i\mu }}} + {{{\mathbf{L}}}_{{ww\mu }}}{{{\mathbf{U}}}_{{i\mu }}}, \\ \end{gathered} $где ${\mathbf{L}}$ – искомые операторы рассеяния. Для однородной решетки с одинаковыми ЭИ все операторы рассеяния также идентичны, поэтому для них индекс $\mu $ можно опустить.
Суммируя в выражении (3) по всем ЭИ, кроме μ-го, и подставляя в него соотношения (4), получаем основные уравнения МОМР:
(5)
${{{\mathbf{A}}}_{{s\mu }}} = \sum\limits_{\nu = - \infty }^\infty {^{{(\mu )}}{{{\mathbf{L}}}_{{ss}}}{{{\mathbf{K}}}_{{\mu ,\nu }}}{{{\mathbf{A}}}_{{s\nu }}}} + {{{\mathbf{L}}}_{{sw}}}{{{\mathbf{U}}}_{{i\mu }}},$(6)
${{{\mathbf{U}}}_{{r\mu }}} = \sum\limits_{\nu = - \infty }^\infty {^{{(\mu )}}{{{\mathbf{L}}}_{{ws}}}{{{\mathbf{K}}}_{{\mu ,\nu }}}{{{\mathbf{A}}}_{{s\nu }}}} + {{{\mathbf{L}}}_{{ww}}}{{{\mathbf{U}}}_{{i\mu }}}.$Верхний символ (μ) означает суммирование по всем ЭИ кроме μ-го. Наибольший интерес представляет записанная в матричной форме система линейных алгебраических уравнений (СЛАУ) (5), которая описывает взаимодействие ЭИ через свободное пространство.
Основные положения МКИ. Определим компенсирующий источник (КИ) следующим образом. Он ассоциирован с некоторым ЭИ с индексом $\xi $ и создает рассеянные волны с амплитудным вектором Vξ. Тогда уравнение (5) при наличии КИ приобретает новый вид:
(7)
$\begin{gathered} {{{\mathbf{A}}}_{{s\mu }}} = \sum\limits_{\nu = - \infty }^\infty {^{{(\mu )}}{{{\mathbf{W}}}_{{\mu ,\nu }}}{{{\mathbf{A}}}_{{s\nu }}}} + {{{\mathbf{L}}}_{{sw}}}{{{\mathbf{U}}}_{{i\mu }}} + {{{\mathbf{V}}}_{\xi }}{{\delta }_{{\mu ,\xi }}}, \\ {{{\mathbf{W}}}_{{\mu ,\nu }}} = {{{\mathbf{L}}}_{{ss}}}{{{\mathbf{K}}}_{{\mu ,\nu }}}, \\ \end{gathered} $где ${{\delta }_{{\mu ,\xi }}}$ – символ Кронекера, равный единице при совпадении индексов $\mu ,\xi $. Назовем матрицы ${\mathbf{W}}_{{\mu ,\nu }}^{{}}$ матрицами взаимодействий. Отметим, что в силу периодичности решетки матрица взаимодействий зависит только от разности индексов $\mu - \nu $, т.е. является матрицей Теплица.
Определим матрицу взаимодействий при $\mu - \nu = 0$ как нулевую матрицу. Тогда в СЛАУ (7) можем распространить суммирование на все элементы решетки. Применим далее к соотношению (7) дискретное преобразование Фурье (ДПФ). Предварительно введем функции ${{{\mathbf{a}}}_{{i,s}}}\left( \kappa \right),$ ${\mathbf{\omega }}\left( \kappa \right),$ ${\mathbf{u}}\left( \kappa \right),$ являющиеся ДПФ соответственно последовательностей ${{{\mathbf{A}}}_{{i,s\mu }}},$ ${{{\mathbf{W}}}_{\mu }},$ ${{{\mathbf{U}}}_{{i\mu }}}.$ Теперь можем записать результат применения ДПФ к выражению (7) и найти вектор ${{{\mathbf{a}}}_{s}}$:
(8)
${{{\mathbf{a}}}_{s}}\left( \kappa \right) = {{\left( {{\mathbf{E}} - {\mathbf{\omega }}\left( \kappa \right)} \right)}^{{ - 1}}}\left( {{{{\mathbf{L}}}_{{sw}}}{\mathbf{u}}\left( \kappa \right) + {{{\mathbf{V}}}_{\xi }}\exp \left( {i\kappa \xi P} \right)} \right),$где $P$ – период решетки.
С помощью обратного ДПФ находим искомые векторы ${{{\mathbf{A}}}_{{s\mu }}}$:
(9)
${{{\mathbf{A}}}_{{s\mu }}} = \sum\limits_{\nu = - \infty }^\infty {{{{\mathbf{G}}}_{{s\mu ,\nu }}}{{{\mathbf{L}}}_{{sw}}}{{{\mathbf{U}}}_{{i\nu }}}} + {{{\mathbf{G}}}_{{s\mu ,\xi }}}{{{\mathbf{V}}}_{\xi }}.$(10)
${{{\mathbf{G}}}_{{s\mu ,\xi }}} = \frac{P}{{2\pi }}\int\limits_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } P}} \right. \kern-0em} P}}^{{\pi \mathord{\left/ {\vphantom {\pi P}} \right. \kern-0em} P}} {{{{\left( {{\mathbf{E}} - {\mathbf{\omega }}\left( \kappa \right)} \right)}}^{{ - 1}}}\exp \left( { - i\kappa (\mu - \xi )P} \right)d\kappa } .$Если в решетке присутствует множество КИ, то в формуле (9) необходимо осуществить суммирование по всем источникам. Назовем функцию индексов μ, ξ – ${{{\mathbf{G}}}_{{s\mu ,\xi }}}$ функцией Грина бесконечной решетки для рассеянных волн. Нам будет полезно получить выражение для функции Грина возбуждающих волн ${{{\mathbf{G}}}_{{i\mu ,\xi }}}$, которая связывает векторы${{{\mathbf{A}}}_{{i\mu }}}$ с КИ:
(11)
$\begin{gathered} {{{\mathbf{G}}}_{{i\mu ,\xi }}} = \frac{P}{{2\pi }} \times \\ \times \,\,\int\limits_{ - \pi /P}^{\pi /P} {{\mathbf{Q}}\left( \kappa \right){{{\left( {{\mathbf{E}} - {\mathbf{\omega }}\left( \kappa \right)} \right)}}^{{ - 1}}}\exp \left( { - i\kappa (\mu - \xi )P} \right)d\kappa } . \\ \end{gathered} $(12)
${{{\mathbf{A}}}_{{i\mu }}} = \sum\limits_{\nu = - \infty }^\infty {{{{\mathbf{G}}}_{{i\mu ,\nu }}}{{{\mathbf{L}}}_{{sw}}}{{{\mathbf{U}}}_{{i\nu }}}} + \sum\limits_\xi {{{{\mathbf{G}}}_{{i\mu ,\xi }}}{{{\mathbf{V}}}_{\xi }}} .$Приведем соотношение, связывающее функции ${{{\mathbf{G}}}_{{i\mu ,\xi }}}$ и ${{{\mathbf{G}}}_{{s\mu ,\xi }}}$:
(13)
${{{\mathbf{L}}}_{{ss}}}{{{\mathbf{G}}}_{{i\mu ,\xi }}} + {\mathbf{E}}{{\delta }_{{\mu ,\xi }}} = {{{\mathbf{G}}}_{{s\mu ,\xi }}}.$Режим квазипериодического возбуждения решетки является типовым режимом работы ФАР. В этом режиме векторы ${{{\mathbf{U}}}_{{i\nu }}}$ имеют вид
где ${{\kappa }_{0}}$ – заданный параметр, определяющий фазовые сдвиги между каналами решетки в квазипериодическом режиме. Кроме того, этот вектор определяет углы излучения решетки в свободное пространство. Находим ДПФ последовательности векторов ${{{\mathbf{U}}}_{{i\nu }}}$ – ${\mathbf{u}}\left( \kappa \right)$, применяя формулу суммирования Пуассона [5]:
(15)
${\mathbf{u}}\left( \kappa \right) = 2\pi {{{\mathbf{U}}}_{0}}\delta {{(\kappa - {{\kappa }_{0}})} \mathord{\left/ {\vphantom {{(\kappa - {{\kappa }_{0}})} P}} \right. \kern-0em} P},$где $\delta (\kappa - {{\kappa }_{0}})$ – дельта функция. Выражения для амплитудных векторов в квазипериодическом режиме имеют следующий вид:
(16)
$\begin{gathered} {{{\mathbf{A}}}_{{s\mu }}} = {{{\mathbf{q}}}_{{s0}}}{{{\mathbf{U}}}_{0}}\exp ( - i{{\kappa }_{0}}\mu P) + \sum\limits_\xi {{{{\mathbf{G}}}_{{s\mu ,\xi }}}{{{\mathbf{V}}}_{\xi }}} , \\ {{{\mathbf{A}}}_{{i\mu }}} = {{{\mathbf{q}}}_{{i0}}}{{{\mathbf{U}}}_{0}}\exp ( - i{{\kappa }_{0}}\mu P) + \sum\limits_\xi {{{{\mathbf{G}}}_{{i\mu ,\xi }}}{{{\mathbf{V}}}_{\xi }}} , \\ {{{\mathbf{q}}}_{{i0}}} = {\mathbf{Q}}\left( {{{\kappa }_{0}}} \right){{\left( {{\mathbf{E}} - {\mathbf{\omega }}\left( {{{\kappa }_{0}}} \right)} \right)}^{{ - 1}}}{{{\mathbf{L}}}_{{sw}}}, \\ {{{\mathbf{q}}}_{{s0}}} = {{\left( {{\mathbf{E}} - {\mathbf{\omega }}\left( {{{\kappa }_{0}}} \right)} \right)}^{{ - 1}}}{{{\mathbf{L}}}_{{sw}}}. \\ \end{gathered} $Приведем далее СЛАУ, к которой сводится граничная задача о решетке с дефектами. Под дефектом мы понимаем любой ЭИ, имеющий операторы рассеяния ${{{\mathbf{L}}}^{d}}$, отличающиеся от операторов рассеяния ${\mathbf{L}}$ регулярной решетки. Соотношения (4) для дефекта имеют вид
(17)
$\begin{gathered} {\mathbf{A}}_{{s\mu }}^{{}} = {\mathbf{L}}_{{^{{ss\mu }}}}^{d}{\mathbf{A}}_{{i\mu }}^{{}} + {\mathbf{L}}_{{sw\mu }}^{d}{{{\mathbf{U}}}_{{i\mu }}}, \\ {\mathbf{U}}_{{r\mu }}^{{}} = {\mathbf{L}}_{{ws\mu }}^{d}{\mathbf{A}}_{{i\mu }}^{{}} + {\mathbf{L}}_{{ww\mu }}^{d}{\mathbf{U}}_{{i\mu }}^{{}}. \\ \end{gathered} $Их можно рассматривать в качестве граничных условий для амплитудных векторов на дефекте в регулярной решетке. В большей степени нас интересует первое уравнение из (17), так как оно позволяет найти векторы ${\mathbf{A}}_{{i,s\mu }}^{{}}$. И затем с помощью второго соотношения (17) не составляет труда найти векторы ${\mathbf{U}}_{{r\mu }}^{{}}$.
Допустим, что анализируемая неоднородная решетка является по-прежнему однородной, но в ЭИ с дефектами введены КИ. Тогда из уравнений (7) и (17) получаем
(18)
${{{\mathbf{V}}}_{\xi }} = \left( {{\mathbf{L}}_{{ss\xi }}^{d} - {{{\mathbf{L}}}_{{ss}}}} \right){\mathbf{A}}_{{i\xi }}^{{}} + \left( {{\mathbf{L}}_{{sw\xi }}^{d} - {{{\mathbf{L}}}_{{sw}}}} \right){{{\mathbf{U}}}_{{i\xi }}}.$С использованием найденной выше функции Грина можем выразить амплитудные векторы ${\mathbf{A}}_{{i\xi }}^{{}}$ через КИ и получить для них искомую СЛАУ, описывающую решетку с дефектами:
(19)
$\begin{gathered} {{{\mathbf{V}}}_{\xi }} - \Delta {{{\mathbf{L}}}_{{ss\xi }}}\sum\limits_{\nu = - \infty }^\infty {{{{\mathbf{G}}}_{{i\xi ,\nu }}}{{{\mathbf{V}}}_{\nu }}} = \\ = \Delta {{{\mathbf{L}}}_{{ss\xi }}}\sum\limits_{\nu = - \infty }^\infty {{{{\mathbf{G}}}_{{i\xi ,\nu }}}{{{\mathbf{L}}}_{{sw}}}{{{\mathbf{U}}}_{{i\nu }}}} + \Delta {{{\mathbf{L}}}_{{sw\xi }}}{{{\mathbf{U}}}_{{i\xi }}}, \\ \Delta {{{\mathbf{L}}}_{{ss\xi }}} = {\mathbf{L}}_{{ss\xi }}^{d} - {{{\mathbf{L}}}_{{ss}}}, \\ \Delta {{{\mathbf{L}}}_{{sw\xi }}} = {\mathbf{L}}_{{sw\xi }}^{d} - {{{\mathbf{L}}}_{{sw}}}. \\ \end{gathered} $В правой части (19) находятся известные величины. В квазипериодическом режиме уравнение (19) имеет следующий вид:
(20)
$\begin{gathered} {{{\mathbf{V}}}_{\xi }} - \Delta {{{\mathbf{L}}}_{{ss\xi }}}\sum\limits_{\nu = - \infty }^\infty {{{{\mathbf{G}}}_{{i\xi ,\nu }}}{{{\mathbf{V}}}_{\nu }}} = \\ = \left( {\Delta {{{\mathbf{L}}}_{{ss\xi }}}{{{\mathbf{q}}}_{{i0}}} + \Delta {{{\mathbf{L}}}_{{sw\xi }}}} \right){{{\mathbf{U}}}_{0}}\exp ( - i{{\kappa }_{0}}\xi P). \\ \end{gathered} $В заключение данного раздела приведем соотношения, описывающие эффективный алгоритм вычисления матрицы ${\mathbf{Q}}(\kappa )$, необходимой для применения МКИ:
(21)
$\begin{gathered} {\mathbf{Q}}(\kappa ) = \sum\limits_{\mu = - {{\mu }_{m}}}^{{{\mu }_{m}}} {^{{(0)}}\left( {{{{\mathbf{K}}}_{\mu }} - {{{\mathbf{K}}}_{{a\mu }}}} \right)\exp (i\kappa \mu P)} + {{{\mathbf{Q}}}_{a}}(\kappa ), \\ {{{\mathbf{Q}}}_{a}}(\kappa ) = \sum\limits_{\mu = - \infty }^\infty {^{{(0)}}{{{\mathbf{K}}}_{{a\mu }}}\exp (i\kappa \mu P)} . \\ \end{gathered} $В первом выражении (21) суммирование ведется в конечных пределах, задаваемых параметром ${{\mu }_{m}}$, а во втором – в бесконечных пределах по всем элементам решетки, за исключением нулевого. Асимптотическое выражение для матрицы связи ${{{\mathbf{K}}}_{{a\mu }}}$ взято из работы [13]:
(22)
$\begin{gathered} {{{\mathbf{K}}}_{{a\mu }}} = \left( {{{{{\mathbf{\tilde {a}}}}}_{{1\mu }}}{{{\left( {\left| \mu \right|P} \right)}}^{{ - 1}}} + {{{{\mathbf{\tilde {a}}}}}_{{2\mu }}}{{{\left( {\left| \mu \right|P} \right)}}^{{ - 2}}}} \right)\exp ( - ik\left| \mu \right|P), \\ {{{{\mathbf{\tilde {a}}}}}_{{1,2\mu N,M}}} = {{{\mathbf{a}}}_{{1,2N,M}}}\exp ( - i({{m}_{N}} - {{m}_{M}}){{\varphi }_{\mu }}), \\ \end{gathered} $где $M$ – номер пространственной гармоники μ-го ЭИ, а $N$ – номер гармоники нулевого ЭИ, $m$ – азимутальный индекс гармоник, ${{r}_{\mu }}$,${{\varphi }_{\mu }}$ – радиальная и азимутальная координаты μ-го ЭИ в системе координат нулевого ЭИ, ${{{\mathbf{a}}}_{{1,2}}}$ – известные матрицы. Отметим, что для линейной решетки угол ${{\varphi }_{\mu }}$ принимает два значения: 0 при $\mu > 0$ и $\pi $ при $\mu < 0$.
Для матрицы ${{{\mathbf{Q}}}_{a}}(\kappa )$ в работе [9] получены следующие соотношения:
(23)
$\begin{gathered} {{{\mathbf{Q}}}_{a}}(\kappa ) = {{{\mathbf{a}}}_{1}}{{\left( {{{S}_{1}}((k - \kappa )P){\mathbf{q}} + {{S}_{1}}((k + \kappa )P)} \right)} \mathord{\left/ {\vphantom {{\left( {{{S}_{1}}((k - \kappa )P){\mathbf{q}} + {{S}_{1}}((k + \kappa )P)} \right)} P}} \right. \kern-0em} P} + \\ + \,\,{{{\mathbf{a}}}_{2}}{{\left( {{{S}_{2}}((k - \kappa )P){\mathbf{q}} + {{S}_{2}}((k + \kappa )P)} \right)} \mathord{\left/ {\vphantom {{\left( {{{S}_{2}}((k - \kappa )P){\mathbf{q}} + {{S}_{2}}((k + \kappa )P)} \right)} {{{P}^{2}}}}} \right. \kern-0em} {{{P}^{2}}}}, \\ \end{gathered} $(24)
$\begin{gathered} {{{\mathbf{q}}}_{{N,M}}} = \exp ( - i\pi ({{m}_{N}} - {{m}_{M}})), \\ {{S}_{1}}(x) = \ln ({1 \mathord{\left/ {\vphantom {1 {(1}}} \right. \kern-0em} {(1}} - \exp ( - ix))). \\ \end{gathered} $Ряд для функции S2(x) суммировать аналитически не удается, но для него можно предложить приближенное выражение, выбирая в котором параметр ${{N}_{m}}$ достаточно большим, можно рассчитать искомую функцию с любой требуемой точностью:
(25)
$\begin{gathered} {{S}_{2}}(x) = \left( {1 + \left( {\exp (ix) - 1} \right)\ln \left( {1 - \exp ( - ix)} \right)} \right) + \\ + \,\,\sum\limits_{n = 1}^{{{N}_{m}}} {\exp ( - inx)\left( {\frac{1}{{{{n}^{2}}}} - \frac{1}{{n(n + 1)}}} \right)} . \\ \end{gathered} $На практике достаточно взять параметр ${{N}_{m}}$ в пределах 5…7.
3. АНАЛИЗ РЕШЕТКИ СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
Рассмотрим теперь непериодическую решетку. Пусть причина непериодичности связана с тем, что некоторый параметр $x$ разный у разных ЭИ. Таким образом, мы можем говорить о множестве значений параметра ${{x}_{\mu }}$. Представим ${{x}_{\mu }}$ следующим образом:
где $x$ – некоторое номинальное среднее значение параметра, а $\Delta {{x}_{\mu }}$ – его отклонение, которое, как мы предполагаем, является малой величиной.
Отклонение параметра ${{x}_{\mu }}$ от номинала приводит к изменениям операторов рассеяния (4):
где ${\mathbf{L}}{\kern 1pt} '$ – производная оператора ${\mathbf{L}}$ в точке ${{x}_{\mu }} = x$. Мы предполагаем, что соотношения вида (26) могут быть записаны для всех четырех типов операторов (4).
Нетрудно видеть, что выражение (26) является разложением оператора ${\mathbf{L}}_{{^{\mu }}}^{{}}$ в ряд Тейлора, в котором удержаны только линейные слагаемые. Отклонение $\Delta {{x}_{\mu }}$ должно быть достаточно малым, чтобы приближенное равенство (26) выполнялось с приемлемой точностью.
В соответствии с МКИ каждый ЭИ, отличающийся от номинального, является дефектом решетки, который мы описываем при помощи КИ ${{{\mathbf{V}}}_{\xi }}$. С учетом (26) и (18) получаем
(27)
${{{\mathbf{V}}}_{\xi }} = \Delta {{x}_{\xi }}\left( {{\mathbf{L}}_{{ss}}^{'}{{{\mathbf{A}}}_{{i\xi }}} + {\mathbf{L}}_{{sw}}^{'}{{{\mathbf{U}}}_{{i\xi }}}} \right).$С точностью до слагаемых пропорциональных первой степени малых параметров $\Delta {{x}_{\xi }}$ нам достаточно найти вектора ${\mathbf{A}}_{{i\xi }}^{{}}$ в нулевом приближении, то есть для периодической решетки с номинальными параметрами. Сделаем это для наиболее интересного режима квазипериодического возбуждения, воспользовавшись соотношением (16):
(28)
${{{\mathbf{A}}}_{{i\xi }}} = {{{\mathbf{q}}}_{{i0}}}{{{\mathbf{U}}}_{0}}\exp ( - i{{\kappa }_{0}}\xi P).$В формуле (16) мы приняли во внимание только первое слагаемое, имеющее нулевой порядок малости. Подставим далее выражение (28) в (27):
(29)
${{{\mathbf{V}}}_{\xi }} = \Delta {{x}_{\xi }}\left( {{\mathbf{L}}_{{ss}}^{'}{{{\mathbf{q}}}_{{i0}}} + {\mathbf{L}}_{{sw}}^{'}} \right){{{\mathbf{U}}}_{0}}\exp ( - i{{\kappa }_{0}}\xi P).$Соотношение (29) теперь представляет КИ через известные параметры решетки.
Амплитуды рассеянных волн в нулевом приближении имеют следующий вид:
(30)
${{{\mathbf{A}}}_{{s\mu }}} = {{{\mathbf{q}}}_{{s0}}}{{{\mathbf{U}}}_{0}}\exp ( - i{{\kappa }_{0}}\mu P).$Добавка к ним $\Delta {{{\mathbf{A}}}_{{s\mu }}}$, обусловленная отклонениями параметра $\Delta {{x}_{\mu }}$, находится с помощью функции Грина (10):
(31)
$\begin{gathered} \Delta {{{\mathbf{A}}}_{{s\mu }}} = \sum\limits_\xi {\Delta {{x}_{\xi }}} {{{\mathbf{G}}}_{{s\mu ,\xi }}}{{{\mathbf{v}}}_{0}}\exp ( - i{{\kappa }_{0}}\xi P), \\ {{{\mathbf{v}}}_{0}} = \left( {{\mathbf{L}}_{{ss}}^{'}{{{\mathbf{q}}}_{{i0}}} + {\mathbf{L}}_{{sw}}^{'}} \right){{{\mathbf{U}}}_{0}}. \\ \end{gathered} $Добавка к амплитудам возбуждающих волн $\Delta {{{\mathbf{A}}}_{{i\mu }}}$ находится аналогично (31) с помощью соотношения (11):
(32)
$\Delta {{{\mathbf{A}}}_{{i\mu }}} = \sum\limits_\xi {\Delta {{x}_{\xi }}} {{{\mathbf{G}}}_{{i\mu ,\xi }}}{{{\mathbf{v}}}_{0}}\exp ( - i{{\kappa }_{0}}\xi P).$Соотношения (31), (32) дают в первом приближении решение граничной задачи для непериодической бесконечной решетки. Далее будем считать параметр $\Delta x$ случайной величиной с нулевым математическим ожиданием и дисперсией ${{\sigma }_{x}}$. Соотношения (31), (32) являются базовыми для вывода интересующих нас статистических оценок характеристик решетки.
4. ДИСПЕРСИЯ ОТРАЖЕННЫХ ОТ ВХОДОВ РЕШЕТКИ ВОЛН
Найдем теперь, используя соотношение (6), поправки к амплитудам отраженных от входов ЭИ волн $\Delta {{{\mathbf{U}}}_{{r\mu }}}$:
(33)
$\begin{gathered} \Delta {{{\mathbf{U}}}_{{r\mu }}} = \sum\limits_{\nu = - \infty }^\infty {^{{(\mu )}}\left( {{{{\mathbf{L}}}_{{ws}}}{{{\mathbf{K}}}_{{\mu ,\nu }}}\Delta {{{\mathbf{A}}}_{{s\nu }}} + \Delta {{x}_{\mu }}{\mathbf{L}}_{{ws}}^{'}{{{\mathbf{K}}}_{{\mu ,\nu }}}{{{\mathbf{A}}}_{{s\nu }}}} \right)} + \\ + \,\,\Delta {{x}_{\mu }}{\mathbf{L}}_{{ww}}^{'}{{{\mathbf{U}}}_{{i\mu }}}. \\ \end{gathered} $В квазипериодическом режиме для этого же можем воспользоваться соотношениями (30), (31):
(34)
$\begin{gathered} \Delta {{{\mathbf{U}}}_{{r\mu }}} = \\ = \sum\limits_{\xi = - \infty }^\infty {\Delta {{x}_{\xi }}\left( {{{{\mathbf{L}}}_{{ws}}}{{{\mathbf{G}}}_{{i\mu ,\xi }}}{{{\mathbf{v}}}_{0}} + {{{\mathbf{w}}}_{0}}{{\delta }_{{\mu ,\xi }}}} \right)\exp ( - i{{\kappa }_{0}}\xi P)} , \\ \end{gathered} $где ${{\delta }_{{\mu ,\xi }}}$ – символ Кронекера.
Выражение (34) описывает добавки к амплитудам отраженных от входов ЭИ волн, которые обусловлены отклонениями параметра $x$ от своего номинального значения.
Далее найдем усредненные значения величин ${{\left| {\Delta {{{\mathbf{U}}}_{{r\mu }}}} \right|}^{2}},$ которые равны ${{\sigma }_{{u\mu }}}$ – дисперсии модуля случайной составляющей амплитуды отраженной волны. При этом будем исходить из того, что случайные параметры $\Delta {{x}_{\xi }}$ статистически независимы и имеют одинаковые значения дисперсии.
С учетом этих допущений получаем
(35)
$\sigma _{{u\mu }}^{2} = \sigma _{x}^{2}\sum\limits_{\xi = - \infty }^\infty {{{{\left| {{{{\mathbf{L}}}_{{ws}}}{{{\mathbf{G}}}_{{i\mu ,\xi }}}{{{\mathbf{v}}}_{0}} + {{{\mathbf{w}}}_{0}}{{\delta }_{{\mu ,\xi }}}} \right|}}^{2}}} .$Для вычисления ряда в формуле (35) воспользуемся выражением (11) и также учтем, что
(36)
${{\delta }_{{\mu ,\xi }}} = \frac{P}{{2\pi }}\int\limits_{ - \pi /P}^{\pi /P} {\exp ( - i\kappa (\mu - \xi )P)d\kappa } .$В результате получаем
(37)
$\sigma _{u}^{2} = \frac{{\sigma _{x}^{2}P}}{{2\pi }}\int\limits_{ - \pi /P}^{\pi /P} {{{{\left| {{{{\mathbf{L}}}_{{ws}}}{\mathbf{Q}}(\kappa ){\mathbf{d}}(\kappa ){{{\mathbf{v}}}_{0}} + {{{\mathbf{w}}}_{0}}} \right|}}^{2}}d\kappa } ,$где ${\mathbf{d}}(\kappa ) = {{\left( {{\mathbf{E}} - {\mathbf{\omega }}\left( \kappa \right)} \right)}^{{ - 1}}}.$
Как видно из выражения (37), дисперсия отраженной волны не зависит от номера ЭИ $\mu $, поэтому соответствующий индекс в обозначении дисперсии опущен.
Соотношение (37) описывает интересующую нас дисперсию случайной составляющей отраженной волны. Важно отметить, что статистически, т.е. в рамках усредненных параметров, решетка осталась однородной, также как исходная структура с номинальными значениями параметров. Данный результат не означает, что однородной будет каждая конкретная реализация решетки, которая должна состоять из неодинаковых ЭИ.
Если ЭИ имеет несколько независимых случайных параметров, то в рамках линейного приближения необходимо суммировать квадраты дисперсий $\sigma _{{ui}}^{2}$($i$ – номер параметра). При этом все они находятся с помощью выражения (37).
5. НЕКОГЕРЕНТНОЕ ПОЛЕ ИЗЛУЧЕНИЯ И ЕГО СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Соотношение (31), которое описывает приращения амплитуд рассеянных волн, является основой для определения статистических параметров поля излучения. Случайное нарушение периодичности решетки приводит к появлению в пространстве случайного некогерентного поля. Наша задача состоит в том, чтобы выразить его через отклонения параметра Δxξ и найти дисперсию его вектора Пойнтинга.
Для последующего анализа соотношения (31) исходными являются формулы, связывающие приращения электрического и магнитного полей $\Delta \vec {E}$ и $\Delta \vec {H}$ через приращения амплитуд (31):
(38)
$\Delta \vec {E} = \sum\limits_\mu {\Delta {{{\mathbf{A}}}_{{s\mu }}}{{{{\mathbf{\vec {E}}}}}_{{s\mu }}}} ,\,\,\,\,\Delta \vec {H} = \sum\limits_\mu {\Delta {{{\mathbf{A}}}_{{s\mu }}}{{{{\mathbf{\vec {H}}}}}_{{s\mu }}}} $,(векторы ${{{\mathbf{\vec {E}}}}_{{s\mu }}}$, ${{{\mathbf{\vec {H}}}}_{{s\mu }}}$ введены выше, см. формулу (2)).
Для дальнейшего анализа нам удобно воспользоваться представлением ВСГ в виде двойных интегралов Фурье:
(39)
$\begin{gathered} \left[ \begin{gathered} {{{{\mathbf{\vec {E}}}}}_{{s\mu }}} \hfill \\ {{{{\mathbf{\vec {H}}}}}_{{s\mu }}} \hfill \\ \end{gathered} \right] = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\left[ \begin{gathered} {{{{\mathbf{\vec {e}}}}}_{s}} \hfill \\ {{{{\mathbf{\vec {h}}}}}_{s}} \hfill \\ \end{gathered} \right]} } \exp ( - i{{\kappa }_{1}}(x - \mu P) - \\ - \,\,i{{\kappa }_{2}}y - iqz)d{{\kappa }_{1}}d{{\kappa }_{2}}, \\ q = \sqrt {{{k}^{2}} - \kappa _{1}^{2} - \kappa _{2}^{2}} . \\ \end{gathered} $Функции ${{{\mathbf{\vec {e}}}}_{s}}$, ${{{\mathbf{\vec {h}}}}_{s}}$ известны [15] и выражаются весьма громоздким образом, поэтому мы их не приводим в явном виде.
Нам также будут полезны соотношения (10), (37), представляющие функцию Грина в виде интеграла Фурье. Подставим их и выражение (39) в формулы (38) и осуществим суммирование по индексу $\mu $ с помощью формулы Пуассона [5], которая сводит сумму экспонент к сумме дельта-функций. Используя свойство дельта-функции, берем интеграл по ${{\kappa }_{1}}$. В результате получаем
(40)
$\begin{gathered} \Delta \vec {E} = \sum\limits_\xi {\Delta {{x}_{\xi }}} \sum\limits_{n = - \infty }^\infty {\int\limits_{ - \pi /P}^{\pi /P} {\int\limits_{ - \infty }^\infty {{\mathbf{d}}(\alpha ){{{\mathbf{v}}}_{0}}{{{{\mathbf{\vec {e}}}}}_{s}}({{\kappa }_{{1n}}},{{\kappa }_{2}})} } } \times \\ \times \,\,\exp ( - i(\xi P({{\kappa }_{0}} - \alpha ) + {{\kappa }_{{1n}}}x + {{\kappa }_{2}}y + {{q}_{n}}z))d\alpha d{{\kappa }_{2}}, \\ {{\kappa }_{{1n}}} = \alpha + {{2\pi n} \mathord{\left/ {\vphantom {{2\pi n} P}} \right. \kern-0em} P},\,\,\,\,{{q}_{n}} = \sqrt {{{k}^{2}} - \kappa _{{1n}}^{2} - \kappa _{2}^{2}} . \\ \end{gathered} $Соотношение (40) описывает полное поле, создаваемое решеткой. Нас интересует только его часть – поле излучения, которое переносит энергию на бесконечность. Используем данное обстоятельство для преобразования соотношения (40). Соотношение (40) является разложением поля по гармоникам Флоке. Номер гармоники совпадает с индексом суммирования в выражении (40) $n$. В типовом случае только небольшая часть гармоник является распространяющимися. Ограничимся анализом ситуации, в которой распространяется только одна гармоника Флоке с нулевым номером. Отметим, что при произвольном угле сканирования этому ограничению удовлетворяет решетка с периодом, меньшим половины длины волны в свободном пространстве.
Таким образом, мы можем избавиться от ряда в соотношении (40), оставив только нулевой его член:
(41)
$\begin{gathered} \Delta \vec {E} = \sum\limits_\xi {\Delta {{x}_{\xi }}} \int\limits_{ - k}^k {\int\limits_{ - \infty }^\infty {{\mathbf{d}}(\alpha ){{{\mathbf{v}}}_{0}}{{{{\mathbf{\vec {e}}}}}_{s}}(\alpha ,{{\kappa }_{2}})} } \times \\ \times \,\,\exp ( - i(\xi P({{\kappa }_{0}} - \alpha ) + \alpha x + {{\kappa }_{2}}y + {{q}_{0}}z))d\alpha d{{\kappa }_{2}}. \\ \end{gathered} $Дальнейшие преобразования связаны с интегралом по переменной ${{\kappa }_{2}}$. Как следует из соотношения (41), он описывает зависимость поля от координат y, z. Найдем его приближенное выражения в дальней зоне. Для этого введем полярные координаты:
Здесь угол $\varphi $ отсчитывается от оси 0z. Его не следует путать с углом в сферической системе координат. Радиус $\rho $ задает расстояние от оси 0х до точки наблюдения.
Введем также новую переменную интегрирования:
(43)
${{\kappa }_{2}} = {{k}_{e}}\sin \psi ,\,\,\,\,{{q}_{0}} = {{k}_{e}}\cos \psi ,\,\,\,\,{{k}_{e}} = \sqrt {{{k}^{2}} - {{\alpha }^{2}}} ,$(44)
$\begin{gathered} \Delta \vec {E} = \sum\limits_\xi {\Delta {{x}_{\xi }}} \int\limits_{ - k}^k {\int\limits_{ - \infty }^\infty {{\mathbf{d}}(\alpha ){{{\mathbf{v}}}_{0}}{{{{\mathbf{\vec {e}}}}}_{s}}(\alpha ,{{\kappa }_{2}})} } \times \\ \times \,\,\exp ( - i(\xi P({{\kappa }_{0}} - \alpha ) + \alpha x + \\ + \,\,{{k}_{e}}\rho \cos (\psi - \varphi )){{k}_{e}}\cos \psi d\alpha d\psi . \\ \end{gathered} $В формуле (41) мы изменили пределы интегрирования по переменной $\alpha $. Данное изменение обусловлено тем, что параметр ${{k}_{e}}$ является действительной величиной при $\left| \alpha \right| < k$. При мнимых значениях ${{k}_{e}}$ соотношение (44) описывает затухающие на бесконечности поля. Далее методом перевала [14] вычислим интеграл (44) при условии ${{k}_{e}}\rho \gg 1$:
Аналогичное выражение можно без труда получить для вектора магнитного поля, заменяя ${{{\mathbf{\vec {e}}}}_{s}}(\alpha ,\lambda )$ на ${{{\mathbf{\vec {h}}}}_{s}}(\alpha ,\lambda )$. Найдем продольную компоненту вектора Пойнтинга ${{\Pi }_{\rho }}$:
Будем искать усредненное по реализациям значение вектора Пойнтинга. Тогда с учетом отсутствия корреляции между отклонениями $\Delta {{x}_{\xi }}$ получаем
(47)
$\begin{gathered} {{{\bar {\Pi }}}_{\rho }} = \frac{{\sigma _{x}^{2}}}{2}\sum\limits_\xi {\int\limits_{ - k}^k {\int\limits_{ - k}^k {{{{\left[ {{{{\vec {R}}}_{e}}(\alpha )\vec {R}_{h}^{ * }(\beta )} \right]}}_{\rho }}} } } \times \\ \times \,\,\exp ( - i(\xi P(\beta - \alpha ))d\alpha d\beta , \\ {{{\vec {R}}}_{{e,h}}}(\alpha ) = {\mathbf{d}}(\alpha ){{{\mathbf{v}}}_{0}}\left[ \begin{gathered} {{{{\mathbf{\vec {e}}}}}_{s}}(\alpha ,\lambda ) \hfill \\ {{{{\mathbf{\vec {h}}}}}_{s}}(\alpha ,\lambda ) \hfill \\ \end{gathered} \right] \times \\ \times \,\,\exp ( - i(\alpha x + {{k}_{e}}\rho ))\cos \varphi \sqrt {\frac{{2\pi {{k}_{e}}}}{\rho }} . \\ \end{gathered} $Сумма по $\xi $ вычисляется с помощью упомянутой выше формулы Пуассона, которая также позволяет взять интеграл по $\beta $, используя свойство дельта-функции $\delta (\beta - \alpha )$:
(48)
$\begin{gathered} {{\Pi }_{\rho }} = \frac{{2{{\pi }^{2}}\sigma _{x}^{2}{{{\cos }}^{2}}\varphi }}{{P\rho }} \times \\ \times \,\,\int\limits_{ - k}^k {k_{e}^{2}{{{\left[ {\left( {{\mathbf{d}}(\alpha ){{{\mathbf{v}}}_{0}}{{{{\mathbf{\vec {e}}}}}_{s}}(\alpha ,\lambda )} \right)\left( {{\mathbf{d}}{\text{*}}(\alpha ){\mathbf{v}}_{0}^{ * }{\mathbf{\vec {h}}}_{s}^{ * }(\alpha ,\lambda )} \right)} \right]}}_{\rho }}} d\alpha \,. \\ \end{gathered} $Формула (48) описывает пространственное распределение дисперсии потока мощности некогерентного поля. Как видим, дисперсия вектора Пойнтинга не зависит от координаты х, но она изменяется в плоскости YOZ. Энергетическая диаграмма направленности некогерентного поля может быть получена из (48).
6. АНАЛИЗ РЕШЕТКИ ЛЕНТОЧНЫХ ВИБРАТОРОВ
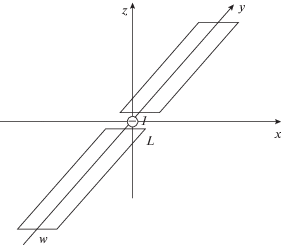
Для проверки представленной выше теории ее использовали при анализе решетки ленточных вибраторов со случайными длинами (рис. 2). В работе [13] приведена реализация метода МОМР-РВСГ для случая ленточной вибраторной решетки. В ней описан алгоритм расчета операторов рассеяния ${\mathbf{L}}$. Алгоритм вычисления функции Грина бесконечной вибраторной решетки строится по соотношениям из разд. 1 [9].
Наряду с исследованием бесконечной решетки были проведены расчеты статистических характеристик линейки с конечным, но достаточно большим числом вибраторов ${{N}_{v}}$, которое в численных экспериментах было равно 21. В такой структуре достаточно удаленные от краев элементы ведут себя также, как элементы бесконечной решетки. Отметим, что моделируемая решетка состояла из неодинаковых вибраторов со случайными длинами. Для нее провели серию статистических испытаний, состоящую из ${{N}_{t}}$ расчетов. При этом набор длин вибраторов ${{L}_{\xi }}$ при каждом испытании задавался генератором случайных чисел с математическим ожиданием $L$ и дисперсией ${{\sigma }_{L}}$.
Для центрального элемента решетки рассчитывали амплитуду отраженной волны и находили дисперсию ее модуля. Исследовали зависимость дисперсии от параметра ${{N}_{t}}$ с целью определения предела при ${{N}_{t}} \to \infty $. Предельное значение дисперсии использовали для сравнения с результатом, получаемым по формуле (37).
На рис. 3 и 4 показаны характеристики бесконечной решетки с детерминированными параметрами: $P = 17$, $L = 13.85$, $w = 1$. Здесь и далее все размеры приводятся в миллиметрах. На рис. 3 представлена зависимость модуля коэффициента отражения ${{S}_{{11}}}$ от входа излучателя для одиночного вибратора и для вибратора в составе синфазной решетки ($\theta = 0$), на рис. 4 – частотная зависимость модуля коэффициента отражения бесконечной решетки для углов сканирования $\theta = 0,15,30,45,60$ град. Сканирование идет в плоскости XOZ. Видно, что увеличение угла $\theta $ сначала улучшает согласование структуры. Однако начиная с некоторого критического угла, наблюдается резкий всплеск коэффициента отражения, который связан с появлением побочного дифракционного лепестка.
Рис. 3.
Частотная зависимость модуля коэффициента отражения для одиночного вибратора (1) и для вибратора в составе бесконечной решетки (2).
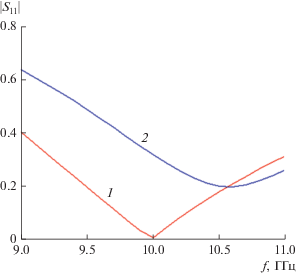
Рис. 4.
Частотная зависимость модуля коэффициента отражения вибраторной решетки в режиме сканирования при θ = 0 (1), 15 (2), 30 (3), 45 (4), 60 град (5).
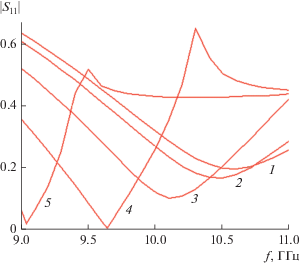
На рис. 5 показана частотная зависимость дисперсии модуля амплитуды отраженной волны для углов сканирования $\theta = 0,15,30,45,60$ град. Дисперсия длины вибратора ${{\sigma }_{L}}$ принята равной 0.2. Видно, что существенные изменения частотной зависимости дисперсии ${{\sigma }_{u}}$ наблюдаются в зоне появления побочных дифракционных лепестков.
Рис. 5.
Частотная зависимость дисперсии амплитуды отраженной волны при θ = 0 (1), 15 (2), 30 (3), 45 (4), 60 град.
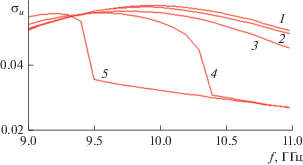
Интересно рассмотреть различные приближенные способы вычисления дисперсии ${{\sigma }_{u}}$. Кривые 1–5 на рис. 5 были получены с помощью соотношения (37). В нем разные члены учитывают разные виды взаимодействий волн в решетке.
Наиболее простой смысл имеет слагаемое ${\mathbf{L}}_{{ww}}^{'},$ входящее в параметр ${{{\mathbf{w}}}_{0}}$. Оно описывает вклад в изменение амплитуды отраженной волны, который порождает изменение коэффициента отражения уединенного вибратора. При этом взаимодействие элементов решетки через свободное пространство никак не учитывается. Можно сказать, что обсуждаемое слагаемое описывает дисперсию отраженной волны в приближении элементарной теории антенных решеток.
Более сложный смысл имеет слагаемое ${\mathbf{L}}_{{ws}}^{'}{{{\mathbf{q}}}_{{i0}}}.$ Оно учитывает вклад в случайную составляющую отраженной волны, порождаемый полем решетки нулевого приближения, т.е. решетки с детерминированными номинальными параметрами. При этом случайный характер отраженных волн возникает благодаря тому, что оператор ${{{\mathbf{L}}}_{{ws}}}$ содержит случайную составляющую, пропорциональную в линейном приближении его производной ${\mathbf{L}}_{{ws}}^{'}.$
Наиболее сложный вид имеет слагаемое из формулы (37), пропорциональное оператору ${{{\mathbf{L}}}_{{ws}}}$. Оно описывает вклад в отраженную волну от случайной части поля в решетке. В линейном приближении он пропорционален детерминированной части оператора рассеяния ${{{\mathbf{L}}}_{{ws}}}$.
Расчет дисперсии ${{\sigma }_{u}}$ можно проводить, учитывая одно, два и, наконец, все три слагаемых, т.е. по наиболее сложной формуле (37), получая при этом приближения разной степени точности. Присвоим им номера 1, 2, 3. Отметим, что в вычислительном смысле первые два приближения намного проще третьего, так как интеграл в них берется элементарно, а при использовании соотношения (37) возникает необходимость численного интегрирования весьма сложной функции.
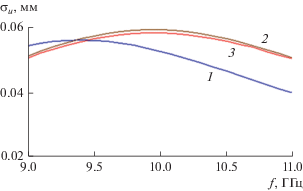
На рис. 6 показана частотная зависимость дисперсии ${{\sigma }_{u}}$ для геометрических параметров, приведенных выше, и нулевого угла сканирования. Номер кривой совпадает с номером приближения. Видно, что наиболее грубое приближение 1 весьма сильно отличается от точного результата, который соответствует кривой 3. При этом приближение 2 весьма близко к расчету по формуле (37). Отметим, что указанная близость сохраняется в весьма широком диапазоне изменения параметров решетки и углов сканирования, что позволяет предположить, что она не является результатом случайного сочетания параметров, а отражает важную особенность взаимодействия поля в решетке.
Рис. 6.
Частотная зависимость дисперсии амплитуды отраженной волны рассчитанная при помощи моделей 1–3 (кривые 1–3 соответственно).
Рассмотрим результаты численного эксперимента по прямому определению дисперсии амплитуд отраженных волн методом статистических испытаний (схема численного эксперимента описана в начале данного раздела). На рис. 7 показан пример расчета амплитуд отраженных волн в вибраторной решетке с ${{N}_{{v}}} = 21$. Сплошная кривая получена для решетки с детерминированными параметрами, а также показаны три реализации с разными случайными наборами длин вибраторов. Дисперсия длины ${{\sigma }_{L}}$, как и раньше, равна 0.2.
Рис. 7.
Распределение амплитуд отраженных волн в каналах решетки при статистических испытаниях для решетки с детерминированными параметрами (кривая 1), также показаны три реализации (кружочки, квадраты и ромбы) с разными случайными наборами длин вибраторов.
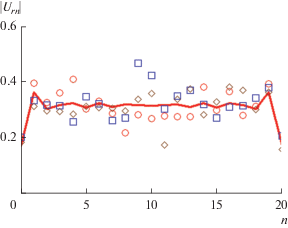
В решетке был выделен центральный элемент, параметры которого близки к параметрам элемента в составе бесконечной решетки. Подтверждением этого может служить кривая на рис. 7. Видно, что на краях решетки наблюдаются достаточно большие осцилляции в распределении амплитуд отраженных волн. В центре они ослаблены настолько, что ими можно уже пренебречь. Затухание осцилляций является свидетельством того, что влияние краевых эффектов в данной области решетки незначительно и ее параметры близки к параметрам бесконечной структуры.
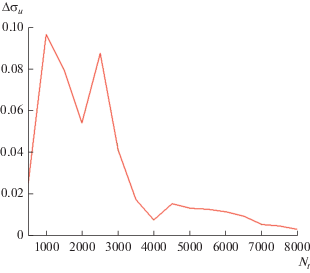
На рис. 8 показана зависимость параметра $\Delta {{\sigma }_{u}}$ от числа испытаний ${{N}_{t}}$. Указанный параметр определяется следующим образом:
(49)
$\Delta {{\sigma }_{u}} = \left| {\frac{{{{\sigma }_{u}}({{N}_{t}}) - {{\sigma }_{t}}}}{{{{\sigma }_{t}}}}} \right|,$где ${{\sigma }_{t}}$ – теоретическая оценка дисперсии, а ${{\sigma }_{u}}({{N}_{t}})$ – дисперсия, определяемая по методу статистических испытаний. Таким образом, параметр $\Delta {{\sigma }_{u}}$ имеет смысл относительной погрешности теоретического расчета дисперсии.
Кривая на рис. 8 получена для синфазной решетки с параметрами, приведенными выше. Видна явная тенденция к уменьшению погрешности $\Delta {{\sigma }_{u}}$ при увеличении числа испытаний. Таким образом, можно сделать вывод, что построенная теоретическая схема расчета статистических параметров решетки находит подтверждение при использовании прямого метода статистических испытаний.
Список литературы
Гупта К., Гардж Р., Чадха Р. Машинное проектирование СВЧ устройств. М.: Радио и связь, 1987.
Воскресенский Д.И., Котов Ю.В., Овчинникова Е.В. // Антенны. 2005. № 11. С. 7.
Шифрин Я.С. Вопросы статистической теории антенн. М.: Сов. радио, 1970.
Инденбом М.В. Антенные решетки подвижных обзорных РЛС. Теория, расчет, конструкции. М.: Радиотехника, 2015.
Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. М.: Мир, 1974.
Mailoux R.J. Phased array antennas handbook. N.-Y.: Artech House, 2005.
Банков С.Е., Курушин А.А., Гутцайт Э.М. Решение оптических и СВЧ задач с помощью HFSS. М.: Оркада, 2012.
Банков С.Е., Курушин А.А. Электродинамика для пользователей САПР СВЧ. М.: Солон-Пресс, 2018.
Бaнкoв C.E. // PЭ. 2020. T. 65. № 2. C. 118.
Бaнкoв C.E. // PЭ. 2005. T. 50. № 9. C. 23.
Xiao G.B., Mao J.F., Yuan B. // IEEE Trans. 2008. V. AP-56. № 12. P. 3723.
Xiang S., Xiao G., Tian X., Mao J. // IEEE Trans. 2013. V. AP-61. № 11. P. 5453.
Бaнкoв C.E. // PЭ. 2020. T. 65. № 1. C. 31.
Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь, 1983.
Стрэттон Дж.А. Теория электромагнетизма. М.: Гостехтеориздат, 1948.
Дополнительные материалы отсутствуют.
Инструменты
Радиотехника и электроника