Радиотехника и электроника, 2020, T. 65, № 4, стр. 353-362

ВВЕДЕНИЕ

Одним из способов создания стелс-объектов является размещение на их поверхности электродинамических структур с управляемыми характеристиками излучения и рассеяния, так называемых “умных” обшивок [1–5]. Концепция умных поверхностей, связанная с управляемым рассеянием объектов, сформировалось еще в 60–70-е гг. ХХ в. [6–9]. Электрофизические свойства многих из таких структур можно описать с помощью импедансных граничных условий [10–12]. Обоснованность применения импедансных граничных условий подтверждена как для плоских, так и для криволинейных поверхностей, в том числе для сверхпроводников гладких и шероховатых поверхностей, и устройств на их основе [13]. В работах [14, 15] впервые продемонстрирована возможность эффективного управления полем рассеяния объектов с помощью сосредоточенных и распределенных комплексных импедансных нагрузок.

Проектирование объектов с заданными излучающими и рассеивающими свойствами предполагает постановку и решение обратных задач электродинамики или задач синтеза. Известно немало работ, посвященных синтезу граничных условий на телах различной формы по заданным характеристикам излучения и рассеяния (например, [16–25]), где рассмотрены задачи синтеза двумерных изотропных импедансных поверхностей по заданным характеристикам излучения и рассеяния на согласованной поляризации. Так, в работе [16] предложен метод решения обратной задачи для импедансной антенны, реактансный рельеф которой выбирался параллельным вещественной части вектора Пойнтинга. На найденной поверхности затем определялся закон распределения реактанса. Позднее в работе [17] предложенный в [16] метод был обобщен на случай синтеза цилиндрических импедансных рассеивателей. Здесь по известному падающему полю и заданной диаграмме рассеяния из уравнений Максвелла определена форма реактансного рассеивателя, совпадающая с одной из замкнутых поверхностей, на которой вещественная часть вектора Пойнтинга равна нулю. В работах [18, 19] форма объекта полагалась заданной (плоская [18] или цилиндрическая [19]), а поверхностный реактанс определялся по требуемой диаграмме направленности (ДН). Условие чистой реактивности импеданса достигнуто за счет специально вводимых медленных (непространственных) волн. Система ограничений на значения комплексных амплитуд токов, связанная с условием чистой реактивности импеданса, сведена к поиску условного экстремума квадратичной формы при наличии квадратных ограничений типа равенств на значения неизвестных.

В [20, 21] рассмотрены задачи синтеза пассивного импеданса (${\text{Re}}Z \geqslant 0$), что, по замыслу авторов, должно было дать дополнительные возможности по управлению характеристиками рассеяния объектов. Задача решалась приближенно – методом линейного программирования путем сведения интегрального уравнения к переопределенной системе алгебраических уравнений.

В работах [22, 23] строго и в приближении физической оптики решены задачи синтеза для плоскости и для двумерных тел произвольной формы. В отличие от работ [16–21] здесь законы распределения изотропного неоднородного импеданса найдены в явном виде. Получены выражения для коэффициентов отражения, определен класс реализуемых диаграмм для пассивных отражателей (${\text{Re}}Z \geqslant 0$).

Функциональные возможности импедансных отражателей с управляемыми характеристиками можно дополнительно расширить за счет перевода отраженной волны на кросс-поляризацию [24–26]. Так, в [24] методом интегральных уравнений исследовано анизотропное импедансное “умное” покрытие (смарт-покрытие), обеспечивающее перевод поля рассеяния произвольного цилиндра на кросс-поляризацию. Показано, что при этом на согласной поляризации цилиндрическая поверхность эквивалентна “черному” телу закона Кирхгофа [27]. В работах [25, 26] в результате решения задачи синтеза удалось в явном виде получить законы распределения реактансов частой решетки ортогональных импедансных полос и их ориентации на плоскости, которые обеспечивают переотражение падающей волны линейной поляризации в заданном направлении с одновременным поворотом плоскости поляризации на 90°.

Дальнейшее совершенствование умных покрытий возможно за счет трансформации поляризации отраженного поля по любому наперед заданному закону.

Работы, посвященные этой проблематике, существуют и связаны в основном с антенной тематикой (см., например, [28–33]). Так, в [28] дана обширная библиография работ по разработке поляризаторов отражательного типа. В [30] сообщается о свойствах поляризационного преобразования частотно-селективных поверхностей на примере микрополосковых структур, преобразующих линейную поляризацию в круговую. Однако они рассчитаны на ограниченный диапазон углов падения. Преимущества отражательного поляризатора, предложенного в работах [28, 29], включают в себя: низкий профиль, небольшие масса и размер, широкополосная работа, низкие тепловые потери и угловая стабильность. В [31] разработан аналитический метод синтеза бианизотропных рассеивателей, расположенных в узлах квадратной сетки, для проектирования поляризационных трансформаторов. Для упрощения синтеза предложенный метод рассматривается только для нормального падения волны. Численные результаты показали хорошее соответствие экспериментальных результатов и теории. Однако в работах [28–31] рассмотрены структуры, работающие только при нормальном падении волны либо на зеркально отраженных лучах.

В отличие от указанных выше работ в [32, 33] рассмотрены задачи синтеза анизотропных структур, переотражающих падающие поля в заданном (незеркальном) направлении с поворотом (трансформацией) ее плоскости поляризации, безотносительно к реализующим их конструкциям. Показано, что такой эффект возможно достичь только с помощью частой решетки ортогональных неоднородных реактансных полос, имеющих помимо неоднородного реактанса еще и переменную на импедансной плоскости ориентацию. Законы распределения реактанса и ориентации полос получены в явном виде. Очевидно, что в практических приложениях реализация реактансных структур с переменной ориентацией может оказаться весьма трудоемкой, неоправданно дорогостоящей задачей, особенно на поверхности рассеивателя сложной формы. Таким образом, ранее решались задачи синтеза анизотропной плоскости, переводящей отраженную волну на кросс-поляризацию. Задача синтеза анизотропной импедансной структуры по заданному направлению и поляризации (трансформации поляризации падающей волны в требуемую, в том числе круговую) при ограничениях на конструкцию реализующей импеданс (конструктивный синтез) ставится впервые.

Цель данной работы – решение задачи синтеза анизотропной плоскости в виде частой решетки ортогональных реактансных полос фиксированной ориентации, по заданному направлению отражения электромагнитной волны с требуемой трансформацией поляризации.

1. ПОСТАНОВКА ЗАДАЧИ

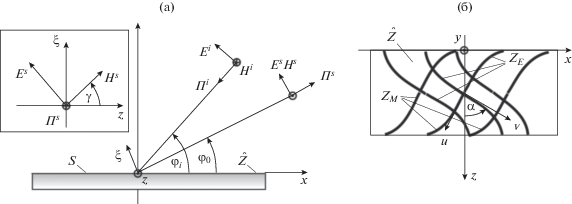
Пусть на идеально проводящей плоскости S (y = 0) (рис. 1a, 1б) реализована анизотропная структура в виде частой решетки ортогональных импедансных полос (лент) ${{Z}_{E}},~{{Z}_{M}},$ вплотную прилегающих друг к другу и ориентированных под углом α к оси z (см. рис. 1б). В этом случае на плоскости S выполняются импедансные граничные условия Леонтовича [12]:

где в системе координат $\left\{ {\vec {v},\vec {u},\vec {n} = - {{{\vec {1}}}_{y}}} \right\}$ (см. рис. 1б) тензор импеданса $\hat {Z}$ имеет диагональный вид

Здесь и далее компоненты тензора импеданса и вектор напряженности электрического поля нормированы на характеристическое сопротивление свободного пространства $W = 120\pi ~\,\,{\text{Ом}}.$ В общем случае, как показано в работах [32, 33], параметры структуры могут меняться вдоль оси $x{\text{\;}}$ (${{Z}_{E}}\left( x \right)$, ${{Z}_{M}}\left( x \right)$ и $\alpha \left( x \right)$). Вдоль оси z система однородна (см. рис. 1), следовательно, задача двумерна.

На плоскость S с направления ${{\varphi }_{i}}$ падает плоская электромагнитная волна (см. рис. 1а) с векторами ${{\vec {E}}^{i}},{{\vec {H}}^{i}}:$

где $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ ($\lambda $ – длина падающей волны).

Необходимо найти компоненты ${{Z}_{E}}\left( x \right),$ ${{Z}_{M}}\left( x \right)$ тензора (2) реактанса

с постоянной ориентацией полос системы $\left( x \right) = {\text{const,}}$ обеспечивающие отражение волны ${{\vec {E}}^{s}},~{{\vec {H}}^{s}}$ от плоскости y = 0 в заданном направлении ${{{\varphi }}_{0}}$ с требуемой поляризацией: где ${{E}_{0}} = \Upsilon {{H}_{0}}$ и ${{\Phi }_{0}},$ ${{\Psi }_{0}}$ – заданные амплитуды и фазы ортогональных составляющих отраженного поля, определяющие поляризацию отраженной волны.

2. КОЭФФИЦИЕНТЫ ОТРАЖЕНИЯ НЕОДНОРОДНОЙ ИМПЕДАНСНОЙ ПЛОСКОСТИ

Поскольку падающие (4) и отраженные (6) волны являются однородными плоскими волнами, то можно ввести в рассмотрение коэффициенты отражения ${{P}_{{m,n}}}~\left( {m = 1,2;n = 1,2} \right)$ [34] следующим образом:

Запишем импедансные граничные условия (3) в декартовой системе координат:

Представляя полные поля в виде суммы падающих (4) и отраженных (6) волн и выражая ${{E}_{x}}$ и ${{H}_{x}}$ через ${{H}_{z}}$ и ${{E}_{z}}$ (см. формулы (4), (6)), из (8) и (9) получим представление рассеянных полей $E_{z}^{s}$, $H_{z}^{s}$ через падающие $E_{z}^{i}$, $H_{z}^{i}:$

где

Сопоставляя формулы (10) и (11) с формулами (7) и учитывая формулы Вайнштейна–Сивова для ${{Z}_{{11}}}$ и ${{Z}_{{22}}}$, получим выражения для ${{P}_{{m,n}}}$ неоднородной анизотропной плоскости с системой ортогональных полос (лент) ${\text{\;}}{{Z}_{M}},{\text{\;}}{{Z}_{E}}$ (см. рис. 1б):

Формулы (12) для однородной импедансной плоскости, когда ${{{\varphi }}_{0}} = \pi - {{\varphi }_{i}},$ переходят в общеизвестные [34].

Строго говоря, полученные соотношения справедливы только в том случае, когда импедансная структура обеспечивает отражение единственной однородной плоской волны (6). На самом деле, в силу требований физической (${\text{Re}}\left( {{{Z}_{E}}} \right) \geqslant 0$; ${\text{Re}}\left( {{{Z}_{M}}} \right) \geqslant 0$) и технической (например, $\alpha \left( x \right) = {\text{const}}$) реализации пассивного импеданса (не требующего размещения на поверхности синтезируемого рефлектора дополнительных источников ЭМВ) создать структуру, обеспечивающую условия (6) возможно, как показано в работе [23] на примере решения задач синтеза и анализа неоднородной изотропной плоскости, только для направления обратного рассеяния. В остальных случаях помимо заданного луча появляется как минимум еще одна плоская однородная волна, отраженная в зеркальном направлении. В общем же случае [23] помимо заданной неоднородная импедансная плоскость будет порождать множество других отраженных однородных плоских и поверхностных волн, тогда выражения (12) уже нельзя считать строгими.

На данном же этапе считаем, что полученные коэффициенты отражения являются неоднородными функциями (зависящими от координаты х) и содержат в общем случае неизвестные пока функции ${{Z}_{E}}\left( x \right)$; ${{Z}_{M}}\left( x \right)$ и $\alpha \left( x \right).$ О них известно лишь то, что они должны обеспечить синтезируемой структуре заданный режим отражения однородной плоской волны и подлежат определению из требуемых диаграмм рассеяния. В процессе решения задачи синтеза (см. далее разд. 4) будут определены условия реализации таких структур (класс реализуемых диаграмм рассеяния).

3. ДИАГРАММА РАССЕЯНИЯ

В точке наблюдения $p\left( {r,\varphi } \right)$, расположенной в дальней зоне $\left( {r \to \infty } \right)$, в цилиндрической системе координат диаграммы рассеяния в Е‑ и Н‑плоскостях (${{F}_{E}}\left( \varphi \right)$ и ${{F}_{H}}\left( \varphi \right)$) для фрагмента реактансной плоскости $x \in \left[ { - L,L} \right]$ можно представить через коэффициенты отражения (7) и соотношения (4), (6) в следующем виде:

где

Как видим, составляющие ${{F}_{{{\text{т}}E,H}}}\left( \varphi \right)$ диаграммы направленности определяют теневой лепесток (поле рассеяния “черного” тела Кирхгофа) и не зависят ни от поверхностного импеданса, ни от поляризации падающей волны, имеют одинаковую форму и отличаются только комплексными амплитудами.

Полученные формулы позволят найти пока еще неизвестные законы распределения импеданса полос ${\text{\;}}{{Z}_{M}},{\text{\;}}{{Z}_{E}}$, обеспечивающих заданный режим отражения волн на согласной и кроссовой поляризациях.

4. СИНТЕЗ РЕАКТАНСНОЙ ПЛОСКОСТИ

Рассмотрим задачу синтеза на примере анизотропной плоскости, переотражающей падающую с направления ${{\varphi }_{i}}$ однородную плоскую Н-поляризованную волну (4) ($E_{z}^{i} = 0,$ ${\text{\;}}H_{0}^{i} = {{1{\text{\;}}A} \mathord{\left/ {\vphantom {{1{\text{\;}}A} m}} \right. \kern-0em} m}$) в отраженную волну заданной поляризации $\left( {\Upsilon ,~~\Delta \Psi = {{\Phi }_{0}} - {{\Psi }_{0}}} \right)$ в направлении ${{\varphi }_{0}}$. Необходимые законы распределения чисто реактивного импеданса (реактанса) полос (3) ${{Z}_{E}} = i{{X}_{E}}\left( x \right),$ ${{Z}_{M}} = i{{X}_{M}}\left( x \right)$ и их ориентацию $\alpha $ на плоскости S, обеспечивающие максимумы диаграмм рассеяния в направлении $\varphi = {{\varphi }_{0}},$ можно найти непосредственно из подынтегральных выражений для диаграмм рассеяния (13), которые с учетом (7) примут вид

где $U\left( {x,\varphi } \right) = \left\{ {\left( {\sin \varphi - \sin {{\varphi }_{i}}} \right){\Delta }} \right.$ + $\left( {\sin \varphi + } \right.$ $\left. { + \,\,\sin {{\varphi }_{0}}} \right)\left. {{{P}_{{22}}}{\Delta }} \right\};$ $\chi \left( {x,\varphi } \right) = kx\left( {\cos \varphi + \cos {{\varphi }_{i}}} \right).$

Подынтегральные выражения в формулах (14) и (15) представляют собой в общем случае быстро осциллирующие функции. Очевидно, что максимальная амплитуда отраженной волны в заданном направлении может быть достигнута за счет такого выбора реактансов, при которых в (14) и (15) будут выполняться условия:

Равенства (16) в подынтегральных выражениях (14) и (15) означают, что реактансная структура (см. рис. 1) создает в заданном направлении $\varphi = {{\varphi }_{0}}$ однородную плоскую волну. Это система двух комплексных уравнений относительно четырех неизвестных действительных функций: ${{X}_{E}}\left( x \right),$ ${{X}_{M}}\left( x \right),$ $\alpha \left( x \right)$ и ${{H}_{0}}$.

Исследования [23] показывают, что отражение на согласной поляризации только однородной плоской волны возможно лишь для углов ${{\varphi }_{0}} = {{\varphi }_{i}}$ и ${{\varphi }_{0}} = \pi - {{\varphi }_{i}}.$ При этом ее амплитуда равна амплитуде падающей волны ${{H}_{0}} = H_{0}^{i}.$

Отраженная однородная плоская волна только на кроссовой поляризации (твист-эффект) возможна [25] в любом направлении, но с амплитудой ${{E}_{0}} = \sqrt {{{\sin {{\varphi }_{i}}} \mathord{\left/ {\vphantom {{\sin {{\varphi }_{i}}} {\sin {{\varphi }_{0}}}}} \right. \kern-0em} {\sin {{\varphi }_{0}}}}} H_{0}^{i}.$ Ориентация полос в этом случае оказывается переменной величиной $\alpha \left( x \right)$. Система (16) для реактансной структуры (3), поворачивающей плоскость поляризации отраженной волны на произвольный угол (${{E}_{0}}~\,\,{\text{и}}\,\,~{{H}_{0}} \ne 0$) в заданном направлении (${{\varphi }_{0}} \ne {{\varphi }_{i}}$ и ${{\varphi }_{0}} \ne \pi - {{\varphi }_{i}}$), строгого решения не имеет [33].

Рассмотрим приближенное решение системы (16). Условия возникновения отраженных лучей на обеих поляризациях в направлении $\varphi = {{\varphi }_{0}}$ можно получить и непосредственно из равенства только аргументов в формулах (16):

где ${\text{arg}}\left( {{{P}_{{12}}}} \right) = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - {\text{arg}}\Delta .$

Это система двух действительных уравнений, и из нее можно найти только две действительные функции, ${{X}_{E}}\left( x \right)$ и ${{X}_{M}}\left( x \right)$. В этом случае неизвестный угол $\alpha \left( x \right)$ либо необходимо задавать, либо находить из дополнительных условий, например, из условия получения максимальной амплитуды отраженного в заданном направлении поля. Параметры $\Upsilon $ и ${{H}_{0}}$ в уравнениях не входят и поэтому будут неконтролируемыми. В результате амплитуда ${{H}_{0}}$ отраженной волны на импедансной поверхности $\left( {\left| {U\left( {x,{{\varphi }_{0}}} \right){{\Delta }^{{ - 1}}}} \right|} \right)$ будет функцией координаты $x{\text{\;}}\left( {{{H}_{0}}\left( x \right)} \right)$, т.е. отраженная волна окажется неоднородной. Поскольку мы синтезируем поляризатор с заданным параметром $\Upsilon $, то эту систему следует дополнить еще одним уравнением, содержащим $\Upsilon $. Так, разделив в системе (16) одно уравнение на другое, получим еще одно комплексное уравнение:

Выражения (17), (18) представляют собой систему четырех действительных уравнений относительно трех неизвестных действительных функций ${{X}_{E}}\left( x \right),$ ${{X}_{M}}\left( x \right),$ $\alpha \left( x \right)$:

Таким образом, система (19) оказывается переопределенной, ее можно решить приближенно – методом “обмена” Штифеля [35].

В качестве примера рассмотрим два частных случая: отраженное поле имеет линейную поляризацию и имеет круговую поляризацию. Поскольку задача синтеза здесь решена приближенно, то диаграммы рассеяния получены строго [36] (методом интегральных уравнений) для фрагмента импедансной структуры длиной $L$ (см. рис. 1).

1. Линейная поляризация – $\Delta \Psi = 0.$ В соответствии с [35] получим приближенную взаимосвязь между реактансами полос, дающую равную невязку (разность между их решениями) решений второго и третьего уравнений системы (19):

Из первого уравнения системы (19) с учетом (20) найдем ориентацию системы полос на плоскости в допущении, что она фиксирована $\alpha \left( x \right) = {\text{const}}$:

В результате из четвертого уравнения (17) найдем искомые значения реактанса полос:

В качестве примера рассмотрим синтез реактансной структуры, поворачивающей параллельно поляризованную падающую под углом ${{\varphi }_{i}} = 30^\circ $ волну на 45° ($\Upsilon = 1$), переотражая ее в направлении ${{\varphi }_{0}} = 60^\circ .$ Законы распределения ${{X}_{E}}\left( x \right)$ и ${{X}_{M}}\left( x \right)$ приведены на рис. 2а, а диаграммы рассеяния для фрагмента плоскости $L = 6{\text{\;}}$ с такой структурой – на рис. 2б. В соответствии с (21) угол $\alpha $ в этом случае равен $22.6^\circ $. Здесь кривая 1 соответствует диаграмме на согласной поляризации $Fh\left( \varphi \right)$, а кривая 2 – кроссовой $Fe\left( \varphi \right)$.

Для структуры с заданными ${{\varphi }_{i}} = 60^\circ ,$ ${{\varphi }_{0}} = 30^\circ $ и $\Upsilon = 1$ на рис. 3а приведены распределения реактанса, а на рис. 3б – диаграммы рассеяния.

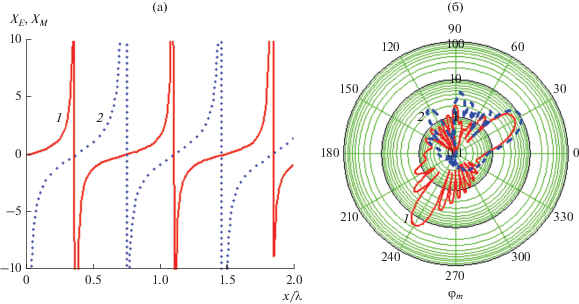
Анализ полученных результатов показывает, что помимо основного лепестка в отраженном поле появляются ярко выраженные дополнительные лепестки. В первом случае (см. рис. 2) это зеркальный лепесток на согласной поляризации. Во втором случае (см. рис. 3) – зеркальный лепесток на кросс-поляризации и лепесток на обеих поляризациях в направлении, близком к нормали ($\varphi \approx 90^\circ $).

2. Круговая поляризация – $\Delta \Psi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},\,\,~\Upsilon = 1$. В системе уравнений (19) положим ${{{\Psi }}_{0}} = 0;{\text{\;}}$ ${{{\Phi }}_{0}} = \Delta {\Psi }{\text{.}}$ Из первого и третьего уравнений системы (19) для угла ориентации реактансных полос получим [32] следующее решение:

Закон распределения реактансов полос можно найти из второго и четвертого уравнений (21). При этом ${{X}_{E}}\left( x \right),$ ${{X}_{M}}\left( x \right)$ являются функциями координаты $x$ импедансной плоскости. В соответствии с (23) угол $\alpha \left( x \right)$ также является переменной величиной. Приближенное решение для постоянной ориентации реактансных полос ($\alpha = {\text{const}}$) примет [32] вид

Таким образом, если для постоянной ориентации полос в случае линейной поляризации эта величина зависит от угла ${{\varphi }_{0}}$ (см. (21)), то для круговой поляризации вне зависимости от углов падения и отражения система имеет постоянную ориентацию на плоскости, равную $\alpha = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}.$ Из (23), строго говоря, это решение следует только при углах ${{\varphi }_{i}} = {{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$

С учетом (20) из второго и четвертого уравнений системы (19) для реактанса получим

На рис. 4а–4в приведены результаты синтеза структуры по заданным параметрам ${{\varphi }_{i}} = 30^\circ ,$ ${{\varphi }_{0}} = 60^\circ ,$ $\Delta {\Psi } = 90^\circ ,$ $\alpha \left( x \right) = 45^\circ $ и $\Upsilon = 1.$

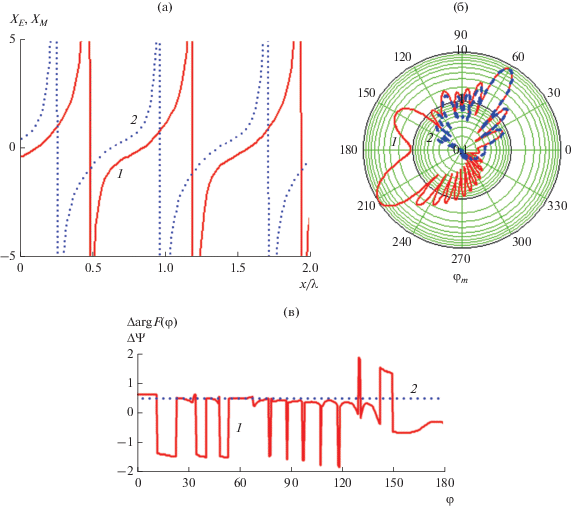
Как видим, диаграммы на согласной и кроссовой поляризациях практически полностью совпадают в секторе $ \pm 60^\circ $ относительно основного лепестка φ₀ = 60°. Кроме того, разность фаз (см. рис. 4в) между ними в этом же секторе составляет $\Delta {\Psi } = 90^\circ $ (скачки кривой равны $2\pi )$. Следовательно, отраженное поле в секторе углов 0°…120° имеет круговую поляризацию. Вместе с тем на согласной поляризации наблюдается зеркальный луч (см. рис. 4а и 4б).

На рис. 5а–5в приведены результаты синтеза структуры с параметрами ${{\varphi }_{i}} = 60^\circ ,$ ${{\varphi }_{0}} = 30^\circ ,$ $\Delta {\Psi } = 90^\circ ,$ $\alpha \left( x \right) = 45^\circ $ и $\Upsilon = 1.$ И в данном случае в отраженном поле на обеих поляризациях появляются неконтролируемые лепестки. Причем в направлении нормали амплитуда дополнительного лепестка становится соизмеримой с уровнем основного. На согласной поляризации появляются дополнительно еще и лепестки в направлениях $120^\circ $ и $150^\circ .$

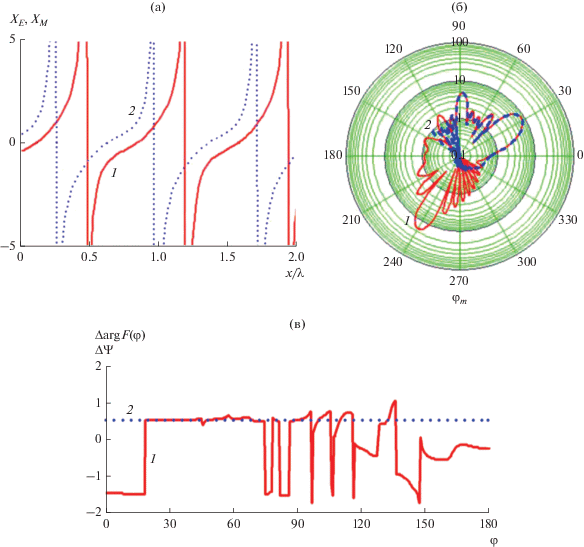
Отраженное поле в секторе углов ${{\varphi }_{0}} \pm 60^\circ $ $\left( { - 30^\circ \ldots 110^\circ } \right)$ имеет круговую поляризацию (амплитуды лучей на обеих поляризациях одинаковы, а сдвиг фаз $~\Delta {\Psi }$ равен $90^\circ $) (см. рис. 5в).

ЗАКЛЮЧЕНИЕ

Таким образом, впервые решена задача синтеза анизотропной реактансной структуры, ориентированной под фиксированным углом, переотражающей падающую линейно поляризованную волну в заданном направлении на требуемой поляризации. Получены выражения для коэффициентов отражения. В явном виде найдены компоненты тензора анизотропного импеданса. Найден класс реализуемых с помощью реактансной структуры диаграмм рассеяния. Предложенные решения дают высокую точность в основном и ближайших боковых лепестках. При ${{\varphi }_{i}} < {{\varphi }_{0}}$ в секторе углов ${{\varphi }_{0}} \pm 60^\circ .$ Вне этих углов могут появляться неконтролируемые лепестки значительной амплитуды. Показано, что если необходимо получить результаты в более широком секторе углов, то необходимо решать задачу синтеза по заданной диаграмме рассеяния в данном секторе с привлечением методов оптимизации. В этом случае предложенные решения могут выступать в качестве первого приближения решения задачи. Как показали многочисленные расчеты при φ_i < φ₀ точность предложенных решений достаточна.